A Note on the Calculation of Empirical P Values from Monte Carlo Procedures

To the Editor:

It has become commonplace in the statistical analysis of genetic data to use Monte Carlo procedures to calculate empirical P values. The reasons for this include the following: (1) many test statistics do not have a standard asymptotic distribution; (2) even if a standard asymptotic distribution does exist, it may not be reliable in realistic sample sizes; and (3) calculation of the exact sampling distribution through exhaustive enumeration of all possible samples may be too computationally intensive to be feasible. In contrast, Monte Carlo methods can be used to obtain an empirical P value that approximates the exact P value without relying on asymptotic distributional theory or exhaustive enumeration. Examples of procedures for genetic analysis that use simulation methods to determine statistical significance are CLUMP (Sham and Curtis 1995), MCETDT (Zhao et al. 1999), and a new test of linkage for a second locus conditional on information from an already-known locus (Cordell et al. 2000).

In this letter, we would first like to draw attention to the fact that some currently available genetic-analysis programs (including some of our own) use a method of calculating empirical P values that is not strictly correct. Typically, the estimate of the P value is obtained as 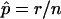, where n is the number of replicate samples that have been simulated and r is the number of these replicates that produce a test statistic greater than or equal to that calculated for the actual data. However, Davison and Hinkley (1997) give the correct formula for obtaining an empirical P value as (r+1)/(n+1). The reasoning is roughly as follows: if the null hypothesis is true, then the test statistics of the n replicates and the test statistic of the actual data are all realizations of the same random variable. These realizations can be ranked, and then the probability, under the null hypothesis, that the test statistic from the actual data has the observed rank or a higher rank is (r+1)/(n+1), the proportion of all possible rankings of the realizations that fulfill this criterion.

It is perhaps worth explicitly making the point that this procedure utilizes the ranks, rather than the actual values, of the test statistics. Another approach to the Monte Carlo estimation of significance would be to use the simulated test statistics to estimate the shape of the probability distribution and then to calculate a P value from this, but the use of ranks renders the process distribution free and is used almost universally.

Given that the most accurate estimate of the P value is actually (r+1)/(n+1), any procedure that uses r/n will tend to underestimate the P value if the null hypothesis is true—although, in most circumstances, to only a small degree. For example, if r=5 and n=500, then the correct estimate of the P value is 6/501=0.012, rather than .01. The effect is greatest when r is small: for r=1 and n=500, the correct P value is 2/501=.004, rather than .002, and, for r=0 and n=500, the correct P value is 1/501=.002, rather than 0. It is straightforward to demonstrate this effect in practice. We wrote a small computer program to generate a random number, x, to represent a test statistic observed under the null hypothesis. It then generates n more random numbers, to obtain an empirical estimate of the P value associated with x, where r is the number of replicates obtained that are ⩾x. We repeated this procedure 10⁶ times, using a value of 500 for n and counting the number of times that we obtained an empirical P value ⩽.01. When we used r/n to estimate the P value, we obtained a P value of .01 on 12,103 of 10⁶ occasions, whereas, when we used (r+1)/(n+1), this P value was obtained on 10,106 of 10⁶ occasions. This confirms that use of r/n to estimate P values is anticonservative.

Using (r+1)/(n+1) also avoids the problem of obtaining a P value of 0 when the observed test statistic is greater than those in any of the replicates. For n replicates, the minimum possible estimate of the P value becomes 1/(n+1). Thus, to obtain a very small P value, it will be necessary to simulate a large number of replicates. Another way of viewing this issue is as follows. Although use of (r+1)/(n+1) produces an unbiased estimate of the true P value (in contrast to use of r/n), this procedure will consistently overestimate small P values but will underestimate large P values. In fact, the expectation of (r+1)/(n+1) is (np+1)/(n+1), so that the bias is (1-P)/(n+1). Once again, when n is large, this overestimation is unlikely to be important.

It is helpful to provide some quantification of the effects that we describe. Typically, the true P value will be unknown, and judgments will need to be made on the basis of the observed values of r and n.

First, any methodology that utilizes r/n to estimate the P value will tend to underestimate the actual P value by a factor of ∼r/(r+1). Often, it will be possible to recalculate the true estimate of the P value, but, in some situations, the estimated P value may not be stated explicitly (e.g., when multiple tests are applied and only corrected P values are provided). In any event, if r⩾4, then the bias in the estimate of the P value will not be likely to lead to any serious error in interpretation. If r<4, then perhaps results should be treated with some suspicion and a larger number of simulations should be performed.

Second, if r is small, then small P values will tend to be overestimated, and potentially important results could be missed. Obviously, if one uses n=19, observes r=0, and estimates a P value of (r+1)/(n+1)=.05, then the true P value might be as low as 10^-6 or 10^-12. One would hope that any researcher obtaining r=0 would want to repeat the procedure using larger n. The question obviously arises of what value of r is “enough”—that is, what value should one observe to be reasonably confident that one is not wildly overestimating the P value? For given values of the true P value and of n, we can use a binomial distribution to calculate the probability that a value of r will be obtained such that (r+1)/(n+1) will overestimate P by a factor of ⩾2. The following examples are chosen such that, for a true P value of .01, the stated values of r and n will yield an estimate of ⩾.02: with n=149, P_r⩾2=0.44; with n=249, P_r⩾4=.24; with n=449, P_r⩾8=.085; and with n=549, P_r⩾10=.052. As it turns out, the probabilities associated with these values of r remain very similar, albeit not identical, if different P values are used, along with appropriate values for n chosen to yield an overestimate by a factor of 2. For example, the corresponding probabilities of r exceeding the threshold values of 2, 4, 8, and 10, if the true P value is .00001, are .44, .24, .087, and .054, respectively. It should perhaps be emphasized that this tendency to overestimate small P values is not purely a consequence of using (r+1)/(n+1) rather than r/n as an estimate: use of r/n would give corresponding probabilities (with a true P value of .00001) of .26, .14, .051, and .031. From these observations, we can construct the general rule that, if one observes r=2, then there is a strong possibility that one may be overestimating the P value by a factor of ⩾2, whereas, if one observes r⩾10, then such a large overestimate is fairly unlikely.

Finally, although we have said that use of r/n rather than (r+1)/(n+1) is anticonservative to only a small degree—which would be unlikely to have an important effect on interpretation (at least provided r⩾4)—there is one situation in which even a small bias could be important: when the power of different methods is being compared. We have noted that the true P value associated with r=5 and n=500 is .012, rather than .01. This means that a Monte Carlo method that used r/n to estimate the P value might find 20% more observations significant at a level of .01 compared with an accurate method. One might be concerned that, if one performed a power study comparing two such methods, the Monte Carlo method might be found to be considerably more powerful than the other method, such a finding being an artifact of the anticonservative nature of the Monte Carlo method. In fact, we have carried out extensive simulations and have found this not to be the case. We simulated affected sib-pair samples with allele-sharing probabilities increased above the null hypothesis value of 0.5 and measured the power of a Monte Carlo method using r/n compared to the power of an exact binomial method to detect this deviation. Once again, we found that, at least for values of r⩾4, the power of the two methods was very similar and that the theoretically anticonservative nature of the Monte Carlo test did not, after all, have important practical implications. The reason for this seems to be that the Monte Carlo test does not measure significance, but only estimates it, and that the effect of the anticonservative bias is almost exactly counterbalanced by the tendency to overestimate small P values.

We therefore draw the following conclusions. First, taking r/n rather than (r+1)/(n+1) as an estimate of the P value is essentially incorrect and should not be used. However, in practice, doing so is unlikely to have any serious implications either in individual tests or in power comparisons between methods, at least when r⩾4. Second, Monte Carlo methods provide an estimate, rather than a measure, of the P value. This implies that they tend to overestimate P values that are, in reality, small, and, hence, they may have less power than other methods. This effect decreases as r increases and becomes fairly unimportant when r⩾10. We therefore recommend that, for all applications, enough replicates are obtained to ensure that r⩾10.