A mechanically coupled reaction-diffusion model for predicting the response of breast tumors to neoadjuvant chemotherapy

Abstract

There is currently a paucity of reliable techniques for predicting the response of breast tumors to neoadjuvant chemotherapy. The standard approach is to monitor gross changes in tumor size as measured by physical exam and/or conventional imaging, but these methods generally do not show whether a tumor is responding until the patient has received many treatment cycles. One promising approach to address this clinical need is to integrate quantitative in vivo imaging data into biomathematical models of tumor growth in order to predict eventual response based on early measurements during therapy. In this work, we illustrate a novel biomechanical mathematical modeling approach in which contrast enhanced and diffusion weighted magnetic resonance imaging data acquired before and after the first cycle of neoadjuvant therapy are used to calibrate a patient-specific response model which subsequently is used to predict patient outcome at the conclusion of therapy. We present a modification of the reaction-diffusion tumor growth model whereby mechanical coupling to the surrounding tissue stiffness is incorporated via restricted cell diffusion. We use simulations and experimental data to illustrate how incorporating tissue mechanical properties leads to qualitatively and quantitatively different tumor growth patterns than when such properties are ignored. We apply the approach to patient data in a preliminary dataset of eight patients exhibiting a varying degree of responsiveness to neoadjuvant therapy, and we show that the mechanically coupled reaction-diffusion tumor growth model, when projected forward, more accurately predicts residual tumor burden at the conclusion of therapy than the non-mechanically coupled model. The mechanically coupled model predictions exhibit a significant correlation with data observations (PCC = 0.84, p < 0.01), and show a statistically significant >4 fold reduction in model/data error (p = 0.02) as compared to the non-mechanically coupled model.

1. Introduction

In the neoadjuvant setting, breast cancer patients receive therapy to reduce tumor burden to a size more amenable to surgery. Neoadjuvant therapy (NAT) also provides an excellent opportunity to observe tumor sensitivity to a particular regimen. However, if the primary tumor is unresponsive, the treatment could be changed to another, potentially more effective, approach thereby avoiding unnecessary side effects and toxicities. With numerous therapy options now available, development of a method to predict response early in the course of NAT is highly significant. This is especially relevant as targeted therapies, which are frequently cytostatic rather than cytotoxic, find increasing use in the neoadjuvant setting. Unfortunately, evaluation of the effectiveness of NAT by conventional means currently requires a long period of clinical observation, at the risk of letting unresponsive tumors become unresectable. Currently, the response of breast tumors to NAT is monitored by gross changes in tumor size as measured by physical exam, conventional (i.e., morphological) magnetic resonance imaging (MRI), and/or ultrasound, but these methods generally do not show whether a tumor is responding until the patient has received several treatment cycles. New methods are needed to guide therapeutic interventions in this important patient group.

One promising approach to address this clinical need is to integrate quantitative data available from emerging imaging modalities into physically realistic biomathematical models of tumor growth (Garg and Miga, 2008; Hogea et al., 2008; Szeto et al., 2009; Ellingson et al., 2011; Atuegwu et al., 2011; Atuegwu et al., 2012b; Harpold et al., 2007; Rockne et al., 2010; Swanson et al., 2011; Wang et al., 2009). While some conditions can be diagnosed and monitored through conventional imaging, conventional imaging alone is often insufficient to characterize therapeutic responses (Ratain and Eckhardt, 2004; Tuma, 2006). The combination of quantitative data provided by advanced medical imaging approaches to initialize and guide a mechanistic understanding provided by mathematical models may be a compelling strategy for these complex evaluations.

It is well-known that empirical evidence supports distinct links between the disruption of the normal structural architecture and load-bearing nature of tissue and uncontrolled growth in cancer, with movement of tumor cells mechanically restricted by surrounding tumor and healthy tissue (Paszek and Weaver, 2004; Paszek et al., 2005; Paszek et al., 2004; Huang and Ingber, 2005). Specifically, the mechanical behavior of the extracellular matrix has been shown to affect growth, differentiation, and motility (Engler et al., 2004; Engler et al., 2002; 2005; Lo et al., 2000; Yeung et al., 2005). For example, it has been conclusively demonstrated that accumulation of mechanical stress through increased substrate matrix stiffness inhibits cancer cell growth/diffusion in an aggressiveness dependant manner, with more aggressive cancer cells penetrating extracellular matrix more effectively than their less aggressive counterparts (Helmlinger et al., 1997; Stein et al., 2007; Cheng et al.). Due to the strong implication of the role of mechanics in tumor growth, there has been a concomitant increase in biomathematical models of tumor growth that incorporate constraints governed by tissue mechanical properties (Wasserman and Acharya, 1996; Kyriacou et al., 1999; Mohamed and Davatzikos, 2005; Hogea et al., 2008; Hogea et al., 2006; Gevertz et al., 2008; Garg and Miga, 2008). These modeling approaches link tumor cell motility with surrounding tissue stiffness and solid stress accumulation. While understanding of the link between tissue mechanics and tumor growth continues at the cellular level with molecular pathways slowly being uncovered (Provenzano et al., 2008a; Provenzano et al., 2008b; Conklin et al., 2011; Keely, 2011), and at the diagnostic level with applications being pursued in breast (Barr, 2010; Barr et al., 2012; Sinkus et al., 2007), prostate (Dresner et al., 1998; Lorenz et al., 2000; Kallel et al., 1999), liver (Yin et al., 2007; Sandrin et al., 2003), thyroid (Lyshchik et al., 2005), and brain (Rose et al., 1998), there is still a need to understand how these structural biomarkers could translate into the clinical setting.

While there is an abundance of tumor growth modeling approaches, they are often not of the form that can be easily applied to patient specific predictive modeling. These complex multi-parametric models often use a multitude of model parameters that are either taken from values in the literature or empirically derived and therefore are not applicable to modeling tumor response in individual patients. It is therefore highly desirable to cast such models in a way such that parameters can be derived from patient-specific non-invasive imaging-based methods and projected forward to predict eventual, patient-specific outcomes. Early approaches towards patient specific tumor growth modeling have shown preliminary successes (Atuegwu et al., 2011; Atuegwu et al., 2012b; Harpold et al., 2007; Rockne et al., 2010; Swanson et al., 2011; Szeto et al., 2009; Wang et al., 2009). However, given the important role of mechanics in tumor growth, there is a critical lack of understanding at the interface of mechanically coupled tumor growth models and imaging. In an early approach, a simplified framework was suggested whereby parameter optimization of a 1-D model of spatio-temporal growth and deformation of surrounding tissue (mass-effects) was used to model glioma growth (Hogea et al., 2008). Parameter optimization between the initial and final time points was driven by user selected landmarks and tumor growth was modeled by a reactive-advective-diffusive tumor cell growth equation coupled with mechanics within the advective term through a local pressure gradient produced by changes in tumor cell density. Following parameter optimization between the initial and final time points, the model result at the final time point was observed to visually agree with the experimental observation (Hogea et al., 2008).

In this work, we use a simplified mechanically coupled reaction-diffusion tumor growth model linked to the surrounding tissue stiffness via the diffusive term (Garg and Miga, 2008) to model and predict tumor response to NAT in simulations and experimental patient data. Estimation of tumor growth parameters within the model are driven by differences in tumor cell distributions measured early in the course of therapy (i.e., before and after one cycle of NAT). Using the model, we then predict the tumor burden at the conclusion of NAT and compare to experimental observations. Our approach represents a novel application of biomechanics coupled tumor growth models to the clinically significant problem of patient-specific non-invasive imaging-derived predictive models of tumor response to therapy.

2. Methods

2.1 Subject description

Simulation studies were based on imaging data obtained from four healthy women (ages 23–42 years; mean: 34.5 years) with no history of breast diseases. Breast cancer patient data studies included patients who were undergoing NAT as a component of their clinical care. Further inclusion criteria included: 1) no previous systemic therapies for breast cancer, and 2) histologically documented invasive carcinoma of the breast with a sufficient risk of recurrence based on pre-treatment clinical parameters of size, grade, age and nodal status to warrant the use of NAT. Participating patients provided informed written consent to an Institutional Review Board approved study. The initial retrospective study compared modeling results from eight patients exhibiting varying degrees of response to therapy; from complete pathological response (defined as no residual viable tumor on histologic analysis in breast or nodes at the completion of therapy), to no (or partial) pathological response (defined as any residual invasive tumor on histologic analysis in breast or nodes at the completion of therapy).

2.2 MRI Data acquisition

MRI was performed using a Philips 3T Achieva MR scanner (Philips Healthcare, Best, The Netherlands). A 16-channel double-breast coil was used for all patients and healthy subjects. For the healthy subjects, THRIVE (T₁ High Resolution Isotropic Volume Examination) structural data was acquired via a 400×400×129 acquisition matrix over a 20 cm × 20 cm × 12.9 cm transverse field of view (FOV) with one signal acquisition, and TR/TE/α = 6.43 ms/3.4 ms/10°. For the patient studies, dynamic contrast enhanced MRI (DCE-MRI) and diffusion weighted MRI (DW-MRI) were also acquired. For the DCE-MRI study, the acquisition matrix was 192×192×20 (full-breast) over a sagittal square FOV (22 cm²) with slice thickness of 5 mm, one signal acquisition, TR/TE/α= 7.9 ms/1.3 ms/20°, and a SENSE factor of 2. Each 20-slice set was collected in 16 seconds at 25 time points for approximately 6.7 minutes of scanning. A catheter placed within an antecubital vein delivered 0.1 mmol/kg (9 – 15 mL, depending on patient weight) of the contrast agent gadopentetate dimeglumine, Gd-DTPA, (Magnevist, Wayne, NJ) at 2 mL/sec (followed by a saline flush) via a power injector (Medrad, Warrendale, PA) after the acquisition of three baseline dynamic scans.

Diffusion weighted MR imaging (DW-MRI) was acquired with a single-shot spin echo (SE) echo planar imaging (EPI) sequence in three orthogonal diffusion encoding directions, with b-values of 0 and 500 or 600 s/mm², FOV = 192×192 (uni-lateral), and an acquisition matrix of 96×96 reconstructed to 144×144. SENSE parallel imaging (acceleration factor = 2) and spectrally-selective adiabatic inversion recovery (SPAIR) fat saturation were implemented to reduce image artifacts. Subjects were breathing freely with no gating applied. The patient DW-MRIs consisted of 12 sagittal slices with slice thickness = 5 mm (no slice gap), TR = 3080 ms, TE = ‘shortest’ (41 or 60 ms), Δ= 19.8 or 29 ms, and δ= 10.7 or 21 ms, respectively, NSA = 10.

2.3 MRI data analysis

For the patient data, DCE-MRI, DW-MRI, and anatomical T₁-weighted MR images were acquired at three time points: prior to beginning NAT (baseline), after one cycle of NAT (post one cycle, typically one week after the initial time point), and at the conclusion of NAT (final, typically 8–12 weeks after the initial time point). Critical to the modeling approach is that all MR images for each patient are registered at each time point, as well as longitudinally co-registered across all time points. For each time point, the DCE-MRI, DW-MRI, and structural MRI were collected within the same imaging session with minimal patient motion, so that these image sets are readily co-registered for each patient. To register the MR data acquired at the different time points, the DCE-MRI scans from the baseline and post one cycle time points were spatially aligned to the final time point using a constrained, non-rigid approach that employs an adaptive basis algorithm with a tumor volume preserving constraint (Li et al., 2009; Li et al., 2010).

Following registration, DCE-MRI data sets at each time point were used to define a tumor region-of-interest (ROI) by comparing the average of the baseline pre-contrast images (DCE-MRI time points 1–3) and the average of the dynamic enhanced post-contrast images (DCE-MRI time points 4–25). The tumor ROI was manually outlined on the difference image between the pre- and post-contrast images. Voxels in the manually drawn ROI exhibiting 80% signal intensity increase between the pre- and post-contrast infusion data were used to define the tumor voxels. The threshold of 80% DCE-MRI signal intensity enhancement was empirically determined to provide highest degree of correlation between tumor volume determined by DCE-MRI at the final time point with the with tumor volume at the time of surgery (data not shown).

The DW-MRI data sets were fit to Eq. (1) to return apparent diffusion coefficient (ADC) values on a voxel-by-voxel basis:

$$\mathit{ADC}=\frac{{\sum }_{i=x,y,z}ln(S_0/S_i)/b_i}{3},$$ (1)

where i is the direction of diffusion-weighting, b_i is the amount of diffusion-weighting imparted to the sample, S₀ denotes the signal intensity in the absence of diffusion gradients, and S_i is the signal intensity in the presence of the diffusion-sensitizing gradient. Using Eq. (2), the ADC data for the voxels satisfying the DCE-MRI threshold criteria of 80% enhancement were transformed to an estimate of tumor cell number, N(x̄,t) as described in (Anderson et al., 2000; Atuegwu et al., 2012b):

$$N(\overline{x},t)=\theta \left(\frac{{\mathit{ADC}}_w-\mathit{ADC}(\overline{x},t)}{{\mathit{ADC}}_w-{\mathit{ADC}}_{min}}\right),$$ (2)

where θ is the carrying capacity (i.e., the total number of tumor cells that fit within a voxel), ADC_w is the ADC of free water at 37° C (3 × 10⁻³ mm²/s), ADC(x̄,t) is the ADC value at position (x,y) in image space, and ADC_min is the minimum ADC value which corresponds to the voxel with the largest number of cells. Details of this approach are provided in (Anderson et al., 2000; Atuegwu et al., 2011). To calculate θ, we assumed spherical tumor cells with a sphere packing density of 0.7405 (Martin et al., 1997). We assumed a nominal tumor cell radius of 10 μm to arrive at a tumor cell volume of 4189 μm²; from this value, and the voxel volume, the maximum tumor cell number can be determined for a given voxel. We note that Eq. (2) assumes that the voxel consists entirely of tumor cells; i.e., it contains no blood vessels, supportive tissue, or other cell types. We return to this limiting assumption in the Discussion section.

2.4 Qualitative description of the biomechanical model

Considering the hypothetical situation of a tumor growing within an elastic medium of breast tissue, we qualitatively describe our formulation of the biomechanics coupled tumor growth model. As a patient’s breast tissue represents a heterogeneous material made up of adipose, fibroglandular, and tumor tissue, we must also consider a heterogeneous tissue elasticity distribution. The outward growth of a tumor within the breast causes an external force on the surrounding tissue, inducing deformation of that tissue. This phenomenon is typically referred to as a “mass effect”. This growth/deformation event leads to an increase in the distortion energy state of the surrounding tissue, the amount of which depends on the stiffness of the surrounding tissue. Here we use the von Mises stress as a metric of distortion energy and a directionality-invariant descriptor of the overall loading condition (tension, compression, and shear). Since it is well known that tumors are sensitive to their mechanical micro-environmental stress fields and exhibit reduced outward growth/expansion when subjected to high stress (Helmlinger et al., 1997; Stein et al., 2007; Cheng et al.), we therefore hypothesize that accumulated mechanical distortion energy has an inhibitory effect on tumor cell growth by affecting invasiveness, represented in our model by the apparent tumor cell diffusion coefficient, D; note this is not the same parameter as the water apparent diffusion coefficient measured via DW-MRI. Therefore, in our model, the growth event directly leads to a reduction in the tumor cell diffusion coefficient, with an even greater reduction in areas of higher stiffness. This reduction in tumor cell diffusion acts to restrict the ability of the tumor to invade the surrounding tissue. Our model (Garg and Miga, 2008) represents a reformulated, but analogous approach of other mechanically coupled tumor growth models (Wasserman and Acharya, 1996; Kyriacou et al., 1999; Mohamed and Davatzikos, 2005; Hogea et al., 2008; Hogea et al., 2006; Gevertz et al., 2008).

2.5 Biomechanical modeling approach

Following the work of Garg and Miga (2008), the coupled set of PDE’s governing the model are shown in Eqs. (3) – (5):

$$\frac{\partial N(\overline{x},t)}{\partial t}=\nabla ·\left(D\nabla N(\overline{x},t)\right)+k(\overline{x})N(\overline{x},t)\left(1-\frac{N(\overline{x},t)}{\theta }\right),$$ (3)

$$D=D_o{e}^{-\gamma {\sigma }_{vm}(\overline{x},t)},$$ (4)

$$\nabla ·G\nabla \stackrel{\rightharpoonup }{u}+\nabla \frac{G}{1-2\nu }(\nabla ·\stackrel{\rightharpoonup }{u})+\lambda \nabla N(\overline{x},t)=0,$$ (5)

Eq. (3) models the rate of change of tumor cell number at a particular location and time as the sum of random cell diffusion (the first term on the right hand side of the equation) and logistic growth (the second term). The apparent cell diffusion term, D, is linked to surrounding tissue stiffness via Eq. (4), where σ_vm is the von Mises stress, γ is an empirically derived coupling constant, and D₀ is the diffusion of tumor cells in the absence of stress. Eq. (5) describes linear elastic, isotropic mechanical equilibrium subject to an external expansive force determined by changes in tumor cell number, N(x̄,t), and a coupling constant λ, and governs the response of the displacement vector, u, to tumor cell growth. G represents shear modulus, G = E/(2(1+v)), where E and v are material properties of Young’s modulus and Poisson’s ratio, respectively.

The 2-D coupled forward model (Eqs. (3) – (5)) under the plane strain approximation is simultaneously solved for tumor cell number and displacement vector at each node in the FE mesh through a custom-built fully explicit, finite difference in time domain, finite element simulation written in MATLAB (Mathworks, Natick, MA). Finite element meshes for all models were composed of three-node triangular elements with an average edge length of approximately 4 mm. A mesh edge length sensitivity analysis was performed and less than 1% error was found with further mesh refinement. Implicit within each time step of the forward tumor growth model is a calculation of von Mises stress (based on the displacement vector and material properties) which is governed by changes in tumor cell number. At breast tissue boundaries, the conditions imposed reflect both the diffusive flux of tumor cells, and tissue displacement to be zero, respectively. Poisson’s ratio was assigned at 0.45 for all tissues, consistent with the near-incompressible soft tissue nature of breast tissue while avoiding numerical instabilities within the FE solution.

2.6 Simulation studies

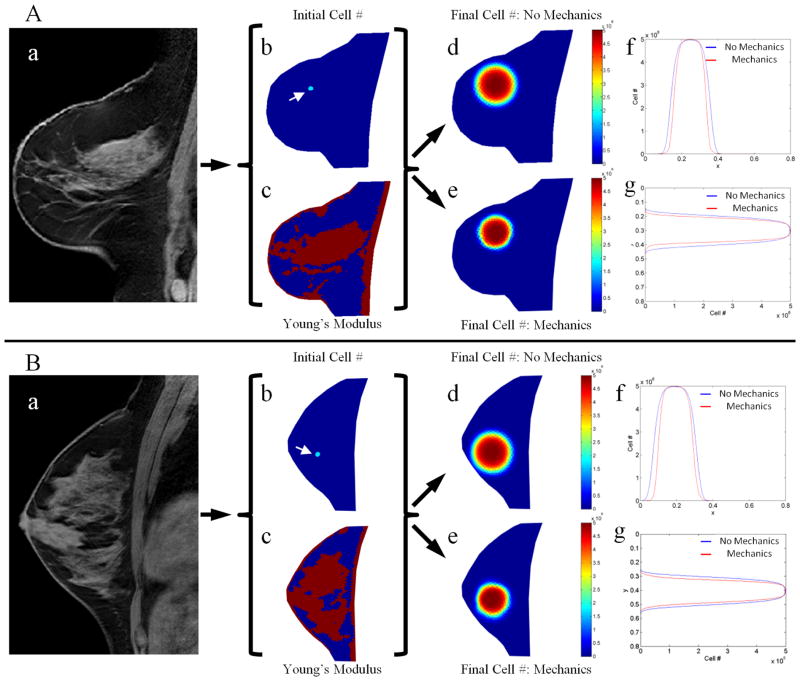
Structural MR data from four healthy subjects was segmented by signal intensity into regions of adipose and fibroglandular tissue, and Young’s modulus was assigned at 2 kPa and 4 kPa for each tissue, respectively (McKnight et al., 2002). 2-D finite element triangular meshes were generated for each subject using the central slice of the MR structural data. Simulated tumors were seeded at a single node within the breast mesh by selecting a random node corresponding to an interior region of adipose tissue and assigning an initial tumor cellularity for that node as the maximum tumor cell carrying capacity, θ. The model (Eqs. (3) – (5)) was then used to project tumor growth forward in time with and without mechanical coupling for each subject. Global values for all simulation studies were assigned for proliferation rate (k), tumor cell diffusion (D₀), and mechanical coupling coefficient (γ) as: 0.5 day⁻¹, 1 mm²/day, and 2 × 10⁻³, respectively. Time stepping was assigned with Δt = 5 × ⁻² days for a duration of 20 days (400 iterations). Horizontal and vertical line profiles through the center of the final simulated tumor volume were calculated and used to show the spatial distribution and density of tumor cells for both models.

2.7 Experimental studies

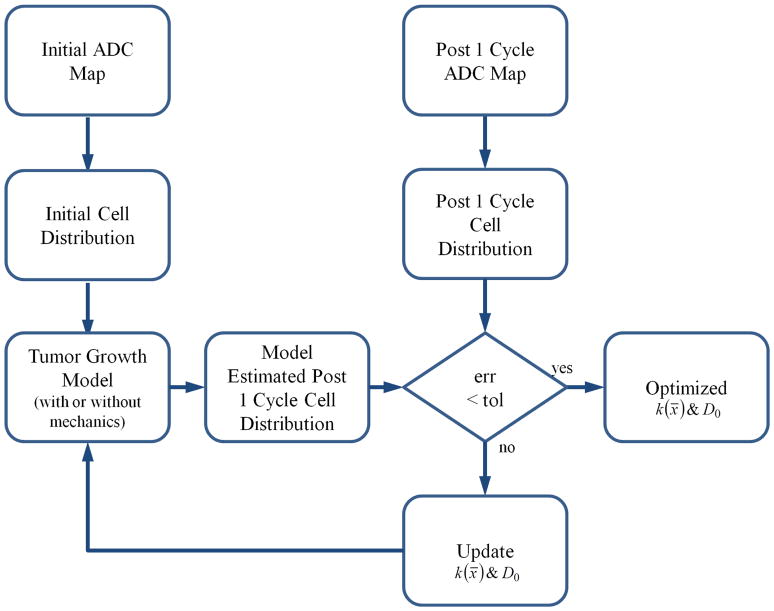
Figure 1 shows the modeling approach for characterizing tumor cell growth and diffusion by mechanically coupling a reaction-diffusion tumor growth model to the surrounding tissue properties. A Levenberg-Marquardt least squares non-linear optimization was used to estimate the spatially varying proliferation rate and global tumor cell diffusion term (k(x̄) and D₀, respectively) between the tumor cell numbers at the baseline and post one cycle time points. Note that k(x̄) can have positive or negative values, describing either proliferation or cell death, respectively. Following optimization and parameter estimation between the first two time points, the k(x̄) and D₀ parameters were fixed and the model was projected forward in time in order to predict tumor cellularity and response to NAT at the final time point. For mechanics coupled models, the mechanical coupling coefficient (γ) was empirically determined and assigned as 2 × 10⁻³. Time stepping was assigned with Δt = 5 × 10⁻² days for a patient-specific duration that corresponded to the time between either: initial time point and post one cycle time point (for parameter optimization), or post one cycle time point and final time point (for projection).

Figure 1.

Inverse modeling approach for characterizing tumor cell growth parameters. The initial and post one cycle ADC maps of the tumor are used to assign the tumor cell distributions at these time points as described by Eq. (2). Utilizing the tumor cell growth model either with or without mechanical coupling, a model estimated tumor cell distribution is compared to the observed distribution at the post 1 cycle time point. Levenberg-Marquardt optimization is then used to reconstruct a map of proliferation, k(x̄), and the tumor cell diffusion coefficient, D₀, iteratively until the model/data error is minimized below a preset tolerance. These parameters are then used to project the model forward in time to estimate tumor cellularity at a final time point.

Pearson correlation coefficients and concordance correlation coefficients were calculated between the observed total cell number at the final time point and the model-estimated total cell number at the final time point (for both the mechanics coupled and non-mechanics coupled reaction-diffusion tumor growth models). Pearson correlation coefficient and concordance correlation coefficient were used to determine the degree of relationship and agreement among the model projections and data observations, respectively. Total cell number error was calculated and statistical analysis for reduction in error between the model projections and observations at the final time point was performed using the Wilcoxon test. Statistical significance was set at p < 0.05.

3. Results

3.1 Simulation studies

Simulations were performed to determine differences in tumor growth patterns when including mechanical coupling from the surrounding tissue as compared to tumor growth patterns that neglect mechanical coupling. Several healthy subjects were used to initialize simulations so that we could observe differences that arise from varying patterns of adipose and fibroglandular tissue. Figure 2 shows the results for simulation studies based on two subjects. Comparing the tumor cell number data from the models with and without mechanics coupling, the tumor cell distribution from the no mechanics coupling results in a uniformly round distribution with consistent radial decay in tumor cell density. Conversely, the mechanics coupled tumor cell number data shows non-uniformity in shape and density in areas of higher Young’s modulus and an overall reduced size, indicative of restricted diffusion due to mechanical effects. For example, in Figure 2A the material properties in the area of the tumor seed are seen to strongly vary in the vertical direction, with adipose tissue (lower mechanical properties) seen above the tumor seed and fibroglandular tissue (higher mechanical properties) seen below the tumor seed. The vertical line profile (Figure 2Ag) is seen to have a stronger tumor cell diffusion restriction in the area of fibroglandular tissue versus adipose tissue, whereas the horizontal line profile (Figure 2Af) represents a more homogeneous material property region and shows the mechanics coupled model is only slightly uniformly restricting diffusion of tumor cells as compared to the no mechanics model. This can be visually confirmed by observing the difference between mechanics coupled and non-mechanics coupled tumor cell density plots in Figure 2Ad and Figure 2Ae. A similar trend (although expressed in the horizontal direction) can be observed in Figure 2B.

Figure 2.

Simulations of tumor growth with and without mechanical coupling for two different healthy subjects (Panels A and B). Tumor growth was simulated by using a T₁ image (a) to seed a tumor at the initial time point (b, white arrows), generating a Young’s modulus map (c) by segmenting adipose (blue voxels) and fibroglandular tissue (red voxels), assuming growth parameters, and then projecting the model forward in time to a final time point either using a model without mechanical coupling (d) or with mechanical coupling (e). Horizontal (f) and vertical (g) line profiles through the center of the simulated tumor shows the spatial distribution of tumor cell number for both models, highlighting areas of restricted cell diffusion in the mechanics coupled model in areas of higher tissue elasticity.

3.2 Experimental studies

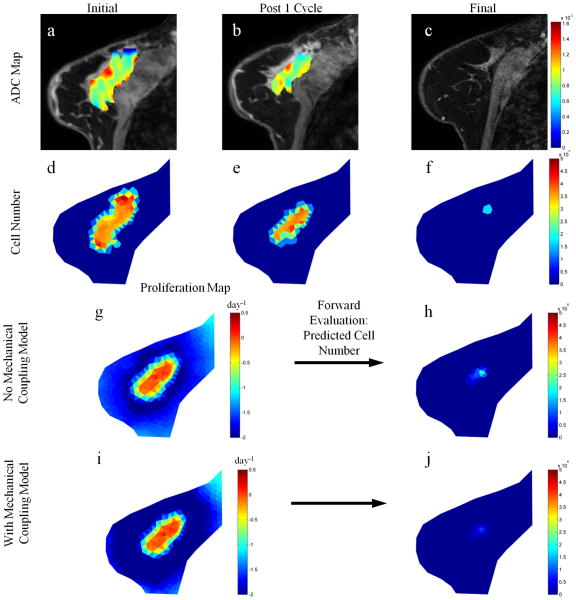
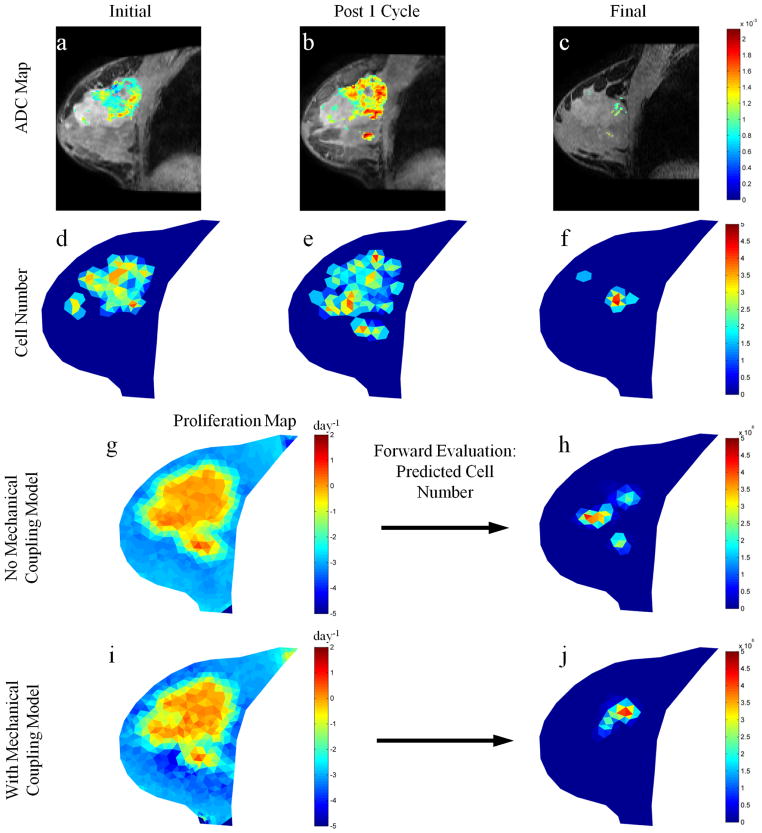
Figures 3 and 4 show parameter reconstructions with and without mechanical coupling for tumors from two representative patients; Fig. 3 displays a patient achieving pathological complete response (i.e., a responder), while Fig.4 presents a patient with residual disease at the time of surgery (i.e., a non-responder). Comparisons of the non-mechanics coupled proliferation rate maps with the mechanics coupled maps for these patients show subtle spatial differences between reconstructed parameter maps with no drastic changes in proliferation rate magnitude; a maximum proliferation rate of approximately 0.2 day⁻¹ was observed for both models in the responsive case, respectively, and a maximum proliferation rate of approximately 2.0 day⁻¹ was observed for both models in the partially responsive case, respectively. Thus, there was a dramatic 10 fold difference in cell proliferation between the two patients, showing an increase in proliferative capacity of tumor cells for a patient whose clinical outcome results in residual tumor at the conclusion of therapy. Additionally, the mechanics coupled model predictions at the final time point for both patients results in excellent agreement with the observed data as compared to the non-mechanics coupled model in both tumor cell number and spatial distribution. Comparing the final tumor burden predictions for both models in each tumor (Figure 3h and j and Figure 4h and j, respectively) with their respective observations of final tumor burden (Figure 3f and Figure 4f) the spatial distributions of the mechanics coupled model predictions are seen to exhibit excellent agreement whereas the non-mechanics couple model are spatially less accurate.

Figure 3.

Parameter reconstruction and forward model evaluation for a responsive tumor. ADC maps (for voxels satisfying the DCE-MRI enhancement threshold criteria) overlaid on T₁ structural images at initial (a), post one cycle (b), and final (c) time points are converted to cell number distributions at respective time points (d–f). Parameter optimization between initial and post one cycle time points using a model without mechanical coupling, as described in Figure 1, is used to reconstruct tumor cell diffusion coefficient and a map of proliferation (g) which is used to predict the final cell number (h). This process is repeated for the model with mechanical coupling (i and j). The predicted final cell number for the model with mechanical coupling (j) is shown to have excellent agreement with the observed final cell number (f).

Figure 4.

Parameter reconstruction and forward model evaluation for a non-responsive tumor. ADC maps (for voxels satisfying the DCE-MRI enhancement threshold criteria) overlaid on T₁ structural images at initial (a), post one cycle (b), and final (c) time points are converted to cell number distributions at respective time points (d–f). Parameter optimization between initial and post one cycle time points using a model without mechanical coupling, as described in Figure 1, is used to reconstruct tumor cell diffusion coefficient and a map of proliferation (g) which is used to predict the final cell number (h). This process is repeated for the model with mechanical coupling (i and j). The predicted final cell number for the model with mechanical coupling (j) is shown to have better agreement with the observed final cell number (f).

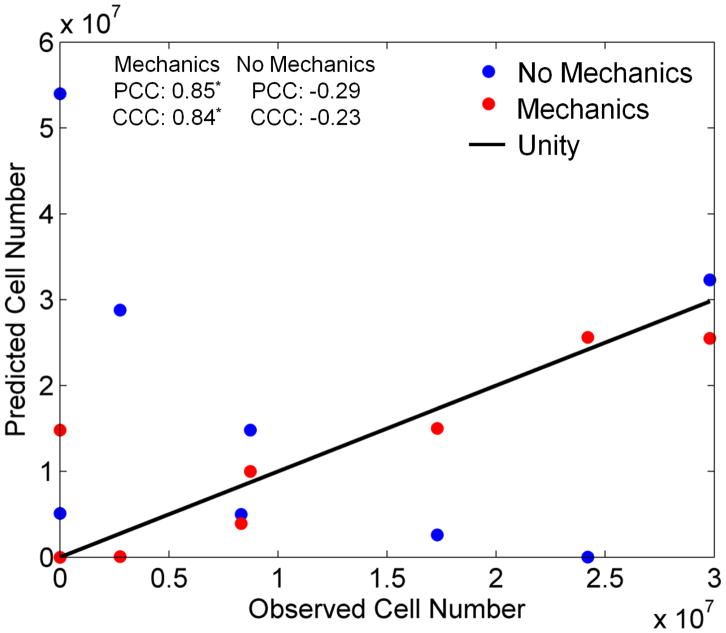
Broadening our view to the larger patient cohort (n = 8), in Figure 5 we see the same trend whereby the mechanically coupled tumor growth model more accurately replicates the observed total tumor cell number at the final time point the than the non-mechanically coupled tumor growth model. The Pearson and concordance correlation coefficients for projected total cell number for the mechanics coupled model are 0.85 and 0.84, respectively (p < 0.01); the Pearson and concordance correlation coefficients for the non-mechanics coupled model are −0.29 and −0.23, respectively (not significant). This indicates there is a very strong and statistically significant correlation and agreement between the mechanics coupled model and the observed data for total cell number, whereas there is a much reduced and non-significant correlation between the traditional reaction-diffusion model and the observed data. Comparing the model-to-data error at the final time point, we see a statistically significant 4.36 fold reduction in the average total cell number prediction error for the mechanically coupled model as compared to the non-mechanically coupled model (p = 0.02).

Figure 5.

Comparison of the observed and predicted total tumor cell number for each patient at the final point for the mechanics coupled (red circles) and non-mechanics coupled (blue circles) models. The line of unity is represented by the black line. The mechanics coupled model is shown to have better agreement with the observed cell number than the traditional non-mechanics coupled reaction-diffusion tumor growth model.

4. Discussion

In this effort, we presented a mechanically constrained modeling approach to integrate quantitative in vivo imaging data into biomathematical models of tumor growth in order to predict eventual response based on early measurements after the first cycle of NAT. The simulation results indicate that the incorporation of mechanics within the biomathematical model substantially impacts the behavior of the model (i.e., the resulting tumor growth magnitude and distribution) by restricting the diffusion of tumor cells, with greater restriction in areas of higher stiffness. The experimental results show clear differences in the tumor cell proliferation rates between tumors with different tumor burden outcomes. Additionally, since the therapeutic system is intact, we are able to use the parameters optimized between the initial and post one cycle of NAT time points to project the model forward in time and compare the model predictions to experimental data for tumor cell number at the final time point. The results indicate that our incorporation of mechanics into the tumor growth modeling approach allows for a statistically significant and more accurate prediction of total tumor cell number at the final time point, with a significant correlation to clinical observations. While preliminary, our modeling results provide excellent agreement with clinical observations and suggest that an imaging-based modeling approach to the prediction of tumor response which incorporates mechanical coupling may provide valuable early feedback during the course of NAT, and our results provide considerable enthusiasm for further studies with more patients. Furthermore, it is very important to note that there is a paucity of efforts in the mathematical modeling literature where in vivo clinical measurements are used to generate hypotheses that can actually be tested in individual cancer patients. The framework presented here contributes one such approach to this very important problem.

While mechanical properties are currently assumed from accepted values in the literature for fibroglandular and adipose tissue types identified in the structural MRI for each patient, the next step is to use MRI-based elasticity imaging methods to generate subject-specific estimates of spatial elasticity to initialize the mechanics coupled tumor growth modeling approach detailed in this study. We have developed one such method that is appropriate for elastographic analyses of breast cancer patients. “Modality independent elastography” (MIE) involves imaging a tissue of interest before and after compression, and then applying a finite element soft-tissue biomechanical model within a nonlinear optimization framework in order to determine the elastic properties of the tissue (Miga, 2003; Miga et al., 2005; Ou et al., 2008; Pheiffer et al., 2011). More specifically, MIE reconstructs elastic properties of tissue by incorporating a biomechanical finite element model into the non-rigid registration of images acquired under different static deformations. Spatial estimates of the modulus of elasticity are then returned from MIE analysis. Incorporation of MIE into the tumor growth modeling methodology presented in this study would then allow for an entirely non-invasive imaging-driven biomathematical modeling approach for the estimation of tumor burden outcome at the conclusion of NAT and perhaps contribute to increasing the accuracy and patient-specificity of our predictions.

It should be noted that there are several limitations in our current approach. The assumption of a constant proliferation rate in time, following parameter optimization between the initial and post one cycle time points, implicitly assumes a linear effect with NAC treatment. This assumption is clearly an simplification of the true nature of response to NAC. While the dynamics of temporal proliferation rate changes are scientifically interesting, it is clinically impractical to collect enough imaging time points throughout the course of therapy to accurately update the proliferation map. Additionally, the assumption of a linear elastic constitutive law yields an inherently simplistic material model. Breast tissue is clearly not a purely elastic medium, and is often modeled using a viscoelastic assumption. However in the limit of the relatively long time course of tumor growth-induced tissue deformation, the assumption of dampening of time-dependant viscoelastic effects is a valid one. Hyperelasticity has also been used to model breast tissue, however it is also important to note that the goal of this study was to generate a novel first-order link between quantitative in vivo imaging data and cell growth/diffusion models to the structure of the surrounding tissue, not to generate the most accurate multi-physics model of tumor growth. Another limitation of the study is the assumption that the only type of tissue in each voxel is tumor cells. More recently, we have attempted to correct this assumption by incorporating parameters available from quantitative analysis of DCE-MRI data (Atuegwu et al., 2012a). In particular, such an analysis provides estimates of the plasma and extravascular extracellular volume fractions. This enables a more accurate estimation of the carrying capacity of a particular voxel. Another limitation of the current study is the use of central slice MR data and two-dimensional mathematical models of tumor growth. The use of full volumes and three-dimensional mathematical models will likely provide more accurate predictions of tumor cell growth, and future studies in a larger patient population will focus on this extension of the modeling approach. We note that our current approach has no inherent barriers towards three-dimensional implementation. Lastly, we must recognize that the mechanical coupling (Eq. (4)) represents an intuitive but yet still proposed hypothesis that links tumor proliferation and the impact on the surrounding tissue matrix. While components of the expression are either fit to data (D_o), or derived from the mechanics (σ_vm), the strength of that relationship (γ) and coupling form need to be explored further.

Nevertheless, we have demonstrated how readily available in vivo imaging data obtained early in the course of NAT can be used to parameterize and calibrate a biomechanical model of tumor growth to predict tumor cell number and spatial distribution at the conclusion of treatment. This biomechanical model-driven approach was shown to have significantly greater accuracy in predicting the tumor burden at the conclusion of therapy than when the mechanics of tumor growth and stiffness of the surrounding breast tissue is ignored. These results indicate that the integration of quantitative, in vivo imaging data with appropriate mechanically coupled mathematical models of tumor growth is a promising avenue of investigation.