Concordance between distributed EEG source localization and simultaneous EEG-fMRI studies of epileptic spikes

Abstract

In order to analyze where epileptic spikes are generated, we assessed the level of concordance between EEG source localization using distributed source models and simultaneous EEG-fMRI which measures the hemodynamic correlates of EEG activity. Data to be compared were first estimated on the same cortical surface and two comparison strategies were used: (1) MEM-concordance: a comparison between EEG sources localized with the Maximum Entropy on the Mean (MEM) method and fMRI clusters showing a significant hemodynamic response. Minimal geodesic distances between local extrema and overlap measurements between spatial extents of EEG sources and fMRI clusters were used to quantify MEM-concordance. (2) fMRI-relevance: estimation of the fMRI-relevance index α quantifying if sources located in an fMRI cluster could explain some scalp EEG data, when this fMRI cluster was used to constrain the EEG inverse problem. Combining MEM-concordance and fMRI-relevance (α) indexes, each fMRI cluster showing a significant hemodynamic response (p <0.05 corrected) was classified according to its concordance with EEG data. Nine patients with focal epilepsy who underwent EEG-fMRI examination followed by EEG recording outside the scanner were selected for this study. Among the 62 fMRI clusters analyzed (7 patients), 15 (24%) found in 6 patients were highly concordant with EEG according to both MEM-concordance and fMRI-relevance. EEG concordance was found for 5 clusters (8%) according to α only, suggesting sources missed by the MEM. No concordance with EEG was found for 30 clusters (48%) and for 10 clusters (16%) α was significantly negative, suggesting EEG-fMRI discordance. We proposed two complementary strategies to assess and classify EEG-fMRI concordance. We showed that for most patients, part of the hemodynamic response to spikes was highly concordant with EEG sources, whereas other fMRI clusters in response to the same spikes were found distant or discordant with EEG sources.

Introduction

Identification and understanding of the underlying mechanisms involved during the generation of interictal spikes is a key issue (Luders and Awad, 1992). Interictal spikes are transient events, characteristic of epilepsy, that occur between seizures. As opposed to seizures, spikes are generated by the brain without producing clinical signs, therefore, the use of multi-modal imaging is convenient when investigating them. In the present study, we evaluated two non-invasive modalities that can be used to explore the generators of interictal spikes: (1) Electroencephalography (EEG) source localization using distributed source methods, which measures a current density along the cortical surface at each time sample of the spike (Baillet et al., 2001; Grova et al., 2006b) and (2) simultaneous EEG-functional Magnetic Resonance Imaging (fMRI), which measures the hemodynamic correlates of EEG activity (Gotman et al., 2006). The main generators of brain electrical activity are the large pyramidal neurons found in the cortical layer V, which are oriented perpendicularly to the cortical surface (Speckmann et al., 2004). They are the main contributors to the signal measured on the surface of the scalp using EEG. Electroencephalogram provides information regarding neuronal activity at high temporal resolution (~1 ms), but only weak spatial localization can be achieved from scalp recordings. Functional neuroimaging techniques such as fMRI or Positron Emission Tomography (PET) can measure neuronal activity indirectly through oxygenation, blood flow and metabolism changes with a spatial resolution of a few millimeters.

Simultaneous recordings of fMRI and intracortical neural signals have shown correlations between the Blood Oxygenation Level Dependent (BOLD) signal changes measured by fMRI and the activity of the main generators of the EEG signals (Logothetis et al., 2001). These results support the existence of a coupling between EEG sources and fMRI signals. Using well controlled evoked potential experiments, good correlations, within 10–16 mm, have been reported between fMRI results and equivalent current dipoles (ECD) estimated from electric or magnetic scalp measurements (Sanders et al., 1996; Korvenoja et al., 2001; Thees et al., 2003). EEG and fMRI are exploring different physiological phenomena with complementary temporal and spatial resolutions (~1 ms and ~1 cm for EEG source localization and ~1 s and ~3 mm for fMRI (Menon et al., 1998)) and discrepancies between fMRI and electro-physiological results have also been reported (Nunez and Silberstein, 2000; Gonzales Andino et al., 2001; Korvenoja et al., 2001).

Simultaneous EEG-fMRI acquisition constitutes a unique technique to study the hemodynamic changes correlated with interictal epileptic activity detected on the scalp EEG acquired within the scanner (Salek-Haddadi et al., 2003; Gotman et al., 2006). EEG-fMRI concordance was usually reported by comparing fMRI results with scalp topography of the discharges (Krakow et al., 2001; Archer et al., 2003; Al-Asmi et al., 2003; Kobayashi et al., 2005a), but the results have rarely been compared with EEG source localization. Average Euclidian distance larger than 3 cm between EEG generators modeled by ECDs and fMRI results suggested no clear concordance (Lemieux et al., 2001; Bagshaw et al., 2005; Bénar et al., 2006). ECDs have been widely used to localize epileptic spikes and their accuracy was assessed by comparison with intracortical recordings (Merlet and Gotman, 1999). Generators of spikes are known to be spatially extended, as at least 6 cm² of cortex need to be active to detect a spike on scalp EEG (Ebersole, 1997). Hence, ECD can model at best the center of mass of the generator and can also be misleading in presence of spatially extended sources (Kobayashi et al., 2005b), whereas EEG source localization using distributed source methods is probably more appropriate to recover spike generators with their spatial extent (Grova et al., 2006b). As fMRI responses to interictal spikes are rarely focal (Kobayashi et al., 2006a), spatial extent of EEG sources should be taken into account when studying concordance between EEG sources and fMRI results. In this study, we propose a new methodology to quantify “EEG-fMRI concordance”. We will denote as “EEG-fMRI concordance” the concordance between fMRI responses to epileptic spikes interpolated on the cortical surface and EEG sources of these spikes estimated on the same cortical surface using distributed models.

Providing accurate estimation of the levels of “EEG-fMRI concordance” is of particular interest. Concordance between EEG sources and fMRI results may give further evidence that fMRI responses indeed reflect hemodynamic changes linked to spike generation, in agreement with a presumed neurovascular coupling at the time of a spike. Discordance or complementarities between EEG sources and fMRI responses can provide insights that the underlying structure of spike generators may be organized as a distributed network, parts of this network being able to generate either EEG or fMRI detectable signals. Such a situation could occur especially because fMRI does not require synchronization among large populations of neurons to detect a significant response, whereas EEG does.

The purpose of this study is to measure quantitatively and classify the levels of EEG-fMRI concordance among all fMRI responses and EEG sources detected for a specific epileptic spike. We first propose a dedicated method to address such a difficult quantification problem. This method was then applied to nine patients with focal epilepsy. Our overall objective was to demonstrate that the underlying structure of spike generators may be organized as a distributed network, where one can detect and classify concordant and discordant EEG sources and fMRI responses. Quantification of “EEG-fMRI concordance” remains a difficult task and the issues are twofold: (i) EEG sources and fMRI responses should be quantified on the same spatial support, such as the cortical surface, and appropriate comparison metrics are required; to address this issue, fMRI clusters showing a significant BOLD response to interictal spikes assessed by standard event-related analysis (Bagshaw et al., 2004) were selected and interpolated onto the cortical surface (Grova et al., 2006a) to be compared with EEG source localization results. (ii) As an ill-posed inverse problem, EEG source localization does not admit any unique solution, unless prior information is added. Quantification of “EEG-fMRI concordance” should take into account the choice of such prior information. This is why we propose two complementary comparison strategies:

• (1)MEM-concordance: each fMRI cluster was compared with EEG sources estimated using the Maximum Entropy on the Mean (MEM) approach (Amblard et al., 2004; Grova et al., 2006b). Minimal geodesic distances between local extrema and overlap measurements between spatial extents of EEG sources and fMRI clusters were used to quantify MEM-concordance. As prior information assumed by the MEM approach was very general and completely independent from fMRI results, MEM-concordance provides insights regarding EEG-fMRI concordance from results obtained completely independently from each other.

• (2)fMRI-relevance: using an fMRI-relevance index α, we tested the ability of each fMRI cluster to be a relevant prior in the EEG inverse problem (Daunizeau et al., 2005). Significantly positive α means that sources located within this fMRI cluster could clearly explain some scalp EEG data, whereas significantly negative α means that sources located within this fMRI cluster could not explain scalp EEG data.

Combining MEM-concordance and fMRI-relevance (α) indexes, each fMRI cluster showing a significant hemodynamic response (p<0.05 corrected), was classified according to its concordance with EEG data.

Material and methods

In the first five sections, we will describe patient selection, data acquisition, anatomical MRI preprocessing methods (cortical surface segmentation), fMRI preprocessing methods (statistical analysis and interpolation of significant BOLD responses on the cortical surface) and EEG preprocessing methods (spike detection and averaging, and EEG source localization). The sixth section will introduce MEM-concordance methodology and notably how to measure geodesic distances and overlap measurements between EEG sources estimated with the MEM and fMRI results. The seventh section will describe fMRI-relevance methodology and the fMRI-relevance index α. In the last section, we will present how each fMRI cluster showing a significant hemodynamic response was classified according to its concordance with EEG data.

Patient selection

Nine epileptic patients were selected according to the following criteria: (1) all patients underwent an EEG-fMRI examination followed by an EEG recording session outside the scanner immediately afterwards. This EEG recording will be referred to as the prolonged EEG to distinguish it from the EEG recorded during scanning. It was used for source localization. (2) All patients had focal epilepsy with not more than two distinct types of spikes identified on the EEG within the scanner. (3) Spikes acquired within and outside the scanner were consistent and there were at least two events of a particular spike type on the prolonged EEG. (4) Only patients for whom the anatomical MRI did not show large morphological abnormalities (e.g., lesions, surgical resections) were selected, so an accurate segmentation of the cortical surface could be computed. Nine subjects already described in Bagshaw et al. (2005) were selected for this study. Written informed consent was obtained in accordance with the regulations of the Research Ethics Board of the Montreal Neurological Institute and Hospital.

Data acquisition

The EEG-fMRI sessions were carried out in a 1.5T Siemens Sonata scanner (Siemens, Erlangen, Germany) using 21 Ag/AgCl MR compatible electrodes and an EMR32 amplifier recording at a sampling rate of 1 kHz (Schwarzer, Munich, Germany). A standard Echo Planar Imaging (EPI) fMRI sequence was used (voxel dimensions 5×5×5 mm, 25 slices, 64×64 matrix, TE=50 ms, TR=3 s, ip angle 90°) and an anatomical T1-weighted scan was also acquired prior to fMRI recording (~170 sagittal slices, 1 mm slice thickness, 256×256 matrix, TE=9.2 ms, TR=22 ms, flip angle 30°). The fMRI data were acquired in runs of 120 images taking 6 min each. The gradient artifact was removed off-line using FEMR software (Schwarzer; Hoffmann et al. (2000)). The patient’s head was immobilized using a vacuum-bag filled with polystyrene spheres (S&S X-ray products, New York, USA). The scanning session lasted approximately 2 h, with 5 to 12 runs of fMRI data acquired for each patient. Following the EEG-fMRI scanning session, the patient was taken from the scanner to the clinical EEG department. Starting from the 10–20 system for electrode placement acquired in the scanner, extra electrodes were added according to the 10–10 system leading to a total of 44 electrodes. Approximately 45 min of EEG data was acquired at a sampling rate of 200 Hz with the patient in a relaxed position (Harmonie, Stellate, Montreal, Canada).

MRI preprocessing: cortical surface segmentation

To provide a comparison driven by the anatomy of each subject, fMRI BOLD responses and EEG sources were estimated on the same spatial support defined by the cortical surface. The cortical surface was obtained from a tesselated surface of the white matter/gray matter interface segmented from the MRI of each subject (Mangin, 1995), using the BrainVISA software.¹ This method provides a very accurate description of the cortical surface, consisting on average of 40,000 vertices with a mean intervertices distance around 1 mm or less. The distributed source model used to perform EEG source localization was obtained by down-sampling this surface by a ratio of 10, providing a model of p ≃ 4000 sources (mean intervertices distance ≃ 7 mm). fMRI results were interpolated at each vertex of the same surface.

fMRI preprocessing

Estimation of fMRI clusters showing a significant BOLD response

An experienced neurophysiologist reviewed filtered EEGs acquired in the scanner and marked the spikes, which provided an event-related paradigm for fMRI data analysis. The fMRI data were first motion corrected and smoothed (6 mm full width at half maximum (FWHM)) using the software package from the Brain Imaging Center of the Montreal Neurological Institute.² Models and signals were prewhitened with an auto-regressive filter of order 1, and low frequency drifts in the signal were modeled with a third order polynomial fitted to each run. Statistical analysis was performed using fMRIStat (Worsley et al., 2002). Each data set was analyzed with four monophasic, single gamma functions peaking after 3, 5, 7 and 9 s with an FWHM of 5.2 s, as described in Bagshaw et al. (2004). The analysis described below was repeated for each HRF. For each run j, the method provided an estimate of the effect of interest e_j and its standard deviation s_j, and thus a t-statistic t_j = e_j/s_j. The data of each run were then registered and resampled to the position of the first run using a rigid transformation (three rotations and three translations). Results for all runs of a subject were combined using a fixed effects model, leading to an estimation of the global statistics e, s and t=e/s for each subject.

The resulting t-statistic images were thresholded using the minimum given by a Bonferroni correction and random field theory, taking into account the non-isotropic spatial correlation of the errors. The FWHM of the inter-run analysis was first estimated at each voxel from the residuals of the previous analysis. Assuming the FWHM map sufficiently uniform throughout the brain, we used the averaged brain FWHM (ranging from 7.51 to 12.97 mm among subjects, mean: 9.57 mm) to perform a cluster size test (Worsley et al., 2002). All voxels showing a t value higher than 3.17 or lower than −3.17 (uncorrected p<0.001) located within a mask of the brain were considered for this cluster analysis. Every cluster showing a corrected p<0.05 for its spatial extent was considered significant, and thus selected for the comparison study.

Interpolation of significant fMRI results on the cortical surface

For comparison with EEG source localization results, fMRI t-maps were interpolated on the cortical surface used for EEG source localization. We used the method recently proposed in Grova et al. (2006a): each vertex of the cortical surface was associated to an interpolation kernel, i.e., a small local volume of interest, over which volumic fMRI t-values were integrated. The value resulting from this integration was associated to the corresponding vertex of the cortical surface. This interpolation method was designed to automatically adapt a trade-off between choosing large enough interpolation kernels, because of the distributed nature of the hemodynamic response, and avoiding mixing data from different anatomical structures. Starting from each vertex of the cortical surface, interpolation kernels were generated using a 3D geodesic Voronoï diagram within an anatomical mask. Resulting interpolation kernels adapt their volume and shape to the local morphology of the cortex of each subject. Only fMRI information located within a close neighborhood of the cortical surface was thus considered for the interpolation, and possible BOLD responses located far from the cortical surface were automatically discarded.

Before interpolation, fMRI 3D t-maps were resampled over the anatomical MRI using nearest neighbor interpolation. For each of the four HRF analysis, each selected fMRI cluster had its t-values integrated over each interpolation kernel. fMRI t-values of each cluster being thresholded before interpolation (see Estimation of fMRI clusters showing a significant BOLD response), all vertices of the cortical surface showing a non-null interpolated t-value were considered to belong to this particular cluster.

EEG preprocessing

Spikes detection and averaging

Detection and averaging of interictal spikes from the prolonged EEG was performed as described in Bagshaw et al. (2005). Epileptic spikes were identified semi-automatically using BESA 2000 (MEGIS Software GmbH, Germany), following the method of Bast et al. (2004). The EEG was band pass filtered between 1.6 Hz and 35 Hz and then manually inspected to identify a typical spike, showing similar morphology to those marked on the EEG acquired within the scanner. A pattern matching algorithm combined with visual inspection was then used to identify all segments similar to this typical spike. The selected events were used to form an average spike, on which source localization methods were applied. In order to determine at which time points of the average spike the spatio-temporal maps of EEG sources should be compared with fMRI results, we identified main EEG time peaks of the average spike as local maxima of the maximum field power over all the sensors. These time peaks will be denoted t_j.

EEG source localization using distributed models

The distributed source model assumes that the main generators of EEG potentials consist of a large number of dipolar sources distributed on the cortical surface; the orientation of each dipole being perpendicular to the surface. Using this anatomical constraint, the relationship between source amplitudes and scalp potentials is expressed by the following linear model (Dale and Sereno, 1993):

$$\mathbf{M}=\mathbf{G}·\mathbf{J}+\mathbf{E}$$ (1)

where M is a n×t matrix of the EEG signal measured at n electrodes and t time samples. J is the p×t unknown matrix of amplitudes of the p dipoles along the time. G indicates the n×p lead field matrix (forward operator) associated with the fixed positions and orientations of the p dipolar sources of the model. G is obtained by solving the forward problem, by estimating the influence on the sensors of each dipole location and orientation given by the distributed model (Mosher et al., 1999). Data are corrupted by an additive measurement noise E (n×t matrix).

The source model was composed of p≃4000 dipolar sources distributed over the cortical surface previously described. Electrode positions were located on the MRI of each subject, as the 19 electrodes used within the scanner were visible on a 3D rendering of the head surface segmented from the MRI. The remaining electrodes were placed manually. The forward matrix G was calculated according to a three-layer spherical model (de Munck, 1988), using the Brainstorm software.³ Conductivities were set to 0.33 S/m for brain and scalp and 0.0165 S/m for skull, corresponding to a skull/brain conductivities ratio of 1/20 (Oostendorp et al., 2000).

Although the inverse problem becomes linear when using a distributed source model, it is still an ill-posed problem as the forward matrix G is under-determined (p ≫ n). The inverse problem admits no unique solution unless a priori information regarding the distribution of the sources J is added to regularize the problem. The two proposed comparison strategies, i.e., MEM-concordance and fMRI-relevance, rely respectively on the two following regularization techniques:

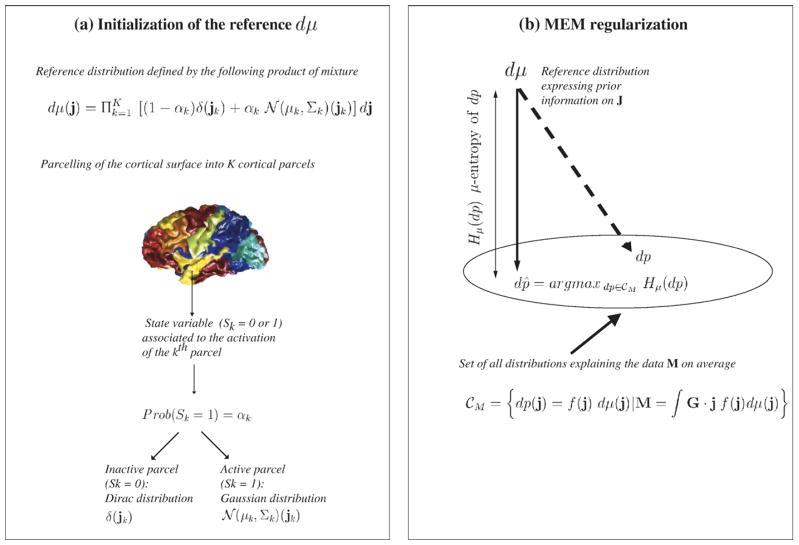
• Maximum Entropy on the Mean (MEM) model (Appendix A): Within the MEM approach, prior information regarding J is expressed using a reference distribution dμ.

  The objective is to estimate J as a realization of a random multivariate variable following a distribution dp(j)=Prob(J=j). Regularization is introduced by writing the solution of the form dp(j)=f (j) dμ(j), where f (j) is a μ-density to be found such that it explains the data in average (noise being zero mean):

  $$\mathbf{M}=\int \mathbf{G}·\mathbf{j}f(\mathbf{j})d\mathrm{\mu }(\mathbf{j})$$ (2)

  Among all the distributions dp satisfying the constraint (2), the MEM solution dp̂ =f̂ dμ is the one with maximum μ-entropy, i.e., the solution that makes the least assumption regarding missing information (Amblard et al., 2004; Grova et al., 2006b). The great advantage of the MEM framework relies on a very flexible way to define prior information, through the distribution dμ. The model dμ used in this study assumes that brain activity may be described by K cortical parcels showing an homogeneous activation state. Each parcel is characterized by an activation state and a probability of being active. Whenever active, the current distribution within each cortical parcel is described by a Gaussian distribution. More details regarding the MEM principle and the definition of dμ are provided in Appendix A and in Grova et al. (2006b). The spatio-temporal current density map corresponding to the MEM solution is the mean value of the density dp̂ and will be denoted Ĵ_MEM.

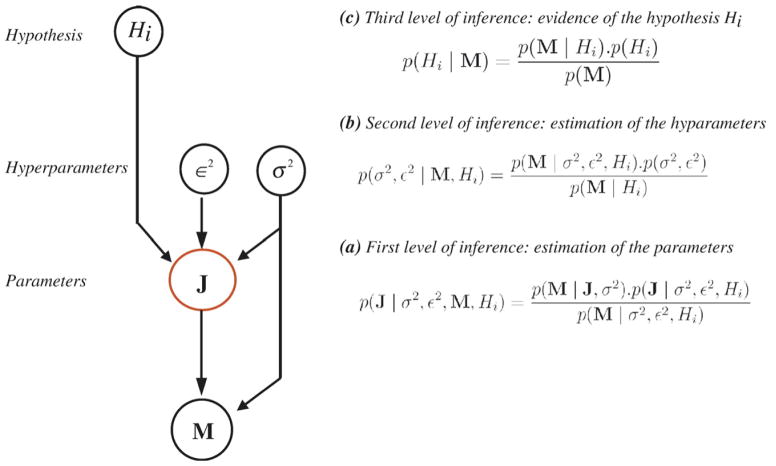
• Hierarchical Bayesian model used by fMRI-relevance (Appendix B): Hierarchical models offer another elegant way of introducing prior information. Assuming E_τ, the additive noise in Eq. (1) at time sample τ, to be zero-mean Gaussian with variance σ²I_n (I_n being the identity matrix of dimension n), a set of mutually independent hyperparameters (σ², ε²) and a specific hypothesis (H_i), the a priori distribution of J may be stated as follows (Daunizeau et al., 2005):

  $$p(\mathbf{J}\mid {\sigma }^2,{\epsilon }^2,H_i)=\prod _{\tau =1}^t\mathcal{N}\left({\mathbf{0}}_p,\frac{{\sigma }^2}{{\epsilon }^2}{\left({\mathbf{L}}^{{(H_i)}^T}{\mathbf{L}}^{(H_i)}\right)}^{-1}\right)$$ (3)

  where 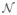denotes a Gaussian distribution and 0_p a zero column vector of length p. According to this model, J_τ at time sample τ is then assumed to be zero-mean Gaussian with prior covariance $\frac{{\sigma }^2}{{\epsilon }^2}{\left({\mathbf{L}}^{{(H_i)}^T}{\mathbf{L}}^{H_i}\right)}^{-1}$. Any specific hypothesis H_i actually corresponds to a model affecting the prior covariance of the sources. To assess fMRI-relevance, a non-informative hypothesis (H₀) will be compared to an informative hypothesis (H₁) derived from fMRI results (see fMRI-relevance: assessing the relevance of fMRI-based prior in the EEG inverse problem).

  Bayesian inference allows integrating every source of uncertainty of the model (σ², ε², H_i) while estimating the solution Ĵ. Under these assumptions, the Maximum A Posteriori (MAP) estimator Ĵ_MAP is obtained by minimizing the following cost function:

  $${\widehat{\mathbf{J}}}_{\text{MAP}}={\text{argmin}}_{\mathbf{J}}[{\Vert \mathbf{M}-\mathbf{G}·\mathbf{J}\Vert }^2+{\epsilon }^2{\Vert {\mathbf{L}}^{(H_i)}·\mathbf{J}\Vert }^2]$$ (4)

  This minimization aims at tuning a trade-off between data fit ||M−G·J|| and respect to prior information ||L^(Hi) · J||, while adapting the scale hyperparameter ε² (see Appendix B and Daunizeau et al. (2005) for details).

MEM-concordance: comparison between each fMRI cluster and MEM sources

As summarized in the first part of Fig. 1, MEM-concordance addressed one particular question: are there sources of EEG activity estimated with the MEM in agreement with each significant fMRI cluster?

Fig. 1.

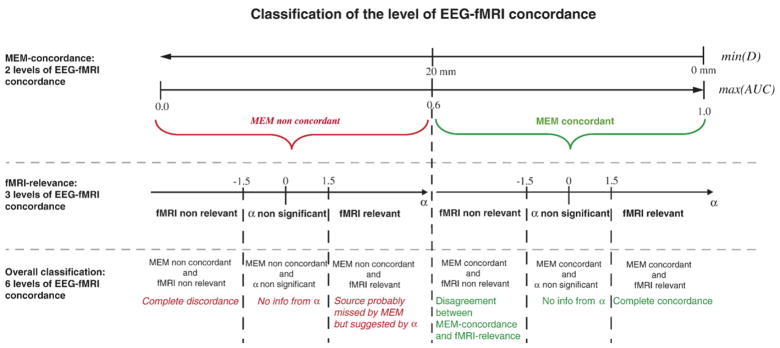
Summary of the method to classify the six levels of EEG-fMRI concordance for each fMRI cluster according to MEM-concordance (min(D) and max (AUC)) and fMRI-relevance (α). For MEM concordant results, the interpretation of the corresponding classification according to α (fMRI non-relevant, α non-significant and fMRI relevant) is presented using green font. For MEM non-concordant results, the interpretation of the corresponding classification according to α(fMRI non-relevant, α non-significant and fMRI relevant) is presented using red italic font.

MEM-concordance is an asymmetrical comparison regarding fMRI data. fMRI volumic t-maps were thresholded according to the methodology described in Estimation of fMRI clusters showing a significant BOLD response. Consequently, every vertex of the cortical surface belonging to an fMRI cluster does represent a significant BOLD response. On the other hand, detecting significant EEG sources from Ĵ_MEM using a t-statistic was not feasible as it required the estimation of the covariance of Ĵ_MEM. Selecting significant EEG sources based on a single threshold was thus not straightforward. MEM results were thus selected by detecting vertices showing local extrema of |Ĵ_MEM|. Two comparison metrics taking into account the morphology of the cortical surface were then used:

• (1) minimal geodesic distance between each fMRI cluster and the closest local extremum of |Ĵ_MEM|.

• (2) overlap measurements between spatial extents of MEM sources and each fMRI cluster.

The estimated current density map Ĵ_MEM is a spatio-temporal map of EEG activity, whereas fMRI clusters on the cortical surface represent static data. To take into account EEG spike propagation during the analysis, comparison between static fMRI clusters and EEG sources was then only performed at the peaks of the average spike t_j (i.e., peaks of the maximum field power as defined in Spikes detection and averaging).

Minimum geodesic distance between local extrema of MEM sources and fMRI clusters

At each peak of the average spike t_j, the local extrema of the MEM current density map was defined as each vertex i of the cortical surface, where |Ĵ_MEM (i, t_j)| was greater than all its neighbors and greater than the full width half max of the current density distribution, max_i (|Ĵ_MEM (i, t_j)|)/2. For each significant fMRI cluster and at each peak of the spike t_j, we measured the minimum geodesic distance D between each vertex of the fMRI cluster and each MEM local extremum. This metric is asymmetrical because only local extrema were considered from MEM current density maps, whereas all the vertices showing a significant BOLD response were considered for each fMRI cluster.

Overlap measurements between spatial extents of MEM sources and fMRI clusters

Comparing the spatial extents of each fMRI cluster with the MEM current distribution at t_j requires thresholding the MEM distribution. Ideally, one would compute a t-statistic on Ĵ_MEM and threshold it accordingly. As it was not straightforward, we estimated overlap measurements at all possible thresholds of |Ĵ_MEM| and integrated them. To do so, a Receiver Operating Characteristic (ROC) curve approach was used, considering each fMRI cluster as the reference for comparison. To assess the detection accuracy of a method when a reference is available, ROC curves are generated by plotting the sensitivity against the false positive detection rate, for different detection thresholds. The Area Under the ROC Curve (AUC) is a well-known criterion to assess detection accuracy (Metz, 1986). Usually, the reference reflects some ground truth regarding the object to be detected, and detection errors are assessed by comparing this reference to the results of the method for different thresholds. Whereas no ground truth was available for the present comparison, we used ROC methodology to assess the concordance between each fMRI cluster and the current distribution |Ĵ_MEM| at t_j. Each fMRI cluster was then considered as the reference for the estimation of sensitivity and false positive rate at different thresholds of |Ĵ_MEM| ranging between 0 and max_i(|Ĵ_MEM(i, t_j)|). AUC should be interpreted carefully, as we are not measuring detection errors as is usually the case when using ROC curves. If we consider a set of randomly selected pairs of EEG sources located inside (index i′) or outside (index i) the fMRI cluster, the AUC criterion represents the following probability:

$$\text{AUC}=p(\mid {\widehat{\mathbf{J}}}_{\text{MEM}}(i^{\prime },t_j)\mid >\mid {\widehat{\mathbf{J}}}_{\text{MEM}}(i,t_j)\mid )$$ (5)

To interpret AUC as the probability that EEG sources located inside the fMRI cluster have higher amplitude |Ĵ_MEM| than sources located outside the fMRI cluster, one should theoretically provide the same number of sources inside and outside the fMRI cluster to estimate ROC parameters. In Grova et al. (2006b), we proposed a method specifically dedicated to this issue. A non-biased estimation of AUC is obtained by randomly drawing outside the fMRI cluster as many fictitious sources as sources located inside the fMRI cluster. The AUC is then measured using this set of pairs of sources. This random drawing is repeated 100 times and the proposed metric of EEG-fMRI concordance is the average AUC over these 100 trials.

fMRI-relevance: assessing the relevance of fMRI-based prior in the EEG inverse problem

As summarized in the second part of Fig. 1, fMRI-relevance compared EEG and fMRI localizations by the indirect route of testing the relevance of each fMRI cluster as prior information for the EEG inverse problem. Using a Bayesian model comparison approach (Daunizeau et al., 2005), we estimated a relevance index α that quantifies whether EEG generators located within each fMRI cluster could partly explain scalp EEG data. This relevance index α is the logarithm of a Bayes’ factor (Gelman et al., 1998) comparing the evidences of two prior models: a non-informative hypothesis (H₀) and an informative hypothesis (H₁) defined from each fMRI cluster. The evidence of each model H_i (i =0, 1) was estimated as p(H_i|M), the posterior probability of H_i, given the data M (see Appendix B for details).

Assessing the relevance of each fMRI cluster in the EEG inverse problem is equivalent to the following hypothesis test:

$$\{\begin{array}{l}{H}_0:\text{All}\text{sources}\text{have}\text{a}\text{priori}\text{the}\text{same}\text{energy}(\text{minimum}\text{norm}\text{assumption})\hfill \\ H_1:\text{Sources}\text{located}\text{within}\text{an}\text{fMRI}\text{cluster}\text{are}\text{likely}\text{to}\text{have}\text{more}\text{energy}\hfill \end{array}$$ (6)

Within the proposed hierarchical linear model, any hypothesis H_i corresponds to a model a affecting the prior covariance of the sources, as mentioned in EEG source localization using distributed models. Starting from the general a priori model (H_i) described in Eq. (3), the non-informative model H₀ was stated as:

$$H_0:p(\mathbf{J}\mid {\sigma }^2,{\epsilon }^2,H_0)=\prod _{\tau =1}^{t}N\left(0_p,\frac{{\sigma }^2}{{\epsilon }^2}{\mathbf{I}}_p\right)$$ (7)

where I_p denotes the identity matrix of dimension p. Similarly, for each fMRI cluster interpolated on the cortical surface, the informative model H₁ was stated as:

$$H_1:p(\mathbf{J}\mid {\sigma }^2,{\epsilon }^2,H_1)=\prod _{\tau =1}^{t}N\left(0_p,\frac{{\sigma }^2}{{\epsilon }^2}\mathbf{f}(\mathbf{Z})\right)$$ (8)

where f represents a coupling function between fMRI and EEG sources. Here we defined Z as the absolute value of the t-values of the fMRI cluster after interpolation on the cortical surface. The following coupling function was used (Babiloni et al., 2003):

$$\mathbf{f}(\mathbf{Z})={\mathbf{I}}_p+\frac{\mathrm{\Delta }-1}{max(\mathbf{Z})}\text{diag}(\mathbf{Z})$$ (9)

This model allows an increased discrepancy of the fMRI-favored sources from their zero prior mean. The parameter Δ tunes the weight of the fMRI constraint in the prior covariance matrix, it was empirically set to Δ=10 as suggested by Babiloni et al. (2003) and evaluated by Daunizeau et al. (2005).

The relevance of each fMRI cluster in the EEG inverse problem solution was quantified as the logarithm of the Bayes’ factor comparing the evidence of prior models H₀ and H₁:

$$\alpha =ln\frac{p(H_1\mid \mathbf{M})}{p(H_0\mid \mathbf{M})}$$ (10)

Using Bayesian inference, α was estimated by integrating all the levels of uncertainties of the parameters and hyperparameters of both hierarchical models H₀ and H₁. This integration took into account the whole signal of the spike, i.e., the main peak and the following slow wave. α is therefore a global metric summarizing EEG-fMRI concordance over the whole spike. Such a metric includes how much each fMRI cluster could contribute to the measured EEG signal at some point during spike propagation, as opposed to D and AUC that were estimated only at the main peaks of the spike (t_j).

Classification of the level of concordance between EEG sources and fMRI responses

MEM-concordance results regarding the minimal geodesic distance (D) between local extrema of MEM sources and fMRI clusters were classified using a threshold of 20 mm. Regarding spatial extents of MEM sources and fMRI clusters, an AUC value close to 1 means that EEG sources were mainly located within the fMRI cluster, and that no other EEG sources were found elsewhere. It is therefore a stringent index of concordance, as a perfect match is not expected between |Ĵ_MEM| at t_j and each fMRI cluster. In order to allow the occurrence of some false positives, i.e., other EEG sources located far from the selected fMRI cluster at t_j, we used a threshold of 0.6 to classify AUC results. Moreover, for each fMRI cluster, D and AUC were estimated at each time peak t_j of the average spike. Spike propagation being detectable in EEG only (high temporal resolution), it was taken into account in MEM-concordance results by considering only the best comparison measurements among all time peaks t_j, i.e., the minimum geodesic distance min(D) and the maximum area under the ROC curve max(AUC). According to MEM-concordance (min(D) and max(AUC)), the following two levels classification of EEG-fMRI concordance were considered:

• MEM concordant defined by min(D) ≤20 mm and max (AUC)≥0.6: a MEM source was close to the fMRI cluster.

• MEM non-concordant defined by min(D)>20 mm or max (AUC)<0.6: no MEM source was close to the fMRI cluster.

To classify fMRI-relevance results, a threshold of 1.5 was considered. An fMRI-relevance index α>1.5 means that the posterior probability of the informative model (H₁) given the data M was 4.5 times greater than the posterior probability of the non-informative model (H₀). In other words, the fMRI cluster associated to the model H₁ was in good agreement with the EEG data, i.e., both EEG data and the fMRI prior were “pulling the EEG source solution in the same direction”. Conversely, an fMRI-relevance index α<−1.5 means that EEG data and the fMRI prior were “pulling the EEG source solution in opposite directions”. A discordance between this fMRI cluster and the EEG is then suspected, as it is very unlikely that sources located within this fMRI cluster could contribute to the measured EEG data. According to fMRI-relevance (α), the following three level classification of EEG-fMRI concordance was proposed:

• fMRI relevant defined by α>1.5: the fMRI cluster constitutes a relevant constraint for EEG source localization.

• α non-significant defined by α ∈[−1.5; 1.5]: there was no significant difference when using or not the fMRI cluster to constrain the EEG source localization.

• fMRI non-relevant defined by α<−1.5: the fMRI cluster was not a relevant constraint for EEG source localization.

Combining the two levels of MEM-concordance and the three levels of fMRI-relevance, the concordance of each fMRI cluster with EEG data was classified according to the following six level classification summarized in Fig. 1:

• MEM concordant and fMRI relevant: complete EEG-fMRI concordance.

• MEM concordant and α non-significant: concordance according to MEM and no additional information provided by α.

• MEM concordant and fMRI non-relevant: disagreement between MEM-concordance and fMRI-relevance.

• MEM non-concordant and fMRI relevant: source probably missed by the MEM, but suggested by α.

• MEM non-concordant and α non-significant: no concordance according to MEM and no additional information provided by α.

• MEM non-concordant and fMRI non-relevant: complete EEG-fMRI discordance.

Results

Summary of results

Two of the nine patients were excluded as they did not show any significant cortical BOLD response (Patients 5 and 7). Among the seven other patients, 62 fMRI clusters were analyzed, corresponding to significant positive or negative BOLD responses obtained with the four HRF analysis: 31 clusters of activations (positive BOLD response) and 31 clusters of deactivations (negative BOLD response). We found no disagreement between MEM-concordance and fMRI-relevance, i.e., none of the fMRI cluster was classified as MEM concordant and fMRI non-relevant. This class was omitted in Tables 1 and 2. We will first illustrate some typical observations before providing quantitative results.

Table 1.

Classification of the level of EEG-fMRI concordance

Name	BOLD response	Non-studied response	MEM non-concordant and fMRI non-relevant	MEM non-concordant and α non-significant	MEM concordant and α non-significant	MEM non-concordant and fMRI relevant	MEM concordant and fMRI relevant
Patient 1	Positive	Cerebellum L: 3,5				Sup-post-temp R: 9	Sup-post-temp R: 3, 5, 7
	Negative		Parietal R: 5,7
Patient 2	Positive			Subcortical/Ant-insula/Basal ganglia L: 3 Mesial-temp-pole/Amygdala R: 3			Temp-pole L: 3
	Negative			Entorhinal cortex R: 3 Mesial Parietal R (artifact): 3			Middle/Inf-temp gyrus L: 3
Patient 3	Positive		Insula/Basal ganglia/Thal R: 5 Frontal L (artifact); 9	Supramarginal/Angular gyrus R: 3	Supramarginal/Post-temp L: 5
	Negative			Basal-post-temporo-occ L: 7 Parietal R: 7		Mesial-parietal/Occ R: 3	Temp/Occ L: 3, 5 Temp/Occ R: 3 Mesial-parietal/Temp/Occ R: 5, 7, 9
Patient 4	Positive						Occ R: 3
	Negative	None
Patient 5	Positive	None
	Negative	None
Patient 6	Positive			Subcortical/Inferior-frontal L: 3 Inferior-frontal L: 5 Diencephalon L: 5
	Negative	Cerebellum R: 5		Insula L: 3 Parietal R (artifact): 9 Central region L (artifact): 9
Patient 7	Positive	Cerebellum R: 3
Patient 8	Positive		Occ-horn-ventricle L: 3	Mesial-occ L: 3, 7 Fourth ventricle: 7 Mesial-post-occ L: 7 Mesial-occ bilat (artifact, vessel: tentorium cerebellum): 9 Brainstem/cerebellum L: 9	Fronto-central region L: 7	Frontal L	Frontal L: 3 Precentral region L: 3 Frontal F1+F2 (including SMA) L: 5
	Negative		Basal ganglia/Third ventricle R: 3 Basal ganglia/Frontal subcortical L: 3, 5 Ant-frontal R: 7 Parietal L: 9	Basal ganglia R: 5 Ant-insula +Fronto-operculum L: 7 Fronto-temporal L: 7 Ant-frontal R+Basal ganglia/Caudate R: 9 Parietal R: 9 (almost pertinence <0)		Ant-cingulate R: 5 Ant-frontal bilat+Basal ganglia/Caudate R: 7
Patient 9	Positive			Parietal R: 3 Mesial-occ L: 5 Mesial-occ R: 5 Mesial-occ bilat: 7			Parietal L: 3
	Negative			Mid-cingulate bilat: 3

Each fMRI cluster described by its anatomical location is classified according to its concordance with EEG data according to both MEM-concordance and fMRI-relevance. For each cluster, the HRF(s) used to detect it is indicated after its anatomical description.

Table 2.

Summary of the classification of EEG-fMRI concordance levels

Name	# spikes in prolonged EEG	# spikes in fMRI scanner	# deactivation clusters	# activation clusters	MEM non-concordant and fMRI non-relevant	MEM non-concordant and α non-significant	MEM concordant and α non-significant	MEM non-concordant and fMRI relevant	MEM concordant and fMRI relevant
Patient 1	23	18	2	4	2	0	0	1	3
Patient 2	6	4	3	3	0	4	0	0	2
Patient 3	73	91	9	4	2	3	1	1	6
Patient 4	34	14	0	1	0	0	0	0	1
Patient 6	6	2	3	3	0	6	0	0	0
Patient 8	38	13	12	11	6	11	1	3	2
Patient 9	11	56	2	5	0	6	0	0	1
Total	–	–	31	31	10 (16%)	30 (49%)	2 (3%)	5 (8%)	15 (24%)

For each subject, we indicated the number of spikes used to create the average spike from the prolonged EEG, the number of spikes selected for fMRI data analysis, the number of fMRI clusters showing activations and deactivations and the classification of these clusters according to the 5 levels of EEG-fMRI concordance. The last row indicates the distribution of the classification levels for all the 62 clusters analyzed.

Illustrative cases showing different levels of EEG-fMRI concordance

All four patients selected for illustration had additional information available to confirm our results. Three underwent intracranial EEG investigation as part of a presurgical evaluation. The fourth had a focal cortical dysplasia. Intracranial recordings were reviewed by experienced electro-encephalographers in order to determine which pattern of interictal spiking activity was the most likely to correspond to scalp EEG spikes (see Bénar et al., 2006). It was considered that a necessary condition for the spikes to be visible on scalp EEG was that they involved several intracranial electrode contacts, including superficial contacts or epidural electrodes. Such a criterion was used to ensure that similar events were selected on scalp and intracranial recordings, even if these signals were not recorded simultaneously. Intracranial electrode contacts considered active were identified and represented in red within a 3D display of the patient’s MRI and cortical surface. Intracranial electrode coordinates were registered onto the patient’s MRI, using anatomical landmarks and 3D locations of electrodes and landmarks provided by the neuronavigation system that guided the implantation (SNN Neuronavigation System Inc., Mississauga, Ontario, Canada). The intracranial EEG results were only used to qualitatively confirm an overall spatial agreement with MEM sources and fMRI clusters.

Illustrative case showing excellent EEG-fMRI concordance (patient 3)

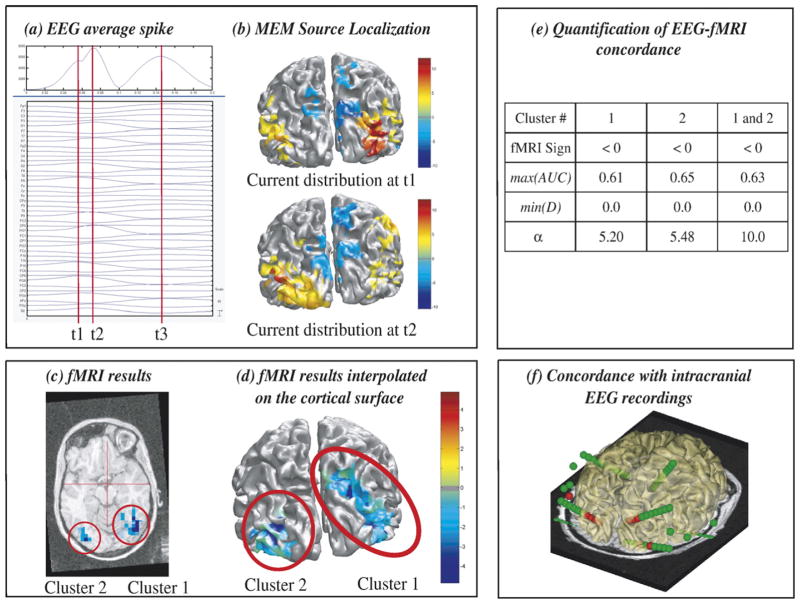
Results of the analysis done in patient 3 are summarized in Fig. 2. Spikes were bilateral occipital. Three peaks (t₁, t₂, t₃) of the maximum field power were identified on the average spike from the prolonged EEG (Fig. 2a). t₁ and t₂ showed a fast propagation of the discharge from the right occipital (maximal negativity at PO8 electrode) to the left occipital region (maximal negativity at PO7 electrode). MEM results confirmed this propagation from right to left occipital regions (Fig. 2b). Most significant fMRI responses (Figs. 2c and d) consisted in BOLD deactivation located in the right temporo-occipital and mesial–parietal area (cluster 1) and in the left temporo-occipital area (cluster 2). Visual inspection showed that fMRI cluster 1 was concordant with the MEM sources estimated at t₁, whereas cluster 2 corresponded to the MEM sources found at t₂. MEM-concordance and fMRI-relevance results confirmed these trends (Fig. 2e). α>5 for both clusters suggests that sources located in these areas could explain scalp EEG data. Moreover, when both clusters were used together as a prior for EEG source localization, we found a highly significant relevance index (α=10.0), suggesting that these two regions were involved. On the other hand, only the EEG data provide information regarding the direction of the propagation of the discharge, from right to left. Brain areas suggested by EEG sources and fMRI results were in good agreement with the one detected using intracranial recordings, electrode contacts identified as active during these spikes being presented in red in Fig. 2f.

Fig. 2.

Analysis of patient 3 showing excellent EEG-fMRI concordance. (a) Signal and maximum field power of the average spike, local peaks (t₁, t₂, t₃) considered for MEM-concordance are represented using red vertical lines. (b) MEM source localization estimated at t₁ and t₂, the positive and the negative parts of Ĵ_MEM being thresholded upon the level of background activity, using Otsu’s threshold estimated on |Ĵ_MEM| (Otsu, 1979). (c) t-values of the two most significant fMRI clusters obtained with the HRF peaking 5 s after the spike, superimposed on the 3D anatomical MRI. (d) Same fMRI clusters after interpolation onto the cortical surface. (e) MEM-concordance and fMRI-relevance metrics for cluster 1, cluster 2 and when considering both clusters together. (f) 3D representation of the position of the intracranial EEG electrodes with one MRI axial slice and the cortical surface (yellow slightly transparent), active contacts being represented in red. Visual inspection (b and d) and quantitative results (e) showed an excellent EEG-fMRI concordance within right and left occipital regions, and were confirmed by intracranial EEG recordings (f).

Illustrative case suggesting EEG-fMRI concordance during spike propagation (patient 1)

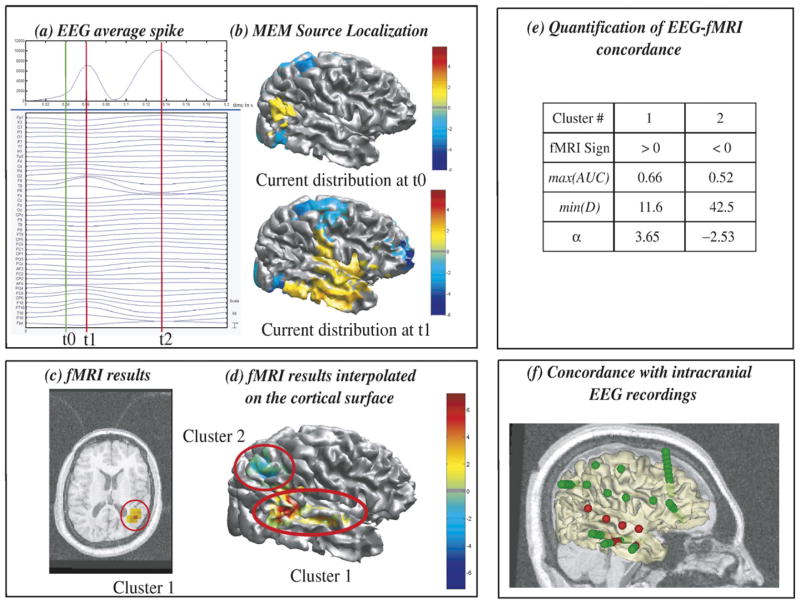
Results from patient 1 are summarized in Fig. 3. Spikes were right temporal. At the main peak of the fast wave t₁, the average spike showed a maximum negativity at T8 electrode (Fig. 3a). MEM results at t₁ consisted in an extended right lateral temporal source (Fig. 3b). The most significant fMRI results were a right superior posterior temporal cluster showing activation (cluster 1) and a right parietal cluster showing deactivation (cluster 2). Most significant clusters are presented in Figs. 3c and d. Visual inspection suggested some overlap between the spatial extents of cluster 1 and the MEM sources at t₁ (Figs. 3b and d), as confirmed by MEM-concordance results (min(D)=11.6 mm and max(AUC)= 0.66). Moreover, the relevance index α=3.65 estimated using the entire duration of the spike suggested that EEG sources in the superior posterior temporal fMRI cluster could explain some scalp EEG data. Exploring the evolution of MEM sources along the duration of the spike, we found at t₀, 25 ms before the main peak t₁, a superior posterior temporal source particularly concordant with cluster 1 (Figs. 3b and d). Evolution of the scalp potentials and MEM source localization from t₀ to t₁ suggested a propagation of the discharge from superior posterior temporal (PO4 electrode) to lateral temporal regions (T8 electrode). Considering MEM results alone, such an origin of the spike at t_o should be considered with caution, but associated with the fMRI-relevance index α=3.65 one can have more confidence in this result. Conversely, α=−2.53 found for the right parietal deactivation (cluster 2) suggested that this area was not involved in EEG spike generation. These results were in good agreement with the intracranial recordings that confirmed the involvement of both the superior posterior temporal area found with MEM and fMRI and the lateral temporal area found only with MEM (Fig. 3f).

Fig. 3.

Analysis of patient 1 suggesting EEG-fMRI concordance during spike propagation. (a) Signal and maximum field power of the average spike, local peaks (t₁, t₂) considered for MEM-concordance are represented using red vertical lines. (b) MEM source localization, thresholded as in Fig. 2b, estimated at t₁ and t₀, an additional time point showing some early activity located at PO4 electrode (green vertical line in panel a) and in the right superior posterior temporal area on the cortex. (c) t-values of the two most significant fMRI clusters obtained with the HRF peaking 5 s after the spike, superimposed on the 3D anatomical MRI. (d) Same fMRI clusters after interpolation onto the cortical surface. (e) MEM-concordance and fMRI-relevance metrics for cluster 1 and cluster 2. (f) 3D representation of the position of the intracranial EEG electrodes with one MRI sagittal slice and the cortical surface (yellow slightly transparent), active contacts being represented in red. Comparisons between fMRI and MEM results at t₁ suggested partial spatial overlap between sources. α=3.65 for cluster 1 suggested a good EEG-fMRI concordance, which could be slightly detectable in MEM results at t₀. These results were confirmed by intracranial EEG recordings (f).

Illustrative case showing partial EEG-fMRI concordance (patient 8)

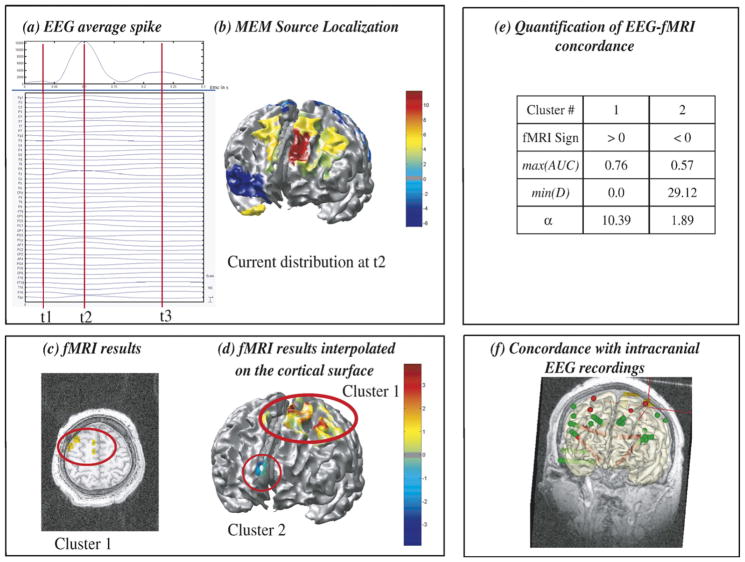
Results from patient 8 are summarized in Fig. 4. Widespread frontal spikes showed a maximum negativity at Fz electrode with a left predominance. At the main peak of the average spike (t₂), MEM showed a widespread frontal source, involving mainly the left frontal region close to the midline. The topography of the electric potentials was more complex than in the two previous examples and other MEM sources less intense but widespread were found in the left parietal, right orbito-frontal and right temporal pole regions. fMRI results were also complex and widespread, with many large clusters of activations or deactivations involving many different areas (Table 1). The two most significant fMRI clusters (Figs. 4c and d) were a large activation in the first and second left frontal gyri, including supplementary motor area (cluster 1) and the other a deactivation in the right anterior cingulate region (cluster 2). Visual inspection (Figs. 4b and d) as well as MEM-concordance and fMRI-relevance results (Fig. 4e) confirmed a good correspondence between the main frontal MEM source and fMRI cluster 1. This cluster showed the highest fMRI-relevance index of our study (α=10.39), suggesting that EEG sources located in this area could clearly explain some scalp EEG data. Although cluster 2 did not show any concordance with MEM results (min(D)=29.12 and max (AUC) the fMRI-relevance index α=1.89>1.5 suggested that sources located in the right anterior cingulate region could explain some scalp EEG data. Intracranial recording results (Fig. 4f) supported these findings but also illustrated the complexity of the case, as spikes involved many contacts in the lateral and mesial frontal regions, including those close to clusters 1 and 2.

Fig. 4.

Analysis of patient 8 showing partial EEG-fMRI concordance. (a) Signal and maximum field power of the average spike, local peaks (t₁, t₂, t₃) considered for MEM-concordance are represented using red vertical lines. (b) MEM source localization, thresholded as in Fig. 2b, estimated at the main peak of the spike t₂. (c) t-values of the two most significant fMRI clusters obtained with the HRF peaking 5s after the spike, superimposed on the 3D anatomical MRI. (d) Same fMRI clusters after interpolation onto the cortical surface. (e) MEM-concordance and fMRI-relevance metrics for cluster 1 and cluster 2. (f) 3D representation of the position of the intracranial EEG electrodes with one MRI coronal slice and the cortical surface (yellow slightly transparent), active contacts being represented in red. EEG source localization, fMRI and intracranial EEG results showed a complex and widespread distribution of the activity involved at the time of the spike. However, excellent EEG-fMRI concordance was found within a widespread left frontal source (fMRI cluster 1). No MEM source was found concordant with the right anterior cingulate BOLD deactivation (cluster 2), although α=1.89 suggested that sources located in this region could explain some scalp EEG data, which was confirmed by intracranial EEG results (f).

Illustrative case showing EEG-fMRI concordance within a focal cortical dysplasia (patient 9)

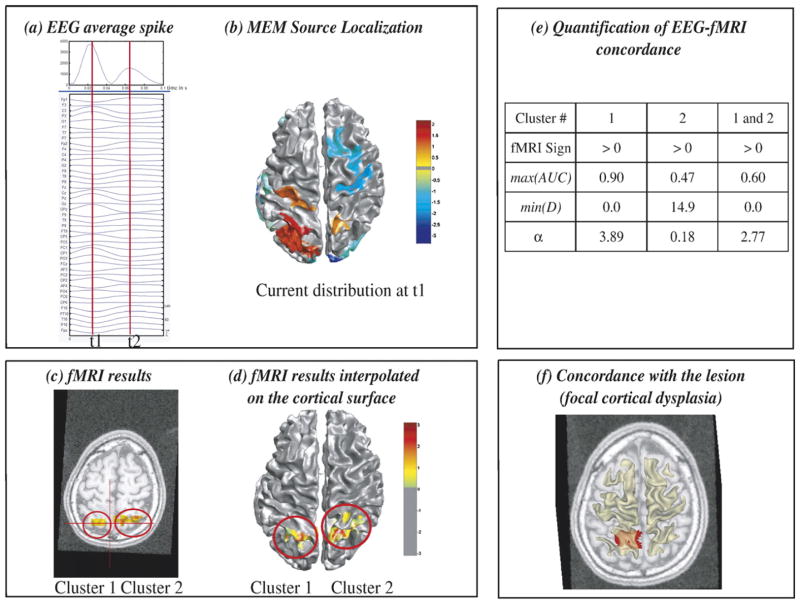
Results of the analysis done in patient 9 are summarized in Fig. 5. Left centro-parietal spikes were selected. At the peak of the fast wave t₁, the average spike showed maximum negativity at CP1 electrode (Fig. 5a). At t₁, MEM found a left parietal source (Fig. 5b). The two most significant fMRI clusters were in the left and right parietal regions (Figs. 5c and d). Visual inspection (Figs. 5b and d) as well as MEM-concordance and fMRI-relevance results (Fig. 5e) showed a very good concordance between MEM source and fMRI cluster 1, both being located within the left parietal focal cortical dysplasia (Fig. 5f). The relevance index α showed that using only the left parietal cluster (cluster 1) was more relevant (α=3.89) than using both right and left parietal fMRI clusters as prior information for the EEG inverse problem (α=2.77).

Fig. 5.

Analysis of patient 9 showing partial EEG-fMRI concordance within a focal cortical dysplasia. (a) Signal and maximum field power of the average spike, local peaks (t₁, t₂) considered for MEM-concordance are represented using red vertical lines. (b) MEM source localization estimated at t₁, thresholded as in Fig. 2b. (c) t-values of the two most significant fMRI clusters obtained with the HRF peaking 3 s after the spike, superimposed on the 3D anatomical MRI. (d) Same fMRI clusters after interpolation onto the cortical surface. (e) MEM-concordance and fMRI-relevance metrics for cluster 1, cluster 2 and when considering both clusters together. (f) Left parietal focal cortical dysplasia manually segmented and superimposed in red on an axial MRI slice, together with the cortical surface (yellow slightly transparent). Visual inspection (b and d) and quantitative results (e) confirmed an excellent EEG-fMRI concordance within the dysplastic lesion (f). α suggested that considering only cluster 1 as prior information in the EEG inverse problem was more relevant than considering both cluster 1 and cluster 2.

Classification of the level of EEG-fMRI concordance

The different levels of concordance with EEG found for each fMRI cluster are presented in Tables 1 and 2. For each patient, fMRI clusters fell within almost all the classes of EEG-fMRI concordance, except the one suggesting disagreement between MEM-concordance and fMRI-relevance methods (class MEM concordant and fMRI non-relevant). Six of seven patients had at least one fMRI cluster in complete concordance with EEG data (class MEM concordant and fMRI relevant). In three patients out of seven, we also found fMRI clusters completely discordant with EEG data (class MEM non-concordant and fMRI non-relevant). In the only patient showing no fMRI cluster in good concordance with EEG (patient 6), fMRI data were noisy and only two spikes were detected during the simultaneous EEG-fMRI recording.

Among the 62 fMRI clusters considered in this analysis, 15 (24%) were highly concordant with EEG according to both MEM-concordance and fMRI-relevance (class MEM-concordant and fMRI-relevant). EEG concordance was found for 5 clusters (8%) according to α only, suggesting sources probably missed by the MEM. No concordance with EEG was found for 30 clusters (48%). Finally, α was significantly negative for 10 clusters (16%). This means that no EEG source located in these clusters could explain any part of scalp EEG data, which suggests EEG-fMRI discordance.

Distributions of MEM-concordance and fMRI-relevance metrics

Distributions of MEM-concordance (min(D) and max(AUC)) and fMRI-relevance (α) metrics are represented in Fig. 6 for all 62 fMRI clusters. All these metrics were uniformly distributed over their range of values, explaining why we found fMRI clusters classified within almost all classes of EEG-fMRI concordance for each patient (Table 2). No difference was found when comparing the levels of EEG-fMRI concordance from clusters representing activations or deactivations (Fig. 6). Deactivation or activation clusters could be either concordant or discordant with EEG results. We found no effect of the HRF model (peak 3, 5, 7 or 9) on the level of EEG-fMRI concordance (results not shown).

Fig. 6.

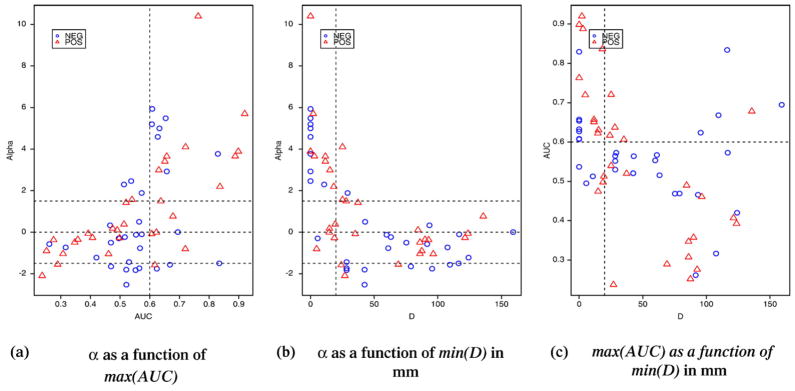
Distributions of MEM-concordance (min(D) and max(AUC)) and fMRI-relevance (α) metrics for all the 62 clusters considered in this study. Clusters corresponding to activations are represented in red triangles, and deactivations in blue circles. Thresholds used for classification are displayed using dashed lines. There is overall a good agreement between α, min(D) and max(AUC) and they are uniformly distributed over their whole range of values. In most cases, fMRI-relevance was then in agreement with MEM-concordance and all levels of EEG-fMRI concordance were observed. More discrepancies were observed between max(AUC) and min(D), especially for highest min(D) values (c), suggesting that these two metrics were complementary and necessary to quantify MEM-concordance.

Overall, there was a good agreement between MEM-concordance (min(D) and max(AUC)) and fMRI-relevance (α) metrics (Fig. 6). More discrepancies were observed between max(AUC) and min(D). We found a widespread distribution of max(AUC) for the highest min(D) values (Fig. 6c), suggesting that these two metrics proposed to quantify MEM-concordance were complementary and necessary to compare source localization, using distributed source models, and fMRI results interpolated onto the cortical surface. α results were in good agreement with MEM results. Highest α values were observed when MEM exhibited a source close to or completely overlapping the corresponding fMRI cluster. No concordance or discordance (α<−1.5) was observed for fMRI clusters that were due to artifacts, as indicated on Table 1. For instance, fMRI artifacts were suspected when we found widespread fMRI activity within one axial slice, whereas adjacent slices did not show any response. Other clusters could be artifact when the BOLD response was found within the ventricles or in the tentorium cerebellum.

Fig. 7a shows that almost all the largest fMRI clusters (volume>10 mm³) were highly relevant for EEG source localization (α>1.5). Knowing that an epileptic spike will only be visible on the scalp if EEG sources cover a sufficient area or cortex (at least 6 cm²), it was not surprising to observe concomitant large fMRI responses in these regions. The fMRI responses concordant with EEG were either activation or deactivation, also fMRI clusters showing deactivation tend to be slightly larger than the ones showing activations (Fig. 7a). Most of the fMRI clusters found relevant for the EEG inverse problem (α>1.5) were also highly significant clusters (corrected p<0.01) as showed on Figs. 7b and c.

Fig. 7.

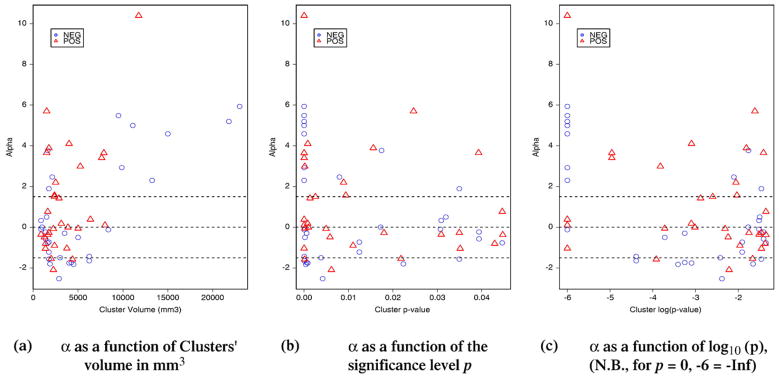
Distribution of the fMRI-relevance index α as a function of: (a) the volume of each cluster, (b) the corrected significance level of the cluster p and (c) its logarithm log₁₀(p). Each point corresponds to one of the 62 clusters considered in this study. Clusters corresponding to activations are represented in red triangles, and deactivations in blue circles. Thresholds used for classification are displayed using dashed lines. Almost all the largest fMRI clusters (volume>10 mm³) were highly relevant for EEG source localization (α>1.5). The fMRI responses concordant with EEG were either activation or deactivation, also fMRI clusters showing deactivation tend to be slightly larger than the ones showing activations (a).

Discussion

In the first section, we will discuss the method we proposed to compare EEG sources and fMRI responses to spikes. In the second section, we will discuss what we learned from this comparison regarding the underlying phenomena linked to spike generation measured by EEG and fMRI.

A new methodology to assess EEG-fMRI concordance during epileptic spikes

We proposed a new methodology to quantify the level of concordance between EEG sources and BOLD responses to epileptic spikes. We first addressed important issues to make possible this difficult comparison: (1) EEG sources and fMRI results were estimated on the same cortical surface before being compared, (2) the ill-posed nature of the EEG inverse problem was taken into account by combining two complementary approaches, MEM-concordance and fMRI-relevance.

Assessment of EEG-fMRI concordance driven by the anatomy of each subject

The proposed framework to assess EEG-fMRI concordance was driven by the anatomy of each subject: the common spatial support used to estimate and compare EEG and fMRI data was the cortical surface segmented from the MRI of each subject. Therefore, a source (EEG or fMRI) located far from the cortical surface was not considered in this study. To our knowledge, this study was the first attempt to compare EEG sources and fMRI results estimated onto the same cortical surface. Appropriate comparison metrics taking into account the morphology of the cortical surface were also proposed (D and AUC).

In most previous studies, the whole brain volume was the common spatial support used to compare fMRI results with EEG or MEG sources. Indeed, EEG or MEG sources were estimated using either Equivalent Current Dipoles (ECDs) (Sanders et al., 1996; Lemieux et al., 2001; Bagshaw et al., 2005) or dipole scanning approaches on 3D grids (Seeck et al., 1998; Van der Meij et al., 2001; Mulert et al., 2004; Bénar et al., 2006). Consequently, the comparison metric was the Euclidian distance within the whole brain volume. The main generators of electrical activity being the large pyramidal neurons (Speckmann et al., 2004), constraining EEG source localization to the cortical surface as proposed by Dale and Sereno (1993), is a fair assumption. Moreover, as opposed to ECDs, distributed source models can recover spike generators with their spatial extent, especially using the MEM (Grova et al., 2006b).

fMRI data were acquired and analyzed on a 3D voxel grid covering the whole brain volume. Analysis involved a multiple HRFs approach (Bagshaw et al., 2004) to take into account the temporal variability of BOLD responses to spikes and to increase detection sensitivity. For each HRF, every cluster showing a significant BOLD response was selected using a cluster size test (Worsley et al., 2002) and its t-values were interpolated onto the cortical surface (Grova et al., 2006a). This interpolation method was designed to take into account the local morphology of the cortical surface and the distributed nature of the hemodynamic response. fMRI results became available on the same cortical surface as the one used to constrain EEG source localization. This interpolation method could as well be applied on raw fMRI data to perform, as for EEG data, an analysis of fMRI data constrained to the cortical surface (Andrade et al., 2001). However, evaluating the added-value of such a constrained approach was out of the scope of this study.

MEM-concordance: concordance between fMRI clusters and MEM sources

MEM-concordance was proposed to compare EEG sources and fMRI results obtained independently from each other. Geodesic distances (D) between local extrema and overlap measurements between spatial extents (AUC) of EEG sources estimated with the MEM and fMRI clusters were used to quantify MEM-concordance.

The geodesic distances (D) between fMRI clusters and MEM local extrema quantify EEG-fMRI concordance taking into account the morphology of the cortical surface. Euclidian distance was the only comparison metric reported to assess EEG-fMRI or MEG-fMRI concordance, when sources were estimated using ECDs (Sanders et al., 1996; Lemieux et al., 2001; Bagshaw et al., 2005), dipole scanning approaches (Van der Meij et al., 2001; Bénar et al., 2006) or the LORETA distributed source method (Mulert et al., 2004; Seeck et al., 1998). Following the convoluted structure of the cortical surface, the geodesic distance is able to consider as distant sources located on both side of a sulcus, whereas the Euclidian distance between these sources is small. Geodesic distance is then a concordance index more selective than the Euclidian distance.

Our approach was also the first to compare EEG sources and fMRI responses by taking into account their spatial extents on the cortical surface. Therefore, we proposed a ROC curve analysis assuming the fMRI cluster to be the reference with which MEM sources had to be compared. For each fMRI cluster interpolated on the cortical surface, the metric AUC integrated overlap measurements over all possible thresholds of MEM current density maps. Although this comparison was asymmetric as we only took into account MEM sources located close to fMRI clusters, results suggested that both D and AUC were complementary and necessary to quantify MEM-concordance.

fMRI-relevance: relevance of each fMRI cluster for the EEG inverse problem

fMRI-relevance compared EEG and fMRI localizations by the indirect route of testing the relevance of each fMRI cluster as prior information for the EEG inverse problem. This study is the first attempt to apply on clinical data the fMRI-relevance index α we proposed and validated on simulated data in Daunizeau et al. (2005). As it allowed to answer different questions than MEM-concordance, fMRI-relevance brought new and complementary information in the analysis of EEG-fMRI concordance. fMRI clusters with an α greater than 1.5 suggested the presence of sources sometimes missed by the MEM (e.g., cluster 1 at t₀ in Fig. 3 and cluster 2 in Fig. 4). Conversely, only fMRI clusters with an α lower than −1.5 indicated that no current source within or close to this fMRI cluster could contribute to scalp EEG data (e.g., cluster 2 in Fig. 3).

Using fMRI data to constrain the EEG inverse problem should be considered with caution and may be misleading, especially when the constraint is too strong such as in ECDs approaches (Gonzales Andino et al., 2001; Korvenoja et al., 2001; Bagshaw et al., 2005). Distributed source models proved to be an elegant way to introduce and control smooth constraints derived from fMRI results, in the EEG inverse problem (Liu et al., 1998; Dale et al., 2000; Babiloni et al., 2003). By combining hierarchical models and Bayesian inference techniques (Phillips et al., 2005; Daunizeau et al., 2005), the uncertainties associated to all parameters and hyperparameters of the models could be taken into account during the estimation. Model comparison, using for instance Bayes’s factor (Gelman et al., 1998), is then feasible and it was first applied to EEG source localization by Trujillo-Barreto et al. (2004) who compared different anatomical priors. The behavior of fMRI-constrained source localization in the presence of accurate or inaccurate fMRI priors was previously analyzed using extensive simulations (Liu et al., 1998; Babiloni et al., 2003; Phillips et al., 2005; Daunizeau et al., 2005). In most cases, only fMRI priors concordant with EEG sources were tested, even in the presence of additional EEG sources with no fMRI correspondence. The influence of fMRI priors non-concordant with simulated EEG sources was tested by Daunizeau et al. (2005) and Phillips et al. (2005). The results of these simulation studies help to achieve more confidence in the meaning of a fMRI-relevance index α significantly positive or negative. Our results obtained with clinical data confirmed the added-value of using α when analyzing EEG-fMRI concordance. However, the specificity of α should also be considered, which could be tested by comparing our results to the estimation of α using false fMRI clusters generated randomly in the brain. This was out of the scope of this study.

Why is it important to consider both MEM-concordance and fMRI-relevance approaches?

We proposed two complementary comparison strategies to assess EEG-fMRI concordance: MEM-concordance and fMRI-relevance. The overall agreement observed between these two approaches increased the confidence we have in our results. They were also complementary, especially because fMRI-relevance could answer different questions than MEM-concordance, such as assessing if sources located within or close to an fMRI cluster could explain some scalp EEG data or not. We found no case of contradiction or complete disagreement between the two methods (class MEM concordant and fMRI non-relevant). Moreover, fMRI clusters were observed within the five other classes of EEG-fMRI concordance, what confirmed this complementarity and emphasized the complexity of the underlying mechanisms associated with epileptic spikes generation.

The use of both MEM-concordance and fMRI-relevance was necessary to adequately take into account spike propagation when comparing EEG sources and fMRI responses. EEG is sensitive to spike propagation as it measures brain activity at the order of the millisecond, whereas fMRI data integrate a slow hemodynamic phenomenon over seconds. EEG sources corresponding to the main steps of such a propagation were considered in the analysis, as MEM-concordance metrics were only quantified at the main peaks of the spike. For each cluster, only the time peak for which we measured the most concordant result was considered and reported (cf. min(D) and max(AUC) indices). Using MEM-concordance, we showed in Fig. 2 that fMRI cluster 1 was in better concordance with the MEM source estimated at time t₁ than at time t₂, whereas fMRI cluster 2 was in better concordance with the MEM source at time t₂ than at time t₁. EEG sources can propagate rapidly and some EEG-fMRI concordance could be missed just by considering few time samples, as for instance the superior posterior temporal source at t₀ in Fig. 3. By integrating EEG-fMRI concordance metrics over the whole duration of the spike, α can address this issue and measure how much each fMRI cluster could contribute to the measured EEG signal at some point during spike propagation. As suggested by Ebersole (2000), one must check whether different voltage topographies appear over the course of the spike, indicating propagation. α may also provide clues where to analyze more carefully source localization results (see for instance the MEM source at t₀ in Fig. 3, confirmed by α=3.65 for cluster 1).

What did we learn from studying EEG-fMRI concordance?

EEG-fMRI concordance and source localization

Good correlations within 10–16 mm have been reported in evoked potential experiments (Sanders et al., 1996; Korvenoja et al., 2001; Mulert et al., 2004). However, such a good concordance is not found when analyzing the generators of interictal spikes (Lemieux et al., 2001; Bagshaw et al., 2005). Using the same data as in this study, Bagshaw et al. (2005) reported an average Euclidian distance greater than 3 cm between the location of the ECD and the nearest fMRI voxel showing a significant response. Similar EEG-fMRI discrepancies were reported by Bénar et al. (2006), who compared fMRI responses with statistical maps showing which dipoles on a 3D grid are the most likely to contribute to a solution involving one, two or three ECDs. These studies suggested that the ECD may not be the appropriate model for spike localization. Our MEM results indicate a better EEG-fMRI concordance than results reported in Bagshaw et al. (2005) and Bénar et al. (2006) on the same data. Indeed, we found at least one fMRI cluster classified as MEM-concordant for six of seven patients. Our results showed that distributed source approaches, and notably the MEM approach, are well suited to assess EEG-fMRI concordance for epileptic spikes. A possible explanation may be the ability of the MEM technique to recover accurately the spatial extent of spike generators, as evaluated in Grova et al. (2006b). ECD localization may be misleading in presence of spatially extended generators (Kobayashi et al., 2005b). EEG sources detected using distributed source localization methods may over-estimate spatial extent by bleeding over adjacent lobes or sulci (every source showing similar orientation in neighboring sulci along the cortical surface will tend to show similar activity). Describing brain activity using a model composed of K cortical parcels associated with their probability of being active, the MEM technique is able to stop such bleeding by switching off the contribution of some parcels during the estimation, providing a more accurate estimate of the spatial extent of the source.

Toward a better understanding of the phenomena underlying spike generation

Our results demonstrate that the underlying structure of spike generators may be organized as a distributed network, where part of this network is able to generate detectable EEG signals, detectable fMRI signals or both. For each patient, we found fMRI clusters in almost all the five classes of EEG-fMRI concordance. Part of the hemodynamic response to spikes was highly concordant with EEG sources, but as a response to the same EEG spikes, there were also other BOLD responses distant or even discordant with EEG sources. This highlights the complex nature of the underlying phenomenon linked to spike generation and propagation. Using the proposed classification scheme defined with MEM-concordance and fMRI-relevance indices, we detect parts of this network where strong concordance between EEG sources and fMRI response was found, as well as other parts where EEG-fMRI discordance was suspected. When such an information was available, MEM-concordance and fMRI-relevance results were confirmed by intracranial EEG recordings (Figs. 2–4). EEG-fMRI concordant results were also found within a focal cortical dysplasia (Fig. 5). These observations increased the confidence we have in our findings, although more patients should be considered for evaluation.

Whereas the nine patients of this study were not selected based on their fMRI findings, EEG-fMRI concordance was not quantified for two patients, as they did not show any significant fMRI results. This observation is in agreement with the fact that EEG-fMRI analysis of interictal spike suffer from weak sensitivity. Indeed, Bagshaw et al. (2004) showed that using four HRFs resulted in an increased sensitivity from 45% when using the standard HRF alone, to 62.5%. Our results suggest that more advanced fMRI analysis techniques could be considered in regions where EEG sources were detected.

fMRI clusters identified as fully concordant with EEG data according to both MEM-concordance and fMRI-relevance could be considered to study in greater detail the coupling between electrophysiological and hemodynamic phenomena. A very simple coupling function was considered in this study (Eq. (9)). The proposed fMRI-relevance index α may also test and compare different coupling functions, such as the more complex ones proposed by Babiloni et al. (2003). In the illustrative cases, we showed that combining more than one fMRI cluster in the prior model may lead to a better fMRI-relevance. For instance, α increased when cluster 1 and 2 were considered together in patient 3 (Fig. 2). Combining different clusters may also lead to a decrease of α (Fig. 5). fMRI-relevance may then help to identify the optimal set of fMRI clusters suspected to be concordant with EEG data during an interictal spike. The proposed method to assess EEG-fMRI concordance is then appropriate to identify brain region where a coupling between electrophysiological and hemodynamic phenomena is highly suspected. Such coupling could then be further investigated using dedicated data fusion approaches (Dale and Halgren, 2001; Pflieger and Greenblatt, 2001; Kiebel and Friston, 2004).

Another originality of the proposed method was its ability to identify areas where EEG and fMRI localizations were considered discordant (class MEM non-concordant and fMRI non-relevant). There may be two ways to interpret this discordance. On one hand, a problem during fMRI analysis occurred and the corresponding clusters may be a false positive or an artifact. This assumption may be tested by better analyzing the fMRI signal in such a region, using HRF estimation techniques for instance (Marrelec et al., 2003). If, however, a significant HRF is found in these regions, then a decoupling between EEG sources and BOLD response may have occurred, and this phenomenon needs to be explained.

Many physiological phenomena may explain discrepancies between electrophysiological sources and BOLD responses (Nunez and Silberstein, 2000; Gonzales Andino et al., 2001). Nunez and Silberstein (2000) suggested that different cell assemblies are responsible for electro-magnetic and hemodynamic signatures. Indeed, there is no need for synchronization of neuronal firing to obtain an increase of BOLD response. For instance, the cortical stellate cells provide a closed field structure and are thus electrically and magnetically invisible, whereas they are known to have a large metabolic contribution. Conversely, a few percent of synchronously active neurons may generate large EEG/MEG oscillating signals such as the alpha rhythm, without much energy consumption.

By construction, both imaging techniques considered in this study are only sensitive to the epileptic discharges that are sufficiently spatially extended to generate a spike seen on scalp EEG (Ebersole, 1997). Many phenomena linked to the generation and propagation of a spike may not be measured by scalp EEG, and propagated sources can already be involved at the time point of the peak of the spike on the scalp (Alarcon et al., 1994). Conversely, one can measure a BOLD response as soon as it correlates with scalp EEG. Because of the inertia of the hemodynamic phenomena, detected BOLD responses could also correspond to events that occurred slightly before or after the main spike seen on scalp EEG. For instance, distant BOLD responses located in sub-cortical or contralateral regions are often found (Kobayashi et al., 2006a) and may reflect such phenomena. Whereas only interictal discharges were considered in this study, we have shown that during the electrographic seizures of one patient, a right focal temporal EEG discharge corresponding to a right temporal MEM source was associated to a huge BOLD response involving almost the whole hemisphere (Kobayashi et al., 2006b).

Similar EEG-fMRI concordance levels were found for clusters corresponding either to BOLD activation or deactivation. We previously suggested that positive BOLD responses were likely to be more meaningful than negative ones regarding the presumed epileptogenic area (Kobayashi et al., 2005a). In our small group of patients, we showed that both kinds of BOLD responses provided similar levels of concordance with EEG. The reasons why a BOLD deactivation may be either completely concordant (e.g., clusters 1 and 2 in Fig. 2) or discordant with EEG sources (e.g., cluster 2 in Fig. 3) remain unclear. Although Shmuel et al. (2006) showed recently a tight coupling between negative BOLD and decreased neuronal activity using simultaneous recording of fMRI and intracortical EEG data in the macaque visual areas, little is known regarding the meaning of negative BOLD responses. Even more precaution should then be considered when analyzing fMRI and EEG responses to epileptic spikes, which is a pathological situation. It is generally accepted that BOLD deactivation is caused by a decrease in energy consumption and that an epileptic spike requires the synchronization of neuronal firing over a fairly extended area to be detected on scalp EEG. As the BOLD does not depend on neuronal synchronization, we may then assume that a cortical region showing less active cells but more synchronous cells may generate at the same time BOLD deactivation and an EEG spike. EEG-fMRI discordance may also be explained by BOLD deactivation associated to a suspension of the default state of the brain (Raichle et al., 2001) that could be interpreted as a decrease of the level of attention during the spike. These fMRI deactivations, completely discordant with EEG data, were found when studying spike and wave discharges in patients with idiopathic generalized epilepsy (Gotman et al., 2005). Deactivations within the network associated to the default state of the brain could also be detected partially or completely after focal spikes, and cluster 2 in patient 1 (Fig. 3) may be part of this network. Analyzing more data using the method proposed here as well as more detailed analysis of fMRI results will help us to better understand these complex phenomena linked to spike generation and propagation.

Conclusion

We propose a new framework to analyze EEG-fMRI concordance by comparing BOLD responses to interictal spikes using EEG-fMRI simultaneous acquisition with EEG source localization. An important contribution was to propose an anatomically informed method to compare these two sources of information on the same spatial support, the cortical surface. Two complementary strategies were considered, MEM-concordance and fMRI-relevance, in order to classify each significant fMRI cluster according to its level of concordance with EEG data. Our main result was that for most patients, part of the hemodynamic response to epileptic spikes was highly concordant with EEG sources, and as a response to the same spikes other fMRI clusters were found distant or discordant with EEG sources. Our results emphasized the complex nature of the underlying phenomenon linked to spike generation and propagation. We propose an original method to identify cortical areas where electro-physiological and hemodynamic phenomena may be coupled during spike generation.

Appendix A. MEM regularization of the EEG inverse problem

The reference distribution dμ used to incorporate prior information within the MEM framework is described in Fig. 8a. This very general model assumes that brain activity may be described by K a priori independent cortical parcels showing an homogeneous activation state. Each cortical parcel k was characterized by an activation state S_k (=0 or 1), described by a probability of being active: Prob(S_k =1)= α_k. j_k denotes the intensity of the p_k sources in the kth parcel, δ is the Dirac distribution that allows to shut down the activity when the parcel is inactive (S_k =0). The Gaussian distribution (μ_k, Σ_k) (j_k) with mean μ_k and covariance Σ_k describes the current distribution within the kth parcel when it is assumed to be active (S_k =1). The initialization of the parameters of this model is described with more details in Grova et al. (2006b).

Fig. 8.

Principle of source localization using MEM principle: (a) definition of the reference distribution dμ expressing prior information on J, (b) principle of MEM regularization, estimation of the solution dp̂ explaining the data M in average with maximum μ-entropy. dp̂ is the distribution explaining the data M in average closest to dμ in the sense of Kullback–Leibler divergence.

The principle of MEM regularization of the EEG inverse problem is summarized in Fig. 8b. Considering this prior model dμ, the MEM solution dp̂ within the k^th parcel is found to be:

$$\begin{array}{l}{\widehat{\mathbf{J}}}_{\text{MEM}}^{\mathbf{k}}={\widehat{\alpha }}_k\left[{\mu }_k+{\sum }_k{\mathbf{G}}_k^T\stackrel{\sim }{\lambda }\right]\text{with}\\ {\widehat{\alpha }}_k=\frac{{\alpha }_k}{{\alpha }_k+(1-{\alpha }_k)exp(-F_{\mu ,k}({\mathbf{G}}_k^T\stackrel{\sim }{\lambda }))}\end{array}$$ (A.1)

where G_k is the n × p_k submatrix of G and the “free energy” term F_μ,k corresponding to the kth parcel is defined as:

$$F_{\mu ,k}\left({\mathbf{G}}_k^T\stackrel{\sim }{\lambda }\right)={\mu }_k^T{\mathbf{G}}_k^T\stackrel{\sim }{\lambda }+\frac{1}{2}{\stackrel{\sim }{\lambda }}^T{\mathbf{G}}_k{\sum }_k{\mathbf{G}}_k^T\stackrel{\sim }{\lambda }$$ (A.2)

where λ̃ is the maximum of a non-linear optimization within a n-dimensional space (Amblard et al., 2004).

Appendix B. Hierarchical linear model and Bayesian inference

Fig. 9 presents a graph representation of the hierarchical linear model of data generation stated in Eq. (3). To estimate the evidence of any hypothesis or prior model H_i, three levels of Bayesian inference are needed to integrate every source of uncertainty of the model (Daunizeau et al., 2005):

Fig. 9.

Graph representation of the hierarchical linear model of data generation and description of three levels of Bayesian inference used to estimate the evidence of any prior model H_i.

• First level of inference: Estimation of the parameters J

  Fig. 9a presents Bayesian inference used to estimate the unknown parameters of interest J, assuming a specific prior model (H_i) and a set of mutually independent hyperparameters (σ², ε²). p(J|σ², ε², M, H_i) defines the posterior probability density function (pdf) to be estimated. p(M|J, σ²) represents the data likelihood and p(J|σ², ε², H_i) is the prior pdf of J stated in Eq. (3). Under specific assumptions regarding prior distributions using Gaussian distributions, it is possible to estimate Ĵ_MAP, the Maximum a Posteriori (MAP) estimate of J, given H_i and a set of hyperparameters (σ², ε²) linked to the variance of the noise and of the sources.

• Second level of inference: Estimation of the hyperparameters (σ², ε²)

  Fig. 9b presents Bayesian inference used to integrate in the model the source of variability due to the choice of the hyperparameters (σ², ε²). p(σ², ε² |M, H_i) defines posterior pdf to be estimated. p(M|σ², ε², H_i) is the data likelihood, estimated by integrating over J the numerator of the first level Bayes’ rule (Fig. 9a). p(σ², ε²) is the prior pdf of the hyperparameters, which is generally a non-informative distribution assumed to be independent from H_i. A method to estimate the posterior pdf and then the MAP estimate of σ² and ε² is described in Daunizeau et al. (2005).

• Third level of inference: Estimation of the relevance of the hypothesis H_i

  Fig. 9c presents Bayesian inference used to integrate in the model the source of variability due to the choice of the hypothesis H_i. The model evidence p(H_i | M) to be estimated is the posterior probability of the ith hypothesis H_i given the data M. p(M|H_i) is the data likelihood of H_i, estimated by integrating over σ² and ε² the numerator of the second level Bayes’ rule (Fig. 9b). A numerical method to estimate p(M|H_i) using an integration of a 1-dimension function is detailed in Daunizeau et al. (2005). p(H_i) is the prior distribution of the hypothesis. In our context, in order not to privilege any hypothesis, we assume uniform probability: p(H₀)= p(H₁)=1/2.