Temporal/spatial resolution improvement of in vivo DCE-MRI with compressed sensing-optimized FLASH

Abstract

Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) provides critical information regarding tumor perfusion and permeability by injecting a T₁ contrast agent, such as Gd-DTPA, and making a time-resolved measurement of signal increase. Both temporal and spatial resolutions are required to be high to achieve an accurate and reproducible estimation of tumor perfusion. However, the dynamic nature of the DCE experiment limits simultaneous improvement of temporal and spatial resolution by conventional methods. Compressed sensing (CS) has become an important tool for the acceleration of imaging times in MRI, which is achieved by enabling the reconstruction of subsampled data. Similarly, CS algorithms can be utilized to improve the temporal/spatial resolution of DCE-MRI, and several works describing retrospective simulations have demonstrated the feasibility of such improvements. In this study, the fast low angle shot sequence was modified to implement a Cartesian, CS-optimized, sub-Nyquist phase encoding acquisition/reconstruction with multiple two-dimensional slice selections and was tested on water phantoms and animal tumor models. The mean voxel-level concordance correlation coefficient for Ak_ep values obtained from ×4 and ×8 accelerated and the fully sampled data was 0.87±0.11 and 0.83±0.11, respectively (n=6), with optimized CS parameters. In this case, the reduction of phase encoding steps made possible by CS reconstruction improved effectively the temporal/spatial resolution of DCE-MRI data using an in vivo animal tumor model (n=6) and may be useful for the investigation of accelerated acquisitions in preclinical and clinical DCE-MRI trials.

1. Introduction

Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) provides critical information regarding tumor perfusion/permeability by the dynamic measurement of signal increase after injection of a T₁ contrast agent (CA) [1–6]. DCE-MRI employs sequential acquisition of MR images after an intravenous injection of a CA. The T₁ value of water shortens with the accumulation of a paramagnetic CA, such as Gd-DTPA. In the tissue region of interest, the CA usually arrives faster and in larger concentrations in well-perfused, highly vascular and permeable regions. Thus, the MR image displays a characteristic time signal intensity change related to the CA concentration in the voxel. The vascular perfusion and permeability information of a tumor can be obtained from quantitative modeling of the DCE data [7,8]. Both high temporal and spatial resolutions are required to obtain accurate and reproducible measurements of tumor perfusion/blood flow and permeability [1–4]. However, the dynamic nature and signal-to-noise considerations of the DCE experiment limit simultaneous enhancement of temporal and spatial resolution by conventional data acquisition methods.

For the acceleration of dynamic MR images, various processing algorithms with reduced k-space data have been proposed and implemented, such as keyhole [9], Reduced-encoding Imaging by Generalized-series Reconstruction (RIGR) [10], k–t Broad-use Linear Acquisition Speed-up Technique (k–t BLAST) [11] and k–t FOCal Underdetermined System Solver (k–t FOCUSS) [12]. Compressed sensing (CS) theory was recently established and proves that only a small fraction of the samples necessary for a regular linear reconstruction (i.e., fast Fourier transformation, Hadamard) is sufficient to reconstruct sparse or compressible signals given certain restrictions on the sampling [13–15]. It has the potential to significantly accelerate data acquisition in many MRI applications without the need of any reference images. Magnetic resonance images have long been known to be sparse under various spatial transformations, such as discrete wavelet transform or Fourier transformation (typically a temporal-sparsifying transform), from general research in image compression and work specific to the archival of medical data [16–18]. Furthermore, the ability to easily manipulate the sampling in a conjugate space of the image, i.e., k-space, makes it straightforward to obey the sampling requirements. Accordingly, following CS theory, dynamic MR images can be reconstructed by solving an l₁-norm minimization problem, i.e., minimizing the l₁-norm of the compressed image that is consistent with the acquired data [11,12].

DCE-MRI is an appealing application of the CS algorithm in particular. The negative influence of poor temporal resolution in determining pharmacokinetic parameters from DCE-MRI has recently been simulated [19]. A possible reduction of number of phase encoding steps of dynamic image acquisition with CS will lead to spatial/temporal resolution enhancement of the dynamic uptake curve and thus will improve the accuracy in extracting perfusion data from DCE-MRI. Consequently, several retrospective simulations from fully sampled DCE-MRI data have been performed [20–27]. For example, resolution enhancements of 10-fold in a phantom model [23], 4-fold in an animal model [24,27] and 6-fold to ~10-fold in breast DCE-MRI [23,25,26] were simulated with the CS algorithm from a subsampling of fully acquired dynamic images. On the other hand, to the best of our knowledge, an actual demonstration of either temporal or spatial resolution enhancement with a CS-optimized pulse sequence, which is a critical extension of previous feasibility studies, has not been done as of today for in vivo DCE-MRI studies.

In this work, we demonstrate the actual enhancement of spatial/temporal resolution of in vivo DCE-MRI in an animal model with a Cartesian CS-optimized fast low angle shot (FLASH) sequence with multiple two-dimensional (2D) slice selections in a manner similar to k–t FOCUSS [12]. The FLASH sequence is a widely accepted protocol for acquiring both preclinical and clinical in vivo DCE-MRI data. Therefore, the acceleration of DCE-MRI data acquisitions with this sequence combined with established CS reconstruction has the potential to benefit many preclinical and clinical investigations of tumor perfusion/permeability trials with straightforward implementation and with full compatibility with other acceleration techniques, such as parallel imaging or half k-space imaging [27].

This paper is organized as follows: (1) Design parameters necessary for the development of a Cartesian CS-assisted FLASH sequence were optimized by subsampling the phase encoding steps on the fully sampled DCE-MRI data of animal tumors. (2) The phase encoding steps of the conventional Bruker FLASH sequence have been modified with a CS-optimized phase encoding table, and undersampled data were reconstructed using a standard CS algorithm. Water phantom experiments were performed to check the functionality of the sequence and to establish the baseline stability of a new CS-FLASH sequence as a control sample. (3) Finally, actual improvements of the spatial/temporal resolutions of preclinical DCE-MRI data were demonstrated on mouse flank tumor xenografts by comparing uptake curves and corresponding DCE-MR images and Ak_ep maps from the CS-FLASH sequence with those obtained using the conventional FLASH sequence.

2. Methods and materials

2.1. Optimization of CS-FLASH parameters for acquisition and reconstruction

Compressed sensing can be described as reconstructing image/signal from subsampled data by optimizing for the reconstruction’s sparsity under some predetermined compressive transformation. This is achieved by minimizing the l₁-norm of the compressed reconstruction that is constrained to match the acquired data by solving the following constrained optimization problem:

$$\text{minimize}{\Vert \Psi s\Vert }_1,$$

$$\text{subject to}{\Vert Fs-k\Vert }_2<\epsilon ,$$

where the underlying image of interest is a vector s and Ψ denotes the linear operator that transforms s from a pixel into a sparse representation, such as Fourier transformation or discrete wavelet transformation. k is the undersampled k-space data, F is the undersampled Fourier transform which converts the image domain into the k-space domain, and ε controls the fidelity of the reconstruction to the measured data and is usually set to below the noise level of k-space [28,29].

For the implementation of a Cartesian CS-FLASH for DCE-MRI applications, five design variables were optimized for both, acquisition and reconstruction: (1) the optimal compressive transform, (2) the undersampling scheme for the phase encoding steps, (3) the incoherent sampling schemes along the temporal dimensions, (4) the constraint of reconstruction and (5) the rate of acceleration. Optimized parameters in each step were passed on to the next optimization process and used for the determination of parameters of interest at each stage. Optimizations were performed using a slice of a Dunning R3327-AT prostate tumor in a rat with heterogeneous perfusion/permeability, which was previously reported [6].

First, the proper compressive transformations along the image and time domain were selected by comparing the relationship between the fraction of coefficients after compression and the fraction of the total signal for several different processing algorithms with multiple combinations of transformations. In addition, subsampled data were created from fully sampled DCE-MRI data and reconstructed with CS algorithms with various transformations. Respective optimal transforms along the image and time domain were selected by minimizing the residual values between the CS-reconstructed and the fully reconstructed image.

Second, the undersampling of the phase encoding steps followed a random sampling scheme. The center k-space points in these schemes were always sampled, and the remaining points were sampled with Gaussian weighting. This scheme ensures a sampling bias towards small k values with a good signal-to-noise ratio (SNR), while still collecting enough data for larger k-values to reconstruct the details of the image as well as maintaining sampling incoherence for CS. Different random phase encoding schemes were applied to next time points as this variation maintains incoherent sampling for the CS reconstruction along the time axis, while reconstructing multiple time points simultaneously improves the compression of the stack of image frames.

Third, to determine the optimal size of the sampling scheme along the temporal dimensions of DCE-MRI, different random phase encoding schemes unique to each time point were repeated after every n time points for the full reconstruction of the time signal curves after administration of the CA. Subsampled data from the fully sampled DCE-MRI data were reconstructed with varying segment sizes n. The residual between the CS-reconstructed and fully reconstructed image was analyzed as a function of the segment size n. This avoids an unnecessarily large phase encoding array for the CS-FLASH sequence and increases the flexibility of the implementation of the CS-FLASH sequence, while the required number of temporal acquisitions can be adjusted for the study of interest.

Fourth, the constraint ε controls the reconstruction’s least squares difference to the acquired data and also impacts the total computation time required for the reconstruction [29]. In general, it should be set at or below the total noise level of the acquired samples, where it will add this noise in addition to the error from subsampling from the ideal reconstruction [28]. A looser constraint (ε), which may be convenient as it will usually result in faster reconstruction times, will also cause the reconstruction to deviate significantly from the actual data as the algorithm overcompresses the image. Constraints and reconstruction time requirements were optimized based on our fully sampled DCE-MRI data by analyzing the residual between the CS reconstruction with different constraints and the fully reconstructed image.

Finally, the degradation of image quality and corresponding Ak_ep parameters was studied with ×4, ×8, ×10, ×12 and ×16 acceleration factors with optimized design parameters. Residuals values with respect to regular reconstruction of fully sampled DCE-MRI were calculated for both image and Ak_ep maps. Dynamic modeling of the uptake curve for each subsampled image was performed with the Hoffmann/Brix model [7] to compare perfusion parameters.

All reconstructions were performed on a personal computer with an Intel Core i3 3.19-GHz central processing unit and 4 GB of memory on the Windows 7 platform. The data were processed by software developed with MATLAB R2010a (MathWorks, Natick, MA, USA) by using two external packages: spgl1 v.1.7 for the l₁-norm minimization [30] and Wavelab v.8.02 for applying wavelet transform to images [31].

2.2. Statistical and DCE-MRI analysis

For the quantitative comparison of the image and Ak_ep values of various CS reconstructions with different parameters, the concordance correlation coefficient (CCC) value was used as a standard metric. The CCC value quantifies the degree of agreement for each voxel intensity of the CS reconstruction with respect to that of a fully reconstructed image and was evaluated using [27,32]:

$${\rho }_c=\frac{2\rho {\sigma }_x{\sigma }_y}{{\sigma }_x^2+{\sigma }_y^2+{({\mu }_x-{\mu }_y)}^2},$$

where σ, µ and ρ refers to standard deviation, mean and correlation coefficient of each case, respectively. The CCC value was used to determine how far the CS reconstructed data deviate from 45° line on a square scatter plot with respect to fully reconstructed data. The accuracy and precision of data, which are characterized by the nearness and tightness of the data’s major axis to the 45° line in the scatter plot, increase the CCC value, reaching the value of 1 when both data are identical and, thus, in perfect concordance [32].

Ak_ep values from the Hoffmann/Brix model were used for the measurement of DCE parameters. Many different parameters from various models can be used for the analysis, but many of them require the measurement of an arterial input function (AIF) for each animal. Characterization of an individual AIF in preclinical studies is known to be very difficult and could be misleading when measurement errors exist, especially for the longitudinal investigations employed in this study. On the other hand, the Ak_ep value (k_ep is the movement of Gd-DTPA between the interstitial space and plasma and A is the amplitude in the two compartment model) reflects both the degree of relative MR signal enhancement and an exchange rate, and thus characterizes the velocity of MR signal increase without requiring an AIF measurement in each animal and was shown to provide relevant information regarding tumor perfusion/permeability. Consistency and simplicity in DCE-MRI fitting with Ak_ep offer a practical and relevant way to verify the efficacy of the new sequence. Ak_ep values were evaluated on each voxel of DCE-MRI uptake curve using the following equation [7]:

$$\frac{S(t)}{S(0)}=1+A{k}_{ep}\left(\frac{e^{-k_{ep}t}-e^{-k_{el}t}}{k_{el}-k_{ep}}\right).$$

2.3. Development of CS-FLASH and application to in vivo DCE-MRI

To experimentally verify the improvement in spatial/ temporal resolution, we modified the phase encoding scheme of the FLASH pulse sequence with a CS-optimized phase encoding table and called it CS-FLASH. In the conventional FLASH sequence, the phase encoding steps are repeated in the same way for all slices and repetitions. Therefore, one predefined phase step array is sufficient. In CS-FLASH, the phase encoding steps are reduced by 3/4 or 7/8 for ×4 or ×8 compression, respectively. The remaining 1/4 or 1/8 steps are all different for the temporal repetitions and predefined by the sequence. Therefore, a three-dimensional phase encoding array with predefined phase step gradient values has to be provided in the CS-FLASH pulse sequence with the indices of the phase encoding steps and repetition along the temporal direction. These index orders are passed to the CS reconstruction to recreate the sampling table. Water phantom data were acquired to ensure both the proper functionality of the pulse sequence and the stability of the baseline. The data were acquired using the new Cartesian CS-FLASH sequence with a matrix size of 128 (read) × 128 (phase) × 32 (time points) for eight slices (1 mm thick) on an 11.7 T nuclear MR system (Bruker BioSpin, Billerica, MA, USA) at ×4 and ×8 undersamplings, respectively.

The Institutional Animal Care and Use Committee of the Korea Basic Science Institute approved the in vivo animal experiments conducted in this study. For the animal tumor model, U-87 MG (human glioblastoma–astrocytoma, epithelial-like) cells [33], suspended in phosphate-buffered saline (PBS; pH 7.4), were subcutaneously implanted into the flank of female mice (10⁶ cells/0.05 ml PBS per mouse). The CA Gd-DTPA (0.015 mmol/ml; Dotarem, Laboratoire Guerbet, Aulnay-sous-Bois, France) was injected as a bolus into the tail vein, followed by the serial acquisition of dynamic MR images of the tumors with FLASH or CS-FLASH sequences for each animal.

To verify the temporal resolution improvement at a fixed spatial resolution, the matrix size was varied according to the number of phase encodes and repetitions while holding the total number of points constant. For three different animals, they were 128×128×128, 128×32×512 and 128×16×1024 (read, phase, repetitions) for FLASH, CS-FLASH (×4) and CS-FLASH (×8), respectively. The total acquisition time was 1640 s for each sequence. The subsampled dynamic MR images were reconstructed based on optimized CS parameters. For all experiments, repetition time/echo time (TR/TE) was 100/2.2 ms, and eight slices with 1.5-mm slice thickness were collected. The potential advantage of improved temporal resolution is discussed.

In parallel, to verify the spatial resolution improvement at a fixed temporal resolution, a longitudinal DCE-MRI study was performed on three animals. Initial DCE-MRI experiments were performed with regular FLASH. After 5 h (allowing for clearance of the Gd-DTPA), DCE-MRI experiments were repeated with CS-FLASH (×4) and CS-FLASH (×8) on the same animals at the same temporal resolution (4.2 s). TR/TE was 130/3.1 ms, and four slices with 1.5-mm slice thickness were collected. CS reconstructions were used to demonstrate the spatial resolution improvements of the CS-FLASH acquired DCE-MRI data with fixed temporal resolutions. Relatively long TR values were used to demonstrate the acquisition of high-spatial/temporal resolution (up to 156 µm × 156 µm × 1.5 mm / 4.2 s) DCE-MRI data with multiple slices for enhanced volume coverage.

3. Results

3.1. Optimization of CS-FLASH parameters

3.1.1. Compressive transforms

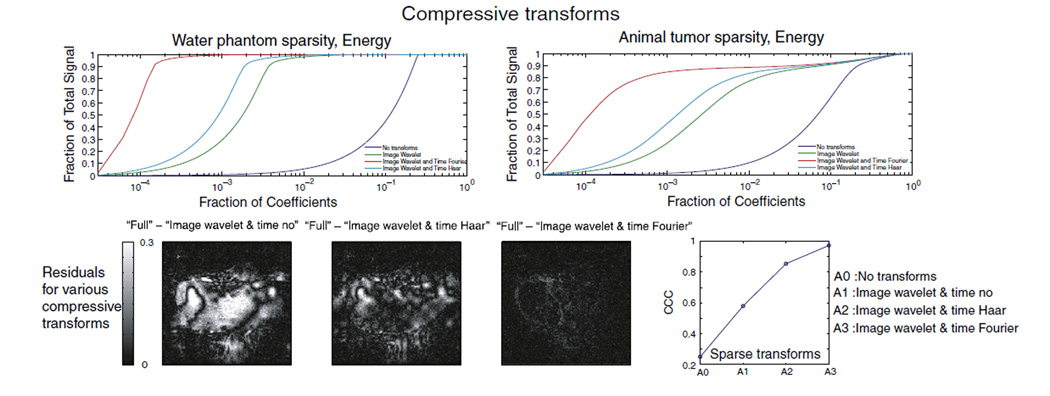
To choose the proper compressive transformation for the MR images, we plotted the relationship between the fraction of coefficients after compression (in decreasing order of signal intensity) and the fraction of the total signal for several different processing algorithms for a water phantom and an animal tumor as shown in the top row of Fig. 1: (a) no transform, (b) wavelet (symlet) transform only along the image axes, (c) wavelet (symlet) transform along the image axes with Haar transform along the time axis and (d) wavelet (symlet) transform for image compression with the Fourier transform along the time axis. Phase encoding steps were undersampled according to the scheme shown in Fig. 2A for 32 repetitions along the time dimension, and constraints were set to the noise level of the image (ε=σ). Wavelet compression along the image axes and the Fourier transform along the time axis were sparser than in all the other cases. Alternatively, CS-reconstructed images were generated with several different combinations of compressive transforms along the image and temporal dimension. Their corresponding residual values with respect to the fully reconstructed image are shown in the bottom row of Fig. 1. The fully reconstructed images were normalized to their maximum intensity voxel, and the CS-reconstructed images were normalized to the same value for their direct comparison. For a clear visualization, the maximum scale of residual plots was set to 30% of the maximum signal intensity of the fully reconstructed image. The CCC was calculated for each combination of transforms, as shown in the bottom row Fig. 1, and an optimal value of CCC=0.974 was obtained for the wavelet transform along the image dimensions and the Fourier transform along the time dimension. Based on these observations, CS was implemented here by applying the wavelet transform along the image dimensions (Wavelab) and Fourier transform along the time dimension.

Fig. 1.

In the top row, the accumulated signal is plotted against the corresponding fraction of coefficients for selected types of transform applied to a water phantom and an animal tumor. No transform (blue), image wavelet only (green), image wavelet (symlet) and time Haar (turquoise), image wavelet (symlet) and time Fourier (red). In the bottom row, the residual values of each CS-reconstructed image against fully sampled/reconstructed images are plotted for various transforms along with the corresponding CCC values.

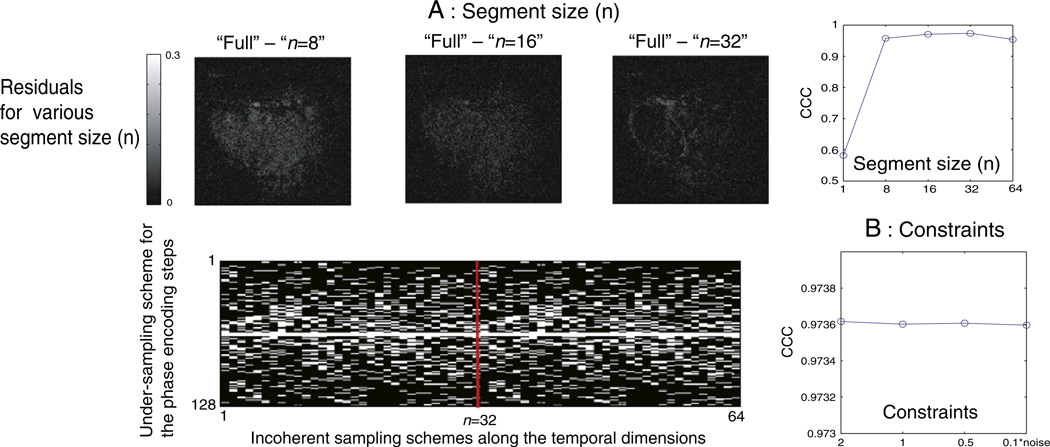
Fig. 2.

(A) Residual images and CCC values are plotted as a function of segment size (n). Optimized sampling scheme of phase encoding steps (full phase encoding 128) are shown for 64 time points. The same scheme was repeated for every n time points (here 32). (B) The CCC values for CS-reconstructed images with tightening tolerance, ε, to the acquired data, spanning ε=2σ, σ, 1/2σ, σ/10.

3.1.2. Segment size (n)

The segmentation of CS phase encoding schemes to n time points reduces the burden of reconstruction time as it reduces the data input size for CS reconstruction. For example, necessary input data size reduces from a single vector of 128 (read) × 32 (phase) × 128 (repetitions) to four 128×32×32 vectors when temporal encoding steps were segmented to n=32 at ×4 subsamplings. It also resolves memory overflow issues in the spectrometer that can occur when using a fully randomized phase encoding table for arbitrary number of repetitions. It also ensures the flexible implementation of study-dependent, varying temporal acquisition requirements. To estimate a suitable segment size n, each block of n time points out of 256 repetitions was reconstructed separately, and the residuals from the CS-reconstructed images with respect to the fully reconstructed image were evaluated as shown in Fig. 2A. Corresponding CCC values were calculated for n=1, 8, 16, 32 and 64, and the value appeared to saturate near 0.974 for n=32, as shown in Fig. 2A. The resulting, optimized phase encoding scheme for ×4 undersampling with a segment size of 32 is shown in Fig. 2A.

3.1.3. Constraints (ε)

With the optimized sampling scheme for sparse transforms and number of repetitions (n), we subsampled (×4) the phase encoded signal of a fully acquired DCE-MRI data set, ran CS reconstruction with a variable ε chosen based on the noise level σ and compared the result to the fully sampled MR image to verify the optimum value of the constraint for CS reconstructions. No significant difference between the constraint in the range of ε=2σ, σ, 0.5σ, 0.1σ was observed, and the results of steady CCC values are shown in Fig. 2B.

3.1.4. Acceleration factors

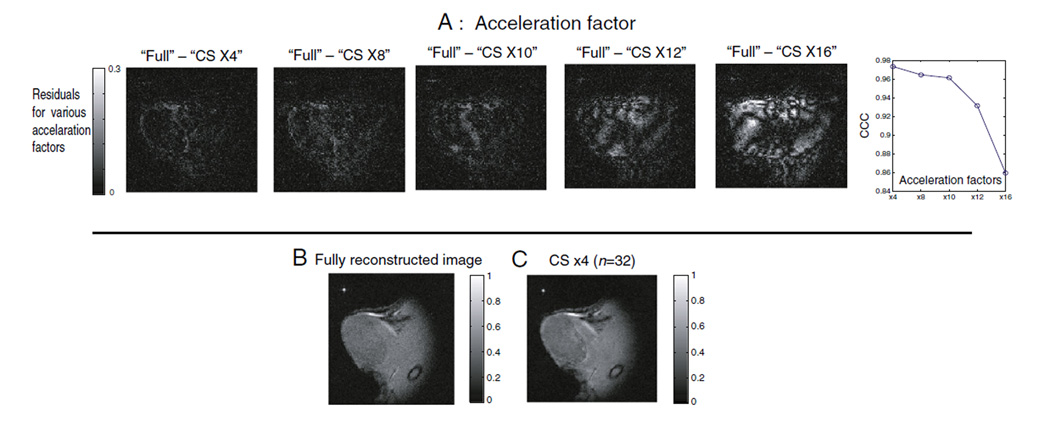
Finally, the CS reconstruction was validated at five different acceleration factors, i.e., ×4, ×8, ×10, ×12, ×16 subsampling of phase encoding steps with optimized compressive transforms, segment size along temporal dimensions (n=32) and constraints (ε=σ). The residual images and the corresponding CCC values plotted as a function of acceleration factor are shown in Fig. 3A. As the subsampling factor increases for the CS-reconstructed MR images, significant degradation of the image quality is visually apparent from the residual images at and above ~×10 subsampling. As reference, the fully reconstructed MR image is shown in Fig. 3B and compared to a ×4-accelerated, CS-reconstructed image with optimized parameters, as shown in Fig. 3C.

Fig. 3.

(A) Residual images and CCC values are plotted as a function of acceleration factors. For clear visualization, the maximum scale of residual plots was set to 30% of the maximum signal intensity of the fully reconstructed image. To calculate a representative number for the retained sparse coefficients for each of the CS reconstruction, fraction of coefficient of each CS-reconstructed image for each acceleration factor was divided by that of fully sampled image at 95% signal level. It shows that 88.46%, 80.05%, 77.90%, 76.18% and 71.19% of sparse coefficients of compressed representations were retained for ×4, ×8, ×10, ×12 and ×16 subsamplings for this animal tumor, respectively. (B) Fully acquired and reconstructed image. (C) CS (×4) reconstructed image with optimized parameters. In (B) and (C), fully reconstructed image was normalized to its maximum intensity voxel, and CS reconstructed images were normalized to the same value for their direct comparison.

3.2. Correlation of Ak_ep values between fully and CS reconstructed DCE-MRI

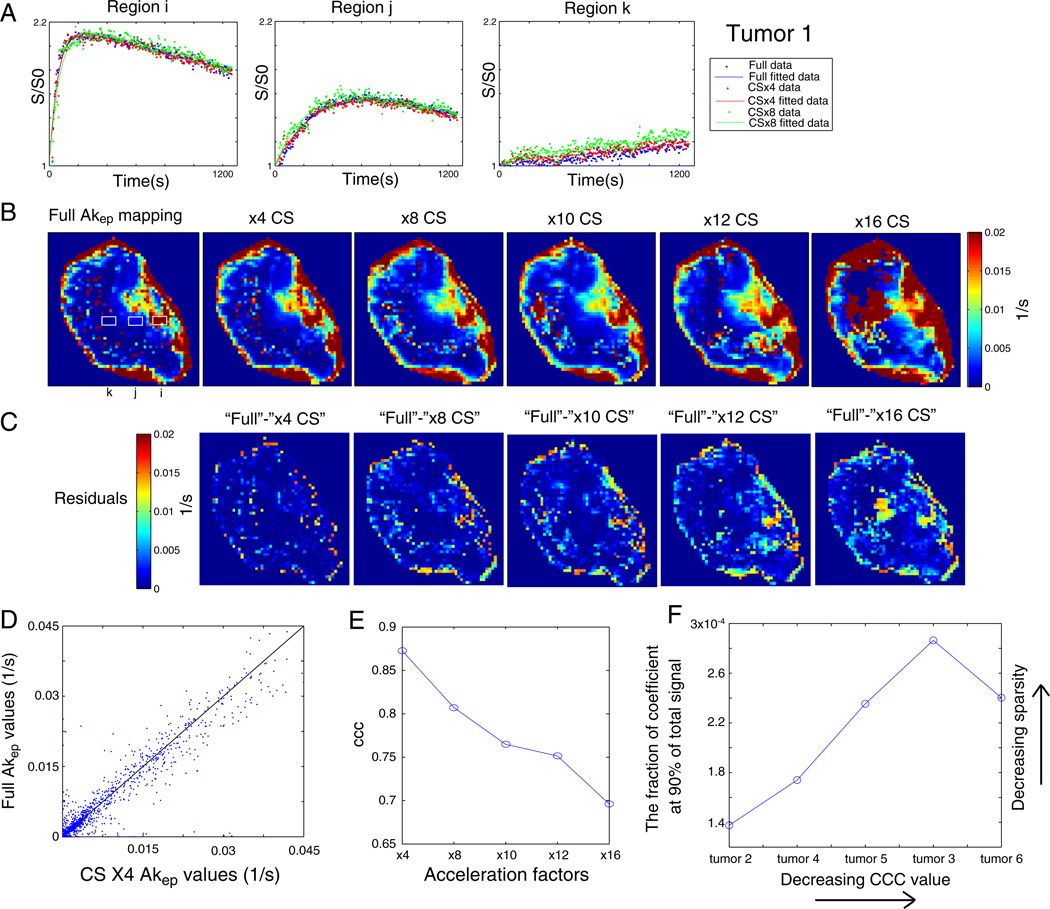
As DCE-MRI measures a time-resolved signal increase curve, the feasibility of applying CS to DCE-MRI must be validated not only with (a) individual image quality at each time point, but also with (b) a change in characteristic contrast uptake curve and (c) fitting of perfusion/permeability value (Ak_ep), all with optimized CS parameters. Subsequently, from DCE-MRI images reconstructed with different acceleration factors, an Ak_ep map was generated for each reconstruction by least squares fitting of the dynamic uptake curves for each individual pixel to the Hoffmann/Brix model [7]. Fig. 4 shows the Hoffmann interpretation of these CS reconstructions. Fig. 4A displays representative contrast uptake curves from three different regions of a tumor marked with the solid squares labeled (i), (j) and (k) on the Ak_ep map obtained from fully sampled data as shown in Fig. 4B. The fast (i), intermediate (j) and slow (k) initial slopes of uptake curves are shown at ×4 and ×8 subsampling along with the fully sampled data. The agreement between the fully sampled and CS-reconstructed images for the different characteristic uptake curves demonstrates the potential of CS-assisted DCE-MRI for even very heterogeneous tumors such as the one evaluated here. Fig. 4B shows the Ak_ep map of fully sampled data and corresponding Ak_ep maps for six different acceleration factors. High Ak_ep values around the tumor rim and low Ak_ep values in the core region are apparent on the CS-reconstructed images, which are qualitatively consistent with corresponding Ak_ep values from the full reconstruction. However, regional deviations from the full reconstruction emerge increasingly with increasing acceleration factors. To quantify this, the residual images (Fig. 4C) were obtained from CS-reconstructed data with respect to Ak_ep maps obtained from fully reconstructed data, and the corresponding CCC values (Fig. 4E) were evaluated as a function of acceleration factors. The CCC value decreased from 0.87 (×4) to 0.7 (×16) with increasing acceleration factor for this tumor. Some discrepancies were observed at the boundary of the images, where abrupt change in the signal intensity tends to occur. A scatter plot of Ak_ep values obtained from fully reconstructed data versus Ak_ep values obtained from ×4-undersampled and CS-reconstructed data shown in Fig. 4D emphasizes the good correlation between these data as well.

Fig. 4.

(A) Representative uptake curves from three different regions of the tumor marked with solid squares indicated as (i), (j) and (k). Fast (i), intermediate (j) and slow (k) CA uptake curves are shown at ×4 and ×8 subsampling along with fully sampled data. (B) The Ak_ep map of fully sampled data and the corresponding Ak_ep maps at different CS acceleration factors are shown. (C) Residuals of Ak_ep maps from the CS reconstructions with respect to those from full reconstructions are shown. (D) A scatterplot visualizes the quantitative comparison between Ak_ep maps from ×4 CS and full reconstructions. (E) The CCC values are shown as a function of acceleration factors. (F) The relationship between the fraction of coefficients and the fraction of total signal after compressive transforms for different tumors.

Single slices of five more tumors were similarly evaluated, confirming the soundness of the optimized pulse parameters. The superior performance of the CS algorithm for more homogeneous samples is attested by the improved CCC values (0.99 for ×4 and 0.97 for ×8) for tumors with a spatially uniform distribution of Ak_ep value as demonstrated in Supplementary Fig. 1 for tumor 2. Table 1 summarizes the CCC values of six tumors at ×4, ×8 CS reconstructions with optimized parameters. Mean(±S.D.) CCC values of 0.87±0.11 and 0.83± 0.11 for ×4 and ×8 CS reconstruction, respectively, substantiate the potency of CS with optimized parameters. Observed variations in CCC values among different tumors appear to depend on the sparsity of DCE-MRI data after compressive transforms. As shown in Fig. 4F, 90% of the signal after compression was supported with fewer coefficients in tumors with high CCC values than in tumors with lower CCC values, which indicates the more homogeneous spatiotemporal nature of tumor with high CCC values. Observed relatively low CCC values of tumors 3 and 6 appear to be the result of the extremely heterogeneous nature of perfusion/permeability with large region of necrosis as shown in Supplementary Fig. 1F, where the Ak_ep distribution of each tumor is shown in the order of decreasing CCC values.

Table 1.

CCC values of Ak_ep values comparing fully acquired and CS-reconstructed DCE-MR images for six slices of different animal tumors

	CCC (×4)	CCC (×8)
Tumor 1 (SNR=6.87)	0.87	0.83
Tumor 2 (SNR=6.18)	0.99	0.97
Tumor 3 (SNR=9.64)	0.77	0.74
Tumor 4 (SNR=5.82)	0.96	0.93
Tumor 5 (SNR=5.36)	0.91	0.86
Tumor 6 (SNR=7.32)	0.70	0.63
Mean(±S.D.)	0.87±0.11	0.83±0.11

Signal-to-noise ratio (SNR_mult) of fully sampled FLASH data of each tumor was estimated as well [34].

3.3. Temporal/spatial resolution enhancement of in vivo DCE-MRI with CS-FLASH

3.3.1. Water phantom

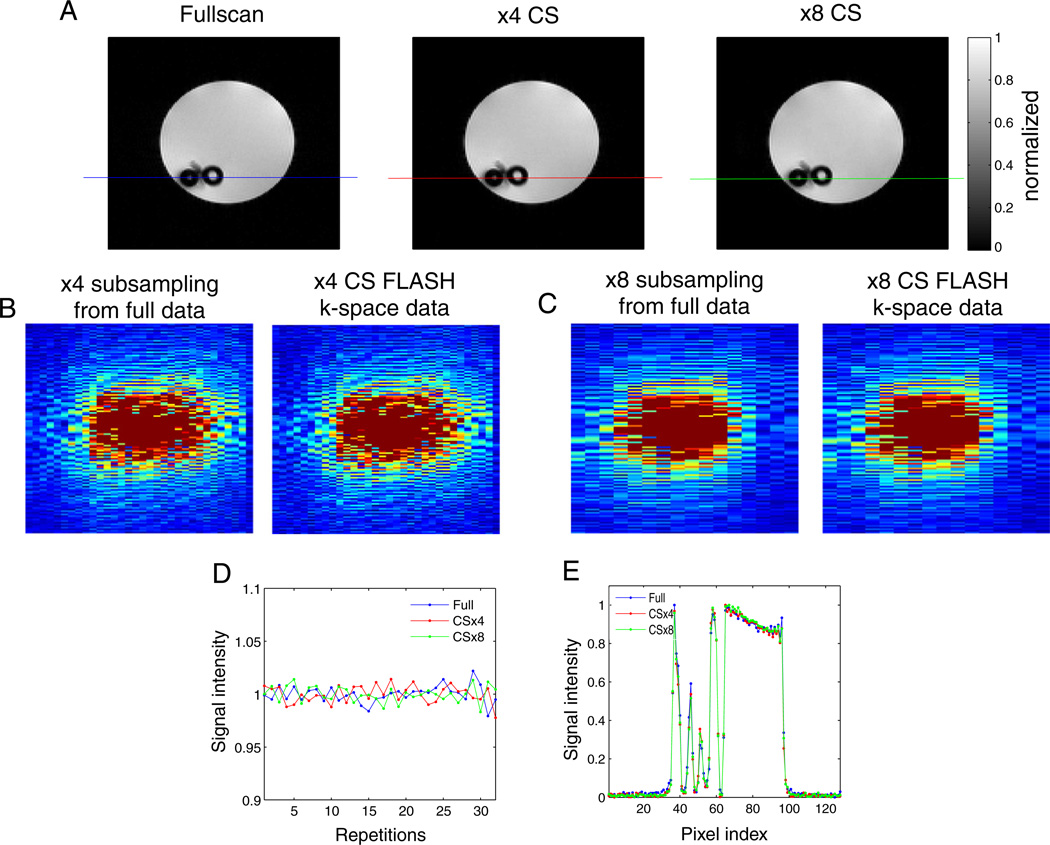
The modified CS-FLASH sequence with optimal parameters was tested on a water phantom as a control sample to establish the functionality of the desired phase encoding scheme and to evaluate the stability of the pulse sequence with repeated acquisitions with random jumps in phase encoding steps. Reconstructed MR images of a water phantom acquired with the newly modified CS-FLASH sequence at ×4 and ×8 subsampling, respectively, were compared to the fully sampled MR image acquired with the conventional FLASH sequence (Fig. 5A). The k-space data from ×4 and ×8 CS-FLASH acquisitions superimpose the subsampled ×4 and ×8 k-space data obtained from fully acquired data with optimized CS phase encoding schemes, confirming the exact acquisition of desired phase encoding signals with the new CS-FLASH sequence as shown in Fig. 5B – C. The intensity of the water signal in the spin density images appears stable throughout the 32 randomized, undersampled phase encoding steps of the image acquisition with the CS-FLASH sequence and comparable to that of the regular FLASH sequence (Fig. 5D). The water intensity profiles across the sample (as indicated by the lines in Fig. 5A) demonstrate that no spatial or intensity information is lost (Fig. 5E). The Pearson correlation coefficient comparing the subsampled MR images with the fully acquired MR image was 0.9985 for ×4 and 0.9986 for the ×8 undersamplings. A higher correlation of CS-reconstructed images with respect to fully sampled MR images than that obtained for tumors appears to be the result of the simple, homogeneous spatial and temporal nature of the water phantom. As demonstrated in Fig. 1, showing the relation between the fraction of coefficients and the fraction of total signal, 90% of the signal after compression was supported with far fewer coefficients in the water phantom than in a tumor (0.015% and 3.82% of the coefficients for the water phantom and tumor, respectively). This is a direct consequence of the much simpler nature of the water phantom, especially along the time dimension where it does not vary. With the l₂-norm normalized to 1, the l₁-norms of the water phantom and the animal tumor were 4.58×10⁻⁵ and 300×10⁻⁵, respectively. The smaller l₁-norm of the water phantom data quantifies the compression of the water phantom’s reconstruction compared to a tumor’s reconstruction under the metric assumed in the application of CS.

Fig. 5.

(A) The water phantom image from a regular FLASH sequence along with the CS-reconstructed MR image acquired with the new CS-FLASH sequence. (B–C) The k-space data from ×4 and ×8 CS-FLASH acquisitions and the subsampled ×4 and ×8 k-space data obtained from fully acquired data with optimized CS phase encoding schemes. (D) The intensity of the water signal in the spin density images throughout the 32 randomized, undersampled phase encoding steps of the image acquisition with the CS-FLASH. (E) The water intensity profiles across the sample (as indicated by the lines in A). The Pearson correlation coefficient comparing the subsampled MR images with the fully acquired MR image was 0.9985 for ×4 and 0.9986 for the ×8 undersamplings.

3.3.2 In vivo xenografts

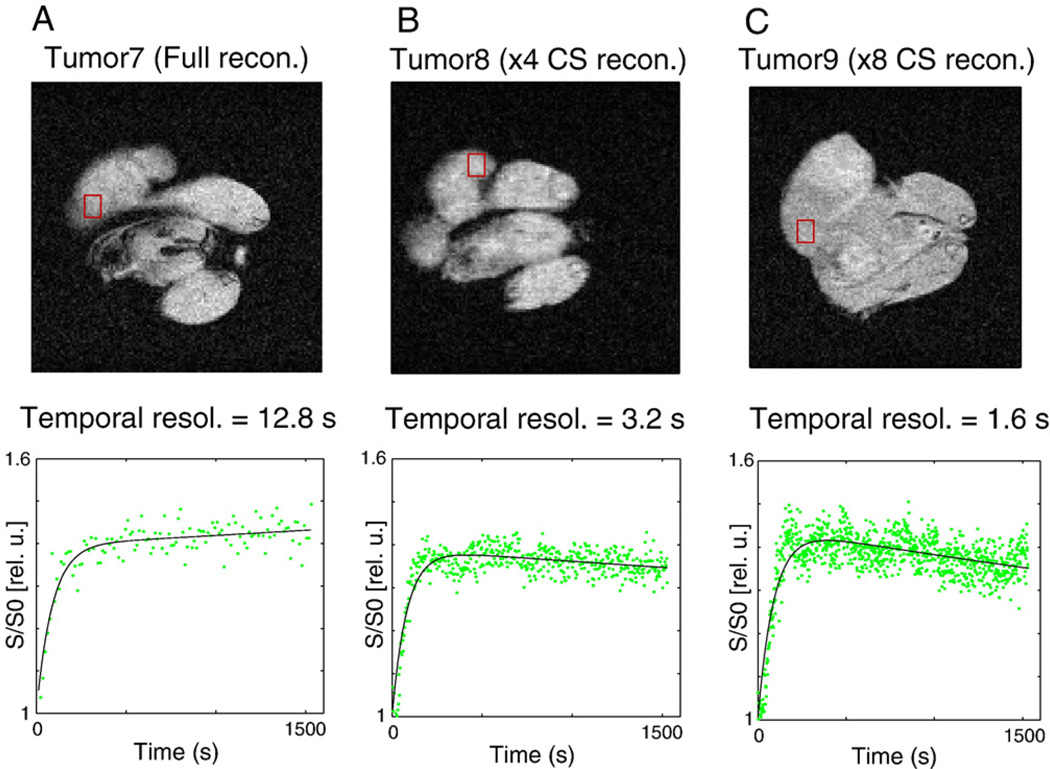
The in vivo experiments focused on demonstrating actual temporal and spatial resolution enhancement of DCE-MRI data in tumor xenografts. To test the actual temporal resolution improvement in vivo, DCE-MRI was performed on three different animals injected with Gd-DTPA using the conventional FLASH sequence, the ×4 CS-FLASH or the ×8 CS-FLASH at a fixed spatial resolution. Fig. 6A shows a fully sampled MR image and representative contrast uptake curves acquired using the conventional FLASH sequence with a matrix size of 128×128 (in-plane resolution of 234 µm × 234 µm) and a temporal resolution of 12.8 s. Fig. 6B – C shows CS-reconstructed MR images (234 µm × 234 µm in-plane resolution) and corresponding representative contrast uptake curves at ×4 and ×8 subsampling increasing the temporal resolutions to 3.2 s and 1.6 s, respectively. Here, three different tumors were used for the DCE-MRI experiment, and thus, the contrast uptake curves vary qualitatively for different acceleration factors. Nevertheless, the increase in the number of time points for the same total acquisition times (1640 s) clearly demonstrates the increased temporal resolution that is achieved with the CS-FLASH sequence and corresponding reconstruction as compared to the full acquisition and reconstruction.

Fig. 6.

(A) A fully sampled MR image and a representative contrast uptake curves acquired using the conventional FLASH sequence with a matrix size of 128×128 (in-plane resolution of 234 µm × 234 µm) and a temporal resolution of 12.8 s. (B–C) CS-reconstructed MR images (234 µm × 234 µm in-plane resolution) and corresponding representative contrast uptake curves at ×4 and ×8 subsamplings are shown with increased temporal resolutions of 3.2 s and 1.6 s, respectively.

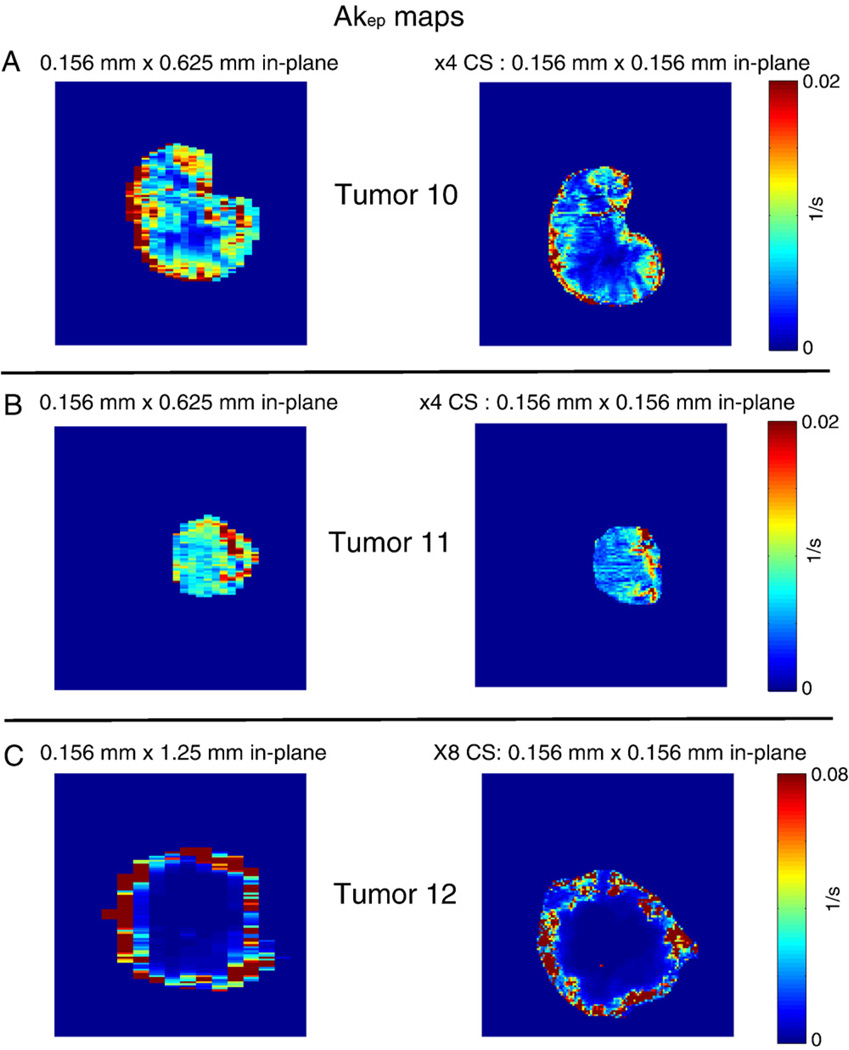
To test the spatial resolution improvement achieved at a fixed temporal resolution, a longitudinal DCE-MRI study was performed on three animals. Initial DCE-MRI experiments were performed with regular FLASH with a matrix size of either 128×32 or 128×16 with a 2-cm field of view. After clearance of the CA (5 h), DCE-MRI experiments were repeated with CS-FLASH (×4) and CS-FLASH (×8), with the same temporal resolutions (4.2 s) as the initial experiments. Ak_ep maps from the regular Fourier-reconstructed images with limited spatial resolution are shown for three tumors in Fig. 7 along with their corresponding Ak_ep maps from CS-reconstructed images for ×4 (Fig. 7A – B) and ×8 (Fig. 7C) undersamplings, respectively. As the tumor slices between DCE-MRI scans were difficult to align when repositioning the flank tumor in the MR coil, a quantitative comparison of Ak_ep values was not performed as before. However, qualitative agreements of the heterogeneous Ak_ep distribution between longitudinal scans are apparent, and the spatial resolution of the Ak_ep maps was increased by a factor of 4 or 8 in one spatial dimension (from 625 µm or 1.25 mm to 156 µm) at the same temporal resolution used for the full acquisitions. The Ak_ep values from the ×4 CS reconstruction of tumor 10 appeared to be lower than those of the preceding regular reconstruction (Fig. 7B). This was likely the result of slice misalignment or inconsistency in the physiological perfusion between the two longitudinal experiments, rather than an artifact of CS, considering the fact that each pair had identical temporal resolutions. A clear benefit of the CS-FLASH sequence and CS reconstruction over the traditional FLASH sequence was demonstrated by the increased spatial resolution.

Fig. 7.

Ak_ep maps from the regular Fourier-reconstructed images with limited spatial resolution are shown for three tumors along with their corresponding Ak_ep maps from CS-reconstructed images for ×4 (A–B) and ×8 (C) undersamplings, respectively.

4. Discussion and conclusions

We enhanced the spatial and temporal resolution for the acquisition of in vivo DCE-MRI by up to eight times with a newly modified Cartesian CS-FLASH sequence with multiple 2D slice selections. To the best of our knowledge, this is the first experimental implementations of a CS-optimized FLASH sequence in animal models showing improved spatial/ temporal resolution of DCE-MRI. Experiments were designed to show an enhancement of temporal resolution at fixed spatial resolution and vice versa with our CS-FLASH sequence. Improved spatial resolution of the Ak_ep map with equivalent temporal resolution demonstrates the clear advantage of the CS-FLASH sequence with better delineation of tumor regions and finer characterization of perfusion-driven tumor micro-environments. The immediate advantage of an improved temporal resolution is twofold: For one, in regions of fast contrast enhancement (e.g., arteries or leaky tumor vasculature), the temporal resolution can be increased to obtain enough points to accurately follow the pattern of the contrast uptake curve and avoid underestimating Ak_ep values, as demonstrated in Supplementary Fig. 2. Secondly, if the temporal resolution is already sufficient to fully characterize the contrast uptake curves, the extra time can be used to increase either spatial resolution or number of image slices.

As the FLASH sequence is widely accepted for the acquisition of T₁-weighted MR images in DCE-MRI for in vivo studies, the acceleration of this sequence has the potential to benefit ongoing preclinical and clinical investigations of tumor perfusion and permeability. For example, improved temporal/spatial resolution may benefit the measurement of the AIF in small animals, which is very challenging to obtain by conventional acquisition methods due to the extremely fast contrast uptake and the small arterial regions. Improved temporal/spatial resolution with CS-FLASH may increase the robustness of the AIF measurement in small animal studies and thus facilitate the application of the Tofts model [8] for preclinical studies. The observed sporadic intensity discrepancies between CS-reconstructed images and Ak_ep values with fully acquired images near the boundary of abruptly changing signal intensity must be further investigated. The results of such an investigation may prove useful for complementary tumor boundary refinement methods. In conclusion, the results presented here offer a promising and straightforward process for improving the spatial and temporal resolution of DCE-MRI with the standard CS algorithm for the modified FLASH sequence with multiple 2D slice selections, and may find potential applications to benefit many preclinical and clinical trials investigating tumor perfusion and permeability.

Supplementary materials related to this article can be found online at doi:10.1016/j.mri.2012.02.001.