Studying Parents and Grandparents to Assess Genetic Contributions to Early-Onset Disease

Abstract

Suppose DNA is available from affected individuals, their parents, and their grandparents. Particularly for early-onset diseases, maternally mediated genetic effects can play a role, because the mother determines the prenatal environment. The proposed maximum-likelihood approach for the detection of apparent transmission distortion treats the triad consisting of the affected individual and his or her two parents as the outcome, conditioning on grandparental mating types. Under a null model in which the allele under study does not confer susceptibility, either through linkage or directly, and when there are no maternally mediated genetic effects, conditional probabilities for specific triads are easily derived. A log-linear model permits a likelihood-ratio test (LRT) and allows the estimation of relative penetrances. The proposed approach is robust against genetic population stratification. Missing-data methods permit the inclusion of incomplete families, even if the missing person is the affected grandchild, as is the case when an induced abortion has followed the detection of a malformation. When screening multiple markers, one can begin by genotyping only the grandparents and the affected grandchildren. LRTs based on conditioning on grandparental mating types (i.e., ignoring the parents) have asymptotic relative efficiencies that are typically >150% (per family), compared with tests based on parents. A test for asymmetry in the number of copies carried by maternal versus paternal grandparents yields an LRT specific to maternal effects. One can then genotype the parents for only the genes that passed the initial screen. Conditioning on both the grandparents’ and the affected grandchild’s genotypes, a third log-linear model captures the remaining information, in an independent LRT for maternal effects.

Introduction

Designs based on the genotyping of affected individuals and their parents allow the detection of markers in linkage disequilibrium with disease genes (Spielman et al. 1993). The maternal genome may influence risk for the offspring through phenotypes expressed during pregnancy. Thus, the mother’s role as maintainer of the prenatal environment is complementary to her role as provider of genes. Maternally mediated genetic effects can be detected in two ways: risk-related alleles will have a higher frequency in mothers than in fathers of affected individuals, and transmissions from maternal grandparents to mothers of affected individuals will also appear distorted (Lande and Price 1989; Mitchell 1997; Wilcox et al. 1998).

Data from case-parent triads can be analyzed for offspring-mediated effects by the transmission/disequilibrium test (TDT) or by likelihood-based methods (Self et al. 1991; Schaid and Sommer 1993; Spielman et al. 1993; Weinberg et al. 1998). The log-linear model with a corresponding likelihood-ratio test (LRT) can be applied by standard software (e.g., SAS) and can detect maternally mediated effects (Wilcox et al. 1998), and imprinting (Weinberg 1999b).

For early-onset diseases—such as birth defects, autism, insulin-dependent diabetes, and schizophrenia—grandparents may often be available, and the present article will instead consider transmissions from grandparents to affected grandchildren. The idea is that, under a global null hypothesis in which there are neither maternally mediated nor offspring-mediated effects linked to the allele under study, transmissions from grandparents should be random under Mendelism. Under an alternative in which there are offspring-mediated effects, any susceptibility allele will be preferentially transmitted. Under alternatives involving maternally mediated phenotypic effects, there will be two measurable consequences for grandparents: maternal grandparents will have an elevated prevalence of the allele, compared with paternal grandparents; and, for a given set of grandparental genotypes, the transmissions will favor the maternal pathway.

A well-known problem plagues analyses of case-parent triads: any family in which both parents are homozygous is noninformative. The smallest possible such loss occurs in a population that is in Hardy-Weinberg equilibrium, with allele prevalence, p, of 1/2, in which, on average, a fraction p⁴ + 2p²(1 − p)² + (1 − p) ⁴ = 1/4 of families are useless. By contrast, many fewer families are noninformative when studying transmissions from grandparents; for example, with a p value of 1/2, the proportion of noninformative families is p⁸ + 2p⁴(1 − p)⁴ + (1 − p) ⁸ = 1/64. This marked improvement suggests that the use of grandparents could enhance statistical efficiency.

The present article proposes a design in which the unit of analysis is a family, consisting of one affected proband, two parents, and four grandparents. A log-linear model measures violations of Mendelian transmission, conditioning on grandparental mating types. With a large number of markers, an alternative two-stage strategy can be used. Computation of statistical power is enabled by χ² noncentrality parameters (Schaid 1999; Longmate 2001), on the basis of the expected value of the log likelihood.

Omnibus Procedure

Suppose a modest number of diallelic genes are to be studied and that all seven family members have been genotyped. Let MM, MF, FM, and FF denote the numbers of copies of the variant allele carried by the mother’s mother, the mother’s father, the father's mother, and the father's father, respectively. Let C, M, and F denote the numbers of copies carried by the child, the mother, and the father, respectively.

One can define grandparental mating types by analogy with parental mating types (Schaid and Sommer 1993). First, note that each grandparental couple falls into one of six mating-type categories, defined in the usual way. This produces a total of 6×6=36 pairs of mating types for the grandparents. The treatment as equivalent of reflections of mating type across the maternal versus the paternal grandparents yields 21 distinct grandparental categories (see table 1 for a listing). For example, we aggregate the grandparent sets—(MM = 1, MF = 2, FM = 0, FF = 1) and (MM = 0, MF = 1, FM = 2, FF = 1)—into the same grandparental-mating-type category. Conditioning on grandparental mating type is what will enable us to avoid the assumption of Hardy-Weinberg equilibrium and thereby to achieve robustness against population stratification. In the omnibus analysis, the triad (consisting of M, F, and C) is treated as the outcome, within each of the 21 categories of grandparental mating type. The number of combinations (i.e., families) possible with a diallelic gene is 435 (of which 148 are usefully distinct).

Table 1.

Probabilities for Various Mother-Father-Child Outcomes, Conditional on Grandparental Mating Types

	Probabilitya for Outcome
Grandparental Mating Type	000	010	011	100	101	021	201	121	122	211	212	110	111	112	222	NonzeroOutcomesb
00 00	32	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1
00 01	16	4	4	4	4	0	0	0	0	0	0	0	0	0	0	5
00 02	0	8	8	8	8	0	0	0	0	0	0	0	0	0	0	4
00 11	8	4	4	4	4	4	4	0	0	0	0	0	0	0	0	7
00 12	0	4	4	4	4	8	8	0	0	0	0	0	0	0	0	6
00 22	0	0	0	0	0	16	16	0	0	0	0	0	0	0	0	2
01 01	8	4	4	4	4	0	0	0	0	0	0	2	4	2	0	8
01 02	0	4	4	4	4	0	0	0	0	0	0	4	8	4	0	7
01 11	4	3	3	3	3	2	2	1	1	1	1	2	4	2	0	14
01 12	0	2	2	2	2	4	4	2	2	2	2	2	4	2	0	13
01 22	0	0	0	0	0	8	8	4	4	4	4	0	0	0	0	6
02 02	0	0	0	0	0	0	0	0	0	0	0	8	16	8	0	3
02 11	0	2	2	2	2	0	0	2	2	2	2	4	8	4	0	11
02 12	0	0	0	0	0	0	0	4	4	4	4	4	8	4	0	7
02 22	0	0	0	0	0	0	0	8	8	8	8	0	0	0	0	4
11 11	2	2	2	2	2	2	2	2	2	2	2	2	4	2	2	15
11 12	0	1	1	1	1	2	2	3	3	3	3	2	4	2	4	14
11 22	0	0	0	0	0	4	4	4	4	4	4	0	0	0	8	7
12 12	0	0	0	0	0	0	0	4	4	4	4	2	4	2	8	8
12 22	0	0	0	0	0	0	0	4	4	4	4	0	0	0	16	5
22 22	0	0	0	0	0	0	0	0	0	0	0	0	0	0	32	1

^aProbabilities shown are multiplied by 32.

^bNo. of outcomes for which probability is nonzero.

We wish to assess whether the genotypes for the families observed are consistent with simple Mendelian transmission. To do this, we categorize each of the families into 1 of the 148 nonzero cells, as shown in table 1. The proportions falling into the various cells within each grandparental mating type (i.e., each row of the table) should follow the multinomial distribution given by the probabilities in the table, under a null hypothesis in which the gene under study is not related to increased risk, either through linkage disequilibrium, direct effects, or maternal effects. Note that only two of the grandparental mating types are noninformative, because they allow only one outcome.

The corresponding likelihood can be derived, with some simplifying assumptions. Let k(MM,MF,FM,FF) denote the grandparental-mating-type index corresponding to the four observed genotypes: MM, MF, FM, and FF. After the application of Bayes's theorem, the probability P[M,F,C|k(MM,MF,FM,FF),child affected] is proportional to P[childaffected|M,F,C,k(MM,MF,FM,FF)] × P[M,F,C|k(MM,MF,FM,FF)]. Let S_M (R_C) denote the relative penetrance when the mother (offspring) carries M (C) copies, compared to the penetrance when the mother (offspring) carries no copies of the allele. Suppose that maternally mediated effects and offspring-mediated effects combine multiplicatively, so that P(disease|MM,MF,FM,FF,M,C) is proportional to the product, S_MR_C. Then, the above probability is proportional to S_MR_CP[M,F,C|k(MM,MF,FM,FF)].

One can fit a log-linear model to test the hypothesis that S_M=1=R_C for all M and C, as follows:

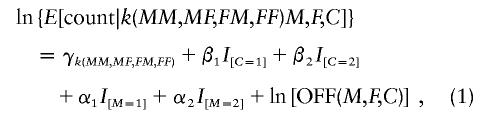where E denotes the expectation; the γ values are stratification parameters that impose the conditioning on grandparental mating types; I_[C=1], I_[C=2] and I_[M=1], I_[M=2] are indicator variables that are 1 (or 0) according to whether the bracketed equality holds true (or false); and OFF(M,F,C) is as provided in table 1. Here, ln[OFF(M,F,C)] is a term with its coefficient constrained to be 1 (called an “offset”). One can use standard Poisson regression software to fit this model to the 148 observed cell counts and to derive estimates and confidence intervals for R₁ = exp(β₁), R₂ = exp(β₂), S₁ = exp(α₁), and S₂ = exp(α₂).

One can test the global null hypothesis in the usual way, by constructing a 4-df χ² statistic on the basis of the comparison between the log-likelihood under the above formulation and the null log-likelihood obtained by omitting the genetic predictor variables. If only direct effects (or maternally mediated effects) are considered to be biologically plausible, then one can instead do a 2-df test, by including only the β (or the α) parameters, or a 1-df test, by entering only the variable C (or M), in place of the four indicator variables. The latter represents a natural generalization of the TDT to the study of transmission across multiple generations.

Noncentrality parameters for the test statistics were calculated for a range of specified scenarios, by calculating the log likelihood of expected data for assumed parameter values (Schaid 1999; Longmate 2001), for both stratified and Hardy-Weinberg populations. The noncentrality parameter allows the calculation of approximate power for any hypothetical number of families.

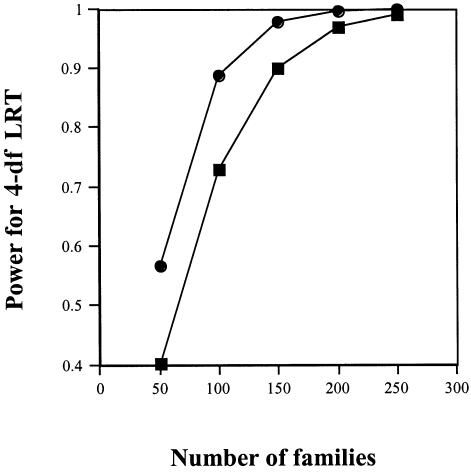
Figure 1 gives example power curves for the LRT (with 4 df). One (the upper curve) corresponds to a scenario with genetic population stratification (equal subpopulations with baseline risks of 0.01 and 0.03 and allele prevalences of 0.05 and 0.10, respectively), where S₁=1.5, S₂=2.0 and R₁=2.0, R₂=4.0.

Figure 1.

Power (omnibus test) for a study of families, for two scenarios: R₁, R₂, S₁, and S₂, respectively, of 2, 4, 1.5, and 2 (upper curve) and of 1, 3, 2, and 2 (lower curve). (Calculations assumed a stratified population in which half have a baseline risk of 0.01 and an allele prevalence of 0.05 and the other half have a baseline risk of 0.03 and an allele prevalence of 0.10.) The omnibus null hypothesis is that the allele under study is not linked or not associated with a risk-conferring gene and that there are no maternally mediated genetic effects.

Because of concern about sparseness of data when families are distributed over 148 cells, the power results for 100 families on the basis of the upper curve were confirmed by performing a simulation of 1,000 such studies. The empirical power based on simulations was 0.883, compared with the theoretical power (shown in the graph) of 0.887. Corresponding results for the lower curve were 0.718 (simulated power) and 0.729 (calculated power), values that are statistically compatible. The empirical size was also confirmed by simulating 1,000 studies under the corresponding null scenario. The rate of rejection of the null hypothesis was 0.042, which is compatible with the nominal 0.05. Thus, sparseness of the count data does not seem to be a problem.

One can use the expectation-maximization algorithm to include data from families in which some individuals were not available or in which there was evident nonpaternity, as has been described for case-parent data (Weinberg 1999a). Also, a straightforward extension of the same model permits assessment of imprinting (Weinberg et al. 1998).

When one wishes to screen multiple markers, an alternative three-test strategy may be preferred over the omnibus procedure. This strategy involves an initial phase in which only grandparents and the affected grandchild are genotyped and a subsequent phase in which genotyping may be done for the parents. Because we will be conditioning on grandparental genotypes, the proposed two-phase approach can be applied only to the subset consisting of complete families.

Phase I: Analyses Based Only on Grandparents and the Affected Grandchild

After DNA has been collected from affected individuals, their parents, and their grandparents, phase I analyses involve the genotyping of grandparents and affected grandchildren at all markers, setting aside the parental DNA. (Presumably, nonpaternity can be detected on the basis of markers in the grandparents, as compared with grandchildren.) The first test will assess maternally mediated effects, by the measurement of asymmetry in allele counts between the maternal and paternal grandparents. A second test, which is independent of the first, will then condition on the grandparental genotypes and assess transmissions from grandparents to affected grandchildren.

Test 1: Asymmetry between Maternal and Paternal Grandparents

The first test targets genetic effects that are maternally mediated. Let X denote the difference between the number of copies carried by maternal grandparents minus the number of copies carried by paternal grandparents—that is, X=MM+MF-FM-FF. Regardless of whether the alleles are in Hardy-Weinberg equilibrium, the numbers of families that fall into the various combinations of k(MM,MF,FM,FF) and X will follow a multinomial distribution. If the only marker genotype related to risk is that of the grandchild (and there is no imprinting) or if the marker is completely unrelated to risk, then, because there are no maternally mediated genetic effects, for each given grandparental mating type k(MM,MF,FM,FF), X and −X should be equally likely. Hence, δ is 0 in the following:

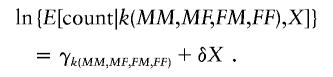As is always the case for LRTs, the model need be strictly true only under the null hypothesis. Under alternatives where there are maternally mediated genetic effects, the maternal grandparents will on average carry more copies of the susceptibility allele, pushing δ to be positive.

Testing this hypothesis (δ=0) is straightforward, using standard software and a χ² LRT statistic, with 1 df. One first fits a model with only indicator variates for the grandparental mating types and then fits a model augmented by inclusion of X. The difference between the deviances (−2 times the log-maximized likelihood) for the two nested models is asymptotically χ-squared under the null hypothesis that there are no maternally mediated genetic effects.

Assortative mating could theoretically produce false-positive test 1 results, because the mating-symmetry assumption underlies the approach. This issue goes away in phase II, in which a confirmatory test is not subject to this theoretical source of bias.

Test 2: Distortion in Transmissions from Grandparents to Affected Grandchildren

Let i=MM+MF and j=FM+FF be the total number of copies carried by the maternal and paternal grandparents, respectively. Under the composite null hypothesis of no linkage or no association for offspring-dependent genetic effects and no maternally mediated genetic effects, the probability that C is 0, 1, or 2, respectively, conditional on the grandparents and assuming Mendelian inheritance and nondifferential survival to the time of study (as required for the TDT), can be written as functions of i and j, as follows:

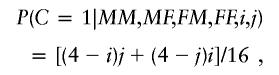and

To see how these are derived, consider, for example, that the probability that the grandchild inherits one copy of the allele of interest from the maternal side and one from the paternal side is just (i/4)(j/4), or ij/16, because, on each side of the family, each of the four alleles has an equal chance of transmission. Denote those conditional probabilities as OFF₀(i,j), OFF₁(i,j), and OFF₂(i,j), respectively.

Note that, because these three functions are each symmetric in the arguments i and j, the conditional probabilities for C do not depend on the value of X. This implies that test 2, which is based on the distribution of C conditional on the grandparental mating type but not on X, will be equivalent to one that conditions on X as well. Hence, test 2 is statistically independent of test 1, because it conditions on all the information used in test 1.

Consider now a hypothetical experiment in which one genotypes N individuals—at random—from the population, together with their four grandparents. Then, regardless of whether the gene is in Hardy-Weinberg equilibrium, the numbers of families that fall into the various cells corresponding to the possible (MM,MF,FM,FF,C) will follow the multinomial distribution described by the following log-linear model:

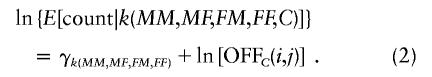If, on the one hand, instead of sampling at random, one samples only families in which the grandchild is affected by the disease of interest and the marker under study is not linked or not associated with the disease, then model (2) should again apply. If, on the other hand, the marker is associated with a relative penetrances of R₁ when one copy is inherited and R₂ when two copies are inherited (either because of direct effects or because the marker is in linkage disequilibrium with a disease gene), then the model becomes

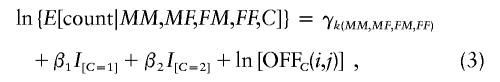where β₁ is ln(R₁) and β₂ is ln(R₂). An LRT of the hypothesis that β₁=β₂=0 can then be based on the difference in the deviance (−2 times the maximized log likelihood) between the maximum-likelihood fits under the two models.

For the test to be valid, the above model does not need to be (and will not be) literally true under all alternatives to the null hypothesis, but only under the null where both β values are 0. In general, the genetic model will not be known, and the 2-df approach is needed. However, more-restricted alternatives to the null hypothesis can be specified, if the investigator has reason to impose them.

As an alternative to model (3), one can simply fit variable C linearly, as is implicit under the TDT. Such an approach yields a 1-df test of a broad null hypothesis, that there are neither offspring-mediated nor maternally mediated genetic effects.

Phase II: Genotypes of the Parents Are Studied

In the next phase, parents are genotyped for markers that were identified in phase I analyses. Because test 3 conditions both on the grandparental genotypes and on the grandchild’s genotype (i.e., on all the information used in phase I analyses), this third test is statistically independent of both phase I tests.

Test 3: Maternal Effects, Based on Asymmetric Transmissions through Parents

The remaining information includes only the conditional probability for a set of parental genotypes, given the grandparents’ genotypes and the genotype of the affected child. Consider a scenario in which there may be both maternally mediated and offspring-mediated genetic effects. Let R₀(j) be the baseline risk in grandchildren descended from the jth grandparental mating type. Then, by standard manipulations of conditional probabilities,

where M′ and F′ range through all choices of 0, 1, and 2. Thus, a log-linear model that stratifies jointly on the genotypes of all four grandparents and also on the genotype of the affected grandchild will be valid and will permit maximum-likelihood estimation of the relative risks due to maternally mediated genetic effects:

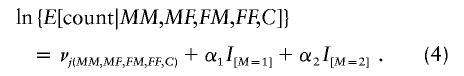Here, the ν_{j(MM,MF,FM,FF,C)} values denote stratification parameters that are distinct for all the distinct combinations of the 36 distinct pairs of maternal and paternal grandparents’ mating types, together with the grandchildren's genotypes that they could have produced. LRTs for maternal effects at this stage will be robust against bias due to population stratification and also resistant to possible assortative mating, because joint parental transmissions, rather than associations, are being assessed. Interestingly, there remains no information about the relative penetrances, R_C, following this conditioning. One can alternatively modify model (4) to perform a 1-df test, based on comparison of the models with and without the variable M.

Methods for Evaluation of Operating Characteristics of the Proposed Test Scheme

Test 1: Asymmetry across Maternal versus Paternal Grandparents

The grandparental-asymmetry test is compared with several alternative approaches to the study of maternally mediated effects. The proposed test resembles the 2-df test proposed by Weinberg et al. (1998) and Wilcox et al. (1998), except that, in the latter, asymmetry is assessed across the parents, rather than the grandparents, by inclusion of the variables I_[M=1] and I_[M=2] as predictors in a log-linear model for triads that stratifies on parental mating types. A related 1-df test for maternal effects is constructed by inclusion of the variable M in place of the two indicator variables. Also considered are results for the TDT proposed by Mitchell (1997), on the basis of transmissions from maternal grandparents to mothers, both in the 1-df form (corresponding to the TDT) and in the 2-df form.

Test 2: Transmission Distortion from Grandparents to Affected Grandchild

One can perform the test for apparent distortion in transmissions from grandparents to affected grandchildren as either a 1-df test or a 2-df test. Each test is compared with the corresponding test on the basis of transmissions from parents. Again, the 1-df parental-transmission test is closely related to the TDT, and power results approximate those for the TDT under a model where R₂ equals the square of R₁ (i.e., where the usual TDT should be at its best).

Test 3: Maternal Effects, Conditioning on Both Grandparental Genotypes and That of the Affected Grandchild

Powers are computed for various maternal-effects scenarios, with and without population stratification.

Results

Test 1 Results: Asymmetry across Grandparents

Table 2 provides χ² parameters and powers for selected scenarios. The parameters selected were intended to provide a variety of possible genetic models—including dominant, recessive, and allele-dose models—as when S₁ and S₂ are 2 and 4, respectively. All scenarios were based on the same population, with genetic stratification. One subpopulation had an allele prevalence of 0.05 and a baseline penetrance of 0.01, and a second subpopulation (equal in size) had an allele prevalence of 0.10 and a penetrance of 0.03. Mating was assortative, confined to the respective subpopulations. This construction produces an extreme form of genetic population stratification, enabling us to confirm the robustness of the approach.

Table 2.

Noncentrality Parameters and Powers for Testing for Maternally Mediated Genetic Effects by Using LRTs Based on Either Grandparents, Parents, or a Mother and Her Parents

	χ2 Noncentrality Parameter (Power)b for
		Parental Asymmetry Testd with		Maternal Grandparents Teste with
Scenarioa	Grandparental Asymmetry Testc with 1 df	1 df	2 df	1 df	2 df
1, 1, 1, 1	.0000 (.05)	.0000 (.05)	.0000 (.05)	.0000 (.05)	.0000 (.05)
2, 2, 1, 1	.0000 (.05)	.0000 (.05)	.0000 (.05)	.0103 (.30)	.0104 (.23)
1, 1, 2, 2	.0212 (.54)	.0381 (.79)	.0400 (.72)	.0368 (.77)	.0408 (.73)
1, 1, 3, 3	.0603 (.93)	.1030 (1.00)	.1078 (.99)	.0969 (.99)	.1098 (.99)
1, 1, 2, 4	.0283 (.66)	.0492 (.88)	.0492 (.81)	.0498 (.88)	.0498 (.81)
1, 1, 3, 9	.0859 (.99)	.1375 (1.00)	.1375 (1.00)	.1424 (1.00)	.1424 (1.00)
1, 1, 1, 2	.0003 (.06)	.0006 (.06)	.0027 (.09)	.0006 (.06)	.0040 (.12)
1, 1, 1, 3	.0012 (.08)	.0023 (.10)	.0083 (.19)	.0025 (.11)	.0127 (.28)

^aThe numbers denoting each scenario represent R₁, R₂, S₁, and S₂, respectively.

^bThe χ² noncentrality parameter is found by multiplying the entry in the table by the number of families to be studied. Example powers (for a level-.05 test) are given in parentheses for studies with 200 families. Calculations assumed a stratified population in which half have a baseline risk of .01 and an allele prevalence of .05 and the other half have a baseline risk of .03 and an allele prevalence of .10.

^cTest 1.

^dWilcox et al. 1998.

^eMitchell 1997.

The noncentrality parameters in the first row of table 2 show that under the global null all tests achieve their nominal type I error rates of 0.05. This behavior was confirmed by simulations (not shown).

Under alternatives to the null hypothesis, one computes approximate power for any hypothetical number of families by multiplying the parameters given by the number of families and using the corresponding noncentral χ² distribution to calculate the probability of exceeding the critical value for the selected α level. For example, for 200 families, if S₁ and S₂ (the relative risks associated with one and two maternal copies, respectively) are 2 and 4, then the power of the 1-df grandparental asymmetry test is 0.66, which is the area under the upper tail (past the 0.05 critical value, 3.84) of the noncentral χ² distribution with 1 df and noncentrality parameter (0.0283)(200) = 5.66. Evidently, the four tests based on parents are similar in power, and the grandparental asymmetry test is less powerful.

Note that the test based on transmissions from maternal grandparents to the mother is not specific to maternally mediated effects. For example, with 200 families, R₁=R₂=2, and no maternally mediated effects (table 2, second row), this test rejects with probability 0.30. This elevated rejection rate happens because sampling is restricted to families in which the grandchild has the disease, which weights the sampling in favor of families in which the deleterious allele did transmit through the parents. By contrast, effects mediated through the grandchild’s genotype do not inflate the type I error rate for either of the two symmetry-based tests.

Test 2 Results: Transmissions from Grandparents

Simulations (not shown) confirm that, under the global null hypothesis, the 2-df test with nominal size 0.05 has empirical size consistent with 0.05. However, if there are maternally mediated effects, then they will produce an apparent distortion in transmission to the grandchild, because the grandchild will (via the mother) have inherited the susceptibility allele more often than the null model predicts. Thus, in this setting, the null hypothesis must be broad, specifying that there are neither offspring-mediated nor maternally mediated genetic effects.

Table 3 gives χ² parameters for various scenarios. Power for 200 families is good for modest effects of the inherited gene and less impressive for maternally mediated effects. The strongest benefit is realized when there are both offspring genotype effects and maternal effects, as seen in the last two rows of table 3.

Table 3.

Noncentrality Parameters and Powers for TDTs Based on Grandparents as Compared with Parents, Together with Asymptotic Relative Efficiencies^[Note]

	χ2 Noncentrality Parameter (Power)b for
	Grandparental-Transmission Testd with		Parental-Transmission Test with
Scenarioa	1 df	2 df	1 dfe	2 df	AREc for Grandparents vs. Parents
1, 1, 1, 1	.0000 (.05)	.0000 (.05)	.0000 (.05)	.0000 (.05)	…
2, 2, 1, 1	.0576 (.92)	.0632 (.90)	.0368 (.77)	.0408 (.73)	1.57
2, 4, 1, 1	.0785 (.98)	.0785 (.95)	.0498 (.88)	.0498 (.81)	1.58
1, 1, 2, 4	.0092 (.27)	.0093 (.21)	.0000 (.05)	.0000 (.05)	∞
1, 1, 3, 9	.0276 (.65)	.0282 (.56)	.0000 (.05)	.0000 (.05)	∞
1, 3, 1, 1	.0037 (.14)	.0177 (.37)	.0025 (.11)	.0127 (.28)	1.48
1, 3, 2, 2	.0289 (.67)	.0479 (.80)	.0051 (.17)	.0216 (.44)	5.67
2, 4, 1.5, 2	.1248 (1.00)	.1248 (1.00)	.0582 (.93)	.0582 (.87)	2.14

Note.— Calculations assumed a stratified population in which half have a baseline risk of .01 and an allele prevalence of .05 and the other half have a baseline risk of .03 and an allele prevalence of .10.

^aThe numbers denoting each scenario represent R₁, R₂, S₁, and S₂, respectively.

^bExample powers (for a level-.05 test) are given in parentheses for studies with 200 families.

^cBased on 1-df LRTs. ARE = asymptotic relative efficiency.

^dTest 2.

^eBased on the log-linear model with parental mating type and C as predictors.

The ratios of noncentrality parameters for two tests provide their large-sample relative efficiencies—that is, the ratio of sample sizes that would be required for the respective two to achieve a particular power at any specified α level. Under an assumed model with R₁=2, R₂=4, S₁=1, S₂=1, and Hardy-Weinberg equilibrium, the asymptotic relative efficiencies for the 1-df test based on grandparents, as compared with the 1-df test based on the case-parent triads, ranged from 1.5 to 1.6 for allele prevalences <0.5.

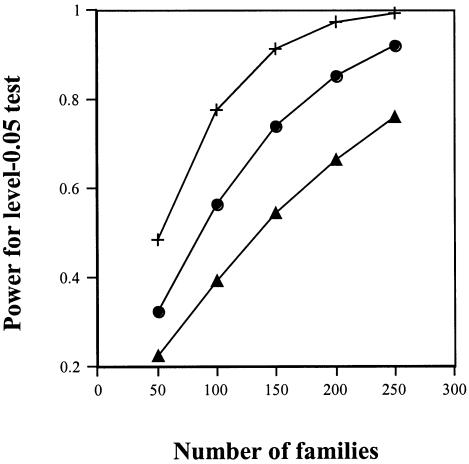
Figure 2 displays power curves for the parent-based LRT and the grandparent-based LRT, both with 1 df (using variable C). These curves use the calculated noncentrality parameters (and an α level of 0.05), under a scenario in which R₁ is 2, R₂ is 3, and the prevalence of the variant allele is 0.05.

Figure 2.

Power for R₁=2, R₂=3, S₁=1, and S₂=1, for the 1-df grandparents test (middle curve) (i.e., test 2) as compared with the 1-df parents test (lowest curve) and the 1-df grandparents test (with C as predictor variable) in the presence of a maternal-effect background (upper curve) where S₁=1.5 and S₂=2.0. (Prevalence of variant allele is 0.05, with no population stratification.)

Test 3 Results

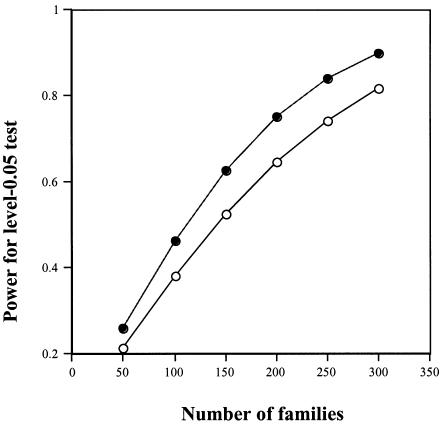
Simulations (not shown) confirm that test 3 is specific to maternally mediated effects and that the empirical type I error rate is consistent with nominal size 0.05 under the maternal null model. Figure 3 displays power curves for this test, for choices of S₁ and S₂, and for a scenario with population stratification (two equal-sized subpopulations with baseline risks of 0.01 and 0.03 and allele prevalences of 0.05 and 0.10). The assumed α level is 0.05.

Figure 3.

Power for the conditional maternal-effects test (i.e., test 3, with 1 df), conditional on the genotypes of both grandparents and the affected grandchild. Scenarios are R₁=1, R₂=1, S₁=2, and S₂=4 (upper curve) and R₁=1, R₂=1, S₁=2, and S₂=2 (lower curve). (Calculations assumed a stratified population in which half have a baseline risk of 0.01 and an allele prevalence of 0.05 and the other half have a baseline risk of 0.03 and an allele prevalence of 0.10.)

Discussion

When the disease of interest occurs early enough in life that grandparents are available, the proposed design offers improved power over approaches that use affected individuals and their parents. Although inclusion of three generations of individuals increases the number of distinct possible families (with a diallelic gene) from 15 to 435 (which can be grouped for analysis into 148 meaningfully distinct and informative family types), a log-linear model can still be used to detect apparent transmission distortions. Simulations suggest that sparseness of the resulting count data is not a problem.

The intuition underlying the proposed three-test strategy is as follows: In the first test, one can look for evidence for maternally mediated effects, by assessing the asymmetry between the genotype frequencies for maternal compared with paternal grandparents of affected individuals. In the second test, one can condition on those grandparental genotypes and look for apparent distortion in transmissions from grandparents to affected grandchildren; such distortion does not admit an unambiguous interpretation because it can reflect both maternally mediated effects and offspring-mediated effects, but, in general, the transmission test is more sensitive to the latter than to the former. A third test (which can be omitted, particularly when maternal effects were not found in the first test) then conditions on both the grandparental genotypes and the genotype of the affected grandchild; apparent distortions away from equal transmission through the mother and through the father can provide further evidence of maternally mediated effects. These three tests are mutually independent, because the information in the data has been partitioned into three orthogonal components.

The fact that, once we condition on the genotypes of grandparents and their grandchild, the distribution of parental genotypes depends only on maternal effects and not on direct, offspring-mediated effects reveals that, once we have studied the grandparents and grandchild, parents provide no additional information for genes that act only through direct, offspring-mediated mechanisms. Hence, one may reasonably elect to stop after phase I and not genotype parents at all.

When many markers are to be considered and maternal effects are judged likely (as with a pregnancy complication), the proposed approach allows one to screen for maternal effects in phase I, in which most of the unrelated markers can be eliminated, because they fail to reach statistical significance in test 1. Because the approach is sequential and the tests are statistically independent, the composite type I error rate for maternally mediated effects is a product: if tests 1 and 3 have α levels of 0.1 and 0.2, respectively, then the composite type I error rate is 0.02; by contrast, if both were always performed, with markers considered significant if significant in either test, then the type I error rate would instead be 1-(.9)(.8), or 0.28, yielding many false positives. In this way, the sequential design, with independent testing, alleviates the multiple-testing problem.

The power results for the detection of maternally mediated genetic effects by using tests 1 and 3 were disappointing. However, because these tests are independent and we can multiply their type I error rates, it makes sense to set both α levels high. If tests 1 and 3 are performed at α levels 0.10 and 0.20, then the powers would be substantially higher than those shown (which used an α level of 0.05). (The power for the sequential procedure for the detection of maternal effects is, however, the product of the two powers.) More quantitative conclusions regarding optimization of the design are beyond the scope of the present article.

Although 67% more assays are required to genotype grandparents and grandchildren than to genotype parents and children, calculations of the χ² noncentrality parameters revealed that the statistical relative efficiency (for the 1-df LRT) for transmission studies based on grandparents (test 2) versus the 1-df test based on parents is typically >1.5. This observation is important in settings in which a rare disease is to be studied and identification and recruitment of a sufficient number of families is the limiting challenge, rather than the cost of genotyping.

As an example, suppose that there are no maternally mediated effects, but only direct effects due to the grandchild’s genotype, and suppose that we can afford to genotype 450 people. The results of the present article show that a study of 90 case subjects and their grandparents (5×90 genotypes) is nearly as informative as would be a study of 150 case subjects and their parents (3 × 150 genotypes) analyzed via the TDT. The point is that it may be far more feasible to find 90 affected families than 150 affected families. If there are also maternal effects, then the 90 families with grandparents will provide a much more powerful transmission test than would 150 families with only parents.

A concern that arises in planning a study that uses grandparents is that, for some families, the grandparents will not all be available. However, if they are missing for reasons unrelated to the genes under study, one can make good use of the incomplete family sets, by applying the expectation-maximization algorithm, as described elsewhere. Although simulations of such a strategy are beyond the scope of the present article, the power results would be expected to resemble those seen in the case-parents context (Weinberg 1999a), in which one can capture much of the information from incomplete families.

Especially for conditions that occur during development or early life, one should consider the possibility that the gene under study is imprinted—that is, the variant allele has a different effect depending on whether it was maternal or paternal in origin. Any genes identified through the asymmetry tests (1 and 3) could be maternally mediated but could also be subject to imprinting. This possibility can be explored by extending the omnibus model (eq. [1]) and by performing LRTs for imprinting.

In general, the investigator who discovers alleles of apparent importance in tests 1 or 2 will often wish to genotype the parents and fit the omnibus model (eq. [1]) and its extensions. This strategy will allow the analyst to fully use incomplete families, to explore parent-of-origin effects and joint effects of the maternal and offspring genotypes, and to estimate relative penetrances, by using all of the data.