Critical Damping Conditions for Third Order Muscle Models: Implications for Force Control

Short abstract

Experimental results presented in the literature suggest that humans use a position control strategy to indirectly control force rather than direct force control. Modeling the muscle-tendon system as a third-order linear model, we provide an explanation of why an indirect force control strategy is preferred. We analyzed a third-order muscle system and verified that it is required for a faithful representation of muscle-tendon mechanics, especially when investigating critical damping conditions. We provided numerical examples using biomechanical properties of muscles and tendons reported in the literature. We demonstrated that at maximum isotonic contraction, for muscle and tendon stiffness within physiologically compatible ranges, a third-order muscle-tendon system can be under-damped. Over-damping occurs for values of the damping coefficient included within a finite interval defined by two separate critical limits (such interval is a semi-infinite region in second-order models). An increase in damping beyond the larger critical value would lead the system to mechanical instability. We proved the existence of a theoretical threshold for the ratio between tendon and muscle stiffness above which critical damping can never be achieved; thus resulting in an oscillatory free response of the system, independently of the value of the damping. Under such condition, combined with high muscle activation, oscillation of the system can be compensated only by active control.

Introduction

One's ability to exert controlled forces on the environment, such as when manipulating fragile objects, is very important in everyday life. This suggests that force regulation is a necessary component of motor control. In robotics, an effective way to implement force control is by imposing a low contact impedance with critical damping, and using admittance control to regulate force output [1,2]. Human limbs can be modeled as second order mechanical systems, under the assumption that tendons are much stiffer than muscle fibers. The mechanical properties of muscle fibers alone render the implementation of the aforementioned direct force control strategy as not efficient. Several studies have demonstrated that the exertion of force onto the environment results in an increase in muscle stiffness [3–5] and a reduction of muscle damping to under critical values [6,7].

Modeling tendons and contractile elements independently requires higher than second order muscle-tendon models [8]. The presence of a tendon elastic element favors an oscillatory response to external disturbances that normally needs to be eliminated [9]. We demonstrated that a higher order model always exhibits an oscillatory free response and cannot be critically dampened for mechanical parameters included within the normal physiological range. This requires the force controller implemented by the central nervous system (CNS) to employ active feedback and feed-forward regulation. We propose that oscillations, whether part of an external disturbance or of the system's response, can be actively compensated for by the CNS with a position control approach, as long as a predictive model of the perturbation, and an internal model of the system's biomechanics are available. This model of control is in agreement with findings previously published by our group that showed how the implementation of an internal feed-forward model trajectory can be part of a force-regulation strategy [10].

Methods

Given $\overrightarrow{q}\left(t\right)$ as a vector of generalized variations of position coordinates (angles, Cartesian coordinates, muscle lengths, etc.) describing the motion of a mechanical system, we can define Dⁿq as the set representing the position coordinates variations and their derivatives with respect to time up to the n-th order so that

$$D^{n}q=(\frac{d^{n}q}{{\mathit{dt}}^n},...,\frac{d^{2}q}{{\mathit{dt}}^2},\frac{d^{1}q}{{\mathit{dt}}^1},q)$$

in general $n\in \mathbf{Q}$ [11].

A mechanical system of given inertia must comply with the Lagrange–d'Alembert principle (see Figs. 1(c), 2(b),2(d)) so that

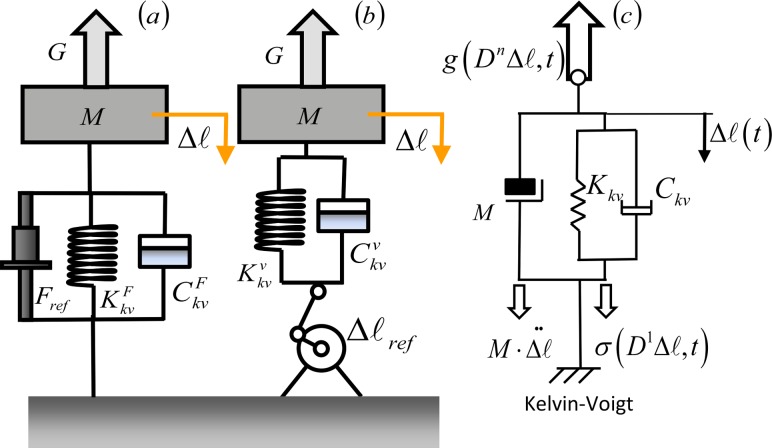
Fig. 1.

Force control models of second-order mechanical systems. (a) Direct force control. (b) Indirect force control via position control. (c) Generalized impedance model of a second order mechanical system indicating the force fields that appear in the d'Alembert equation, Eq. (1).

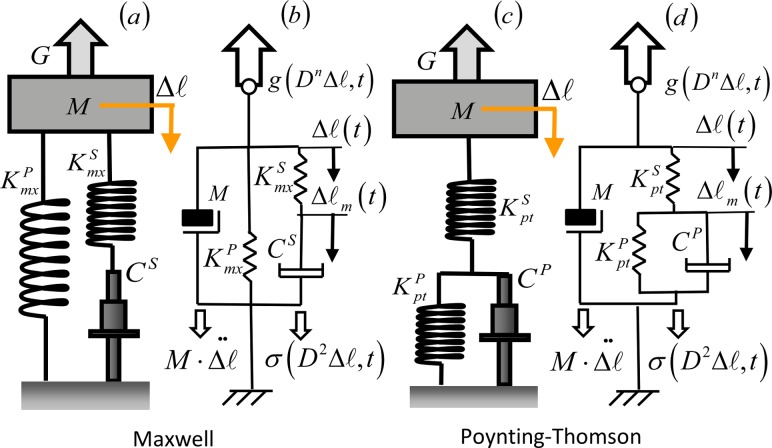
Fig. 2.

Third-order mechanical models of muscle-tendon systems. (a) Maxwell model (b) generalized impedance schematics of Maxwell model (c) Poynting-Thomson model (d) generalized impedance schematics of the PT model. (b) and (d) indicate the force fields that appear in the d'Alembert equation, Eq. (1). Each force field is a function of the mechanical paramenters of the elements that generate it.

$$M(q,t)\frac{d^2}{{\mathit{dt}}^2}\left(\overrightarrow{q}\left(t\right)\right)+\overrightarrow{\sigma }(D^{n}q,t)=\overrightarrow{g}(D^{n}q,t)$$ (1)

where M(q, t) is the inertial matrix of the system in the chosen coordinate frame, $\overrightarrow{g}(D^{n}q,t)$ is the external force field, and $\overrightarrow{\sigma }(D^{n}q,t)$ is the internal force field generated by the mechanical network [12]. Each force field should be expressed in any frame of reference, through a Jacobian transformation, maintaining the structure of Eq. (1) unaltered [13]. We will provide models of a muscle-tendon system acting on a limb through a single joint and use the following variable nomenclature: $\overrightarrow{x}$ represents the trajectory of the controlled endpoint of the limb as a vector in a Cartesian, inertial reference system, ${\theta }^{\to }$ is the joint angle, and $\overrightarrow{\Delta \ell }$ represents the change in length of the muscle-tendon system, which can be due to muscle activation, or the consequence of a displacement perturbation at the endpoint.

When the muscle-tendon system is modeled as a second order Kelvin-Voigt (KV) system, represented in Fig. 1(c), the internal viscoelastic force field $\sigma (D^n\Delta \ell ,t)$ is described by the following differential equation:

$$\sigma (D^1\Delta \ell ,t)=-C_{\mathit{kv}}·\stackrel{.}{\Delta \ell }\left(t\right)-K_{\mathit{kv}}·\Delta \ell \left(t\right)$$ (2)

Direct Versus Indirect Force Control in Second-Order Systems.

Figure 1 shows the implementation of direct and indirect force control on a one degree-of-freedom (DOF) mass-muscle-tendon system, modeled as a second order KV. The parameter $K_{\mathit{kv}}^F$ represents the lumped stiffness of the muscle-tendon system. In a direct force control setup (Fig. 1(a)), the reference force F _ref(t) is applied to the inertial load, which includes the inertia of the limb. When a positional perturbation Δx(t) is applied to the endpoint, it results in a muscle length variation $\Delta \ell \left(t\right)$, and the stiffness is modulated to maintain the total applied force constant. On the other hand, an indirect force control can be implemented using a position control strategy (Fig. 1(b)): when a displacement perturbation Δx(t) is applied, a compensating variation of the muscle length $\Delta {\ell }_{\mathrm{ref}}\left(t\right)$ is imposed to generate the compensating force $K_{\mathit{kv}}^v\Delta {\ell }_{\mathrm{ref}}\left(t\right)+C_{\mathit{kv}}^v\stackrel{.}{\Delta \ell }{}_{\mathrm{ref}}\left(t\right)$ and maintain the total applied force constant. When the control system cannot track the force at a high enough rate, indirect force control requires a priori knowledge of the perturbation Δx(t) to preplan the variation of muscle length accordingly in a feed-forward fashion. In this case, to provide an accurate compensating force, the control system must rely on an internal model of its dynamics. A low $K_{\mathit{kv}}^F$ is preferable for a direct force control strategy, while indirect force control benefits from higher $K_{\mathit{kv}}^v$ for the endpoint trajectory to accurately comply with the displacement disturbance through a controlled variation of the muscle length. The oscillations generated by the disturbance are passively eliminated when $C_{\mathit{kv}}$ is above the critical limit. This is particularly important when a direct force control strategy with low stiffness is implemented. An indirect force control requires prediction and tracking of position disturbances to properly regulate force; therefore the passive elimination of residual intrinsic oscillations is less critical, as long as the controller can account for them; therefore the system can be underdamped.

Third Order Model.

A more realistic representation of the mass-muscle-tendon system than the KV includes independent models of the physical properties of tendon and muscle fibers. Models typically used are linearized Hill models [8] defined in either Maxwell (MX) or Poynting-Thomson (PT) form, both of which are extensions of the KV model. In Fig. 2(a) the muscle-tendon system is represented as a Maxwell model with the contractile element C^S (including muscle damping) in series with the elastic element $K_{\mathrm{mx}}^S$ (tendon stiffness), both parallel to the elastic element $K_{\mathrm{mx}}^P$ (muscle stiffness). Figure 2(c) represents the muscle-tendon system as a Poynting-Thomson (PT) model with element $K_{\mathrm{pt}}^S$ (tendon stiffness) in series with the parallel of $K_{\mathrm{pt}}^P$ (muscle stiffness), and C^P (contractile element incorporating muscle damping). These two linear, time-invariant models are mechanically equivalent [14]. We show that the interaction of either muscle-tendon model with an inertial system (e.g., the mass of bones and connective tissues) give rise to a third order system. Equation (1) is a general model for a time-variant linear system whose oscillating solutions can be found both in the time and frequency domains by means of classical control theory. Assuming the system is stationary (i.e., the resonant angular frequency ω(t) is constant), classical Laplace transform techniques can be used to recast Eq. (1),

$$\mathrm{M}{s}^2\overrightarrow{\Delta \mathrm{L}}\left(s\right)+\overrightarrow{\Sigma }\left(s\right)=\overrightarrow{\mathrm{G}}\left(s\right)$$ (3)

where M, $\overrightarrow{\Delta \mathrm{L}}$, $\overrightarrow{\Sigma }$, and $\overrightarrow{\mathrm{G}}$ are the Laplace transforms of the term M, $\overrightarrow{\Delta \ell }$, $\overrightarrow{\sigma }$, $\overrightarrow{g}$ expressed in the time domain. Dividing both members of Eq. (3) by the Laplace transform of the displacement perturbation we can express the transfer function of the system to external displacement as

$$\mathrm{M}{s}^2+\frac{\overrightarrow{\Sigma }\left(s\right)}{\overrightarrow{\Delta \mathrm{L}}\left(s\right)}=\frac{\overrightarrow{\mathrm{G}}\left(s\right)}{\overrightarrow{\Delta \mathrm{L}}\left(s\right)}$$ (4)

For the PT model shown in Fig. 2(d), the force applied to the tendon (${\mathrm{\Sigma }}_{\mathrm{pt}}^S\left(s\right)=K_{\mathrm{pt}}^S·\Delta {\mathrm{L}}_T\left(s\right)$) and the force at the muscle (${\mathrm{\Sigma }}_{\mathrm{pt}}^P=C^{P}s·\Delta {\mathrm{L}}_m+K_{\mathrm{pt}}^P·\Delta {\mathrm{L}}_m$) are the same and the total elongation of the muscle-tendon system is the sum of the elongations of the muscle and tendon (i.e., $\Delta \mathrm{L}=\Delta {\mathrm{L}}_m+\Delta {\mathrm{L}}_T$). Thus we can write the following expression:

$$\frac{\Sigma \left(s\right)}{\Delta \mathrm{L}\left(s\right)}=\frac{K_{\mathrm{pt}}^S{Z}_{\mathrm{pt}}^P}{K_{\mathrm{pt}}^S+Z_{\mathrm{pt}}^P}=\frac{K_{\mathrm{pt}}^S(C^{P}s+K_{\mathrm{pt}}^P)}{C^{P}s+K_{\mathrm{pt}}^P+K_{\mathrm{pt}}^S}$$ (5)

Substituting Eq. (5) into Eq. (4), and multiplying both members by $s+(K_{\mathrm{pt}}^P/C^P)+(K_{\mathrm{pt}}^S/C^P)$ we obtain

$$(\mathrm{M}{s}^3+\frac{\mathrm{M}}{C^P}(K_{\mathrm{pt}}^S+K_{\mathrm{pt}}^P)s^2+K_{\mathrm{pt}}^{S}s+\frac{K_{\mathrm{pt}}^S·K_{\mathrm{pt}}^P}{C^P})=\frac{\overrightarrow{\mathrm{G}}\left(s\right)}{\overrightarrow{\Delta \mathrm{L}}\left(s\right)}$$ (6)

During a free response, the external force is null (i.e., $g(D^n\Delta \ell ,t)=0$) so the governing equation of a PT model in the time domain is [15]

$$M·\stackrel{\dots }{\Delta \ell }+\frac{M}{C^P}(K_{\mathrm{pt}}^S+K_{\mathrm{pt}}^P)\stackrel{..}{\Delta \ell }+K_{\mathrm{pt}}^S\stackrel{.}{\Delta \ell }\hspace{1em}+\hspace{1em}\frac{K_{\mathrm{pt}}^S·K_{\mathrm{pt}}^P}{C^P}\Delta \ell =0$$ (7)

The governing equation of Maxwell models can be obtained in a similar way: the impedance of the serial elements is

$$Z_{\mathrm{mx}}^S=\frac{{\mathit{sC}}^S{K}_{\mathrm{mx}}^S}{{\mathit{sC}}^S+K_{\mathrm{mx}}^S}$$

and the transfer function of the viscoelastic system is

$$\frac{\Sigma \left(s\right)}{\Delta \mathrm{L}\left(s\right)}=K_{\mathrm{mx}}^p+\frac{{\mathit{sC}}^S{K}_{\mathrm{mx}}^S}{{\mathit{sC}}^S+K_{\mathrm{mx}}^S}$$ (8)

Substituting Eq. (8) into Eq. (4), multiplying both terms by $s+(K_{\mathrm{mx}}^S/C^S)$, and transforming in the time domain we obtain the governing differential equation of a Maxwell system in the following form:

$$M·\stackrel{\dots }{\Delta \ell }+\frac{M}{C^S}{K}_{\mathrm{mx}}^S\stackrel{..}{\Delta \ell }+(K_{\mathrm{mx}}^S+K_{\mathrm{mx}}^P)\stackrel{.}{\Delta \ell }+\frac{K_{\mathrm{mx}}^S·K_{\mathrm{mx}}^P}{C^S}\Delta \ell =0$$ (9)

The PT and MX systems are equivalent when the corresponding coefficients of Eq. (7) and Eq. (9) are equal [14],

$$\begin{array}{ccc}\multicolumn{1}{c}{\{\begin{array}{c}\multicolumn{1}{c}{\frac{K_{\mathrm{mx}}^S}{C^S}=\frac{(K_{\mathrm{pt}}^S+K_{\mathrm{pt}}^P)}{C^P}}\\ \multicolumn{1}{c}{K_{\mathrm{mx}}^S+K_{\mathrm{mx}}^P=K_{\mathrm{pt}}^S}\\ \multicolumn{1}{c}{\frac{K_{\mathrm{mx}}^S·K_{\mathrm{mx}}^P}{C^S}=\frac{K_{\mathrm{pt}}^S·K_{\mathrm{pt}}^P}{C^P}}\end{array}}& \hfill \Rightarrow \hfill & \hfill \{\begin{array}{c}\multicolumn{1}{c}{K_{\mathrm{mx}}^P=\frac{K_{\mathrm{pt}}^S·K_{\mathrm{pt}}^P}{K_{\mathrm{pt}}^S+K_{\mathrm{pt}}^P}}\\ \multicolumn{1}{c}{K_{\mathrm{mx}}^S+K_{\mathrm{mx}}^P=K_{\mathrm{pt}}^S}\\ \multicolumn{1}{c}{\frac{K_{\mathrm{pt}}^S+K_{\mathrm{pt}}^P}{K_{\mathrm{mx}}^S}=\frac{C^P}{C^S}}\end{array}\hfill \end{array}$$ (10)

Results

System's Oscillatory Behavior.

Having demonstrated the equivalency of the two third-order models we can use Eq. (7), omit the subscript and apply the following substitutions:

$$\begin{array}{ccc}\multicolumn{1}{c}{A=(K^S+K^P);}& \hfill B=K^S;\hfill & \hfill C=K^S·K^P\hfill \end{array}$$ (11)

The characteristic polynomial of Eq. (7) can be written as follows:

$$s^3+\frac{A}{C^P}{s}^2+\frac{B}{M}s+\frac{C}{M·C^P}=0$$ (12)

The solution of the characteristic polynomial can be obtained using Cardano's method. Two auxiliary variables can be defined

$$\begin{array}{c}\multicolumn{1}{c}{Q=-{\left(\frac{A}{3C^P}\right)}^2+\frac{B}{3M}R=-{\left(\frac{A}{3C^P}\right)}^3+\frac{\mathit{AB}}{6{\mathit{MC}}^P}-\frac{C}{2{\mathit{MC}}^P}}\end{array}$$ (13)

The discriminant of the cubic equation can be computed as $\Delta =Q^3+R^2$ [16]. The sign of the discriminant determines the type of solution for Eq. (12); the roots of a cubic polynomial can be [15,16]

• three distinct real roots (Δ < 0)

• three real roots, at least two of which are equal (Δ = 0)

• one real root and two complex conjugate roots (Δ > 0)

We show that the sign of the discriminant can be expressed as a function of the ratio between the tendon stiffness K^S and the muscle stiffness K^P. A third-order model has an oscillating free response only if the solution of Eq. (12) includes complex roots, i.e., if Δ > 0 (see Fig. 3). From Eq. (13), the discriminant can be expressed as a function of the muscle damping as follows [15]:

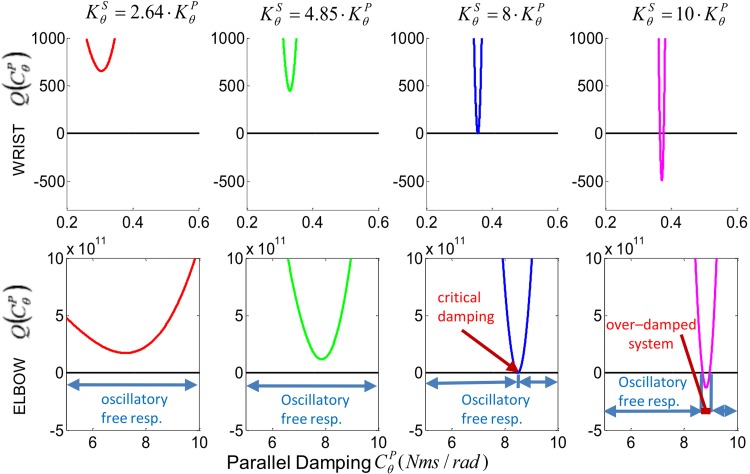
Fig. 3.

Discriminant of Poynting-Thomson model's characteristic polynomial shown as a function of muscle damping $C_{\theta }^P$ for four values of tendon/muscle stiffness ratio κ (2.64, 4.85, 8, 10). The function is shown for both wrist (top) and elbow (bottom). For κ < 8 the discriminant is positive, independent of the value of $C_{\theta }^P$, which translate in a free oscillatory response of the system. If κ ≥ 8 a finite interval of damping values exists within which the system does not present an oscillatory free response.

$$\Delta \left(C^P\right)=Q^3+R^2=\frac{1}{108{\left(C^P\right)}^4{M}^3}\left(4B^3{\left(C^P\right)}^4-M\left(A^2{B}^2+18ABC-27C^2\right){\left(C^P\right)}^2+4M^2{A}^{3}C\right)$$ (14)

By solving Eq. (14) for Δ(C^P) > 0 we find the region in the solution domain where the model presents an oscillating free response. The first multiplicative term in Eq. (14) is always positive and the expression within the parenthesis is a bi-quadratic form. Hence, to find the solutions to Δ = 0, we can substitute ${\left(C^P\right)}^2=v$ and solve the following quadratic equation [15]:

$$\Omega \left(v\right)=(4{\mathit{Bv}}^2-M(A^2{B}^2+18\mathit{ABC}-27C^2)v+4M^2{A}^{3}C)=0$$ (15)

Since $\nu ={\left(C^P\right)}^2\ge 0$, the solutions can only be positive and the following two conditions apply [15]:

$$\{\begin{array}{c}\multicolumn{1}{c}{{\Delta }_{\Omega }=M^2{(\mathit{AB}-9C)}^3(\mathit{AB}-C)\ge 0}\\ \multicolumn{1}{c}{(A^2{B}^2+18\mathit{ABC}-27C^2)\ge 0}\end{array}$$ (16a, 16b)

The expression (16a) represents the condition for the discriminant of Eq. (15) to be non-negative and Eq. (16b) can be clarified by writing Eq. (15) in its monic form,

$$v^2-(v_1+v_2)v+(v_1·v_2)=0$$ (17)

The coefficient of the first degree term has the same sign as the sum of the two solutions (which are both positive since C^P≥ 0).

The inertia M ²> 0 and the following expression is true:

$$\mathit{AB}-C=(K^S+K^P)K^S-K^S·K^P={\left(K^S\right)}^2>0$$ (18)

So the condition defined by Eq. (16a) is equivalent to the following:

$$(\mathit{AB}-9C)\ge 0,\hspace{1em}\mathrm{i}.\mathrm{e}.\hspace{1em}(K^S+K^P)K^S-9·K^S·K^P\ge 0$$ (19)

Assuming that the stiffness of the tendon is proportional to the stiffness of the muscle, we can define $K^S=\kappa ·K^P$, with κ > 0. Substituting in Eq. (19) we obtain the following sufficient condition for Eq. (16b),

$$\kappa (\kappa -8){\left(K^P\right)}^2\ge 0\iff \kappa \ge 8$$ (20)

Incidentally, repeating the calculation starting from Eq. (11), the parameters A, B, and C in Eq. (11) can be defined as

$$\begin{array}{ccc}\multicolumn{1}{c}{A=K_{\mathrm{mx}}^S;}& \hfill B=(K_{\mathrm{mx}}^S+K_{\mathrm{mx}}^P);\hfill & \hfill C=K_{\mathrm{mx}}^S·K_{\mathrm{mx}}^P\hfill \end{array}$$ (21)

Equation (18) assumes the same form and the same threshold condition holds true for $\kappa =K_{\mathrm{mx}}^S/K_{\mathrm{mx}}^P$.

Equations (7) and (9) have two complex conjugate roots for κ < 8, which translates to a free oscillatory response of the third-order mechanical system, independently of the damping. On the other hand, for κ ≥ 8 there exists a finite interval of damping values within which the system does not present an oscillatory free response (see Fig. 3).

Conditions for Stability.

When the system is under-damped, Eq. (12) has always one real root r ₁ and two complex conjugate roots r _2,3. Using Cardano's methods for the solution of cubic algebraic equations, we can calculate the real root defining the following auxiliary variables [16]:

$$\begin{array}{c}\multicolumn{1}{c}{S=\sqrt[3]{R+\sqrt{\Delta \left(C^P\right)}}T=\sqrt[3]{R-\sqrt{\Delta \left(C^P\right)}}}\end{array}$$ (22)

thus obtaining

$$r_1=-\frac{A}{3·C^p}+(S+T)$$ (23)

Equation (12) can be recast using the following polynomial decomposition:

$$P(s)=(s-r_1)(s^2+(\frac{A}{C^P}+r_1)s+\frac{B}{M}+\frac{A}{C^P}{r}_1+r_1^2)\begin{array}{c}\multicolumn{1}{c}{}\end{array}=(s-r_1)(s^2+2\xi \omega s+{\omega }_n^2)$$ (24)

where

$$\begin{array}{c}\multicolumn{1}{c}{\begin{array}{cc}\multicolumn{1}{c}{}& \hfill 2\xi {\omega }_n=\frac{A}{C^P}+r_1\hfill \\ \multicolumn{1}{c}{}& \hfill {\omega }_n^2=\frac{B}{M}+\frac{A}{C^P}{r}_1+r_1^2\hfill \end{array}}\end{array}$$ (25)

The coefficients in Eq. (25) were obtained using Ruffini's rule [17]. Equation (25b) represents the square of the angular natural frequency of the system ${\omega }_n^2$, which is a quadratic function of the real root r ₁. The complex roots of the polynomial P(s) can be found by solving Eq. (25b),

$$\begin{array}{c}\multicolumn{1}{c}{r_{2,3}=-\frac{\frac{A}{C^P}+r_1}{2}\pm \frac{1}{2}\sqrt{{\left(\frac{A}{C^P}\right)}^2-2·\frac{A}{C^P}{r}_1-4·\frac{B}{M}-3·r_1^2}=\alpha \pm j\omega }\end{array}$$ (26)

The real part of all roots (r ₁ and α) need to be nonpositive for the oscillatory system to be stable, hence

$$-\frac{A}{C^P}\le r_1\le 0$$ (27)

Unlike for a second-order system, for a third-order system both the resonant frequency and the natural frequency ω_n are functions of the damping.

Stiffness and Length Ratio.

Measuring the ratio between the tendon and muscle stiffnesses has been the object of several experimental works. Wren and colleagues reported 0.5 < κ < 3 in several studies with animal subjects [17]. In humans, results obtained by Loram et al. [19] suggest that κ < 8 is always true for the soleus and gastrocnemius. Cook and McDonagh found that muscle and tendon stiffnesses are approximately equal for the first dorsal intraosseus muscle (index abductor) at full activation [20]. An approximate value for κ can also be estimated from the biomechanical characteristics of the muscle-tendon system. The tendon can be approximated with a purely elastic element [21–23], tendon stiffness is a function of its tissue mechanical properties and geometry,

$$K^S=\frac{A_{T}E}{{\ell }_T}$$ (28)

where A_T is the average cross section of the tendon, E is the elastic modulus, and ${\ell }_T$ is its length.

The modulation of force is optimal when the muscle is activated in the configuration of isometric tetanic contraction at the muscle's optimum length, corresponding to a plateau in the length-tension curve. In such configuration, the muscle stiffness is [21,24],

$$K_0^P=\gamma \frac{P_0}{{\ell }_f}$$ (29)

Here, γ = 24.5 is an experimental constant [21], ${\ell }_f$ is the length of the muscle fibers and P ₀ is the isometric force calculated as $P_0=\mathrm{PCSA}·p_s$, where PCSA is the physiological cross-sectional area, and p_s = 22.5 N/cm² is the specific tension of the muscle fibers [21,25,26]. Hence, the stiffness ratio can be calculated for each muscle-tendon as follows:

$$\kappa =\frac{E}{\gamma ·p_s}\frac{A_T}{\mathit{PCSA}}\frac{{\ell }_f}{{\ell }_T}$$ (30)

We can lump all muscle-tendon systems acting on the same articulation into an equivalent muscle and equivalent tendon. Since the force acting on a single muscle-tendon system is the same for the muscle and the tendon, the stiffness ratio is the inverse of the ratio between the elongations of the muscle and the tendon,

$$P_o=K^P\Delta {\ell }_m=K^S\Delta {\ell }_T\Rightarrow \kappa =\frac{\Delta {\ell }_m}{\Delta {\ell }_T}$$ (31)

We assume that the elongation of the equivalent muscle and equivalent tendon are the average of the elongations across the elements that compose them. Thus, the equivalent stiffness ratio at the joint is the average of the stiffness ratios across muscle-tendon systems.

The rotational stiffness of each muscle-tendon system at the joint can be calculated from the equation of torque τ_o,

$$\begin{array}{c}\multicolumn{1}{c}{{\tau }_o=K_{\theta }·\Delta \theta =P_o·l_m=K·\Delta {\ell }_w·l_m=K·(\Delta \theta ·l_m)·l_m\Rightarrow K_{\theta }=K·l_m^2}\end{array}$$ (32)

where K is the stiffness of the muscle-tendon system K _θ is the rotational stiffness at the joint, $\Delta {\ell }_w$ is the elongation of the whole muscle-tendon system, l_m is its moment arm, and Δθ is the rotation of the body segment. Assuming that each muscle contributes to the rotational stiffness of the joint on which it acts, we can estimate the lumped joint stiffness by first calculating the equivalent stiffness of the series between each muscle and corresponding tendon and then adding each muscle-tendon stiffness (parallel of springs).

Numerical Examples.

We validated our result numerically using the biomechanical parameters of five main muscles acting across the wrist and the elbow reported in [21,27–35] and summarized in Tables 1 and 2, respectively. The moment arm l_m is calculated for the joint angle θ = 0, defined as the configuration in which both the wrist and the elbow are completely extended. Using Eq. (32), the equivalent tendon and muscle stiffnesses calculated at isometric tetanic contraction for the wrist and elbow joints are $K_{\theta }^S=50.1\mathrm{\hspace{1em}}\mathrm{N}\mathrm{m}/\mathrm{rad}$ and $K_{\theta }^P=18.9\mathrm{\hspace{1em}}\mathrm{N}\mathrm{m}/\mathrm{rad}$, and $K_{\theta }^S=864.8\mathrm{\hspace{1em}}\mathrm{N}\mathrm{m}/\mathrm{rad}$ and $K_{\theta }^P=178\mathrm{\hspace{1em}}\mathrm{N}\mathrm{m}/\mathrm{rad}$, with a stiffness ratios of κ_wrist = 2.64 and κ_elbow = 4.85, respectively. Figure 3 shows a numerical analysis for the two joints with κ = 2.64, 4.58, 8, and, 10, using $M_{\theta }^{\mathrm{wrist}}=0.002\mathrm{\hspace{1em}}\mathrm{kg}/{\mathrm{m}}^2$ and $M_{\theta }^{\mathrm{elbow}}=0.12\mathrm{\hspace{1em}}\mathrm{kg}/{\mathrm{m}}^2$ as the value of the inertia with respect to the joints [36]. For κ < 8 the modulation of $C_{\theta }^P$ does not produce any critical or over-damped condition in neither of the two joints. Furthermore, the values of $C_{\theta }^P$ for which the system is overdamped when κ > 8 are included in a very narrow interval. Specifically, for κ = 10, we obtained $0.366<C_{\theta }^P<0.377$ for the wrist, and $8.694<C_{\theta }^P<8.964$ for the elbow, respectively. Differently from a second-order system, the free response of an over-damped third-order mechanical system can become oscillatory when the damping is increased.

Table 1.

Parameters used in Eqs. (28)–(32) to estimate the stiffness of the tendons and muscle fibers with respect to the wrist. E is the elastic modulus, A_T is the average cross section of the tendon, PCSA is the physiological cross section area of the muscle, ${\ell }_f$ is the length of the muscle fibers, ${\ell }_T$ is the tendon length, l_m is the average moment arm of the muscle, P ₀ is the maximum isometric force, $K_{\theta }^P$ is the joint stiffness generated by the parallel element (muscle fibers), $K_{\theta }^S$ is the joint stiffness generated by the serial element (tendon), κ is the ratio between stiffness components. Muscles are extensor carpii radialis brevis (ECRB), extensor carpii radialis longus (ECRL), extensor carpii ulnaris (ECU), flexor carpii radialis (FCR), flexor carpii ulnaris (FCU).

	E	AT	PCSA	${\ell }_f$	${\ell }_T$	$\frac{{\ell }_f}{{\ell }_T}$	lm	Po	$K_{\theta }^P$	$K_{\theta }^S$
Wrist	(MPa)	(mm2)	(cm2)	(m)	(m)		(cm)	(N)	(Nm/rad)	(Nm/rad)	κ
ECRB	726.1	14.6	2.401	0.071	0.204	0.346	1.60	54.023	4.786	13.303	2.77
ECRL	438.1	14.2	1.300	0.127	0.264	0.476	1.50	29.250	1.267	5.300	4.13
ECU	721.6	15.7	2.100	0.059	0.215	0.272	0.60	47.250	0.709	1.896	2.67
FCR	595.4	17.7	2.119	0.060	0.230	0.259	1.60	47.678	5.001	11.715	2.34
FCU	448.0	27.4	3.636	0.042	0.208	0.202	1.40	81.810	9.376	11.589	1.23

Table 2.

Parameters used in Eqs. (28)–(32) to estimate the stiffness of tendons and muscle fibers with respect to the elbow. E is the elastic modulus, A_T is the average cross section of the tendon, PCSA is the physiological cross section area of the muscle, ${\ell }_f$ is the length of the muscle fibers, ${\ell }_T$ is the tendon length, l_m is the average moment arm of the muscle, P ₀ is the maximum isometric force, $K_{\theta }^P$ is the joint stiffness generated by the parallel element (muscle fibers), $K_{\theta }^S$ is the joint stiffness generated by the serial element (tendon), κ is the ratio between stiffness components. Muscle denominations are biceps long head (BLH), biceps short head (BSH), triceps long head (TLH), brachialis (BRC), brachioradialis (BRD).

	E	AT	PCSA	${\ell }_f$	${\ell }_T$	$\frac{{\ell }_f}{{\ell }_T}$	lm	Po	$K_{\theta }^P$	$K_{\theta }^S$
Elbow	(MPa)	(mm2)	(cm2)	(m)	(m)		(cm)	(N)	(Nm/rad)	(Nm/rad)	κ
BLH	244.0	63.93	3.330	0.136	0.176	0.771	4.70	74.925	29.816	195.340	6.552
BSH	244.0	48.00	3.220	0.150	0.183	0.821	4.70	72.450	26.140	141.608	5.417
TLH	108.0	143.4	6.700	0.063	0.249	0.253	2.30	150.750	31.013	32.850	1.059
BRC	176.0	95.00	9.000	0.090	0.060	1.500	2.60	202.50	37.265	188.379	5.055
BRD	176.0	46.50	3.000	0.160	0.127	1.260	7.70	67.500	61.282	382.070	6.235

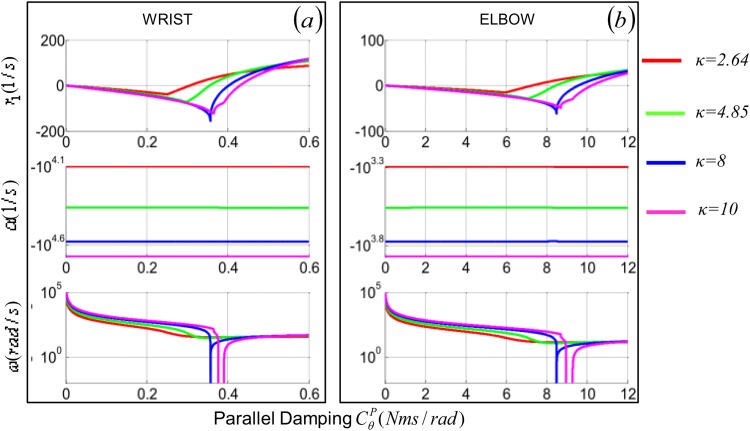
Figure 4 illustrates how the roots of the characteristic polynomial change as a function of C^P. The minimum of r ₁ (most stable configuration of the system) coincides with the minimum of Δ(C^P) in Fig. 3. As the damping increases beyond Δ(C^P), so does r ₁. Not only increasing the damping of the system does not attenuate vibration when κ < 8, but it could also undermine stability. An increase in damping above the minimum of Δ(C^P) would increase the value of the real root monotonically to the point of becoming positive (Fig. 4(a)), thus, making the system unstable. This behavior is quite different from that of a second order system, for which an increase of damping never introduces instabilities.

Fig. 4.

Roots of Poynting-Thomson model's characteristic polynomial shown as functions of the damping $C_{\theta }^P$ for four values of tendon/muscle stiffness ratio κ (2.64, 4.85, 8, 10). The top row represents the real root; center and bottom rows represent the real and imaginary part of the two complex conjugate root, respectively.

For κ ≥ 8 in the specific example, α (the real part of the complex roots r _2,3) is always negative as C^P increases and the resonant frequency of the system ω (the imaginary part of r _2,3) is null between the two critical damping values.

Discussion and Conclusions

We presented a series of analytical tools to investigate force control of human subjects when the interaction of the muscle-tendon system (either in its Poynting-Thomson or Maxwell form) with the limb inertia is described as a third-order system. We established that when the stiffness of the series elastic element is less than eight times the stiffness of the parallel elastic element, both models exhibit an oscillatory free response, independently of the value of the damping. For higher ratios of series to parallel stiffness, the model is over-damped for damping values included within a finite interval between two separate critical limits.

A numerical simulation of the wrist and elbow joints revealed that at maximum isotonic contraction the interval of over-critical damping is very limited. This suggests that the force controller must be capable of dealing with the oscillatory behavior proper of the system's biomechanics.

The transfer function of either the PT or MX isolated muscle-tendon system is first order, having one zero and one pole (see Eqs. (5) and (8)), with no complex conjugate double poles. This means that muscle-tendon systems disconnected from an inertial element cannot exhibit any oscillatory behavior and in experiments where isolated muscle-tendon systems are stretched or released, the absence of any visible oscillations is the expected response. On the other hand, a vibrational free response can appear when the viscoelastic force of the muscle-tendon system interacts with the inertial force of a limb segment and the muscle is highly activated.

While the muscle-tendon models used in this work are approximations limited to a linearized, but physiologically consistent, region of the force-length-velocity curve, they provide a realistic account of the ‘‘contraction dynamics” which arises from the interaction between the stiffness of the tendon in series with the contractile muscle element. Our analysis could be extended to more complex Hill-type muscle models encompassing a wider range of the nonlinear force-length-velocity curve [37,38], as well as including different activation dynamics and reflex contributions [23,39] and history dependent muscle force generation [38].

We propose that force control of the mass-muscle-tendon system can be accomplished indirectly by controlling the position of the muscle-tendon interface, or $\Delta {\ell }_m(t)$ in Fig. 2. Golgi tendon organs (GTO) are located at the conjunction between muscle and tendon and can be modeled as force transducers used by the CNS [40]. It is possible that their position at the interface provides a linear relationship with maximum sensitivity between the force transmitted and elongation of the tendon, therefore providing positional information for the controlled variable z(t) [40]. In robotics, the indirect force control of a system presents a compliant element (tendon) acting as stabilizing impedance buffers between the force-generating element (muscle) and the environment, is referred to as serial elastic control [41]. Advantages include a high shock tolerance and reduction of chatter at the end-effector, thanks to low passive impedance at high frequencies, and the possible use of actuators with relatively low-fidelity force output. Elastic energy can also be stored and released by the elastic element, potentially improving efficiency in harmonic applications. In muscle-tendon systems, the system is relatively forgiving of collisions and other high frequencies environmental disturbances. The elasticity of tendons is also used to store and release energy during rhythmic movements, demanding little mechanical work from the muscle.

Prediction of Low Frequency Oscillations.

Intrinsic oscillations can be compensated by actively varying the length of the muscle-tendon system. It is plausible that the CNS employs different control pathways depending on the time scale of the disturbance. For perturbations whose semiperiod is less than 150 ms, spinal reflexes might provide most of the active compensation for residual oscillation, given their fast acting control loop [42], while compensation of lower frequency perturbations could have a voluntary phasic component [43]. In both cases, we can assume that an internal model of the biomechanical behavior of the muscle-tendon system is encoded by the CNS [10,44].

It is plausible that the same control strategy could be used to predict and compensate for externally introduced vibrational disturbances. Previous studies of our group point to the formation of predictive models of external perturbations during force control tasks [10,45]. When the power spectral density of the disturbance is concentrated at few specific frequencies vibrational disturbances can be predicted and compensated for as demonstrated in [10]. Perturbations whose power spectrum P_c is equally distributed on a wide frequency band are less predictable. However, the power transferred to the inertial load by each perturbation component $x_c(t)=X_c\sin ({\omega }_c·t)$ is a constant, and in the form,

$$\{\begin{array}{c}\multicolumn{1}{c}{{\mathrm{P}}_c=F·{\stackrel{·}{x}}_c=M·{\stackrel{\mathrm{··}}{x}}_c·{\stackrel{·}{x}}_c}\\ \multicolumn{1}{c}{=-{\mathit{MX}}_c^2{\omega }_c^3\sin ({\omega }_c·t)\cos ({\omega }_c·t)}\\ \multicolumn{1}{c}{=-\frac{{\mathit{MX}}_c^2{\omega }_c^3}{2}\sin (2·{\omega }_c·t)}\end{array}$$ (33)

Thus, each amplitude X_c must be inversely proportional to the corresponding angular frequency ω_c. Perturbation components with lower frequency and higher amplitude also result in higher force disturbances transmitted through the tendon. Tendon stiffness can be considered constant, therefore if position control of the muscle-tendon interface is used to indirectly control force, the lower frequency components of the perturbation also provide the larger, and therefore more identifiable error signals. Disturbance compensation in this case is partial, but primarily directed against the components transmitting the highest elastic forces. Further experimentation is needed to identify the frequency ranges in which such force control strategy can be implemented.

Our results confirmed that, when coupled with an inertial load and under high levels of muscle activation, the muscle-tendon system can exhibit an oscillatory free response [12,46–48]. This suggests that nonparametric techniques based on measuring free vibrational responses to impulsive perturbations are a viable tool to identify the system's biomechanical properties [12,47–49].