Multiphasic Finite Element Framework for Modeling Hydrated Mixtures With Multiple Neutral and Charged Solutes

Short abstract

Computational tools are often needed to model the complex behavior of biological tissues and cells when they are represented as mixtures of multiple neutral or charged constituents. This study presents the formulation of a finite element modeling framework for describing multiphasic materials in the open-source finite element software febio. ¹ Multiphasic materials may consist of a charged porous solid matrix, a solvent, and any number of neutral or charged solutes. This formulation proposes novel approaches for addressing several challenges posed by the finite element analysis of such complex materials: The exclusion of solutes from a fraction of the pore space due to steric volume and short-range electrostatic effects is modeled by a solubility factor, whose dependence on solid matrix deformation and solute concentrations may be described by user-defined constitutive relations. These solute exclusion mechanisms combine with long-range electrostatic interactions into a partition coefficient for each solute whose value is dependent upon the evaluation of the electric potential from the electroneutrality condition. It is shown that this electroneutrality condition reduces to a polynomial equation with only one valid root for the electric potential, regardless of the number and valence of charged solutes in the mixture. The equation of charge conservation is enforced as a constraint within the equation of mass balance for each solute, producing a natural boundary condition for solute fluxes that facilitates the prescription of electric current density on a boundary. It is also shown that electrical grounding is necessary to produce numerical stability in analyses where all the boundaries of a multiphasic material are impermeable to ions. Several verification problems are presented that demonstrate the ability of the code to reproduce known or newly derived solutions: (1) the Kedem–Katchalsky model for osmotic loading of a cell; (2) Donnan osmotic swelling of a charged hydrated tissue; and (3) current flow in an electrolyte. Furthermore, the code is used to generate novel theoretical predictions of known experimental findings in biological tissues: (1) current-generated stress in articular cartilage and (2) the influence of salt cation charge number on the cartilage creep response. This generalized finite element framework for multiphasic materials makes it possible to model the mechanoelectrochemical behavior of biological tissues and cells and sets the stage for the future analysis of reactive mixtures to account for growth and remodeling.

1. Introduction

Many biological cells, as well as most biological tissues, consist of a porous solid matrix imbibed with an interstitial fluid. This fluid typically consists of water and charged or neutral solutes, including salt ions, nucleic acids, amino acids, carbohydrates, and larger molecular species, such as proteins, polysaccharides, proteoglycans, DNA, RNA, etc. In many tissues, the solid matrix includes charged molecular species, such as bound or enmeshed proteoglycans, which impart it with a fixed charge density. In a continuum mechanics framework, it is possible to model mechanics and transport in tissues and cells using mixture theory [1,2], where various constituents may be modeled as either a solid, a solute, or the solvent.

Mixture theory has been applied successfully for the modeling of various biological tissues and cells. For example, biphasic models that include a neutral porous solid matrix and a pure interstitial fluid (no solutes) have been used for the modeling of the arterial wall [3] and articular cartilage [4–6]. Triphasic [7] and quadriphasic [8] models that include a charged solid matrix and an interstitial fluid consisting of a solvent and two monovalent counterions have been used to model mechanoelectrochemical phenomena in cartilage [9–14] and chondrons [15,16], intervertebral disc [17,18], arterial wall [19], cornea [20], and brain [21]. Biphasic-solute models, consisting of a mixture of a neutral solid and an interstitial fluid containing one or more neutral solutes, have also been used to model the response of cells to osmotic loading [22–24] and the transport of nutrients in dynamically loaded engineered gels and tissue constructs [25,26].

The set of governing equations for mixture models increases in size in direct proportion to the number of constituents modeled. Furthermore, even under infinitesimal strains, the governing equations for mixtures that include solutes are nonlinear [7,8,25,27]. Therefore, few analytical solutions are available for mixture models and numerical methods become a necessity when modeling common phenomena or experimental configurations. The finite element method has been applied successfully for the modeling of biphasic tissues under infinitesimal [28,29] and finite [30,31] deformations; commercial finite element codes are similarly available for modeling porous deformable media under finite deformations (abaqus 2 and marc 3) using Biot's consolidation (poroelasticity) theory [32]. (As shown by Bowen [33] and Mow and Lai [34], the mixture framework reproduces Biot's poroelasticity equations in the case of a biphasic mixture in the limit of infinitesimal strains.)

Finite element implementations of triphasic/quadriphasic charged porous media have been presented by several authors, applicable to infinitesimal [17,35–39] and finite deformations [40], under specialized conditions where the interstitial fluid includes only two monovalent counterions. Other investigators have used the analogy between thermal diffusion and solute transport to simulate a triphasic medium under infinitesimal deformation [41] or have constrained their triphasic finite element analyses to modeling the equilibrium response to Donnan osmotic swelling under finite deformation [19,42]. The neutral transport of solutes in porous deformable media was addressed by Sengers et al. [43], who formulated a finite element implementation of a biphasic (uncharged) medium, undergoing finite deformation, with solute transport and biosynthesis. Steck et al. [44] and Zhang and Szeri [45] used a commercial finite element code to combine mass (solute) transport with a poroelastic analysis using a two-stage solution procedure. In general, these prior implementations have not addressed the possibility that solutes might be excluded from a fraction of the pore space [46]. Recently, we implemented the biphasic-solute theory [47] into the open-source finite element software febio [48], where partial solute exclusion was described using the concept of solubility [24,25]. This implementation also highlighted the importance of modeling the well-recognized phenomenon of increased hindrance of the solute by the porous solid matrix [46], which retards the flow of solutes relative to the solvent and also produces interesting coupling effects between mechanical loading and solute transport [25,26,49].

In biological systems, it is sometimes necessary to model more than two solutes in order to produce accurate insight into biological and physiological phenomena. For example, to understand basic cell physiology, it may be necessary to analyze models that include many different ions, such as Na⁺, K⁺, Ca²⁺, Cl⁻, and ${\mathrm{HCO}}_3^{-}$, while also accounting for the charged nature of cytoskeletal proteins. Similarly, to analyze transport of growth factors in tissues, it may be necessary to model the charged solid matrix, interstitial ions, and charged growth factor. A framework for describing a mixture with any number of electrolytes has been formulated by Gu et al. [27], though this framework has not yet been generalized to account for solubility effects. Furthermore, few solutions for this generalized framework have been presented in the literature, undoubtedly due to the complexity associated with modeling such mixtures.

The objectives of the current study are to extend Gu et al.'s [27] multielectrolyte theory to account for the solubility of solutes, as well as their increased hindrance, within the deformable charged porous solid matrix; to generalize earlier finite element implementations of specialized triphasic/quadriphasic mixtures to account for any number of neutral solutes and ions whose charge number is an arbitrary signed integer; and to formulate a framework that facilitates the application of electric current as a boundary condition. This novel finite element formulation and implementation is verified against newly derived analytical as well as alternative numerical solutions, as may be achieved under various special cases. Furthermore, initial validations of this framework are presented, whereby finite element predictions are shown to agree with classical experimental findings involving current-generated stress in cartilage and loading of cartilage in electrolytes containing cations of various charges.

2. Finite Element Implementation

2.1. Governing Equations.

A detailed presentation of the governing equations for multiphasic mixtures may be found in the paper by Gu et al. [27]. The generalization of their mixture framework to incorporate tensorial permeability and diffusivity, momentum exchange between solute and solid, and solute steric volume exclusion from the porous solid was described in detail in our recent presentation of finite element modeling of biphasic-solute mixtures [47]. Though that study only included a single neutral solute, the resulting governing equations are substantially similar to the more general case of multiphasic mixtures. Therefore, to avoid repetition of modeling assumptions and derivations starting from fundamental axioms of mass and momentum balance, we refer the reader to the previous publication and herein provide the details that extend the previous presentation to the multiphasic case of charged solutes. The reader will also find details in a recent book chapter [50].

In a multiphasic mixture, the deformation of the solid matrix is represented by the solid displacement u. The interstitial fluid pressure is p. The molar concentration of solutes (on a solution-volume basis) is c ^α, where α represents any of the solute species. The solid matrix Cauchy stress is ${\mathbf{\sigma }}^s$, and the mixture stress is $\mathbf{\sigma }=-p\mathbf{I}+{\mathbf{\sigma }}^s$, where I is the identity tensor. The boundaries of the mixture are defined on the solid matrix. Each mixture constituent is assumed to be intrinsically incompressible, though the mixture may change volume as interstitial fluid flows into or out of the solid matrix pores. The volume fraction of the solid (in the current configuration) is denoted by φ^s and that of the solvent is φ^w. It is assumed that the volume fraction of solutes is negligible relative to the solid and solvent content; thus, ${\varphi }^s+{\varphi }^w\approx 1$.

In a finite element implementation of multiphasic materials, since the solid matrix displacement u must remain continuous across adjoining elements, it may be used as a nodal variable (degree of freedom). However, based on mass, momentum, and energy continuity requirements across interfaces, p and c ^α are not necessarily continuous across element boundaries; therefore, they may not be used as nodal variables [36]. The quantities that satisfy continuity are the mechanoelectrochemical potentials of the solvent and solutes [51,52]. Since these potentials are defined relative to arbitrary reference states, they are not convenient for use as nodal variables. Instead, based on standard constitutive relations from physical chemistry that relate these potentials to fluid pressure and solute concentrations, it is possible to define the following variables [36,47]: the effective fluid pressure

$$\tilde{p}=p-R\theta \Phi \sum _{\alpha }{c}^{\alpha }$$ (2.1)

and the effective solute concentration

$${\tilde{c}}^{\alpha }=c^{\alpha }/{\tilde{\kappa }}^{\alpha }$$ (2.2)

In these expressions, R is the universal gas constant; θ is the absolute temperature; Φ is the osmotic coefficient, a nondimensional property that describes the deviation of the osmotic pressure from the ideal behavior known as van't Hoff's law [53]; ${\tilde{\kappa }}^{\alpha }$ is the partition coefficient of solute α relative to an ideal solution [54,55]. This partition coefficient may be further described by

$${\tilde{\kappa }}^{\alpha }=\frac{{\kappa }^{\alpha }}{{\gamma }^{\alpha }}\exp (-\frac{z^{\alpha }{F}_c\psi }{R\theta })$$ (2.3)

where the nondimensional property κ^α is the solubility of solute α in the mixture, representing the fraction of the interstitial pore volume that is accessible to the solute [25]; and γ^α is the activity coefficient of solute α, a nondimensional property that describes the deviation of the solute chemical potential from the ideal behavior of a very dilute solution [56]. The ratio ${\stackrel{\wedge }{\kappa }}^{\alpha }\equiv {\kappa }^{\alpha }/{\gamma }^{\alpha }$ may be interpreted as the effective solubility of solute α [47]. Here, ψ is the electric potential, F_c is Faraday's constant; and z ^α is the charge number of solute α. For a neutral solute (z ^α= 0), the partition coefficient reduces to the effective solubility. Constitutive relations must be provided for Φ and ${\stackrel{\wedge }{\kappa }}^{\alpha }$; in febio, it is assumed that these material functions depend at most on J = det F, where F is the deformation gradient of the solid and ${\tilde{c}}^{\beta }$ of all the solutes. For ideal mixtures in the context of physical chemistry, Φ = 1 and ${\stackrel{\wedge }{\kappa }}^{\alpha }=1$.

Physically, since $R\theta \Phi \sum _{\alpha }{c}^{\alpha }$ is the osmotic (chemical) contribution to the fluid pressure, $\tilde{p}$ may be interpreted as that part of the total (mechanochemical) fluid pressure that does not result from osmotic effects; thus, it is the mechanical contribution to p. Similarly, the effective solute concentration ${\tilde{c}}^{\alpha }$ represents the true contribution of the molar solute content to its electrochemical potential.

The volume flux of solvent relative to the solid is $\mathbf{w}={\varphi }^w({\mathbf{v}}^w-{\mathbf{v}}^s)$, where v ^w is the solvent velocity and v ^s is the solid velocity (the time derivative of u). The molar flux of solute α relative to the solid is ${\mathbf{j}}^{\alpha }={\varphi }^w{c}^{\alpha }({\mathbf{v}}^{\alpha }-{\mathbf{v}}^s)$, where v ^α is the solute velocity. Using the momentum balance equations for the solvent and solutes, it is possible to relate these fluxes to gradients in $\tilde{p}$ and ${\tilde{c}}^{\alpha }$ according to

$$\mathbf{w}=-\tilde{\mathbf{k}}·(\mathrm{grad}\tilde{p}+R\theta \sum _{\beta }\frac{{\tilde{\kappa }}^{\beta }}{d_0^{\beta }}{\mathbf{d}}^{\beta }·\mathrm{grad}{\tilde{c}}^{\beta })$$ (2.4)

$${\mathbf{j}}^{\alpha }={\tilde{\kappa }}^{\alpha }{\mathbf{d}}^{\alpha }·(-{\varphi }^w\mathrm{grad}{\tilde{c}}^{\alpha }+\frac{{\tilde{c}}^{\alpha }}{d_0^{\alpha }}\mathbf{w})$$ (2.5)

with

$$\tilde{\mathbf{k}}={[{\mathbf{k}}^{-1}+\frac{R\theta }{{\varphi }^w}\sum _{\alpha }\frac{{\tilde{\kappa }}^{\alpha }{\tilde{c}}^{\alpha }}{d_0^{\alpha }}(\mathbf{I}-\frac{{\mathbf{d}}^{\alpha }}{d_0^{\alpha }})]}^{-1}$$ (2.6)

In these expressions, d ^α is the diffusivity tensor of solute α in the mixture (solid + fluid), which accounts for the increased hindrance affected by the porous solid matrix on the solute; $d_0^{\alpha }$ is the isotropic diffusivity of the solute in free solution (fluid); $\tilde{\mathbf{k}}$ is the hydraulic permeability tensor of the porous solid to the interstitial fluid (solvent + solutes); and k is the hydraulic permeability tensor of the porous solid to the interstitial solvent. Constitutive relations must be provided for k, d ^α, and $d_0^{\alpha }$, which relate them to state variables, such as solid matrix strain and suitable measures of solute concentrations.

Under quasistatic conditions, in the absence of external body forces, the momentum balance for the mixture is

$$\mathrm{div}\hspace{1em}\mathbf{\sigma }=0$$ (2.7)

When the volume fraction of solutes is negligible compared to solid and solvent content, the mass balance for the mixture reduces to

$$\mathrm{div}\hspace{1em}({\mathbf{v}}^s+\mathbf{w})=0$$ (2.8)

The mass balance for the solid produces the relation

$${\varphi }^s={\varphi }_r^s/J$$ (2.9)

where ${\varphi }_r^s$ is the solid volume fraction in the reference state. The mass balance for solutes may be written in a form convenient for a finite element formulation where the mixture boundaries are defined on the solid matrix

$$\frac{1}{J}\frac{D^s}{\mathit{Dt}}\left(J{\varphi }^w{\tilde{\kappa }}^{\alpha }{\tilde{c}}^{\alpha }\right)+\mathrm{div}{\mathbf{j}}^{\alpha }=0$$ (2.10)

where $D^s(·)/\mathit{Dt}$ is the material time derivative in the spatial frame following the solid.

If it is assumed that there can be no charge accumulation in the mixture, this electroneutrality condition must be enforced with the following constraint:

$$\sum _{\alpha }{z}^{\alpha }{\tilde{\kappa }}^{\alpha }{\tilde{c}}^{\alpha }=0$$ (2.11)

where the sum is taken over all constituents. Multiplying the mass balance in Eq. (2.10) with z ^α, taking the sum over all constituents, and making use of the above electroneutrality constraint produces

$$\mathrm{div}\sum _{\alpha }{z}^{\alpha }{\mathbf{j}}^{\alpha }=0$$ (2.12)

or, equivalently $\mathrm{div}{\mathbf{I}}_e=0$, where ${\mathbf{I}}_e=F_c\sum _{\alpha }{z}^{\alpha }{\mathbf{j}}^{\alpha }$ is the electric current density (the net rate of flow of electric charge per unit area of the mixture). Thus, the electroneutrality condition produces a constraint on the current density vector field in the mixture.

In most biological mixtures, the solvent is water and thus neutral (z^w= 0). The charge on the solid matrix is described as a net fixed charge density $c^F\equiv z^s{c}^s$. For solids, c^F may be used in lieu of a molar concentration and associated charge number. The mass balance equation for the solid also applies to the fixed charge density, producing

$$c^F=\frac{1-{\varphi }_r^s}{J-{\varphi }_r^s}{c}_r^F$$ (2.13)

where $c_r^F$ is the fixed charge density in the reference configuration.

2.2. Virtual Work and Weak Form.

The virtual work integral for a mixture of intrinsically incompressible constituents combines the balance of momentum for the mixture, the balance of mass for the mixture, and the balance of mass for each of the solutes. In addition, for charged mixtures, the current condition of Eq. (2.12) may be enforced as a penalty constraint on each solute mass balance equation,

$$\begin{array}{c}\multicolumn{1}{c}{\delta W={\int }_b\delta \mathbf{v}·\mathrm{div}\hspace{1em}\mathbf{\sigma }d\upsilon +{\int }_b\delta \tilde{p}\hspace{1em}\mathrm{div}({\mathbf{v}}^s+\mathbf{w})d\upsilon \hspace{1em}+\sum _{\alpha \ne s,w}{\int }_b\delta {\tilde{c}}^{\alpha }[\frac{1}{J}\frac{D^s}{\mathit{Dt}}\left(J{\varphi }^w{\tilde{\kappa }}^{\alpha }{\tilde{c}}^{\alpha }\right)+\mathrm{div}{\mathbf{j}}^{\alpha }+\sum _{\beta \ne s,w}{z}^{\beta }\mathrm{div}{\mathbf{j}}^{\beta }]d\upsilon }\end{array}$$ (2.14)

where δv is the virtual velocity of the solid, $\delta \tilde{p}$ is the virtual effective fluid pressure, and $\delta {\tilde{c}}^{\alpha }$ is the virtual molar energy of solute α. Here, b represents the mixture domain in the spatial frame and $d\upsilon$ is an elemental volume in b. Applying the divergence theorem, δW may be split into internal and external contributions to the virtual work, $\delta W=\delta W_{\mathrm{ext}}-\delta W_{\mathrm{int}}$, where

$$\delta W_{\mathrm{int}}={\int }_b\mathbf{\sigma }:\delta \mathbf{d}d\upsilon +{\int }_b(\mathbf{w}·\mathrm{grad}\delta \tilde{p}-\frac{\delta \tilde{p}}{J}\frac{D^{s}J}{\mathit{Dt}})d\upsilon \hspace{1em}+\sum _{\alpha \ne s,w}{\int }_b[{\mathbf{j}}^{\alpha }·\mathrm{grad}\delta {\tilde{c}}^{\alpha }-\frac{\delta {\tilde{c}}^{\alpha }}{J^s}\frac{D^s}{\mathit{Dt}}\left(J{\phi }^w{\tilde{\kappa }}^{\alpha }{\tilde{c}}^{\alpha }\right)]d\upsilon \hspace{1em}+\sum _{\alpha \ne s,w}{\int }_b\mathrm{grad}\delta {\tilde{c}}^{\alpha }·\sum _{\beta \ne s,w}{z}^{\beta }{\mathbf{j}}^{\beta }d\upsilon$$ (2.15)

$$\delta W_{\mathrm{ext}}={\int }_{\partial b}(\delta \mathbf{v}·\mathbf{t}+\delta \tilde{p}{w}_n+\sum _{\alpha }\delta {\tilde{c}}^{\alpha }{\tilde{j}}_n^{\alpha })\mathit{da}$$ (2.16)

In these expressions, $\delta \mathbf{d}=(\mathrm{grad}\delta \mathbf{v}+{\mathrm{grad}}^T\delta \mathbf{v})/2$, $\partial b$ is the boundary of b, and da is an elemental area on $\partial b$. In this finite element formulation, u, $\tilde{p}$, and ${\tilde{c}}^{\alpha }$ are used as nodal variables, and essential boundary conditions may be prescribed on these variables. Natural boundary conditions are prescribed to the mixture traction, $\mathbf{t}=\mathbf{\sigma }·\mathbf{n}$, normal fluid flux, $w_n=\mathbf{w}·\mathbf{n}$, and normal effective solute flux, ${\tilde{j}}_n^{\alpha }\equiv j_n^{\alpha }+\sum _{\beta }{z}^{\beta }{j}_n^{\beta }$, where $j_n^{\alpha }={\mathbf{j}}^{\alpha }·\mathbf{n}$ and n is the outward unit normal to $\partial b$. To solve the system δW = 0 for nodal values of u, $\tilde{p}$, and ${\tilde{c}}^{\alpha }$, a Newton scheme is used to solve the resulting equations iteratively. In Newton's method, the nonlinear equations are linearized about a known configuration using a Taylor series expansion. The solution is obtained by iteration and involves the formation and factorization of a stiffness matrix. Therefore, it is necessary to linearize these equations along increments in each of these variables [57], as shown, for example, in Ref. [47], to produce the (nonsymmetric) stiffness matrix needed for the evaluation of incremental changes Δu, $\Delta \tilde{p}$, and $\Delta {\tilde{c}}^{\alpha }$ in this iterative scheme.

If the mixture is charged, it is also necessary to solve for the electric potential ψ using the electroneutrality condition in Eq. (2.11). This equation may be rewritten as a polynomial in ζ,

$$\sum _{i=0}^n{a}_i{\zeta }^i=0$$ (2.17)

where

$$\zeta =\exp (-\frac{F_c\psi }{R\theta })$$ (2.18)

$$a_i=\{\begin{array}{c}\multicolumn{1}{c}{z^{\alpha }{\stackrel{\wedge }{\kappa }}^{\alpha }{\tilde{c}}^{\alpha }\hspace{1em}i=z^{\alpha }-z^{min}{c}^F\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}i=-z^{min}}\end{array}$$ (2.19)

and $z^{min}=\underset{\alpha }{min}{\zeta }^{\alpha }$. If we also let $z^{max}=\underset{\alpha }{max}{\zeta }^{\alpha }$, it follows that the polynomial degree is $n=z^{max}-z^{min}$. Since more than one solute may share the same charge number z ^α, the coefficients a_i should represent summations of $z^{\alpha }{\stackrel{\wedge }{\kappa }}^{\alpha }{\tilde{c}}^{\alpha }$ over all such solutes. This polynomial will have n roots, though they may not all be real. Only real positive roots are valid, since $\psi =-R\theta \left(\ln \zeta \right)/F_c$ according to Eq. (2.18). Using Descartes' rule of signs, an inspection of the coefficients a_i shows that there is only one sign change in the polynomial, regardless of the sign of c^F, implying that there will always be only one positive root ζ, which must thus be real. Therefore, there cannot be any ambiguity in the calculation of ψ, irrespective of the polynomial degree. Newton's method is used to solve for the positive real root when n > 2. In the special case of a mixture having two equivalent counterions ($\alpha =+,-$ and $z^{+}=-z^{-}\equiv z$), this polynomial may be solved in closed form to produce

$$\psi =\frac{1}{z}\frac{R\theta }{F_c}\ln \left(\frac{2z{\stackrel{\wedge }{\kappa }}^{+}{\tilde{c}}^{+}}{-c^F+\sqrt{{\left(c^F\right)}^2\hspace{1em}+\hspace{1em}4z^2\left({\stackrel{\wedge }{\kappa }}^{+}{\tilde{c}}^{+}\right)\left({\stackrel{\wedge }{\kappa }}^{-}{\tilde{c}}^{-}\right)}}\right)$$ (2.20)

Using the above relations, it follows that ${\tilde{\kappa }}^{\alpha }={\stackrel{\wedge }{\kappa }}^{\alpha }{\zeta }^{z^{\alpha }}$. An examination of Eq. (2.15) shows it is necessary to evaluate $D^s{\tilde{\kappa }}^{\alpha }/\mathit{Dt}$ to obtain the internal virtual work. This evaluation is performed using the chain rule,

$$\frac{D^s{\tilde{\kappa }}^{\alpha }}{\mathit{Dt}}=\frac{\partial {\tilde{\kappa }}^{\alpha }}{\partial J}\frac{D^{s}J}{\mathit{Dt}}+\sum _{\beta }\frac{\partial {\tilde{\kappa }}^{\alpha }}{\partial {\tilde{c}}^{\beta }}\frac{D^s{\tilde{c}}^{\beta }}{\mathit{Dt}}$$ (2.21)

where the derivatives of the partition coefficient ${\tilde{\kappa }}^{\alpha }$ are given by

$$\frac{\partial {\tilde{\kappa }}^{\alpha }}{\partial J}=\frac{\partial {\stackrel{\wedge }{\kappa }}^{\alpha }}{\partial J}{\zeta }^{z^{\alpha }}+z^{\alpha }{\tilde{\kappa }}^{\alpha }\frac{1}{\zeta }\frac{\partial \zeta }{\partial J}\frac{\partial {\tilde{\kappa }}^{\alpha }}{\partial {\tilde{c}}^{\beta }}=\frac{\partial {\stackrel{\wedge }{\kappa }}^{\alpha }}{\partial {\tilde{c}}^{\beta }}{\zeta }^{z^{\alpha }}+z^{\alpha }{\tilde{\kappa }}^{\alpha }\frac{1}{\zeta }\frac{\partial \zeta }{\partial {\tilde{c}}^{\beta }}$$ (2.22)

In these expressions, the derivatives of ${\stackrel{\wedge }{\kappa }}^{\alpha }$ are obtained from the user-defined constitutive relations. Derivatives of ζ may be evaluated by differentiating the electroneutrality condition in Eq. (2.11) to produce

$$\frac{1}{\zeta }\frac{\partial \zeta }{\partial J}=-\frac{\frac{\partial c^F}{\partial J}+\sum _{\alpha }{z}^{\alpha }{\zeta }^{z^{\alpha }}{\tilde{c}}^{\alpha }\frac{\partial {\stackrel{\wedge }{\kappa }}^{\alpha }}{\partial J}}{\sum _{\alpha }{\left(z^{\alpha }\right)}^2{\tilde{\kappa }}^{\alpha }{\tilde{c}}^{\alpha }}\frac{1}{\zeta }\frac{\partial \zeta }{\partial {\tilde{c}}^{\beta }}=-\frac{z^{\beta }{\tilde{\kappa }}^{\beta }+\sum _{\alpha }{z}^{\alpha }{\zeta }^{z^{\alpha }}{\tilde{c}}^{\alpha }\frac{\partial {\stackrel{\wedge }{\kappa }}^{\alpha }}{\partial {\tilde{c}}^{\beta }}}{\sum _{\alpha }{\left(z^{\alpha }\right)}^2{\tilde{\kappa }}^{\alpha }{\tilde{c}}^{\alpha }}$$ (2.23)

The relations in Eqs. (2.17)–(2.23) provide the method to evaluate ${\tilde{\kappa }}^{\alpha }$ and its various derivatives. A basic algorithmic scheme for the finite element implementation of this method is outlined in Fig. 1.

Fig. 1.

Basic algorithmic scheme for finite element implementation of multiphasic materials

3. Verifications

A broad range of problems may be analyzed using multiphasic materials, which may serve as verification of the current implementation. Since multiphasic materials subsume biphasic (neutral solid + solvent) and biphasic-solute (neutral solid + solvent + single neutral solute) materials, the multiphasic implementation has been verified against analytical solutions and existing finite element implementations for such materials [47,48,58]. For brevity, details of those verifications are not reported here. Instead, this study focuses on verification problems that address the new capabilities of the multiphasic implementation.

3.1. The K-K Model for Osmotic Loading of a Cell.

In 1958, Kedem and Katchalsky [59] proposed a model to describe the response of biological cells to osmotic loading (altering the concentration of the cell's bathing environment). In this classic model, the cell is modeled as a gel-filled semipermeable membrane; the membrane sustains negligible stress and is selectively permeable to the solvent (water) and certain types of solutes (classified as permeant), whereas other (impermeant) solutes cannot transport across it. In this model, the intracellular fluid contains at least one impermeant solute; osmotic loading may be performed with either a permeant or an impermeant solute. The material properties for this model include the membrane hydraulic conductivity, L_p, the membrane solute permeability P ^α and Staverman's reflection coefficient σ^α (permeant solutes only), and the intracellular volume fraction of “osmotically active water” in the reference configuration; this latter property corresponds to $1-{\varphi }_r^s$ in the above mixture notation. In this model, it is implicit that solvent and solutes diffuse much more slowly across the cell membrane than within the protoplasm. Given these assumptions, a coupled set of nonlinear ordinary differential equations may be posed and solved for the time-varying cell volume V(t) and number of moles n ^α(t) for each permeant solute in the intracellular space when the cell is subjected to osmotic loading with such permeant solutes; when osmotic loading is performed with an impermeant solute, only one differential equation remains for the unknown V(t).

In 2006, it was shown that governing equations of the K–K model for cells may be reproduced using mixture theory [22], providing relations between the membrane properties (L_p, P ^α, σ^α) and the multiphasic material properties described above. To reproduce this K–K cell model in febio for the purpose of verifying the implementation of multiphasic materials, a spherical model of a cell is created that incorporates two multiphasic regions: (1) the protoplasm (radius r ₀), consisting of a mixture with a neutral porous solid matrix (compressible neo-Hookean material [57] with Young's modulus E_Y and Poisson's ratio $\nu$) and referential solid volume fraction ${\varphi }_r^s$, an isotropic and constant hydraulic permeability ($\mathbf{k}=k\mathbf{I}$), an impermeant solute α = n, and a permeant solute α = p. For both solutes, the diffusivity is set to one-half the corresponding free diffusivity value, ${\mathbf{d}}^{\alpha }=\frac{1}{2}\hspace{1em}{d}_0^{\alpha }\mathbf{I}$; the effective solubility of the impermeant solute is set to unity, ${\stackrel{\wedge }{\kappa }}^n=1$, whereas that of the permeant solute, ${\stackrel{\wedge }{\kappa }}^p$, is left as a user-defined parameter. (2) The cell membrane (thickness h), consists of a mixture with a neutral porous solid matrix (uncoupled Mooney–Rivlin material [57] with shear modulus μ and bulk modulus κ, with $\kappa >>\mu$ to prevent membrane compaction under elevated transmembrane osmotic gradients while simultaneously producing negligible membrane tension) and referential solid volume fraction ${\varphi }_r^s$, an isotropic and constant hydraulic permeability ($\mathbf{k}=k\mathbf{I}$), and only the permeant solute α = p with constant, isotropic diffusivity ${\mathbf{d}}^p=\frac{1}{2}\hspace{1em}{d}_0^p\mathbf{I}$.

Initially, the protoplasmic solute concentrations are set to $c^n=c_0$ (a user-defined parameter) and c^p= 0. This initial configuration requires that the extracellular bath also contains an impermeant solute with the same concentration c ₀ (prescribed as a boundary condition on the outer cell membrane surface). Osmotic loading with the permeant solute is achieved by prescribing $c^p=c_{1}H\left(t\right)$ on the outer cell membrane surface, where H(t) is the unit step function. These initial and boundary conditions need to be suitably converted to corresponding values for the effective fluid pressure and solute concentrations, since the nodal variables in the finite element model are $\tilde{p}$ and ${\tilde{c}}^{\alpha }$. Assuming that the ambient fluid pressure in the bath is p = 0 and the ambient electric potential is ψ = 0, the initial conditions are $\tilde{p}=-R\theta c_0$ and ${\tilde{c}}^p=0$ in the intracellular space and in the membrane and ${\tilde{c}}^n=c_0$ in the intracellular space. The boundary conditions on the outer membrane surface are $\tilde{p}=-R\theta (c_0+c_{1}H\left(t\right))$ and ${\tilde{c}}^p=c_{1}H\left(t\right)/{\stackrel{\wedge }{\kappa }}^p$.

To replicate the assumptions of the K–K model, the intracellular permeability k and solute diffusivities $d_0^{\alpha }$ are taken to be much larger than the corresponding membrane values of k and $d_0^p$. Similarly, since the membrane is assumed to sustain negligible stress, its shear modulus μ is taken to be much smaller than the peak osmotic pressure magnitude acting across it, Rθc ₁; however, to prevent the compaction (and possible inversion) of the finite elements forming the cell membrane, the bulk modulus κ is taken to be comparable to Rθc ₁. Since the K–K model does not attribute any stiffness to the intracellular environment, E_Y is similarly taken to be much smaller than Rθc ₁; $\nu$ is taken to be zero to preclude any resistance to volume changes. The finite element mesh uses 8-node hexahedral elements and takes advantage of the spherical symmetry by modeling only a small arc along the azimuth and elevation and employing symmetry planes along both directions. Only a single element is used along the radial direction for the intracellular space (since the K–K model assumes a homogeneous response there); similarly, a single element is used through the thickness of the membrane.

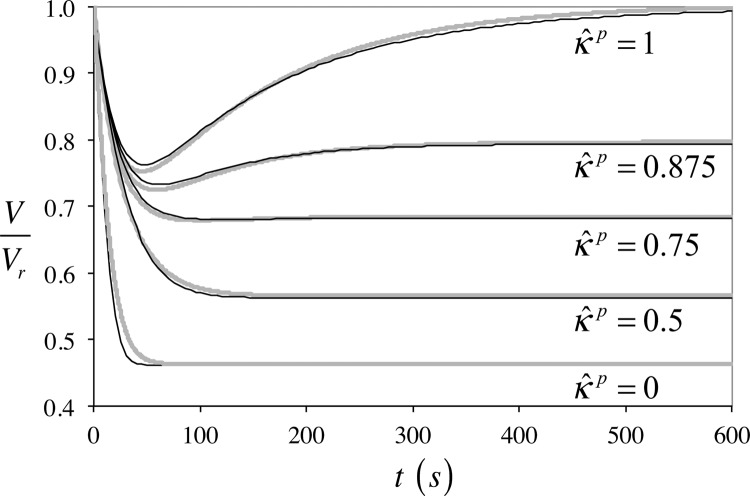
The response of the cell volume to osmotic loading is presented in Fig. 2 for different values of ${\stackrel{\wedge }{\kappa }}^p$, showing a comparison of the febio results against the numerical solution of the K–K equations using a fourth-order Runge–Kutta scheme as described in our earlier study [22]. The observed agreement verifies the accuracy of febio for this problem over a range of large deformations, taking into account transport of one (in the membrane) or two (in the cell protoplasm) neutral solutes through a neutral porous solid matrix. Small differences between the two solutions may be attributed to the fact that certain idealized assumptions of the K–K model (zero stiffness for the membrane and protoplasm, infinitely fast transport of solute and solvent in the protoplasm, membrane permeant solute concentration exactly equal to the mean of intra- and extracellular values) cannot be reproduced exactly in the finite element representation.

Fig. 2.

Cell volume response to osmotic loading: V is the current cell volume and V_r is its volume in the reference configuration. Black curves are the responses from the K–K model and gray curves are the finite element solutions. For the finite element model, the membrane thickness is 10 nm and its properties are ${\varphi }_r^s=0.3$, $\mu =2.5\mathbf{kPa}$, $\kappa =2.5\mathbf{MPa}$, $k=5\times {10}^{-7}\mu {\mathbf{m}}^4/\mathbf{nN}·\mathbf{s}$, $d_0^p=1.43\times {10}^{-3}\mu {\mathbf{m}}^2/\mathbf{s}$, and ${\stackrel{\wedge }{\kappa }}^p=1$; the protoplasm has a radius of $10\mu \mathbf{m}$, and its properties are ${\varphi }_r^s=0.3$, $E_Y=2.5\mathbf{kPa}$, $\nu =0$, $k=5\times {10}^{-3}\mu {\mathbf{m}}^4/\mathbf{nN}·\mathbf{s}$, $d_0^p=d_0^n=14.3\mu {\mathbf{m}}^2/\mathbf{s}$, and ${\stackrel{\wedge }{\kappa }}^p$ values are indicated on the graph. For the K–K model, the equivalent membrane properties are reported in Ref. [22]. For these analyses, $c_0=0.3\mathbf{M}$ and $c_1=1\mathbf{M}$ (see text).

The physical explanation for the observed response stems from the imbalance in osmolarity between the intracellular and extracellular environments, which drives the fluid flux into or out of the cell, thus altering its volume. Substituting Eq. (2.1) into the solvent flux relation in Eq. (2.4), assuming ideal physicochemical relations, and recognizing that $p\approx 0$, since neither the membrane nor the protoplasm can sustain stress, we find that $\mathbf{w}=R\theta \tilde{\mathbf{k}}·\sum _{\beta }(\mathbf{I}-{\mathbf{d}}^{\alpha }/d_0^{\alpha })·\mathrm{grad}\hspace{1em}{\tilde{c}}^{\beta }$. This relation makes it evident that solvent will initially exude from the cell when the extracellular osmolarity exceeds the intracellular value due to the prescribed increase in permeant solute concentration. However, as the cell shrinks, the intracellular osmolarity increases, due to the fact that impermeant solutes cannot leave the cell; combined with the increasing intracellular permeant solute concentration, the osmolarity gradient eventually reverses itself (when ${\stackrel{\wedge }{\kappa }}^p\stackrel{<}{{~}_{\mathrm{x}}}1$), producing a volume recovery, or subsides (when ${\stackrel{\wedge }{\kappa }}^p$ is sufficiently smaller than unity), producing no further reduction in volume.

3.2. Donnan Osmotic Swelling.

Osmotic forces arise in a multiphasic material as a result of gradients in the osmolarity of the interstitial fluid or, equivalently, gradients in solute concentrations. Such gradients may be enabled by properties of the multiphasic material, such as semipermeable membranes that selectively allow transport of the solvent and certain solutes or electric charges fixed to the solid matrix that produce an imbalance in the concentrations of interstitial fluid anions and cations due to the electroneutrality condition. When a multiphasic material with a charged solid matrix is immersed in an electrolyte whose ions may transport into or out of the porous material, the electroneutrality condition enforces an imbalance in the osmolarities of the interstitial fluid and external bathing solution. This charge-induced imbalance produces an osmotic pressure difference known as the Donnan osmotic pressure [60]. In a multiphasic material with a deformable solid matrix, this Donnan pressure may produce nonnegligible swelling, depending on the magnitude of the interstitial osmotic pressure relative to the stiffness of the porous solid matrix [7,19].

When the interstitial fluid and bathing solution contain two monovalent counterions ($z^{+}=1$, $z^{-}=-1$), an analytical solution may be obtained for the dependence of the osmotic pressure on the fixed charge density c^F and bathing solution concentration c _* as a result of the existence of a closed-form solution for the electric potential ψ (Eq. (2.20)). Furthermore, if the solid matrix deformation is homogeneous, the solution to this deformation reduces to a set of nonlinear algebraic equations. For example, if the solid matrix is isotropic, the homogeneous deformation becomes isotropic with $\mathbf{F}=\lambda \mathbf{I}$, where λ is the stretch ratio along any direction. For a neo-Hookean solid with Lamé constants λ_s and μ_s, assuming ideal physicochemical conditions, Azeloglu et al. [19] have shown that λ must satisfy

$${\mu }_s({\lambda }^2-1)+3{\lambda }_s\left(\ln \lambda \right)-{\lambda }^{3}R\theta [\sqrt{{\left(\frac{(1-{\varphi }_r^s)c_r^F}{{\lambda }^3-{\varphi }_r^s}\right)}^2+\hspace{1em}{\left(2c_{*}\right)}^2}-2c_{*}]\hspace{1em}=0$$ (3.1)

under traction-free conditions on the boundaries (free swelling). Such a homogeneous state for the deformation is typically achieved under steady-state conditions when solvent and solute fluxes have subsided.

These homogeneous free-swelling conditions are easily reproduced in a representative finite element model in febio by using a single cuboid hexahedral element with symmetry constraints on three orthogonal faces (zero normal displacement, and zero solvent and solute normal fluxes, the latter being natural boundary conditions); on the remaining three faces, the mixture traction is zero (a natural boundary condition), the effective fluid pressure is $\tilde{p}=-2R\theta c_{*}$ (under the assumption that the ambient bath pressure is zero), and the effective solute concentrations are ${\tilde{c}}^{\alpha }=c_{*}$ ($\alpha =+,-$) (under the assumption that the ambient bath electric potential is zero). Since steady-state conditions are sought, the selection of k, d ^α, and $d_0^{\alpha }$ is arbitrary in the finite element analysis.

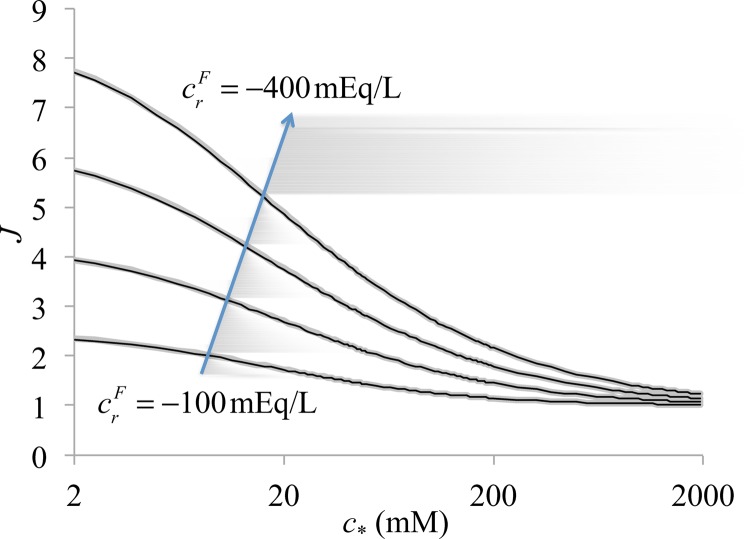
A comparison of the febio solution with a numerical solution to Eq. (3.1) is provided in Fig. 3 for representative values of λ_s, μ_s, and ${\varphi }_r^s$ and a range of values for $c_r^F$ and $c_{*}$. Agreement is observed over the entire range, providing a verification of the finite element code with regard to the interaction between Donnan osmotic pressure and solid matrix deformation.

Fig. 3.

Donnan osmotic swelling of a triphasic material (${\varphi }_r^s=0.2$) with a neo-Hookean solid (${\lambda }_s=0$, ${\mu }_s=0.25\hspace{1em}\mathbf{MPa}$). The relative volume $J={\lambda }^3$ is plotted for four different values of $c_r^F$ (ranging from $=100$ to $=400\hspace{1em}\mathbf{mEq}/\mathbf{L}$ by increments of $=100\hspace{1em}\mathbf{mEq}/\mathbf{L}$) over a range of values for the bath concentration c _* (θ = 293 K). The numerical solution to Eq. (3.1) is given by the thin black curves, and the finite element solution is represented by the thicker gray curves.

3.3. Current Flow in an Electrolyte.

Electrolytes conduct electricity as a result of the net transport of ionic charges. Consider a monovalent salt, such as NaCl, placed in a rigid impermeable chamber of length h, having impermeable silver-silver chloride (Ag/AgCl) electrodes at each end (Fig. 4). A prescribed current density I ₀ is passed through the electrolyte, and we would like to determine the ion concentrations and electric potential throughout the electrolyte as a function of time. When analyzing problems involving electrodes, it is important to understand the nature and interactions of the electrode with the electrolyte solution. In the case of Ag/AgCl electrodes in contact with a NaCl solution, a chemical reaction occurs at the electrodes that converts silver to silver chloride, or vice versa, according to

Fig. 4.

Schematic for current flow in an electrolyte

$${\mathrm{Ag}}_{(\mathrm{s})}^0+{\mathrm{Cl}}^{-}\rightleftharpoons {\mathrm{AgCl}}_{(\mathrm{s})}+e^{-}$$ (3.2)

At the anode, the silver metal reacts with a chloride ion from the electrolyte solution to produce an insoluble silver-chloride salt that gets deposited onto the electrode; an electron is freed at the junction to flow through the electrode. At the cathode, the silver-chloride salt dissociates into silver metal, which remains on the electrode, and a chloride ion that gets released into the solution; an electron is captured from the electrode in this process.

This problem is set up to be one-dimensional in space, with ion transport occurring along the $z-\mathrm{direction}$ over the range $0\le z\le h$. Accordingly, the current density is also directed along z; based on the charge numbers of Na ⁺and Cl⁻, this current density is given by $I_0=F_c(j^{+}-j^{-})$. For a one-dimensional problem, I ₀ must remain uniform over z, based on Eq. (2.12). From the chemical reaction described in Eq. (3..2), it follows that $j^{+}=0$ at the electrodes and throughout the electrolyte (since sodium ion does not react with the electrodes), whereas $j^{-}=-I_0/F_c$ (since chloride ion is exchanged with the electrodes). Combining these conditions with the electroneutrality constraint and the remaining governing equations of mixture theory (in the absence of a charged solid matrix), it can be shown that the electrolyte concentration $c(z,t)$ (where $c\equiv c^{+}=c^{-}$ based on electroneutrality) in response to a step increase in the current density from zero to I ₀ is given by

$$\frac{c(z,t)}{c_0}=1+{\stackrel{\wedge }{I}}_0[\frac{2z}{h}-1+\frac{8}{{\pi }^2}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{{(2n-1)}^2}\hspace{1em}\sin \left[(n-\frac{1}{2})\pi (\frac{2z}{h}-1)\right]\exp (-{(2n-1)}^2{\pi }^2\frac{d_{0}t}{h^2})]$$ (3.3)

where c ₀ is the initial homogeneous electrolyte concentration, d ₀ is the electrolyte free diffusivity related to the ion diffusivities via

$$\frac{1}{d_0}=\frac{1}{2}(\frac{1}{d_0^{+}}+\frac{1}{d_0^{-}})$$ (3.4)

and ${\stackrel{\wedge }{I}}_0$ is the nondimensional current density given by

$${\stackrel{\wedge }{I}}_0=\frac{{\mathit{hI}}_0}{4d_0^{-}{F}_c{c}_0}$$ (3.5)

At steady state, the solution reduces to

$$\underset{t\to \infty }{lim}\hspace{1em}\frac{c(z,t)}{c_0}=1+{\stackrel{\wedge }{I}}_0(\frac{2z}{h}-1)$$ (3.6)

It should be noted that this solution is only valid for ${\stackrel{\wedge }{I}}_0\le 1$, since higher values produce meaningless negative concentrations in Eq. (3.3). The physical explanation is that the upper-limiting case ${\stackrel{\wedge }{I}}_0=1$ represents the (normalized) current density at which the requisite rate of chloride ion oxidation at the anode is balanced by the maximum rate at which chloride ions from the bulk solution can diffuse toward the anode to sustain the oxidation reaction; since diffusion is driven by the concentration gradient, the highest possible gradient in a linearly varying concentration field at steady-state occurs when the chloride ion concentration reduces to zero at z = 0.

This problem is simulated in febio by using a triphasic material with two monovalent counterions ($z^{+}=1$, $z^{-}=-1$). Though the actual material consists of a pure fluid (solvent + ions), all multiphasic models in febio must include a porous solid matrix, since the finite element mesh is defined on the solid. For this problem, the solid matrix is modeled to be neutral ($c_r^F=0$) with zero solid volume fraction $({\varphi }_r^s=0)$. The solid matrix stiffness has no effect on the solution, since this problem produces no solid deformation; therefore, a stress-strain constitutive model and corresponding material properties may be selected arbitrarily for the solid (e.g., neo-Hookean with Young's modulus equal to 10 MPa and Poisson's ratio equal to zero). Similarly, the permeability of the solid to the solvent, k, has no effect on the solution, since there is no solvent flux in this problem (one-dimensional problem with impermeable boundaries); thus, $\mathbf{k}=k\mathbf{I}$ with $k={10}^{-3}{\mathrm{mm}}^4/\mathrm{N}·\mathrm{s}$ may be selected arbitrarily. Since the solid matrix should not hinder solute transport in this simulation of a pure fluid, the ion diffusivities are set to ${\mathbf{d}}^{\alpha }=d_0^{\alpha }\mathbf{I}$ ($\alpha =+,-$) with $d_0^{+}=1.0\times {10}^{-3}{\mathrm{mm}}^2/\mathrm{s}$ and $d_0^{-}=1.2\times {10}^{-3}{\mathrm{mm}}^2/\mathrm{s}$. A cuboid geometry is selected for this analysis, with $h=1\mathrm{mm}$ along the $z-\mathrm{direction}$. Ideal physicochemical conditions are assumed to prevail; thus, ${\stackrel{\wedge }{\kappa }}^{\alpha }=1$ and $\Phi =1$. A biased mesh of 40 elements along z is employed, with an increasingly finer mesh near z = 0 and z = 1.

The current density I ₀ is prescribed by letting $j_n^{+}=0$ and $j_n^{-}={10}^{-1}\mathrm{nmol}/{\mathrm{mm}}^2·\mathrm{s}$ at z = 0 (where the outward normal to the boundary points in the negative $z-\mathrm{direction}$), producing a current density $I_0=9.65\mu \mathrm{A}/{\mathrm{mm}}^2$ (with $F_c=9.65\times {10}^{-5}\mathrm{C}/\mathrm{nmol}$) along the positive $z-\mathrm{direction}$. Since febio requires that solute flux boundary conditions for solute α be imposed as ${\tilde{j}}_n^{\alpha }\equiv j_n^{\alpha }+\sum _{\beta }{z}^{\beta }{j}_n^{\beta }$ (see Eq. (2.16)), the actual flux conditions in the finite element model are ${\tilde{j}}_n^{+}=-j_n^{-}$ and ${\tilde{j}}_n^{-}=0$. Similarly, since the current density is uniform along z, the same boundary conditions are applied at z = 1 with $j_n^{-}=-{10}^{-1}\mathrm{nmol}/{\mathrm{mm}}^2·\mathrm{s}$ (since the outer normal on that boundary is along the positive $z-\mathrm{direction}$). Initially, the ion concentration is taken to be $c_0=150\mathrm{mM}$ throughout the chamber. If it is assumed that the electric potential ψ is initially zero, it follows from Eqs. (2.2) and (2.3) that ${\tilde{\kappa }}^{\alpha }=1$ and ${\tilde{c}}^{\alpha }=c_0$ initially.

While it may seem that these boundary conditions are sufficient to solve this problem, it should be noted that, since there are no boundary conditions on ${\tilde{c}}^{\alpha }$ at z = 0 or z = h, there are no constraints imposed on the reference electric potential in the chamber. In other words, the electrolyte solution is not electrically grounded and the value of ψ may float randomly. A numerical solution can be obtained for this set of initial and boundary conditions, but convergence is very poor and the final solution may show random numerical fluctuations in ψ, even while grad ψ remains well-behaved. To ground the electrolyte in the chamber and produce a stable numerical solution with good convergence properties, the effective solute concentrations at the midpoint of the chamber are constrained to remain constant, ${\tilde{c}}^{\alpha }(h/2,t)=c_0$; this constraint satisfies the electroneutrality condition while also imposing ψ = 0 at z = h/2, thereby successfully grounding the solution.

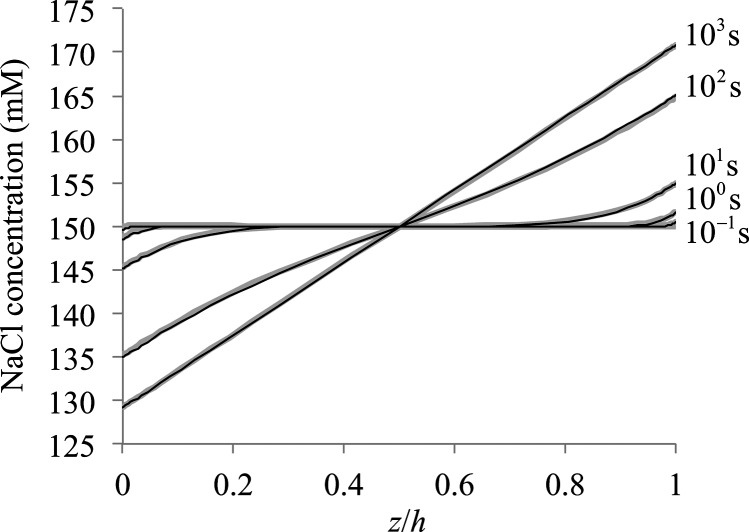
A comparison of the febio solution with the analytical solution of Eq. (3.3) is presented in Fig. 5 at several representative time points, showing agreement across all values of z and t. This verification problem demonstrates that this multiphasic implementation may properly solve problems of mass transport and electric conduction in an electrolyte.

Fig. 5.

One-dimensional current flow in NaCl. The concentration of NaCl along the entire length of the domain is provided at selected time points. Black curves represent the analytical solution and gray curves represent the finite element solution.

4. Illustrations

4.1. Current-Generated Stress in Cartilage.

In 1987, Frank and Grodzinsky [61] demonstrated experimentally that passing an alternating electric current across an articular cartilage sample that is clamped between two electrodes produces an alternating stress response. They observed that the stress magnitude and phase angle decreased with increasing input current frequency. They proposed a theoretical framework to describe this electromechanical response, which extended porous media theories by including electrokinetic equations relating the current density to gradients in fluid pressure and electric potential while also accounting for the dependence of the interstitial fluid flux on those same gradients [62]. The primary distinction between their electromechanical model and the subsequent triphasic theory of Lai et al. [7] is that the former does not include an explicit description of ions. Whereas the electromechanical model has been shown to reproduce the experimental observation of current-generated stress [62], the triphasic theory has not yet been used to analyze this problem.

To simulate this current-generated stress phenomenon in febio, a triphasic material is used with negative fixed charge density and monovalent counterions Na⁺ and Cl⁻ ($z^{+}=1$, $z^{-}=-1$). The solid matrix is modeled as neo-Hookean (Young's modulus = 0.24 MPa, Poisson's ratio = 0), the hydraulic permeability is isotropic and constant ($\mathbf{k}=k\mathbf{I}$ with $k={10}^{-3}{\mathrm{mm}}^4/\mathrm{N}·\mathrm{s}$), and the solute diffusivities are taken to be half their respective values in free solution (${\mathbf{d}}^{\alpha }=\frac{1}{2}\hspace{1em}{d}_0^{\alpha }\mathbf{I}$, $d_0^{+}=1.0\times {10}^{-3}{\mathrm{mm}}^2/\mathrm{s}$, and $d_0^{-}=1.6\times {10}^{-3}{\mathrm{mm}}^2/\mathrm{s}$). Ideal physicochemical conditions are assumed (Φ = 1, ${\stackrel{\wedge }{\kappa }}^{\alpha }=1$). The geometry for this problem is presented in Fig. 6; the mesh distribution is identical to the finite element model for current flow through an electrolyte, as described above. The material has a thickness h = 1 mm in its reference (stress-free) configuration; it is assumed to be inside a rigid confining chamber with impermeable side walls (the chamber is not modeled explicitly, but displacement constraints prevent lateral motion). The bottom end of the chamber (z = 0) is an impermeable rigid Ag/AgCl electrode with zero axial displacement and flux boundary conditions specified as $w_n(0,t)=0$, ${\tilde{j}}_n^{+}(0,t)=I_e\left(t\right)/F_c$ ($F_c=9.65\times {10}^{-5}\mathrm{C}/\mathrm{nmol}$), and ${\tilde{j}}_n^{-}(0,t)=0$, where $I_e\left(t\right)$ is the prescribed current density (positive along the negative $z-\mathrm{direction}$). At the top end (z = h), a rigid porous (free-draining) Ag/AgCl electrode acts as an indenter that constrains the material (zero axial displacement). This porous electrode is assumed to be immersed in a well-mixed electrolyte bath with zero ambient pressure and electric potential; thus, effective solute boundary conditions at z = h are ${\tilde{c}}^{+}(h,t)={\tilde{c}}^{-}(h,t)=c_0$, where c ₀ is the electrolyte bath concentration ($c_0=150\hspace{1em}\mathrm{mM}$) and the effective pressure is $\tilde{p}=-2R\theta c_0$ ($R=8.314\times {10}^{-3}\mathrm{mJ}/\mathrm{nmol}·\mathrm{K}$ and $\theta =293\hspace{1em}\mathrm{K}$).

Fig. 6.

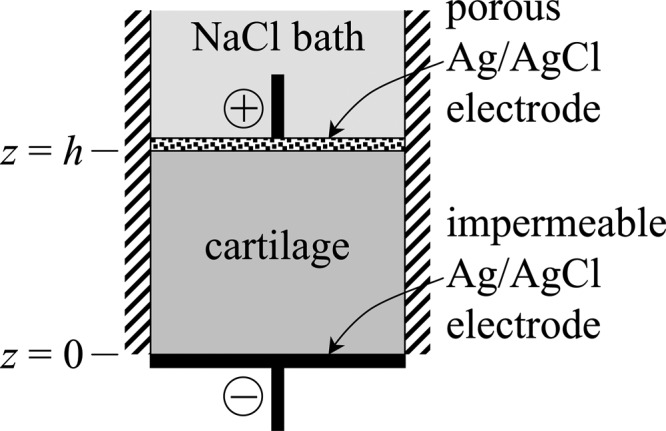
Schematic for configuration of current-generated stress analysis in cartilage

Initial conditions inside the material are given by ${\tilde{c}}^{+}(z,0)={\tilde{c}}^{-}(z,0)=c_0$ and $\tilde{p}(z,0)=-R\theta (c^{+}+c^{-})$, where c ⁺and c ⁻ are the actual ion concentrations. There are two ways to determine these concentrations: (1) The value of ψ may be evaluated from the closed-form solution in Eq. (2.20) (which requires knowledge of J in order to also evaluate c^F from Eq. (2.13)) and then substituted into Eq. (2.3) to evaluate ${\tilde{\kappa }}^{\alpha }$ and then into Eq. (2.2). This method is not sufficiently general, since a closed-form expression is not always available for ψ, nor is J necessarily known at t = 0. (2) Let $c_r^F=0$ at t = 0, implying that $\psi (z,0)=0$ and $c^{+}=c^{-}=c_0$; then decrease $c_r^F$ to the desired value ($c_r^F=-150\mathrm{mEq}/\mathrm{L}$) using a steady-state analysis for computational efficiency to achieve the desired initial conditions for a charged solid matrix.4 As $c_r^F$ is decreased, and since the triphasic material is exposed to an external bath without restriction on electrolyte transport, ion exchanges take place and a Donnan osmotic pressure is produced. Since the material is clamped between the two electrodes, it now exerts a tare stress on the electrodes equal in magnitude to the Donnan pressure. Once this state is achieved, the transient response to $I_n\left(t\right)$ may be initiated.

For this illustrative example, a step increase in current is applied (with a magnitude of $4\times {10}^{-6}\mathrm{A}/{\mathrm{mm}}^2$) and the transient response is monitored until a steady state is achieved. The current-generated stress is observed to increase slowly over time, with a characteristic time constant on the order of $~{10}^3\mathrm{s}$ (Fig. 7(a)). Relative to the tare stress ($~0.09\mathrm{MPa}$), the current-generated compressive stress rises in magnitude by an additional $~0.08\hspace{1em}\mathrm{MPa}$ at steady state. A plot of the ion concentrations c ^α ($\alpha =+,-$) at various time points is presented in Fig. 7(b). The stress is generated because the application of the current produces an increasing concentration of Cl⁻ at the impermeable cathode (z = 0), where this ion is being released; even though Cl ⁻is simultaneously absorbed at the porous anode (z = h), its concentration does not decrease substantially there, due to the plentiful supply from the external bath. The net result is that the osmolarity ($c^{+}+c^{-}$) of the interstitial fluid increases over the entire range of z, producing an increase in the osmotic pressure, which is responsible for the increased stress.

Fig. 7.

Current-generated stress. (a) Stress response σ_zz as a function of time, inclusive of the tare stress resulting from the initial Donnan osmotic pressure. (b) Concentrations c ⁺of Na⁺ and c ⁻ of Cl⁻ along the axis z of the tissue at selected time points t (t = 0 s corresponds to the state immediately prior to current application; remaining time points increase from 10⁰s to 10⁴s by decade).

4.2. Effect of Cation Charge on Creep Response of Cartilage.

In 1963, Sokoloff reported on the creep response of articular cartilage in solutions containing monovalent, divalent, or trivalent cations [63]. He observed that the creep deformation in divalent cation solutions (such as CaCl₂, BaCl₂, and MgCl₂) was significantly greater than with monovalent cation solutions (e.g., NaCl, KCl, and LiCl). He also observed that trivalent cation solutions (e.g., AlCl₃, LaCl₃, and FeCl₃) produced a response substantially similar to divalent cation solutions. To examine whether these findings may be replicated from theory, unconfined compression creep analyses are performed on cylindrical cartilage models in febio, using bathing solutions where the cation is either monovalent (0.15 M NaCl), divalent (0.11 M CaCl₂), or trivalent (0.085 M AlCl₃).

The cartilage solid matrix is modeled using a continuous isotropic fiber distribution to represent the collagen, where each fiber bundle has a power-law response with a modulus ξ = 2 MPa and exponent β = 2.5 [42], a neo-Hookean ground matrix with Young's modulus E_Y = 0.1 MPa and Poisson's ratio $\nu =0$ to represent the nonelectrostatic contribution of the proteoglycans [64] and a fixed charged density $c_r^F=-200\hspace{1em}\mathrm{mEq}/\mathrm{L}$ to represent the proteoglycan charges. The permeability tensor is assumed to be isotropic and dependent on J via a combined power/exponential law [6] with a zero-strain permeability of $k_0={10}^{-3}{\mathrm{mm}}^4/\mathrm{N}·\mathrm{s}$, a power-law exponent given by α = 2, and an exponential rate given by M = 4. The ions diffusivity tensors are taken to be isotropic and constant with $d_0^{+}={10}^{-3}{\mathrm{mm}}^2/\mathrm{s}$, $d_0^{-}=1.6\times {10}^{-3}{\mathrm{mm}}^2/\mathrm{s}$, and ${\mathbf{d}}^{\alpha }=\frac{1}{2}\hspace{1em}{d}_0^{\alpha }\mathbf{I}$. Room temperature was assumed in the analysis (θ = 293 K).

A rigid, impermeable, frictionless loading platen is used to apply the load on the cartilage for the creep response. Using a steady-state analysis, the fixed-charge density is reduced from zero to the desired negative value of $c_r^F$, allowing the tissue to swell radially and circumferentially while constrained axially by the initially stationary loading platen. Then, using a transient analysis, a step load is prescribed on the loading platen, corresponding to a mean engineering contact stress ${\sigma }_0=0.8\mathrm{MPa}$, and the engineering strain is examined.

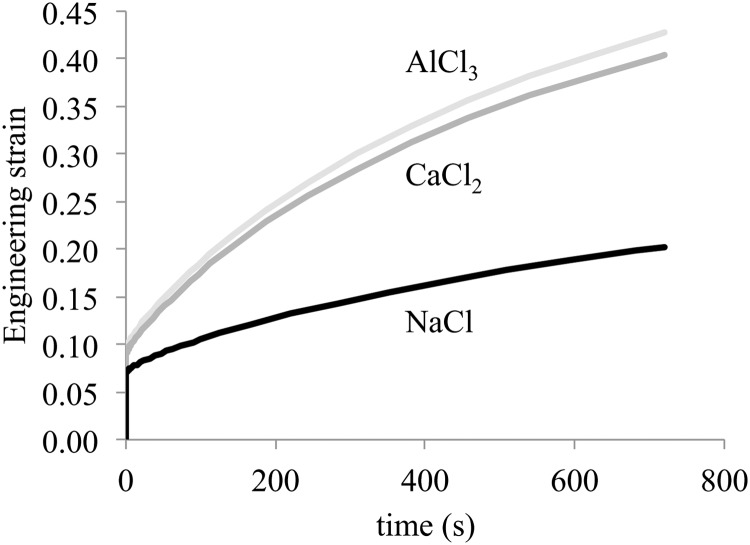
The creep responses for the three solutions are presented in Fig. 8. Upon application of the load, the tissue undergoes a nearly isochoric instantaneous axial compression and lateral expansion at t = 0⁺ followed by a time-dependent increase in deformation as its interstitial fluid exudes. The deformation in the CaCl₂ solution is considerably greater than that in NaCl; however, the deformation in AlCl₃ is only slightly greater than in CaCl₂. These results are in remarkable agreement with the experimental observations of Sokoloff [63]. They indicate that the experimental observations may be explained substantially by the differences in electrostatic and Donnan osmotic mechanisms, whereby the Donnan osmotic pressure is substantially reduced when switching from NaCl (0.146 MPa before application of the creep load) to CaCl₂ (0.061 MPa), but not much more when switching to AlCl₃ (0.040 MPa).

Fig. 8.

Effect of cation charge on the creep response of cartilage: The compressive engineering strain is reported for three solutions corresponding to a monovalent (NaCl), divalent (CaCl₂), and trivalent (AlCl₃) cation

5. Discussion

This study presents the finite element implementation of multiphasic materials using the framework of mixture theory. The multiphasic material consists of a solid matrix, a solvent, and any number of neutral or charged solutes. The finite element implementation is valid for three-dimensional analyses where the solid matrix may undergo finite deformation. Each constituent is intrinsically incompressible, though the porous solid matrix may undergo volume changes as interstitial fluid is exchanged with the pore space. To the best of our knowledge, this represents the first implementation of such a general mixture theory framework for applications to biological tissues and cells.

To successfully implement this formulation, it was necessary to provide a general method to solve for the unknown electric potential when the mixture includes any number of multivalent ions, as shown in Eqs. (2.17)–(2.19). It was found that the resulting polynomial equation only admits one valid solution, eliminating any ambiguity in the selection of the correct root. It was also necessary to enforce the divergence-free current condition of Eq. (2.12) as a constraint in the mass balance equation for every solute, as shown in Eq. (2.15), instead of enforcing it once for the entire mixture. This approach preserved symmetry in the equations for all the solutes, from which the effective normal flux ${\tilde{j}}_n^{\alpha }$ emerged as the natural boundary condition for these constituents. Since ${\tilde{j}}_n^{\alpha }=j_n^{\alpha }+I_e/F_c$, where I_e is the component of the current density normal to the surface, this boundary condition makes it easy to prescribe an electric current while also accounting for the type of electrode used for current transmission, as illustrated in Figs. 4 and 6.

The finite element implementation of this study also uniquely incorporates the well-recognized phenomenon of solute partitioning by accounting for steric volume exclusion and short-range electrostatic interactions via the solubility, κ^α, as well as long-range electrostatic interactions via the expression of Eq. (2.3) for the partition coefficient, ${\tilde{\kappa }}^{\alpha }$. The formulation accounts for the dependence of the partition coefficient on solid deformation as well as solute concentrations, as expressed in Eqs. (2.21)–(2.23).

Another distinctive characteristic of this formulation is the use of the effective fluid pressure $\tilde{p}$ and effective solute concentration ${\tilde{c}}^{\alpha }$ instead of the mechanoelectrochemical potentials of these species as essential variables. This approach preserves full consistency with the meaning of fluid pressure and solute concentration in related biphasic-solute and biphasic frameworks, while also providing a compact and elegant form for the flux relations of Eqs. (2.4) and (2.5). This formulation accepts every possible combination of mechanical, chemical, and electrical essential boundary conditions, making it straightforward to analyze the full complexity of multiphasic systems.

Several verification problems were presented that demonstrated the ability of the code to replicate known solutions, including problems that involve large deformations resulting from osmotic effects. The analytical solution of Eq. (3.3) for current flow in an electrolyte is original and was derived from first principles using the governing equations and boundary conditions presented above. It demonstrates the interesting phenomenon that such electrolytes can only carry a finite amount of current. Producing an agreement between the finite element solution and this analytical result required electrical grounding of the multiphasic medium by suitably prescribing specific conditions as presented above. Though the physical need for electrical grounding of circuits is a well-recognized phenomenon, the concept of electrical grounding of multiphasic media has not been addressed in prior studies of multiphasic materials. This concept is critical for a subset of multiphasic problems where all the mixture boundaries are impermeable to ions.

Furthermore, some illustrative problems were presented that replicate known experimental findings, such as current-generated stress and the influence of salt cation charge in cartilage, that are rarely addressed from theory. The current-generated stress analysis in Sec. 4.1 is the first such study to demonstrate this fundamental mechanism in a formulation that explicitly models the ions that carry the electric current. Though Frank and Grodzinsky's earlier electromechanical model proposed equations to describe current-generated stress [62], their framework did not explicitly model ions; instead, it provided an equation for electrokinetics that related electric current density to the gradient in fluid pressure and electric potential. The solution presented in Fig. 7 demonstrates that the phenomenon of current-generated stress may be predicted in a charged tissue directly as a result of ions flowing through it. In this multiphasic framework, the transient stress response to a step change in the current depends explicitly on the ion diffusivities, whereas the magnitude of the stress depends explicitly on the fixed-charge density. The multiphasic framework also explicitly accounts for the fact that the transference of energy at the electrodes is dependent on the nature of the electrodes and ions present in the tissue.

Similarly, the analysis of the response of cartilage to loading in electrolyte solutions having different cation charges, Sec. 4.2, is the first theoretical verification of the experimental findings reported by Sokoloff [63]. This example illustrated the ability of the finite element implementation to solve problems with multivalent ions just as easily as with monovalent ions. Furthermore, by facilitating the examination of the fluid pressure response, it helped reinforce the physical explanation for those findings.

Due to the potential complexity of multiphasic analyses and because of the limited collective experience of the research community with this framework, it may take a certain amount of effort to set up well-posed problems using this finite element implementation, especially when modeling charged constituents. Pitfalls that are otherwise familiar in finite element analyses, such as analysis failures when applying excessive loads in a finite deformation problem or lack of convergence when using excessively large penalty parameters for nearly incompressible solids, may not be as intuitive or familiar in multiphasic problems. Over time, users need to develop an intuitive understanding of the underlying physics of multiphasic problems to minimize such pitfalls in their finite element analyses.

For example, in the cell osmotic loading analysis (Fig. 2), it was necessary to model the solid matrix of the membrane using a nearly incompressible material with uncoupled strain energy contributions from the dilatational and distortional components of the deformation [57,65,66], because the initial large disparity in osmolarity between the extracellular and intracellular environments would otherwise produce excessive volumetric changes to the membrane that would lead to analysis failure; by using a large modulus for the dilatational response, volumetric changes could be kept sufficiently small, while using a small modulus for the distortional response ensured that the membrane had negligible resistance to area changes, consistent with the idealized assumptions of the K–K model. These modeling assumptions are consistent with the well-recognized behavior of cell plasma membranes as two-dimensional liquids. Similarly, in the electrolyte current flow analysis (Fig. 5), it was necessary to “ground” the electric potential to produce stable numerical results; this grounding is identical to the requirement in real electrical circuits, making it easier to understand intuitively.

The finite element implementation of multiphasic material behavior requires the identification of variables that are continuous across multiphasic boundaries. For the solvent and solutes, neither the pressure p nor the concentration c ^α satisfy this continuity requirement under general conditions. To identify such continuous variables, it is necessary to adopt a general form for the constitutive relations relating the mechanoelectrochemical potential to p and the c ^α. From these relations, the effective fluid pressure $\tilde{p}$ and solute concentrations ${\tilde{c}}^{\alpha }$ emerge as suitable nodal variables. The material functions Φ and ${\stackrel{\wedge }{\kappa }}^{\alpha }$ emerging from these relations must be described by explicit constitutive relations that accurately model the physicochemical behavior of the mixture. Assuming that the interstitial fluid is an ideal solution (Φ = 1 and ${\stackrel{\wedge }{\kappa }}^{\alpha }=1$), as commonly done in introductory chemistry textbooks, is strictly an oversimplification that would be equivalent to assuming that, for example, all elastic solids may be described by Hooke's law. This ideal physicochemical behavior may not accurately describe the results of real experiments, except for specialized conditions. Nonideal responses may be characterized from direct experimental measurements of the osmotic pressure of solutions, such as proteoglycan or chondroitin sulfate solutions, which may be used to formulate suitable constitutive relations for Φ [67–70]. Alternatively, microscopically based models of electrostatic interactions between charged macromolecules and electrolytes in aqueous solutions may be used to formulate such relations for Φ and γ^α (and thus ${\stackrel{\wedge }{\kappa }}^{\alpha }$), as proposed by Buschmann and Grodzinsky [71]. Similarly, the ability to model phenomena, such as partitioning of interstitial water between the intrafibrillar and extrafibrillar space of a fibrillar matrix [72], may be modeled by choosing suitable relations for Φ and formulating the fixed charge density on an extrafibrillar water volume basis, as shown by Wilson et al. [73]. The multiphasic finite element implementation in the open-source febio code is designed to accommodate any such implementation, thereby allowing deviations from ideal physicochemical behavior.

Finally, in order to properly model evolving conditions in materials and living tissues, it is necessary to account for the chemical reactions that form the basis for growth, remodeling, as well as other phenomena, such as phase transformations in charged gels and cells [74]. Having established a finite element framework for nonreactive multiphasic materials, it now becomes possible to extend this framework to include chemical reactions between any and all of the mixture constituents [52,75–77].

A driving need for developing this framework in open source is the absence of commercial codes that currently reproduce these capabilities. Commercial finite element programs generally provide separate modules for poroelastic analyses and mass transport. They do not offer modules where the governing equations for solid deformation, solvent flux, and solute transport are fully coupled, such as allowing the solid matrix and solutes to be charged, allowing momentum exchanges between the deforming solid and the solutes, or allowing solutes to be partially excluded from the pore space of the solid. An open source implementation implies that all users have unfettered access to the code and may freely extend and modify it, either for using it directly or for verifying other custom or commercial implementations.