The Fine-Scale Functional Correlation of Striate Cortex in Sighted and Blind People

Abstract

To what extent are spontaneous neural signals within striate cortex organized by vision? We examined the fine-scale pattern of striate cortex correlations within and between hemispheres in rest-state BOLD fMRI data from sighted and blind people. In the sighted, we find that corticocortico correlation is well modeled as a Gaussian point-spread function across millimeters of striate cortical surface, rather than degrees of visual angle. Blindness produces a subtle change in the pattern of fine-scale striate correlations between hemispheres. Across participants blind before the age of 18, the degree of pattern alteration covaries with the strength of long-range correlation between left striate cortex and Broca's area. This suggests that early blindness exchanges local, vision-driven pattern synchrony of the striate cortices for long-range functional correlations potentially related to cross-modal representation.

Introduction

Spontaneous neural activity is observed in the absence of structured sensory input or motor output (Arieli et al., 1995, 1996; Fiser et al., 2004; He et al., 2008, 2010), and these signals display informative spatiotemporal synchrony (Fox and Raichle, 2007). Slow fluctuations in the BOLD fMRI signal measured at rest reflect neural activity (Biswal et al., 1995; Greicius et al., 2003) and show correlation across brain regions (Hagmann et al., 2008; Greicius et al., 2009; van den Heuvel et al., 2009; Honey et al., 2009). Recent work has examined correlation structure at a fine (millimeter) scale, for example, revealing that the pattern of resting-state correlations in the somatosensory cortex of the squirrel monkey reflects the representation of individual digits of the hand (Chen et al., 2011). This scale of analysis allows for tests of the relationship between the spontaneous signals and the functional organization of sensory cortex.

In visual cortex, the fine-scale structure of correlations measured with fMRI reveals a pattern aligned with retinotopy (Heinzle et al., 2011; Jo et al., 2012), which is the mapping of the visual field to the 2D surface of cortex. Spontaneous neural signals may be organized by this fundamental, functional property of visual cortex, linking together neurons that share representation of similar positions in the visual world. A limitation to such claims, however, is that these studies have generally not tested whether the pattern of correlations reflect visual function per se or are instead an intrinsic property of cortex that happens to align with retinotopy. This is a plausible concern as retinotopic organization is a spatially smooth gradient of eccentricity and polar angle visual field position across the cortex, and thus could resemble other spatial gradients of spontaneous neural activity, or even non-neural physiologic processes.

The current study asks whether the fine-scale properties of functional correlation reflect subtle, specific properties of retinotopic organization. We examine in particular the first cortical visual area, the striate cortex. We test whether resting-state correlations display “magnification” along the eccentricity axis and enhanced correlation along the vertical meridian between hemispheres, both specific functional properties of the visual cortex.

We then examine how the pattern of fine-scale correlation is altered in blindness. Prior studies demonstrate that the structure (Park et al., 2009; Trampel et al., 2011) and function (Cohen et al., 1999; Sadato et al., 2002; Liu et al., 2007; Bedny et al., 2011; Watkins et al., 2012) of striate cortex are altered in blind people.

To date, studies of resting-state signals in blind people have only examined whole-region correlations, finding a reduction in correlation of extrastriate (although not striate) occipital cortex between hemispheres (Watkins et al., 2012). In animal studies, visual experience drives the pruning of diffuse synaptic connections in the occipital cortex (Innocenti and Price, 2005), leading to the prediction of an altered (perhaps broadened) pattern of fine-scale correlation in the visual cortex of blind humans.

To allow comparisons between blind and sighted subjects within a common framework, we make use of recent methodological advances that establish hemispheric homology and functional assignment based upon cortical surface topology. Gray matter surface alignment using gyral landmarks (Fischl et al., 1999) allows for accurate prediction not only of the boundaries of striate cortex (Hinds et al., 2008) but the assignment of retinotopic polar angle and eccentricity (Benson et al., 2012).

Materials and Methods

Subjects.

A total of 47 subjects participated in resting-state experiments (Table 1; 28 females and 19 males), 25 of whom had severe or complete vision loss, and 22 normally sighted controls. The blind participants (mean age 54) varied in the age at which they lost vision (Table 1), with 16 losing sight before the age of 18. The 22 sighted subjects had normal or corrected-to-normal visual acuity and were on average younger (mean age 37). As normal aging is associated with changes in resting state correlations, which could confound our measures (Zuo et al., 2010; Ferreira and Busatto, 2013), we identified age-matched subgroups of 12 subjects each for our two populations, each of which had a mean age of 48. Participants were screened to exclude those who had recently taken cyclooxygenase-1 inhibitors (e.g., ibuprofen). Handedness was assessed using a standard questionnaire (Bryden, 1982). The study was approved by the University of Pennsylvania Institutional Review Board, and all subjects provided written informed consent.

Table 1.

Subject population demographics^a

ID	Sex/age (yr)/handedness			Age onset/severity (yr)	Visual acuity	Cause/notes
B01*	F	33	L	0/0	LP	Congenital hypoplasia
B03*	F	32	R	0/18	NLP	Retinopathy of prematurity (ROP)
B04*	M	59	R	28/32	NLP	Diabetic retinopathy
B05*	F	23	R	0/18	LP	Congenital cataracts, detached retinas
B06*	F	48	—	0/20	NLP	ROP; glaucoma; vitreous hemorrhage
B07*	F	55	R	8/8	NLP	Uveitis
B08*	F	53	A	0/0	NLP	ROP
B09*	F	61	—	40/50	HM	Retinitis pigmentosa (RP)
B10*	M	58	R	0/0	NLP	ROP
B12*	F	46	R	8/8.5	NLP	RP
B13*	M	58	R	0/0	NLP	ROP
B17*	M	48	R	0/0	HM	ROP
B02	F	69	R	7/7	HM	Cone-rod dystrophy
B11	F	69	R	13/35	HM	Juvenile macular degeneration
B14	F	62	R	0/0	NLP	ROP
B15	M	40	R	36/36	HM	Glaucoma (primary); cataracts (secondary)
B16	F	61	R	0/16	HM	Optic atrophy
B18	M	50	R	0/0	HM	Congenital cataracts
B19	M	53	R	20/35	HM	Congenital infection
B20	F	63	R	54/56	NLP	Diabetic retinopathy; detached retina
B21	M	69	R	0/15	NLP	RP; glaucoma (secondary); detached retinas
B22	F	61	R	14/14	NLP	Retinoblastoma; left eye blind at age of 3; right at 14
B23	M	48	R	12/12	NLP	Trauma
B24	M	62	L	0/9	HM	Congenital cataracts; glaucoma (secondary)
B25	F	69	R	0/0	NLP	Congenital optic atrophy
S01*	M	33	R	—	—	—
S06*	M	41	R	—	—	—
S11*	M	32	R	—	—	—
S13*	F	58	R	—	—	—
S14*	F	52	R	—	—	—
S15*	F	46	R	—	—	—
S16*	M	48	R	—	—	—
S17*	F	68	R	—	—	—
S19*	F	43	R	—	—	—
S20*	F	51	R	—	—	—
S21*	M	58	R	—	—	—
S22*	F	44	R	—	—	—
S02	F	22	R	—	—	—
S03	M	25	A	—	—	—
S04	M	27	R	—	—	—
S05	F	25	R	—	—	—
S07	M	26	R	—	—	—
S08	F	22	R	—	—	—
S09	M	28	R	—	—	—
S10	F	22	R	—	—	—
S12	F	19	R	—	—	—
S18	F	24	R	—	—	—

^aTwenty-five blind (B1–B25) and 22 sighted (S1–S22) individuals participated in the study. The blind population was heterogeneous with respect to age of onset and cause, although all had severe vision loss. R, Right-handed; L, left-handed; A, ambidextrous; NLP, no light perception; LP, best vision light perception only; HM, best vision hand-motion perception; —, missing value.

*Age-matched subgroups of 12 participants each.

MRI.

Scans were acquired using a 3-Tesla Siemens Trio with an 8-channel Siemens head coil. Echoplanar BOLD fMRI data were collected with whole-brain coverage (TR = 3 s; 3 × 3 × 3 mm isotropic voxels; 42 axial slices, interleaved; 64 × 64 voxel in-plane resolution). Head motion was minimized with foam padding. Functional scans were obtained in total room darkness with subjects instructed to keep their eyes closed for a duration of 150 TRs (38 subjects). Nine sighted subjects were scanned under a second protocol, otherwise identical except for a duration of 160 TRs; only the first 150 TRs of these data were used to equate data length across subjects. Stray light in the room was minimized by the use of opaque shades and covering light sources. Continuous pulse oximetry was recorded for 40 of 47 scanning sessions. One or more anatomical images using a standard T1-weighted, high-resolution anatomical scan of Magnetization Prepared Rapid Gradient Echo (3D MPRAGE) (160 slices, 1 × 1 × 1 mm, TR = 1.62 s, TE = 3.09 ms, TI = 950 ms, FOV = 250 mm, FA = 15°) were acquired for each subject.

Image preprocessing.

Anatomical data from the subjects were processed using the FMRIB Software Library (FSL) toolkit (http://www.fmrib.ox.ac.uk/fsl/) to correct for spatial inhomogeneity and to perform nonlinear noise reduction. Brain surfaces were reconstructed and inflated from the MPRAGE images using the FreeSurfer (v5.1) toolkit (http://surfer.nmr.mgh.harvard.edu/) as described previously (Dale et al., 1999; Fischl and Dale, 2000; Salat et al., 2004).

Raw echoplanar (volumetric) data were sinc interpolated in time to correct for the slice acquisition sequence and motion corrected with a six parameter, least-squares rigid body realignment routine using the first functional image as a reference. The echoplanar data in subject space were coregistered to subject-specific anatomy in FreeSurfer using FSL-FLIRT with 6 degrees-of-freedom under a FreeSurfer wrapper (bbregister).

Serial whole-brain (right and left hemisphere) surface maps for each individual TR were registered to a common FreeSurfer template surface pseudo-hemisphere (fsaverage_sym) using the FreeSurfer spherical registration system (Fischl et al., 1999; Greve et al., 2011).

The surface-sampled raw data were smoothed using a 2 mm full-width at half-maximum, 2D Gaussian kernel. Modest spatial smoothing increases the sensitivity and specificity of the final correlation structure (Vincent et al., 2006) while decreasing spatial noise (Greicius et al., 2003). A 0.01–0.08 Hz bandpass filter was then applied to the time series (Biswal et al., 1995; Yeo et al., 2011). The effect of nuisance variance was removed, including the effects of the scan, spikes (periods of raw signal deviation >2 SDs from the mean), head motion as modeled by 3 translation and 3 rotation covariates, and cardiac and respiratory fluctuations (when available). The latter were derived from raw, 50 Hz pulse oximetry measurements taken during BOLD scanning. After aligning raw pulse data with DICOM image time stamps, raw pulse arrays were split into high (cardiac) and low (respiratory) frequency covariates (Verstynen and Deshpande, 2011). Global signal covariates were not included as these may bias correlation measures (Saad et al., 2012).

Test for differences in head motion.

For each subject, absolute head displacement during a given scan was recorded. The Euclidean distance of translational movement of the head from one TR to the next was obtained, then averaged over time. This measure has been shown to scale with artifactual short-range correlation in resting-state studies (Van Dijk et al., 2012; Power et al., 2012).

Striate cortex mean surface area and deformation values.

Regional cortical surface area (mm²) was defined as the sum of the area enclosed by all vertices comprising striate cortex at the gray-white matter boundary. The mean areal deformation warp for striate cortex on the white surface was quantified by obtaining the log of the determinant of the Jacobian matrix (Fischl et al., 2001) for all striate vertices. The SD of these values may be taken as a “goodness of fit” for registration of any one participant's cortical surface anatomy within striate cortex to the anatomical template.

Striate indexing and difference matrices.

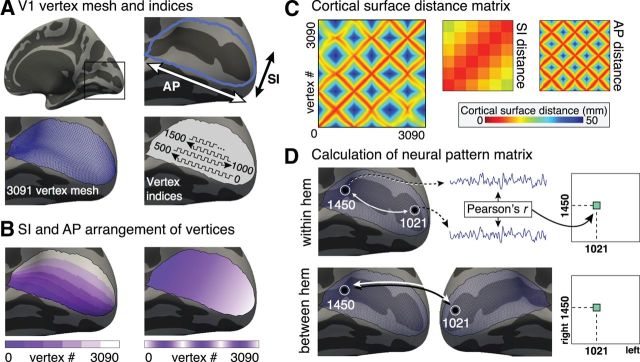
As retinotopic mapping data cannot be collected for blind subjects, we identified 3091 vertices in the occipital cortex of each subject that fall within a probabilistic striate cortex boundary (Hinds et al., 2008). The vertices were indexed (Fig. 1A) so that their ordering reflects a steady progression along the superior–inferior (SI) axis (corresponding to polar angle) and the anterior–posterior (AP) axis (corresponding to eccentricity) (Fig. 1B). The cortical surface distance matrix (Fig. 1C) expresses the Euclidean distance along the flattened cortical surface between any two vertices. Matrices may also be constructed which express distance between the pairs of vertices projected onto either the SI or AP axes.

Figure 1.

Measurement of fine-scale correlation structure. A, V1 vertex mesh and indices. The cortical patch corresponding to striate cortex (area V1) is centered about the calcarine sulcus on the medial aspect of the occipital lobe. V1 was identified by position in surface topology. The two primary axes of striate cortex (AP and SI) are indicated and correspond to the eccentricity and polar angle dimensions of retinotopic organization, respectively. In standard template space, V1 comprises 3091 surface vertices, as outlined on the surface mesh. V1 vertices were indexed as outlined in A (lower right). The selected arrangement was to facilitate visual display of the pattern matrices and has no effects upon the quantitative results of the analyses. B, SI and AP arrangement of vertices. The two panels illustrate the indexing of vertices within area V1 by mapping different shades of color to index values. These color scales demonstrate how the vertices were numbered along 6 discrete bands along the SI dimension (corresponding to polar angle). Within each band, vertices were then numbered along the AP dimension (corresponding to eccentricity). C, Cortical surface distance matrix. The distance along the cortical surface may be calculated for any pair of points within striate cortex. The distances between all possible pairings of vertices are shown as a matrix. The structure seen within the matrix is a consequence of the numbered ordering of the vertices shown in A and B. This structure may be more easily understood by examining the matrices that express distance between points only along the SI or AP directions. D, Calculating the neural pattern matrix. Within the set of indexed V1 vertices, the Pearson's (R) correlation of the resting-state fMRI data between each pair of vertices was obtained. Each pairwise correlation provided one cell of a resulting pattern matrix. The pattern matrix was derived for each subject for both within-hemisphere correlation structure and between-hemisphere correlation structure.

Generating pattern matrices.

Within-hemisphere pattern matrices for the striate cortex from each hemisphere from each participant were generated by obtaining the correlation of the processed time-series for all pairings of the vertices (Fig. 1D). A between-hemisphere pattern matrix was generated for each subject by obtaining the correlation of time-series data from pairings of the vertices in the striate cortex in one hemisphere with those of the other hemisphere. In all, two within-hemisphere pattern matrices (right and left) and one between-hemisphere pattern matrix were generated for each subject; the within-hemisphere matrices for each subject were averaged. Following a Fisher's r-to-z transformation, group mean within-hemisphere and between-hemisphere pattern matrices were created for the sighted and blind groups.

A “corticocortico receptive field” (CCRF) (Heinzle et al., 2011) representation was also constructed and used to test differences in correlation between vertices representing the vertical and horizontal meridia. For each subject, the between-hemisphere CCRFs were separately obtained for those vertices within 45° of the vertical and horizontal meridia. For each CCRF, the difference in mean correlation values (z′) between the center and periphery of the CCRF was calculated (center being defined as within 25% the long axis length of the center of the CCRF plot).

Characterizing digital image structure with simulations.

Although we intend to measure the correlation structure of spontaneous neural activity, some organization in our measure will be induced by extrinsic digital processing from the imaging method and the surface reconstruction approach. To characterize this artifact component of the pattern matrix, we first created spatially uncorrelated (volumetric) random signals, which were then passed through our preprocessing and analysis routines. The analyses from 9 randomly selected subjects were repeated but supplied with this fabricated data containing 150 volumetric image time-series of normally distributed pseudorandom values. The fabricated data were passed through the same image preprocessing routine that matched the analysis conducted for a given subject, including the following: resampling to the standard surface space, 2 mm surface smoothing, bandpass filtering, and linear regression of nuisance covariates. Within- and between-hemisphere pattern matrices were then generated for the simulated, processed time-series data. As before, individual within-hemisphere and between-hemisphere pattern matrices were averaged following a Fisher's r-to-z transformation into group pattern matrices. Ten such simulations were conducted, and the data from all simulations averaged together to produce a representation of the digital image structure induced by the processing pipeline. The resulting structure (Fig. 2, left panels) is a consequence of the surface interpolation technique and the minimal spatial smoothing that was applied to the simulated data. No structure is seen in the simulation for between-hemisphere correlations (Fig. 2, right panels). This is both sensible, given the spatial separation of the hemispheres, and reassuring, as signals from vertices close to the interhemispheric fissure could in principle be mixed.

Figure 2.

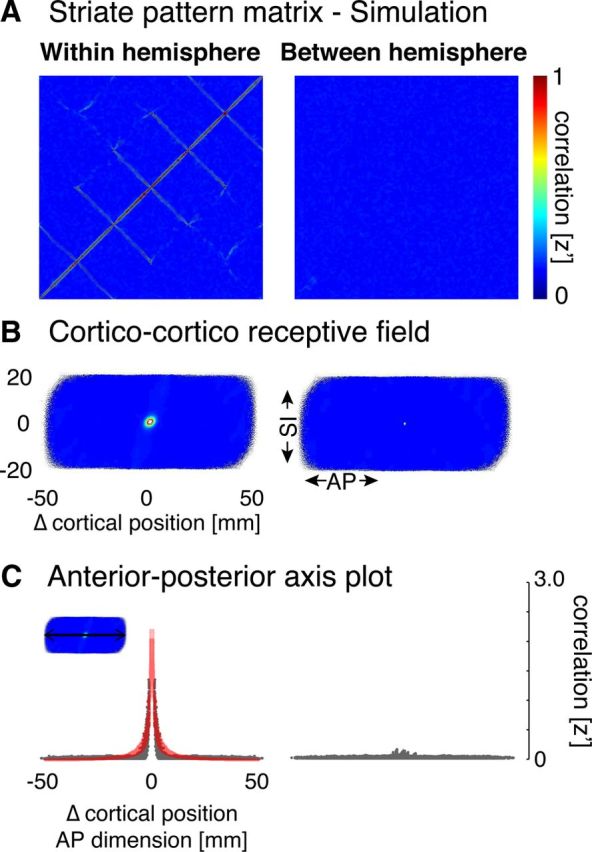
Pattern matrices for simulated fMRI data. A, Within- and between-hemisphere striate pattern matrices. Normally distributed, pseudorandom data were passed through the particular anatomical and image processing routines for 9 randomly selected subjects. The resulting pattern matrices for simulated data were averaged following a Fisher's r-to-z transformation. Structure about the diagonal of the matrix is readily apparent in the within-hemisphere matrix, which we term “digital image structure.” B, Corticocortico receptive field depictions derived from the pattern matrices. Correlation data depicted in A are replotted for the receptive field view by change (in millimeters of cortex) along the AP and SI dimensions. A local, circular area of high correlation within 10 mm of each vertex is seen for the within-hemisphere simulation. C, AP axis plots. A cross-section along the AP dimension of each receptive field plot is shown. Each gray point indicates a given pairing of vertices, with the position along the x-axis given by the distance between the points in millimeters along the AP axis. Red represents the fit of the decaying exponential model.

Model fitting.

The simulations revealed digital image structure in the within-hemisphere pattern matrix that was well fit by a decaying exponential. In empirical data, the local smoothness in correlations appeared to contain both this decaying exponential and a more spatially extended, 2D Gaussian structure. Iterative fitting to group average data was performed in MATLAB (MathWorks) using a weighted nonlinear regression (nlinfit) for within- and between-hemisphere resting correlation patterns. As the digital image structure did not vary between groups, within-hemisphere pattern matrices (both full matrices and CCRF view) had the digital image artifact removed for display purposes using a piecemeal regression based on the decaying exponential component of the best-fit model.

Tests of group differences.

Group differences in the amplitude of fine-scale correlations were tested by obtaining for each subject the average correlation across all cells in the pattern matrix for that subject.

We conducted leave-one-out analyses to test for group differences in the spatial pattern of the correlation matrices. The aggregate pattern matrix of all sighted subjects except one was obtained. The correlation of the pattern matrix of the left-out subject to the aggregate was obtained and termed the pattern similarity score. This was repeated in a typical leave-one-out fashion. For the blind subjects, the pattern matrix for a given subject was correlated with each possible leave-one-out aggregate of the sighted or blind subjects, and the average correlation across these partitions obtained.

Long-range correlation with Broca's area.

An anatomical ROI corresponding to left Broca's area was defined on the FreeSurfer template (fsaverage_sym) as the union of the pars opercularis and pars triangularis (Destrieux et al., 2010). The correlation was then obtained for each subject between the average rest signal within Broca's area and the left striate cortex. A whole cortical surface analysis to test for group differences in long-range correlation with left striate cortex was also conducted following 15 mm FWHM surface smoothing. Signal correlation with the mean left-hemisphere striate signal on a vertex-by-vertex basis for each subject was calculated for the whole brain. Unpaired, two-tailed t tests were used to assess between-group differences. To account for multiple-comparison testing, a cluster-based (whole map), false discovery rate (Heller et al., 2006) was computed and only clusters with q values <0.05 retained.

Results

We obtained BOLD fMRI data from sighted and blind participants while they rested in the scanner in darkness. The location of the striate cortex was defined for each subject based upon the pattern of cortical surface topology, and within this region we obtained the resting state signal correlation of every pair of cortical points. We begin by characterizing the pattern of these striate correlations in sighted subjects and then examine how the correlation structure is altered in blindness.

Striate cortex has a Gaussian point-spread function of correlation within and between hemispheres

Figure 3A (left) is a matrix of average correlation values (across all sighted subjects) between any pair of points in the striate cortex (after modeling and removing the effects of local digital image structure; see Materials and Methods). The pattern within the matrix reflects the particular numerical ordering used to map 2D locations within striate cortex to the rows and columns of cells (Fig. 1A). Visual comparison with model predictions in Figure 1C suggests primarily an effect of cortical surface distance: the correlation between two striate cortex points declines as the surface distance between the pair increases. This effect is present both along the SI axis, corresponding to polar angle, seen as a decline in correlation strength with distance from the diagonal of the matrix, and along the AP axis (corresponding to eccentricity), which produces the diamond-shaped changes in correlation as the indexed vertices traverse from the occipital pole forward along the calcarine sulcus and back.

Figure 3.

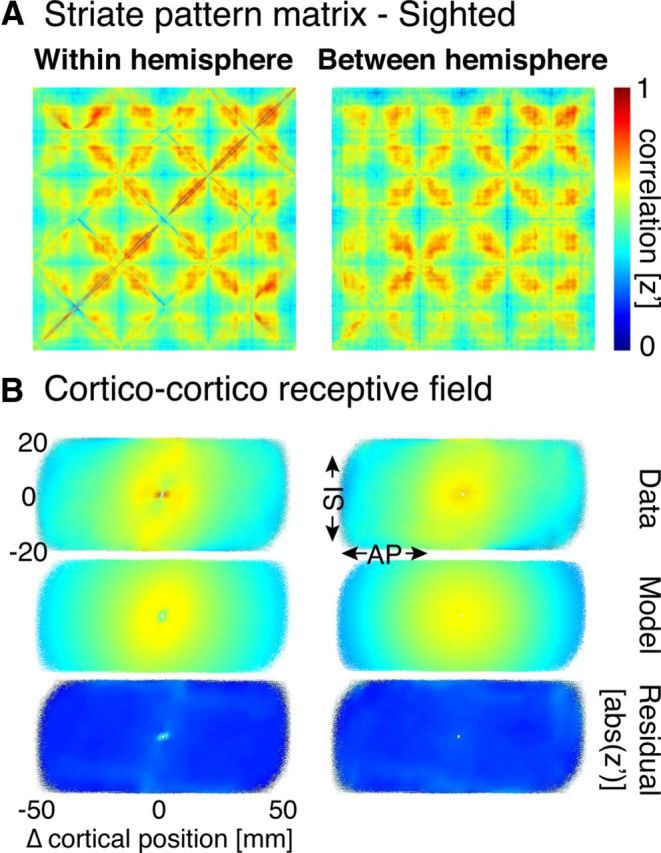
Striate pattern matrices from sighted subjects. A, Within- and between-hemisphere striate pattern matrices. Following a Fisher's r-to-z transformation, the individual pattern matrices from 22 sighted subjects were averaged. The effect of digital image structure in the within-hemisphere modeled and removed from both this representation and in B. B, Corticocortico receptive field depictions derived from the pattern matrices. In the first row, correlation data depicted in A are replotted for the receptive field view by change (in millimeters of cortex) along the AP and SI dimensions. The second row represents the 2D Gaussian fit to these data. The third row represents the absolute value of the residuals of the model fits to the data. Minimal residual structure is seen, supporting the validity of the model.

These data may also be expressed as a CCRF Heinzle et al., 2011) by averaging the 2D field of correlations surrounding each vertex (Fig. 3B, left). A 2D Gaussian was found to fit well the decay in correlation strength with distance and had a similar width in both the AP (AP σ = 17.4 mm) and SI directions (SI σ = 19.7 mm).

We next examined the resting-state pattern matrix derived from between-hemisphere correlations for vertices with mirror-matched visual field positions. We were motivated to test mirror-symmetric points of visual cortex given prior observations of interhemispheric correlations in sensory cortical areas (Heinzle et al., 2011; Jo et al., 2012). The between-hemisphere pattern matrix shows a spatial pattern very similar to the within-hemisphere matrix (the Pearson correlation between the two aggregate matrices is 0.91).

In the CCRF representation (Fig. 3B, right), a local correlation structure is again seen that is fit by a 2D-Gaussian. The width of this local correlation structure was found to be nearly identical to that observed in the within-hemisphere data, in both the AP (σ = 17.4 mm) and SI dimensions (σ = 19.1 mm). Given the spatial separation of the hemispheres, this organization cannot be attributed solely to the physical proximity of adjacent patches of cortex.

Therefore, both the within- and between-hemisphere functional correlations of the striate cortex contain structure that can be described as a Gaussian point-spread function of local correlation of resting signals over ∼20 mm of cortex.

The pattern of striate correlations reflect surface distance, not degrees of visual angle

The Gaussian point-spread of correlation structure within and between hemispheres suggests that nearby (and mirror homologous) regions of cortex share neural signal. Given retinotopic organization, a reasonable hypothesis is that striate cortex correlations reflect the similar receptive field tuning (or mirror symmetric tuning) of nearby neurons. It is possible, however, that the observed functional correlations do not reflect retinotopy per se, but instead physical proximity on the cortical surface (or proximity to a hemisphere symmetric location). These two accounts differ as to whether the proper units in which to model the pattern matrix are those of millimeters of cortical distance, or change in visual angle. As a consequence, these two models make different predictions and thus may be distinguished, in the setting of cortical magnification of eccentricity for which a unit change in cortical distance implies a different change in represented visual angle at different points within the cortex.

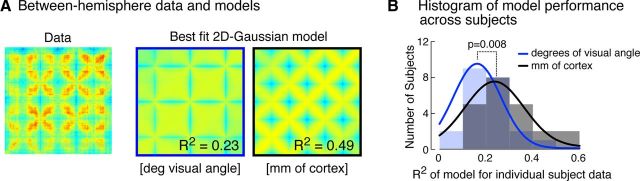
We tested whether the Gaussian point-spread model of local correlation structure better explained the entire pattern matrix whether it was cast in millimeters of cortical distance or degrees of visual angle. This test is difficult to conduct for the within-hemisphere pattern matrix, as there is an additional free parameter (the modeling of digital image structure with an exponential decay; see Materials and Methods). Therefore, we examined model performance in the between-hemisphere pattern matrix. This test is implemented using an anatomically based model of retinotopic organization (Benson et al., 2012), which assigns polar angle and eccentricity values to each vertex within the left and right striate cortices with an accuracy comparable to fMRI retinotopic mapping.

Figure 4A represents the average, between-hemisphere pattern matrix for the 22 sighted participants. Adjacent are the best-fit 2D-Gaussian models, calculated in terms of degrees of visual angle and in terms of millimeters of cortical distance, displayed in matrix form. The model calculated in terms of millimeters of cortical distance is clearly superior, with an R² value twice that of the model that used degrees of visual angle (0.49 vs 0.23).

Figure 4.

Comparison of modeling by visual angle and cortical distance. A, Sighted aggregate, along with models based on visual angle and cortical distance (mm). The between-hemisphere aggregate (n = 22) pattern matrix for the sighted group was modeled using a 2D Gaussian with units either of change in degrees of visual angle or change in cortical position between vertices. The R² of the model fit to the aggregate pattern matrix is shown. B, Histograms of leave-one-out model performance across all sighted subjects. The 2D Gaussian model in units of either cortical position of visual angle was fit to an aggregate pattern matrix derived from 21 subjects. The correlation of this fit to the pattern matrix of the 22nd subject was obtained in a leave-one-out fashion. The Gaussian model cast in units of cortical distance had superior performance.

We formalized this impression using a leave-one-out analysis (see Materials and Methods). Figure 4B presents a histogram of R² values obtained across subjects for the two models. A paired t test confirmed the superior performance of the model that used cortical distance (t₍₂₁₎ df = 2.9, p = 0.008). Although not formally tested, it is visually apparent that the within-hemisphere pattern matrix (Fig. 3A, left) also reflects correlations over millimeters of cortex, as opposed to visual angle.

Having rejected degrees of visual angle as the relevant units of the decline in correlation strength with distance, we next asked whether the correlation function is better characterized by distance in 2D-surface or 3D-volumetric space. A finding in support of the latter would implicate non-neural mechanisms, such as pulsatile blood flow or head motion, as the basis of the correlation measures. Although the surface and volumetric distance measures are strongly correlated, they may be distinguished because of the folding of the cortical surface plane. We repeated the leave-one-out analysis, now comparing a surface-based, 2D Gaussian decay model with a spherical 3D Gaussian decay model based on direct Euclidian distance in the subject's idiosyncratic, 3D volumetric space. The 2D surface-model performed significantly better than the 3D, volumetric model (paired two-tailed t test, t₍₂₁₎ df = 2.8, p = 0.01). An “average” 3D model fit across subjects is not meaningful given individual differences in cortical folding.

This finding suggests that the pattern of resting state correlations in striate cortex within and between hemispheres is best understood as a connection between homologous positions on the cortex that declines in strength with distance along the cortical surface.

Interhemispheric striate correlations do not differ between vertical and horizontal meridia

We asked whether between-hemisphere correlations vary for the vertical and horizontal meridia. In the human striate cortex, only those neurons with receptive fields close to the vertical meridian have monosynaptic, callosal connections (Clarke et al., 2000). Heinzle et al. (2011) observed greater between-hemisphere correlations of areas V1 and V3 for voxels representing the vertical meridian compared with the horizontal meridian. We replicated the Heinzle analysis in our data for between-hemisphere striate correlations and examined the height of the Gaussian point-spread function from individual subjects for vertices located close to the horizontal and vertical meridia of striate cortex. (with height computed as the difference between the center and surround of the Gaussian). No difference was found between those striate cortex points that represent the vertical meridian (mean z′ height = 0.10 ± 0.01 SEM across subjects) and those that represent the horizontal meridian (mean z′ difference = 0.11 ± 0.01 SEM across subjects).

We further examined only those vertex pairings for exactly mirror symmetric locations (the diagonal of the between-hemisphere pattern matrix). Across subjects, there was no greater correlation for pairings drawn from near the vertical meridian compared with the horizontal meridian. Indeed, the trend was for an effect in the opposite direction. In sum, we found no evidence of a special status for between-striate correlations arising from cortical points close to the vertical meridian.

The average pattern of striate correlation is similar in the blind and sighted

We find that the pattern of correlated signals between the striate cortices reflect visual cortex position, as opposed to visual field. Vision may be required, however, to establish or maintain the functional coupling between cortical points as defined by visual field location, even if the spread of correlation around those points is a function of cortical distance. To test this idea, we examined the within and between-hemisphere pattern matrix derived from a population of 25 blind participants (Table 1). Fourteen of these participants have no light perception, whereas the remainder have minimal light or hand-motion perception. The age at vision loss and cause of blindness in the group is also variable, although 18 of the 25 had reached their maximal visual impairment before the age of 18.

Despite the altered visual experience of this group, the average within-hemisphere, resting-state structure found was similar to that of sighted controls (Fig. 5A, left) in both pattern and amplitude. This was seen as well in the corresponding CCRF representation (Fig. 5B, left), which was well fit with the same 2D Gaussian and decaying exponential model fit. The Pearson correlation of the average, within-hemisphere pattern matrices from the blind and sighted populations was 0.78 (0.74 when calculated using only age- and gender-matched subjects). The across-subject, average pattern of between-hemisphere correlation (Fig. 5, right column) also resembled that of the sighted group. In this case, however, there was a greater difference between the sighted and blind groups, with a Pearson correlation of the average, between-hemisphere pattern matrices from the blind and sighted populations of 0.67 (0.53 when calculated using only age- and gender-matched subjects). A quantitative comparison of these pattern matrices is provided below.

Figure 5.

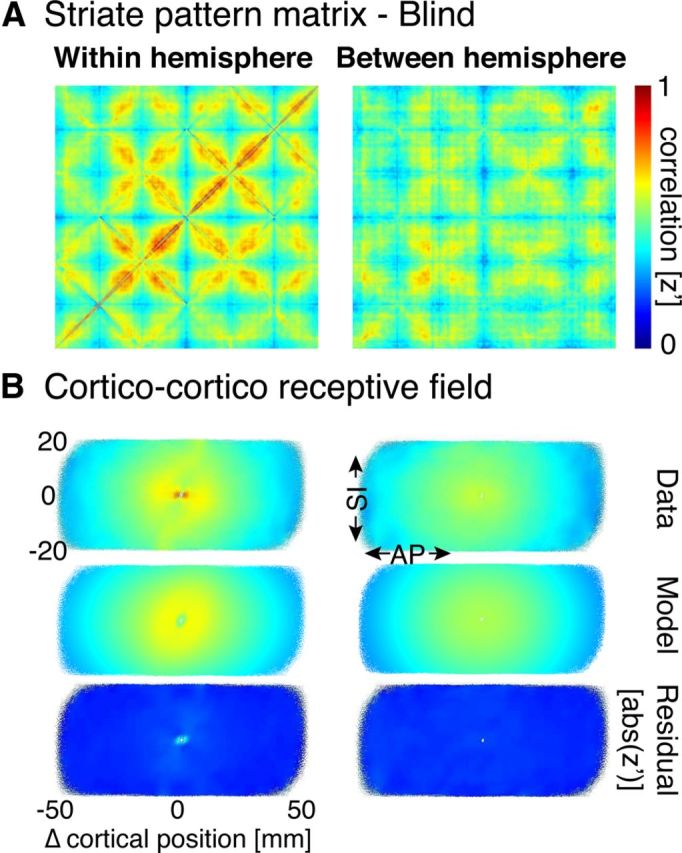
Striate pattern matrices from blind subjects. A, Within- and between-hemisphere striate pattern matrices. Following a Fisher's r-to-z transformation, the individual pattern matrices from 25 blind subjects were averaged. B, Corticocortico receptive field depictions derived from the pattern matrices. Conventions are as in Figure 3B.

For both the within- and between-hemisphere 2D Gaussian fits, the widths were similar but slightly wider than seen in sighted controls (within-hemisphere AP σ = 19.1 mm, SI σ = 14.4 mm; between-hemisphere AP σ = 20.4 mm, SI σ = 19.0 mm). These measures, however, are made in standardized units within a surface template space to which all subjects have been registered. The surface area of V1 tends to be smaller in the blind compared with the sighted (Park et al., 2009), an effect we replicate in our data (striate surface area in the blind: 1890 mm²; sighted: 2530 mm²; unpaired t test: t₍₄₅₎ df = 5.4, p < 0.001). This difference in surface area implies that surface distance measurements in the blind are inflated by 15% when measured in the standard space. After accounting for this effect, the between-hemisphere Gaussian spread of correlation is nearly equal in the blind and sighted when considered in absolute units of millimeters in native surface space.

The blind differ from the sighted in the pattern, not amplitude, of between-hemisphere striate correlation

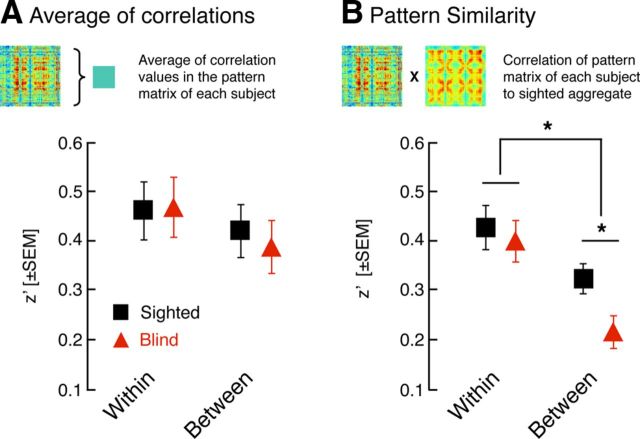
In across-subject, aggregate data, the blind and sighted populations have a similar appearing pattern of fine-scale striate correlation, although there is the suggestion of a group difference between hemispheres. We obtained a measure from our individual subjects to allow a statistical test for group differences.

We examined for each blind and sighted subject the average correlation across all vertices in the within- and between-hemisphere pattern matrices (Fig. 6A). This is a measure of the average amplitude of fine-scale correlation for each individual, independent of the pattern. There was no difference between the populations for either the within-hemisphere (two-tailed t₍₄₂₎ df = 1.5, p = 0.14) or between-hemisphere measure (two-tailed t₍₄₂₎ df = 1.1, p = 0.27). This was the case as well for tests restricted to 12 age- and gender-matched subjects from each group (within t₍₂₂₎ df = −0.1, p = 0.93; between t₍₂₂₎ df = 0.4, p = 0.67).

Figure 6.

Group comparisons of the amplitude and similarity of pattern matrices. A, Average of correlations. The average correlation across all vertices in the within- and between-hemisphere pattern matrices was obtained for each subject and then averaged across the age-matched sighted and blind groups. No differences between the blind and the sighted groups in this measure of the aggregate amplitude of correlation strength were seen. B, Pattern similarity. The within- and between-hemisphere pattern matrix from each subject was correlated with the aggregate pattern matrix across sighted subjects (using a leave-one-out approach). The average of these correlations was obtained within the age-matched sighted and blind groups. The between-hemisphere pattern matrices from blind subjects were consistently less similar to the aggregate sighted matrix.

We next examined the similarity of the pattern matrix obtained for each subject to the aggregate pattern matrix of the sighted subjects (Fig. 6B). This is a measure of the structure of the pattern matrix, independent of its overall amplitude. A leave-one-out approach was used so that the pattern matrix of the subject being examined did not contribute to the aggregate matrix (see Materials and Methods). Within hemisphere, there was no difference between the sighted and blind populations in either the entire (two-tailed t₍₄₈₎ df = −0.8, p = 0.47) or age-matched subgroups (two-tailed t₍₂₂₎ df = −0.4, p = 0.67). Between hemispheres, however, there was a lower average correlation of pattern matrices from individual blind subjects to the sighted aggregate (two-tailed t₍₄₈₎ df = −2.8, p = 0.01). This was also the case in the matched subgroups (two-tailed t₍₂₂₎ df = −2.2, p = 0.04). A t test of the interaction of the effect of group and within-hemisphere/between-hemisphere comparison confirmed that the difference between the groups is greater for the between-hemisphere pattern matrices (two-tailed t₍₂₂₎ df = 3.2, p = 0.004).

There is variability in age of onset of vision loss in our population of blind subjects. We conducted post hoc tests to examine whether individual differences in the structure of the between-hemisphere pattern matrix is related to age at vision loss. We treated age of vision loss as a categorical variable (congenital, less than age 18, after age 18) and did not observe a significant relationship between striate pattern similarity and age of vision loss in an ANOVA (F_(2,22) = 0.219, p = 0.8). Independently tested, each blind group also tended to be different from the sighted group (congenitally blind vs sighted, one-tailed t₍₂₈₎ df = 1.6, p = 0.06; blind before age 18 vs sighted, one tailed t₍₂₉₎ df = 28, p = 0.11; blind after age 18 vs sighted, one tailed t₍₂₉₎ df = 2.5, p = 0.009). We note, however, that there are multiple factors that contribute to the integrated visual deprivation that a given subject experiences (e.g., severity of blindness, trajectory of vision loss, anterior vs posterior segment damage) and that these factors are not controlled in these post hoc groupings.

The finding of a group difference in the pattern of resting-state correlations does not distinguish between two alternatives: (1) the blind population has the same aggregate spatial organization of functional connectivity as the sighted, only more variable in individuals; or (2) the blind population has a systematically different between-hemisphere pattern matrix from that seen in the sighted. To test this idea, we repeated our pattern similarity, leave-one-out analysis, only now comparing it with the aggregate matrix of the blind population. If we found that the data from blind individuals are better correlated with the aggregate of other blind subjects than the aggregate of sighted subjects, this would support a claim that the blind have a systematically different between-hemisphere connectivity structure. This was not found. Instead, essentially the same average correlation was found for blind subjects compared with a blind aggregate (z′ = 0.24) as blind subjects compared with the sighted aggregate (z′ = 0.24, paired t₍₂₄₎ df = 0.31, p = 0.76 for the comparison).

Overall, the effect of blindness upon resting-state, striate correlations is subtle. Averaged across individuals, the blind and the sighted have a generally similar pattern of fine-scale correlation. This suggests that blindness does not produce a systematically different organization of correlations within and between the striate cortices. Further, individual blind subjects do not show a reduction in the average strength of point-to-point striate correlations, either within or between hemispheres. The groups do differ in that the pattern of correlations observed in individual blind subjects is different from that of the sighted (as is shown in Fig. 6B), but these differences are not the same across blind individuals. We next asked whether this individual variation in the blind is related to another, established measure of functional alteration in blindness.

Alteration of the between-hemisphere correlation pattern is related to Broca's area correlation in the blind

Changes in long-range, interregional, functional correlation have been previously reported in the blind. Specifically, left hemisphere occipital areas have been observed to have increased resting signal correlation with anterior language regions (specifically, Broca's area) in the blind (Bedny et al., 2011; Watkins et al., 2012). These alterations in correlation have been proposed to subserve cross-modal representations in occipital cortex.

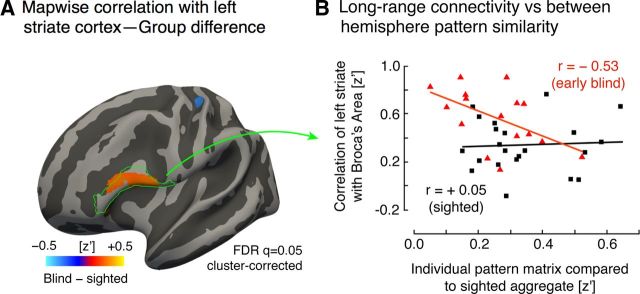
We examined whether individual differences in the striate correlation pattern could be related to the degree of long-range functional correlation between regions. First, we reproduced prior findings of altered long-range correlation in the blind (Fig. 7A). The thresholded map shows that a region within the pars opercularis and pars triangularis (classic Broca's area) has differential functional correlation to the left striate cortex in the blind and sighted, in general agreement with prior findings (Bedny et al., 2011; Watkins et al., 2012), although these prior studies used the lateral occipital cortex as a seed region. Also, in agreement with prior findings, a small area within the somatosensory cortex demonstrated decreased functional correlation to the left striate cortex in the blind population (Liu et al., 2007; Yu et al., 2008; Bedny et al., 2011).

Figure 7.

Differences in striate cortex long range correlation and its relation to pattern similarity. A, Whole-brain group difference in correlation with mean left-hemisphere striate cortex signal. Red represents a larger average correlation with the left striate cortex in the blind group compared with the sighted controls. No differences at this map-wise threshold were found either on the medial surface of the brain or the right hemisphere. The location of Broca's area is indicated in green outline (defined as the union of the pars opercularis and pars triangularis). B, Long-range correlation versus interhemispheric pattern similarity. The between-hemisphere pattern similarity measure from each subject (Fig. 6B) was related to the correlation between the left striate cortex and Broca's area. A significant relationship between these measures was observed for blind group (red triangles), but not for the sighted group (black squares).

Age of onset of blindness was related to long-range Broca's area correlation. An ANOVA that modeled a categorical effect of age of blindness onset (congenital, before 18 years old, or after 18) confirmed lower long-range correlation scores in those who became blind after the age of 18 (t₍₁₉₎ df = −2.4, p = 0.03).

We then asked whether the degree of long-range functional correlation with Broca's area is related to variation in between-hemisphere striate pattern. Effectively, is blindness associated with the exchange of local, synchronous interhemispheric visual cortex correlation for long-range, cross-modal correlation? We modeled long-range functional correlation for the blind participants within an ANOVA that included the between-hemisphere striate pattern similarity score, the categorical effect of age of blindness onset, and the interaction of these. Overall, there was a significant negative relationship between the striate pattern similarity and long-range functional correlation with Broca's area (t₍₁₉₎ df = −2.5, p = 0.02). That is, those blind participants who had more altered between-hemisphere striate signals had a greater left striate correlation with Broca's area. This effect interacted with age of blindness onset, with those participants who were blind at birth or before the age of 18 (Fig. 7B, red triangles) showing a stronger relationship between these two measures (t₍₁₉₎ df = 2.4, p = 0.03).

In the sighted population, no relationship was seen between across-hemisphere pattern similarity in striate cortex and long-range correlation between the left striate and Broca's area (t₍₂₁₎ df = 0.3, p = 0.8; Fig. 7B, gray points).

In a post hoc ANOVA analysis, we asked whether the striate pattern similarity measure itself predicts Broca's correlation in the blind or whether both measures are themselves driven by age of onset of blindness. A direct comparison of the effect of age of blindness onset and the effect of the pattern similarity measure found that these factors were not significantly different in predicting Broca's area correlation (p = 0.24). Therefore, it is possible that age of blindness is the common factor that alters both striate pattern similarity and long-range functional correlation in the blind.

Group differences are not explained by differences in head motion or structural registration

Group differences in head motion may lead to artifactual differences in measured functional correlation. Specifically, head motion enhances correlations locally and between symmetric hemispheric locations while decreasing long-range correlation between regions (Van Dijk et al., 2012; Power et al., 2012). We tested for group differences in head motion by calculating the mean Euclidean displacement of the head (Van Dijk et al., 2012) during the resting-state scan for each subject. The small difference between the groups was not significant (blind group displacement = 0.09 ± 0.055 mm SD, sighted group displacement = 0.07 ± 0.043 mm SD; t₍₄₅₎ df = 1.39, p = 0.17). Moreover, the blind group had slightly greater (albeit insignificantly so) head motion than the sighted group, which would be associated with an artifactual result opposite to that we observe in our data. A further test demonstrated that there was no significant correlation (all p values >0.05) between the individual subject head motion measures and the measures of within-hemisphere pattern similarity (blind r = −0.10; sighted r = 0.24), between-hemisphere pattern similarity (blind r = −0.07; sighted r = 0.18), or long-range functional correlation with Broca's area (blind r = 0.24; sighted r = −0.29).

Our findings also depend upon the ability to identify mirror-homologous patches of cortex within the striate cortex. To do so, we make use of a cortical surface template (Benson et al., 2012) that provides a probabilistic location for the stria of Gennari (Hinds et al., 2008) based upon gyral topology. The decreased between-hemisphere pattern similarity observed in individual blind subjects could in principle be a consequence not of a true reduction in between-hemisphere correlation, but of systematic differences in cortical registration and surface warping in the blind. This is a plausible concern as, while the early blind possess an intact stria of Gennari (Trampel et al., 2011), the surface area is reduced (Park et al., 2009; and as seen in our participants).

We used two tests to determine whether differences across groups and individuals in the quality of anatomical registration and normalization could explain our results. First, we tested whether differences in the degree of anatomical transformation between the two hemispheres could contribute to the between-hemisphere pattern similarity measure. Despite the previously reported smaller overall striate surface area in the blind, the surface area of the two hemispheres is as highly correlated across subjects in the sighted (r = 0.75) and blind (r = 0.79) groups. Thus, there is no tendency in blind subjects to have greater differences in the size of the labeled striate region between hemispheres. Next, we examined the degree of anatomical warping required to register the brain of each subject to the surface template space. Group differences in the magnitude or variability of warping could impair the application of a striate cortex template. This was quantified by obtaining for each subject the mean and SD of the Jacobian areal warp values (Fischl et al., 2001) calculated for each surface vertex within the striate cortex. After accounting for group differences in the mean surface area (which contributes to the Jacobian measure), there was no difference in either mean Jacobian (p = 0.74) or SD (p = 0.67) between the two groups.

Discussion

Our study examines the fine-scale pattern of correlations within BOLD fMRI data collected during darkness. We distinguish the modeling of fine-scale correlation within a cortical region from studies of the relationship between entire cortical regions (Liu et al., 2007; Yu et al., 2008; Watkins et al., 2012). By measuring the point-to-point structure of correlations within a cortical region, we may examine whether resting-state signals are related in a systematic way to the local functional organization of cortex. Here, we asked whether resting-state correlations within and between the striate cortices reflect retinotopic organization, and whether this structure is altered in blindness.

Previous examinations of the fine-scale correlation structure of visual cortex have been conducted in sighted participants. Heinzle et al. (2011) measured the point-to-point correlation of visual area V1 with V3 and established the correspondence of cortical points by functional retinotopic mapping. Aggregating data across cortical locations and subjects, they found approximately circular CCRFs across the cortical surface for the spread of correlations between homologous V1 and V3 locations both within and between hemispheres. Yeo et al. (2011) also reported correlation between nonadjacent patches of V1 and V3, although they observed a gradient of correlation strength primarily along the AP (eccentricity) dimension. Finally, Haak et al. (2012) applied a modeling approach (the population receptive field model) to the structure of correlated signals between retinotopically organized visual areas. These analyses, conducted upon data collected during retinotopic mapping visual stimulation, revealed CCRFs that were well described as a 2D Gaussian function of correlation across the cortical surface.

In the present study, we confirm the observation of Heinzle et al. (2011) of a circular CCRF within striate cortex for spontaneous neural signals, and further demonstrate that this is well modeled by a Gaussian form, as described by Haak et al. (2012). In our data, the point-spread function of correlation within and between striate cortex was constant across the eccentricity dimension. At the level of within-V1 connections, therefore, it seems that equivalent-sized patches of cortex share a functional correlation, as opposed to equivalent areas of the visual field. Instead of retinotopy per se, this functional organization may reflect the equivalent areal pooling across striate cortex of density of retinal ganglion cells (Wässle et al., 1990). Our result is consistent with the findings of Haak et al., 2012 who observed in stimulus-driven signals a negligible dependence of connective field size upon eccentricity position for V1 to V2 connections. This dependence grew, however, for connections of V1 to ever higher level extrastriate regions.

This finding prompted us to ask to what extent striate cortex correlation reflects vision per se, as opposed to a more basic organizational property of cortex. In our population of blind subjects, we found that the structure of within-hemisphere, striate correlation is not altered. This suggests that the properties of neural correlation (e.g., diffuse horizontal connections) (Bosking et al., 1997) that mediate within region, within-hemisphere correlations are independent of visual experience. In contrast, we found that individual blind subjects had a subtle but significant alteration of the pattern of between-hemispheric striate correlation. As the aggregate fine-scale correlation pattern across blind subjects resembles that of the sighted, this finding indicates that our individual blind subjects have variability in their between-hemisphere striate correlation structure that is not systematic across participants. We did not find any difference in the extent of this alteration as a function of the age of onset of blindness, although our study was not well powered to detect such differences.

The degree of the departure from the sighted pattern of correlation was, however, found to be associated with increased correlation between striate cortex and frontal language regions and, to a greater extent, in those blind before the age of 18. This suggests that the degree of alteration of visual cortex is related to more basic aspects of visual deprivation.

Our study is limited in the ability to examine how features of blindness (e.g., age of onset of vision loss, age at maximal vision less, severity of vision loss) relate to the observed differences in functional correlation. One reason for this limitation is that the effect of blindness upon our measures was quite subtle. Although a population of 25 blind subjects is relatively large for studies of this kind, it is insufficient to disentangle the correlated factors that might impact total visual experience before and after maturation of the visual system. At the least, however, the alteration of the pattern of between-hemisphere correlation was present in those who became blind in adulthood. Therefore, ongoing visual input appears necessary to synchronize mirror symmetric patches of cortex between the hemispheres.

The source and function of interhemispheric resting correlation remain unclear. It is generally held that homologous right and left cortical areas communicate through the corpus callosum (for review, see Pietrasanta et al., 2012). Although callosal connections generally synchronize the activity of large groups of neurons (Engel et al., 1991; Kiper et al., 1999; Knyazeva et al., 1999; Carmeli et al., 2007), the extent and distribution of this effect vary over the course of development. In the striate cortex, visual experience drives the transition from the diffusely connected juvenile state to the adult state (Innocenti and Price, 2005) in which callosal connections are localized to the border between visual areas (Manger et al., 2002). Early vision is essential to trigger this reorganization, but not to maintain the adult distribution (Zufferey et al., 1999).

In our study, no difference in correlation strength in the sighted was observed between those points that connect the horizontal and vertical meridia. This suggests that direct monosynaptic connections transversing the corpus callosum are not the source of striatal interhemispheric resting structure. This is in agreement with recent studies of resting-state networks in subjects with chronic callosal disconnection, because of either surgical resection (Corsi-Cabrera et al., 2006; Uddin et al., 2008) or agenesis (Tyszka et al., 2011), who demonstrate preserved between-hemisphere resting correlations (although there is disruption of interhemispheric correlation in the immediate period after corpus callosotomy) (Johnston et al., 2008). Presumably, this synchronization is being mediated by extracallosal, interhemispheric connections. In studies in cats, for example, interhemispheric transfer of visual information for behavior was preserved even after sectioning the optic chiasm and corpus callosum (Peck et al., 1979). In a recent resting-state fMRI study in rhesus monkeys, only sectioning of the callosum and anterior commissure altered regional, between-hemisphere correlations, although even then interhemisphereic correlation of the visual cortex was not affected (O'Reilly et al., 2013). These results implicate the posterior commissure and/or optic tectum as the basis of interhemispheric correlations in the visual system.

Although subcortical interhemispheric connections may contribute to the between-hemisphere striate signal correlation, left unexplained is the fine-scale alignment of this correlation structure. One possibility is the presence of feedback projections from higher visual areas, which contain neurons whose receptive fields span the vertical meridian. Behavioral and neuroimaging studies in callosotomy patients (Clarke et al., 2000; Noudoost et al., 2006) demonstrate bilateral recruitment of higher-level, dorsal visual areas by stimuli presented to a single hemifield. Therefore, hemispheric synchronization of dorsal visual areas may lead in turn to topographically organized synchronization of the striate cortices through feedback projections.

A deeper question is why this correlation structure should have mirror symmetry across the visual field. Although unclear, there is at least evidence of behavioral consequences of visual field symmetry. For example, using Gabor patches placed symmetrically about the vertical meridian, Tanaka et al. (2007) reported an effect upon detection threshold specific to the mirrored retinotopic position, orientation, and phase. Further, patients with occipital lobe damage and consequent visual field scotomas show detection impairments in the (theoretically intact) ipsilesional visual field (Snow and Mattingley, 2006; Snow et al., 2013). To these findings, we add the observation that altered visual experience disrupts the hemispheric symmetry of spontaneous neural activity.

Finally, we examined here the functional properties of striate cortex, the first of many cortical visual areas. Our focus upon striate cortex in part derives from the technique used to assign retinotopic position to points on the cortical surface. The topology of cortical folding (a measure of anatomy) can be used to predict accurately the retinotopic organization of striate cortex (Benson et al., 2012) and permitted the blind and sighted subjects to be assessed within a common framework. It would be of interest to examine how the pattern of correlations within and between the extrastriate visual areas is altered by blindness. We predict that ongoing vision is required as well to synchronize cortical points that share retinotopic assignment across visual areas (e.g., V1-V3). The test of this hypothesis must await the development of an anatomically based approach that can accurately predict retinotopic organization beyond striate cortex.

Notes

Supplemental material for this article is available at https://cfn.upenn.edu/aguirre/wiki/public:data_jneurosci_2013_butt. Additional analyses and raw data tables. This material has not been peer reviewed.