Electroviscous effects in the bordered pit membrane may impact the overall hydraulic conductance of xylem and explain the ion-mediated changes in conductance observed in perfusion experiments.
Abstract
In perfusion experiments, the hydraulic conductance of stem segments ( ) responds to changes in the properties of the perfusate, such as the ionic strength (
) responds to changes in the properties of the perfusate, such as the ionic strength ( ), pH, and cationic identity. We review the experimental and theoretical work on this phenomenon. We then proceed to explore the hypothesis that electrokinetic effects in the bordered pit membrane (BPM) contribute to this response. In particular, we develop a model based on electroviscosity in which hydraulic conductance of an electrically charged porous membrane varies with the properties of the electrolyte. We use standard electrokinetic theory, coupled with measurements of electrokinetic properties of plant materials from the literature, to determine how the conductance of BPMs, and therefore
), pH, and cationic identity. We review the experimental and theoretical work on this phenomenon. We then proceed to explore the hypothesis that electrokinetic effects in the bordered pit membrane (BPM) contribute to this response. In particular, we develop a model based on electroviscosity in which hydraulic conductance of an electrically charged porous membrane varies with the properties of the electrolyte. We use standard electrokinetic theory, coupled with measurements of electrokinetic properties of plant materials from the literature, to determine how the conductance of BPMs, and therefore  , may change due to electroviscosity. We predict a nonmonotonic variation of
, may change due to electroviscosity. We predict a nonmonotonic variation of  with
with  with a maximum reduction of 18%. We explore how this reduction depends on the characteristics of the sap and features of the BPM, such as pore size, density of chargeable sites, and their dissociation constant. Our predictions are consistent with changes in
with a maximum reduction of 18%. We explore how this reduction depends on the characteristics of the sap and features of the BPM, such as pore size, density of chargeable sites, and their dissociation constant. Our predictions are consistent with changes in  observed for physiological values of sap
observed for physiological values of sap  and pH. We conclude that electroviscosity is likely responsible, at least partially, for the electrolyte dependence of conductance through pits and that electroviscosity may be strong enough to play an important role in other transport processes in xylem. We conclude by proposing experiments to differentiate the impact of electroviscosity on
and pH. We conclude that electroviscosity is likely responsible, at least partially, for the electrolyte dependence of conductance through pits and that electroviscosity may be strong enough to play an important role in other transport processes in xylem. We conclude by proposing experiments to differentiate the impact of electroviscosity on  from that of other proposed mechanisms.
from that of other proposed mechanisms.
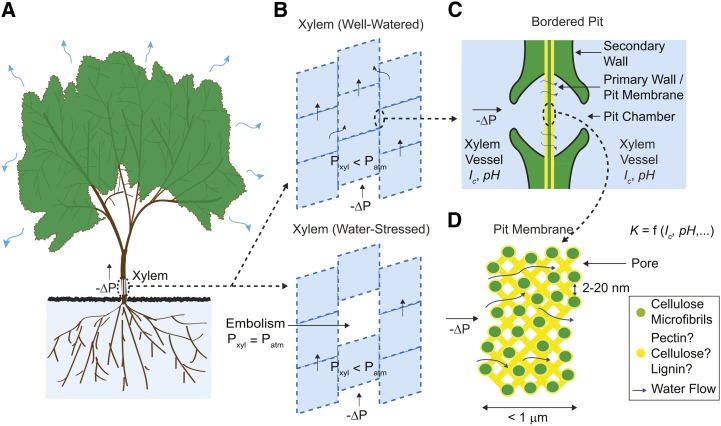
During transpiration, sap flows along a gradient in water potential through the vascular conduits of xylem (Fig. 1A), moving both axially through tracheids and vessel elements of macroscopic cross section (10–700 μm in diameter) and transversally through intertracheid and intervessel structures known as bordered pits (Fig. 1, B–D; Bailey, 1916). In this vascular network, pits can contribute more than 50% of xylem’s total hydraulic resistance (Wheeler et al., 2005; Choat et al., 2006). Pits in angiosperms comprise a nanoporous membrane, the bordered pit membrane (BPM), enclosed by a channel that connects two xylem vessels. This membrane is formed from the primary cell wall and intervening middle lamella (Zwieniecki and Holbrook, 2000) and is covered by a matrix of thin, plaque-like material of unknown composition (Pesacreta et al., 2005; Fig. 1, C and D). Pits redistribute flux to bypass immature vessels in young shoots (Halis et al., 2011) and local emboli (Fig. 1B; Tyree and Ewers, 1991) and function as valves between adjacent vessels, allowing the passage of sap while preventing the spread of embolisms (Konrad and Roth-Nebelsick, 2005; Choat et al., 2008; Jansen et al., 2009) and pathogens (Roper et al., 2007). Pit characteristics also play a role in poorly understood phenomena, such as how embolisms spread between vessels (Christman et al., 2012) and how vessels are actively refilled, i.e. during transpiration (Tyree et al., 1999). Although pits are ubiquitous, it is hard to study their characteristics directly because of their small size; therefore, indirect methods such as stem perfusion experiments are often used.
Figure 1.
Water transport through xylem. A, Global view. B, Segmented architecture of xylem, with both axial and radial flow of sap. C, Cross-sectional view of a pit and its membrane. D, Cross-sectional view of the BPM and its interconnected pore network through which sap flows. The effective hydraulic conductance of an individual pore ( ) depends on its own properties and those of the sap. [See online article for color version of this figure.]
) depends on its own properties and those of the sap. [See online article for color version of this figure.]
The Ionic Effect: BPM-Mediated Response of Xylem Conductance to Sap Composition
Experiments over the previous three decades have challenged the view that xylem forms an inert conduit whose structure solely determines its sap-carrying characteristics; these experiments have provided clues as to the structure and possible functions of pits in regulating flow. The conductance of xylem ( ) has been shown to change rapidly in response to changes in the composition of sap. To the best of our knowledge, Zimmermann (1978) first reported this phenomenon. In a study on stem segments of sugar maple (Acer saccharum), he found that
) has been shown to change rapidly in response to changes in the composition of sap. To the best of our knowledge, Zimmermann (1978) first reported this phenomenon. In a study on stem segments of sugar maple (Acer saccharum), he found that  decreased > 50% upon initial perfusion with distilled water and returned to its original value upon perfusion with tap water or upon reversal of direction of flow. More recent studies using well-defined aqueous solutions confirm that
decreased > 50% upon initial perfusion with distilled water and returned to its original value upon perfusion with tap water or upon reversal of direction of flow. More recent studies using well-defined aqueous solutions confirm that  may vary in response to changes in fluid ionic strength (
may vary in response to changes in fluid ionic strength ( ; van Ieperen et al., 2000; Zwieniecki et al., 2001; López-Portillo et al., 2005; Pittermann et al., 2005; Wheeler et al., 2005; Choat et al., 2006; Hacke et al., 2006; Domec et al., 2007; Nardini et al., 2007; Aasamaa and Sõber, 2010), composition with respect to specific cations (van Ieperen et al., 2000; Zwieniecki et al., 2001; Gascó et al., 2006), pH (Zwieniecki et al., 2001), and concentration of proteins and polysaccharides (Neumann et al., 2010). Further studies indicate that the magnitude (Van Meeteren et al., 1999; Zwieniecki et al., 2001) and direction (van Ieperen et al., 2000; Cochard et al., 2010) of the change in
; van Ieperen et al., 2000; Zwieniecki et al., 2001; López-Portillo et al., 2005; Pittermann et al., 2005; Wheeler et al., 2005; Choat et al., 2006; Hacke et al., 2006; Domec et al., 2007; Nardini et al., 2007; Aasamaa and Sõber, 2010), composition with respect to specific cations (van Ieperen et al., 2000; Zwieniecki et al., 2001; Gascó et al., 2006), pH (Zwieniecki et al., 2001), and concentration of proteins and polysaccharides (Neumann et al., 2010). Further studies indicate that the magnitude (Van Meeteren et al., 1999; Zwieniecki et al., 2001) and direction (van Ieperen et al., 2000; Cochard et al., 2010) of the change in  depend on the species studied and the range of
depend on the species studied and the range of  considered. Here, we refer to this overall phenomenon as the “ionic effect.” In Laurus nobilis, perfusion experiments through segments with and without passages through pits suggest that these changes are mediated by pits (Zwieniecki et al., 2001).
considered. Here, we refer to this overall phenomenon as the “ionic effect.” In Laurus nobilis, perfusion experiments through segments with and without passages through pits suggest that these changes are mediated by pits (Zwieniecki et al., 2001).
Although experiments on stem segments clearly show the ionic effect, questions remain as to whether it occurs in planta as well as its possible physiological role and its mechanism. Studies suggest that plants may exploit the ionic effect to regulate  actively by exchanging ions between xylem and phloem (Zwieniecki et al., 2004), a mechanism that may help maintain flow in the presence of emboli (Trifilò et al., 2008). Still, concerns exist that the ionic effect may be an experimental artifact due to the use of deionized water, an artificial fluid devoid of ions normally present in sap (van Ieperen and van Gelder, 2006; van Ieperen, 2007). This fluid can permanently decrease
actively by exchanging ions between xylem and phloem (Zwieniecki et al., 2004), a mechanism that may help maintain flow in the presence of emboli (Trifilò et al., 2008). Still, concerns exist that the ionic effect may be an experimental artifact due to the use of deionized water, an artificial fluid devoid of ions normally present in sap (van Ieperen and van Gelder, 2006; van Ieperen, 2007). This fluid can permanently decrease  in stem segments and decrease fresh weight in cut flowers (Van Meeteren et al., 1999).
in stem segments and decrease fresh weight in cut flowers (Van Meeteren et al., 1999).
Notwithstanding whether the ionic effect occurs in vivo, here, we explore why it happens and what it reveals about the structure and function of pits. Two mechanisms have been proposed to explain it: (1) the swelling and shrinking of hydrogels within the BPM, and (2) electroviscosity in the pores of the BPM.
Current Models of Flow Regulation through BPMs
BPM Swelling-Shrinking Hypothesis
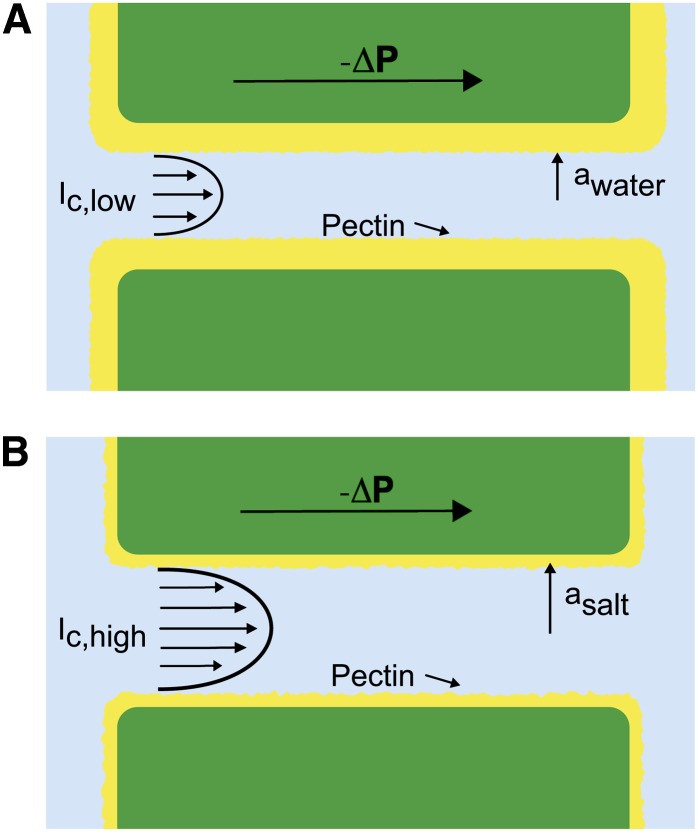
Zimmermann (1978) suggested that the ionic effect could be caused by the swelling or shrinking of hydrogels covering the surface of BPM pores. Swelling could decrease the size of pores traversing the BPM, thus decreasing the pit conductance (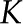 ) and, therefore,
) and, therefore,  as well (Figs. 1D and 2A). This swelling-shrinking behavior of the BPM was later attributed to the Donnan effect that describes changes in the hydration status of polyelectrolytic gels (e.g. pectin; Cochard et al., 2010). At low
as well (Figs. 1D and 2A). This swelling-shrinking behavior of the BPM was later attributed to the Donnan effect that describes changes in the hydration status of polyelectrolytic gels (e.g. pectin; Cochard et al., 2010). At low  , polyelectrolyte gels swell because of the long-range repulsion between bound charges. In the architecture suggested in Figures 1D and 2, this swelling could reduce the effective hydrodynamic radii of pores in the BPM (Figs. 1D and 2A), decreasing
, polyelectrolyte gels swell because of the long-range repulsion between bound charges. In the architecture suggested in Figures 1D and 2, this swelling could reduce the effective hydrodynamic radii of pores in the BPM (Figs. 1D and 2A), decreasing 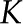 . At high
. At high  , polyelectrolyte gels collapse because ions in the fluid screen the bound charges and reduce the distance over which their mutual repulsion acts; this shrinking could increase the effective pore radius (Fig. 2B), increasing
, polyelectrolyte gels collapse because ions in the fluid screen the bound charges and reduce the distance over which their mutual repulsion acts; this shrinking could increase the effective pore radius (Fig. 2B), increasing 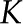 . This model can also explain the observed response to pH: At high pH, the number of charged groups in the gel increases because more bound acids deprotonate, the gel swells, and
. This model can also explain the observed response to pH: At high pH, the number of charged groups in the gel increases because more bound acids deprotonate, the gel swells, and 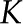 decreases; at low pH, the acids are neutralized, the gel collapses, and
decreases; at low pH, the acids are neutralized, the gel collapses, and 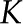 increases. Lee et al. (2012) observed a swelling-shrinking response to changes of ionic strength on individual BPMs of tobacco plants (Nicotiana tabacum) using an atomic force microscope. We note, though, that based on their observations, they suggest an alternative architecture to the one shown in Figure 2: Rather than gel lining the pores in the membrane, they suggest a layer of gel on the surface of the membrane. We are not aware of a simple explanation for how the swelling of the gel in this alternative architecture would affect the conductance of the membrane.
increases. Lee et al. (2012) observed a swelling-shrinking response to changes of ionic strength on individual BPMs of tobacco plants (Nicotiana tabacum) using an atomic force microscope. We note, though, that based on their observations, they suggest an alternative architecture to the one shown in Figure 2: Rather than gel lining the pores in the membrane, they suggest a layer of gel on the surface of the membrane. We are not aware of a simple explanation for how the swelling of the gel in this alternative architecture would affect the conductance of the membrane.
Figure 2.
Hydrogel hypothesis as proposed by Zwieniecki et al. (2001). A, When deionized water (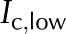 ) flows through a BPM pore, the pectin layer swells, decreasing both the effective pore radius (
) flows through a BPM pore, the pectin layer swells, decreasing both the effective pore radius (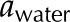 ) and the overall conductance. B, When an ionic solution flows, e.g. KCl (
) and the overall conductance. B, When an ionic solution flows, e.g. KCl (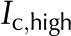 ), the pectin layer shrinks, increasing both the effective pore radius (
), the pectin layer shrinks, increasing both the effective pore radius ( ) and the overall hydraulic conductance. [See online article for color version of this figure.]
) and the overall hydraulic conductance. [See online article for color version of this figure.]
The gel-swelling hypothesis is incompatible with some observations. First, in some species,  has been observed to decrease as
has been observed to decrease as  increases (Cochard et al., 2010), a behavior opposite of that predicted. Second, various studies question whether pectin hydrogels actually exist in the BPM, as reviewed by van Doorn et al. (2011). Third, uncertainties about the distribution of the gels within the membrane make it difficult to predict how swelling should impact conductance (Lee et al., 2012). These arguments suggest that we may need to invoke other phenomena to explain the ionic effect.
increases (Cochard et al., 2010), a behavior opposite of that predicted. Second, various studies question whether pectin hydrogels actually exist in the BPM, as reviewed by van Doorn et al. (2011). Third, uncertainties about the distribution of the gels within the membrane make it difficult to predict how swelling should impact conductance (Lee et al., 2012). These arguments suggest that we may need to invoke other phenomena to explain the ionic effect.
Electrokinetic Flow Model
Under equivalent conditions, liquid flow through an electrically charged channel is always less than flow through an uncharged one (Rice and Whitehead, 1965). This effect is often called the electroviscous effect, or electroviscosity, because the viscosity of the fluid appears to increase. In reality, electroviscosity is an electrokinetic effect in which ions in the fluid cause the observed decrease in conductance (Kirby, 2010). Electroviscosity occurs as follows: (1) When submerged in water, most materials develop a net ionic charge on their surface due to the exchange of ions with the solution; (2) this surface charge then attracts counterions from the liquid and creates a layer of mobile net electric charge in the fluid near the surface (called the Debye layer [DL]); (3) finally, the ions in this layer produce a drag on the uncharged fluid flowing through the channel and decrease the overall flow for a given pressure drop (see “Theory” for detailed description). The strength of this drag depends mainly on two parameters: the electric potential, or voltage, at the surface (usually called the zeta potential,  ), and the
), and the  of the fluid. Stronger potentials produce more drag, while an increased
of the fluid. Stronger potentials produce more drag, while an increased  may increase or decrease drag, depending on the ratio between channel size and DL thickness at the particular
may increase or decrease drag, depending on the ratio between channel size and DL thickness at the particular  .
.
Several observations suggest electroviscosity could be important in the BPM. Measurements show that materials believed to line the BPM surface, such as pectin and lignin (Lee et al., 2012), present moderate to large electric potentials (Table I), though we note there is much controversy as to the presence of noncellulosic components in the BPM (O’Brien and Thimann, 1967; O’Brien, 1970; Choat et al., 2008). Nonetheless, this conclusion is supported by measurements of streaming potentials in xylem, a related electrokinetic phenomenon (Kirby, 2010) that occurs when pressure-driven flow in a charged channel convects ions and creates an electrical potential difference between the ends of the channel (Stamm, 1926; Tyree and Fensom, 1968; Tyree and Zimmermann, 1971). Previous researchers have mentioned electroviscosity as a possible explanation for the ionic effect (Jansen et al., 2011; Nardini et al., 2011). For instance, van Doorn et al. (2011) proposed an analysis of electroviscosity in BPMs. We believe that the analysis of van Doorn et al. errs in its treatment of the electrokinetic processes that lead to electroviscosity by assuming the Debye layer is immobile. As we will show (see Fig. 6), their predictions are qualitatively correct at high  but strongly overpredict the decrease in flow due to electroviscosity.
but strongly overpredict the decrease in flow due to electroviscosity.
Table I. Maximum values of surface potential ( ) reported for plant materials.
) reported for plant materials.
| Material |
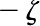 mV
mV
|
Reference |
|---|---|---|
| Sugar beet pectina | 48, 60 | Kuljanin et al. (2008); Nakauma et al. (2008) |
| Kraft lignina | 45 | Dong et al. (1996) |
| Citrus pectina | 33 | Kim et al. (2005) |
| Cellulose fibersa | 15 | Bellmann et al. (2005) |
| Xylem | 14 | Stamm (1926) |
Values shown are for materials processed in acidic or basic solutions at elevated temperatures; these processes likely increase  over its value in vivo. We did not find experimental data on
over its value in vivo. We did not find experimental data on  for these materials in unprocessed conditions. In this study, we take the materials sugar beet pectin and xylem to represent the upper and lower bounds on the magnitude of the surface potential in vivo.
for these materials in unprocessed conditions. In this study, we take the materials sugar beet pectin and xylem to represent the upper and lower bounds on the magnitude of the surface potential in vivo.
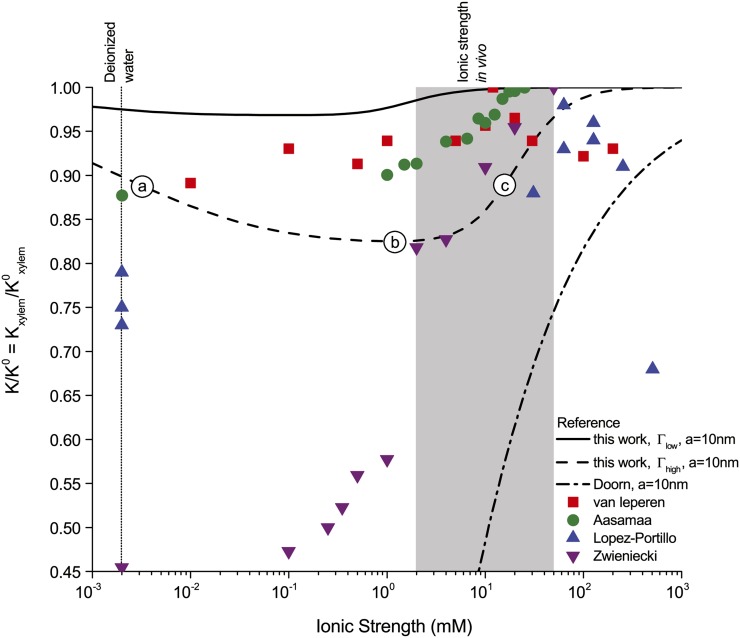
Figure 6.
Relative hydraulic conductance (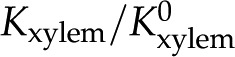 ) versus ionic strength (
) versus ionic strength ( ) for our theoretical predictions, van Doorn’s model, and published experimental data. Theoretical models shown (10-nm pore radius and KCl electrolyte): this work, density of chargeable sites
) for our theoretical predictions, van Doorn’s model, and published experimental data. Theoretical models shown (10-nm pore radius and KCl electrolyte): this work, density of chargeable sites  (solid line); this work,
(solid line); this work,  (dashed line); and van Doorn et al. (2011), dash dot line). Experimental data shown (species, electrolyte, and figure in reference): (1) Chrysanthemum and KCl (Fig. 3 in van Ieperen et al., 2000; red squares); (2) Q. robur with petioles and various salt solutions (Fig. 1A in Aasamaa and Sõber, 2010; green circles); (3) C. erectus and NaCl, (Fig. 3 in López-Portillo et al., 2005; blue triangles); (4) L. nobilis, KCl, and average value of
(dashed line); and van Doorn et al. (2011), dash dot line). Experimental data shown (species, electrolyte, and figure in reference): (1) Chrysanthemum and KCl (Fig. 3 in van Ieperen et al., 2000; red squares); (2) Q. robur with petioles and various salt solutions (Fig. 1A in Aasamaa and Sõber, 2010; green circles); (3) C. erectus and NaCl, (Fig. 3 in López-Portillo et al., 2005; blue triangles); (4) L. nobilis, KCl, and average value of  (Fig. 1C in Zwieniecki et al., 2001; purple triangles). Experimental data were normalized to the largest measured conductance in the particular species and report. [See online article for color version of this figure.]
(Fig. 1C in Zwieniecki et al., 2001; purple triangles). Experimental data were normalized to the largest measured conductance in the particular species and report. [See online article for color version of this figure.]
Motivation and Overview
The purpose of this article is to develop a complete model of electroviscosity in the BPM and ask if this mechanism can explain the available experimental observations of the ionic effect. Specifically, we ask: Is electroviscosity consistent with the observed response of  to
to  , pH, and ionic identity of the sap? To answer this question, we model electrokinetic effects in an idealized model of the BPM and examine how the properties of sap affect the conductance of individual pores in the BPM. We model the pore surface as presenting a number of chemically identical chargeable sites per unit area (Γ), where these sites may dissociate and become electrically charged. A surface with a larger
, pH, and ionic identity of the sap? To answer this question, we model electrokinetic effects in an idealized model of the BPM and examine how the properties of sap affect the conductance of individual pores in the BPM. We model the pore surface as presenting a number of chemically identical chargeable sites per unit area (Γ), where these sites may dissociate and become electrically charged. A surface with a larger  will thus develop a larger net charge and produce stronger electroviscosity. We calculate
will thus develop a larger net charge and produce stronger electroviscosity. We calculate 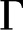 for two materials that represent the low and high end of reported values of
for two materials that represent the low and high end of reported values of  for plant materials: cellulose fiber (
for plant materials: cellulose fiber ( = −15 mV,
= −15 mV, 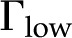 = 6,900/μm2) and sugar beet (Beta vulgaris) pectin (
= 6,900/μm2) and sugar beet (Beta vulgaris) pectin ( = −60 mV,
= −60 mV, 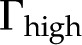 = 120,000/μm2; see Table I). Regardless of their presence in the BPM, these two materials cover an expected range of electroviscosity in the BPM: from weak effects (cellulose) to strong effects (pectin).
= 120,000/μm2; see Table I). Regardless of their presence in the BPM, these two materials cover an expected range of electroviscosity in the BPM: from weak effects (cellulose) to strong effects (pectin).
Subsequently, we assume that the BPM presents the limiting hydraulic resistance in xylem (Wheeler et al., 2005; Choat et al., 2006), such that 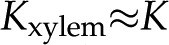 , and compare our predictions with experimental measurements from the literature. Our results thus represent the maximum decrease in
, and compare our predictions with experimental measurements from the literature. Our results thus represent the maximum decrease in  expected due to electroviscosity, for cellulose and pectin individually; experimental results above this threshold cannot be explained by electroviscosity. This analysis suggests that electroviscosity would produce similar changes in
expected due to electroviscosity, for cellulose and pectin individually; experimental results above this threshold cannot be explained by electroviscosity. This analysis suggests that electroviscosity would produce similar changes in  in the physiological range of composition of the sap as those predicted by the swelling-shrinking hydrogel hypothesis. Therefore, we propose various experiments that could differentiate between these two phenomena in the BPM. We conclude by discussing the possible implications of electrokinetic effects, if they are important in plants, for the management of flow and refilling of embolisms in xylem.
in the physiological range of composition of the sap as those predicted by the swelling-shrinking hydrogel hypothesis. Therefore, we propose various experiments that could differentiate between these two phenomena in the BPM. We conclude by discussing the possible implications of electrokinetic effects, if they are important in plants, for the management of flow and refilling of embolisms in xylem.
Theory
This section presents a brief overview of electrokinetic phenomena implicated in the hypothesis of electroviscosity in xylem. We explain how surfaces develop electric charge in water and how this charge affects the fluid. Subsequently, we introduce four interrelated electrokinetic phenomena: electroosmosis, electroviscosity, streaming current, and streaming potential.
Surface Electric Charge and Potential
Solid surfaces in aqueous solution usually develop net electric charge (Fig. 3). At equilibrium with solution, chargeable sites exchange ions with the fluid and may produce an excess electric charge on the surface (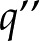 [C/m2]). For instance, carboxylic acids present in certain plant materials are chargeable sites: They are more likely to lose a proton and become negatively charged (COOH
[C/m2]). For instance, carboxylic acids present in certain plant materials are chargeable sites: They are more likely to lose a proton and become negatively charged (COOH 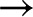 COO−+ H+) as the fluid pH rises above their dissociation constant (
COO−+ H+) as the fluid pH rises above their dissociation constant (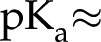 3.5). For simplicity, we model a surface as having only one type of chargeable site, a corresponding
3.5). For simplicity, we model a surface as having only one type of chargeable site, a corresponding 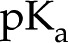 and a density of chargeable sites per unit area
and a density of chargeable sites per unit area 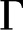 (m−2), as shown in Figure 3. On such a surface, the surface charge density is proportional to the number of sites that have liberated a proton (
(m−2), as shown in Figure 3. On such a surface, the surface charge density is proportional to the number of sites that have liberated a proton (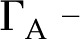 [m−2]) and their charge (
[m−2]) and their charge (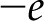 ):
):
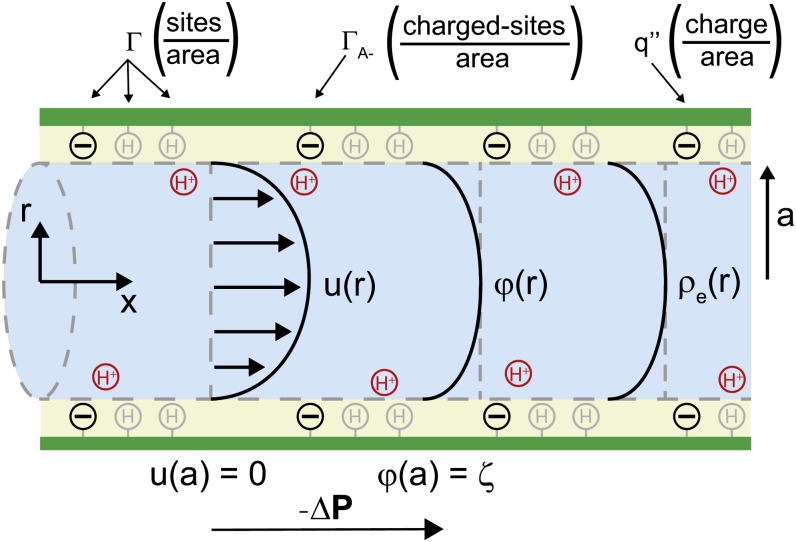
Figure 3.
Idealized model of a BPM pore. A pressure difference 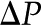 applied between the ends of the cylindrical channel drives fluid flow. The velocity (u), electric potential (
applied between the ends of the cylindrical channel drives fluid flow. The velocity (u), electric potential (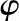 ), and charge density (
), and charge density (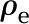 ) in the fluid vary across the radial coordinate (r) but are constant along the axial direction (
) in the fluid vary across the radial coordinate (r) but are constant along the axial direction (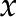 ). At the surface, the velocity is 0 [
). At the surface, the velocity is 0 [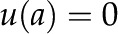 ] and the electric potential is maximum [
] and the electric potential is maximum [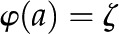 ]. The surface contains a density of chargeable sites (
]. The surface contains a density of chargeable sites (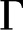 ), some of which lose a proton (H+) and become negatively charged (
), some of which lose a proton (H+) and become negatively charged ( ), thereby producing a net electrical charge at the surface (
), thereby producing a net electrical charge at the surface (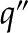 ).[See online article for color version of this figure.]
).[See online article for color version of this figure.]
where 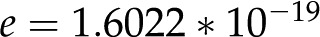 C is the elementary charge (Behrens and Grier, 2001). The specific magnitude of
C is the elementary charge (Behrens and Grier, 2001). The specific magnitude of 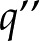 thus depends on the number of ions that dissociate and is a function of the properties of both the surface and the fluid. For all else equal, a surface with more chargeable sites will have higher surface charge density. Similarly, an increase in pH will increase
thus depends on the number of ions that dissociate and is a function of the properties of both the surface and the fluid. For all else equal, a surface with more chargeable sites will have higher surface charge density. Similarly, an increase in pH will increase 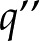 for acid groups, since more chargeable sites will deprotonate and
for acid groups, since more chargeable sites will deprotonate and  will increase.
will increase.
A charged surface attracts counterions from solution. It creates a layer of net ionic charge, the DL, and a corresponding electric potential in the fluid ( 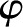 [V]). Both the fluid and the ions in the DL are mobile. The volume density of ionic charge,
[V]). Both the fluid and the ions in the DL are mobile. The volume density of ionic charge, 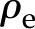 [C m−3], is largest near the surface and decays toward 0 away from it. The characteristic length over which
[C m−3], is largest near the surface and decays toward 0 away from it. The characteristic length over which 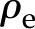 decays is called the Debye length (
decays is called the Debye length ( 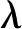 [m]) and is usually taken to be the thickness of the DL. The DL thickens with increases in solution temperature (
[m]) and is usually taken to be the thickness of the DL. The DL thickens with increases in solution temperature ( 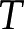 [K]) and permittivity (
[K]) and permittivity ( 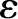 [C V−1 m−1]) and decreases in solution
[C V−1 m−1]) and decreases in solution  . Its thickness is given by:
. Its thickness is given by:
 |
where 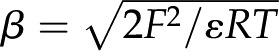 ,
, 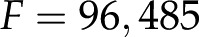 C mol−1 is Faraday’s constant, and
C mol−1 is Faraday’s constant, and 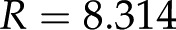 J mol−1 K−1 is the universal gas constant (Kirby, 2010). For example, at room temperature,
J mol−1 K−1 is the universal gas constant (Kirby, 2010). For example, at room temperature, 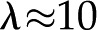 nm for
nm for 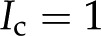 mm, and
mm, and 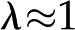 nm for
nm for 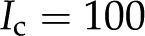 mm. The solution
mm. The solution  depends on the concentration of ions in solution (
depends on the concentration of ions in solution (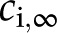 [mol/m3]) and their valence (
[mol/m3]) and their valence (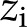 ):
):
 |
As with 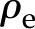 , the potential
, the potential 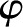 is largest near the surface and decreases to 0 over the length
is largest near the surface and decreases to 0 over the length 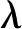 . The potential at the surface is commonly called the zeta potential, or
. The potential at the surface is commonly called the zeta potential, or  [V].
[V].
Electrokinetic Matrix
In a channel with electrically charged walls, the fluid flow, 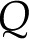 [m3/s], electrical current,
[m3/s], electrical current, 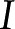 [A], pressure gradient,
[A], pressure gradient, 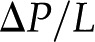 [Pa/m], and electric field,
[Pa/m], and electric field, 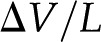 [V/m], are coupled by the electrokinetic matrix (Kirby, 2010):
[V/m], are coupled by the electrokinetic matrix (Kirby, 2010):
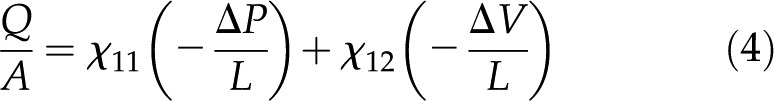 |
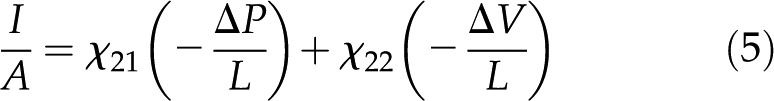 |
where the coefficients 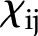 (members of the electrokinetic matrix) capture the interplay between the surface and fluid properties and are derived in “Materials and Methods.” When an electric field is applied between the ends of a charged channel, it drives the ions in the DL across the channel; these charges drag neutral fluid molecules and create net fluid flow (
(members of the electrokinetic matrix) capture the interplay between the surface and fluid properties and are derived in “Materials and Methods.” When an electric field is applied between the ends of a charged channel, it drives the ions in the DL across the channel; these charges drag neutral fluid molecules and create net fluid flow (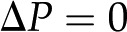 in Eqs. 4 and 5). This effect is known as electroosmosis. Conversely, when a pressure gradient is applied, it creates a net fluid flow; this flow convects the charges in the DL and creates a flow of electrical current known as the streaming current (
in Eqs. 4 and 5). This effect is known as electroosmosis. Conversely, when a pressure gradient is applied, it creates a net fluid flow; this flow convects the charges in the DL and creates a flow of electrical current known as the streaming current ( in Eqs. 4 and 5). If there exists an electrical path between the ends of the channel, distinct from the ionic path created by the electrolyte that fills the channel, then the convection of charge by pressure-driven flow will lead to a net streaming current. If there is no electrical path between the ends, then the charges convected by pressure-driven flow will accumulate downstream and produce an electric potential (
in Eqs. 4 and 5). If there exists an electrical path between the ends of the channel, distinct from the ionic path created by the electrolyte that fills the channel, then the convection of charge by pressure-driven flow will lead to a net streaming current. If there is no electrical path between the ends, then the charges convected by pressure-driven flow will accumulate downstream and produce an electric potential ( ). This potential, called the streaming potential, drives an ionic current against the convection such that there will be no net ionic current (I = 0 in Eqs. 4 and 5).
). This potential, called the streaming potential, drives an ionic current against the convection such that there will be no net ionic current (I = 0 in Eqs. 4 and 5).
Electroviscosity
Figure 4 presents the interplay of these electrokinetic processes in defining the electroviscosity: As fluid flows through a charged channel without a closed electrical circuit, the resulting streaming potential decreases the permeability of the channel, K. Macroscopically, the channel appears to present a lower 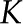 than predicted by Hagen-Poiseuille for the radius of the conduit and the viscosity of the fluid. From Equations 4 and 5, setting
than predicted by Hagen-Poiseuille for the radius of the conduit and the viscosity of the fluid. From Equations 4 and 5, setting 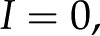 the net volumetric flow in a cylindrical channel, taking into account electroviscosity, is given by:
the net volumetric flow in a cylindrical channel, taking into account electroviscosity, is given by:
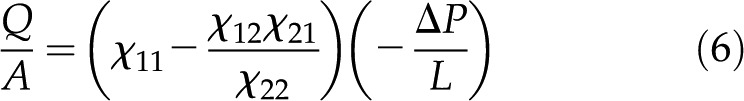 |
Figure 4.
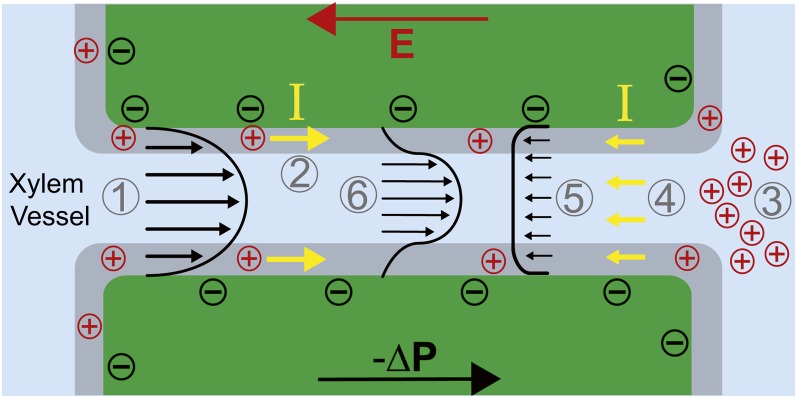
Electroviscosity. Pressure-driven flow (1) sweeps cations in the Debye layer (gray region; 2) and creates a buildup of positive charges at the distal end of the pore (3). Accumulated positive charges produce an electric field (E) that drives an ionic current, I, opposite to the direction of pressure-driven flow (4). These charges drag fluid molecules as they move, creating an opposing electroosmotic flow (5) and decreasing net forward flow through the pore (6). [See online article for color version of this figure.]
In Equation 6, we can identify 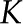 as:
as:
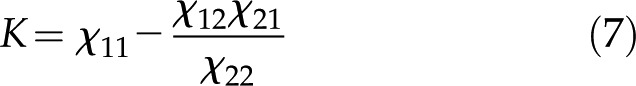 |
The maximum conductance (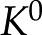 ), which occurs in an uncharged channel (
), which occurs in an uncharged channel ( ), is given by the Hagen-Poiseuille equation for a cylinder:
), is given by the Hagen-Poiseuille equation for a cylinder:
 |
where 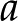 is the cylinder radius. Dividing Equation 7 by Equation 8, the conductance of a charged channel relative to an uncharged one is:
is the cylinder radius. Dividing Equation 7 by Equation 8, the conductance of a charged channel relative to an uncharged one is:
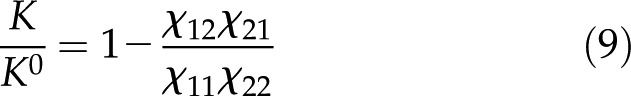 |
We will use the ratio in Equation 9 as a measure of the magnitude of electroviscosity in the channel. If there is no surface charge, the relative conductance, 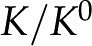 , is one.
, is one.
We use standard electrokinetic theory (Kirby, 2010) to calculate the electrokinetic coefficients, 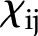 . One important note is that we account for the dependence of
. One important note is that we account for the dependence of  on the properties of the fluid (pH,
on the properties of the fluid (pH,  , and
, and 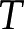 ), the properties of the surface material (
), the properties of the surface material (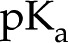 and
and 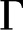 ), and the radius of the channel (Behrens and Grier, 2001). This calculation is necessary because the value of
), and the radius of the channel (Behrens and Grier, 2001). This calculation is necessary because the value of  strongly influences the magnitude of electrokinetic effects, and, as will be seen in the results,
strongly influences the magnitude of electrokinetic effects, and, as will be seen in the results,  varies substantially with the fluid and surface properties and channel radius.
varies substantially with the fluid and surface properties and channel radius.
RESULTS
We now exploit the model described in the previous section to explore the ionic effect on flow through a BPM pore. We discuss the dependence of 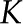 on
on  , pH,
, pH, 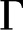 ,
, 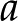 , and ionic identity. We then compare these predictions with experimental measurements from the literature. In the “Discussion,” we use these predictions to propose experiments and further comparisons with data from the literature.
, and ionic identity. We then compare these predictions with experimental measurements from the literature. In the “Discussion,” we use these predictions to propose experiments and further comparisons with data from the literature.
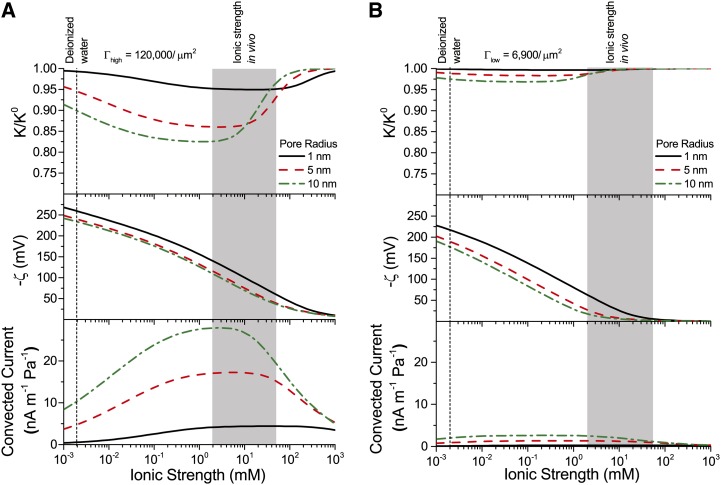
Conductance as a Function of Ionic Strength, Density of Chargeable Sites, and Pore Size
With our model, we first explore how conductance varies as a function of  for the high and low limits of the expected density of acid groups on the walls of the pore (
for the high and low limits of the expected density of acid groups on the walls of the pore (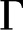 ) and for various pore sizes. We use the properties of a simple, one-to-one electrolyte (KCl) previously exploited in many experiments (van Ieperen et al., 2000; Cochard et al., 2010). Figure 5 presents our predictions for relative conductance (
) and for various pore sizes. We use the properties of a simple, one-to-one electrolyte (KCl) previously exploited in many experiments (van Ieperen et al., 2000; Cochard et al., 2010). Figure 5 presents our predictions for relative conductance (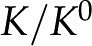 ), surface potential (
), surface potential ( ), and convected current as a function of
), and convected current as a function of  . These results are shown for both materials with
. These results are shown for both materials with 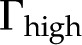 (Fig. 5A) and
(Fig. 5A) and 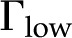 (Fig. 5B) and pores of radii of 1, 5, and 10 nm; these radii cover the range reported from colloidal gold perfusion studies (Choat et al., 2003; Pérez-Donoso et al., 2010). We note the following: The higher density of chargeable sites (
(Fig. 5B) and pores of radii of 1, 5, and 10 nm; these radii cover the range reported from colloidal gold perfusion studies (Choat et al., 2003; Pérez-Donoso et al., 2010). We note the following: The higher density of chargeable sites (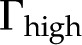 ) leads to larger variations in conductance with
) leads to larger variations in conductance with  (Fig. 5A) than does the lower density (
(Fig. 5A) than does the lower density (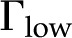 ; Fig. 5B), and
; Fig. 5B), and 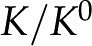 varies nonmonotonically for both cases with minima the depths of which grow with increasing radius and positions of which move to lower
varies nonmonotonically for both cases with minima the depths of which grow with increasing radius and positions of which move to lower  with increasing pore radius. Although, in general,
with increasing pore radius. Although, in general, 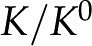 varies nonmonotonically with
varies nonmonotonically with  , it increases monotonically with
, it increases monotonically with  in the physiological range of
in the physiological range of  (2–50 mm; Schurr and Schulze, 1995; Herdel et al., 2001; Siebrecht et al., 2003) for the larger pore sizes.
(2–50 mm; Schurr and Schulze, 1995; Herdel et al., 2001; Siebrecht et al., 2003) for the larger pore sizes.
Figure 5.
Relative conductance (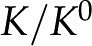 ) versus ionic strength for 1- to 10-nm pores and density of chargeable sites
) versus ionic strength for 1- to 10-nm pores and density of chargeable sites 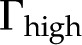 (A) and
(A) and 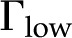 (B); the corresponding zeta potential (
(B); the corresponding zeta potential ( ) and convected current are also shown. Properties used are as follows: KCl electrolyte in pure water; pH = 7;
) and convected current are also shown. Properties used are as follows: KCl electrolyte in pure water; pH = 7; 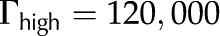 μm−1; and
μm−1; and 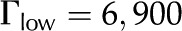 μm−1. [See online article for color version of this figure.]
μm−1. [See online article for color version of this figure.]
In looking for insights into this behavior, we first turn to the surface potential (Fig. 5, second row). This potential shows much weaker dependence on the density of surface charge than does 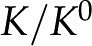 , and it grows monotonically with decreasing ionic strength. On the other hand, the variations of convected current (“2” in Fig. 4) mirror those of the electroviscous decrease in conductance and thus help elucidate its origins (Fig. 5, bottom row). First, for
, and it grows monotonically with decreasing ionic strength. On the other hand, the variations of convected current (“2” in Fig. 4) mirror those of the electroviscous decrease in conductance and thus help elucidate its origins (Fig. 5, bottom row). First, for 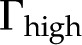 , the net charge in the DL is higher such that more charge is convected with the pressure-driven flow than for
, the net charge in the DL is higher such that more charge is convected with the pressure-driven flow than for 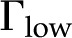 ; the convection of more charge leads to a stronger electroviscous drag. At sufficiently large
; the convection of more charge leads to a stronger electroviscous drag. At sufficiently large  , the DL is more densely charged but very thin, such that little charge is convected. Furthermore, at high Ic, the electrical conductance of the solution increases to the point that it significantly reduces the streaming potential (i.e. it acts as a short circuit). At low
, the DL is more densely charged but very thin, such that little charge is convected. Furthermore, at high Ic, the electrical conductance of the solution increases to the point that it significantly reduces the streaming potential (i.e. it acts as a short circuit). At low  , the DL is thick compared with the radius of the pore (
, the DL is thick compared with the radius of the pore (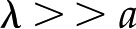 ) but contains a sparse distribution of charge: The flow convects little charge and produces minimal electroviscous resistance. The minimum of conductance and the maximum of convected current occur when the thickness of the DL is approximately equal to the pore radius (
) but contains a sparse distribution of charge: The flow convects little charge and produces minimal electroviscous resistance. The minimum of conductance and the maximum of convected current occur when the thickness of the DL is approximately equal to the pore radius (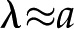 ).
).
Comparison with Experiments: Conductance versus Ionic Strength
We now compare our theoretical predictions with experimental data from the literature. By assuming that bordered pits form the limiting hydraulic resistance in xylem, such that 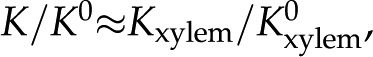 we calculate the maximum decrease in
we calculate the maximum decrease in  expected due to electroviscosity. Figure 6 presents our predictions for
expected due to electroviscosity. Figure 6 presents our predictions for  of BPM pores with
of BPM pores with  and
and  , alongside theoretical predictions by van Doorn et al. (2011) and data from experimental studies. Measurements shown are for angiosperms for studies in which
, alongside theoretical predictions by van Doorn et al. (2011) and data from experimental studies. Measurements shown are for angiosperms for studies in which  was measured across a range of
was measured across a range of  . We selected representative data from each reference (given in caption). We begin by remarking that the model by van Doorn et al. (2011) (black dash-dot line) qualitatively captures the drop in
. We selected representative data from each reference (given in caption). We begin by remarking that the model by van Doorn et al. (2011) (black dash-dot line) qualitatively captures the drop in  with decreasing
with decreasing  that was observed in some studies but predicts a larger drop in
that was observed in some studies but predicts a larger drop in 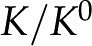 than observed experimentally for
than observed experimentally for 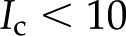 mm. Our model (black solid line for
mm. Our model (black solid line for 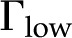 and black dashed line for
and black dashed line for 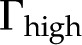 ) also captures this decrease of
) also captures this decrease of  with decreasing
with decreasing  across the physiological range, consistent with the results of van Doorn et al. Indeed, within this range, the trend reported for L. nobilis (purple triangles; Zwieniecki et al., 2001), Dendranthema × grandiflorum Tzvelev (Chrysanthemum) (red squares; van Ieperen et al., 2000), and Quercus robur (green circles, Aasamaa and Sõber, 2010) are compatible in both trend and magnitude with our predictions, given a value of
across the physiological range, consistent with the results of van Doorn et al. Indeed, within this range, the trend reported for L. nobilis (purple triangles; Zwieniecki et al., 2001), Dendranthema × grandiflorum Tzvelev (Chrysanthemum) (red squares; van Ieperen et al., 2000), and Quercus robur (green circles, Aasamaa and Sõber, 2010) are compatible in both trend and magnitude with our predictions, given a value of 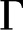 between
between 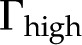 and
and 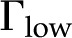 . These experimental studies are reviewed by Nardini et al. (2011), where 28 out of 35 experiments on different species, made by various research groups, show a response that falls within, or close to, our predicted range (
. These experimental studies are reviewed by Nardini et al. (2011), where 28 out of 35 experiments on different species, made by various research groups, show a response that falls within, or close to, our predicted range (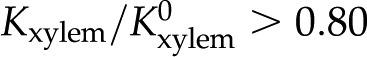 ), with five out of seven outliers showing
), with five out of seven outliers showing 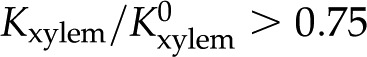 . In general, our predictions are consistent with the experimental data at physiologically relevant values of
. In general, our predictions are consistent with the experimental data at physiologically relevant values of  but are incompatible with various experimental measurements outside of this range: L. nobilis shows
but are incompatible with various experimental measurements outside of this range: L. nobilis shows 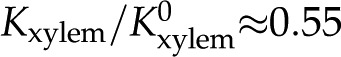 for
for 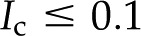 mm, while Conocarpus erectus (blue triangles, López-Portillo et al., 2005) shows
mm, while Conocarpus erectus (blue triangles, López-Portillo et al., 2005) shows 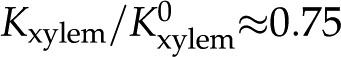 for deionized water and
for deionized water and 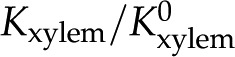 drops to approximately 0.65 for
drops to approximately 0.65 for 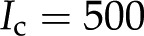 mm. In all of these cases, the reported responses were significantly larger than we predict based on electroviscosity.
mm. In all of these cases, the reported responses were significantly larger than we predict based on electroviscosity.
Our model can also explain the three distinct responses of  , increase, decrease, and no effect, to an increase in
, increase, decrease, and no effect, to an increase in  reported in the literature (Cochard et al., 2010). Consider a hypothetical BPM with the characteristics of
reported in the literature (Cochard et al., 2010). Consider a hypothetical BPM with the characteristics of 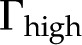 in Figure 6: An increase from 2 mm (“b” in the figure) to 10 mm KCl (“c”) produces an increase in
in Figure 6: An increase from 2 mm (“b” in the figure) to 10 mm KCl (“c”) produces an increase in  , a change from deionized water (“a”) to 10 mm KCl (“c”) produces no difference in
, a change from deionized water (“a”) to 10 mm KCl (“c”) produces no difference in  , and an increase in
, and an increase in  from deionized water (“a”) to a 2 mm KCl solution (“b”) produces a decrease in
from deionized water (“a”) to a 2 mm KCl solution (“b”) produces a decrease in  .
.
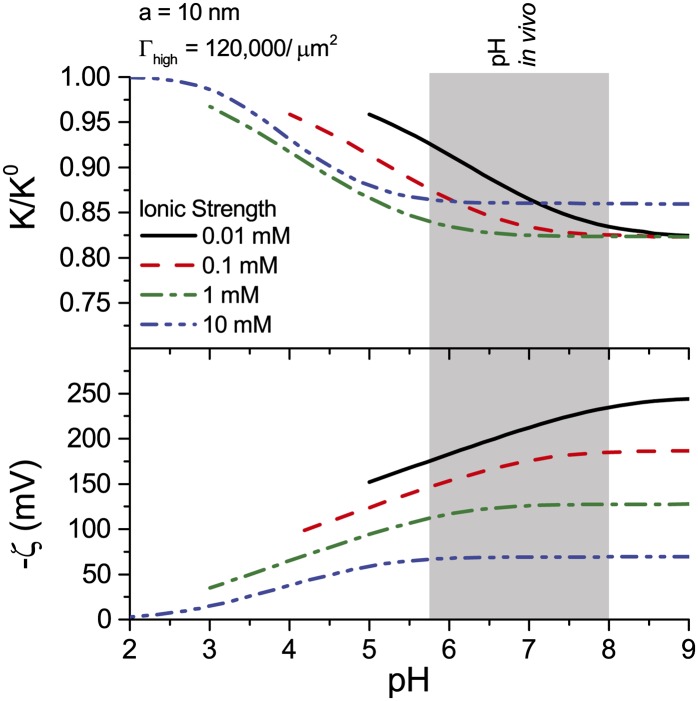
Conductance as a Function of pH and Ionic Strength
The hydraulic conductance of xylem has been shown to increase in response to a decrease in pH of the perfusing solution (Zwieniecki et al., 2001). We find that electroviscosity presents a similar behavior: Conductance is maximum at low pH and decreases to a minimum for 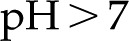 (Fig. 7). For
(Fig. 7). For 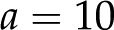 nm and
nm and 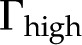 , this minimum is
, this minimum is 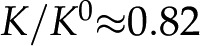 . The surface potential follows an opposite trend: It is near 0 at low pH but saturates to its maximum value at
. The surface potential follows an opposite trend: It is near 0 at low pH but saturates to its maximum value at 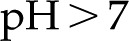 (Fig. 7). As the pH is increased, surface chargeable sites deprotonate, producing a larger
(Fig. 7). As the pH is increased, surface chargeable sites deprotonate, producing a larger  , a denser ionic layer, and a stronger electroviscous decrease in
, a denser ionic layer, and a stronger electroviscous decrease in 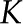 . This effect is pronounced at low pH, yet for in vivo values of
. This effect is pronounced at low pH, yet for in vivo values of  (1 and 10 mm) and pH (5.8–8; Marschner, 1995), changes in pH produce only small changes in
(1 and 10 mm) and pH (5.8–8; Marschner, 1995), changes in pH produce only small changes in 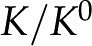 (approximately 2%). These predictions are qualitatively consistent with experiments but are too small to explain the large responses observed experimentally. For example, in the study by Zwieniecki et al. (2001),
(approximately 2%). These predictions are qualitatively consistent with experiments but are too small to explain the large responses observed experimentally. For example, in the study by Zwieniecki et al. (2001),  at
at 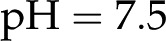 was 75% of its value at
was 75% of its value at 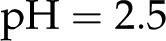 .
.
Figure 7.
Relative hydraulic conductance (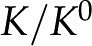 ) and zeta potential (
) and zeta potential ( ) versus fluid pH in the BPM for various ionic strengths. Properties used: KCl electrolyte in pure water,
) versus fluid pH in the BPM for various ionic strengths. Properties used: KCl electrolyte in pure water, 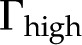 density of chargeable sites, and
density of chargeable sites, and 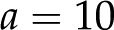 nm. [See online article for color version of this figure.]
nm. [See online article for color version of this figure.]
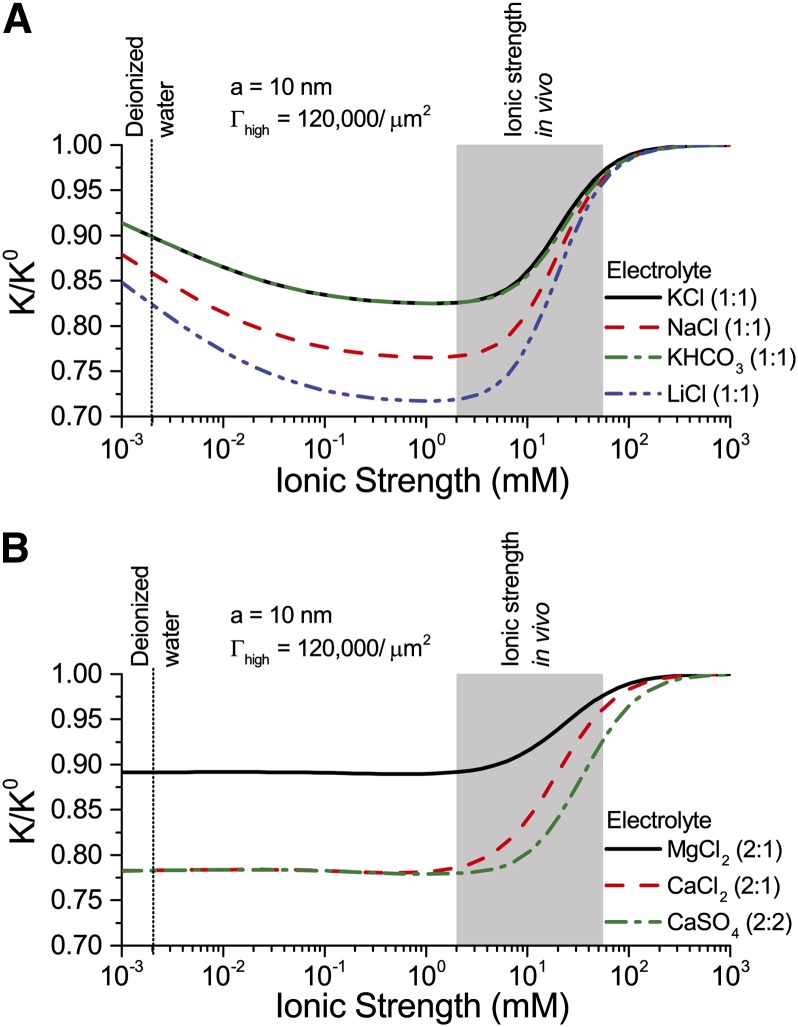
Conductance as a Function of Ion Identity and Ionic Strength
The identity of ions in the sap in perfusion experiments has been shown to affect  (van Ieperen et al., 2000; Zwieniecki et al., 2001; Gascó et al., 2006). We now examine this behavior from an electrokinetic perspective. We look at how both the electrophoretic mobility (
(van Ieperen et al., 2000; Zwieniecki et al., 2001; Gascó et al., 2006). We now examine this behavior from an electrokinetic perspective. We look at how both the electrophoretic mobility (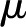 ) and valence of ions in the electrolyte affect
) and valence of ions in the electrolyte affect 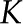 . Figure 8 shows
. Figure 8 shows 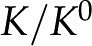 versus
versus  for a solution with various monovalent (Fig. 8A) or divalent (Fig. 8B) cations. As before,
for a solution with various monovalent (Fig. 8A) or divalent (Fig. 8B) cations. As before, 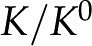 shows a nonmonotonic relationship with
shows a nonmonotonic relationship with  . Conductance is higher for cations with larger mobility, yet is nearly independent of anion mobility or valence. Due to the negative surface charge, cations outnumber anions in the solution within the pore; therefore, the overall electrical conductivity of the solution, and its influence on electroviscous drag, is largely determined by the characteristics of the cations. Cations with larger mobilities increase the solution electrical conductivity and thus decrease both the streaming potential and the electroviscous drag. For instance,
. Conductance is higher for cations with larger mobility, yet is nearly independent of anion mobility or valence. Due to the negative surface charge, cations outnumber anions in the solution within the pore; therefore, the overall electrical conductivity of the solution, and its influence on electroviscous drag, is largely determined by the characteristics of the cations. Cations with larger mobilities increase the solution electrical conductivity and thus decrease both the streaming potential and the electroviscous drag. For instance, 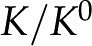 for a solution of LiCl is lower than
for a solution of LiCl is lower than 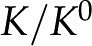 for a solution of KCl at all values of
for a solution of KCl at all values of  (
(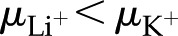 ). Divalent cations (Fig. 8B) show a similar trend to that of monovalent cations (Fig. 8A), but
). Divalent cations (Fig. 8B) show a similar trend to that of monovalent cations (Fig. 8A), but 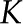 is minimum below
is minimum below 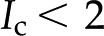 mm. These predictions, that higher mobility ions decrease flow more, have been reported in some studies, while others report no effect. In L. nobilis, perfusion of a 100 mm KCl solution increased flow by 35% over deionized water, whereas 100 mm NaCl increased flow by only 22% (Gascó et al., 2006), where
mm. These predictions, that higher mobility ions decrease flow more, have been reported in some studies, while others report no effect. In L. nobilis, perfusion of a 100 mm KCl solution increased flow by 35% over deionized water, whereas 100 mm NaCl increased flow by only 22% (Gascó et al., 2006), where  . By contrast, a study in Chrysanthemum reported negligible difference in
. By contrast, a study in Chrysanthemum reported negligible difference in  between solutions of 10 mm KCl, NaCl, K2SO4, MgSO4, and CaCl2 (van Ieperen et al., 2000). Regardless of the ionic identity, in the physiologically relevant range,
between solutions of 10 mm KCl, NaCl, K2SO4, MgSO4, and CaCl2 (van Ieperen et al., 2000). Regardless of the ionic identity, in the physiologically relevant range, 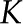 increases with an increase in
increases with an increase in  for the pore size (10 nm) and pH (7) chosen in our model.
for the pore size (10 nm) and pH (7) chosen in our model.
Figure 8.
Relative hydraulic conductance (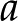 ) versus ionic strength for an electrolyte with monovalent cations (A) or divalent cations (B). Properties used: given electrolyte in pure water,
) versus ionic strength for an electrolyte with monovalent cations (A) or divalent cations (B). Properties used: given electrolyte in pure water, 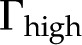 density of chargeable sites,
density of chargeable sites, 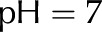 , and pore radius
, and pore radius 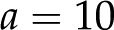 nm. The electrophoretic mobilities of the cations (
nm. The electrophoretic mobilities of the cations (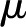 ) are related as follows:
) are related as follows: 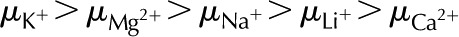 (see Table II). Anion mobilities have negligible effect on
(see Table II). Anion mobilities have negligible effect on  . [See online article for color version of this figure.]
. [See online article for color version of this figure.]
DISCUSSION
Our comparisons with available measurements indicate that electroviscosity is compatible with the qualitative trends of most studies in the physiological range of  and pH and shows reasonable quantitative agreement with some experiments. Outside this range, experimental reports diverge both qualitatively (monotonic versus nonmonotonic) and quantitatively; thus, we cannot draw any definitive conclusions regarding their compatibility with our predictions. We hypothesize various reasons for these discrepancies: experimental artifacts, model idealizations, and competing effects.
and pH and shows reasonable quantitative agreement with some experiments. Outside this range, experimental reports diverge both qualitatively (monotonic versus nonmonotonic) and quantitatively; thus, we cannot draw any definitive conclusions regarding their compatibility with our predictions. We hypothesize various reasons for these discrepancies: experimental artifacts, model idealizations, and competing effects.
Two experimental artifacts may exaggerate the ionic effect. First, wounding responses in perfusion experiments (i.e. from cutting or perforating the stem) may gradually obstruct xylem vessels with parenchyma cell outgrowth and secretions (Sun et al., 2008), producing an exaggerated decrease in  . Second, various published experiments use deionized water as a baseline measurement of
. Second, various published experiments use deionized water as a baseline measurement of  ; this fluid has an
; this fluid has an  far below plant sap and may cause an exaggerated ionic effect unlikely to exist in vivo (van Ieperen, 2007). Because it lacks dissolved ions, deionized water purges naturally present ions from the xylem surface and promotes deprotonation; consequently, its perfusion may increase the surface charge and
far below plant sap and may cause an exaggerated ionic effect unlikely to exist in vivo (van Ieperen, 2007). Because it lacks dissolved ions, deionized water purges naturally present ions from the xylem surface and promotes deprotonation; consequently, its perfusion may increase the surface charge and  , thus producing stronger electroviscosity, lower
, thus producing stronger electroviscosity, lower 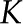 , than predicted by our model of constant surface composition. This removal of ions could explain why
, than predicted by our model of constant surface composition. This removal of ions could explain why  continues to decrease over time as deionized water is perfused through stems (Zimmermann, 1978; Zwieniecki et al., 2001; Cochard et al., 2010), and the pH of this solution is higher upon exiting the stem (Gascó et al., 2008). On the other hand,
continues to decrease over time as deionized water is perfused through stems (Zimmermann, 1978; Zwieniecki et al., 2001; Cochard et al., 2010), and the pH of this solution is higher upon exiting the stem (Gascó et al., 2008). On the other hand,  stabilizes when a solution with higher
stabilizes when a solution with higher  (5–10 mm KCl; Zimmermann, 1978) or low pH (Sperry et al., 1988) is used. In a charged channel, a solution with large
(5–10 mm KCl; Zimmermann, 1978) or low pH (Sperry et al., 1988) is used. In a charged channel, a solution with large  does not strip ions from the walls to the same extent, and thus keeps
does not strip ions from the walls to the same extent, and thus keeps  constant; a solution with low pH discourages deprotonation and thus lowers
constant; a solution with low pH discourages deprotonation and thus lowers  , eliminating the electroviscous resistance. In both circumstances, flow is stable, close to its maximum value.
, eliminating the electroviscous resistance. In both circumstances, flow is stable, close to its maximum value.
In our analysis, the pores of the BPM are modeled as rigid, perfect cylinders, but this geometry may not accurately represent the complex and variable structure of the BPM. First, a recent study that imaged a BPM using atomic force microscopy suggests that a BPM may be better modeled as a bundle of fibers, the surface of which is covered with a layer of gel (Lee et al., 2012). This distinct architecture (i.e. from that depicted in Fig. 1D) could change the magnitude and dependence of electroviscosity on ionic strength. Second, studies suggest that theoretical calculations tend to underpredict the magnitude of electroviscosity in porous media (Huisman et al., 2000). Third, our analysis predicts that large surface potentials are created at low  (Fig. 5). In a real system, this potential would cause the pore walls to repel each other and therefore increase the overall pore size (van Doorn et al., 2011), an effect not accounted for in our model.
(Fig. 5). In a real system, this potential would cause the pore walls to repel each other and therefore increase the overall pore size (van Doorn et al., 2011), an effect not accounted for in our model.
We cannot exclude the possible role played by other mechanisms in defining the observed trends. In particular, the hypothesis of gel swelling (Fig. 2) could lead to the same trends in the physiological range and increase the overall ionic response. For instance, pectin could show both strong electroviscosity and hydrogel swelling. Conductance might then be influenced by a combination of these effects.
Proposed Experiments
Exploiting our theoretical predictions, we now propose three experiments, the outcomes of which should be either compatible or incompatible with an electrokinetic origin of the ionic effect. In these experiments, we propose changes in parameters that should not affect the hydration state of hydrogels such that the presence or absence of changes in the ionic effect could be attributed to electroviscosity and not to swelling of hydrogels. We aim to decrease electroviscosity by varying the following parameters: (1) the viscosity of the DL, (2) the electrophoretic mobility of the cations, and (3) the streaming potential. According to Figures 5 and 7, electroviscosity produces the greatest decrease in flow at pH > 6 and  approximately 2 to 3 mm; therefore, these experiments should be performed in this range to produce the strongest response.
approximately 2 to 3 mm; therefore, these experiments should be performed in this range to produce the strongest response.
(1) Perfuse a stem segment with a 2 mm KCl solution at constant pressure until flow rate stabilizes. At this point, change the solution to 2 mm KCl with 0.4 weight percent methylcellulose. Experiments in synthetic channels indicate that methylcellulose increases the viscosity near the channel surface and consequently reduces both the amount of charge convected and the electroviscous resistance (Hjertén, 1967). Although the overall viscosity of the fluid increases, flow rate should increase if the reduced conductance is due to electroviscosity. Methylcellulose is a neutral molecule, so it will not change the ionic strength of the fluid and should not affect the swelling of hydrogels in the BPM.
(2) Perfuse a stem segment with a 2 mm LiCl solution at constant pressure until flow rate stabilizes. At this point, change the solution to 2 mm KCl. The electrophoretic mobility of K+ is larger than that of Li+; therefore, the KCl solution is more conductive, produces a weaker streaming potential, and should increase flow rate. From Figure 8A, we predict that  for any given
for any given  and that flow rate should be independent of the identity of anions in solution. This cation-dependent conductance has been shown previously in synthetic systems (Huisman et al., 2000). Cations with larger valence, e.g. Ca2+ and La3+, may confound the results because of their larger tendency to bind to the surface (Kirby and Hasselbrink, 2004).
and that flow rate should be independent of the identity of anions in solution. This cation-dependent conductance has been shown previously in synthetic systems (Huisman et al., 2000). Cations with larger valence, e.g. Ca2+ and La3+, may confound the results because of their larger tendency to bind to the surface (Kirby and Hasselbrink, 2004).
(3) Perfuse a stem segment with a 2 mm KCl solution at constant pressure until flow rate stabilizes. At this point, create an electrical short circuit in the segment by providing an external electrical path through which the convected charges return to the source reservoir. Because charges can flow freely through the external conductive path, there should be little streaming potential in the stem segment, the electroviscous resistance should diminish, and flow should increase. This short circuit is used in the microfluidics literature to measure the streaming current by forcing the streaming potential to be 0 (ΔV = 0 in Eq. 4; Werner et al., 2001). We note that complete elimination of the streaming potential is challenging due to the polarization of the electrodes, but any observed increase in flow with addition of this external electrical path would provide evidence that electroviscosity is at least partially responsible for the reduction of flow.
Ecophysical Implications
Our analysis suggests that plants may use several mechanisms to enhance sap transport through BPMs in an active manner, possibly in response to emboli. First, by locally increasing the sap’s  in the physiologically relevant range of 2 to 20 mm, conductance through the BPM could increase by up to 15% (Fig. 5). This increase could occur if voltage-gated ion channels such as outward K+ rectifiers released K+ from adjacent cells, thereby increasing K+ concentration locally in the sap. Similarly, Ca2+ could be released into the xylem by calcium-permeable channels that are activated by plasma membrane depolarization (Buchanan et al., 2000). Second, plants may be able to alter the ionic composition of sap to increase conductance through the pore (Figs. 5 and 7). This increase might be accomplished by selective ion loading into pits from adjacent parenchyma cells or via coupling to the phloem. Evidence from stem perfusion studies highlights the importance of BPM to ion-mediated flow; these studies suggest that plants may be able to alter the ionic composition of sap to mitigate the decreased conductance resulting from embolisms (Gascó et al., 2006). This mechanism would allow plants to maintain sap transport capacity and, consequently, photosynthesis, during prolonged drought conditions.
in the physiologically relevant range of 2 to 20 mm, conductance through the BPM could increase by up to 15% (Fig. 5). This increase could occur if voltage-gated ion channels such as outward K+ rectifiers released K+ from adjacent cells, thereby increasing K+ concentration locally in the sap. Similarly, Ca2+ could be released into the xylem by calcium-permeable channels that are activated by plasma membrane depolarization (Buchanan et al., 2000). Second, plants may be able to alter the ionic composition of sap to increase conductance through the pore (Figs. 5 and 7). This increase might be accomplished by selective ion loading into pits from adjacent parenchyma cells or via coupling to the phloem. Evidence from stem perfusion studies highlights the importance of BPM to ion-mediated flow; these studies suggest that plants may be able to alter the ionic composition of sap to mitigate the decreased conductance resulting from embolisms (Gascó et al., 2006). This mechanism would allow plants to maintain sap transport capacity and, consequently, photosynthesis, during prolonged drought conditions.
As BPM surfaces may be electrically charged, the various electrokinetic effects discussed in the theory section may play a role in other plant functions. For instance, changes in flow upon embolization may lead to changes in distributions of streaming potentials around embolized vessels and serve to trigger refilling (Zwieniecki and Holbrook, 2009; Secchi and Zwieniecki, 2012). Take a typical BPM that is 130-nm thick and 5 µm in diameter (Schmid and Machado, 1968), with 10-nm pores and 0.5 porosity. Assuming sap with  mm KCl, a pressure drop of 100 Pa across this BPM (Gregory and Petty, 1973) produces a flow rate of approximately 0.1 pL/s and a streaming potential of 8 µV in our model (Eqs. 4 and 5). The local change in this streaming potential upon embolization might be sufficient to trigger a refilling program in adjacent parenchymal cells. We also note that, if plants could generate a small electric field across the pit (e.g. based on active membrane processes in adjacent parenchymal cells), it would create electroosmotic flow across the BPM, an effect that could be used to drive sap back into embolized vessels. The possibility that electric potentials in plants may generate flow has been previously proposed for phloem sieve plates as a way to drive water flow through the xylem network (Fensom, 1957; Spanner, 1958; Spanner, 1979). Taking the previously discussed scenario, a modest 10-mV voltage difference across a BPM would create a flow rate of approximately 50 pL/s; this flow could refill a typical xylem segment (Hacke et al., 2006) in 1 min to 33 h. We further note that this refilling mechanism could change the constraints on models of vessel refilling previously proposed (Zwieniecki and Holbrook, 2009).
mm KCl, a pressure drop of 100 Pa across this BPM (Gregory and Petty, 1973) produces a flow rate of approximately 0.1 pL/s and a streaming potential of 8 µV in our model (Eqs. 4 and 5). The local change in this streaming potential upon embolization might be sufficient to trigger a refilling program in adjacent parenchymal cells. We also note that, if plants could generate a small electric field across the pit (e.g. based on active membrane processes in adjacent parenchymal cells), it would create electroosmotic flow across the BPM, an effect that could be used to drive sap back into embolized vessels. The possibility that electric potentials in plants may generate flow has been previously proposed for phloem sieve plates as a way to drive water flow through the xylem network (Fensom, 1957; Spanner, 1958; Spanner, 1979). Taking the previously discussed scenario, a modest 10-mV voltage difference across a BPM would create a flow rate of approximately 50 pL/s; this flow could refill a typical xylem segment (Hacke et al., 2006) in 1 min to 33 h. We further note that this refilling mechanism could change the constraints on models of vessel refilling previously proposed (Zwieniecki and Holbrook, 2009).
CONCLUSION
This study presents a rigorous model of the ionic effect based on electrokinetic processes in the BPM. Comparisons of the predictions of this model with available experimental data show qualitative agreement in the physiological range of  and pH. The large quantitative differences in experimental measurements across species and the lack of exact, species-dependent knowledge of the properties (pore size, structure, and surface chemistry) of BPMs make it impossible to test this proposed mechanism definitively. Future experiments should aim at the thorough characterization of each species of interest and employ manipulations that specifically affect the physical basis of a given hypothetical mechanism (e.g. electrokinetic or swelling of hydrogels). We suggest three such experiments to test the electrokinetic hypothesis. We emphasize that more than one mechanism may underlie the observed behavior. Finally, we point to the possibility that electrokinetic effects described by our model may be involved in other processes within the xylem, distinct from the ionic effect. We hope that this exposition on possible electrokinetic processes in xylem may help in the development of clear, testable hypotheses for the operation of these phenomena in planta.
and pH. The large quantitative differences in experimental measurements across species and the lack of exact, species-dependent knowledge of the properties (pore size, structure, and surface chemistry) of BPMs make it impossible to test this proposed mechanism definitively. Future experiments should aim at the thorough characterization of each species of interest and employ manipulations that specifically affect the physical basis of a given hypothetical mechanism (e.g. electrokinetic or swelling of hydrogels). We suggest three such experiments to test the electrokinetic hypothesis. We emphasize that more than one mechanism may underlie the observed behavior. Finally, we point to the possibility that electrokinetic effects described by our model may be involved in other processes within the xylem, distinct from the ionic effect. We hope that this exposition on possible electrokinetic processes in xylem may help in the development of clear, testable hypotheses for the operation of these phenomena in planta.
MATERIALS AND METHODS
In this article, we develop a model of the BPM to investigate how electroviscosity may influence the membrane’s hydraulic conductance ( ). The BPM hydraulically connects two adjacent vessels, transporting sap through its irregular network of pores. Two models have been proposed for the structure of the membrane: (1) as a permeable gel through which sap diffuses (Lee et al., 2012) or (2) as traversed by a number of discrete pores through which sap flows (Zwieniecki et al., 2001; Fig. 1D). We take perspective (2) and idealize the BPM as comprised of many identical, straight, rigid, cylindrical pores through which sap is driven by a pressure gradient (Fig. 4). This model can be modified to account for the irregularity of BPMs by using data on tortuosity and pore size distribution (Yao and Santiago, 2003). These assumptions overlook the deformation of pores due to hydrogel swelling (Zwieniecki et al., 2001) or electrostatic surface repulsion (van Doorn et al., 2011). Nevertheless, electroviscosity will be present in nanometer channels regardless of their specific geometry, and we believe that these assumptions capture the dominant characteristics of this phenomenon.
). The BPM hydraulically connects two adjacent vessels, transporting sap through its irregular network of pores. Two models have been proposed for the structure of the membrane: (1) as a permeable gel through which sap diffuses (Lee et al., 2012) or (2) as traversed by a number of discrete pores through which sap flows (Zwieniecki et al., 2001; Fig. 1D). We take perspective (2) and idealize the BPM as comprised of many identical, straight, rigid, cylindrical pores through which sap is driven by a pressure gradient (Fig. 4). This model can be modified to account for the irregularity of BPMs by using data on tortuosity and pore size distribution (Yao and Santiago, 2003). These assumptions overlook the deformation of pores due to hydrogel swelling (Zwieniecki et al., 2001) or electrostatic surface repulsion (van Doorn et al., 2011). Nevertheless, electroviscosity will be present in nanometer channels regardless of their specific geometry, and we believe that these assumptions capture the dominant characteristics of this phenomenon.
In the following sections, we determine the electroviscosity-induced change in 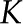 as follows: we (1) derive the electric potential distribution [
as follows: we (1) derive the electric potential distribution [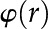 ] and charge density distribution [
] and charge density distribution [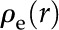 ], (2) determine the relationship between surface charge (
], (2) determine the relationship between surface charge (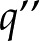 ) and zeta potential (
) and zeta potential ( ), (3) extract approximate values for the density of chargeable sites (
), (3) extract approximate values for the density of chargeable sites (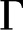 ) from experimental data on plant derived materials, and (4) numerically solve for the electrokinetic matrix coefficients (Eqs. 4 and 5) to calculate
) from experimental data on plant derived materials, and (4) numerically solve for the electrokinetic matrix coefficients (Eqs. 4 and 5) to calculate 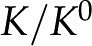 . The parameters used are presented in Table II (electrophoretic mobilities) and Table III (general parameters).
. The parameters used are presented in Table II (electrophoretic mobilities) and Table III (general parameters).
Table II. Electrophoretic mobility of ions used in analysis.
| Ion | Electrophoretic Mobility 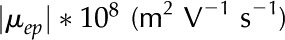
|
|---|---|
| Ca2+ | 3.1 |
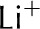 |
4.0 |
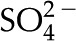 |
4.1 |
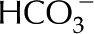 |
4.6 |
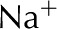 |
5.2 |
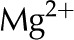 |
7.3 |
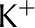 |
7.6 |
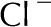 |
7.9 |
Table III. Parameters used in the analysis.
| Parameter | Value |
|---|---|
| Temperature | 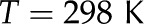 |
| Viscosity of water | 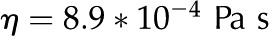 |
| Permittivity of water |
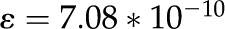 F/m F/m |
| pH of water | 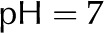 |
 of deionized water at room conditionsa of deionized water at room conditionsa
|
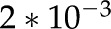 mm mm
|
| Surface dissociation constantb | 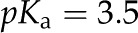 |
| Number of chargeable sites, cellulose | 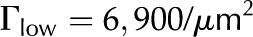 |
| Number of chargeable sites, sugar beet pectin | 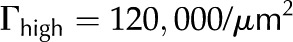 |
Deionized water exposed to the atmosphere absorbs carbon dioxide (CO2) from the air. The CO2 dissolves in the water and dissociates by 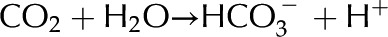 and
and 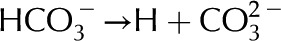 ; in equilibrium
; in equilibrium 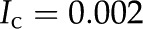 mm (Butler, 1982).
mm (Butler, 1982).
bRepresentative value of 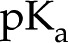 for a carboxylic acid.
for a carboxylic acid.
We assume that (1) the electric field in both axial and azimuthal directions is small compared with the radial field, (2) the fluid properties are constant throughout the channel with the values for bulk liquid water (viscosity and permittivity), (3) the electrophoretic mobilities of the ions are constant and independent of the solution  , and (4) the liquid is incompressible and the flow is in the Stokes (or creeping flow) regime.
, and (4) the liquid is incompressible and the flow is in the Stokes (or creeping flow) regime.
Surface Charge and Electric Potential
Under standard electrokinetic assumptions, the electric field [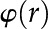 ] and charge distribution [
] and charge distribution [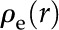 ] in the channel are related by the Poisson equation, which in one-dimensional cylindrical coordinates simplifies to:
] in the channel are related by the Poisson equation, which in one-dimensional cylindrical coordinates simplifies to:
 |
The charge density at a specific location is given by summing over the concentration of ionic species [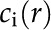 ] and their valence (
] and their valence (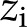 ),
),
where the ionic concentration is given by the Boltzmann distribution:
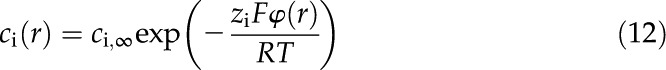 |
The charge density (Eq. 11) and the Boltzmann distribution (Eq. 12) together become:
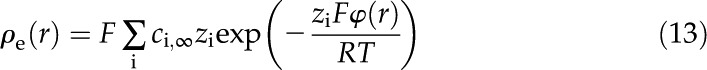 |
The charge distribution (Eq. 13) is substituted into the Poisson equation (Eq. 10) to get the Poisson-Boltzmann (PB) equation, a differential equation that describes 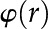 in the channel,
in the channel,
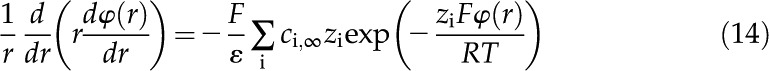 |
This equation is solved by enforcing charge neutrality in the bulk
and using two boundary conditions: (1) a wall potential
and (2) symmetry at the channel center
 |
The PB equation (Eq. 14) is nonlinear and generally must be solved numerically. Here, this equation is first solved for 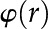 using an analytical approximation, and this approximate solution is used as an initial guess to solve the PB equation (Eq. 14) numerically.
using an analytical approximation, and this approximate solution is used as an initial guess to solve the PB equation (Eq. 14) numerically.
Analytical Approximation and Numerical Solution of 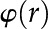
In a cylindrical channel with a monovalent electrolyte (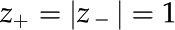 ) and a small surface potential (
) and a small surface potential (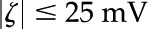 ), the PB equation is approximated well by the Debye-Hückel approximation (Rice and Whitehead, 1965):
), the PB equation is approximated well by the Debye-Hückel approximation (Rice and Whitehead, 1965):
 |
The derivative of Equation 18 is:
 |
where  and
and  are the 0 order and 1st order modified Bessel functions of the first kind, respectively. Using Equations 18 and 19 as an initial guess, the PB equation (Eq. 14) is solved for
are the 0 order and 1st order modified Bessel functions of the first kind, respectively. Using Equations 18 and 19 as an initial guess, the PB equation (Eq. 14) is solved for 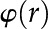 and its derivative
and its derivative 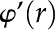 using a numerical solver for boundary value problems, together with the two boundary conditions in Equations 16 and 17. The symmetry boundary condition is applied at an offset from 0 (
using a numerical solver for boundary value problems, together with the two boundary conditions in Equations 16 and 17. The symmetry boundary condition is applied at an offset from 0 (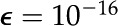 ) to avoid division by zero errors. The numerical value of the boundary condition
) to avoid division by zero errors. The numerical value of the boundary condition  is determined in the next section.
is determined in the next section.
ζ Potential and Surface Charge
We proceed to determine  through both a chemical and an electrical balance between surface and solution in the channel. For the chemical balance, we adapt an analysis for the interaction between a silicon surface and a dilute electrolyte (Behrens and Grier, 2001) to represent the dissociation of charges and the surface potential in our model:
through both a chemical and an electrical balance between surface and solution in the channel. For the chemical balance, we adapt an analysis for the interaction between a silicon surface and a dilute electrolyte (Behrens and Grier, 2001) to represent the dissociation of charges and the surface potential in our model:
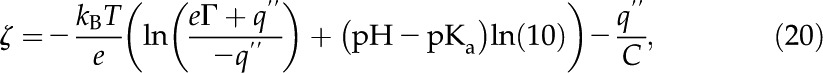 |
where 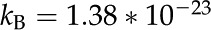 J K−1 is Boltzmann's constant,
J K−1 is Boltzmann's constant, 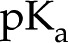 is the surface dissociation constant, and
is the surface dissociation constant, and  (F/m2) is the Stern layer capacitance. Here, we use
(F/m2) is the Stern layer capacitance. Here, we use 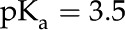 for a carboxylic acid and disregard the contribution of the capacitance of the Stern layer because it is negligible for carboxyl surface groups (Behrens and Grier, 2001). Another necessary relationship between
for a carboxylic acid and disregard the contribution of the capacitance of the Stern layer because it is negligible for carboxyl surface groups (Behrens and Grier, 2001). Another necessary relationship between  and
and  comes from electroneutrality: The net charge at the surface must be balanced by the net charge in the fluid. Per unit axial length of the channel wall, this relationship is
comes from electroneutrality: The net charge at the surface must be balanced by the net charge in the fluid. Per unit axial length of the channel wall, this relationship is
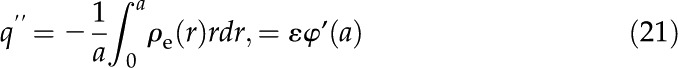 |
commonly known as the Grahame equation (Grahame, 1947), where we substituted 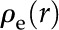 from Equation 10. Equations 20 and 21 together become
from Equation 10. Equations 20 and 21 together become
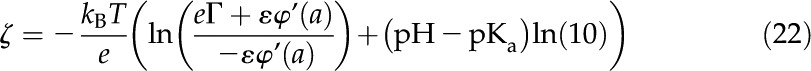 |
Equation 22 is solved using a numerical equation solver that takes an initial guess 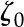 and, together with the method for numerical solution of
and, together with the method for numerical solution of 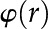 and
and 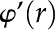 explained in the previous section, iteratively solves for
explained in the previous section, iteratively solves for  .
.
Determination of Γ from Experimental Measurements
To calculate  for a particular material and fluid combination, we first need to determine the material’s density of chargeable sites per unit area (
for a particular material and fluid combination, we first need to determine the material’s density of chargeable sites per unit area ( ). Because values of
). Because values of  for plant materials were not found in the literature, we derive approximate values for
for plant materials were not found in the literature, we derive approximate values for 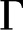 from experimental measurements of
from experimental measurements of  in the literature. For a particular material, we use a value of
in the literature. For a particular material, we use a value of  measured at (1) an elevated pH, e.g.
measured at (1) an elevated pH, e.g. 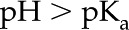 , and (2) at elevated
, and (2) at elevated  , e.g.
, e.g. 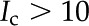 mm. Under condition (1), most of the surface chargeable sites are deprotonated, and the amount of surface charge is approximately
mm. Under condition (1), most of the surface chargeable sites are deprotonated, and the amount of surface charge is approximately
Under condition (2),  is small and the Debye-Hückel approximation applies. Therefore, Equation 19 is inserted into Equation 21 to give:
is small and the Debye-Hückel approximation applies. Therefore, Equation 19 is inserted into Equation 21 to give:
 |
In addition, under condition (2), the Bessel terms in the surface charge approximation (Eq. 24) become
 |
Finally, we combine the DL definition (Eq. 2) and Equations 23 to 25 to give
 |
The value of  approximated this way allows us to determine
approximated this way allows us to determine  for any fluid properties, through the chemical and electrical equilibrium (Eq. 22) and the numerical solution of the PB equation (Eq. 14).
for any fluid properties, through the chemical and electrical equilibrium (Eq. 22) and the numerical solution of the PB equation (Eq. 14).
We verified the accuracy of our derivation of  and numerical solutions by comparing the values we calculate for
and numerical solutions by comparing the values we calculate for  against the data of
against the data of  versus
versus  for sugar beet (Beta vulgaris) pectin (Nakauma et al., 2008;
for sugar beet (Beta vulgaris) pectin (Nakauma et al., 2008; 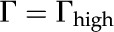 ) and for cellulose (Bellmann et al., 2005;
) and for cellulose (Bellmann et al., 2005; 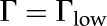 ). We find good agreement between our predictions and the experimental data.
). We find good agreement between our predictions and the experimental data.
Electroviscosity in Nanochannels
This analysis of flow is based on an article by Bowen and Jenner (1995), but without the assumption that the electrolyte is symmetrical. Here, the coupling coefficients for the electrokinetic matrix (Eqs. 4 and 5) are determined. The relative conductance can then be calculated from these coefficients (Eq. 9).
Once  is known, the total flow in the channel is determined through the Stokes equation:
is known, the total flow in the channel is determined through the Stokes equation:
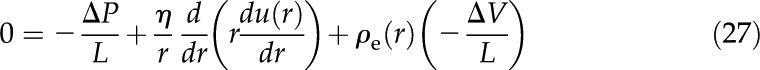 |
This equation is a steady state force balance for a fluid element. It balances the forces due to pressure (first term), viscous friction (second term), and electric fields (third term). We substitute 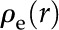 from Equation 10 into Equation 27 and integrate the resulting equation with the following boundary conditions: no-slip [
from Equation 10 into Equation 27 and integrate the resulting equation with the following boundary conditions: no-slip [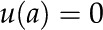 ], symmetry [
], symmetry [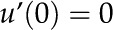 and
and 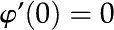 ], and wall potential [
], and wall potential [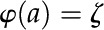 ]. Subsequently, the velocity profile is
]. Subsequently, the velocity profile is
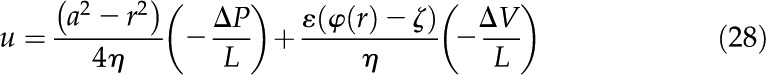 |
We integrate the velocity profile over the channel to get the flow per unit area:
 |
Using the notation of the electrokinetic matrix (Eq. 4), this integral gives the coupling coefficients for flow
 |
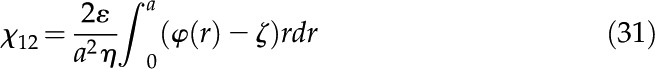 |
Next, the coupling coefficients for the electrical current are determined. The electrical current through a particular radial location is the sum of the current convected by the flow (first term) and the current conducted by the electric field (second term)
where the electrical conductance is given by the density of ions, their mobility, and their valence
We substitute Equation 12 in the previous equation to get
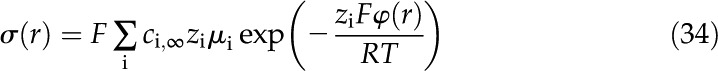 |
Equations 32 and 33 show that the current at a specific location depends on the density of charge (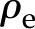 and
and 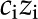 ) and the driving force (
) and the driving force (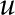 and
and 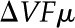 ). The electrical current is integrated over the channel cross section to find the average current per unit area
). The electrical current is integrated over the channel cross section to find the average current per unit area
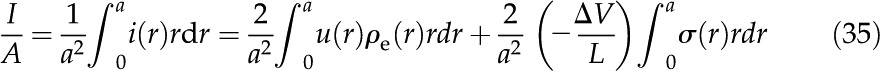 |
Equations 10 and 28 are then substituted into Equation 35; after integration by parts twice, the coupling coefficients for electric current are
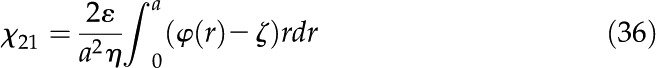 |
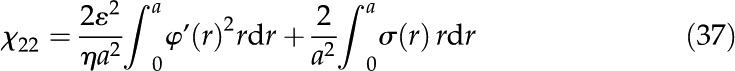 |
The numerical values of coupling coefficients were calculated by numerically integrating the expressions presented here, where the previously discussed numerical solution for  was used. Our calculations of electroviscosity were compared against the numerical solution proposed by Bowen and Jenner (1995), and good agreement was found. The MATLAB code used to calculate all the properties presented is available upon request from the authors.
was used. Our calculations of electroviscosity were compared against the numerical solution proposed by Bowen and Jenner (1995), and good agreement was found. The MATLAB code used to calculate all the properties presented is available upon request from the authors.
Acknowledgments
We thank Maciej A. Zwieniecki, N. Michelle Holbrook, and Fulton Rockwell for helpful discussions on the experimental aspects of measuring the ionic effect and Brian J. Kirby and Alexander C. Barbati for their valuable comments on the article.
Glossary
- DL
Debye layer
- BPM
bordered pit membrane
- PB
Poisson-Boltzmann
References
- Aasamaa K, Sõber A. (2010) Sensitivity of stem and petiole hydraulic conductance of deciduous trees to xylem sap ion concentration. Biol Plant 54: 299–307 [Google Scholar]
- Bailey IW. (1916) The structure of the bordered pits of conifers and its bearing upon the tension hypothesis of the ascent of sap in plants. Bot Gaz 62: 133–142 [Google Scholar]
- Behrens SH, Grier DG. (2001) The charge of glass and silica surfaces. J Chem Phys 115: 6716–6721 [Google Scholar]
- Bellmann C, Caspari A, Albrecht V, Doan TTL, Mäder E, Luxbacher T, Kohl R. (2005) Electrokinetic properties of natural fibres. Colloids Surf A Physicochem Eng Asp 267: 19–23 [Google Scholar]
- Bowen WR, Jenner F. (1995) Electroviscous effects in charged capillaries. J Colloid Interface Sci 173: 388–395 [Google Scholar]
- Buchanan BB, Gruissem W, Jones RL (2000) Biochemistry and Molecular Biology of Plants, Ed 1. American Society of Plant Physiologists, Rockville, MD [Google Scholar]
- Butler JN (1982) Carbon Dioxide Equilibria and Their Applications, Ed 1. Addison-Wesley, Reading, MA [Google Scholar]
- Choat B, Ball M, Luly J, Holtum J. (2003) Pit membrane porosity and water stress-induced cavitation in four co-existing dry rainforest tree species. Plant Physiol 131: 41–48 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choat B, Brodie TW, Cobb AR, Zwieniecki MA, Holbrook NM. (2006) Direct measurements of intervessel pit membrane hydraulic resistance in two angiosperm tree species. Am J Bot 93: 993–1000 [DOI] [PubMed] [Google Scholar]
- Choat B, Cobb AR, Jansen S. (2008) Structure and function of bordered pits: new discoveries and impacts on whole-plant hydraulic function. New Phytol 177: 608–625 [DOI] [PubMed] [Google Scholar]
- Christman MA, Sperry JS, Smith DD. (2012) Rare pits, large vessels and extreme vulnerability to cavitation in a ring-porous tree species. New Phytol 193: 713–720 [DOI] [PubMed] [Google Scholar]
- Cochard H, Herbette S, Hernández E, Hölttä T, Mencuccini M. (2010) The effects of sap ionic composition on xylem vulnerability to cavitation. J Exp Bot 61: 275–285 [DOI] [PubMed] [Google Scholar]
- Domec JC, Meinzer FC, Lachenbruch B, Housset J. (2007) Dynamic variation in sapwood specific conductivity in six woody species. Tree Physiol 27: 1389–1400 [DOI] [PubMed] [Google Scholar]
- Dong DJ, Fricke AL, Moudgil BM, Johnson H. (1996) Electrokinetic study of kraft lignin. Tech Assoc Pulp Pap Ind J 79: 191–197 [Google Scholar]
- Fensom DS. (1957) The bio-electric potentials of plants and their functional significance: I. An electrokinetic theory of transport. Can J Bot 35: 573–582 [Google Scholar]
- Gascó A, Gortan E, Salleo S, Nardini A. (2008) Changes of pH of solutions during perfusion through stem segments: further evidence for hydrogel regulation of xylem hydraulic properties? Biol Plant 52: 502–506 [Google Scholar]
- Gascó A, Nardini A, Gortan E, Salleo S. (2006) Ion-mediated increase in the hydraulic conductivity of Laurel stems: role of pits and consequences for the impact of cavitation on water transport. Plant Cell Environ 29: 1946–1955 [DOI] [PubMed] [Google Scholar]
- Grahame DC. (1947) The electrical double layer and the theory of electrocapillarity. Chem Rev 41: 441–501 [DOI] [PubMed] [Google Scholar]
- Gregory SC, Petty JA. (1973) Valve action of bordered pits in conifers. J Exp Bot 24: 763–767 [Google Scholar]
- Hacke UG, Sperry JS, Wheeler JK, Castro L. (2006) Scaling of angiosperm xylem structure with safety and efficiency. Tree Physiol 26: 689–701 [DOI] [PubMed] [Google Scholar]
- Halis Y, Djehichi S, Senoussi MM. (2011) Vessel development and the importance of lateral flow in water transport within developing bundles of current-year shoots of grapevine (Vitis vinifera L.). Trees (Berl) 26: 705–714 [Google Scholar]
- Herdel K, Schmidt P, Feil R, Mohr A, Schurr U. (2001) Dynamics of concentrations and nutrient fluxes in the xylem of Ricinus communis: diurnal course, impact of nutrient availability and nutrient uptake. Plant Cell Environ 24: 41–52 [Google Scholar]
- Hjertén S. (1967) Free zone electrophoresis. Chromatogr Rev 9: 122–219 [DOI] [PubMed] [Google Scholar]
- Huisman IH, Prádanos P, Calvo JI, Hernández A. (2000) Electroviscous effects, streaming potential, and zeta potential in polycarbonate track-etched membranes. J Membr Sci 178: 79–92 [Google Scholar]
- Jansen S, Choat B, Pletsers A. (2009) Morphological variation of intervessel pit membranes and implications to xylem function in angiosperms. Am J Bot 96: 409–419 [DOI] [PubMed] [Google Scholar]
- Jansen S, Gortan E, Lens F, Lo Gullo MA, Salleo S, Scholz A, Stein A, Trifilò P, Nardini A. (2011) Do quantitative vessel and pit characters account for ion-mediated changes in the hydraulic conductance of angiosperm xylem? New Phytol 189: 218–228 [DOI] [PubMed] [Google Scholar]
- Kim Y, Teng Q, Wicker L. (2005) Action pattern of Valencia orange PME de-esterification of high methoxyl pectin and characterization of modified pectins. Carbohydr Res 340: 2620–2629 [DOI] [PubMed] [Google Scholar]
- Kirby BJ (2010) Micro-and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices, Ed 1. Cambridge University Press, New York [Google Scholar]
- Kirby BJ, Hasselbrink EF., Jr (2004) Zeta potential of microfluidic substrates: 1. Theory, experimental techniques, and effects on separations. Electrophoresis 25: 187–202 [DOI] [PubMed] [Google Scholar]
- Konrad W, Roth-Nebelsick A. (2005) The significance of pit shape for hydraulic isolation of embolized conduits of vascular plants during novel refilling. J Biol Phys 31: 57–71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuljanin TA, Lević LB, Mišljenović NM, Koprivica GB. (2008) Electric double layer and electrokinetic potential of pectic macromolecules in sugar beet. Acta Periodica Technologica 212: 21–28 [Google Scholar]
- Lee J, Holbrook NM, Zwieniecki MA. (2012) Ion induced changes in the structure of bordered pit membranes. Front Plant Sci 3: 55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-Portillo J, Ewers FW, Angeles G. (2005) Sap salinity effects on xylem conductivity in two mangrove species. Plant Cell Environ 28: 1285–1292 [Google Scholar]
- Marschner H (1995) Mineral Nutrition of Higher Plants, Ed 2. Academic Press, London [Google Scholar]
- Nakauma M, Funami T, Noda S, Ishihara S, Al-Assaf S, Nishinari K, Phillips GO. (2008) Comparison of sugar beet pectin, soybean soluble polysaccharide, and gum arabic as food emulsifiers. 1. Effect of concentration, pH, and salts on the emulsifying properties. Food Hydrocoll 22: 1254–1267 [Google Scholar]
- Nardini A, Gascò A, Trifilò P, Lo Gullo MA, Salleo S. (2007) Ion-mediated enhancement of xylem hydraulic conductivity is not always suppressed by the presence of Ca2+ in the sap. J Exp Bot 58: 2609–2615 [DOI] [PubMed] [Google Scholar]
- Nardini A, Salleo S, Jansen S. (2011) More than just a vulnerable pipeline: xylem physiology in the light of ion-mediated regulation of plant water transport. J Exp Bot 62: 4701–4718 [DOI] [PubMed] [Google Scholar]
- Neumann PM, Weissman R, Stefano G, Mancuso S. (2010) Accumulation of xylem transported protein at pit membranes and associated reductions in hydraulic conductance. J Exp Bot 61: 1711–1717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Brien T. (1970) Further observations on hydrolysis of the cell wall in the xylem. Protoplasma 69: 1–14 [Google Scholar]
- O’Brien T, Thimann K. (1967) Observations on the fine structure of the oat coleoptile III. Correlated light and electron microscopy of the vascular tissues. Protoplasma 63: 443–478 [Google Scholar]
- Pérez-Donoso AG, Sun Q, Roper MC, Greve LC, Kirkpatrick B, Labavitch JM. (2010) Cell wall-degrading enzymes enlarge the pore size of intervessel pit membranes in healthy and Xylella fastidiosa-infected grapevines. Plant Physiol 152: 1748–1759 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesacreta T, Groom L, Rials T. (2005) Atomic force microscopy of the intervessel pit membrane in the stem of Sapium sebiferum (Euphorbiaceae). IAWA J 26: 397–426 [Google Scholar]
- Pittermann J, Sperry JS, Hacke UG, Wheeler JK, Sikkema EH. (2005) Torus-margo pits help conifers compete with angiosperms. Science 310: 1924. [DOI] [PubMed] [Google Scholar]
- Rice CL, Whitehead R. (1965) Electrokinetic flow in a narrow cylindrical capillary. J Phys Chem 69: 4017–4024 [Google Scholar]
- Roper MC, Greve LC, Warren JG, Labavitch JM, Kirkpatrick BC. (2007) Xylella fastidiosa requires polygalacturonase for colonization and pathogenicity in Vitis vinifera grapevines. Mol Plant Microbe Interact 20: 411–419 [DOI] [PubMed] [Google Scholar]
- Schmid R, Machado R. (1968) Pit membranes in hardwoods: fine structure and development. Protoplasma 204: 185–204 [Google Scholar]
- Schurr U, Schulze ED. (1995) The concentration of xylem sap constituents in root exudate, and in sap from intact, transpiring castor bean plants (Ricinus communis L.). Plant Cell Environ 18: 409–420 [Google Scholar]
- Secchi F, Zwieniecki MA. (2012) Analysis of xylem sap from functional (nonembolized) and nonfunctional (embolized) vessels of Populus nigra: chemistry of refilling. Plant Physiol 160: 955–964 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siebrecht S, Herdel K, Schurr U, Tischner R. (2003) Nutrient translocation in the xylem of poplar: diurnal variations and spatial distribution along the shoot axis. Planta 217: 783–793 [DOI] [PubMed] [Google Scholar]
- Spanner D. (1979) The electroosmotic theory of phloem transport: a final restatement. Plant Cell Environ 2: 107–121 [Google Scholar]
- Spanner DC. (1958) The translocation of sugar in sieve tubes. J Exp Bot 9: 332–342 [Google Scholar]
- Sperry JS, Donnelly JR, Tyree MT. (1988) Seasonal occurrence of xylem embolism in sugar maple (Acer saccharum). Am J Bot 75: 1212–1218 [Google Scholar]
- Stamm AJ (1926) Electroendosmose through wood membranes. In HB Weiser, ed, Colloid Symposium Monograph. Chemical Catalog Co., Inc., New York, pp 246–257 [Google Scholar]
- Sun Q, Rost TL, Matthews MA. (2008) Wound-induced vascular occlusions in Vitis vinifera (Vitaceae): Tyloses in summer and gels in winter1. Am J Bot 95: 1498–1505 [DOI] [PubMed] [Google Scholar]
- Trifilò P, Lo Gullo MA, Salleo S, Callea K, Nardini A. (2008) Xylem embolism alleviated by ion-mediated increase in hydraulic conductivity of functional xylem: insights from field measurements. Tree Physiol 28: 1505–1512 [DOI] [PubMed] [Google Scholar]
- Tyree MT, Ewers FW. (1991) The hydraulic architecture of trees and other woody plants. New Phytol 119: 345–360 [Google Scholar]
- Tyree MT, Fensom DS. (1968) Methods of measuring hydrokinetic pressure gradients in the xylem of plants in situ. Can J Bot 46: 310–315 [Google Scholar]
- Tyree MT, Salleo S, Nardini A, Assunta Lo Gullo M, Mosca R. (1999) Refilling of embolized vessels in young stems of laurel: do we need a new paradigm? Plant Physiol 120: 11–22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyree MT, Zimmermann MH. (1971) The theory and practice of measuring transport coefficients and sap flow in the xylem of red maple stems (Acer rubrum). J Exp Bot 22: 1–18 [Google Scholar]
- van Doorn WG, Hiemstra T, Fanourakis D. (2011) Hydrogel regulation of xylem water flow: an alternative hypothesis. Plant Physiol 157: 1642–1649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Ieperen W. (2007) Ion-mediated changes of xylem hydraulic resistance in planta: fact or fiction? Trends Plant Sci 12: 137–142 [DOI] [PubMed] [Google Scholar]
- van Ieperen W, van Gelder A. (2006) Ion-mediated flow changes suppressed by minimal calcium presence in xylem sap in Chrysanthemum and Prunus laurocerasus. J Exp Bot 57: 2743–2750 [DOI] [PubMed] [Google Scholar]
- van Ieperen W, van Meeteren U, van Gelder H. (2000) Fluid ionic composition influences hydraulic conductance of xylem conduits. J Exp Bot 51: 769–776 [DOI] [PubMed] [Google Scholar]
- Van Meeteren U, van Gelder H, van Ieperen W. (1999) Reconsideration of the use of deionized water as vase water in postharvest experiments on cut flowers. Postharvest Biol Technol 17: 175–187 [Google Scholar]
- Werner C, Zimmermann R, Kratzmu T, Kratzmüller T. (2001) Streaming potential and streaming current measurements at planar solid/liquid interfaces for simultaneous determination of zeta potential and surface conductivity. Colloids Surf A Physicochem Eng Asp 192: 205–213 [Google Scholar]
- Wheeler JK, Sperry JS, Hacke UG, Hoang N. (2005) Inter-vessel pitting and cavitation in woody Rosaceae and other vesselled plants: a basis for a safety versus efficiency trade-off in xylem transport. Plant Cell Environ 28: 800–812 [Google Scholar]
- Yao S, Santiago JG. (2003) Porous glass electroosmotic pumps: theory. J Colloid Interface Sci 268: 133–142 [DOI] [PubMed] [Google Scholar]
- Zimmermann MH. (1978) Hydraulic architecture of some diffuse-porous trees. Can J Bot 56: 2286–2295 [Google Scholar]
- Zwieniecki MA, Holbrook NM. (2000) Bordered pit structure and vessel wall surface properties. Implications for embolism repair. Plant Physiol 123: 1015–1020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwieniecki MA, Holbrook NM. (2009) Confronting Maxwell’s demon: biophysics of xylem embolism repair. Trends Plant Sci 14: 530–534 [DOI] [PubMed] [Google Scholar]
- Zwieniecki MA, Melcher PJ, Feild TS, Holbrook NM. (2004) A potential role for xylem-phloem interactions in the hydraulic architecture of trees: effects of phloem girdling on xylem hydraulic conductance. Tree Physiol 24: 911–917 [DOI] [PubMed] [Google Scholar]
- Zwieniecki MA, Melcher PJ, Michele Holbrook NM. (2001) Hydrogel control of xylem hydraulic resistance in plants. Science 291: 1059–1062 [DOI] [PubMed] [Google Scholar]