Variation in Methods of Predicting Adult Height in Children with Idiopathic Short Stature

Abstract

Objective

Recombinant human growth hormone (GH) is approved for treatment of children with idiopathic short stature (ISS). Endocrinologists often depend on algorithms to predict adult height. As algorithm performance is often included in treatment decision, we sought to evaluate agreement among height prediction formulas.

Methods

We identified 3 commonly used algorithms for height prediction: Bayley-Pinneau (BP), Roche-Wainer-Thissen (RWT), and Khamis-Roche (KR). We constructed simulated samples of children with typical distributions of ages, heights, weights, bone ages, and parental heights seen in patients with ISS, and applied the algorithms to the simulated children to determine if predicted adult height was <160 cm for boys or <150 cm for girls, the 1.2^nd height percentiles for adults.

Results

We found substantial disagreement amongst algorithms in the percentage of simulated children with predicted adult height < 1.2^nd percentile, a cut-off that may influence GH treatment decisions. Using the BP formula, 43% of boys and 81% of girls had predicted adult height below this threshold, whereas only 3% of boys and 0.2% of girls had predicted heights < 1.2^nd percentile using the KR method. RWT predictions fell in between. Overall agreement of the methods was poor (kappa = 0.21) in boys and negative in girls.

Conclusions

Wide variation exists among formulas used to predict adult height. As these algorithms may be used in decisions about whether to initiate GH treatment and to assess GH’s efficacy in research trials, it is important for parents, pediatricians, and investigators to recognize the considerable variation involved in height prediction.

Introduction

Recombinant human growth hormone (GH) was approved by the United States Food and Drug Administration (FDA) in 2003 for treatment of children with idiopathic short stature (ISS), defined by the FDA as height prior to treatment of 2.25 standard deviations (SD) (1.2^nd percentile) below the mean for age without evidence of underlying disease or GH deficiency. While predicted adult height is not part of the FDA criteria for using GH to treat children with ISS, the FDA criteria do include a statement regarding “a growth rate that is unlikely to attain an adult height within the normal range” and the FDA explained the 1.2 percentile cut-off for children as similar to adult heights of 63 inches (160 cm) for men and 59 inches (150 cm) for women (i.e. the 1.2 percentile for adults)¹

Based upon the ISS indication for GH treatment, approximately 400,000 children in the United States now qualify for GH therapy.² The approval of GH for treatment of ISS was based upon two clinical trials, each with a small number of subjects.^{3, 4} One study (n = 33 followed to adult height) was a randomized, placebo-controlled trial, and the other (n = 50 followed to adult height) was an open-label, dose-response trial that compared adult height to predicted adult height. Both trials used the Bayley-Pinneau method of height prediction. Additional studies of GH use in children with ISS have been limited by sample size. A recent Cochrane Library review included 10 randomized controlled trials of GH treatment in a total of 741 children with ISS. The average duration of treatment and height gain varied, and combined results showed height gains over one year of 0 to + 0.7 SD.⁵ The review did not compare near adult heights to predicted adult heights.

The approval of GH treatment for children with ISS has substantial potential costs for the US healthcare system. A 2006 paper by Lee et al. examined the two studies used by the FDA to support approval for ISS to estimate the cost-effectiveness of GH therapy for children with ISS. The cost-effectiveness was estimated at $52,000/inch, and given an average incremental height gain of 1.9 inches over 5 years, the incremental cost per child was nearly $100,000.⁶ At an average cost per child of approximately $100,000, the potential cost of treating all eligible children is approximately $40 billion dollars.⁶ These costs have been recognized by insurers, as many deny coverage of GH for ISS.^{7, 8}

Predicted adult height is often used to evaluate children with short stature, as treatment with GH may not be indicated in a child whose growth is consistent with attainment of a height above the 1.2^nd percentile, per the FDA indication. For example, in a child with constitutional delay, the current height SD score is often considerably lower than predicted and near adult height SD scores.⁹ Thus, to assess appropriateness of treatment with GH in children with ISS, endocrinologists often use an algorithm to predict whether the child’s predicted adult height will be below 1.2^nd percentile, corresponding to below 160 centimeters (63 inches) in adult men and 150 centimeters (59 inches) in adult women. A 2006 survey of pediatric endocrinologists identified predicted target height below the 5^th percentile as a consistent factor in the decision to treat with GH.¹⁰ As the performance of such algorithms is often crucial to decision-making about treatment with GH, we sought to evaluate agreement among formulas used to predict adult height.

Methods

Simulated sample

We constructed a simulated sample of 1000 boys and 1000 girls with the typical distribution of ages, heights, weights, bone ages, and parental heights seen in patients seen for evaluation of short stature, including appropriate upper and lower limits and correlations among the variables. The variable distributions were determined through informal review of our institution’s clinicians, and based upon a study by Grimberg et al. that compared sex differences among referrals for evaluation of decreased growth velocity at a tertiary pediatric care center.¹¹ Grimberg’s study identified differences in referrals by gender, by height (on average, girls had lower height SD scores than boys), and by mid-parental target height.

SAS software (Cary, NC) was used for all analyses in this paper Two triangular distributions of random ages were generated, spanning 6–16 years with a peak at 13 years for boys, and 6–14 years with a peak at 11 years for girls. An initial sample of 2500 boys and 2500 girls was generated to allow for truncations and deletions, detailed below, so as to produce the final planned sample of 1000 boys and 1000 girls. Multivariate normal deviates (z-scores, mean 0 and SD 1) were generated for each child’s height, weight, and bone age, and the parents’ height. We were unable to identify correlations for these parameters in the literature, and we relied upon observations for our initial correlations. We programmed the random number generator to impose a correlation of 0.90 between the child’s height and weight deviates; 0.60 between the parents’ heights; 0.50 between the child’s height and each parent’s height; 0.15 between the child’s weight and bone age; 0.15 between the child’s bone age and each parent’s height; and 0 among the other deviates. Additionally, to test the sensitivity of our findings to the estimated correlation values, we abolished the relatively strong assumed correlations entirely and repeated the full simulation.

The initial sample was shifted and truncated to reflect typical children and families presenting for evaluation of short stature. For girls, the height distribution was shifted by −0.75 and the weight distribution by −0.25 z-scores. An upper limit of −1 was imposed for height; +1 for weight; and +0.25 for parental height. The z-score distributions were further truncated to eliminate extreme values, deleting cases with weight below −3, height below −4 for boys or −4.5 for girls, parental height below −2.5, or difference between chronologic age and bone age beyond ± 2.

The height and weight deviates were converted to centimeters and kilograms using sex- and age-specific norms for U.S. children.¹² We assumed the child’s bone age differed from chronological age by 0 ± 1 years (mean ± SD) and thus calculated bone age in years by adding the bone age z-score to age in years. The parents’ height z-scores were converted to centimeters using the CDC norms for maximum age (20 years)¹² and averaged to generate midparental height. After the deletions described above, 2680 cases remained in the randomly simulated sample, from which the first 1000 boys and first 1000 girls were selected for analysis

Prediction of adult height

We identified three commonly used algorithms for predicting adult height from the literature and through interviews with board-certified pediatric endocrinologists.

The Bayley-Pinneau method (BP)¹³ employs a series of tables that provide the child’s predicted percentage of adult height (%H). The tables are indexed by sex, chronological age, and skeletal age. Chronological age is trichotomized as > 1 year behind skeletal age; within 1 year of skeletal age; or > 1 year ahead of skeletal age. Tables are provided for ages 7–18 years, with omissions at each extreme depending on sex and skeletal age. Using our simulated children’s sex, age, and bone age, we determined the appropriate BP age category, retrieved %H from the BP tables, and calculated predicted adult height as current height divided by %H. Omissions in the tables resulted in unobtainable %H in a few cases, leaving predictions for 975 of the 1000 boys and 991 of the 1000 girls.

The Roche-Wainer-Thissen algorithm (RWT)¹⁴ directly calculates predicted adult height from a linear combination of the child’s recumbent length, weight, and bone age, together with midparental height, using sex- and age-specific coefficients. As described in the RWT methodology paper, we calculated recumbent length to be 1.25 centimeters greater than standing height.¹⁴ Coefficients used in the RWT method are tabulated up to age 14 years for girls and age 16 years for boys.

The Khamis-Roche algorithm (KR)¹⁵ directly calculates predicted adult height from a linear combination of child’s height and weight, together with midparental height. Sex- and age-specific coefficients are provided for ages 4–17.5 years.

We applied each of the three algorithms to calculate a predicted height for each of the 1000 boys and 1000 girls. The predictions were further dichotomized according to whether the child falls in the lowest 1.2 percentile of predicted adult height.

Statistical analysis

Characteristics of the simulated sample were detailed using standard descriptive statistics (mean, standard deviation, range, Pearson correlation) to confirm that they conformed to the intended profile. Predicted adult heights were calculated in cm and converted to z-scores and percentiles using standard growth charts at the age of 20.¹² The distribution of each measure was characterized by the mean and standard deviation over the 1000 boys and 1000 girls, and the algorithms were compared pairwise by the Spearman rank-correlation statistic. The dichotomized height prediction was tabulated separately by sex for each algorithm. Agreement among the three algorithms was assessed by multi-rater kappa,¹⁶ and pairwise agreement was assessed by Cohen’s inter-rater kappa.¹⁷

To test the reproducibility of the simulation, we generated 30 new sets of random heights, weights, and ages for 1000 boys and 1000 girls and examined the variability of the resulting predictions. To test the sensitivity of the simulation to assumed parameters, we repeated it another 30 times with all correlations among height, weight, parental height, and bone age set to zero.

Results

Table 1 shows characteristics of the simulated sample, which adhered closely to intended distributions and correlations. Age ranges within the sample had a mean of 11.5 years for boys and 10.3 years for girls and, by design, the sample included equal numbers of each gender. The average height z-score score for boys was −2.03 ± 0.66 SD, and for girls was −2.50 ± 0.76 SD, reflecting patients who are typically evaluated for short stature. Age, height, and weight were strongly intercorrelated per design, with pairwise Pearson coefficients for these variables ranging 88 – 97% in boys and 77 – 96% in girls. The other simulated variables did not correlate with each other, or with the cluster of height, weight, and age, with a maximum Pearson correlation of 19%.

Table 1. Simulated sample of children with idiopathic short stature.

Characteristics and Pearson correlations between characteristics used to generate simulated sample of children

		Age, years	Height, cm	Weight, kg	Midparental height, cm	Δ Bone age, years
Male (n=1000)	Mean±SD	11.5 ± 2.2	133.1 ± 12.0	33.1 ± 8.5	163.0 ± 3.7	0.0 ± 0.9
	Min	6.1	100.7	16.0	153.5	−2.0
	Max	15.9	163.2	59.2	171.0	+2.0
Correlation:	Age	1	0.92	0.88	−0.03	−0.06
	Height	—	1	0.97	0.11	−0.09
	Weight	—	—	1	−0.06	−0.01
	Midparental height	—	—	—	1	−0.04
	Δ Bone age	—	—	—	—	1
Female (n= 1000)	Mean±SD	10.3 ± 1.6	124.0 ± 9.4	29.4 ± 6.8	163.4 ± 3.5	0.0 ± 0.9
	Min	6.1	99.0	15.8	153.6	−2.0
	Max	13.8	152.4	52.7	171.5	+2.0
Correlation:	Age	1	0.84	0.77	0.03	0.06
	Height	—	1	0.96	0.19	0.02
	Weight	—	—	1	0.02	0.12
	Midparental height	—	—	—	1	−0.03
	Δ Bone age	—	—	—	—	1

Δ Bone age, years = skeletal age minus chronological age

cm = centimeters

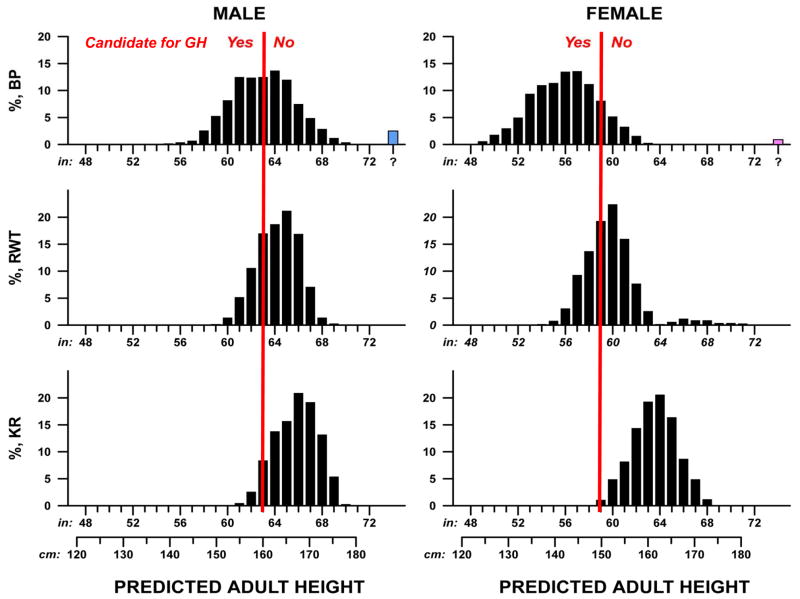
Figure 1 shows the distribution of adult heights as predicted by each algorithm in a single replicate of the simulation (1000 boys, 1000 girls). In each graph, the red line is drawn at the 1.2^nd height percentile. Although this threshold is not a FDA criterion for GH use to treat children with ISS, we were interested in the distribution of and agreements in predicted adult height around the 1.2^nd percentile.

Figure 1.

Distributions of adult heights predicted by using 3 height prediction algorithms. Bars to the left of the red line represent predicted adult heights that are below the 1.2nd percentile for adult height (160 cm or 63 inches for men and 150 cm or 59 inches for women). The blue and pink bars (at extreme right) represent simulated samples that did not allow for height prediction with the BP algorithm because bone age was less than the value required for the algorithm.

Table 2 shows summary statistics for distribution of height as predicted by the three algorithms and for agreement among algorithms, averaged over 30 random replicates. The BP method predicted lowest adult stature for both sexes, with mean height 7 cm below the KR prediction for boys and nearly 10 cm lower for girls. Adult height predictions with RWT fell in between the other two methods. We found substantial disagreement among the three methods in the percentage of simulated patients with predicted adult height below the 1.2 percentile (Figure 1 and Table 2). The BP method predicted adult height below the 1.2^nd percentile in 43% of boys and 81% of girls, whereas the KR method predicted adult height below the 1.2^nd percentile in only 3% of boys and 0.2% of girls. Both the BP and RWT methods predicted short stature in a greater proportion of girls, whereas the KR method predicted short stature in a greater proportion of boys.

Table 2.

Prediction of adult height in simulated samples of children presenting for idiopathic short stature: performance and comparison of three algorithms.^*

	Boys			Girls
	BP	RWT	KR	BP	RWT	KR
Adult height (cm), mean ± SD	161.3±7.0	164.4±4.3	168.4±4.5	143.5±6.9	153.4±6.2	162.8±4.7
Adult height percentile, mean ± SD	5.9±9.9	6.7±6.9	15.9±12.9	1.7±4.5	12.0±19.9	47.7±23.8
Adult height z-score, mean ± SD	−2.16±0.96	−1.74±0.60	−1.18±0.62	−3.04±1.05	−1.54±0.95	−0.08±0.72
PAH < 1.2nd percentile, %†	42.6	17.1	3.9	81.4	26.6	0.1
	BP vs RWT	RWT vs KR	BP vs KR	BP vs RWT	RWT vs KR	BP vs KR
Height, rank correlation‡	0.83	0.89	0.66	0.80	0.70	0.73
PAH < 1.2nd percentile, pairwise kappa§	0.42	0.30	0.10	0.15	0.01	0.00
PAH < 1.2nd percentile, overall kappa	0.21			−0.17

^*BP: Bayley-Pinneau; RWT: Roche-Wainer-Thiessen; KR: Khamis-Roche; PAH: predicted adult height. All parameters averaged over 30 random samples, each sample comprising 1000 boys and 1000 girls.

^† Candidacy for GH treatment defined as predicted adult height <163 cm (63 inches) in boys, <150 cm (59 inches) in girls.

^‡ Spearman correlation coefficient, identical for height in cm, percentile, and z-score.

^§ Kappa coefficient measures agreement among algorithms, ranging from 1 (perfect agreement) to 0 (chance agreement only) to −1 (systematic disagreement).

Rank correlation among methods for predicting a given child’s adult height was moderately strong (0.66–0.89, Table 2); this statistic does not take account of the systematic differences noted above for mean height predicted by the three algorithms. Agreement among the methods in predicting height below the 1.2^nd percentile produced kappas ranging from 0.42 (BP vs RWT in boys) to virtually nil (KR vs BP or RWT for girls). Overall agreement among the methods had a kappa of 0.21 in boys and was negative (worse than chance) in girls (Table 2).

Variation among the 30 replicates was negligible, in keeping with the large sample size in each. Mean height fluctuated by 0.1–0.2 cm around the average displayed in Table 2; mean z-score by 0.02–0.04; pairwise kappa by 0.00–0.05; and similarly for other parameters. Abolishing the assumed correlations among height, weight, parental height, and bone age likewise had negligible effect; the only noticeable impact on Table 2 being attenuation of the mild kappa values.

Discussion

Our study assesses the variation of various height prediction algorithms used for children with short stature. We found wide variation in predicting adult height among commonly used formulas. Our results showed that, on average, the BP method predicts lower adult heights than other methods.

Our study is the first to compare height prediction algorithms using large scale models to represent typical short children who present for endocrine evaluation. The variation in height predictions among methods is important for clinical decision-making and for interpretation of research results. Many research protocols and published studies of GH treatment in children with ISS utilize an endpoint that compares near adult height and predicted adult height.^{4, 18, 19} In addition, predicted adult height has been used by investigators as a marker of growth response to other treatments for children with ISS, including studies of recombinant human insulin-like growth factor 1 (IGF-1),²⁰ or combination therapy with GH and a gonadotropin-hormone releasing agonist.²¹ Use of predicted adult height as an outcome measure in children with ISS should be interpreted cautiously, as we have shown that different height prediction algorithms provide different results.

In addition, although the recent consensus statement on the use of GH as treatment for ISS acknowledges the inaccuracy of predicting adult heights, it concludes that predicted adult height may be helpful in combination with other criteria for determining GH use.²² Thus, practitioners and investigators may continue to rely upon predicted adult height in decision-making.

As demonstrated by studies with small sample sizes, height prediction methods in different patient populations lead to both underestimates and overestimates in predicted adult height, with wide variations in accuracy. Maes et al. compared the accuracy of three height prediction methods in 62 boys and 28 girls with short stature, and found that the BP method was most accurate in short boys, whereas the Tanner-Whitehouse II (TWII) algorithm was most accurate in short girls.²³ We did not use the TWII algorithm in our study because it uses a different technique for assessment of bone age than the BP and RWT algorithms. Roemmich et al. compared three bone age methods and three height prediction models in 23 boys without growth disorders.²⁴ Overall, the TWII method showed underprediction of near adult height, while the other methods (BP, RWT, and RWT with Fels bone age method) led to an overprediction of adult height.²⁴ Sperlich et al. explored accuracy of height predictions in 49 boys with constitutional delay, comparing results of the BP, TWII, and RWT formulas with adult height. While average predicted heights all correlated significantly with average adult heights, individual actual adult heights showed impressive deviations from predicted adult heights.²⁵ More than 30% of the actual adult heights different by more than 5 cm from predicted height using the BP method.²⁵ Height prediction formulas have also been studied in children with tall stature, and a comparison of five height prediction models in children with tall stature concluded that none of the methods was best or most accurate.²⁶ Each method was useful under certain circumstances, with accuracy varying with each subject’s age, gender, and bone age.

A limitation of this paper is the use of simulated patients. However, the sample was generated to reflect a realistic, representative patient population evaluated for short stature, and was used to directly compare three height prediction methods. Prospective studies are needed to assess the accuracy of different height prediction methods in a large cohort of actual children with short stature.

All height prediction methods that utilize bone age are influenced by the reading of bone age, which introduces potential bias and error in height calculations. Most clinicians determine a bone age through comparison of the overall appearance of the radiograph to the standards of Greulich and Pyle, rather than by calculating bone age through assessment of the maturity of individual bones.²⁷ We recognize that the commonly used comparative method of bone age reading may not be ideal, but for this study’s purpose, we assumed that the bone age readings were correct. Recently, a new height prediction algorithm was developed using an automated bone age measurement.²⁸ Automation eliminates inter-rater variability and systematic bias, reducing height prediction error. While this method was approved in Europe, it remains under investigation as a medical device in the United States and is not yet widely used.

We also note that even with consistent and accurate bone age readings, the Greulich and Pyle bone age standards are based upon radiographs of white children from the 1930s, and may not be generalizable to a modern and racially diverse population. Loder et al. found that the Greulich and Pyle standards had decreased accuracy when applied to a contemporary cohort of African American girls and white boys.²⁹ Zhang et al. demonstrated that the Greulich and Pyle standards did not reflect racial differences and found bone age overestimation in Asian and Hispanic children.³⁰ Finally, comparisons done by Roemmich et al. highlighted differences amongst bone age assessment methods, finding bone ages were the most advanced when determined by the TWII method, and youngest with the Greulich and Pyle method.²⁴ Even within healthy individuals studied longitudinally, bone age accuracy varied over time.²⁴ Taken together, these studies indicate that reading bone ages of modern children, even under ideal circumstances, may not be a perfectly accurate science.

In conclusion, we have demonstrated wide variation in predicted adult heights using three commonly used height prediction algorithms. As the three algorithms led to profoundly discrepant predicted heights, future studies are necessary to determine which is most accurate for children with short stature. If automated bone age measurements are found to be more precise than human readers, introduction of this technology may help reduce error in height prediction and allow more accurate comparisons of the different algorithms. Given the substantial medical, psychosocial, and financial implications of using GH for children with ISS, it is important that parents, clinicians, and investigators understand the considerable uncertainty of adult height prediction.

Abbreviations

GH

growth hormone

FDA

Food and Drug Administration

ISS

idiopathic short stature

SD

standard deviation

BP

Bayley Pinneau

RWT

Roche-Wainer-Thissen

KR

Khamis-Roche

TWII

Tanner-Whitehouse