Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Oct 10;3:2914. doi: 10.1038/srep02914

Mechanics of metal-catecholate complexes: The roles of coordination state and metal types

Zhiping Xu 1,a
PMCID: PMC3794374  PMID: 24107799

Abstract

There have been growing evidences for the critical roles of metal-coordination complexes in defining structural and mechanical properties of unmineralized biological materials, including hardness, toughness, and abrasion resistance. Their dynamic (e.g. pH-responsive, self-healable, reversible) properties inspire promising applications of synthetic materials following this concept. However, mechanics of these coordination crosslinks, which lays the ground for predictive and rational material design, has not yet been well addressed. Here we present a first-principles study of representative coordination complexes between metals and catechols. The results show that these crosslinks offer stiffness and strength near a covalent bond, which strongly depend on the coordination state and type of metals. This dependence is discussed by analyzing the nature of bonding between metals and catechols. The responsive mechanics of metal-coordination is further mapped from the single-molecule level to a networked material. The results presented here provide fundamental understanding and principles for material selection in metal-coordination-based applications.

Many biological materials with outstanding mechanical, adhesive and frictional properties benefit from their hierarchical composite structures, within which the reinforcing role of metal complexation in the polymer network phase was recently highlighted1,2. For example, it was reported that the Fe-catecholate (1,2-dihydroxybezene) complexes in mussel byssus cuticles provide effective crosslinking strategies between metal ions and catecholic amino acid dopa (3,4-dihydroxypheylalanine) in mussel foot protein 1 (mfp-1) chains1,3. Granules with high density of these crosslinks resemble the particle-reinforced phase in the composite, and has been correlated to the hardness and high extensibility of the mussel byssus threads. The metal-dopa crosslinks in the matrix were also proposed to endow self-healing properties. Measurements of the mechanical properties after removing metals from the cuticle showed 2-fold decrease in the hardness, suggesting a significant impact of the coordination complex on the material properties3. In the fangs of the wandering spider Cupiennius salei, Zn-His coordination complexes were also found in the matrix of chitin and Zn-containing proteins2. Connection was then identified between the mechanical properties and Zn/Cl enrichment in this fiber-reinforced biocomposite. Moreover, the inhomogeneous metal distribution in the fang might have additional implications in its graded mechanical properties, with an over two-fold increase in hardness and 1.5-fold increase in stiffness measured from the base to the tip2.

The aforementioned examples give prominence to the key roles of metal coordination in defining mechanical properties of crosslinked biopolymers. Coordination complexes form crosslinks when two or more ligands each donate a nonbonding electron pair to empty orbitals in a transition metal ion. A hexadentate mononuclear triple (tris-)Fe-dopa coordination complex was proposed for the mfp-1 crosslinks in the byssus coating3, while bi-, quadr- and hexa-dentate complex can be induced in synthetic materials by tuning pH4. In comparison with other crosslinking strategies in polymeric networks, such as non-bonding (e.g. van der Waals, electrostatic, hydrogen bonds)5 and covalent bonds6, metal-coordination-based crosslinks play a unique role as they are strong (comparable to covalent bonds), responsive to the environment (e.g. pH), and yet reversible (to prevent catastrophic material failure)4,7,8,9. These features have been proposed to offer biological materials a number of desirable mechanical properties in the absence of mineralization, including enhanced hardness, adhesion, toughness, tunability, self-healing capability, efficient energy dissipation upon impact loading, and functions as sacrificial bonds10,11,12.

Recently efforts have been not only made to understand biological materials, but also to develop synthetic materials following these design strategies (Fig. 1). Possible modifications of the proteins and their interfaces were pursued to establish demanding mechanical properties13. Metal-coordination hydrogels were successfully synthesized by several groups4,14,15, which display distinctly dynamic (e.g. responsive, self-healable, tunable, etc.) material properties in contrast to conventional polymers. One excellent example is the pH-responsive gel inspired by the pH jump that proteins experience during maturation of a mussel byssus secretion, which features high stiffness approaching covalently crosslinked gels with additional self-healing capability4,14. In order to develop and optimize bio-inspired materials following the recipes found in nature and explore the limit of maximizing material performance, the understanding of metal-coordination-based crosslinks, especially their mechanical significance, is urged16. A few key questions can be asked readily: (1) what is the nature of the high strength featured by metal-coordination complexes that form in specific chemical environment (e.g. pH)? (2) to what extend the selection of metals (and ligands) would modulate the mechanical properties of the complex? and (3) how would the mechanics of single complex be mapped to the material (e.g. a crosslinked polymer network) level?

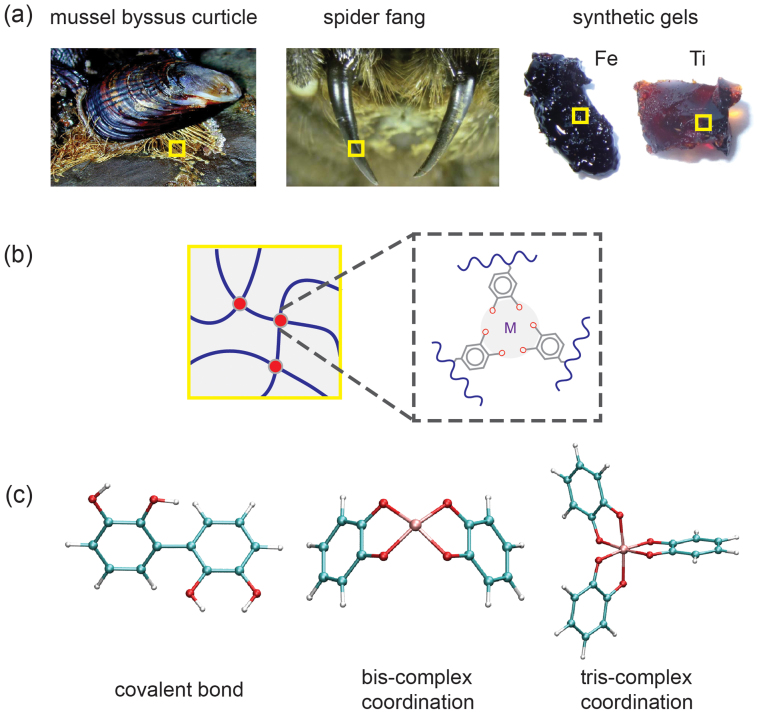
Figure 1. Biological and bio-inspired materials with mechanical properties defined by crosslinked biopolymers.

Figure 1

Open in a new tab

(a) Mechanical properties of biological materials (e.g. mussel byssus1,4, spider fang2) and bioinspired synthetic polymer networks (Fe- and Ti-gels4) are attributed to the presence of unmineralized metals that form crosslinking complexes between biopolymers with funcntional groups such as catechol and dopa. (b) Illustration of a polymeric network crosslinked by metal-coordination complex consisting of metals and catechols. (c) Atomic structures of (from left to right) covalent bonds, bis-catecholate- and tris-catecholate-complexes with coordinate metal-oxygen bonds between metal and catechols. (Images of the mussel byssus curticle and spider fang were taken by Genevieve Anderson and Ken Walker, respectively.)

To address these issues, we present here first a molecule-level study of the coordination complexes. First-principles calculations were performed to investigate representative coordinate and covalent crosslinks, with focus on their structural and mechanical properties. The impact of these crosslinks to mechanics of materials at the network level is then explored, which reveals the responsive hallmark of metal-coordination based biological and bio-inspired materials.

Results

We considered both metal-catecholate coordination complexes and covalent bonds as possible crosslinking mechanisms in biopolymer networks. Ultraviolet-visible (UV) absorption spectra studies showed that at low pH (<7), catechol is reduced and coordination complexes are dissolved instead of crosslinked17. At higher pH, double (bis-) and triple (tris-)complexes form17. On the other hand, covalent bonds could form by an oxidative process under appropriate (pH 8.5) conditions14. Our first-principles calculations start from atomic structures illustrated in Fig. 1c. In the bis-complexes, a planar square coordination complex was assumed, while the metal ion locates in the center of an octahedron for tris-complexes18. Five metals, including Fe, Mn, Ti, Zn, and Ca, were included in our calculations according to their wide appearance in biological (Fe, Mn, Zn, Ca)1,2,19 and synthetic (Fe, Ti)4,14,15 polymer materials. Our geometry optimization results show that all metals form distorted planar square and octahedron configurations with their oxygen donors provided by surrounding catechols18. The lengths of metal-oxygen (MO) bonds lMO were found to be 1.85 (Fe-O), 1.88 (Mn-O), 1.92 (Ti-O), 2.03 (Zn-O), 2.01 (Ca-O) Å in the bis-complexes, and 1.88 (Fe-O), 1.90 (Mn-O), 2.00 (Ti-O), 2.13 (Zn-O), 2.38 (Ca-O) Å in the tris-complexes, respectively. The O-M-O bond angles are distorted from 90° (the angle in undistorted planar squares and octahedrons) for both bis- and tris-complexes (see Table T1 and T2 in the Supporting Information for listed values of bond lengths and angles). In general, these values are within the range of data reported for their oxides20. For example, the Ti-O bond lengths obtained here (1.92 and 2.0 Å) are comparable to the value for TiO2 (1.9–2.0 Å) and Ti2O3 (2.0–2.1 Å)21. The covalent bond thus forming between two catechol groups was also explored, suggesting a length of 1.49 Å for the inter-catechol C-C bond.

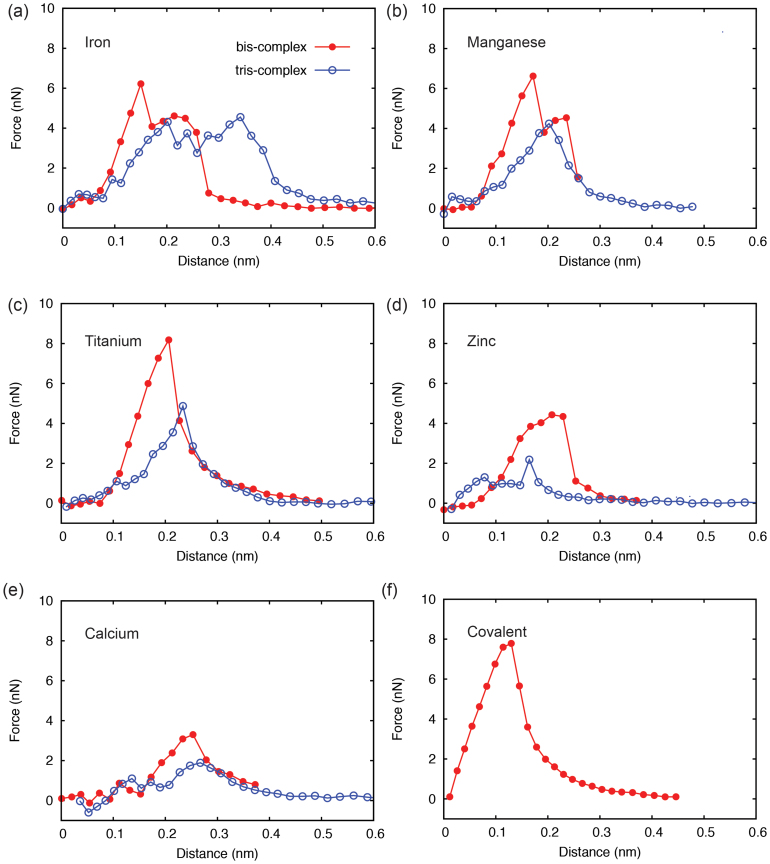
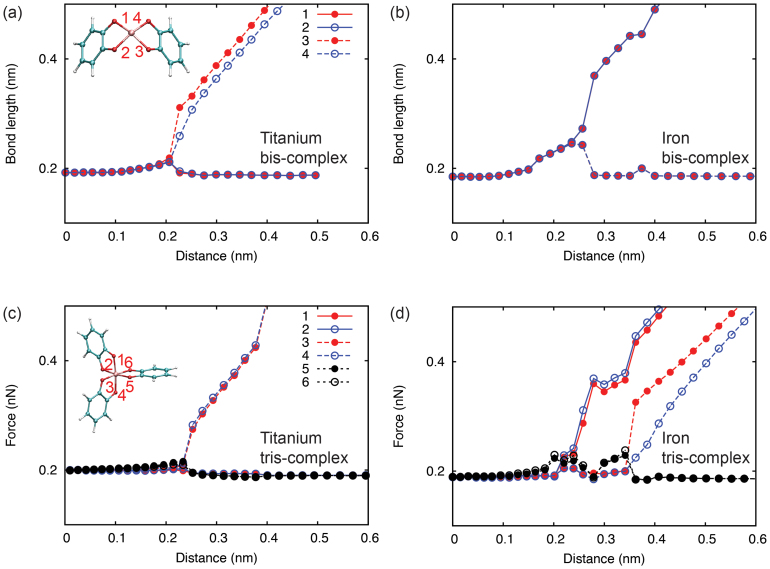
The coordinate bonds are commonly considered to be comparable to, but weaker than covalent bonds. When the polymer network are loaded mechanically as mimicked in this work by pulling apart catechol groups, the metal ion-catechol crosslinks bear tensile loads. The coordination complex thus not only critically defines the stiffness, strength, viscoelasticity, and other overall mechanical behaviors, but also being responsible for the reversibility and tunability of the networked material. Here we quantified the mechanics of crosslinks by displacing and constraining selected carbon atoms in catechols (see Methods section for more details). The force carried by the complex was calculated from the reaction force on the loaded or fixed atoms, and the results are plotted as a function of relative displacement (defined as change in the distance between pulled and fixed carbon atoms) in Fig. 2. It was found that in comparison to the covalent crosslink, the mechanical response of coordination complexes feature a rather complicate profile with multiple peaks, arising form a larger number of degree of freedom involved in the deformation (bond stretching, bond angle bending, etc.). For bis-complex, the ridge was first flattened with negligible responses in the force amplitude. Further stretching led to subsequent breaking of MO bonds (see Fig. 3 and Movie M1 and M2 in Supplementary Information). The irregular profiles of force-displacement curves in Fig. 2, especially those for tris-complexes, can be explained from the dynamics of MO bond distortion and detailed breaking sequence. The Fe-catechol bis-complex first experienced a structural distortion, corresponding to the first peak, and then failed by breaking two Fe-O bonds simultaneously, while for Ti-catechol bis-complex, Ti-O bonds on the pulled catechols broke first. The tris-complexes also showed different bond breaking patterns under tensile loading. For Fe-catechol tris-complex, the two pairs of metal-catechol crosslinks at the left side of the metal ion (Fig. 1c) broke in two steps, resulting in failure at a much larger distance than the Ti-catechol tris-complex, where the breakage of crosslinks right to the metal ion led directly to structural failure (Fig. 3). These distinct behaviors suggest different stabilities of metal-coordination complexes at nonequilibrium conditions, although their structures at equilibrium are quite similar as described above.

Figure 2. Single-molecule mechanics of crosslinks from first-principles calculations.

Figure 2

Open in a new tab

Panels (a–e) plot force-displacement relationships for metal (Fe, Mn, Ti, Zn, Ca)-catechol complexes, and (f) for the covalent crosslink. Metal-coordination shows tensile strength of the complex on the order of a few nN, varying by the type of metals.

Figure 3. Structural distortion and failure of coordination complexes.

Figure 3

Open in a new tab

We plot here changes in the metal-oxygen bond lengths (labeled in the insets) in the metal-coordination complexes with respect to the loading distance (a, c: Ti, b, d: Fe).

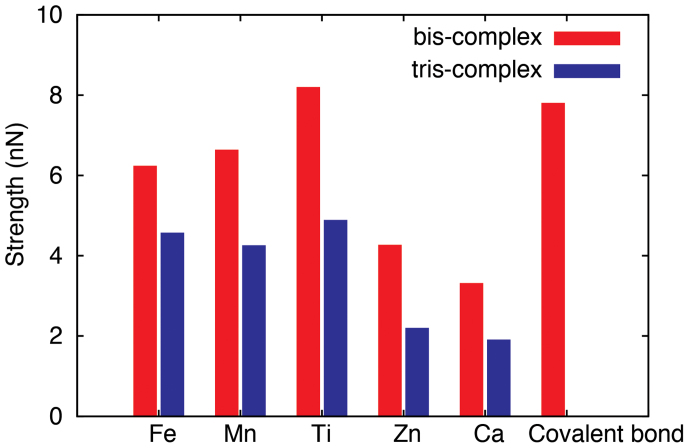
To further assess the roles of metal ions and their coordination states, the whole spectrum of tensile strength for metal-coordination complexes was calculated and summarized in Fig. 4. For bis-complexes, the strength defined as the peak force carried by the crosslink consisting of two MO bonds ranges widely from 3.30 (Ca-O), to 8.18 (Ti-O) nN. Notably, the Fe-catecholate bis-complex features a tensile strength of 6.22 nN, while Ti-coordinate crosslink has a tensile strength of 8.18 nN. It should be noted here that this strength defined for the coordination complex is actually contributed by a pair of M-O bonds that break almost simultaneously (Fig. 3). As a result, single MO bond bears a strength approximately half of that value, i.e. ~3.11 and ~4.09 nN for Fe and Ti respectively. This value is close to half of the strength of a covalent C-C bond (7.79 nN) as calculated here, but several orders higher than the strength of weak non-bonding interactions such as hydrogen bonds, which are usually in the pN range22,23. For the tris-complex under tension, the MO6 octahedron was firstly distorted strongly, being elongated along the loading direction, then dissociated after the metal ion-oxygen bonds break, leaving a bis-complex structure behind (Movie M3 and M4). This dissociation defines the strengths of complexes, ranging from 1.89 (Ca-O) to 4.87 (Ti-O) nN. The dependence of tensile strength on both the coordination state and metal ion types shares the same trend as bis-complexes, i.e. Ti-based coordination complex are the strongest, followed by Fe and Mn featuring similar performance, while Zn and Ca show lower values of the strength. Moreover, we could extract the tensile stiffness from the linearly elastic part of the curve (Fig. S1). The results show that for bis-complexes, Fe-based and Ti-based complex could offer stiffness k of 75.61 and 78.28 N/m respectively, also close to the covalent crosslink with k = 75.77 N/m, which is one order higher than the hydrogen bonds24. Similarly, the stiffness of single M-O bond is half of the stiffness measured for the coordination complex.

Figure 4. Depedence of crosslinking strength on coordination state and metal types.

Figure 4

Open in a new tab

Tensile strength of coordination complexes based on different metals (Fe, Mn, Ti, Zn, Ca) and catechols are plotted and compared with a covalent crosslink between two catechol groups. It should noted that the stength of complexes are contributed by two metal-oxygen bonds and thus the metal coordination could reach up to half of the strength in a covalent bond.

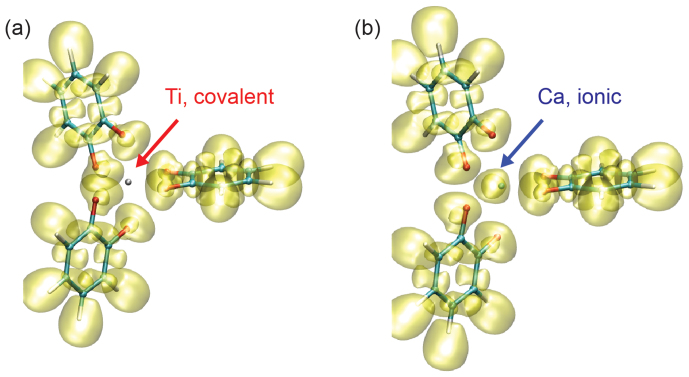
The structural and mechanical properties of the coordination complexes can be clarified further from their electronic structures. Bader atomic charge analysis25 was performed to inspect charge distribution in the complexes. This approach divides the grid-based charge density from quantum mechanical calculations of electrons into atomic volumes. The analysis shows that for bis-complexes, 1.3, 1.7, 1.9, 1.3, and 1.4 electrons are transferred from the metals (Fe, Mn, Ti, Zn, Ca) to the catechol groups. For tris-complexes, the amount of electrons transferred is 1.3, 1.4, 1.8, 1.3, and 1.5 electrons respectively. These results suggest more ionic nature for divalent metal such as Ca, which is correlated to the mechanical strength as identified above. These results elucidate the combined electrostatic and covalent nature of the metal-coordination. To quantify the difference in the metal-catechol bonding characteristics, topological analysis based on electron localization functions (ELFs) was performed for all complexes. ELF is a localized function of the ground-state electron density and wavefunction obtained from the first-principles calculations26. The value of ELF ranges from 0 to 1, where 1 corresponds to the perfect localization as in covalent bonds, and 0.5 corresponds to the electron-gas-like pair probability as in metallic bonds. The bonding nature between metal ions and oxygen atoms in catechols depends on the type of metal. As shown in Fig. 5a and 5b, the results illustrate the nature of coordination bonding compared to the covalent and ionic bonds26. Moreover, there is a distinct contrast in the bonding nature between Ti-O and Ca-O bonds. Further comparative analysis shows that only Ca in the five metals explored here displays distinctly the ionic nature in the coordination complex.

Figure 5. Constractive nature of of metal (Ti, Ca)-catecholate bonding in the coordination complex.

Figure 5

Open in a new tab

Isosurfaces at ELF = 0.5 are plotted here with the atomic structures of tris-complexes. The distribution of ELF shows distinctly covalent and ionic nature for (a) titanium and (b) calcium respectively, which explains their difference in the mechanical properties (Fig. 2).

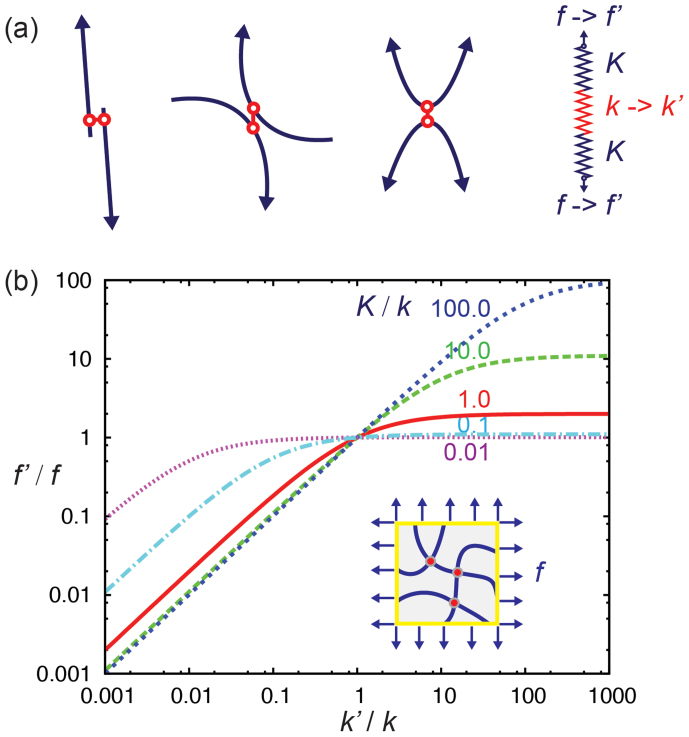
The superior mechanical performance revealed above for single metal-catecholate complex could inspire synthetic materials by incorporating metal coordination. However, how could these merits of individual crosslinks be mapped to the material level remains as a critical question to answer. Especially, the contrastive stiffness of the complex to non-bonding interactions opens promising opportunities in designing highly responsive materials. We now discuss this point using a crosslinked polymer network mode with the assumption of affine deformation. The mechanical response of a typical crosslinked polymeric network can be described using a few representative units (Fig. 6a). When the representative units are loaded, both the polymer chain and crosslink bears an internal force f. We define the effective tensile stiffness of polymers (considering their intrinsic elasticity, thermal fluctuation, and network entanglement) to be K, and the stiffness of crosslinks to be k respectively. At its mechanical equilibration, the nature of coordinate bonds could be modified into a new state with stiffness k′, e.g by tuning the pH, type or concentration of metal ions. Then a response in the force amplitude is generated inside the material. Straightforward analysis shows that response is f′ = fa(1 + b)/(a + b), where a = k′/k is the stiffening factor of crosslinks, and b = K/k is the relative stiffness between the polymer and crosslink. Typical scaling behavior of f′/f with dependence on the stiffness enhancement b is plotted in Fig. 6b. The results show that significant response can be established in a stressed network, which increases with both a and b. For b = 10, a ten-fold stiffening of the crosslink (a = 10, e.g. from hydrogen bonding to metal-coordination) could yield nearly ten-fold response in the internal force carried by the material. We also find that the response is more amplified in the softening situation, i.e. with a < 1.

Figure 6. Responsive mechanics of crosslinked networks.

Figure 6

Open in a new tab

(a) Typical crosslinking structures in a stressed polymer network can be captured in a simple spring model, loaded by force f. (b) Response in the internal forces (f′/f) carried by a pre-stressed networks (the inset), with dependence on the change in tensile stiffness (k′/k) of coordinate crosslinks. K is the effective stiffness of the polymer, and k is the stiffness of the crosslink.

Discussion

It was shown in the results that the highest strength achieved in Ti-catecholate complex could reach half of the covalent strength. Recently, atomic force microscopy (AFM) measurements suggest that the strength of a covalent bond is ~2.0 nN (for silicon-carbon) and ~1.4 nN (gold-sulfur)23. The mechanics of metal coordination in biological materials was characterized as well in AFM7 and surface force apparatus (SFA)9 studies. The results show that a single dopa residue contacting a wet TiO2 surface reveals high strength (~0.8 nN) yet fully reversible, noncovalent interaction7. Moreover Fe ions can mediate the unusually strong interaction between positively charged proteins through metal coordination with dopa9. Although there are some theoretical and experimental evidences showing that mono- and bis-dentate coordination could form between catechol and a TiO2 surface, as a result of dissociative adsorption27, the detailed single-molecule-level chemistry at interfaces in the AFM and SFA experiments is not known. Moreover, the interfacial interaction and stability of metal-coordination complex could be perturbed by its chemistry and environment such as the presence of water28. In spite of these uncertainties that prevent rigorously quantitative comparison, our results that are on the same order as the reported data remain to be conclusive.

To further explain the quantitative discrepancy between our calculations and experimental measurements, it should be noted that the failure of metal coordination complexes has dissociation rates over a range of time scales. Both thermal fluctuation and loading rate will strongly affect the bond dissociation. These effects can be essentially captured by the Bell-Evans model fb = kBTln[rxb/(k0kBT)]/xb, where kB is the Boltzmann factor, T is the temperature, r is the loading rate, xb is the equilibrium bond length, and k0 is the equilibrium dissociation rate7. Recent experiments have shown the evidence that the stiffness and strength of synthetic gels containing metal-coordination crosslinks are rather a function of the dissociation rate than the equilibrium constant15,29. Our quasi-static loading process thus approaches the limit of r = 0 and T = 0. In the force microscopy tests, although finite loading rate would yield a higher strength than that obtained in our calculations, the thermal fluctuation is expected to play a more critical role, which significantly reduces the lifetime of metal-ligand bonds and thus the measured strength of coordination complexes. This may explain the relatively low values reported in experiments. Additionally, although specific metal-coordination complex was modeled here according to experimental evidence17, explicit effects from the chemical environment (pH, ionic strength, salt, etc.) could be critical. For example, water or hydroxyl could fill in the empty octahedral sites in the bis-complex, ions and molecules around could induce charge transfer and polarization as well. The solvent effect for metal ions in aqueous solution could vary for different metals, and thus lead to further contrastive mechanical properties of the complexes30. However, due to the high computational demands to include these effects in first-principles calculations, we leave them to be exploited in our future work.

The nature of coordinate bonds is predominantly electrostatic and partially covalent, which differs for different combination of metal and donor atoms. There are some understandings from a survey of metals in protein structures31, that the covalent contributions follow a certain pattern - K+ < Na+ < Ca2+ < Mn2+ < Fe2+ < Co2+ ~ Ni2+ ~ Cu2+ > Zn2+. In comparison to the metal-donor bond lengths between metal and oxygen in main-chain carbonyl reported in Ref. 31, our results for Zn and Ca are in good agreement (2.13 vs 2.07 Å for Zn and 2.38 vs 2.36 Å for Ca in tris-complex), while values of Fe-O and Mn-O bond lengths are shorter (1.88 vs 2.04 Å for Fe and 2.09 vs 2.19 Å for Ca in tris-complex). This may arise because the transition metal ions with dn configurations are very sensitive to the perturbation in their chemical environment that was not include in this work. Although rigorous comparison between our first-principles calculations results and these referred experimental data cannot be made, the covalent bond length range for all complexes and the more distinct ionic nature identified for Ca-coordination are in reasonable agreement.

In addition to the catechol considered in this work as the electron donor, other ortho-dihydroxy moieties (e.g. dopa, titron)17 and specific amino acids (e.g. His, Ser, Thr, Asn, Gln) could also coordinate with metals17,31. For example, recent work showed that Histidine-rich proteins serve as crosslinking points with nitrogen in the spider fang2. Moreover, experimental evidences were reported for polychaete jaw19,32, Alzheimer Aβ aggregation33, marine and micro-organisms34,35, where other transition metal-coordination strategies play important roles as well. By comparing and understanding these crosslinking mechanisms, extended studies focusing on the material selection (in terms of metal and ligands) are expected to be important in many practical aspects including material science and biomedical applications36,37,38.

Finally at the material level, copolymers containing catechol units were synthesized recently, afforded a dual cross-linking system based on completely different coordination and oxidation chemistries, and competing crosslinking mechanisms14. It was shown that oxidation yields a stable covalently crosslinked gel after excessive acetic acid was added, while metal coordination leads to reversible transition between crosslinking and decrosslinking states. Our affine network model suggests the tunability of network mechanics by controlling either the crosslink (k, k′) or polymer (K). In experiments, change from k to k′ could be established by modulate the metal-coordination state, and the effective stiffness K could be elevated from entropy-controlled value ~kBT/L2 for a flexible polymer chain (L is its size), to much higher values in semiflexible nanostructures, e.g carbon nanotubes and graphene16,39,40,41. By integrating these thoughts, high-performance responsive materials could be accomplished.

In summary, we studied the mechanical properties of metal-catecholate coordination that play critical roles in defining the performance of unmineralized biological materials. Near-covalent stiffness and strength of metal-coordination complexes were found, which depends on the coordination state and type of metals. The mechanical response in polymers crosslinked by metal coordination was predicted through an affine network model. The results, in combination with reported experimental evidences that the chemical environment can tune the coordination state, implying pronounced dynamic mechanical properties. Synthetic materials following this concept could thus offer robustness because of their outstanding mechanical properties, responsiveness because the metal-coordination crosslinks are pH-dependent, reversibility because they can break and reform, and tunability because their strength can be modulated by the metal and chemical environment in question.

Methods

Atomic structures of metal-catecholate-coordination complexes

Metal-based bis-catecholate- and tris-catecholate-coordination complexes were constructed based on the atomic structures of catechols and typical coordination complexes in metal oxides (planar square for the bis-complex and octahedron for the tris-complex). Metal-catecholate complexes were chosen as our model systems here, because catechol and its derivatives are widely present in biological materials, and contained in the side chains of dopa17. Also catechol serves as a minimal model to reduce the computation. Supercells with dimensions of 20, 16, and 16 Å were built. The thickness of vacuum layers was verified to be large enough to model the complexes as isolated molecular systems, by comparing with results using larger supercells.

First-principles calculations

The structure and properties of the coordination complexes were explored using plane-wave-basis-set-based density functional theory (DFT) methods. Spin-polarization was included in the calculations. Generalized gradient approximation (GGA) in Perdew–Burke–Ernzerhof (PBE)42 parameter settings was used for the exchange–correlation functional and Projector Augmented Wave (PAW)43 potentials were used for ion-electron interaction. We used the Vienna Ab-inito Simulation Package (VASP)44 for the calculations. For all results presented, an energy cut-off of 500 eV was used for the plane-wave basis sets. Gamma point was used for the Brillouin zone integration. These settings were verified to achieve a total energy convergence less than 1 meV per atom. For geometry relaxation, the force on atoms converged below 0.01 eVÅ−1. All structures were optimized using the conjugated gradient method. This first-principles approach was successfully applied to similar systems, e.g. adhesion of catechol on TiO227 and silica45. In previous studies, adhesion energy close to experimental measurement was predicted7. However, it should also be noted that the high computational demand prevents DFT calculations to include explicit solvent, and thus the effects of chemical environment (e.g. pH, ionic strength, salt, etc.) could not be directly addressed. In this study, this information was fed into the molecular models instead, as suggested by absorption spectra studies of metal-catecholate complexes17. Optimizing the models in first-principles calculations could eventually solve this issue by minimizing computational demands while keeping the essential chemistry. This is the subject of our ongoing investigation.

Mechanical tensile tests

Tensile loads were applied on selected carbon atoms in the catechols. For the bis-catecholate- and tris-catecholate-complexes, the rightmost two carbon atoms (referring to the metal ion, see Fig. 1c) were displaced further from the other catechols step by step (0.1 Å for each step), while the leftmost two carbon atoms (one in each catechol group) were fixed in the loading direction while not constrained in other directions. Coordinates of all atoms in the system were scaled accordingly after each loading step, to minimize the dependence on the step size. Geometrical optimization calculations were performed after each movement, and the force was evaluated from the reaction force on displaced or constrained atoms. For the covalent bonds between two catechols, the same loading procedure was followed except that displacement and constraints were only applied to one atom in each catechol group.

Author Contributions

Z.X. performed the study and wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary Info Material

srep02914-s1.pdf (361.4KB, pdf)
Supplementary Information

M1. Movie of pulling a Fe-based bis-complex

Download video file (347.7KB, mov)
Supplementary Information

M2. Movie of pulling a Ti-based bis-complex

Download video file (278.8KB, mov)
Supplementary Information

M3. Movie of pulling a Fe-based tris-complex

Download video file (347.6KB, mov)
Supplementary Information

M4. Movie of pulling a Ti-based tris-complex

Download video file (390.1KB, mov)

Acknowledgments

The author thanks Dr. Matthew Harrington and Prof. Peter Fratzl, for their suggestions and comments that helped significantly to improve this work, which was supported by the National Natural Science Foundation of China through Grant 11222217, 11002079, Tsinghua University Initiative Scientific Research Program 2011Z02174, and the Tsinghua National Laboratory for Information Science and Technology of China.

References

  1. Harrington M. J., Masic A., Holten-Andersen N., Waite J. H. & Fratzl P. Iron-clad fibers: A metal-based biological strategy for hard flexible coatings. Science 328, 216–220 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Politi Y. et al. A spider's fang: How to design an injection needle using chitin-based composite material. Adv. Funct. Mater. 22, 2519–2528 (2012). [Google Scholar]
  3. Holten-Andersen N. et al. Metals and the integrity of a biological coating: The cuticle of mussel byssus. Langmuir 25, 3323–3326 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Holten-Andersen N. et al. pH-induced metal-ligand cross-links inspired by mussel yield self-healing polymer networks with near-covalent elastic moduli. Proc. Natl. Acad. Sci. 108, 2651–2655 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Keten S. & Buehler M. J. Nanostructure and molecular mechanics of spider dragline silk protein assemblies. J. Roy. Soc. Interf. 7, 1709–1721 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chou C.-C. & Buehler M. Molecular mechanics of disulfide bonded alpha-helical protein filaments. BioNanoSci. 3, 85–94 (2013). [Google Scholar]
  7. Lee H., Scherer N. F. & Messersmith P. B. Single-molecule mechanics of mussel adhesion. Proc. Natl. Acad. Sci. 103, 12999–13003 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Miserez A., Rubin D. & Waite J. H. Cross-linking chemistry of squid beak. J. Biol. Chem. 285, 38115–38124 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Zeng H., Hwang D. S., Israelachvili J. N. & Waite J. H. Strong reversible Fe3+-mediated bridging between dopa-containing protein films in water. Proc. Natl. Acad. Sci. 107, 12850–12853 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Waite J. H., Qin X.-X. & Coyne K. J. The peculiar collagens of mussel byssus. Matrix Biol. 17, 93–106 (1998). [DOI] [PubMed] [Google Scholar]
  11. Vaccaro E. & Waite J. H. Yield and post-yield behavior of mussel byssal thread: a self-healing biomolecular material. Biomacromolecules 2, 906–911 (2001). [DOI] [PubMed] [Google Scholar]
  12. Harrington M. J. & Waite J. H. Holdfast heroics: Comparing the molecular and mechanical properties of mytilus californianus byssal threads. J. Exp. Biol. 210, 4307–4318 (2007). [DOI] [PubMed] [Google Scholar]
  13. Miserez A. & Guerette P. Integrating materials and life sciences toward the engineering of biomimetic materials. JOM 64, 494–504 (2012). [Google Scholar]
  14. Xu H. et al. Competition between oxidation and coordination in cross-linking of polystyrene copolymer containing catechol groups. ACS Macro Lett. 1, 457–460 (2012). [DOI] [PubMed] [Google Scholar]
  15. Fullenkamp D. E., He L., Barrett D. G., Burghardt W. R. & Messersmith P. B. Mussel-inspired histidine-based transient network metal coordination hydrogels. Macromolecules 46, 1167–1174 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Liu Y., Xie B. & Xu Z. Mechanics of coordinative crosslinks in graphene nanocomposites: A first-principles study. J. Mater. Chem. 21, 6707–6712 (2011). [Google Scholar]
  17. Sever M. J. & Wilker J. J. Visible absorption spectra of metal-catecholate and metal-tironate complexes. Dalton Trans. 7, 1061–1072 (2004). [DOI] [PubMed] [Google Scholar]
  18. Cox P. A. Transition Metal Oxide. (Clarendon Press, 1992). [Google Scholar]
  19. Broomell C. C., Zok F. W. & Waite J. H. Role of transition metals in sclerotization of biological tissue. Acta Biomater. 4, 2045–2051 (2008). [DOI] [PubMed] [Google Scholar]
  20. Shannon R. D. & Prewitt C. T. Effective ionic radii in oxides and fluorides. Acta Cryst. B25, 925–946 (1969). [Google Scholar]
  21. Diebold U. The surface science of titanium dioxide. Surf. Sci. Rep. 48, 53–229 (2003). [Google Scholar]
  22. Keten S. & Buehler M. J. Geometric confinement governs the rupture strength of h-bond assemblies at a critical length scale. Nano Lett. 8, 743–748 (2008). [DOI] [PubMed] [Google Scholar]
  23. Grandbois M., Beyer M., Rief M., Clausen-Schaumann H. & Gaub H. E. How strong is a covalent bond? Science 283, 1727–1730 (1999). [DOI] [PubMed] [Google Scholar]
  24. Xu Z. & Buehler M. J. Mechanical energy transfer and dissipation in fibrous beta-sheet-rich proteins. Phys. Rev. E 81, 061910–061916 (2010). [DOI] [PubMed] [Google Scholar]
  25. Tang W., Sanville E. & Henkelman G. A grid-based bader analysis algorithm without lattice bias. J. Phys.: Condens. Matter 21, 084204–084207 (2009). [DOI] [PubMed] [Google Scholar]
  26. Silvi B. & Savin A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 371, 683–686 (1994). [Google Scholar]
  27. Li S.-C., Chu L.-N., Gong X.-Q. & Diebold U. Hydrogen bonding controls the dynamics of catechol adsorbed on a tio2(110) surface. Science 328, 882–884 (2010). [DOI] [PubMed] [Google Scholar]
  28. Redfern P. C., Zapol P., Curtiss L. A., Rajh T. & Thurnauer M. C. Computational studies of catechol and water interactions with titanium oxide nanoparticles. J. Phys. Chem. B 107, 11419–11427 (2003). [Google Scholar]
  29. Yount W. C., Loveless D. M. & Craig S. L. Strong means slow: Dynamic contributions to the bulk mechanical properties of supramolecular networks. Angew. Chem. 117, 2806–2808 (2005). [DOI] [PubMed] [Google Scholar]
  30. Burgess J. Metal Ions in Solution. (Ellis Horwood, 1978). [Google Scholar]
  31. Harding M. M., Nowicki M. W. & Walkinshaw M. D. Metals in protein structures: A review of their principal features. Cryst. Rev. 16, 247–302 (2010). [Google Scholar]
  32. Broomell C. C., Mattoni M. A., Zok F. W. & Waite J. H. Critical role of zinc in hardening of nereis jaws. J. Exp. Biol. 209, 3219–3225 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Miller Y., Ma B. & Nussinov R. Zinc ions promote alzheimer Aβ aggregation via population shift of polymorphic states. Proc. Natl. Acad. Sci. 107, 9490–9495 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Butler A. Acquisition and utilization of transition metal ions by marine organisms. Science 281, 207–210 (1998). [DOI] [PubMed] [Google Scholar]
  35. Avdeef A., Sofen S. R., Bregante T. L. & Raymond K. N. Coordination chemistry of microbial iron transport compounds. J. Am. Chem. Soc. 100, 5362–5370 (1978). [Google Scholar]
  36. Lee B. P., Messersmith P. B., Israelachvili J. N. & Waite J. H. Mussel-inspired adhesives and coatings. Annu. Rev. Mater. Res. 41, 99–132 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Su J., Chen F., Cryns V. L. & Messersmith P. B. Catechol polymers for ph-responsive, targeted drug delivery to cancer cells. J. Am. Chem. Soc. 133, 11850–11853 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Cranford S. W., de Boer J., van Blitterswijk C. & Buehler M. J. Materiomics: An -omics approach to biomaterials research. Adv. Mater. 25, 802–824 (2013). [DOI] [PubMed] [Google Scholar]
  39. Banerjee S. & Wong S. S. Functionalization of carbon nanotubes with a metal-containing molecular complex. Nano Lett. 2, 49–53 (2001). [Google Scholar]
  40. Liu Y., Xie B., Zhang Z., Zheng Q. & Xu Z. Mechanical properties of graphene papers. J. Mech. Phys. Solids 60, 591–605 (2012). [Google Scholar]
  41. Xu Z., Sun H., Zhao X. & Gao C. Ultrastrong fibers assembled from giant graphene oxide sheets. Adv. Mater. 25, 188–193 (2013). [DOI] [PubMed] [Google Scholar]
  42. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  43. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
  44. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  45. Mian S. A. et al. Density functional theory study of catechol adhesion on silica surfaces. J. Phys. Chem. C 114, 20793–20800 (2010). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Info Material

srep02914-s1.pdf (361.4KB, pdf)
Supplementary Information

M1. Movie of pulling a Fe-based bis-complex

Download video file (347.7KB, mov)
Supplementary Information

M2. Movie of pulling a Ti-based bis-complex

Download video file (278.8KB, mov)
Supplementary Information

M3. Movie of pulling a Fe-based tris-complex

Download video file (347.6KB, mov)
Supplementary Information

M4. Movie of pulling a Ti-based tris-complex

Download video file (390.1KB, mov)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES