Abstract
A number of commonly available density functionals have been tested for their ability to describe the energetics and the geometry at conical intersections in connection with the spin-restricted ensemble referenced Kohn–Sham (REKS) method. The minimum energy conical intersections have been optimized for several molecular systems, which are widely used as paradigmatic models of photochemical rearrangements and models of biological chromophores. The results of the calculations are analyzed using the sign-change theorem of Longuet-Higgins and a method of elementary reaction coordinates of Haas et al. The latter approach helps to elucidate the differences between the geometries at conical intersections as predicted by the multireference wave function ab initio methods and by the density functional methods. Overall, the BH&HLYP density functional yields the best results for the conical intersection geometries and energetics.
1. Introduction
It is established theoretically1−4 and confirmed experimentally4−6 that conical intersections play a vital role as mechanistic features of photochemical reactions providing very efficient funnels for an ultrafast nonadiabatic relaxation of the molecular excited states. The correct description of crossing points between the ground and excited state potential energy surfaces (PESs) of molecules requires a balanced treatment of the dynamic and nondynamic correlation effects.3 The simplest computational method that can be used in the search for conical intersections is the state-averaged7 complete active space self-consistent field (SA-CASSCF)8 method, which, however, misses the major dynamic electron correlation contribution. The latter is introduced via the use of configurational interaction or many-body perturbation theory, thus leading to the well-known MRSDCI and CASPT2 methods, which require a considerably greater computational effort and are restricted in their application to small and medium size molecules. As regards the dynamic electron correlation, density functional theory (DFT)9 represents a more economic alternative to the high-level ab initio wave function methods.10 However, an accurate treatment of the nondynamic electron correlation still remains problematic with the use of practically accessible approximate density functionals.11
The application of density functional methods to the search for conical intersections is an endeavor with quite a mixed success.12 Although the excited states of molecules at the Franck–Condon points can be sufficiently accurately described by the use of the linear-response time-dependent DFT (LR-TDDFT or TDDFT, for brevity), its reliance on the single-reference description of the ground state renders the standard TDDFT inappropriate for the description of the excited state PESs of molecules near the avoided crossing regions and at conical intersections.12,13 A success has been recently reported in the application of the spin-flip TDDFT (SF-TDDFT)14−17 for locating conical intersections in ethylene and stilbene;18,19 however, this approach is not free of certain artifacts.20 In particular, the unphysical states of mixed spin-symmetry and an artificial dependence on the choice of the reference state have been identified by Casida et al.20 as potential pitfalls of the SF-TDDFT approach. Furthermore, an excessive spin-contamination may preclude correct identification of physically meaningful excited states.21
In the present work, an alternative route for describing the strong nondynamic correlation and excited states in DFT will be taken, namely the ensemble approach. The development of practically accessible ensemble DFT method, the spin-restricted ensemble-referenced Kohn–Sham (REKS) method, and its application to the ground and excited (in the state-averaged variant) states of strongly correlated molecular systems have been reported in the past.13,22−24 In this work, the REKS method will be used for describing the energetics and geometry of conical intersections in a number of molecules, which are widely employed as paradigmatic models for understanding the photochemistry and photophysics of organic and biological molecules. The performance of several popular density functionals will be investigated in comparison with the results of high-level ab initio multireference wave function calculations available in the literature.25,26 The results of density functional calculations will be analyzed in chemical terms, where the elementary reaction coordinates of photorearrangement will be employed.27 In section 2 the properties of conical intersection points and the method of calculation will be briefly outlined. The results of the calculations will be described and compared with the literature data in section 4, and in section 5, the conclusions will be drawn.
2. Theory
2.1. Conical Intersections
Conical intersections (CIs) are commonly defined as (manifolds of) points at which Born–Oppenheimer potential energy surfaces (PESs) of two (or more) electronic states, which transform according to the same irreducible representation of the space and spin symmetry group, become degenerate.28 Limiting the discussion to two electronic states, I and J for brevity, the true crossings between their PESs may occur provided that the conditions in eq (1) are fulfilled,
| 1a |
| 1b |
where Ĥ is the electronic Hamiltonian in the Born–Oppenheimer approximation. These conditions, that is, the degeneracy of electronic energies and the vanishing interstate coupling, can only be fulfilled in the space of N–2 internal molecular coordinates.28−30 The gradients of the conditions 1a and 1b with respect to the nuclear coordinates define the branching space of the intersection; that is, two directions in the space of all nuclear coordinates along which the degeneracy of the two PESs is lifted. In the space of the gradient difference vector g⃗ (the gradient of 1a) and the interstate coupling gradient h⃗ (the gradient of 1b), the two PESs near the intersection point have a topography of a double cone, hence the name conical intersection.30
An important criterion for the occurrence of conical intersections has been formulated by Longuet-Higgins and is known as the sign-change theorem:28 Whenever a wave function of the given electronic state in the Born–Oppenheimer approximation is adiabatically transported round a closed path encompassing a conical intersection, the wave function changes its sign. A number of approaches for locating conical intersections based on the sign-change theorem have been proposed in the past;27,31 however, more robust methods of locating CIs are based on the use of branching space vectors. In the present work, the sign-change theorem will be used to demonstrate that the degeneracy points between PESs of two electronic states located using a selection of DFT functionals are indeed the true conical intersections and not weakly avoided crossings. Of note, a criterion similar to the sign-change theorem has been recently proposed in the context of DFT.32
2.2. REKS Methodology
KS DFT is based on the notion that the ground state density of a real many-electron system can be uniquely mapped on the ground state density of a fictitious system of noninteracting particles moving in a suitably modified external potential.9 The existence of such a potential, the KS potential, can be demonstrated using the argument based on the adiabatic theorem of many-body physics.33 Gradually switching off the electron–electron interaction in the Hamiltonian and modifying the external potential such that the ground state density remains unchanged,34 the noninteracting particles limit can be reached, in which the ground state density is represented by N lowest eigenvalues of the noninteracting Hamiltonian, provided that, along the adiabatic connection path, (i) the system remains in its ground state and (ii) the perturbation theory remains valid. If a density can be represented by a single KS determinant built from the lowest eigenvalues of a noninteracting system, such a density is said to be noninteracting pure state v-representable (PS-VR).
The fact that not any physical density is noninteracting PS-VR has been theoretically demonstrated already in the early days of density functional theory. In the works of Lieb,35 of Englisch and Englisch,36 and later, of Kohn and co-workers,37 it has been demonstrated that any physical density is noninteracting ensemble v-representable (E-VR) and that only some densities are PS-VR. E-VR implies that the density is represented by a weighted sum (ensemble) of densities of several KS determinants. That the ensemble representation of the density is not merely a theoretical curiosity and may occur in practical calculations has been demonstrated by Baerends and co-workers38 (E-VR for C2, H2 + H2, and CH2) and by Morrison39 (E-VR for Be-like atomic ions). Using inverse engineering approach to construct the KS potential for the known exact density,40 it has been demonstrated that one needs to switch to the ensemble representation for the density of the noninteracting reference KS system in the cases where strong nondynamic correlation is present in the interacting (physical) limit.
A practically accessible implementation of the ensemble approach in DFT has been achieved in the spin-restricted ensemble-referenced KS (REKS) method, for the first time introduced in refs (22 and 23) and later modified in ref (24). The REKS method is based on a rigorous statement that any positive definite physical density for fermions is ensemble v-representable, cf. Theorems 4.2 and 4.3 and eqs 4.5 and 4.7 in ref (35) and Theorem 5.1 in ref (36). This leads to the formal representation for the density and the ground state energy, given in eqs 2 and 3,
| 2 |
| 3 |
by weighted sums over a finite ensemble of KS states. Provided that the same set of KS orbitals is used to construct the densities of the individual KS determinants in eq 2, the fractional occupation numbers (FONs) of the KS orbitals emerge, as in eq 4,
| 4 |
where a set of orthonormal orbitals φp(r) and their FONs np are introduced.
The implementation of the REKS method used in the present work can treat systems with two active orbitals fractionally occupied by two electrons, that is the REKS(2,2) method. This active space is sufficient to describe the low-spin ground state of a diradical,41 dissociation of a single chemical bond or a situation arising when a double bond is partially broken by an electronic excitation or a conformational change. Based on the analysis of multiconfigurational wave functions the working formulas for the REKS density and total energy, eqs 5 and 6, were derived,
| 5 |
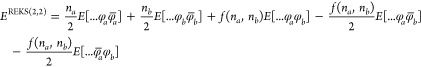 |
6 |
where φk are the doubly occupied core orbitals, φa and φb are the fractionally occupied active orbitals with the occupation numbers na and nb, respectively, f(na,nb) is a function of the occupation numbers the details of which can be found in ref (24), and the unbarred and barred orbitals are occupied with spin-up and spin-down electrons, respectively.
The last three terms in eq 6 represent a DFT analogue of the exchange integral ⟨φaφb|φbφa⟩ in wave function ab initio theory. The occurrence of such a term in eq 6 can be illustrated by the following argument. Let us consider a system of noninteracting electrons (a KS system) in which two frontier orbitals are fractionally occupied by two electrons and all the other orbitals are doubly occupied. The ground state density of such a system (see eq 2 and 4) can be described by eq 5 or, equivalently, by an ensemble of densities of two KS determinants, |...φaφ̅a| and |...φbφ̅b|, with the weighting factors na/2 and nb/2, respectively. According to the exact KS simulations38,39 and theoretical arguments,42 the two fractionally occupied frontier orbitals are energetically degenerate and lie at the Fermi level of the system. Let us now follow the adiabatic connection path between the noninteracting and the fully interacting electronic system33,34 and switch on the electron–electron interaction, however infinitesimally weakly. Because the interaction remains infinitesimally weak, it should not affect the KS orbitals and the energies of all but two electrons, namely the two electrons in the fractionally occupied KS orbitals. For such a situation, the application of quasi-degenerate perturbation theory to obtain the total energy of the system leads to eq 6, in which f(na,nb) = (nanb)1/2.
In the REKS(2,2) method, the algebraic form of the function f(na,nb) is obtained by interpolating between the above limit of an ensemble KS state and a single-reference KS state.24 This is done to eliminate the double counting of the nondynamic electron correlation in the latter case and to guarantee that, for a state that is correctly described by a single-determinant KS Ansatz, the REKS method yields the same energy as the standard KS-DFT.22−24
The REKS(2,2) energy is minimized with respect to the orbitals and FONs of the active orbitals under the constraint of orbital orthonormality and the constraint for active orbital occupation numbers na + nb = 2.22 The orbital orthogonality constraint is imposed by the use of the method of Lagrange multipliers, which leads to the well-known general open-shell self-consistent field equations.43 The number particle constraint for FONs of the active orbitals is explicitly imposed by utilizing the trigonometric relation cos2 ϕ + sin2 ϕ = 1, which enables one to minimize the REKS energy with respect to the FONs of the active orbitals directly thus avoiding the use of Lagrange multipliers. Because, at the variational minimum, the REKS energy is stationary with respect to the FONs of the active orbitals, the respective Lagrange multipliers should have become degenerate had these multipliers been used in the energy minimization.42 Further details of the REKS methodology can be found in refs (22−24). The outlined REKS method can be used in connection with any approximate local or semilocal density functional.
The REKS(2,2) method describes a diradicaloid state (or a state with dissociating single bond or partially dissociating double bond),41 for which the noninteracting KS reference wave function is given by eq 7.
| 7 |
In the delocalized representation of the active orbitals of a diradical,41 this state has a predominantly covalent character and is the ground state of a system with a single strongly correlated electron pair. In the space of two active orbitals ϕa and ϕb, excitation of a single electron from this state leads to an open-shell singlet (OSS) state 8,
| 8 |
which represents the lowest singlet excited state of a biradical.41 The energies of the two states, Φ0 and Φ1, can be obtained with the use of the state-averaged REKS (SA-REKS) method, in which a weighted sum of the energies of these states is minimized with respect to the REKS orbitals and, for the Φ0 state, their fractional occupation numbers.13 In the SA-REKS energy functional, eq 9,
| 9 |
the ground state energy is calculated using the REKS(2,2) method and the OSS excited state energy is calculated using the ROKS method.13,44 Typically, equal weighting factors C0 and C1 are chosen in practical calculations.
The OSS state 8 represents the lowest excited state of a homopolar biradical41 (e.g., ethene at 90° of twist), and it does not mix with its ground state 7. For a heteropolar biradical, either by chemical substitution (e.g., styrene) or geometric distortion (e.g., ethene near the CI), the two states, Φ0 and Φ1, can mix thus leading to the states with partial covalent and partial ionic character.41,45 Within the SA-REKS formalism, this situation can be described by quasi-degenerate perturbation theory, which leads to a simple 2 × 2 secular problem in the space of the two states, Φ0 and Φ1.21 The diagonal elements of the Hamiltonian matrix are given by E0REKS(2,2) and E1, calculated using the SA-REKS orbitals, and the off-diagonal element is given by eq 10,
| 10 |
which is obtained as an element of the Hamiltonian operator taken between the states described by wave functions 7 and 8.21 As the individual determinants in eq 8 are obtained by single excitations from the individual determinants in eq 7, the Hamiltonian matrix element between these wave functions is a combination of the off-diagonal matrix elements of the Fock operator taken between the open-shell orbitals φa and φb. Note that, due to the definition of the Fock operator in open-shell SCF theory, see ref (43) for more detail, the Fock matrix elements should be multiplied by the (fractional) occupation numbers of the respective orbitals. The variational condition in open-shell SCF theory implies that the Fock matrix becomes Hermitian and the off-diagonal matrix elements ⟨φb|naF̂a|φa⟩ and ⟨φa|nbF̂b|φb⟩, where F̂a and F̂b are the Fock operators for the orbitals φa and φb, respectively, become equal to one another. For brevity, these elements are denoted in eq 10 as Wab, which is the off-diagonal Lagrange multiplier22,43,44 for the open-shell orbitals φa and φb in the SA-REKS method.
Provided that equal weighting factors are chosen in eq 9, the state-averaged energy functional remains unchanged upon the application of the described procedure and the SA-REKS orbitals do not have to be reoptimized. Although the correction to the E0REKS(2,2) and E1 energies is sufficiently small, the outlined procedure yields a more realistic description of the ground and excited states, especially when the excitation energy is vanishingly small, such as near a CI. In the following, this approach will be denoted as the state-interaction SA-REKS, or SI-SA-REKS for brevity. The SI-SA-REKS method has been already introduced in ref (21), where it was observed that the SI-SA-REKS method yields a more accurate description of the shape of the potential energy surfaces of PSB3 retinal model near a CI. A more detailed description of the SI-SA-REKS method will be provided elsewhere.
Currently, the analytic energy gradient is available for the REKS(2,2) method, however, is not yet implemented for the individual states in the SA-REKS and SI-SA-REKS methods. This implies that the relaxed density matrix is not yet available for the ground and the excited states in the SA-REKS and SI-SA-REKS approaches and the density matrix is obtained using the state-averaged orbitals only.
The REKS method, as well as the SA-REKS and SI-SA-REKS methods, can be used in connection with any existing GGA, meta-GGA, local or global hybrid exchange-correlation density functional. In practical applications of the SA-REKS and SI-SA-REKS methods, especially in situations where a balanced description of the relative stability of ionic and covalent electronic configurations is needed (e.g., such as in the vicinity of a CI), it was found that hybrid functionals that contain a larger fraction of the exact exchange energy provide for a more accurate description of the excitation energies.13,21 Indeed, the use of the exact (Hartree–Fock) exchange energy mitigates the effect of the electron self-interaction error inherent in the approximate GGA density functionals,11,46 which is important in the context of the present work. In several recent studies that employ TDDFT or SF-TDDFT formalisms, similar observations as regards the performance of hybrid density functionals with increased contribution of the Hartree–Fock exchange energy have been made.17,21
In principle, the Hartree–Fock (HF) exchange energy alone can be used in the context of the REKS, SA-REKS, and SI-SA-REKS methods. With the use of the HF exchange only, the REKS methods do not become exactly equivalent to the respective CASSCF(2,2) approaches, as the dependence of the total energy on the orbital occupation numbers is slightly different in these computational schemes (see discussion after eqs 5 and 6). However, the results yielded by the REKS(2,2)/HF methods are very close to the CASSCF(2,2) results.21,24 There is also a vague analogy between the SI-SA-REKS/HF method and a recently proposed FOMO-CASCI(2,2) approach;47 however, the latter method uses the orbitals obtained from a closed-shell spin-restricted Hartree–Fock calculation with floating orbital occupations, whereas the SI-SA-REKS approach is based on the open-shell SCF theory.
3. Computational Details
The REKS(2,2), SA-REKS, and SI-SA-REKS methods are implemented in the COLOGNE2012 program,48 which was used in the calculations. A series of density functionals ranging from a global hybrid functional, BH&HLYP,49 to a Coulomb-attenuated local hybrid functional, CAM-B3LYP,50 to a meta-GGA hybrid functional, M06-2X,51 have been used in the calculations. For reasons discussed in the end of the previous section, hybrid density functionals with small fraction of the HF exchange have been excluded from consideration. Numeric integration in the density functional calculations employed grids comprising 75 radial points and 302 angular integration points per atom. The SCF convergence criterion of 10–8 for the density matrix was used in all the calculations. To evaluate the importance of the dynamic electron correlation for the geometries and relative energies of the conical intersections, SI-SA-REKS calculations in connection with the HF exchange only have been also carried out.
The 6-31G* basis set was used on all atoms. The ground state equilibrium geometries were optimized using the REKS(2,2) method. The geometries of conical intersections were obtained with the use of the CIOpt program25 interfaced with COLOGNE2012. The algorithm used for the CI optimization employs the penalty function approach in connection with numerically calculated gradients for the ground and excited states obtained using the SI-SA-REKS method. For several species, transition states on the S0 ground electronic state PES have been optimized using the REKS(2,2) method. For all the transition states, it has been confirmed that the molecular Hessian possesses exactly one negative eigenvalue. The Hessian has been calculated by numeric differentiation of the analytic energy gradient using a 0.001 Å increment for the atomic coordinates. The following units are employed throughout the article: all geometric parameters are given in Ångström (Å), the total energies are given in Hartree atomic units (a.u.), and the relative energies are given in electron-volts (eV).
4. Results
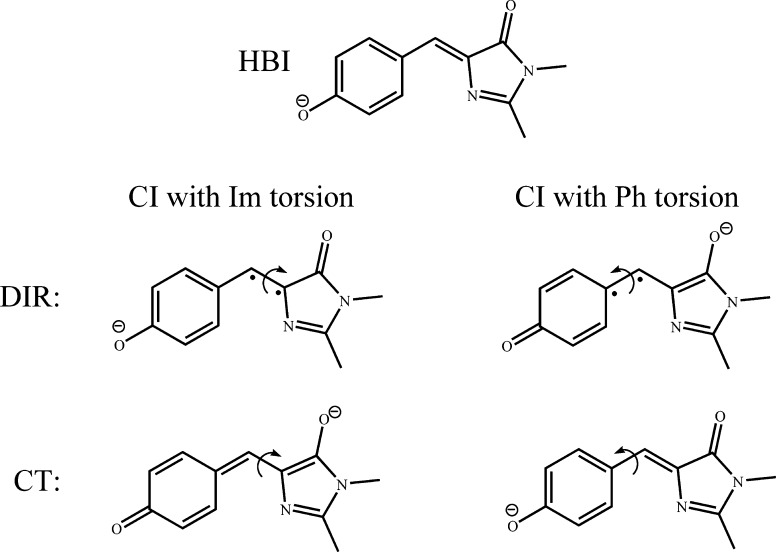
With the use of theoretical method described in the preceding section a number of conical intersections in molecules shown in Scheme 1 have been investigated. The species considered in this work include ethylene, for which two CIs—twisted-pyramidalized (Scheme 1A) and ethylidene (Scheme 1B)—were calculated; methyliminium cation, for which two CIs—twisted (Scheme 1C) and methylimine (Scheme 1D)—were investigated; styrene, for which two twisted-pyramidalized CIs—with pyramidalization on terminal carbon atom (Scheme 1E) and with pyramidalization of phenyl end of the double bond (Scheme 1F)—were studied; stilbene, for which a twisted-pyramidalized CI (Scheme 1G) was computed; penta-2,4-dieniminium cation (the protonated Schiff base, PSB3, a commonly used model of the retinal chromophore), for which a twisted CI (Scheme 1H) was optimized; anionic p-hydroxybenzilideneimidazolinone (HBI, a model of the green fluorescent protein chromophore), for which two twisted-pyramidalized CIs—with torsion of the phenyl ring (Scheme 1I) and with torsion of the imidazole ring (Scheme 1J) were examined.
Scheme 1. Schematic Representation of Conical Intersections Investigated in This Work.
The results of the SI-SA-REKS calculations along with the reference data from the literature are summarized in Table 1, where the relative energies of the Franck–Condon (FC) points and the minimum energy CIs (MECIs) are reported together with the root-mean-square deviations (RMSD) of the MECI geometries optimized with the use of density functionals from the reference ab initio geometries. A complete list of Cartesian coordinates and total energies of the species reported in Table 1 can be found in Supporting Information. The reference energies and geometries at the FC and CI points have been adopted from refs (25 and 26) where calculations have been performed with the use of the multireference configuration interaction with single and double excitations (MRSDCI) method or with the use of the second-order many-body perturbation theory corrected complete active space SCF (CASPT2) approach in connection with medium size basis sets. Further detail on the reference calculations can be found in the original publications.25,26 For HDI, only the CI with phenyl ring torsion was studied using the CASPT2 method;25 however, both CIs, CIPh (Scheme 1I) and CIIm (Scheme 1J), were investigated by the CASSCF method.52 Because the latter approach does not systematically include the dynamic electron correlation, the CASSCF results are not used when benchmarking the density functional calculations.
Table 1. Comparison of the Relative Energies (ΔE, in eV) of the Franck–Condon Points and the Minimum Energy Conical Intersection Points as Well as the Geometries at the Conical Intersection Points Obtained Using Density Functional (SI-SA-REKS) and Wavefunction Ab Initio Methodsa.
| WFTb |
HF |
CAM-B3LYP |
M06-2X |
BH&HLYP |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S0 | S1 | S0 | S1 | S0 | S1 | S0 | S1 | S0 | S1 | |
| Ethylene | ||||||||||
| Franck–Condon Pointc | ||||||||||
| ΔE | 0.000 | 9.330 | 0.000 | 9.644 | 0.000 | 7.855 | 0.000 | 7.819 | 0.000 | 8.338 |
| Twisted-Pyramidalized CIc | ||||||||||
| ΔE | 5.110 | 5.140 | 5.194 | 5.195 | 5.133 | 5.133 | 5.183 | 5.183 | 5.158 | 5.158 |
| RMSD | 0 | 0.0170 | 0.0342 | 0.0538 | 0.0276 | |||||
| Ethylidene CIc | ||||||||||
| ΔE | 4.750 | 4.760 | 4.006 | 4.006 | 4.130 | 4.130 | 5.694 | 5.754 | 4.040 | 4.040 |
| RMSD | 0 | 0.0108 | 0.0727 | 0.3357 | 0.0708 | |||||
| Methyliminium | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Franck–Condon Pointc | ||||||||||
| ΔE | 0.000 | 8.240 | 0.000 | 8.817 | 0.000 | 8.645 | 0.000 | 8.953 | 0.000 | 8.730 |
| Twisted-Pyramidalized CIc | ||||||||||
| ΔE | 3.400 | 3.430 | 3.226 | 3.238 | 4.016 | 4.038 | 4.276 | 4.299 | 3.803 | 3.806 |
| RMSD | 0 | 0.0123 | 0.1039 | 0.1190 | 0.0909 | |||||
| Methylimine CIc | ||||||||||
| ΔE | 5.230 | 5.240 | 4.376 | 4.376 | 4.640 | 4.641 | 5.319 | 5.319 | 4.495 | 4.497 |
| RMSD | 0 | 0.0401 | 0.0533 | 0.0980 | 0.0510 | |||||
| Styrene | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Franck–Condon Pointd | ||||||||||
| ΔE | 0.000 | 0.000 | 6.518 | 0.000 | 5.205 | 0.000 | 5.103 | 0.000 | 5.405 | |
| Twisted-Pyramidalized CI1d,e | ||||||||||
| ΔE | 4.545 | 4.545 | 4.399 | 4.399 | 4.583 | 4.583 | 4.418 | 4.418 | ||
| RMSD | ||||||||||
| Twisted-Pyramidalized CI2d,f | ||||||||||
| ΔE | 5.157 | 5.157 | 4.983 | 4.983 | 5.004 | 5.005 | 5.042 | 5.042 | ||
| RMSD | ||||||||||
| Stilbene | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| trans-Stilbene Franck–Condon Pointg | ||||||||||
| ΔE | 0.000 | 5.730 | 0.000 | 5.726 | 0.000 | 4.285 | 0.000 | 4.224 | 0.000 | 4.366 |
| cis-Stilbene Franck–Condon Pointg | ||||||||||
| ΔE | 0.166 | 6.060 | 0.182 | 4.536 | 0.131 | 4.415 | 0.192 | 4.655 | ||
| Twisted-Pyramidalized CIg | ||||||||||
| ΔE | 4.050 | 4.050 | 4.672 | 4.673 | 4.473 | 4.473 | 4.603 | 4.603 | 4.470 | 4.470 |
| RMSD | 0 | 0.0472 | 0.0246 | 0.0295 | 0.0233 | |||||
| penta-2,4-dieniminium, PSB3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| trans-PSB3 Franck–Condon Pointh | ||||||||||
| ΔE | 0.000 | 3.960 | 0.000 | 4.808 | 0.000 | 4.120 | 0.000 | 4.202 | 0.000 | 4.236 |
| cis-PSB3 Franck–Condon Pointh | ||||||||||
| ΔE | 0.130 | 4.000 | 0.161 | 4.852 | 0.134 | 4.175 | 0.128 | 4.265 | 0.143 | 4.294 |
| Twisted CIh | ||||||||||
| ΔE | 2.040 | 2.040 | 2.476 | 2.476 | 3.051 | 3.053 | 3.349 | 3.352 | 3.012 | 3.013 |
| RMSD | 0 | 0.0281 | 0.0677 | 0.0614 | 0.0509 | |||||
| anionic HBI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Franck–Condon Pointg | ||||||||||
| ΔE | 0.000 | 3.160 | 0.000 | 3.853 | 0.000 | 3.023 | 0.000 | 3.088 | 0.000 | 3.098 |
| Twisted-Pyramidalized CIPhg,i | ||||||||||
| ΔE | 2.560 | 2.550 | 3.261 | 3.261 | 3.481 | 3.481 | 3.962 | 3.962 | 3.405 | 3.405 |
| RMSD | 0 | 0.0612 | 0.0537 | 0.0709 | 0.0299 | |||||
| Twisted-Pyramidalized CIImj,k | ||||||||||
| ΔE | 2.699 | 2.699 | 2.960 | 2.961 | 3.644 | 3.644 | 2.974 | 2.975 | ||
| RMSD | ||||||||||
For the geometries at conical intersection points, the root mean square deviations (RMSD, in Å) of the DFT geometry from the reference wavefunction ab initio geometry are reported.
Multireference wave function ab initio calculations.
MRSDCI results from ref (25).
No reliable reference literature data available for this molecule.
CI with pyramidalization on the terminal carbon atom (see text for more detail).
CI with pyramidalization on the phenyl carbon atom (see text for more detail).
MS-CASPT2 results from ref (25).
MS-CASPT2 results from ref (26).
CI with torsion of the phenyl ring.
CI with torsion of the imidazole ring.
At a brief glance, the SI-SA-REKS method in connection with commonly used density functionals is capable of reproducing the reference data sufficiently accurately. On average, the BH&HLYP functional provides the best agreement with the reference results, in particular for the geometries at CI points. CAM-B3LYP shows similar performance; however, M06-2X displays some conspicuous failures for simple molecules, such as ethylene and methyliminium. In the following, the results of the calculations for individual molecules are analyzed in detail. This analysis is based on the sign-change theorem28 and on the use of elementary reaction coordinates for identifying molecular geometries at which the CIs occur.27
4.1. Ethylene
The twisted-pyramidalized CI in ethylene is the most efficient funnel for nonadiabatic relaxation of the excited state during the photoisomerization about the double bond.3,52−55 The CI occurs as a result of crossing of the ground and the lowest singlet excited state of ethylene near 90° of torsion about the double bond. In the ground electronic state S0, torsion about the double bond leads to a transition state of isomerization, which has a diradical character and, at the simplest level of approximation, can be described by a two-configurational wave function 7.41,45 At this geometry, the lowest excited singlet state S1 can be described by an open-shell singlet wave function, see eq 8, and this state has a zwitterionic character. The S1–S0 energy gap is substantial, 2.90 eV according to the SI-SA-RE-BH&HLYP/6-31G* calculations. Pyramidalization of one of the carbon atoms leads to shifting the (former) π-electron pair toward this atom and to stabilization of the excited state which acquires a charge transfer character.27,45 Simultaneously, the diradicaloid ground state is destabilized and, at a sufficiently large degree of pyramidalization, both states cross forming a CI.
From chemical point of view, the S0 state in the region between the diradicaloid transition state and the CI corresponds to the homolytic π-bond breaking and the S1 state to the heterolytic bond breaking,41,45 and their characters are interchanged after the CI. Hence, it is convenient to analyze the electronic states near the CI in terms of reaction coordinates corresponding to these bond breaking mechanisms.27
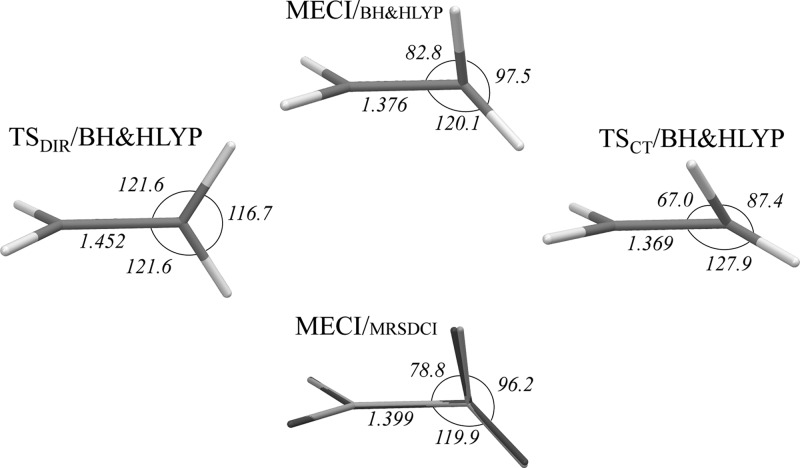
The transition states for the homolytic (TSDIR) and the heterolytic (TSCT, transition state with charge transfer character) breaking of the π-bond on the S0 ground state PES of ethylene were optimized with the use of the REKS(2,2) formalism and characterized by analysis of the vibrational frequencies. The geometries of TSDIR, CI, TSCT, and species optimized using the RE-BH&HLYP/6-31G* method are shown in Figure 1. For comparison, the MECI structure obtained using SI-SA-RE-BH&HLYP/6-31G* calculations is superimposed with the structure obtained by Martínez et al.25 using the MRSDCI/6-31G* method.
Figure 1.
Geometries of TSDIR, MECI, and TSCT points obtained for C2H4 using BH&HLYP functional in connection with REKS and SI-SA-REKS methods. Lower panel shows the MECI/BH&HLYP structure (light gray) superimposed with the reference MRSDCI structure (dark gray) from ref (25). Key geometric parameters (bondlengths in Å and angles in deg) are given.
Using the TSDIR, MECI, and TSCT structures a rigid scan in internal molecular coordinates has been carried out for the S0 and S1 PESs. Following refs (27 and 31), an equilateral triangle was set up around the MECI point with TSDIR and TSCT placed at two of its vertices. The internal molecular coordinates for the remaining vertex structure were obtained in such a way that the MECI point would be at the geometric center of the triangle. The position of any point on the plane defined by the triangle was parametrized by two dimensionless parameters, a1 and a2, see Figure 2.
Figure 2.
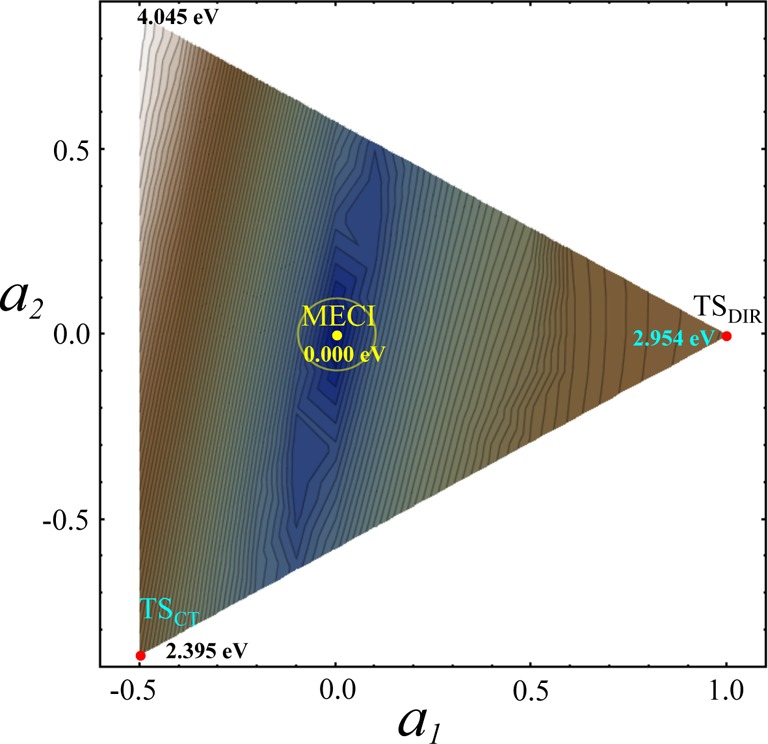
Energy difference (in eV) between the S0 and S1 states of C2H4 obtained using the SI-SA-RE-BH&HLYP/6-31G* method in a rigid scan of the PESs around MECI.
Figure 2 shows the energy difference between the S0 and S1 states obtained for C2H4 using the SI-SA-RE-BH&HLYP/6-31G* method. PESs of the S0 and S1 states are shown in Figure 3. Both figures demonstrate that the crossing point between the S0 and S1 PESs does indeed have the topography of a double cone. To investigate variation of the phase of the SI-SA-REKS wave function transported round a closed path around MECI a number of points have been calculated on a loop with the radius 0.1 shown by a yellow circle in Figure 2. In the plot in Figure 4, the wave function phase angle ϕ is obtained by representing the SI-SA-REKS wave function as cos(ϕ)Φ0 + sin(ϕ)Φ1, see eqs 7 and 8 for definitions, and the angle θ parametrizes the loop starting from the direction from MECI to TSDIR, see Figure 2.
Figure 3.
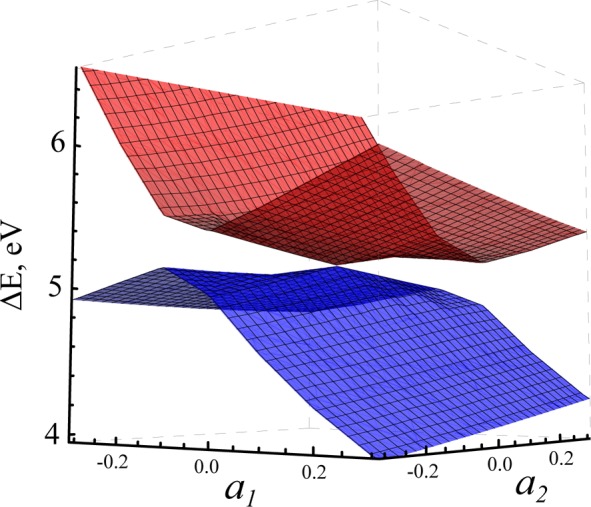
Potential energy profiles of the S0 and S1 states of C2H4 obtained using the SI-SA-RE-BH&HLYP/6-31G* method in a rigid scan around MECI.
Figure 4.
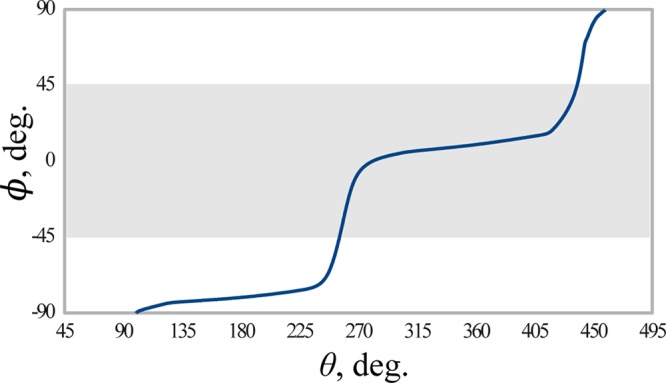
Phase angle ϕ of the SI-SA-RE-BH&HLYP/6-31G* wave function for C2H4 as a function of the angle θ parametrizing a loop of the radius 0.1 around MECI. See Figure 2 for detail of the loop. Shaded area shows the region where the SI-SA-REKS ground state wave function has a predominant diradical character.
Figure 4 demonstrates that the SI-SA-REKS wave function phase does change through π (180°) as one transports it round a closed path around a CI. The shaded area in 4 shows the region where the ground state wave function has a predominant diradical character. This region can be identified in Figure 2 as the segment to the right of MECI and bound from the left by a deep gorge shown by the blue color of varying depth. Although the calculation of the interstate coupling gradient vector h⃗ is not yet implemented for the SI-SA-REKS method, it can be estimated from Figure 2 as the direction normal to the direction of the gorge. Indeed, along the gorge the interstate coupling between S0 and S1 has its minimal magnitude and normal to this direction defines its gradient h⃗. In the coordinates of Figure 2, this is the direction with an azimuth of ca. 14° to the MECI line. The estimated h⃗ vector corresponds predominantly to rotation of the CH2 group of ethylene.
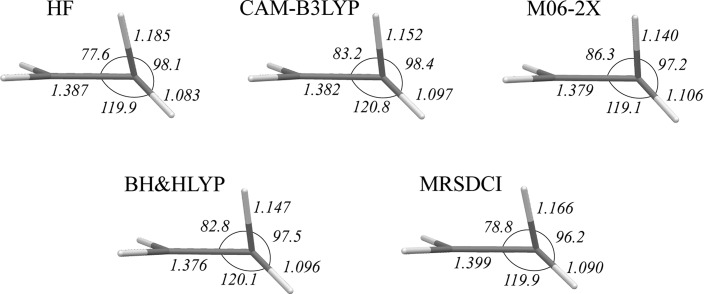
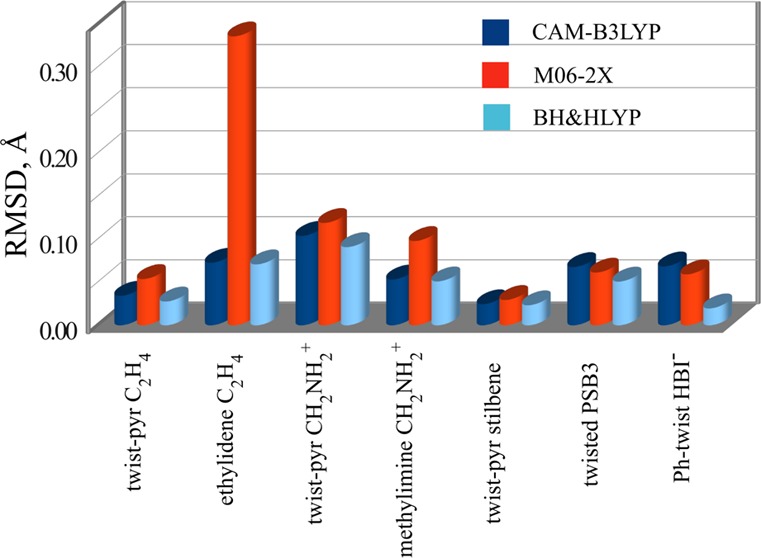
The geometries of MECI points for C2H4 optimized with the use of different density functionals are shown in Figure 5, and Figure 6 shows the S0 and S1 PES profiles calculated along an interpolation pathway connecting TSDIR, MECI, and TSCT structures. Figure 6 illustrates an observation that CI occurs in a proximity of a ground state TS structure that has a higher energy, in this case TSCT. The greater the difference between TSDIR and TSCT energies, the closer is the CI geometry to the TSCT geometry. Thus, the use of the HF energy functional in connection with SI-SA-REKS yields the greatest energy difference between the ground state TSCT and TSDIR geometries and the respective MECI is predicted to lie closer to TSCT than with the use of other functionals. The RMSD between MECI and TSCT geometries obtained with HF is 0.1226 Å, with CAM-B3LYP 0.1751 Å, with M06-2X 0.2039 Å, and with BH&HLYP 0.1623 Å. For comparison, the RMSD between MECI and TSDIR geometries are 0.3602 Å (HF), 0.3304 Å (CAM-B3LYP), 0.3149 Å (M06-2X), and 0.3328 Å (BH&HLYP). Obviously, the geometric proximity of MECI to the TSCT geometry correlates with the energy gap between TSDIR and TSCT. Thus, the HF functional yields MECI the closest to TSCT and M06-2X yields MECI the farthest from TSCT. BH&HLYP and CAM-B3LYP yield MECI geometries at approximately the same distance from the respective TSCT. It can be concluded that the M06-2X functional has the strongest preference for charge-transfer electronic structure than other density functionals, and this shows up in the results obtained with the use of this functional, which are the worst in comparison with the reference wave function ab initio calculations.
Figure 5.
Key geometric parameters of twisted-pyramidalized MECI points optimized for C2H4 with the use of different density functionals.
Figure 6.
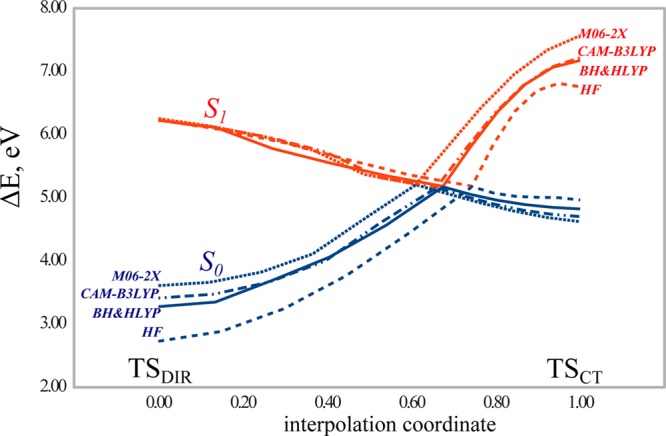
S0 and S1 potential energy profiles of C2H4 obtained along an interpolation pathway connecting TSDIR, twisted-pyramidalized MECI and TSCT structures. All energies are calculated with respect to the energy of the equilibrium ground state conformation.
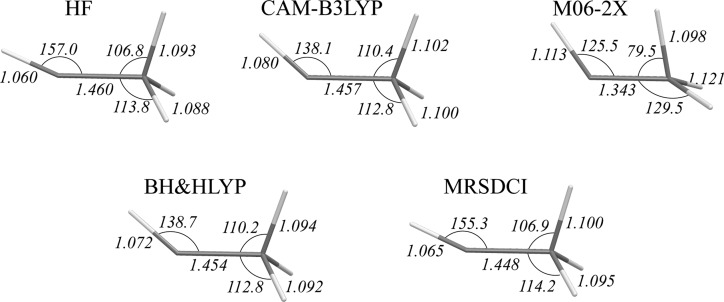
This observation also holds true for the ethylidene MECI in ethylene. Geometries of the ethylidene MECI structures obtained with the use of density functionals are shown in Figure 7. The M06-2X density functional yields a geometry for this CI that deviates strongly from the reference geometry. The distortion is most likely caused by a much too strong attraction between the C–H bonds on the opposite ends of the molecule. M06-2X was parametrized to include some medium range dispersion interaction in the ground states of noncovalently bound systems.51 It is therefore desirable to develop density functionals which would be capable of describing the dispersion interactions in the excited states of molecules as well.
Figure 7.
Key geometric parameters of ethylidene MECI points optimized for C2H4 with the use of different density functionals.
For ethylene, the SI-SA-RE-BH&HLYP calculations have been also performed using the 6-311G** basis set to investigate how strongly the results depend on the basis set size. The twisted-pyramidalized and ethylidene MECI geometries obtained with the use of a bigger basis set deviate only insignificantly from the geometries obtained with a smaller basis set. This is confirmed by RMSD(6-31G* – 6-311G**) of geometries, which for the twisted-pyramidalized MECI amounts to 0.0146 Å and for ethylidene MECI to 0.0032 Å. The excitation energy at the FC point obtained using the SI-SA-RE-BH&HLYP/6-311G** method is 8.112 eV as compared to 8.338 eV when using the 6-31G* basis set (see Table 1). The twisted-pyramidalized MECI obtained using SI-SA-RE-BH&HLYP/6-311G** method lies 5.015 eV above the equilibrium ground state energy (5.158 eV when using the 6-31G* basis), and the ethylidene MECI lies at 4.019 eV (4.040 eV with 6-31G*), which confirms that the basis set extension has only a minor effect on the obtained geometries and relative energies of CIs. For more detail on the SI-SA-RE-BH&HLYP/6-311G** calculations, see Tables 17 and 18 of Supporting Information.
4.2. Styrene and Stilbene
Conical intersections in styrene and stilbene (Scheme 1E, F, G) have been studied in the past with the use of ab initio multireference wave function methods in connection with photoisomerization reactions which these molecules undergo.3,25,54,56,57 For the purpose of the present work, these molecules are interesting because they illustrate the effect of substituents at the double C=C bond on the geometry and relative energy of the conical intersections obtained using density functional calculations.
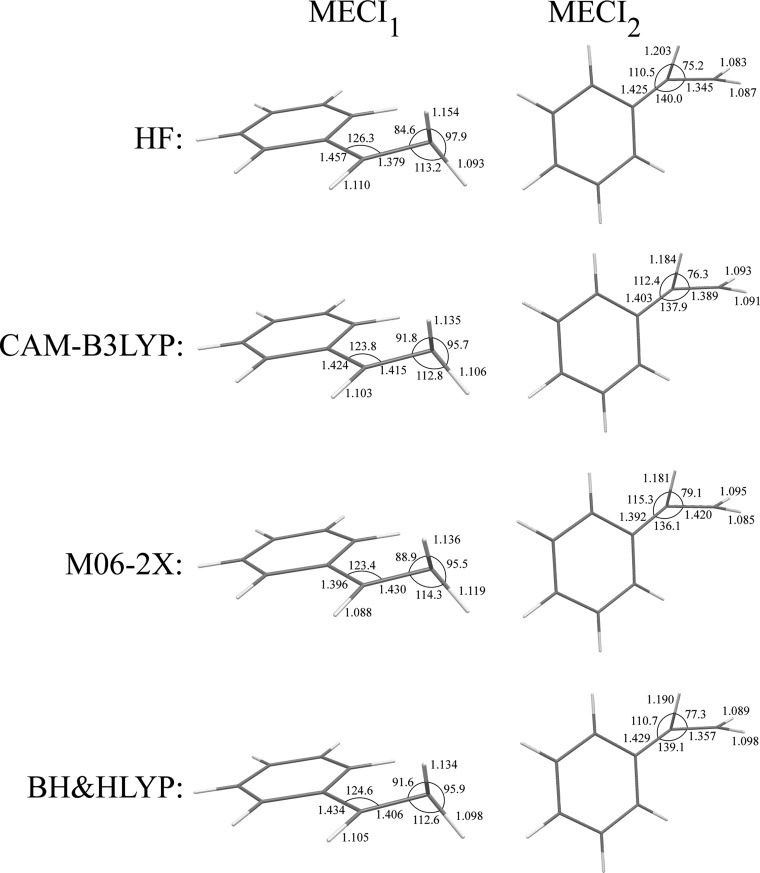
In styrene, the presence of the phenyl ring at one end of the ethylenic double bond creates an asymmetric situation where S0/S1 CIs resulting from twist and pyramidalization of carbon atoms at the opposite ends of the double bond become nonequivalent. Indeed, in the literature two possibilities for low energy conical intersections in styrene were identified, a CI with pyramidalization of the carbon atom bound to phenyl ring56 and a CI with pyramidalization of the terminal carbon atom.57 Unfortunately, a relatively low-level CASSCF approach was used by Bearpark et al.56 and optimization of the CI structure was not attempted with the use of the CASPT2 method by Molina et al.,57 such that the literature results can not be used as a reference for benchmarking the DFT methods. Nevertheless, the two S0/S1 CIs resulting from twist-pyramidalization distortion of the ethylenic bond in styrene have been optimized using the SI-SA-REKS method in connection with various density functionals and the key geometric parameters of the obtained CIs are reported in Figure 8 and their energies relative to the ground state equilibrium conformation of styrene are reported in Table 1.
Figure 8.
Key geometric parameters of twisted-pyramidalized MECI points optimized for styrene with the use of density functionals.
The MECI1 point, where the terminal carbon atom is pyramidalized, lies ca. 0.5 eV below the MECI2 point. This trend can be understood by the following reason: Crossing between the PESs of the states corresponding to the homolytic and heterolytic bond breaking resulting from the torsion of the ethylenic π bond is facilitated by pyramidalization of one or another carbon atom. Pyramidalization leads to shifting the π electron pair toward the pyramidalized end of the double bond, thus leading to a charge transfer electronic structure.45 In the case of styrene, the relative energy of the CT electronic configurations depends on the energy penalty incurred by ionization of the fragments connected by the double bond, for instance, the benzyl radical and methyl radical obtained by a complete breaking of the ethylenic bond and saturating the dangling σ-bonds by hydrogens. According to the BH&HLYP/6-31G* calculations, the ionization potential and the electron affinity of benzyl radical are 6.739 and 0.025 eV, respectively, and those of the methyl radical are 9.523 and −1.969 eV, respectively. Hence, ionizing benzyl and adding electron to methyl, which leads to the MECI1 electronic structure, should incur a lower energy penalty than ionizing methyl and adding electron to benzyl and, consequently, MECI1 has lower energy than MECI2.
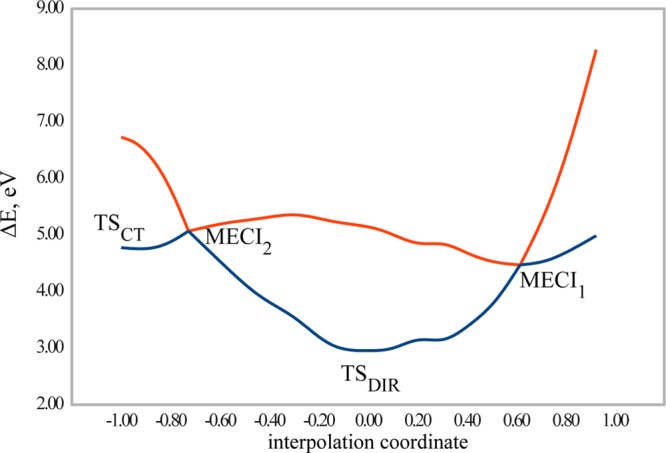
Figure 9 shows the PES profiles of the S0 and S1 states in styrene calculated using the SI-SA-RE-BH&HLYP/6-31G* method along an interpolation coordinate connecting transition state TSCT for the heterolytic double bond breaking where the charge transfer occurs to the phenyl group, MECI2, diradicaloid transition state TSDIR for the homolytic bond breaking, and MECI1. A transition state for the heterolytic bond breaking with charge transfer to the methyl end of the double bond could not be located. It can be seen from the PES profiles in Figure 9 that such a TSCT might have occurred in the nearest vicinity of MECI1. From Table 1, both MECIs lie at least 0.4 eV below the Franck–Condon point of styrene and are therefore easily accessible upon the excitation. However, the reported PES profiles suggest that MECI1 may represent a more efficient funnel for radiationless relaxation of the excited state than MECI2 as there is a slope toward it on the excited state PES.
Figure 9.
Potential energy profiles of the S0 and S1 states of styrene obtained by a rigid scan along an interpolation coordinate connecting for electron transfer to phenyl, MECI2, TSDIR, and MECI1 using the SI-SA-RE-BH&HLYP/6-31G* method. The energies (in eV) are given with respect to the ground state equilibrium energy of styrene.
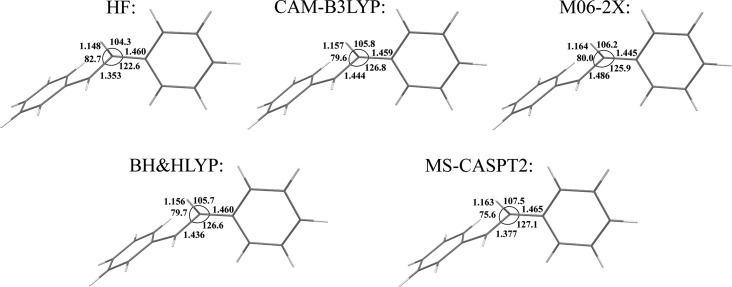
Similar to ethylene, stilbene serves as a paradigmatic system for studying ultrafast photorearrangement of olefins.58 It has been experimentally established that cis-stilbene undergoes an ultrafast isomerization to trans-isomer within ca. 1 ps.58,59 This very short S1 state lifetime was explained by the existence of a twisted-pyramidalized CI accessible from the cis-stilbene Franck–Condon point.3,54 The geometry of the twisted-pyramidalized MECI was optimized with the use of multistate CASPT2 (MS-CASPT2) method by Levine et al.25 This geometry is used as a reference for benchmarking density functionals in the present work.
The twisted-pyramidalized MECI geometry optimized using density functional calculations is compared with the reference MS-CASPT2 geometry in Figure 10. The BH&HLYP and CAM-B3LYP density functionals yield the best agreement with the reference geometry, with M06-2X lagging a little behind in accuracy, see Table 1. The importance of the dynamic electron correlation included into the density functionals is underlined by a visibly worse MECI geometry produced with the use of the HF functional. Interestingly, all the density functionals yield the trans-stilbene FC point below the MECI by ca. 0.1–0.2 eV. BH&HLYP and CAM-B3LYP yield the cis-stilbene FC point 0.185 and 0.063 eV above the respective MECI energy, see Table 1. This energy ordering of the MECI and the FC points generally agrees with the experimentally observed photorearrangement lifetimes in cis- and trans-stilbenes.59 The accessibility of the MECI point from the cis-stilbene FC point predicted by the SI-SA-RE-BH&HLYP/6-31G* and SI-SA-RE-CAM-B3LYP/6-31G* methods agrees with its short lifetime (ca. 1 ps),59 whereas the obtained mild energy penalty to reach MECI from the trans-stilbene FC point is consistent with a longer excited state lifetime (ca. 30 ps).59 The calculated excitation energies of trans- and cis-stilbene, see Table 1, can be compared with the energies experimentally measured in n-hexane, ca. 4.6 and 4.1 eV, respectively.59
Figure 10.
Key geometric parameters of twisted-pyramidalized MECI point optimized for stilbene with the use of density functionals. The MS-CASPT2 geometry is taken from ref (25)
Figure 11 shows the S0 and S1 PES profiles of stilbene obtained with the use of the SI-SA-RE-BH&HLYP/6-31G* method along an interpolation coordinate connecting the structure for the homolytic ethylenic bond breaking and the MECI point. The geometry was optimized using the RE-BH&HLYP/6-31G* method, and it features a torsion about the ethylenic double bond with the Ph–C–C–Ph dihedral angle of 97.2°. The S1 PES is essentially flat in the direction toward MECI, and at the TSDIR geometry, it lies at 4.560 eV, that is, 0.107 eV below the cis FC point. In this regard, the (weakly sloped) MECI topography in stilbene differs from that of ethylene, where the latter lies at the bottom of a potential minimum on the S1 PES, see Figure 6, and thus provides for a much faster photoisomerization rate than in stilbene.3,54
Figure 11.
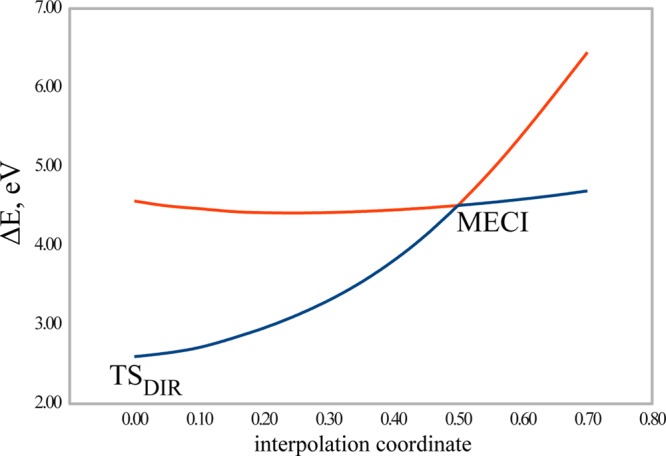
Potential energy profiles of the S0 and S1 states of stilbene obtained by a rigid scan along an interpolation coordinate connecting TSDIR for the homolytic ethylenic bond breaking and MECI using the SI-SA-RE-BH&HLYP/6-31G* method. The energies (in eV) are given with respect to the ground state equilibrium energy of trans-stilbene.
For stilbene, the dependence of the obtained MECI geometry and relative energy on the basis set size was investigated by repeating the SI-SA-RE-BH&HLYP geometry optimizations and energy calculations using the 6-311G** basis set. RMSD(6-31G* – 6-311G**) of the MECI geometry is 0.0344 Å, the relative energy of the S1 trans-FC point with respect to the ground state is 4.305 eV (4.366 eV when using 6-31G*, see Table 1), the relative energy of the S1cis-FC is 4.822 eV (4.655 eV with 6-31G*), and the relative energy of the twisted-pyramidalized MECI is 4.332 eV (4.470 eV with 6-31G*). These results (for more information see Tables 19 and 20 of Supporting Information) confirm that the basis set extension has only a minor effect on the results of calculations.
4.3. Methyliminium Cation
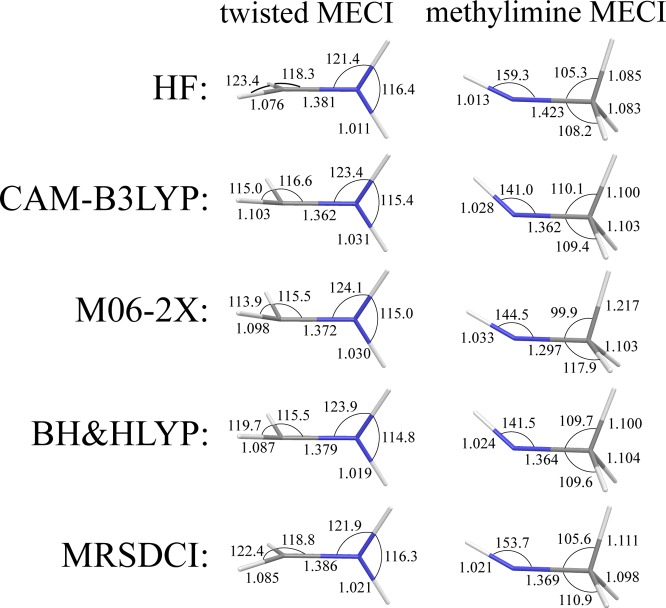
Introduction of the imine nitrogen atom into the methyliminium cation (entries C and D in Scheme 1) results in a strong polarization of the double bond. For this cation, the TSCT for heterolytic breaking of the double C=N bond becomes more stable than the TSDIR for homolytic breaking and the S0/S1 CI occurs in the vicinity of TSDIR. According to the MRSDCI calculations, the twisted MECI can be reached by a pure torsion about the double bond without involving pyramidalization of the carbon or nitrogen atoms.25 SI-SA-REKS calculations undertaken in the present work predict that, at 90° of twist about the C=N double bond, the ground S0 state has a charge transfer character where the π electron pair is transferred toward imine group resulting in a H2N0–C⊕H2 electronic configuration. Thus, to reach the CI at 90° of twist, a slight bending of the methylidene group is needed to destabilize the CT configuration with respect to the diradicaloid electronic configuration. Typically, bending through an angle of ca. 10–20° is sufficient to equalize the energies of the CT configuration (S0) and the diradicaloid configuration (S1) and to reach a CI.
The geometries of the twisted MECI point obtained with the use of SI-SA-REKS method in connection with various density functionals are shown in Figure 12. The best agreement with the reference MRSDCI MECI geometry is achieved with the use of the BH&HLYP density functional. This is also valid for the methylimine MECI geometries, for which SI-SA-RE-BH&HLYP/6-31G* reproduces the reference geometric parameters (with the exception of the H–N–C valence angle) with the best accuracy.
Figure 12.
Key geometric parameters of twisted and methylimine MECI points optimized for methyliminium cation with the use of different density functionals. The MRSDCI geometry is taken from ref (25)
4.4. Penta-2,4-dieniminium Cation, PSB3
PSB3 (penta-2,4-dieniminium cation) is a widely used model of retinal chromophore. Recently, the electronic structure and potential energy surfaces of PSB3 have been studied using a variety of ab initio multireference and single-reference wave function methods as well as density functional methods.21,26,60,61 Using CASSCF, the minimum energy conical intersection in PSB3 was found at a geometry that corresponds to twisting the central C=C double bond through ca. 90° and along a bond length alternation (BLA) pathway that connects a transition state with charge transfer character, TSCT, and a transition state with diradical character, TSDIR. Both transition states feature 90° torsion about the central C=C double bond and differ mostly in the difference between the average length of formally single bonds and the average length of formally double bonds, which defines the BLA coordinate.60
The geometry of MECI optimized for PSB3 with a variety of density functionals used in connection with the SI-SA-REKS method are reported in Figure 13 where they are compared with the reference geometry from the MS-CASPT2 calculations of Keal et al.26 Although the agreement with the reference geometric parameters is reasonably good, especially for the geometry of the allyl fragment, the C–C and C=N bond lengths of the ethyliminium fragment deviate from the CASPT2 values by ca. 0.04–0.05 Å. As has been observed earlier by Huix-Rotllant et al.,21 for PSB3, density functional methods have a tendency to yield much lower energy of TSCT (which corresponds to the heterolytic breaking of the central double bond) than that of TSDIR (holomytic bond breaking). The latter could not even be located with the use of the density functionals employed in this work.
Figure 13.
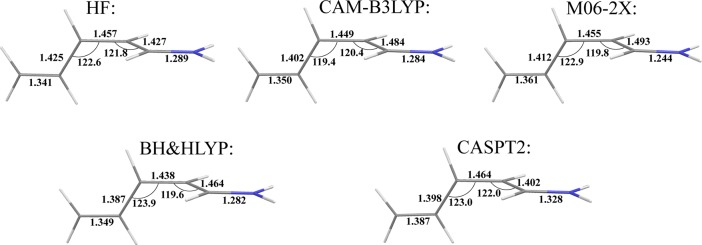
Key geometric parameters of twisted MECI point optimized for PSB3 with the use of different density functionals. The MS-CASPT2 geometry is taken from ref (26)
Figure 14 shows the S0 and S1 PESs of PSB3 along the BLA pathway connecting TSCT with MECI. The crossing between the PESs occurs on an uphill segment of the curves and, after the MECI point, no transition state with diradical character can be found. In the case of the HF energy functional, a possible TSDIR structure may find itself in the nearest proximity of the MECI geometry, and therefore, this transition state could not be located. The CASSCF and CASPT2 methods both predict that the TSCT and TSDIR structures have nearly equal energies (see Figure 2 in ref (60).) and only the MRSDCI method puts TSCT considerably below TSDIR.21,60 As a consequence of nearly equal TSCT and TSDIR energies in CASSCF and CASPT2 calculations, the MECI, which occurs between these structures, has a substantial charge transfer character and the C=N bond of the ethyliminium fragment possesses a noticeably greater single bond character as a result of the charge transfer to this fragment. The SI-SA-REKS calculations predict MECI considerably farther away from the TSCT geometry and the MECI geometry has a more pronounced resemblance of a would-be TSDIR structure. It is noteworthy that the potential energy curves reported in Figure 14 are much closer to the curves obtained using the MRSDCI method.60 However, in the later case, the CASSCF geometries were employed60 whereas they are optimized in the present work.
Figure 14.
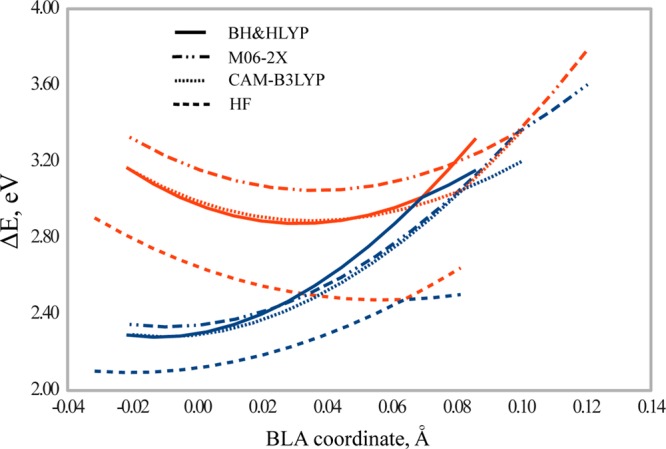
Potential energy profiles of the S0 and S1 states of PSB3 obtained by a rigid scan along the BLA coordinate (in Å) connecting TSCT for the heterolytic C=C bond breaking and MECI using the SI-SA-REKS method in connection with various density functionals. The energies (in eV) are given with respect to the ground state equilibrium energy of cis-PSB3. TSCT is always located at the beginning of the potential energy curves corresponding to individual functionals.
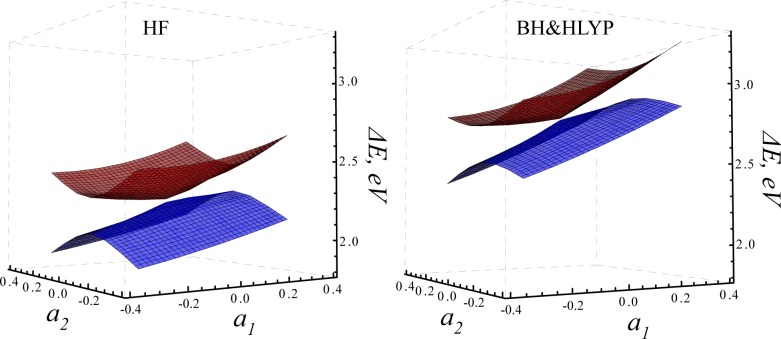
To investigate whether the crossing points obtained for PSB3 satisfy the criteria for conical intersections, the S0 and S1 PESs were scanned in the vicinity of the MECIs optimized using the SI-SA-RE-BH&HLYP/6-31G* and SI-SA-RE-HF/6-31G* methods. The PES profiles in Figure 15 have been obtained in the same way as for ethylene, see Figure 2 and 3, using interpolation within a triangle defined by the TSCT structure and two additional conformations chosen in such a way that the MECI geometry would occur at the center of the triangle. The latter two conformations were obtained by applying a clockwise and counterclockwise torsion about the central C–C bond to the conformation obtained by extrapolation along the BLA coordinate beyond the MECI geometry. According to Gozem et al.,60 the BLA coordinate corresponds to the difference gradient g⃗ direction and twisting about the central C–C bond to the interstate coupling gradient h⃗. Hence, the two directions in Figure 15 should span the branching space of MECI (a⃗2 corresponds to h⃗ and a⃗1 to g⃗).
Figure 15.
Potential energy surfaces of the S0 and S1 states of PSB3 obtained using the SI-SA-RE-HF/6-31G* (left panel) and SI-SA-RE-BH&HLYP/6-31G* (right panel) methods in a rigid scan around MECI. The relative energies are obtained with respect to the ground state energy of the cis-PSB3.
The S0/S1 intersection does indeed have the shape of a double cone and there is no ramming of the S1 PES into the ground state surface as was observed with the use of the conventional density functionals in connection with the standard TD-DFT calculations.21 The further evidence of the proper conical intersection character is presented in Figure 16, which shows the phase of the SA-SA-REKS wave function round a closed loop encompassing the MECI point (see text around Figure 4 for explanation). The S0/S1 interstate coupling is minimal along the BLA coordinate (the discontinuity occurs at zero angle with respect to the TSCT–MECI direction) and the direction normal to it defines the h⃗ vector of the CI branching space. Thus, the SI-SA-REKS method predicts qualitatively the same branching space of the twisted MECI as the ab initio multireference wave function methods.60
Figure 16.
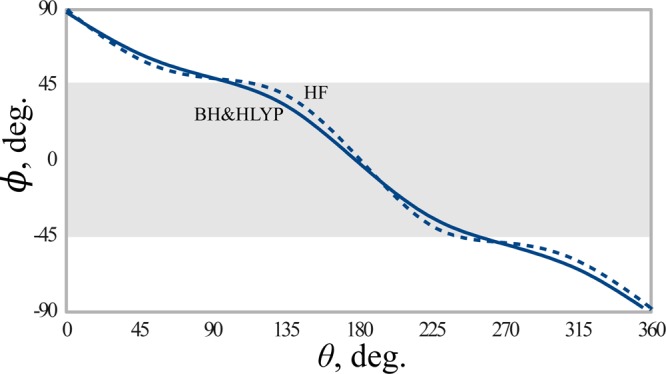
Phase angle ϕ of the SI-SA-RE-BH&HLYP/6-31G* (solid line) and SI-SA-RE-HF/6-31G* (dashed line) wave functions for PSB3 as a function of the angle θ parametrizing a loop of the radius 0.1 around MECI. Shaded area shows the region where the SI-SA-REKS ground state wave function has a predominant diradical character.
4.5. p-Hydroxybenzilideneimidazolinone anion, HBI
p-Hydroxybenzilideneimidazolinone anion (HBI) serves as a model of the anionic state of the chromophore of the green fluorescent protein, a biological molecule that finds a wide application in life sciences for imaging and sensing.62 The spectroscopy and photophysics of HBI represents a considerable interest for synthetic and theoretical chemists, and in a number of studies, the conical intersection seam in this model compound have been investigated with the use of ab initio multireference wavefuction methods.25,52
In the most recent study, Mori and Martínez52 have investigated the CI seam in the anionic HBI using the CASSCF method and have identified two low lying CI points. Of the two CIs, one (CIIm) is obtained by torsion of the imidazole ring and a slight pyramidalization of the methine bridge, another one (CIPh) involves torsion of the phenyl ring accompanied by pyramidalization of the methine bridge. The torsion and pyramidalization result in crossing between the electronic states for which the leading valence electronic configurations are shown in Scheme 2.
Scheme 2. Schematic Representation of the Most Important Valence Configurations Involved in the Formation of Conical Intersections in Anionic HBI.
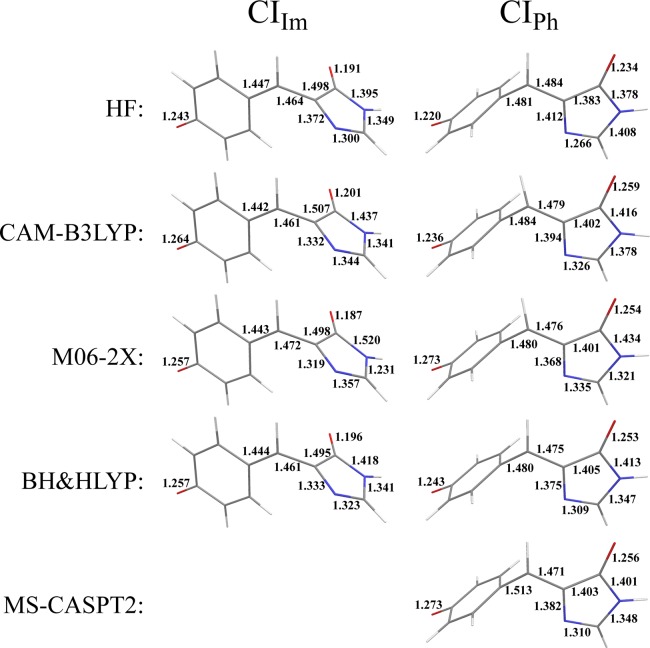
The geometries of the two CI points have been optimized using the SI-SA-REKS method in connection with various density functionals and the results are presented in Figure 17. Although in ref (52) both CIs have been optimized, the dynamic electron correlation was not included into the CASSCF calculations and these geometries are not used in the present work as the reference data. The only CI for which a higher level MS-CASPT2 method was used is the CIPh,25 and its geometry is also shown in Figure 17 for comparison.
Figure 17.
Key geometric parameters of twisted-pyramidalized MECI points optimized for anionic HBI with the use of different density functionals. The left panel shows a CI obtained by the imidazole ring torsion and the right panel shows a CI obtained by the phenyl ring torsion. The MS-CASPT2 geometry for the latter CI is taken from ref (25).
The CIIm point has ca. 0.5 eV lower energy than CIPh, see Table 1. This can be understood by comparing the electron affinity of the fragments formed by breaking methine π-bond as shown in Scheme 2. The homolytic bond breaking leads to diradicaloid (DIR) electronic configurations and heterolytic bond breaking to charge transfer (CT) configurations. The electron affinities were estimated from the energies of fragments formed by breaking the respective methine bond and by saturating the dangling σ-bonds by hydrogens. For both CIs, the CT electronic configurations have the lowest energy and the DIR configurations lie ca. 0.5 eV (CIIm) or ca. 1 eV (CIPh) higher in energy. Therefore, the CIs should occur energetically and geometrically closer to the DIR structures. It is the greater electron affinity (EA) of the p-oxybenzyl fragment as compared to the methylidene imidazolinone fragment (see the DIR configurations in Scheme 2) that makes CIIm more stable. All the density functionals employed in the present work yield ca. 0.8 eV for the difference between EAs of p-oxybenzyl and methylidene imidazolinone which qualitatively agrees with the relative stability of the two CI points.
Generally, the CIPh geometries obtained with the use of density functionals are in a reasonable agreement with the reference MS-CASPT2 geometry.25 It is noteworthy that the geometries of the CIIm and CIPh points obtained with the use of the HF functional are in a good agreement with the CASSCF geometries obtained by Mori and Martínez,52 which are shown in Figure 18. There is also a reasonable agreement between the relative energy of the two CIs obtained by the SI-SA-RE-HF/6-31G* method (0.562 eV) and the SA3-CASSCF(4,3)/6-31G* method (0.401 eV).52
Figure 18.
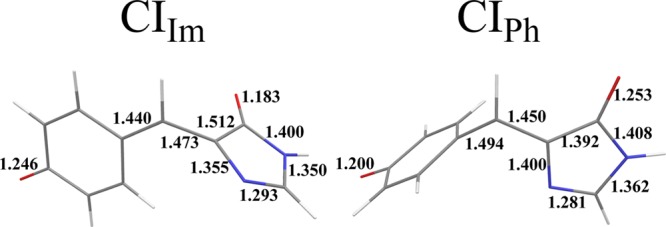
Key geometric parameters of twisted-pyramidalized MECI points optimized for anionic HBI in ref (25). with the use of SA3-CASSCF(4,3)/6-31G* method.
5. Conclusions
A number of popular density functionals employed in connection with the SI-SA-REKS method have been tested for their ability to accurately reproduce the geometries at the conical intersection points between the ground and lowest singlet excited state PESs of several organic molecules. The compounds selected for this study represent paradigmatic models for cis–trans photoisomerization of olefins (ethylene, stilbene) and widely used models of biologically important chromophores (PSB3, HBI).
In the overall assessment, the global hybrid BH&HLYP density functional is capable of producing the MECI geometries in the closest agreement with the reference high-level ab initio multireference wave function calculations. The other two density functionals tested in the present work either offer no advantage over BH&HLYP (local hybrid functional CAM-B3LYP) or yield slightly deteriorated agreement with the reference geometries (meta-GGA hybrid functional M06-2X) while being more time-consuming in practical calculations.
The MECI geometries obtained with the use of SI-SA-REKS method were analyzed by the application of the sign-change theorem,28,29 whereby it was shown that the obtained crossing points satisfy the criteria for conical intersections and the SI-SA-REKS wave function changes sign as it is being transported round a closed path around the crossing point. Furthermore, following Haas et al.,27 analysis of the obtained potential energy surfaces in terms of elementary reaction coordinates corresponding to two possible mechanisms of the π-bond breaking, a heterolytic and a homolytic mechanism, revealed that the energetic and geometric parameters of CI can be estimated from the stationary points on the ground state PES, such as the respective transition states, which correspond to these mechanisms. An even simpler analysis can be based on comparing the electronegativities of fragments obtained by breaking the respective π-bond. Such an analysis enables one to estimate whether the homolytic or the heterolytic bond breaking is the energetically preferred mechanism and to sketch parameters of a possible CI. The latter may be expected to occur closer to the respective transition state (even a hypothesized one) that lies higher in energy. This simple observation can be used for suggesting possible chemical ways of modulating CIs, and its veracity will be tested in subsequent works.
Acknowledgments
M.F. acknowledges financial support provided by the European Union Seventh Framework Programme (FP7/2007-2013) under the IEF grant agreement No. 326652.
Supporting Information Available
Cartesian coordinates and total energies of species discussed in the present article. This material is available free of charge via the Internet at http://pubs.acs.org/.
The authors declare no competing financial interest.
Supplementary Material
References
- Yarkony D. R. Rev. Mod. Phys. 1996, 68, 985–1013. [Google Scholar]
- Bernardi F.; Olivucci M.; Robb M. A. Chem. Soc. Rev. 1996, 25, 321–328. [Google Scholar]
- Levine B. G.; Martínez T. J. Annu. Rev. Phys. Chem. 2007, 58, 613–634. [DOI] [PubMed] [Google Scholar]
- Domcke W., Yarkony D. R., Köppel H., Eds. Conical Intersections. Theory, Computation, and Experiment; Advanced Series in Physical Chemistry; World Scientific: Singapore, 2011; Vol. 17. [Google Scholar]
- Polli D.; Altoe P.; Weingart O.; Spillane K. M.; Manzoni C.; Brida D.; Tomasello G.; Orlandi G.; Kukura P.; Mathies R. A.; Garavelli M.; Cerullo G. Nature 2010, 467, 440–443. [DOI] [PubMed] [Google Scholar]
- Conyard J.; Addison K.; Heisler I. A.; Cnossen A.; Browne W. R.; Feringa B. L.; Meech S. R. Nature Chem. 2012, 4, 547–551. [DOI] [PubMed] [Google Scholar]
- Docken K. K.; Hinze J. J. Chem. Phys. 1972, 57, 4928–4936. [Google Scholar]
- Roos B. O. In Ab Initio Methods in Quantum Chemistry II; Lawley K. P., Ed.; John Wiley and Sons: New York, 1987; pp 399–446. [Google Scholar]
- Kohn W.; Sham L. J. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar]
- Cohen A. J.; Handy N. C. Mol. Phys. 2001, 99, 607–615. [Google Scholar]
- Cremer D. Mol. Phys. 2001, 99, 1899–1940. [Google Scholar]
- Levine B. G.; Ko C.; Quenneville J.; Martínez T. J. Mol. Phys. 2006, 104, 1039–1051. [Google Scholar]
- Kazaryan A.; Heuver J.; Filatov M. J. Phys. Chem. A 2008, 112, 12980–12988. [DOI] [PubMed] [Google Scholar]
- Shao Y.; Head-Gordon M.; Krylov A. I. J. Chem. Phys. 2003, 118, 4807–4818. [Google Scholar]
- Wang F.; Ziegler T. J. Chem. Phys. 2004, 121, 12191–12196. [DOI] [PubMed] [Google Scholar]
- Rinkevicius Z.; Vahtras O.; Ågren H. J. Chem. Phys. 2010, 133, 114104. [DOI] [PubMed] [Google Scholar]
- Bernard Y. A.; Shao Y.; Krylov A. I. J. Chem. Phys. 2012, 136, 204103. [DOI] [PubMed] [Google Scholar]
- Minezawa N.; Gordon M. S. J. Phys. Chem. A 2009, 113, 12749–12753. [DOI] [PubMed] [Google Scholar]
- Minezawa N.; Gordon M. S. J. Phys. Chem. A 2011, 115, 7901–7911. [DOI] [PubMed] [Google Scholar]
- Huix-Rotllant M.; Natarajan B.; Ipatov A.; Wawire C. M.; Deutsch T.; Casida M. E. Phys. Chem. Chem. Phys. 2010, 12, 12811–12825. [DOI] [PubMed] [Google Scholar]
- Huix-Rotllant M.; Filatov M.; Gozem S.; Schapiro I.; Olivucci M.; Ferré N. J. Chem. Theory Comput. 2013, 10.1021/ct4003465. [DOI] [PubMed] [Google Scholar]
- Filatov M.; Shaik S. Chem. Phys. Lett. 1999, 304, 429–437. [Google Scholar]
- Filatov M.; Shaik S. J. Phys. Chem. A 2000, 104, 6628–6636. [Google Scholar]
- Moreira I. d. P. R.; Costa R.; Filatov M.; Illas F. J. Chem. Theory Comput. 2007, 3, 764–774. [DOI] [PubMed] [Google Scholar]
- Levine B.; Coe J. D.; Martínez T. J. J. Phys. Chem. B 2008, 112, 405–413. [DOI] [PubMed] [Google Scholar]
- Keal T. W.; Wanko M.; Thiel W. Theor. Chem. Acc. 2008, 123, 145–156. [Google Scholar]
- Haas Y.; Cogan S.; Zilberg S. Int. J. Quantum Chem. 2005, 102, 961–970. [Google Scholar]
- Longuet-Higgins H. C. Proc. Roy. Soc. London Ser. A 1975, 344, 147–156. [Google Scholar]
- Herzberg G.; Longuet-Higgins H. C. Discuss. Faraday. Soc. 1963, 35, 77–82. [Google Scholar]
- Teller E. J. Phys. Chem. 1937, 41, 109–116. [Google Scholar]
- Fukumoto Y.; Koizumi H.; Makoshi K. Chem. Phys. Lett. 1999, 313, 283–292. [Google Scholar]
- Baer R. Phys. Rev. Lett. 2010, 104, 073001. [DOI] [PubMed] [Google Scholar]
- Noziéres P.; Pines D.. The Theory of Quantum Liquids; Perseus Books Publishing LLC: Cambridge, MA, 1966; pp 296–298. [Google Scholar]
- Becke A. D. J. Chem. Phys. 1988, 88, 1053–1062. [Google Scholar]
- Lieb E. H. Int. J. Quantum Chem. 1983, 24, 243–277. [Google Scholar]
- Englisch H.; Englisch R. Phys. Stat. Sol. B 1984, 124, 373–379. [Google Scholar]
- Ullrich C. A.; Kohn W. Phys. Rev. Lett. 2001, 87, 093001. [DOI] [PubMed] [Google Scholar]
- a Schipper P. R. T.; Gritsenko O. V.; Baerends E.-J. Theor. Chem. Acc. 1998, 99, 329–343. [Google Scholar]; b Schipper P. R. T.; Gritsenko O. V.; Baerends E.-J. J. Chem. Phys. 1999, 111, 4056–4067. [Google Scholar]
- Morrison R. C. J. Chem. Phys. 2002, 117, 10506–10511. [Google Scholar]
- Zhao Q.; Morrison R. C.; Parr R. G. Phys. Rev. A 1994, 50, 2138–2142. [DOI] [PubMed] [Google Scholar]
- Salem L.; Rowland C. Angew. Chem., Int. Ed. 1972, 11, 92–111. [Google Scholar]
- Giesbertz K. J. H.; Baerends E.-J. J. Chem. Phys. 2010, 132, 194108. [DOI] [PubMed] [Google Scholar]
- Hirao K.; Nakatsuji H. J. Chem. Phys. 1973, 59, 1457–1462. [Google Scholar]
- Filatov M.; Shaik S. Chem. Phys. Lett. 1998, 288, 689–697. [Google Scholar]
- Bonačić-Koutecký V.; Koutecký J.; Michl J. Angew. Chem., Int. Ed. 1987, 26, 170–189. [Google Scholar]
- Cremer D.; Filatov M.; Kraka E.; Shaik S. Int. J. Mol. Sci. 2002, 3, 604–638. [Google Scholar]
- Slaviček P.; Martínez T. J. J. Chem. Phys. 2010, 132, 234102. [DOI] [PubMed] [Google Scholar]
- Kraka E.; Filatov M.; Zou W.; Gräfenstein J.; Izotov D.; Gauss J.; He Y.; Wu A.; Polo V.; Olsson L.; Konkoli Z.; He Z.; Cremer D.. COLOGNE2012, Southern Methodist University, 2012.
- Becke A. D. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar]
- Yanai T.; Tew D.; Handy N. C. Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar]
- Zhao Y.; Truhlar D. G. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Mori T.; Martínez T. J. J. Chem. Theory Comput. 2013, 9, 1155–1163. [DOI] [PubMed] [Google Scholar]
- Ben-Nun M.; Martínez T. J. Chem. Phys. 2000, 259, 237–248. [Google Scholar]
- Quenneville J.; Martínez T. J. J. Phys. Chem. A 2003, 107, 829–837. [Google Scholar]
- Virshup A. M.; Chen J.; Martínez T. J. J. Chem. Phys. 2012, 137, 22A519. [DOI] [PubMed] [Google Scholar]
- Bearpark M. J.; Olivucci M.; Wilsey S.; Bernardi F.; Robb M. A. J. Am. Chem. Soc. 1995, 117, 6944–6953. [Google Scholar]
- Molina V.; Merchan M.; Roos B. O.; Malmqvist P.-Å. Phys. Chem. Chem. Phys. 2000, 2, 2211–2217. [Google Scholar]
- Waldeck D. H. Chem. Rev. 1991, 91, 415–436. [Google Scholar]
- Rice J. K.; Baronavski A. P. J. Phys. Chem. 1992, 96, 3359–3366. [Google Scholar]
- Gozem S.; Huntress M.; Schapiro I.; Lindh R.; Granovsky A. A.; Angeli C.; Olivucci M. J. Chem. Theory Comput. 2012, 8, 4069–4080. [DOI] [PubMed] [Google Scholar]
- Gozem S.; Krylov A. I.; Olivucci M. J. Chem. Theory Comput. 2013, 9, 284–292. [DOI] [PubMed] [Google Scholar]
- Tsien R. Y. Annu. Rev. Biochem. 1998, 67, 509–544. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.