The paired t-test as a simple latent change score model

The t-test is a common statistical test of differences in means. Despite the fact that its extension, the paired t-test (t-test_P), appears in most introductory statistics textbooks, it is less known that for repeated variables the t-test_P is in fact a model of change that can be replicated within the Structural Equation Modeling (SEM) framework. We show how to perform the t-test_P with latent change scores (LCS) models, which allow for direct testing of significance of mean changes, and moreover can explain inter-individual (and group) differences in changes over time.

Modeling background

Structural models with latent variables can nowadays replicate virtually any statistical test (Skrondal and Rabe-Hesketh, 2004). It has been shown in particular that a latent growth curve model (LGM) with df = 0 fully replicates the t-test_P statistical tests for two waves of data (Voelkle, 2007) and yields asymptotically identical results. LCS models themselves fully replicate the repeated measures Anova and LGMs models and results, and additionally are much broader and capable to relax their assumptions (McArdle, 2009). We show how a more flexible LCS model with changes correlated with initial levels fully replicates the t-test_P, and moreover can be expanded to test more complex hypotheses of change.

We demonstrate our proposal with a dataset on changes in Hemoglobin A1c (HgA1c) levels among diabetics who participated in a quality improvement study using peer supporters (Phase II–Diabetes eCo-System, Villagra, 2013). HgA1c values range between 5 and 12% (HgA1c > 6.5% defines a diabetic patient, NGSP, 2013). Many studies reporting changes in HgA1c values use the t-test_P to test for significance of changes (e.g., Satoh-Asahara et al., 2013). Hence, we tested the changes in HgA1c in a group of diabetics using the t-test_P, and replicated these results in the LCS framework.

The key feature of the t-test_P is the computation of the sample average of differences (ΔY_21i = Y_2i − Y_1i) which is compared to zero, using an estimate of its standard error that accounts for the covariance between initial levels and changes. Because the t-test_P is testing the significance of Y₁ to Y₂ changes, a natural alternative is to directly specify the change score (Y₂ − Y₁ or ΔY₂₁) in a model of change. Because of known issues around the reliability of the change score (King et al., 2006) and estimation problems due to adding a variable that is a linear combination of two other variables in the same model, the LCS directly inserts the change score in a structural model, however, as a latent variable. Rewriting the ΔY₂₁ = Y₂ − Y₁ equation as LCS₂₁ = Y₂ − Y₁, one can define the true changes (McArdle and Nesselroade, 1994) with the multiple regression:

$$Y_2=0+1\ast Y_1+1\ast {\text{LCS}}_{21}+0$$

where we specifically indicate that the two regression coefficients are fixed to 1 (unity), and the intercept of Y₂ is set to zero, as are the mean and variance of the Y₂ residual error, i.e., the entire variance of Y₂ is explained by the true change LCS₂₁ (see Figure 1).

Figure 1.

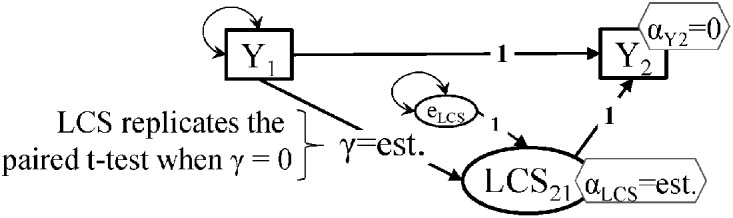
Structural modeling setup for the paired t-test model and the latent change score (LCS) model with self-feedback/mediation (SF/M). Notes: significance of Y₁ to Y₂ changes is captured by the α_LCS intercept; ‘est.’ means parameter is estimated by the model; intercepts are shown in hexagons, variances as double-headed arrows (covariance with itself); the key features of the LCS mode are: (1). No Y₂ residual error; (2). Intercept of Y₂ is set to zero; (3). The auto-regressive path is set to 1; the LCS to Y₂ path is set to 1.

While t-test_p statistical outputs from various software report the correlation between the two repeated measures, the role of this indicator of measure stability is not directly obvious in the t-test_P model. There are two ways in which one can incorporate stability information into the LCS model of change: by specifying a correlation between Y₁ and LCS₂₁ (like McArdle, 2001; Figure 16.3), or with a directed path from Y₁ to LCS₂₁. There is a clear difference in terms of the test of significance of changes in outcome Y between the two setups: the correlation specification tests the significance of the mean of the LCS₂₁ score and yields identical results with the t-test_P, while the γ path specification is testing the significance of the LCS₂₁ intercept; hence, differences in significance level will be observed.

The simple model in Figure 1 is asymptotically equivalent to the t-test_P, when Y₁ is correlated with LCS₂₁, or when the γ path is set to zero (in the directed path setup). The γ path has been called proportional growth (McArdle, 2009), immanent change (Coleman, 1968), self-feedback (McArdle, 2009), or self-mediation (Coman et al., 2013); we label it here as self-feedback/mediation (SF/M). It can be easily shown that the γ coefficient's absolute value is the complement (1 - ρ) of the common auto-regressive (AR1) path, or stability (Kenny, 1979, p. 287), from a simple lagged model Y₁ → Y₂ (Coman et al., 2013): when γ = 0, there is perfect stability (ρ = 1). When an outcome changes in level but under perfect stability (equivalent to the LCS model with zero SF/M), the knowledge of one's initial outcome value Y₁ means perfect prediction of his/her Y₂ follow-up value; the Y₂ intercept in this case tells us by how much Y increases (or decreases) uniformly across the entire sample, i.e., the change is the same in all persons/cases.

This particular case of perfectly stable outcomes is rarely found in real life. Change usually happens within some boundaries, and often those starting off higher on an outcome will change less. The likelihood of this hypothesis can be tested against the data however: since the more relaxed LCS model with SE/M path γ estimated has df = 0, directly forcing γ = 0 on the full LCS model tells us whether the assumption is reasonable or not: a significant χ² of the no-SF/M LCS model, or equivalently: a significant worsening of fit Δχ ²(1), tells us whether the “no SF/M link” hypothesis is tenable.

Results

We performed the t-test_P in MS Excel, then replicated it in the free AMOS 5 (Arbuckle, 2007) software, as a LCS model with Y₁ and LCS₂₁ correlated, then with Y₁ predicting LCS₂₁, then forcing γ = 0 (all our models and data are posted at http://trippcenter.uchc.edu/modeling). To be able to meaningfully compare the results, the outcomes were both centered on the HgA1c₁ mean, and thus the HgA1c₂ mean became −0.395. The t-test_P for significance of HgA1c changes in the diabetic patients (n = 97) indicates a mean of the paired differences of d = −0.395, SE = 0.182, t = −2.173, p = 0.032, and a paired sample correlation ρ = 0.566, p < 0.001. The LCS model with Y₁ and LCS₂₁ correlated yields similar results, whether the correlation is estimated or set to zero, d = −0.395, SE = 0.182, CR = −2.173 (critical ratio), p = 0.0297. The LCS with a SF/M path, however, yields a slightly lower p-value for the test of significance of changes, d = −0.395, SE = 0.171, CR = −2.307, p = 0.021. We note that the LCS model with no SF/M path (γ set to 0) indicated unacceptable misfit, χ ²(1) = 11.423, p = 0.001. This tells us that the path coefficient's γ = 0 constraint is not supported by data.

The difference between p-values from the models with the correlated initial level and changes vs. initial level predicting the changes occurs largely because the LCS model with SF/M path tests the significance of the HgA1c₂ intercept, i.e., the mean changes controlled for HgA1c₁.

To further illustrate our ideas, we re-tested the significance of the HgA1c reported in a recent study (Satoh-Asahara et al., 2013) for their control group (n = 24), from published summary data (means and variances), in the absence of reported information about the Y₁ - Y₂ correlation ρ. A re-test of the original classical paired t-test under the LCS setup replicated the original finding of a non-significant change, for a reasonable ρ = 0.50 correlation assumed between the two repeated measures. For higher values of ρ, however, the LCS t-test_P models began to indicate significant changes for ρ larger than.70; the LCS model with SF/M consistently yielded slightly lower p-values than the t-test_P, and showed significant changes, whereas the t-test_P did not, for ρ 's between 65 and 70.

Conclusions and recommendations

We showed how the classical paired t-test can be replicated in a SEM manner using LCS models, and illustrated the difference in results when one assumes an unexplained correlation between initial scores and changes, as opposed to initial scores predicting the changes. Between-individual and between-group differences in latent changes can be explained by various predictors in simple and more complex dynamical LCS models, hence the t-test_P replicated here as a LCS model with self-SF/M is a first step in building better models of change.

We suggest that researchers perform paired t-tests both in their classical form, which assumes that change is simply correlated with initial levels, and in their more realistic form, where a path from initial level to the LCS is specified. Both these LCS models can be freely replicated by all interested with our input models posted online, using the free version 5 of the AMOS software (Arbuckle, 2007) and summary (or raw) data entered in Microsoft Excel. The LCS setup introduced here allows for models explaining the variability in changes, by predictors like prior levels or even prior changes in other variables (), and can be expanded to more complex models, like recovering latent classes for which the change model differs markedly. One can model in other words heterogeneity in changes or of effects (with mixture LCS models, see AMOS example model online).

Any comparative tests of changes, as commonly performed for instance in Comparative Effectiveness Research (CER, Sox and Greenfield, 2009), can benefit from this accommodation of more flexible models supported by data. CER studies evaluate the success of interventions implemented in different conditions by comparing changes in different groups, like treatment and matched control, or different adaptations of the same intervention. In such multiple-group LCS models, the self-SF/M paths will likely differ also by group or condition, so there is increased chance of misspecification, because models assuming them to be equal or different will fit data better/worse. Estimates of differences in changes between groups will therefore depend on the specific pattern of changes in each group, revealed by the best fitting models. More research seems to be needed to see how the LCS with self-SF/M performs against the simple structural modeling extensions of the classical paired t-test.