Abstract
TAL (transcriptional activator-like) effectors (TALEs) are DNA-binding proteins, containing a modular central domain that recognizes specific DNA sequences. Recently, the crystallographic studies of TALEs revealed the structure of DNA-recognition domain. In this article, molecular dynamics (MD) simulations are employed to study two crystal structures of an 11.5-repeat TALE, in the presence and absence of DNA, respectively. The simulated results indicate that the specific binding of RVDs (repeat-variable diresidues) with DNA leads to the markedly reduced fluctuations of tandem repeats, especially at the two ends. In the DNA-bound TALE system, the base-specific interaction is formed mainly by the residue at position 13 within a TAL repeat. Tandem repeats with weak RVDs are unfavorable for the TALE-DNA binding. These observations are consistent with experimental studies. By using principal component analysis (PCA), the dominant motions are open-close movements between the two ends of the superhelical structure in both DNA-free and DNA-bound TALE systems. The open-close movements are found to be critical for the recognition and binding of TALE-DNA based on the analysis of free energy landscape (FEL). The conformational analysis of DNA indicates that the 5′ end of DNA target sequence has more remarkable structural deformability than the other sites. Meanwhile, the conformational change of DNA is likely associated with the specific interaction of TALE-DNA. We further suggest that the arrangement of N-terminal repeats with strong RVDs may help in the design of efficient TALEs. This study provides some new insights into the understanding of the TALE-DNA recognition mechanism.
Introduction
TAL (transcriptional activator-like) effectors (TALEs) are secreted by plant pathogenic bacteria that cause diseases in plants [1]–[3]. When TALEs are injected into plant cells, they enter the nucleus, bind to effector-specific sequences and manipulate host gene expression [3]–[5]. The DNA-binding domain of TALEs contains multiple (from 1.5 to 33.5), tandemly repeated units [3]. Each repeat comprises 33∼35 (mostly 34) amino acids and shows high sequence conservation except for the residues at position 12 and 13. The two residues, termed repeat-variable diresidues (RVDs), were found to determine DNA-binding specificity [6], [7]. A simple code was established between RVDs and target DNA bases [6], [7], like Asn/Ile (NI) for recognition of adenine (A), His/Asp (HD) for recognition of cytosine (C), Asn/Gly (NG) for recognition of thymine (T) and so on. On one hand, the TALE-DNA recognition code enables the prediction of DNA target sequences of TALEs [6]–[8]. On the other hand, by using this code TALEs can be customized more easily than other known DNA binding proteins to recognize desired DNA sequences [9], [10]. Engineered TALE proteins have been widely used to genome modifications, such as plants [11], [12] and animals (including humans) [13]–[15]. As a result, the DNA-binding domain of TALEs is considered to be an efficient tool for genetic editing [16], [17].
Because of the advantage from the modular nature of TALE-DNA binding, recently many studies focused on the recognition mechanism of TALE-DNA. In 2010, Murakami et al. reported the first structural data of TALE [18], which was a nuclear magnetic resonance (NMR) structure of 1.5 TAL repeats in the protein PthA. However, the length of 1.5-repeat effector is too short to provide more detailed structural data. In 2012, two groups [19], [20] separately published their structural studies of TALEs. The first group led by Shi et al. determined two crystal structures of an engineered 11.5-repeat TALE dHax3 in both DNA-bound and DNA-free states at 1.8 Å and 2.4 Å resolution, respectively [19]. The second group led by Stoddard crystallized a 3.0 Å structure of the naturally occurring TALE PthXo1 with 23.5 repeats bound to DNA [20]. The two groups both described that the repeats self-associate to form a right-handed superhelix and bind with the DNA major groove. In each repeat, the first residue of RVD (position 12) likely plays a structural role in stabilizing the RVD-containing loop for contacting with DNA, and the specific interaction of TALE-DNA is formed solely by the second residue of RVD (position 13). Recently, another two studies by Shi et al. demonstrated that TALE can also recognize modified bases [21] and bind with DNA-RNA hybrids [22]. The recognition efficiencies of different RVD types were investigated by several studies [23]–[25], strongly indicating that RVDs NN and HD contribute most to overall activities of TALEs. Additionally, some other issues were also frequently discussed, which included a reasonable model for TALE-DNA target search and the possible role of flanking elements in TALE [16], [20], [26], [27]. The N-terminal region was suggested to serve as an active site for DNA binding and subsequent target site recognition [27]. These crystallographic and biochemical studies provided a lot of important structural information about the sequence-specific recognition of DNA by TALEs.
In addition to experiments, theoretical approaches were also applied to explore the TALE-DNA recognition mechanism. Moscou et al. [7] developed a computational method to search DNA sequence for TALE target sites and decided the TALE-DNA recognition code. Cong et al. [28] performed the molecular dynamics (MD) simulations and free-energy perturbation (FEP) calculations to further analyze the guanine specificity of RVD Asn/His (NH). The simulations were based on a fragment of the crystal structure of TALE PthXo1 by Stoddard et al. [20]. By using the Rosetta package, Bradley designed the structural models to predict the interactions for the TALE-DNA system [29]. Additionally, a suite of software tools were provided to the efficient TALE design and target prediction [30], [31]. These works improve our understanding of the TALE-DNA interaction. Nevertheless, the crystal structures of TALE dHax3 by Shi et al. [19], in both DNA-free and DNA-bound states, have not been simulated systemically. The comparison of the two crystal structures revealed that the TALE undergoes a dramatic conformational change upon DNA interaction, which was consistent with the previous small-angle X-ray scattering (SAXS) data [18]. The TALE-bound DNA was found largely in the B-form [19], [20]. Meanwhile, the protein-induced deformability of DNA was often linked to the specific recognition of DNA sequences and transcription activation [32]–[35]. Thus, some detailed questions still need to be solved. What interactions at atomic level are formed between the TALE and the DNA? How do the TALE dynamics affect the recognition and binding of TALE-DNA? Does the DNA have the structural deformability when binding with the TALE? Are there any correlations between the structural change of DNA and the sequence-specific recognition by TALE?
In this paper, in order to answer the above questions, the crystal structures of both DNA-free and DNA-bound TALE dHax3 were analyzed by MD simulations. We investigated the interactions between 11.5 TAL repeats and the DNA, and compared the TALE-DNA interactions from different TAL repeats. In addition, principal component analysis (PCA) and free energy landscape (FEL) methods were applied to probe the functional motions of TALEs and identify the dominant conformational states, respectively. Finally, we calculated the structural deformability of the TALE-bound DNA at the base-pair level, and further suggested the association between the conformational change of DNA and the specific interaction of TALE-DNA.
Systems and Methods
The Structures of DNA-free and DNA-bound dHax3 Systems
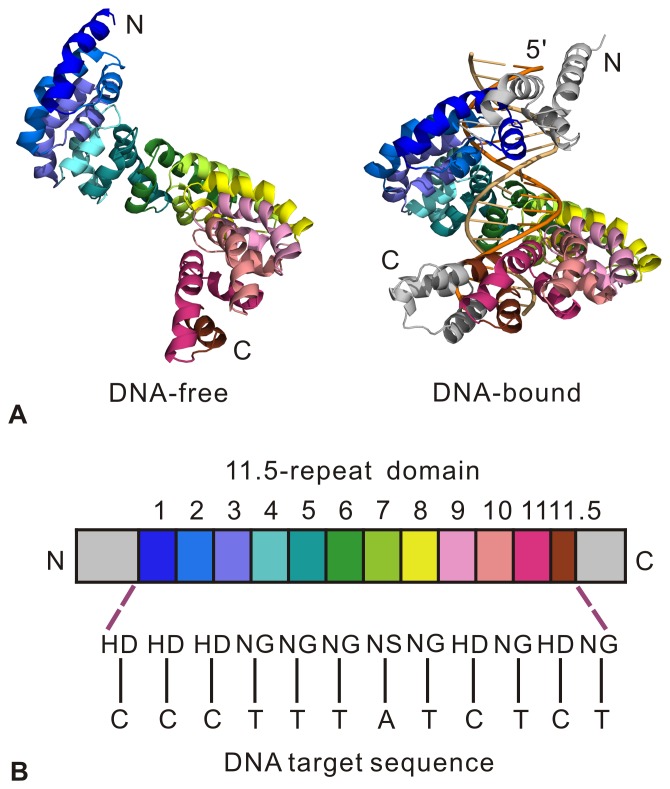
The two crystal structures of DNA-free and DNA-bound dHax3 (PDB codes: 3V6P and 3V6T) [19] each contain an 11.5-repeat TALE (see Figure 1 A). The 11.5 TAL repeats form a right-handed superhelical assembly. The DNA-free dHax3 possesses an extended conformation while that of DNA-bound dHax3 is more compact. In the DNA-bound structure, the superhelix wraps itself along the sense strand of DNA duplex and binds in the major groove of DNA. The 11.5-repeat domain confers DNA sequence specificity, with RVD residues of each repeat recognizing one specific nucleotide (see Figure 1 B).
Figure 1. Structures and domain organization (PDB codes: 3V6P and 3V6T).
(A) The structures of dHax3 in the DNA-free state (left) and DNA-bound state (right). Each structure contains an 11.5-repeat domain, forming a right-handed superhelical assembly. The 11.5 repeats are colored separately. (B) The 11.5-repeat domain mediates DNA binding. Each repeat recognizes one specific nucleotide by using the RVD residues at positions 12 and 13. Single-letter abbreviations for the amino acid residues are as follows: A, Ala; C, Cys; D, Asp; E, Glu; F, Phe; G, Gly; H, His; I, Ile; K, Lys; L, Leu; M, Met; N, Asn; P, Pro; Q, Gln; R, Arg; S, Ser; T, Thr; V, Val; W, Trp; and Y, Tyr.
Molecular Dynamics Simulation
The two simulation systems were set up by VMD 1.9 [36]. Each initial structure was placed in a cubic periodic box filled with TIP3P water molecules. The minimum distance was about 10 Å from the solute unit to the edge of the box. To achieve electroneutrality, 2 Cl− and 29 Na+ ions were added to the DNA-free and DNA-bound systems, respectively. Then, the two MD simulations were carried out with the NAMD 2.6 program [37] using the CHARMM27 all-atom additive force field for nucleic acids [38]. The SHAKE algorithm [39] was used to constrain all bonds involving hydrogen atoms, and particle mesh Ewald (PME) [40] method was applied to evaluate electrostatic interactions. Meanwhile, Lennard-Jones interactions were cut off at 12 Å. Each simulation included two stages. (i) The systems were energetically minimized with 20000 steps and then slowly heated over 0.5 ns from 0 K to 310 K. The positions of dHax3 and DNA were restrained with a harmonic constant of 0.1 kcal·mol−1·Å−2 to keep the stabilization of systems. (ii) The production runs of 20 ns were carried out for each unrestrained system under constant pressure (1 atm) and temperature (310 K) conditions. The pressure and temperature were controlled by the Langevin piston method [41]. The atomic coordinates were saved every 2.0 ps and thus 10000 structures were collected in each system for further analysis.
Principal Component Analysis
Principal component analysis (PCA) can provide a brief picture of motions, which exacts the highly correlated fluctuations from the MD trajectories by applying the dimensionality reduction method. This method is based on the calculation and diagonalization of the covariance matrix. The elements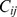 
in the matrix are defined by [42]:
 |
(1) |
where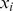 
(
) is the coordinate of the 
th(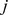
th) atom of the systems, and 
indicates an ensemble average. The eigenvectors (also called the principal modes) of the matrix represent the directions of the concerted motions and the eigenvalues indicate the magnitude of the motions along the direction. Usually, the first few principal components (PCs) describe the most important slow modes of the system, which are related to the functional motions of a biomolecular system [43], [44]. In this article, PCA was performed with Gromacs 4.5 package [45] in order to investigate and compare the functional motions of DNA-free and DNA-bound dHax3.
Free Energy Landscape
Free-energy landscape (FEL) can promote our understanding of biomolecular processes such as molecular recognition, folding and aggregation [42], [44]. The free-energy minima represent the conformational ensemble in stable states which are accessible to a biomolecule under physiological conditions. And the free-energy barriers denote the transient states connecting them. The FEL can be constructed on the basis of PCA [42]. The corresponding expression is
 |
(2) |
where 
and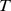 
are the Boltzmann constant and absolute temperature, 
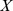stands for the PCs and thus 
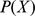is the probability distribution of the molecular system along the PCs. In our study, we calculated the FEL to identify the dominant conformational states with relatively lower energies.
Conformational Analysis of Nucleic Acids
Curves is a widely used nucleic acid conformational analysis program [46]. The program provides a full analysis of DNA structure, including base pair-axis parameters, intra-base and inter-base pair parameters, backbone and groove parameters, etc. In our study, 1000 snapshots were extracted from 20 ns dynamics by sampling every 20 ps. The following parameters were analyzed to describe the DNA structural deformability, including axis bend angles, slides, roll angles, twist angles, rises and groove widths.
Results and Discussion
Convergence Behavior of the Two MD Simulations
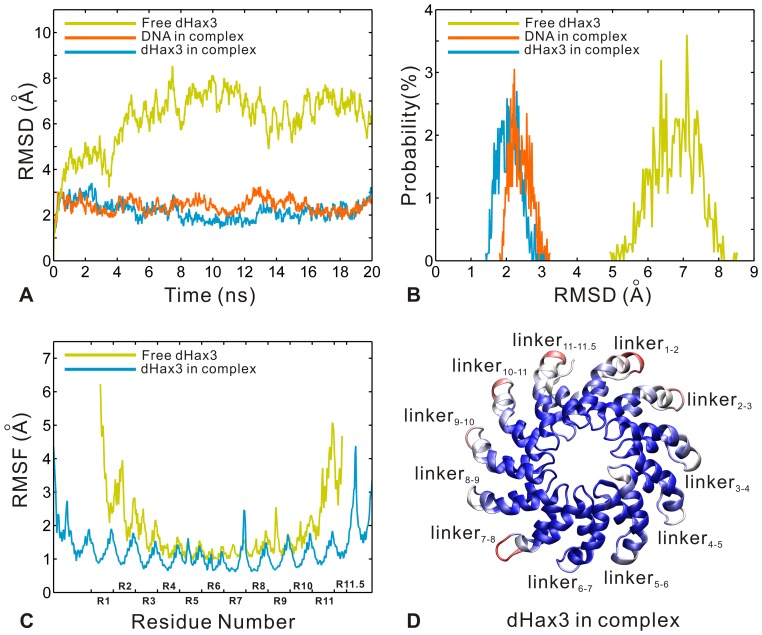
Through 20 ns MD simulations, the systems reached equilibrium by checking the evolutions of potential energies, temperatures and volumes versus time (see Figure S1). The root-mean-square deviation values (RMSDs) were calculated over the dHax3 and DNA backbone atoms relative to the initial structures, and the results are shown in Figure 2 A. The last 15 ns and 17 ns MD trajectories remain comparatively stable and then are taken as the equilibrium portions for the DNA-free and DNA-bound systems, respectively. In view of previous MD studies of protein-DNA [47], [48], this simulation protocol is proper to describe the two systems. Figure 2 B displays the distributional probability of RMSD from the equilibrium trajectories in the two systems. The RMSDs converge to about 2.09 Å, 2.39 Å, and 6.76 Å for the dHax3 in complex, the DNA in complex and the free dHax3, respectively. The RMSDs of the DNA-bound system are significantly lower than those of the DNA-free system. It indicates that the TALE dHax3 is well constrained in the DNA-bound system. The conformational changes along the simulation trajectories are shown in Movie S1 and S2 for the DNA-free and DNA-bound systems, respectively. The detailed mechanism of dHax3 and DNA will be analyzed in the following sections.
Figure 2. Comparative MD analysis of DNA-free dHax3 (yellow) and DNA-bound dHax3 (dHax3: sky blue; DNA: orange) systems.
(A) The RMSD values of the dHax3 and DNA backbone atoms versus simulation time. (B) The probability distribution of RMSD calculated from the equilibrium trajectories. (C) The RMSF values of the dHax3 Cα atoms calculated from the equilibrium trajectories. (D) The cartoon representation of 11.5 TAL repeats for the dHax3 in the DNA-bound system. The residues in red have relatively higher RMSF values (>1.8 Å) while the ones in blue have relatively lower RMSF values (<1 Å). The other regions are colored white.
Furthermore, we also calculated the root-mean-square fluctuation (RMSF) values for Cα atoms of dHax3 from the equilibrium trajectories in the two systems. The result is shown in Figure 2 C, where 11.5 TAL repeats are labeled as R1 to R11.5, respectively. The comparison of RMSF values reveals the markedly reduced fluctuations of the dHax3 in complex (sky blue) relative to the DNA-free dHax3 (yellow). From DNA-free to DNA-bound states, the fluctuation decrease of dHax3 shows two important characteristics. One is that the RVD loop region has less fluctuation than other parts of the repeat. The other is that the two ends of tandem repeats contribute most to the reduction in the fluctuations. Previous studies [19], [20], [29] described that the RVD loop regions in TAL repeats are the DNA binding sites. In the DNA-bound system, almost all RVD loop regions show decreased RMSF values while all linkers between two adjacent TAL repeats still maintain relatively higher RMSF values (see Figure 2 C). The fluctuation decrease in the RVD loop regions implies the importance of the specific binding of TALE-DNA to the system stability. Meanwhile, more remarkable decreases of RMSF values are found in the two ends than the middle of tandem repeats (see Figure 2 C). It indicates that the TALE-DNA binding of the two ends has more contributions to the system stability than that of the middle. In the structure of dHax3, most of the repeats with RVDs HD locate at the ends of the 11.5-repeat effector (see Figure 1 B). RVDs HD were considered to be efficient for the specific recognition of DNA sequence, which are important to the overall TALE activity [24]. Thus, the contribution to the system stability may be associated with the RVD efficiency of the specific recognition. Notably, the linker between repeat 7 and repeat 8 (abbreviated as linker7–8) exhibits an increase in RMSF values in the DNA-bound system compared with the DNA-free system (see Figure 2 C). In order to intuitively observe the fluctuations in the DNA-bound system, 11.5 TAL repeats of the dHax3 are colored according to the RMSF values. The regions with high RMSF values are shown in red (see Figure 2 D). In the crystal structure, the linker7–8 exhibits a slightly loose structure and the other linkers display a relatively more regular helix conformation. The conformational difference leads to the higher RMSF values of the linker7–8. The rest of red regions locate at the linker1–2, linker2–3, linker10–11 and linker11–11.5. Therefore, it is speculated that the dHax3 may possess an important conformational change at the ends of the superhelical structure.
Interactions between the dHax3 and the DNA
The crystallographic study [19] revealed that there are both direct and water-mediated hydrogen bonds in the DNA-bound dHax3 structure. They mediate the important interactions in the TALE-DNA binding. Furthermore, the direct hydrogen bonds can be classified into two types: the specific interaction between amino acid and DNA base; and the nonspecific interaction between amino acid and DNA backbone [49]. Then, we examined the hydrogen bonds between 11.5 TAL repeats and the DNA from the equilibrium trajectory of the DNA-bound system. The hydrogen bonds were calculated by VMD 1.9 [36] with a distance cut-off value of 3.5 Å and an angle cut-off value of 35°. The results are listed in Table 1 (direct hydrogen bonds) and Table 2 (water-mediated hydrogen bonds) with occupancy over 40%. The atom OD1 (OD2) of the residue ASP13 in repeats 1, 2 and 9 (containing RVD HD) accepts a hydrogen bond from the atom N4 of base C. The atom OG of the residue Ser13 in repeat 7 (containing RVD NS) also donates a hydrogen bond to the atom N7 of base A (see Table 1). These base-specific hydrogen bonds are important for the recognition of base C by RVD HD and the recognition of base A by RVD NS [50]. The base T is usually recognized by RVD NG [3], [19], [20], however, no base-specific hydrogen bond is found between bases T and residues Gly13 in all repeats with RVDs NG. Relative to the base C, the base T needs sufficient space to accommodate its 5-methyl group. Due to the lack of side chain in glycine, Gly13 can provide enough space to the base T and make a van der Waals contact with the 5-methyl group of base T [19]. In contrast, any other residues with a side chain at position 13 may introduce steric clash with the base T. Thus, the van der Waals interaction plays a key role in the recognition of base T by RVD NG. Consequently, the efficiency of HD (strong RVD) is considered to be higher than that of NG (weak RVD) [24]. In addition, the residues at position 13, 14, 16 and 17 in the repeats are involved in the phosphate binding with the DNA backbone (see Table 1 and 2). The 17th residue forms direct hydrogen bonds with the phosphate group of DNA. The 13th, 14th and 16th residues form water-mediated hydrogen bonds with the phosphate group of DNA. These nonspecific hydrogen bonds are helpful to the structural stability of the DNA-bound system. The above observed interactions are in agreement with experimental data [19]. Interestingly, although repeat 11.5 is a truncated repeat with only containing the first 20 residues, the half repeat still forms relatively stronger nonspecific interactions with the DNA backbone (see Table 1 and 2). It is suggested that the last half repeat of TALE makes an important contribution to the system stability.
Table 1. TALE-DNA direct hydrogen bonds in 11.5 repeats with occupancy over 40%.
| Repeat | TALE (Residue id*) | Sense-strand DNA base | Occupancy |
| 1 | D301-OD2 (13) | C1-N4 | 47.76% |
| 2 | D335-OD1 (13) | C2-N4 | 49.88% |
| 4 | Q407-NE2 (17) | C3-O1P | 79.65% |
| 6 | Q475-NE2 (17) | T5-O1P | 52.35% |
| 7 | S505-OG (13) | A7-N7 | 66.59% |
| Q509-NE2 (17) | T6-O1P | 72.59% | |
| 8 | Q543-NE2 (17) | A7-O2P | 58.82% |
| 9 | D573-OD1 (13) | C9-N4 | 50.94% |
| Q577-NE2 (17) | T8-O1P | 74.35% | |
| 10 | Q611-NE2 (17) | C9-O1P | 62.12% |
| 11 | Q645-NE2 (17) | T10-O1P | 84.59% |
| 11.5 | R678-NE (16) | C11-O1P | 90.24% |
| R678-NH2 (16) | C11-O1P | 42.82% |
Residue id* is the index of a residue in each TAL repeat sequence. The specific interactions are in bold while non-bold denotes nonspecific interactions.
Table 2. Water-mediated hydrogen bonds in 11.5 repeats with occupancy over 40%.
| Repeat | TALE (Residue id*) | Sense-strand DNA base | Occupancy |
| 2 | G336_O (14) | C2_O2P | 53.18% |
| 3 | K372_N (16) | C2_O2P | 89.29% |
| D369_O (13) | C3_O2P | 78.24% | |
| G370_N (14) | C2_O2P | 53.06% | |
| D369_OD1 (13) | T4_O4 | 47.65% | |
| 4 | K406_N (16) | C3_O2P | 92.94% |
| G403_O (13) | T4_O2P | 54.24% | |
| 5 | K440_N (16) | T4_O2P | 55.41% |
| 7 | G506_N (14) | T6_O2P | 73.53% |
| S505_O (13) | A7_O1P | 50.35% | |
| K508_N (16) | T6_O2P | 57.06% | |
| 8 | K542_N (16) | A7_O1P | 90.82% |
| G539_O (13) | T8_O2P | 74.47% | |
| G540_N (14) | A7_O1P | 44.00% | |
| 9 | K576_N (16) | T8_O2P | 93.53% |
| D573_O (13) | C9_O2P | 73.41% | |
| G574_N (14) | T8_O2P | 66.71% | |
| 10 | K610_N (16) | C9_O2P | 88.24% |
| G607_O (13) | T10_O2P | 70.24% | |
| 11 | K644_N (16) | T10_O2P | 91.29% |
| D641_O (13) | C11_O2P | 70.24% | |
| 11.5 | R678_N (16) | C11_O2P | 93.18% |
| G676_O (14) | T12_O2P | 83.18% |
Residue id* is the index of a residue in each TAL repeat sequence.
Previous study [24] revealed that tandem weak repeats (containing RVDs NG or NI) can compromise TALE function. In this study, RVDs NG locate in repeats 4, 5, 6, 8, 10 and 11.5. According to the above analysis, Gly13 in repeats with RVDs NG forms a van der Waals interaction with the corresponding base T. It is required for the recognition of base T by RVD NG. Thus, we investigated the distance between the Cα of Gly13 and the 5-methyl group of base T for each repeat with RVD NG. Table 3 provides the distance data between them in repeats 4, 5, 6, 8, 10 and 11.5, including initial distances, average distances and distance deviations. The distances of repeats 5 and 6 increase remarkably than those of other repeats. It implies that the repeats 5 and 6 have weak van der Waals interactions relative to repeats 4, 8, 10 and 11.5. Meanwhile, repeats 4, 8, 10 and 11.5 form three or four hydrogen bonds with the phosphate group of bases C3, A7, C9 and C11, respectively (see Table 1 and 2). In comparison, repeats 5 and 6 only have one hydrogen bond with the phosphate group of bases T4 and T5, respectively. Collectively, the TALE-DNA interactions in repeats 5 and 6 are weaker than those in repeats 4, 8, 10 and 11.5. As shown in Figure 1 C, the predecessors of repeats 4, 8, 10 and 11.5 contain RVDs HD or NS while those of repeats 5 and 6 still include RVDs NG. Therefore, tandem weak RVDs (like NG) are unfavorable for the association between TALE and DNA. Our study supports the recommendation of avoiding stretches of weak RVDs in TALE design [24].
Table 3. Distances between the Cα of G13 and the 5-methyl group of thymine in all repeats with RVDs NG.
| Repeat | DInitial a | DAverage b | ΔDc |
| 4 | 3.68 | 3.98 | 0.30 |
| 5 | 3.64 | 4.88 | 1.24 |
| 6 | 5.26 | 7.93 | 2.67 |
| 8 | 3.79 | 3.85 | 0.06 |
| 10 | 3.61 | 3.98 | 0.37 |
| 11.5 | 3.88 | 4.12 | 0.24 |
All distances are measured in the unit of Å.
DInitial is the distance from the crystal structure.
DAverage is the mean value of distances from the equilibrium trajectory.
ΔD describes the deviation between DInitial and DAverage.
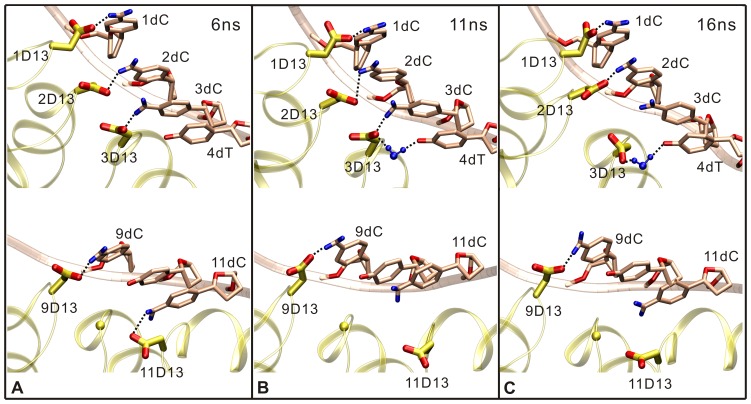
Notably, the interactions between the repeats containing RVDs HD and the DNA are found to vary according to the different positions in the effector. Figure 3 describes the change of specific interactions between the DNA bases and the residues Asp13 in the repeats containing RVDs HD (1, 2, 3, 9 and 11). Repeats 1 and 2, as the beginning of tandem repeats, form the specific interactions with DNA bases C1 and C2, respectively. However, they have less phosphate interactions with the DNA backbone, especially none for repeat 1 (see Table 1 and 2). The residue Asp13 in repeat 3, rather than directly interacting with the atom N4 of base C3 (with occupancy 26.82%), prefers to form a water-mediated hydrogen bond with the atom O4 of base T4 (with occupancy 47.65%). Repeat 9, that locates relatively near the middle of tandem repeats, forms a base-specific hydrogen bond with base C9. Meanwhile, it also maintains the stable phosphate binding with the DNA (see Table 1 and 2). In contrast to repeat 1, repeat 11 at the end of tandem repeats loses the specific hydrogen bond with base C11 (see Figure 3 B and C) and only has the stable phosphate binding with the DNA (see Table 1 and 2). The changes of interactions occur frequently at the head and tail of tandem repeats, which may be related to the functional motions of TALE dHax3.
Figure 3. The change of the specific hydrogen bonds between the TAL repeats and DNA bases at 6(A), 11 ns (B) and 16 ns (C) in the DNA-bound system.
The TAL repeats (yellow), DNA (pink) and water (blue) are depicted with ribbons, tube and CPK models, respectively. During the simulation, 1D13 (the residue Asp13 in repeat 1), 2D13, and 9D13 kept the specific hydrogen bond with 1dC (the base C1 in the DNA target sequence), 2dC, and 9dC, respectively. However, 11D13 lost the specific hydrogen bond with 11dC after 6 ns. Interestingly, 3D13 firstly interacted with 3dC (A). At 11 ns, 3D13 also formed water-mediated hydrogen bond with 4dT (B). Finally, 3D13 only indirectly contacted with 4dT (C).
Slow Modes of the Motions
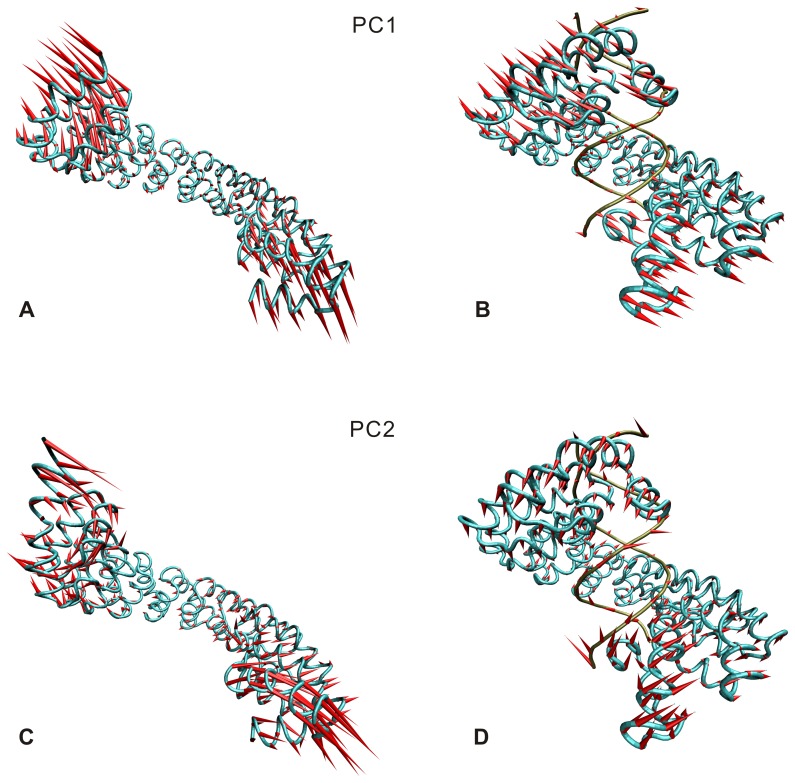
In order to inspect the functional motions of superhelical structure, the PCA analysis was performed for Cα atoms of 11.5 repeats and P atoms of DNA based on the equilibrium trajectories. Figure 4 compares the first and second slowest motion modes of the DNA-free and DNA-bound systems. Similar slow modes are evident in the two systems: the first slowest motion mainly appears as the open-close movements between the two ends of the superhelical structure (see Figure 4 A and B); the second slowest motion shows a twisting around each end (see Figure 4 C and D). In view of the similar motion modes in the DNA-free and DNA-bound systems, the slow motions of two ends are likely to be the intrinsic property of dHax3. It may be associated with TALE function. In addition, the DNA also shows similar but weakened motion trend to the dHax3 in the DNA-bound system.
Figure 4. The first and second slowest motion modes of the DNA-free system (A and C) and DNA-bound system (B and D).
The length of cone is positively-correlated with motive magnitude, and the orientation of cone indicates motive direction. The two systems have the similar slow motions. The first slowest motion mainly appears as the open-close movements between the two ends of the superhelical structure (A and B). The second slowest motion shows a twisting around each end (C and D).
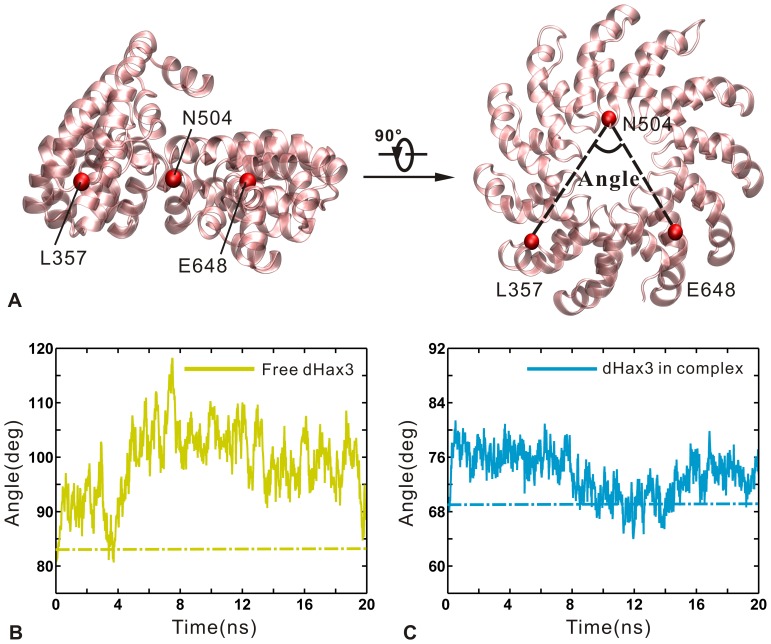
For evaluating the open-close movements in the first slowest motion mode, we define an intramolecular angle to measure the conformational changes. The angle is formed by the three atoms: the Cα atoms of Leu357 (repeat 3), Asn504 (repeat 7) and Glu648 (repeat 11), which are selected from the beginning, middle and end of the superhelical structure, respectively (see Figure 5 A). In the DNA-free system, the angle increases from the initial value about 81° to the maximum value about 115° before 7 ns. Then, the angle rapidly drops down to 100°. After 8 ns, it shows the slightly decreasing trend and fluctuates around 97° (see Figure 5 B). In the DNA-bound system, the angle keeps stable about 76° before 8 ns. From 8∼15 ns, the angle markedly decreases to 64° and then rises back again. After 15 ns, the angle remains about 74° until the end of the simulation (see Figure 5 C). Due to the constraints from the DNA, the angle of DNA-bound dHax3 shows a lower value and a narrower fluctuation range than that of the DNA-free dHax3. Notably, in the two systems the values of intramolecular angle show a positive correlation with the RMSDs of the dHax3 backbone atoms during 20 ns simulation time. Specially, their correlation coefficients are 0.79 for the DNA-free system and 0.64 for the DNA-bound system (see Figure S2 A and B). It indicates that the open-close movements have a major influence on the system stability.
Figure 5. Representation of the intramolecular angle and changes of the angles in the DNA-free and DNA-bound systems.
(A) The cartoon representation of 11.5 TAL repeats, with the intramolecular angle being defined by the Cα atoms of L357 (Leu357), N504 (Asn504) and E648 (Glu648). (B) The intramolecular angle change versus simulation time (solid line) and the value from crystal structure (dotted line) for the DNA-free dHax3. (C) The intramolecular angle change versus simulation time (solid line) and the value from crystal structure (dotted line) for the DNA-bound dHax3.
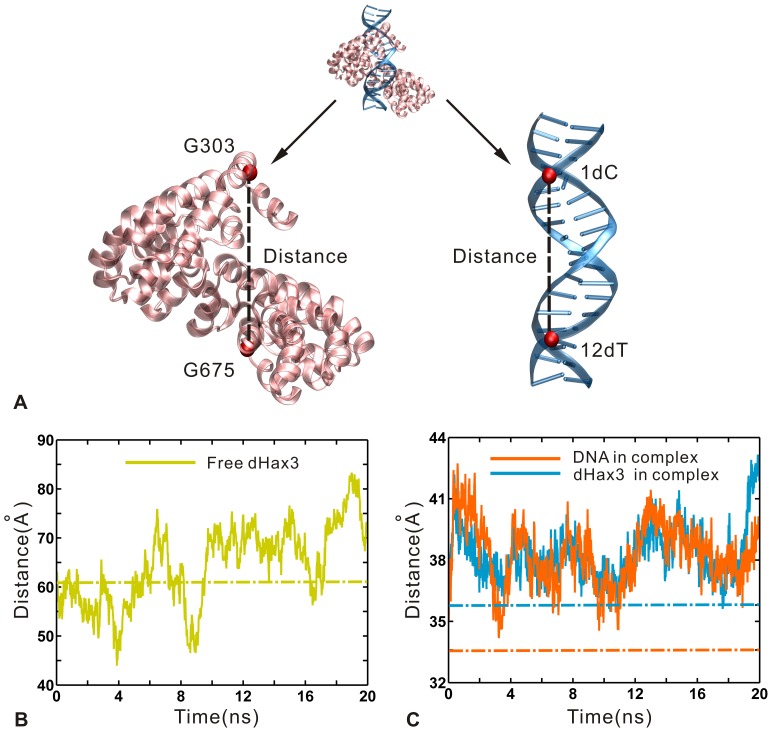
The crystallographic study [19] showed a remarkable difference between the superhelical pitch of DNA-free dHax3 (about 60 Å) and that of DNA-bound dHax3 (about 35 Å). During the simulation, the slow motions are also found to cause the visible change of superhelical pitch. In this study, the pitch change is assessed by the distance between the Cα atoms of Gly303 (repeat 1) and Gly675 (repeat 11.5) for the dHax3, and by the distance between the C3′ atoms of C1 and T12 for the DNA, respectively (see Figure 6 A). In the DNA-free system, the distance fluctuates between 45 Å and 80 Å (see Figure 6 B). In the DNA-bound system, the dHax3 and DNA have the similar distance fluctuation range from 35 Å to 43 Å (see Figure 6 C). On one hand, relative to the DNA-free dHax3, the DNA-bound dHax3 is remarkably compressed by the constraint from the DNA. On the other hand, the DNA is also observed to be pulled by the DNA-bound dHax3 in comparison with the crystal value (see Figure 6 C). Thus, the distance of DNA changes along with that of the dHax3 in the DNA-bound system. Notably, the large fluctuations in distance correspond to the frequent changes of the superhelical pitch. It exhibits a dramatic conformational plasticity of effector, which is likely important for the function of TALEs [18], [19].
Figure 6. Representation of the superhelical pitches and changes of the distances in the DNA-free and DNA-bound systems.
(A) The cartoon representation of 11.5 TAL repeats and the DNA. The superhelical pitch of dHax3 is assessed by the distance between the Cα atoms of G303 (Gly303) and G675 (Gly675) (left), and the pitch of DNA by the distance between the C3′ atoms of 1dC and 12dT (right). (B) The distance change versus simulation time (solid line) and the value from crystal structure (dotted line) in the DNA-free system. (C) The distance change versus simulation time (solid line) and the value from crystal structure (dotted line) in the DNA-bound system.
Functional Conformation Changes of dHax3
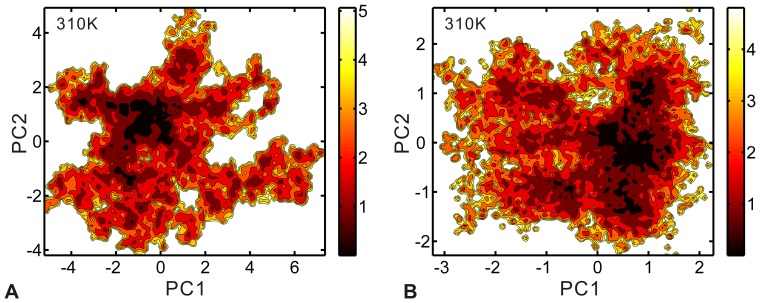
The PCA analysis reveals that the slow motions lead to remarkable conformational changes of dHax3. Then, we further investigated the distribution of conformations along the PCs. Figure 7 displays the free energy contour maps of the two systems at 310 K, with deeper color indicating lower energy. In the DNA-free system, the local minima approximately in the upper left of the FEL (see Figure 7 A). The minima mainly correspond to the conformations from 9∼13 ns and 16∼18 ns (see Figure S3 A). Relative to the DNA-free system, there are more local minima in the DNA-bound system (see Figure 7 B). They are almost in the right of the FEL, of which the largest one lies in the lower right. These minima include the conformations from 4∼8 ns and 15∼20 ns (see Figure S3 B). In the two systems, these stable conformations are almost characterized by a relatively stable intramolecular angle (see Figure 5 B and C). In the DNA-free system, the conformations in the local basin have an intramolecular angle around 100°. In the DNA-bound system, the intramolecular angle values of the local basin are about 75°. It is consistent with the important influence of open-close movements on the system stability in the above PCA analysis.
Figure 7. Free energy contour map versus the principal components PC1 and PC2 at 310-free system (A) and DNA-bound system (B).
Deeper color indicates lower energy.
Compared with the crystal values (DNA-free: 69.1°; DNA-bound: 83.2°), the dHax3 in the two systems is more stable with a more open intramolecular angle when it is relaxed in solvent environment. Meanwhile, there is an important open-close conformational change between the DNA-free and DNA-bound dHax3 systems. The intramolecular angle of the DNA-free dHax3 is always higher than 80° and that of the DNA-bound dHax3 is almost lower than 80°. The conformational plasticity of TALE has been considered to be important for TALE function [18], [19]. Compared with the DNA-bound TALE, the DNA-free TALE presents a relatively more extended and unwound conformation [18], [19], which was suggested to be required for a DNA target search by the unbound TALE [51]. We further speculate that a more open intramolecular angle higher than 80° (for example 100°) is necessary for the DNA target search in the DNA-free TALE. After binding with the target sequence of DNA, the TALE needs to form close contacts with the DNA. Then, it decreases the intramolecular angle to less than 80° (for example 75°). The conformational change of dHax3 is induced by the DNA binding, which is suggested to be an essential step in the TALE-DNA recognition.
Structural Deformability of DNA
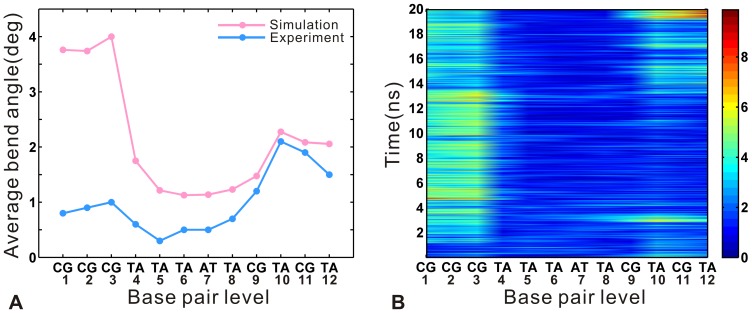
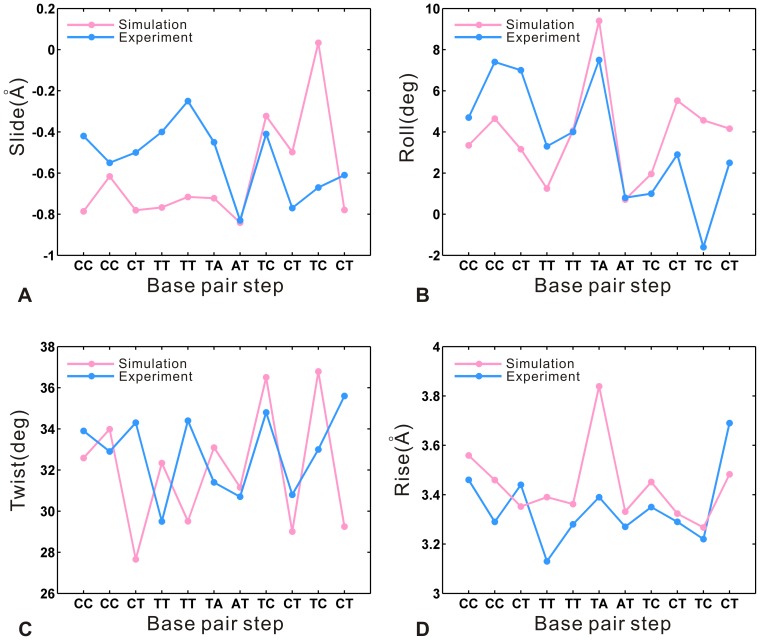
The deformability of DNA plays an important role in the biological processes [32]–[35]. Then, it is necessary to analyze the flexibility of DNA at the base-pair level. The DNA structural parameters are calculated for the DNA target sequence (C1-C2-C3-T4-T5-T6-A7-T8-C9-T10-C11-T12). The previous study [52] indicated that DNA bending is an important structural feature in protein-DNA recognition. Figure 8 A compares the mean bend angle from the equilibrium trajectory with the crystal values along the DNA target sequence. The mean angle shows an increase at all target sites, especially remarkable at the 5′ end (C1-C2-C3). Figure 8 B describes the time evolution (on the vertical axis) of the axis bends (on the horizontal axis) at all base pair steps. During the last 6 ns, the bend angle values of the sites at the 5′ end and 3′ end (T10-C11-T12) are higher than those of the middle sites along the target sequence. It indicates the two ends have a higher bending degree relative to the middle parts. Meanwhile, the DNA bending is associated with the roll and slide of inter-base-pair, for example, the negative values of slide appear with DNA bending into the major groove where roll is positive [53]. Then, Figure 9 compares the average DNA structural step parameters from the equilibrium trajectory with the crystal values, including slide, roll angle, twist angle and rise. As shown in Figure 9 A and B, the bending of DNA is accompanied by the negative slide and positive roll angles. Thus, the DNA sequence shows the increased major groove bending, with higher bend angle values at the ends (see Figure 8 B). The comparison of twist angle is presented in Figure 9 C, where the simulated result shows the decreasing tendency with the average value of 32° relative to 33° in the crystal structure. The previous study [53] indicated that the double helix tends to overwind at the sites of minor groove bending and to underwind at the sites of major groove bending. Meanwhile, overwinding of the helix increases the twist angle and underwinding decreases it [54]. Thus, the reduced twist is associated with the increased major groove bending degree, especially at the sites of the first half of DNA target sequence. Moreover, as shown in Figure 9 D, the rise from the simulated result increases compared with the crystal values. It corresponds to the growth of the distance between the two ends of the DNA target sequence (see Figure 6 C). Altogether, compared with the other positions along the target sequence, the 5′ end is significantly distorted with a more remarkable increase of bend angle and higher bend angle values. The observation suggests that the efficiency of specific recognition is higher at the 5′ end than the other sites along the target sequence.
Figure 8. Changes of axis bend angles along the DNA target sequence.
(A) Comparison of the average values (pink) of the axis bend calculated from the equilibrium trajectory along the d(CCCTTTATCTCT) with the corresponding crystal values (sky blue). (B) Fluctuations of axis bend for all dinucleotide steps along the d(CCCTTTATCTCT) during 20 ns trajectory. The color bar gives the variations in bend from 0° (dark blue) to 10° (dark red).
Figure 9. Comparison of the average values (pink) of base pair step parameters calculated from the equilibrium trajectory along the d(CCCTTTATCTCT) with the corresponding crystal values (sky blue).
(A) Slide. (B) Roll angle. (C) Twist angle. (D) Rise.
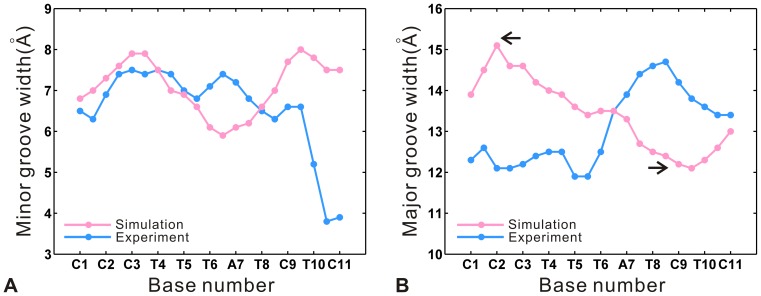
The width of DNA grooves is also an important parameter of DNA structure, which is often correlated with protein-DNA interactions [55], [56]. Figure 10 A and B display the comparison of the average groove widths from the equilibrium trajectory with the crystal values. There are remarkable variations in groove widths at the ends along the target sequence, including the increase of major groove widths at the 5′ end and that of minor groove widths at the 3′ end (see Figure 4 B). The major groove is widened by about 3 Å at the sites of C1-C2-C3 (see Figure 10 B), and the minor groove widths are also increased by about 3.5 Å at the sites of bases C9-T10-C11 (see Figure 10 A). Meanwhile, an opening of the minor groove is often associated with the compression of the major groove [46], [57]. Thus, a decrease of about 2.5 Å in major groove widths occurs at the sites of T8-C9-T10 (see Figure 10 B), which corresponds to the increase of about 3.5 Å in the minor groove widths at the sites of C9-T10-C11. Previous studies [58], [59] indicated that minor groove is narrower in AT-rich central regions (of four or more successive AT base pairs) compared to GC-rich regions. Consequently, our result indicates that the minor groove is compressed by 1.5 Å at the central site of T4-T5-T6-A7-T8 segment relative to the crystal values. Notably, the bases C2 and C9 have more remarkable widths variations in the major groove (see Figure 10 B). By comparing the hydrogen bonds at different sites along the target sequence, it is found that C2 and C9 form relatively stronger specific interactions of TALE-DNA (see Table 1). Although the base A7 also forms one high occupancy hydrogen bond with the residue Ser13 in repeat 7, the interaction previously was designated as nonspecific because NS is nonselective to recognize all four bases [6]. Then, the specific interaction of TALE-DNA is likely favorable for the variations of major groove widths. Further, the sites at the 5′ end of DNA target sequence form more specific interactions than those at the 3′ end (see Figure 3). Correspondingly, the 5′ end shows higher bend angle and more variations in the major groove than the 3′ end (see Figure 8 A and 10 B). It is suggested that the conformational change of DNA is associated with the specific interaction of TALE-DNA. Meanwhile, the 5′ end has more remarkable structural deformability relative to the 3′ end, which also indicates that the N-terminal repeats have more contributions to the specific recognition of TALE-DNA than the C-terminal ones. It is consistent with the previous experimental study [25] that N-terminal repeats are more important to the overall affinity than C-terminal ones. Therefore, we suppose that the arrangement of N-terminal repeats with strong RVDs (that can form specific hydrogen bond with DNA bases, like HD) may be helpful to the efficient design of customized TALEs.
Figure 10. Comparison of the average values (pink) of groove widths calculated from the equilibrium trajectory along the d(CCCTTTATCTCT) with the corresponding crystal values (sky blue).
(A) Minor groove widths. (B) Major groove widths. The widening of the major groove is more remarkable at the sites of C2 and C9.
Conclusions
In this study, MD simulations were performed to investigate the TALE-DNA recognition mechanism. The simulated results indicate that the fluctuations of DNA-bound dHax3 are reduced significantly relative to the DNA-free dHax3. It results from the specific binding between RVDs (repeat-variable diresidues) in the repeats and the DNA. Meanwhile, the N-terminal and C-terminal repeats contribute most to the decreased fluctuations. By calculation of specific and nonspecific hydrogen bonds at the interface, it is found that within a TAL repeat the residue at position 13 forms a specific interaction with the corresponding DNA base, and the residues at position 13, 14, 16 and 17 are important to the phosphate binding with the DNA backbone. The observed interactions in our study are in good agreement with experimental data. The last half repeat of TALE has an important contribution to the nonspecific interactions with the DNA backbone. It suggests that the last half repeat of TALE helps to stabilize the TALE-DNA complex. Moreover, tandem repeats with weak RVDs are shown to be unfavorable for the interaction of TALE-DNA. It is consistent with the previous suggestion of avoiding stretches of weak RVDs in the design of TALEs. The PCA analysis reveals similar slow modes of motions in both DNA-free and DNA-bound systems. The dominant motions of the two systems are both open-close movements between the two ends of the superhelical structure. The movements lead to the changes of the intramolecular angle. It is suggested to be an essential step in the TALE-DNA recognition. By comparing DNA structural parameters, the 5′ end of the target sequence has more remarkable increases of bend angle and variations in major groove widths relative to the 3′ end. It reveals the importance of N-terminal repeats for the specific recognition of TALE-DNA. Meanwhile, the conformational change of DNA is likely related to the specific interaction of TALE-DNA. Therefore, we suppose that the arrangement of N-terminal repeats with strong RVDs may help to construct functional TALEs. This study provides a deeper understanding to the recognition mechanism of TALE-DNA, and may facilitate the TALE design as artificial gene targeting reagents for biotechnological applications.
Supporting Information
The energies (A and B), temperatures (C) and volumes (D) versus simulation time in the two systems. All the energies of potential (blue), kinetic (red) and total ( = potential+kinetic, black) in MD simulations for the DNA-free (A) and DNA-bound (B) systems, respectively. The temperatures and volumes of the DNA-free (orange) and DNA-bound (green) systems, are also given in (C) and (D). The plots of energies, temperatures and volumes level off. It indicates that the equilibriums are reached.
(TIF)
Correlations between the values of intramolecular angle and the RMSDs of the backbone atoms for the DNA-free (A) and DNA-bound (B) dHax3. The correlation coefficients are 0.79 for the DNA-free dHax3 and 0.64 for the DNA-bound dHax3, respectively.
(TIF)
The principal components PC1 and PC2 versus simulation time in the DNA-free (A) and DNA-bound (B) systems. For the free-energy minima in the DNA-free system, the values of PC1 vary from −3.8 to 0.8 and those of PC2 from −0.3 to 1.6 (see Figure 7 A). For the free-energy minima in the DNA-bound system, the values of PC1 vary from 0 to 1.5 and those of PC2 from −1.5 to 1.3 (see Figure 7 B). Then, the time sections can be determined by searching the corresponding intervals of PC1 and PC2 (dotted line). Approximately, the free-energy minima in the DNA-free system (yellow) correspond to the segments of 9∼13 ns and 16∼18 ns, while those in the DNA-bound system (sky blue) correspond to the segments of 4∼8 ns and 15∼20 ns.
(TIF)
This shows the conformational changes of 11.5 TAL repeats along the simulation trajectory in the DNA-free system.
(MPG)
This shows the conformational changes of 11.5 TAL repeats and DNA along the simulation trajectory in the DNA-bound system.
(MPG)
Acknowledgments
We thank the national supercomputing center in Shenzhen (Shenzhen Cloud Computing Center) for the computational support.
Funding Statement
This work was supported by the National Natural Science Foundation of China (31200990, 31372116, 11247018, 31071837, 70971043), Guangdong Province Science and Technology Plan Project (2012B010100029, 2010B080701070), the key Project of Chinese Ministry of Education (211159) and the Science and Technology Bureau Foundation of Sichuan Province (2011JYZ007). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Gu KY, Yang B, Tian DS, Wu LF, Wang DJ, et al. (2005) R gene expression induced by a type-III effector triggers disease resistance in rice. Nature 435: 1122–1125. [DOI] [PubMed] [Google Scholar]
- 2. White FF, Yang B (2009) Host and pathogen factors controlling the rice-Xanthomonas oryzae interaction. Plant Physiology 150: 1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Boch J, Bonas U (2010) Xanthomonas AvrBs3 family-type III effectors: discovery and function. Annual Review of Phytopathology 48: 419–436. [DOI] [PubMed] [Google Scholar]
- 4. Kay S, Hahn S, Marois E, Hause G, Bonas U (2007) A bacterial effector acts as a plant transcription factor and induces a cell size regulator. Science 318: 648–651. [DOI] [PubMed] [Google Scholar]
- 5. Romer P, Hahn S, Jordan T, Strauss T, Bonas U, et al. (2007) Plant pathogen recognition mediated by promoter activation of the pepper Bs3 resistance gene. Science 318: 645–648. [DOI] [PubMed] [Google Scholar]
- 6. Boch J, Scholze H, Schornack S, Landgraf A, Hahn S, et al. (2009) Breaking the code of DNA binding specificity of TAL-type III effectors. Science 326: 1509–1512. [DOI] [PubMed] [Google Scholar]
- 7. Moscou MJ, Bogdanove AJ (2009) A simple cipher governs DNA recognition by TAL effectors. Science 326: 1501–1501. [DOI] [PubMed] [Google Scholar]
- 8. Romer P, Recht S, Strauss T, Elsaesser J, Schornack S, et al. (2010) Promoter elements of rice susceptibility genes are bound and activated by specific TAL effectors from the bacterial blight pathogen, Xanthomonas oryzae pv. oryzae. New Phytologist 187: 1048–1057. [DOI] [PubMed] [Google Scholar]
- 9. Christian M, Cermak T, Doyle EL, Schmidt C, Zhang F, et al. (2010) Targeting DNA double-strand breaks with TAL effector nucleases. Genetics 186: 757–U476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Bogdanove AJ, Voytas DF (2011) TAL effectors: customizable proteins for DNA targeting. Science 333: 1843–1846. [DOI] [PubMed] [Google Scholar]
- 11. Voytas DF (2013) Plant genome engineering with sequence-specific nucleases. Annual Review of Plant Biology 64: 327–350. [DOI] [PubMed] [Google Scholar]
- 12. Zhang Y, Zhang F, Li XH, Baller JA, Qi YP, et al. (2013) Transcription activator-like effector nucleases enable efficient plant genome engineering. Plant Physiology 161: 20–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Geissler R, Scholze H, Hahn S, Streubel J, Bonas U, et al. (2011) Transcriptional activators of human genes with programmable DNA-specificity. PloS One 6: e19509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Wang H, Hu YC, Markoulaki S, Welstead GG, Cheng AW, et al. (2013) TALEN-mediated editing of the mouse Y chromosome. Nature Biotechnology 31: 530–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Hu R, Wallace J, Dahlem TJ, Grunwald DJ, O’Connell RM (2013) Targeting human microRNA genes using engineered Tal-effector nucleases (TALENs). PloS One 8: e63074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Miller JC, Tan SY, Qiao GJ, Barlow KA, Wang JB, et al. (2011) A TALE nuclease architecture for efficient genome editing. Nature Biotechnology 29: 143–U149. [DOI] [PubMed] [Google Scholar]
- 17. Baker M (2012) Gene-editing nucleases. Nature Methods 9: 23–26. [DOI] [PubMed] [Google Scholar]
- 18. Murakami MT, Sforca ML, Neves JL, Paiva JH, Domingues MN, et al. (2010) The repeat domain of the type III effector protein PthA shows a TPR-like structure and undergoes conformational changes upon DNA interaction. Proteins-Structure Function and Bioinformatics 78: 3386–3395. [DOI] [PubMed] [Google Scholar]
- 19. Deng D, Yan CY, Pan XJ, Mahfouz M, Wang JW, et al. (2012) Structural basis for sequence-specific recognition of DNA by TAL effectors. Science 335: 720–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Mak ANS, Bradley P, Cernadas RA, Bogdanove AJ, Stoddard BL (2012) The crystal structure of TAL effector PthXo1 bound to its DNA target. Science 335: 716–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Deng D, Yin P, Yan CY, Pan XJ, Gong XQ, et al. (2012) Recognition of methylated DNA by TAL effectors. Cell Research 22: 1502–1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Yin P, Deng D, Yan CY, Pan XJ, Xi JJ, et al. (2012) Specific DNA-RNA hybrid recognition by TAL effectors. Cell Reports 2: 707–713. [DOI] [PubMed] [Google Scholar]
- 23. Christian ML, Demorest ZL, Starker CG, Osborn MJ, Nyquist MD, et al. (2012) Targeting G with TAL effectors: a comparison of activities of TALENs constructed with NN and NK repeat variable di-residues. PloS One 7: e45383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Streubel J, Blucher C, Landgraf A, Boch J (2012) TAL effector RVD specificities and efficiencies. Nature Biotechnology 30: 593–595. [DOI] [PubMed] [Google Scholar]
- 25. Meckler JF, Bhakta MS, Kim M-S, Ovadia R, Habrian CH, et al. (2013) Quantitative analysis of TALE-DNA interactions suggests polarity effects. Nucleic Acids Research 41: 4118–4128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Mussolino C, Morbitzer R, Lutge F, Dannemann N, Lahaye T, et al. (2011) A novel TALE nuclease scaffold enables high genome editing activity in combination with low toxicity. Nucleic Acids Research 39: 9283–9293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Gao HS, Wu XJ, Chai JJ, Han ZF (2012) Crystal structure of a TALE protein reveals an extended N-terminal DNA binding region. Cell Research 22: 1716–1720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Cong L, Zhou RH, Kuo YC, Cunniff M, Zhang F (2012) Comprehensive interrogation of natural TALE DNA-binding modules and transcriptional repressor domains. Nature Communications 3: 968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Bradley P (2012) Structural modeling of TAL effector-DNA interactions. Protein Science 21: 471–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Cermak T, Doyle EL, Christian M, Wang L, Zhang Y, et al. (2011) Efficient design and assembly of custom TALEN and other TAL effector-based constructs for DNA targeting. Nucleic Acids Research 39: e82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Doyle EL, Booher NJ, Standage DS, Voytas DF, Brendel VP, et al. (2012) TAL Effector-Nucleotide Targeter (TALE-NT) 2.0: tools for TAL effector design and target prediction. Nucleic Acids Research 40: W117–W122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Frantz B, O’Halloran TV (1990) DNA distortion accompanies transcriptional activation by the metal-responsive gene-regulatory protein MerR. Biochemistry 29: 4747–4751. [DOI] [PubMed] [Google Scholar]
- 33. Olson WK, Gorin AA, Lu X-J, Hock LM, Zhurkin VB (1998) DNA sequence-dependent deformability deduced from protein-DNA crystal complexes. Proceedings of the National Academy of Sciences of the United States of America 95: 11163–11168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Garvie CW, Wolberger C (2001) Recognition of specific DNA sequences. Molecular Cell 8: 937–946. [DOI] [PubMed] [Google Scholar]
- 35. Hu JP, Ke GT, Chang S, Chen WZ, Wang CX (2008) Conformational change of HIV-1 viral DNA after binding with integrase. Acta Physico-Chimica Sinica 24: 1803–1810. [Google Scholar]
- 36.Humphrey W, Dalke A, Schulten K (1996) VMD: visual molecular dynamics. Journal of Molecular Graphics 14: 33–38, 27–38. [DOI] [PubMed]
- 37. Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, et al. (2005) Scalable molecular dynamics with NAMD. Journal of Computational Chemistry 26: 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, et al. (2010) CHARMM general force field: a force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. Journal of Computational Chemistry 31: 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Ryckaert JP, Ciccotti G, Berendsen HJC (1977) Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. Journal of Computational Physics 23: 327–341. [Google Scholar]
- 40. Darden T, York D, Pedersen L (1993) Particle mesh Ewald: an N.Log(N) method for Ewald sums in large systems. Journal of Chemical Physics 98: 10089–10092. [Google Scholar]
- 41. Hatano T, Sasa S (2001) Steady-state thermodynamics of Langevin systems. Physical Review Letters 86: 3463–3466. [DOI] [PubMed] [Google Scholar]
- 42. Maisuradze GG, Liwo A, Scheraga HA (2010) Relation between free energy landscapes of proteins and dynamics. Journal of Chemical Theory and Computation 6: 583–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Hu JP, Liu M, Tang DY, Chang S (2013) Substrate recognition and motion mode analyses of PFV integrase in complex with viral DNA via coarse-grained models. PloS One 8: e54929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Wan H, Hu JP, Tian XH, Chang S (2013) Molecular dynamics simulations of wild type and mutants of human complement receptor 2 complexed with C3d. Physical Chemistry Chemical Physics 15: 1241–1251. [DOI] [PubMed] [Google Scholar]
- 45. Van der Spoel D, Lindahl E, Hess B, Groenhof G, Mark AE, et al. (2005) GROMACS: fast, flexible, and free. Journal of Computational Chemistry 26: 1701–1718. [DOI] [PubMed] [Google Scholar]
- 46. Lavery R, Moakher M, Maddocks JH, Petkeviciute D, Zakrzewska K (2009) Conformational analysis of nucleic acids revisited: Curves. Nucleic Acids Research 37: 5917–5929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Salsbury FR, Clodfelter JE, Gentry MB, Hollis T, Scarpinato KD (2006) The molecular mechanism of DNA damage recognition by MutS homologs and its consequences for cell death response. Nucleic Acids Research 34: 2173–2185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Negureanu L, Salsbury FR (2012) Insights into protein-DNA interactions, stability and allosteric communications: a computational study of MutS alpha-DNA recognition complexes. Journal of Biomolecular Structure & Dynamics 29: 757–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Jalili S, Karami L (2012) Study of intermolecular contacts in the proline-rich homeodomain (PRH)-DNA complex using molecular dynamics simulations. European Biophysics Journal with Biophysics Letters 41: 329–340. [DOI] [PubMed] [Google Scholar]
- 50. Mahfouz MM, Li LX, Shamimuzzaman M, Wibowo A, Fang XY, et al. (2011) De novo-engineered transcription activator-like effector (TALE) hybrid nuclease with novel DNA binding specificity creates double-strand breaks. Proceedings of the National Academy of Sciences of the United States of America 108: 2623–2628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Mak AN-S, Bradley P, Bogdanove AJ, Stoddard BL (2013) TAL effectors: function, structure, engineering and applications. Current Opinion in Structural Biology 23: 93–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Rohs R, Sklenar H, Shakked Z (2005) Structural and energetic origins of sequence-specific DNA bending: Monte Carlo simulations of papillomavirus E2-DNA binding sites. Structure 13: 1499–1509. [DOI] [PubMed] [Google Scholar]
- 53. Tolstorukov MY, Colasanti AV, McCandlish DM, Olson WK, Zhurkin VB (2007) A novel roll-and-slide mechanism of DNA folding in chromatin: implications for nucleosome positioning. Journal of Molecular Biology 371: 725–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Strick TR, Allemand JF, Bensimon D, Croquette V (1998) Behavior of supercoiled DNA. Biophysical Journal 74: 2016–2028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Nekludova L, Pabo CO (1994) Distinctive DNA conformation with enlarged major groove is found in Zn-finger-DNA and other protein-DNA complexes. Proceedings of the National Academy of Sciences of the United States of America 91: 6948–6952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Prabakaran P, Siebers JG, Ahmad S, Gromiha MM, Singarayan MG, et al. (2006) Classification of protein-DNA complexes based on structural descriptors. Structure 14: 1355–1367. [DOI] [PubMed] [Google Scholar]
- 57. Chenoweth DM, Dervan PB (2009) Allosteric modulation of DNA by small molecules. Proceedings of the National Academy of Sciences of the United States of America 106: 13175–13179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Yoon C, Prive GG, Goodsell DS, Dickerson RE (1988) Structure of an alternating-B DNA helix and its relationship to A-tract DNA. Proceedings of the National Academy of Sciences of the United States of America 85: 6332–6336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Stella S, Cascio D, Johnson RC (2010) The shape of the DNA minor groove directs binding by the DNA-bending protein Fis. Genes & Development 24: 814–826. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The energies (A and B), temperatures (C) and volumes (D) versus simulation time in the two systems. All the energies of potential (blue), kinetic (red) and total ( = potential+kinetic, black) in MD simulations for the DNA-free (A) and DNA-bound (B) systems, respectively. The temperatures and volumes of the DNA-free (orange) and DNA-bound (green) systems, are also given in (C) and (D). The plots of energies, temperatures and volumes level off. It indicates that the equilibriums are reached.
(TIF)
Correlations between the values of intramolecular angle and the RMSDs of the backbone atoms for the DNA-free (A) and DNA-bound (B) dHax3. The correlation coefficients are 0.79 for the DNA-free dHax3 and 0.64 for the DNA-bound dHax3, respectively.
(TIF)
The principal components PC1 and PC2 versus simulation time in the DNA-free (A) and DNA-bound (B) systems. For the free-energy minima in the DNA-free system, the values of PC1 vary from −3.8 to 0.8 and those of PC2 from −0.3 to 1.6 (see Figure 7 A). For the free-energy minima in the DNA-bound system, the values of PC1 vary from 0 to 1.5 and those of PC2 from −1.5 to 1.3 (see Figure 7 B). Then, the time sections can be determined by searching the corresponding intervals of PC1 and PC2 (dotted line). Approximately, the free-energy minima in the DNA-free system (yellow) correspond to the segments of 9∼13 ns and 16∼18 ns, while those in the DNA-bound system (sky blue) correspond to the segments of 4∼8 ns and 15∼20 ns.
(TIF)
This shows the conformational changes of 11.5 TAL repeats along the simulation trajectory in the DNA-free system.
(MPG)
This shows the conformational changes of 11.5 TAL repeats and DNA along the simulation trajectory in the DNA-bound system.
(MPG)