A Mathematical Model for Scanning and Catalysis on Single-stranded DNA, Illustrated with Activation-induced Deoxycytidine Deaminase^,

Background: A random walk mathematical model is proposed to analyze enzyme scanning and catalysis on ssDNA.

Results: The model depicts AID scanning ssDNA in short in random movements, catalyzing C deaminations with minute efficiencies.

Conclusion: Clonal mutational data determine scanning dynamics and C deamination efficiencies for AID.

Significance: Random walk mathematics can be used to analyze molecular mechanisms generating mutational diversity.

Abstract

We formulated a master equation-based mathematical model to analyze random scanning and catalysis for enzymes that act on single-stranded DNA (ssDNA) substrates. Catalytic efficiencies and intrinsic scanning distances are deduced from the distribution of positions and gap lengths between a series of catalytic events occurring over time, which are detected as point mutations in a lacZα-based reporter sequence containing enzyme target motifs. Mathematical analysis of the model shows how scanning motions become separable from the catalysis when the proper statistical properties of the mutation pattern are used to interpret the readouts. Two-point correlations between all catalytic events determine intrinsic scanning distances, whereas gap statistics between mutations determine their catalytic efficiencies. Applying this model to activation-induced deoxycytidine deaminase (AID), which catalyzes C→U deaminations processively on ssDNA, we have established that deaminations of AGC hot motifs occur at a low rate, ∼0.03 s⁻¹, and low efficiency, ∼3%. AID performs random bidirectional movements for an average distance of 6.2 motifs, at a rate of about 15 nucleotides per second, and “dwells” at a motif site for 2.7 s while bound >4 min to the same DNA molecule. These results provide new and important insights on how AID may be optimized for generating mutational diversity in Ig genes, and we discuss how the properties of AID acting freely on a “naked” ssDNA relate to the constrained action of AID during transcription-dependent somatic hypermutation and class-switch recombination.

Introduction

Enzymes that scan dsDNA seeking targets to attack have been subject to extensive analyses, both experimental (1–7) and modeling (8–11). Examples include DNA glycosylase-catalyzed excision of uracil (1, 2) and oxidized bases such as 8-oxoG (3, 4); mismatch repair proteins working in concert to remove DNA polymerase-catalyzed misincorporated bases and looped out structures resulting from short insertions and deletions (6, 7); and endonucleases that catalyze the cleavage of dsDNA at restriction motifs (5, 12). In contrast, enzymes that act on ssDNA have been investigated to a far lesser extent. The mathematical modeling of dsDNA-scanning enzymes relies heavily on first passage time analyses (10, 11) to treat high efficiency catalysts, for example, restriction endonucleases and DNA glycosylases. Our mathematical model, which is designed to treat ssDNA-scanning enzymes that operate at any catalytic efficiency, is new.

AID³ is a member of the APOBEC family of C deaminases (13, 14). AID is expressed in B-cells, playing an essential role in ensuring immunological diversity by initiating somatic hypermutation and class-switch recombination in immunoglobulin variable and switch regions, respectively (15, 16). When assayed biochemically, purified AID converts C→U using ssDNA as a substrate (17–19), showing no measurable activity on dsDNA, RNA, or RNA-DNA hybrid molecules (17).

Here, we developed a mathematical model to investigate scanning and catalysis on ssDNA, in terms of a one-dimensional random walk. This class of stochastic models has played an extensive and important role in diverse areas of statistical physics that encompass theories of polymer dynamics (20–22), structures of interfaces (23), and electron transport and trapping (24). We have now added a new biological application, enzyme catalysis. We investigated AID-catalyzed C deaminations on ssDNA to illustrate the model and to reveal elemental properties of scanning and catalysis that are specific to AID.

The study integrates the model and experimental data in the following way. Under “Experimental Procedures,” we have derived a general mathematical model for scanning dynamics and catalysis, including the equations needed to design and interpret the experiments. A detailed mathematical development required for a rigorous application of a master equation scan matrix to the model is given in the supplemental data, in which we also discuss several new and unanticipated mathematical insights derived from the equations. Under “Results,” we have used the model to analyze the experimental data.

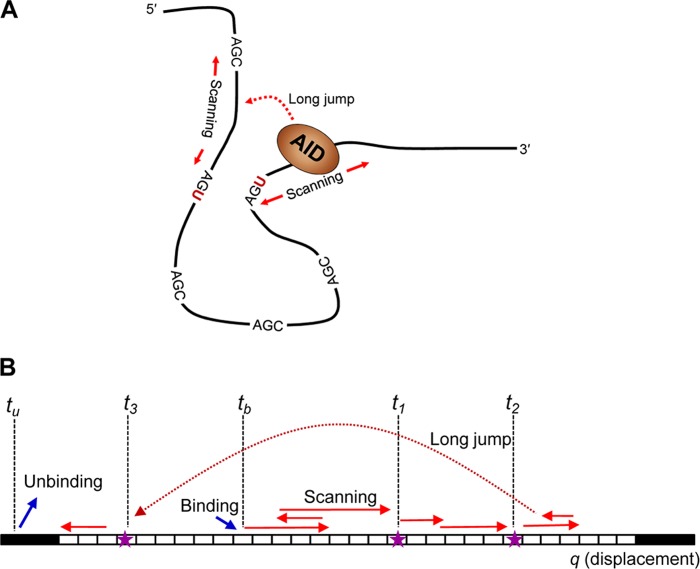
Previous biochemical studies show that AID binds to ssDNA, scans randomly (short hops/slides, longer jumps/intersegmental transfers), and catalyzes C deaminations, favoring WRC motifs (W = A/T, R = A/G) (18, 25) (see Fig. 1A). AID acts processively, catalyzing variable numbers of C→U deaminations on the same ssDNA substrate (18, 25). A “typical” DNA clone depicting AID displacement and catalysis is illustrated in Fig. 1B. One thing to notice is that where the deaminations occur in space provides no explicit information about when they occur in time, nor do the clonal data reflect the deamination efficiency, namely, how many times AID encounters a particular trinucleotide motif before it acts at that motif.

FIGURE 1.

Events leading to a mutation pattern on an ssDNA acted upon by a deaminase enzyme, e.g. AID. A, schematic representation of AID motion (scanning and jumps) and catalysis in three-dimensional space on ssDNA containing multiple AGC hot motifs. B, a projection of AID actions in one-dimensional space for a substrate consisting of a number of trinucleotide motifs (white boxes) that can be deaminated by the enzyme. The enzyme binds to the substrate on a random sequence-independent position at time t_b and moves along the substrate by a sequence of random motions including a combination of scanning (sliding or short hops) and possibly long jumps or intersegmental transfers. The enzyme catalyzes C→U mutations along its trajectory, dropping markers (stars) at time t₁, t₂, … The enzyme eventually unbinds at time t_u. This sequence of events can be mapped onto an abstract one-dimensional sequence space on which the stochastic model is formulated.

We developed a mathematical model that specifies precisely how to use the clonal data to obtain scanning length distributions for AID and catalytic efficiencies. We show that a two-point correlation function, which measures the pairwise distance between all deaminations on every clone, can be used to determine the excursion length distribution for AID by using clonal deamination data collected at two time points. The most salient mathematical insight is that although the combined distribution for all of the clones with C→U deaminations is used to decipher the displacement dynamics of AID on ssDNA, the catalysis does not appear explicitly in the expression for the two-point correlation function. In other words, although scanning and catalysis are closely coupled physically, scanning per se can be determined independently from catalysis using the mathematics, which we have shown is not the case for computer simulations of random scanning and catalysis by AID (25). This key result that enables scanning to be determined independently is contained in Equation 5 (see “Experimental Procedures”). The catalytic efficiency is then obtained by determining the distribution of gap distances between deaminations using a subset of clones containing two deaminations (see Equation 3 under “Experimental Procedures”).

The mathematics is much simpler and considerably more “transparent” when using a repetitive target sequence that is homogeneous. Accordingly, we used a tandemly repeated series of AGC hot motifs as a deamination target cassette embedded in a lacZα mutational reporter gene (25). There is, however, no serious difficulty generalizing the analysis to investigate inhomogeneous sequences, such as a mix of hot and non-hot motifs. This initial study looks at AID operating unconstrained on ssDNA. However, AID in “real life” acts on transcribed dsDNA. The model can readily be modified to accommodate a unidirectional scanning process to analyze deaminations occurring during transcription of dsDNA in a lacZα reporter assay (25, 26). Other APOBEC C deaminases can be characterized in a similar manner taking the approach described here.

EXPERIMENTAL PROCEDURES

Mathematical Model for Scanning Dynamics and Catalysis on ssDNAs

To formulate a mathematical model, we mapped events occurring on the ssDNA onto a one-dimensional coordinate q along its chain contour. Although the conformation of an ssDNA molecule in physical three-dimensional space can be complex (see Fig. 1A), this mapping onto an abstract space q (see Fig. 1B) is always possible and common in theories of linear polymers (21). The motions of AID bound to the DNA are represented by a stochastic trajectory q(t), and the deposition of mutation markers at random times t₁, t₂, … characterizes its catalysis. Fig. 1 illustrates the sequence of events that must occur to produce the mutation patterns in the clone readouts. 1) AID associates by binding to a random position on the sequence at time t_b. 2) The bound AID moves along q via short scanning motions and possibly long jumps (short excursions in sequence space may arise from small distance diffusive motions, whereas long displacements in sequence space may result from various physical mechanisms such as persistent sliding, jumping, and intersegmental transfer (7, 12, 27)). 3) AID deposits C→U deaminations along its stochastic trajectory at random times according to the kinetics of its catalysis, producing markers at the positions where deaminations occur (depicted in Fig. 1B by stars). 4) The enzyme eventually unbinds from the substrate at time t_u.

The experiments employ a DNA construct with m motifs that can be deaminated. We use a master equation (28) to describe the motions of AID.

p⃗(t) is an m component column vector with components p_q(t), giving the time-dependent probabilities of finding the enzyme on motif q = 1, 2, … , m, and W is a transition matrix with elements W_q′q specifying the transfer rate from motif q to q′ due to the motions of the enzyme. Both short range scanning motions as well as long jumps can be incorporated into a single W. The scan matrix W completely encapsulates the dynamics of the stochastic motions of AID on its substrate. ssDNAs may exist in many distinct conformational states and each clone may have a potentially different W; thus, W in Equation 1 is understood as an ensemble average over the clone conformations. The formal solution to Equation 1 is

where the propagator K(t) exp(tW)contains all the essential information needed to characterize the stochastic motions of the enzyme. The matrix elements of the propagator K_q′q(t) give the probability of finding the enzyme on motifs q′ at time t if it had started out on motif q at time 0. Any motif sequence dependence or possible directional bias in the scanning motions may easily be incorporated into the model with an inhomogeneous and/or anisotropic W. Appropriate generalizations of W can be made to model any substrate, and for any finite substrate, the propagator K(t) can always be computed by diagonalizing W, which for a large gene, e.g. variable region (∼1–2 kb), would have to be done numerically. The marker positions and their clustering patterns are related to the moments of K(t).

The catalysis occurs as a secondary stochastic process on top of the scanning dynamics. The deamination kinetics depends on the scanning trajectory q(t) because different motifs have distinct catalytic efficiencies and each scanning trajectory visits different motifs at different times. Despite this entanglement between the two stochastic processes, the catalysis can always be characterized by an inhomogeneous Poisson process (29), although the time sequence of deaminations occurring on the substrate {t₁, t₂, t₃, … t_n} is in general dependent on q(t), and this can lead to substantial mathematical complexities.

Homogeneous Substrates

The mathematics simplifies considerably when the substrate sequence is homogeneous. The elements of W become both isotropic (i.e. W becomes a Toeplitz matrix (30) whose elements depend only on the distance between motifs) as well as symmetric when there is no directional bias to the scanning. Furthermore, the catalytic kinetics reduces to a homogeneous Poisson process with a single deamination efficiency because all motifs are now identical. In a homogeneous Poisson process, the waiting time between two sequential deaminations is distributed exponentially according to P_W(τ) = s_m⁻¹exp (−s_mτ), where s_m is the mutation rate. It is easy to show that the second-order correlations in the propagator K(t) are related to the distribution of gap distances between two markers in clones with exactly two mutations

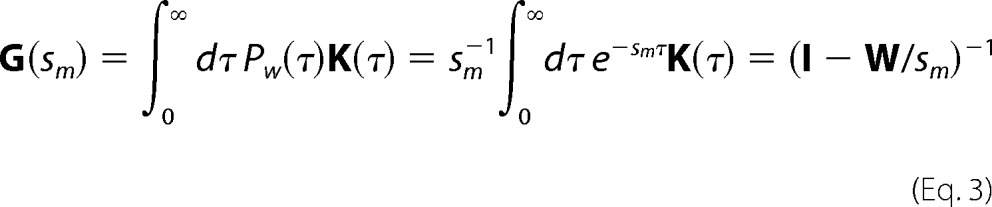where element G_q′q of the matrix G is the joint probability of observing markers at positions q and q′ and I is the identity matrix. Equation 3 suggests that the experimentally observed gap distribution between two markers on a homogeneous substrate behaves as an analog Laplace transform computer of the dynamic propagator K(t) of the enzyme, essentially a read-out of the time-ordered correlations between the position of the enzyme q(t) with its position q(t-τ) where the previous deamination occurred, weighted by exp(−s_mτ). Similar relationships exist between third-order correlations of the propagator K and the gap distribution in clones with three mutations and so on.

More relevant for the analysis of the experiment clones are the time-scrambled correlation functions, the lowest order of which are given by the two-point correlation matrix F(t), whose elements F_q′q(t) are the joint probability of observing a marker at q and another marker at q′ on the same clone but with any number of intervening markers between them (including zero) and over all clones with any number of mutations on them, within time t. Referring again to Fig. 1B, we see that the matrix elements of F(t) come from two deamination events with any number of other deaminations between them, and the appropriate modification to Equation 3 for computing F(t) is to replace the waiting time distribution P_W(τ), which applies for two sequential deaminations, with the appropriate waiting time distribution Q_W(τ) for any number of intervening mutation events. Accounting for the time between binding to the first deamination and the time after the second deamination until unbinding, the final expression for the two-point correlation function is easily shown to be

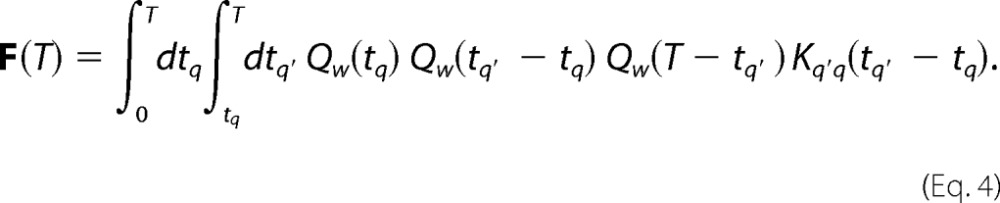One can prove that the waiting time distribution Q_W(τ) for any number of events in time τ for a Poisson process is time-independent (see supplemental data), yielding the simple expression

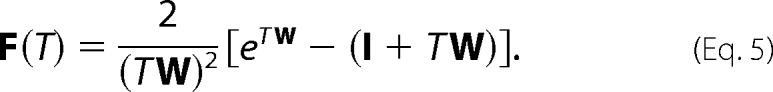Other higher order time-scrambled correlation functions can be derived in an analogous fashion.

Generation of lacZα Clones Containing AID-catalyzed C→U Deaminations Detected as C→T Mutations

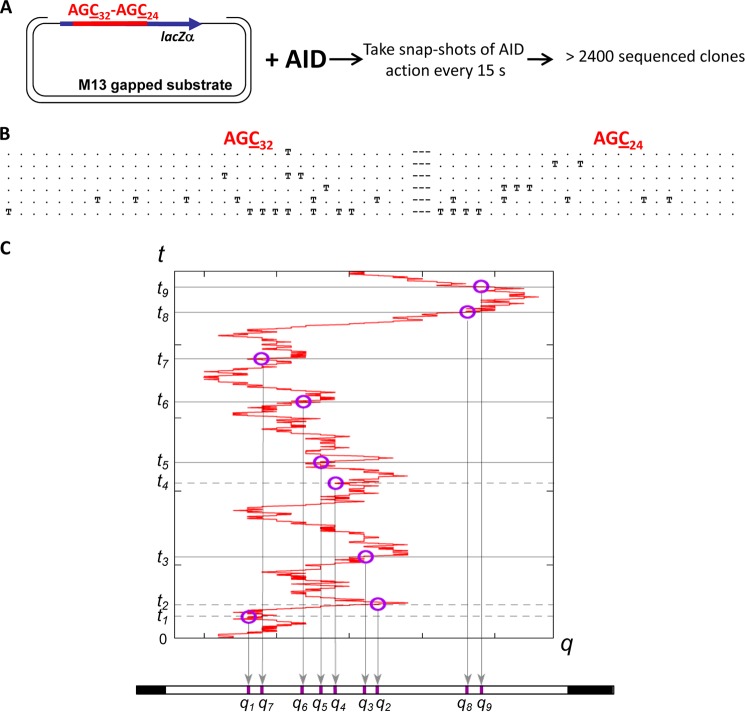
A DNA substrate containing 56 AGC hot motifs (AGC₃₂–AGC₂₄) deamination reporter cassette embedded in lacZα (see schematic in Fig. 1B) was incubated with AID, and deamination reactions were quenched at 15, 30, 45, 60, 120, 300, and 600 s. C→U deaminations in AGC motifs create stop codons within the lacZα reading frame that result in mutant M13 phage clones. Deaminations are detected as C→T mutations in sequenced mutated clones (25). To ensure that virtually all deaminations on individual substrates were caused by a single AID molecule, AID and ssDNA concentrations were chosen so that the fractions of mutated clones were always less than about 2%, as prescribed by Poisson statistics (25). Two incubation times, 45 and 120 s were used to determine AID scanning parameters, distances, and dwell times, as proscribed by Equation 4; the 300-s time point was used to verify that the deaminations had spread uniformly over the entire reporter cassette.

RESULTS

The mapping of the three-dimensional AID scanning and deamination events on ssDNA (Fig. 1A) onto a one-dimensional displacement coordinate q along the chain contour (Fig. 1B) illustrates the key point that catalysis and enzyme motions are scrambled in such a way that when a specific deamination occurred, it was not directly related to where along the chain it is positioned. However, once a deamination has occurred, if a second deamination is more likely to occur at a location more or less in the vicinity of the first deamination, i.e. if “scanning” is favored over “long jump” (Fig. 1), then the locations in deamination positions are correlated with deamination times.

Herein lies the key to disentangling catalysis from scanning dynamics; the disentanglement is achieved by measuring the two-point correlation function F(T) (see Equation 5). This measurement requires that the entire clonal data set for AID-catalyzed deaminations be obtained at two time points (see Fig. 3A). Each clone can contain any number of deaminations. The intuitive point to keep in mind is that the two-point correlations measure the spreading in deamination positions with longer and longer incubations. We will show that just two time points are needed to determine the scanning dynamics unambiguously. A second point to keep in mind is that no assumptions are being made regarding whether or not scanning is favored over long jump (Fig. 1). The data are used to determine the displacement dynamics; a predominance of large displacements would erase the two-point correlations, which, as we will show, is not the case. We will now describe the connection between the model and experiment.

FIGURE 3.

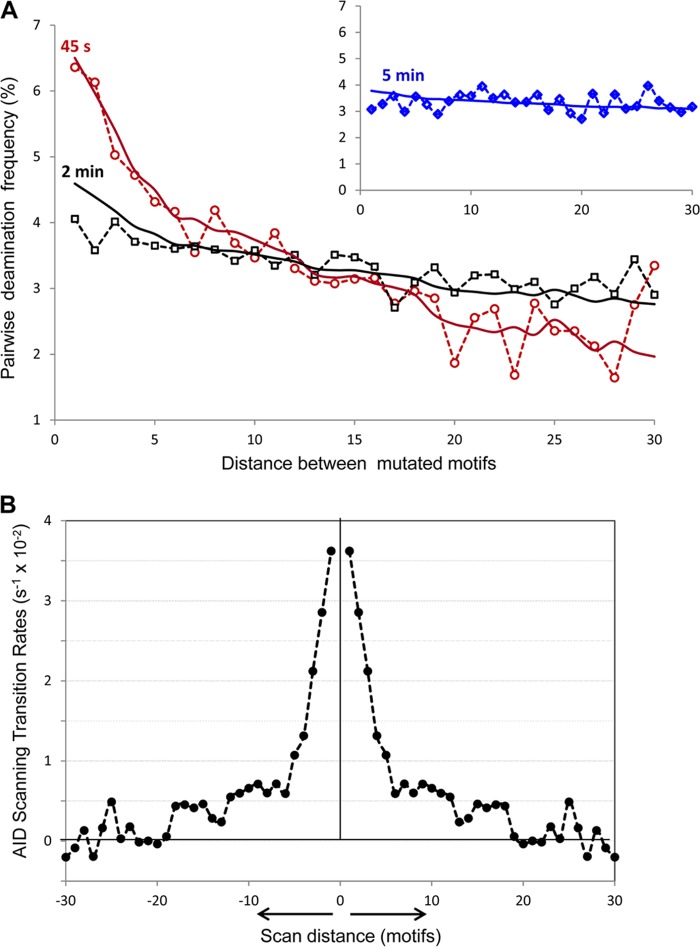
Analysis of AID scanning by two-point correlation function. A, distribution of pairwise deaminations separated by 1–30 motifs in experimental clones with ≥2 mutations at 45 s (open red circles), 2 min (open black squares), and 5 min (open blue diamonds, inset). Solid lines represent the predicted pairwise distributions at 45 s (red), 2 min (black), and 5 min (blue, inset), using the two-point correlation function (Equation 5) with the AID scanning matrix W shown in B. B, AID scanning matrix (W) obtained from inverted experimental data. 0 on the x axis denotes the initial position of the enzyme on ssDNA. The y axis shows the AID transition rates from the initial position 0 to positions on the left and on the right at distances ranging from 1 to 30 motifs (3–90 nt). The negative transition rates originate from noise in the data at long scan distances (>20 motifs). These are shown because they are required in the calculation to conserve total probability.

Analyzing AID C→U Clonal Deamination Data Using the One-dimensional Random Walk Model

Fig. 2 shows how a mutation record is derived from a scanning trajectory q(t) and the associated deamination kinetics. Circles along q(t) indicate where deaminations have occurred. When mapped onto the coordinate q, these correspond to markers on the substrate ssDNA. Notice that the markers only provide a “flattened” record of the positions where mutations have occurred, in the sense that the time-ordered sequence of deamination events has been collapsed onto a single coordinate q. The mutations deposited by AID on the substrate DNA provide a read-out of the stochastic scanning dynamics and the C→U catalytic deaminations kinetics. Although the time ordering is scrambled in the flattened read-outs, nonetheless, the positions of the mutations on the clones contain dynamic signatures from the scanning motions and the catalytic deamination kinetics. Using the model equations derived under “Experimental Procedures” (see the “Homogeneous Substrates” paragraph), we can interpret the statistics and correlations between these markers in a large clonal data set to decipher the dynamic characters of the intrinsic scanning and catalytic activities of AID independently and uniquely.

FIGURE 2.

Time-course experiment to analyze AID random scanning and stochastic deamination on ssDNA. A, an M13mp2 phage construct containing an ssDNA region with 32 AGC deamination motifs on the left side and 24 AGC motifs on the right side separated by a 9-nt linker region was subjected to AID deamination for a duration from 15 s to 10 min at 37 °C. AID deaminations at AGC motifs are detected as C→T mutations in individual M13 mutant phage clones (25). B, representative mutated clones with 1, 2, 3, 4, and ≥5 mutations. T and dot symbols denote deaminated and non-deaminated AGC motifs, respectively. C, a scanning trajectory of AID on an ssDNA combined with stochastic deamination events depositing a random sequence of markers at positions q₁, q₂, … at time t₁, t₂, … on the ssDNA substrate.

Two-point Correlations

Disentangling the catalysis from the scanning dynamics is achieved by measuring the two-point correlations F(T) given by Equation 4. The elements of the two-point correlation matrix F(T) are the joint probability of observing a marker at q and another marker at q′ on the same clone, with any number of intervening markers between them (including zero), and over all clones with any number of mutations on them for an incubation time T. F(T) is isotropic, and the distance dependence of its matrix elements corresponds to the experimental two-point correlations derived from the complete clone data, which are shown in Fig. 3A for three incubation times. The data have been corrected for finite-sized effects where the number of motif pairs with a certain separation decreases linearly with gap distance.

Equation 5 reveals a remarkable feature of the two-point correlation function; it contains information about the scanning dynamics independently from the mutation kinetics, i.e. F(T) has no dependence on the deamination rate s_m. This result suggests that the dynamics of the scanning motions can be determined uniquely by analyzing the statistical correlations between all pairs of markers from the entire population of clones in our data set with two or more mutations, and this can be done with absolutely no interference from the kinetics of the catalysis, although the marker read-outs originate from a convolution between these two dynamical processes. This seemingly surprising result is an essential consequence of the underlying homogeneous Poisson statistics of the deamination kinetics.

The diagonal value of F(T) corresponding to zero displacements cannot strictly be derived from clone data by simply analyzing the correlations between deaminations. (See the supplemental data for details.) However, it is easy to get around this problem by measuring F at two different times T₁ < T₂.

The following protocol has been used to directly solve for the scan matrix W, utilizing the experimentally determined two-point correlation functions at T₁ = 45 s and T₂ = 120 s. 1) Apply a short time Taylor expansion of Equation 5 to the experimentally measured two-point correlation function at T₁ to establish an initial approximation for W. Use this to estimate the diagonal value of F, F_qq(T₁), at zero distance. 2) Insert this estimate for the diagonal value F_qq(T₁) as an input into the experimentally measured F(T₁). Invert F(T₁) using Equation 5 to obtain W. 3) With W from step 2, use Equation 5 to compute the expected two-point correlation function F(T₂) at the second time T₂ as the output. Compare the output F(T₂) against experimental data, using a χ² analysis to either accept or reject the input F_qq(T₁). 4) Refine the estimate for the diagonal value of F(T₁) and return to step 2. Repeat this procedure to converge to the best input value F_qq(T₁).

Applying the Model to Evaluate AID Scanning Distances from the Clonal Data

The mathematical solution and the analysis protocol described above were applied to invert the experimental clone read-outs to analytically compute the scan matrix W. Before the inversion, the two-point correlation function data F(T₁) at T₁ = 45 s in Fig. 3A were smoothed by averaging every three data points, and data for distances >25 motifs were not used for the inversion because of their large statistical uncertainties (i.e. their counts were lower than the statistical noise). Inserting the estimate for the missing diagonal value F_qq for F(45 s) (see steps 2–4 above) and renormalizing the sum to unity over all distances within the cassette, we inverted it according to Equation 5 to compute W. Using this W, we then calculated the expected F(T₂) at T₂ = 120 s and evaluated its fitness as a model for the experimental data for F(120 s) using a χ² test. The best fit produced the W matrix whose elements are shown in Fig. 3B.

The scan matrix obtained from the analytical inversion of experimental data shows that a majority of the motions of AID on ssDNAs are confined to small excursions of fewer than five motifs (15 nt) (Fig. 3B). Physically, these transitions in the W matrix correspond to short range scanning motions, slides, or hops. In addition to these, there is a broad distribution of longer range displacements reaching distances up to about 20 motifs (60 nt). The statistical quality of the two-point correlation function used for the inversion does not permit a very accurate estimate of the scan transition rates for distances larger than these, but the overall shape of the scan matrix is quite clear from Fig. 3B. AID makes excursions along its substrate ssDNA predominantly by short scanning motions with transition distances of 5 motifs or fewer. These account for more than 60% of all transitions originating from each motif. Augmenting these is a broad distribution of longer jumps up to about 20 motifs, which occur at lower frequencies and comprise 40% of all transitions. Averaging over the entire distribution of scan distances, the mean scan length is ∼6.2 motifs (∼19 nt). The total transition rate out of a motif q, which is the sum over all off-diagonal elements Σ_q′≠q W_q′q, equals 0.36 s⁻¹. The mean dwell time of AID on a single trinucleotide motif, which is the inverse of the total flow rate out, is therefore 2.7 s.

Analytical predictions for the two-point correlation function F(t) derived from the scan matrix in Fig. 3B are shown superimposed on the experimental data in Fig. 3A for t = 45 s, 2 min, and 5 min. The time course of the two-point correlation function demonstrates convincingly that the scanning of AID on an ssDNA is highly processive. If the deaminations had been deposited by the repeated binding and unbinding of different enzymes onto the same substrate, the marker positions would exhibit no spatial correlation at all. In fact, because the time evolution of the two-point correlation function is a consequence of the action of the propagator K(t) (see Equation 2, “Experimental Procedures”) over time driven by the same scan matrix W, the remarkable agreement between the analytical calculated F(t) with experiment provides unequivocal evidence for the processivity of AID and its ability to repeatedly scan the same DNA strand.

Applying the Model to Evaluate AID Catalytic Efficiency from the Clonal Data

After W has been determined by the four step protocol described above, it is then a simple matter to use Equation 3 to determine the value of the mutation rate s_m that would best reproduce the experimental gap distribution, which is shown in Fig. 4. Because the substrate is homogeneous, elements of the G matrix are functions only of the distance between motif pairs. This subset of clones with exactly two mutations corresponds to 540 out of a total population of >2400 clones collected. On a finite cassette, the number of motif pairs with a certain separation decreases linearly with gap distance. Therefore, the statistical quality of the gap distribution at large separations also deteriorates rapidly. Short distance data are much more reliable than longer distance data. An analysis of the G matrix presents some interesting mathematical complexities, which (intended primarily for the aficionado) we discuss in the supplemental data. The reporter cassette we have employed has 32 AGC motifs followed by 3 “silent” motifs and then another 24 AGCs (25). This cassette design was made to pick out any possible directional bias in the motions of AID, which the data clearly showed was absent (25). These 3 silent motifs on the background of a 59-motif cassette sequence that is otherwise homogeneous produce only negligible effects on the analysis, namely <3/59, ∼5% on the gap statistics.

FIGURE 4.

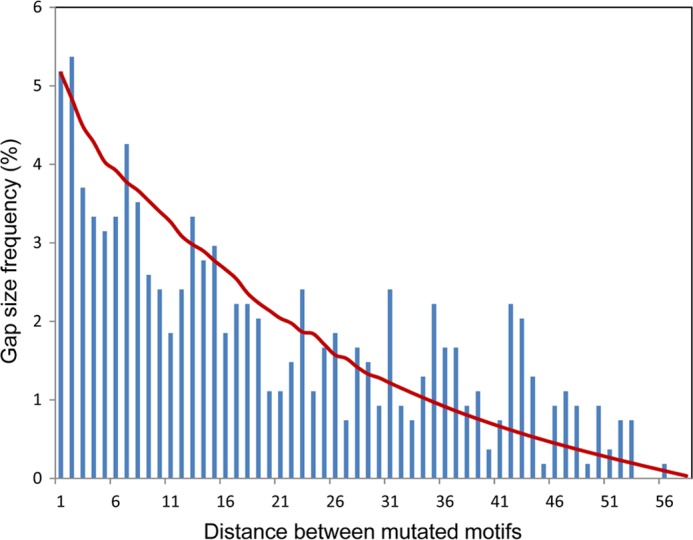
Distribution of the gap distances between two consecutive deaminations in experimental clones with exactly 2 mutations. The red line represents the gap distance distribution predicted from the Laplace transform of the propagator K coming from the scanning matrix W (Fig. 3B) and deamination efficiency of 2%.

Fig. 4 shows the gap distribution derived from the Laplace transform of the propagator K coming from the W matrix (Fig. 3B) at a deamination rate s_m = 0.01 s⁻¹, using Equation 3. Utilizing a χ² analysis, we have determined that a range of deamination rates from 0.0025 to 0.03 s⁻¹ produces good fits to the experiments. Using these, we can derive an estimate for the mutation efficiency of AID in conjunction with the mean dwell time obtained above. These data suggest that the deamination efficiency of AID, given by the product of its mutation rate and the mean dwell time, is in the range of 0.7–8%, with best fits to the data at 3–5%. Experimental measurement of the mutation count per clone suggests a deamination rate of roughly 0.03 s⁻¹, which is in good agreement with these analytical predictions.

Measurement of AID-catalyzed Deamination Rate and Estimation of AID Binding Lifetime

To ensure that virtually all deaminations on individual substrates were caused by a single AID molecule, AID and ssDNA concentrations were chosen so that the fractions of mutated clones were always less than about 2%, as prescribed by Poisson statistics (25). The numbers of mutations/clone occurring as a function of exposure time to AID showed that at a very short (15 s) incubation time, almost all clones have 3 or fewer mutations, with an average of 1.36 mutations per clone (Fig. 5). At longer incubation times from 30 to 120 s, there was a linear increase in the numbers of mutations/clone, with an average of 2.2 and 4.9 mutations/clone at 45 and 120 s, respectively (Fig. 5). Because deaminations on each clone resulted from the action of a single enzyme, the linear increase in the average number of mutations/clone indicates that AID remained bound to the same DNA for the duration of the experiment; otherwise, early dissociation of AID in bulk solution would alter the linear time-dependent increase in the numbers of mutations/clone. From the data, we calculated that AID added one deamination every ∼35 s (implying a deamination rate ∼0.03 s⁻¹) (Fig. 5). The number of mutations/clone continues to increase with increasing AID incubation times of 300 and 600 s, although the increase is no longer linear with time (Fig. 5). Because the fractions of deaminated motifs at long incubation times are high, 16% (∼8.8 mutated motifs out of 56 total) at 300 s and 23% (13/56) at 600 s, the observed break in the linear increase in the numbers of mutations/clone is likely caused by a “target saturation” effect (i.e. AID has a fewer number of available motifs to deaminate at longer times), rather than enzyme dissociation, because the fraction of mutated clones remains less than about 2% at 10 min. When saturation was considered, the predicted average numbers of mutations/clone showed an excellent fit to the experimental data (Fig. 5), suggesting that AID is likely to remain bound to ssDNA for at least 5 min.

FIGURE 5.

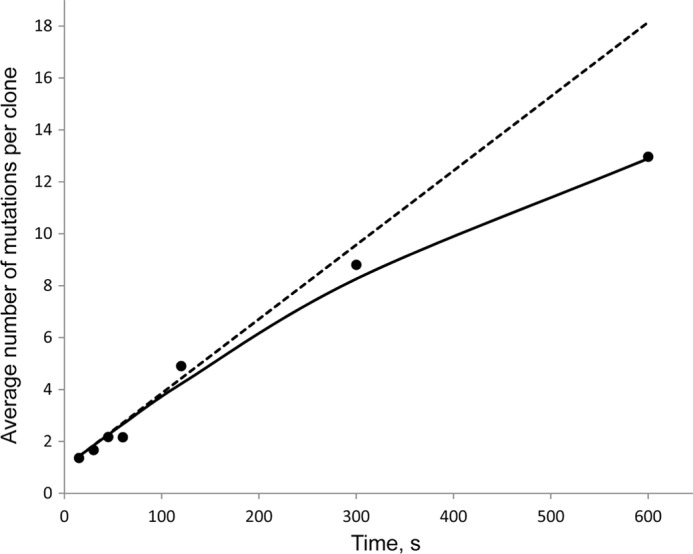
Time-dependent accumulation of AID-catalyzed mutations (black circles) on deaminated clones. The linear rise in the average number of deaminations per clone from 15 to 120 s indicates a long lifetime of AID on ssDNA and corresponds to AID deamination rate of 1 deamination per 35 s (0.029 s⁻¹). The solid line represents the predicted average numbers of deamination per clone if AID remains bound to ssDNA for the duration of the experiment and deaminates the 56-motif cassette with a rate of ∼0.03 s⁻¹ when the “target saturation effect” was considered. The dashed line represents the predicted values without considering the “target saturation effect.”

DISCUSSION

In contrast to a paucity of information regarding enzymes that scan and catalyze reactions on ssDNA, proteins that scan double-stranded DNA (dsDNA), searching for motifs to bind (lac repressor protein) and to cut (restriction endonucleases) and for rare damaged DNA bases to excise (DNA glycosylases), have been well characterized structurally and catalytically. Diffusion models have been advanced to understand targeting efficiency of dsDNA-scanning enzymes (8–11, 27, 31–34), e.g. uracil glycosylase, which often needs to locate as little as a single specific target in 10⁶-10⁷ bp (2). In essence “a needle in a haystack,” the errant target base is removed efficiently ∼70% (1).

The opposite appears to be true for AID. AID encounters large numbers of trinucleotide target motifs when deaminating C→U in immunoglobulin (Ig) switch and variable regions (15, 16) with surprisingly low efficiencies. Our objective is to provide a tractable general mathematical model to examine the salient properties of enzymes that scan ssDNA randomly, which although confronting large numbers of target motifs mainly do “nothing,” and instead only catalyze a reaction occasionally. Why would an enzyme be designed to avoid catalysis? The answer is key to generating mutational diversity. With AID serving as the “poster child” for this peculiar type of inefficient catalytic mechanism, experiments studying the mutation patterns resulting from its action on an ssDNA substrate deserve a rigorous mathematical analysis. The enzymatic properties that need to be identified include intrinsic scanning distances, motif dwell times, catalytic rates, and most importantly, catalytic efficiencies. Defined as the fraction of motif encounters that result in a catalytic conversion, the catalytic efficiency of AID is surprisingly low (25) (Fig. 5).

The principal mathematical challenge is to effect a definitive separation of scanning from catalysis. The elements of the scan matrix W in the stochastic model in Equation 1 describe the random movements of AID along the substrate ssDNA. The C→U deaminations (identified as C→T mutations in the WRC motif reporter cassette, Fig. 2, A and B) serve as markers that record where AID had been present on the DNA. Although the W matrix elements have no explicit dependence on deamination rates or efficiencies, the marker records are a convolution of both scanning and catalysis dynamics. Using the ensemble of clones containing ≥2 mutations, the scanning dynamics of AID has been determined by measuring the two-point correlation function between all pairs of mutations (Equation 5), as prescribed by the “Scan Dynamics Recipe.” Having deposited a mutation at one motif, an AID molecule is more likely to mutate a nearby one, the correlation between them decreasing with increasing motif distance (Fig. 3A). This correlation distance reflects the enzyme's loss of memory of its earlier whereabouts due to its random scanning motions, and the challenge is to derive a rigorous mathematical approach to extract dynamic (i.e. time-dependent) information about the motions of AID from the static mutation records it leaves on the sequence where all time-ordering information has been scrambled. A mathematical solution for the two-point correlation function reveals that the dynamics of the scanning motions is entirely separable from the catalysis (Equation 5, Fig. 3).

An accurate recovery of the dynamic scanning motions (W matrix off-diagonal elements) from the data requires that clonal mutation data be obtained for more than a single time point; in fact, two time points proved to be entirely satisfactory (45 s and 2 min, Fig. 3A). One clearly sees that the range of diffusive excursions increases significantly between 45 s and 2 min, with the high frequency of short scans (1–5 motifs) observed at 45 s, reduced, and spread into longer distances at 2 min (Fig. 3A). For illustration, a third time point at 5 min is included to show that the displacement of AID has spread to become uniform over the entire substrate (Fig. 3A, inset). An important point to make is that virtually all of the mutated clones (illustrated in Fig. 2B) have been acted on by one AID molecule (25) (Fig. 5). This observed time progression in the spread of marker correlation demonstrates unequivocally that the function of AID on ssDNAs is highly processive. Corroborating this, less than about 2% of the input DNA contain 1 or more mutations, which in accord with Poisson statistics means that >98% of the mutated clones are acted on by just one enzyme molecule (25). We strongly suspect that processive scanning may turn out to be a hallmark of other members of the APOBEC family of C deaminases, as we have shown for Apo3G (35, 36).

By directly inverting the correlation functions recorded from experimental clone data, we are able to recover the scan matrix W with exquisite details. Although the experimental data are noisy, inverting the correlation function mathematically to retrieve W reveals a remarkably consistent picture for the scanning dynamics. Short scanning motions (slides/hops) spanning ≤5 motifs (15 nt) comprise >60% of the transitions; about 40% of the transitions are composed of longer scans (jumps/intersegmental transfers) in a range of 6–20 motifs (Fig. 3B). These long jumps in one-dimensional space (Fig. 1B) could correspond to short displacements in three-dimensional space (Fig. 1A). The scans are weighted toward smaller displacements with a mean scan length of roughly 6.2 motifs (18–19 nt). From the W matrix, the total transition rate out of a motif of AID is predicted to be 0.36 s⁻¹, which implies that AID remains bound to each motif for an average dwell time of 2.7 s.

Having obtained the dynamic scanning motions, it is straightforward to determine the catalytic parameters for AID. Here, we need to examine the subset of the mutated clones having exactly two mutations. The deamination rate, s_m, is calculated from Equation 3 by determining a χ² best fit of the distribution of gap distances, G_q′q, between the two mutations (Fig. 4). The analytically predicted range of deamination rates is 0.0025–0.03 s⁻¹, which agrees with an independent measurement for the average deamination rate of about 0.029 s⁻¹; the average deamination rate and minimum residence time of about 4 min for a molecule of AID remaining bound to the same ssDNA substrate are determined by the linear increase in mutations/clone (Fig. 5). By both direct measurement and analytical prediction, AID catalyzes roughly 1 deamination every 35 s, whereas remaining bound at a motif for slightly less than 3 s. The deamination efficiency (deamination rate × motif dwell time) ranges from 0.7 to 8%, with a best fit estimate of 3–5%.

It is instructive to briefly contrast our previous simulations of random scanning and deamination for AID (25) with this analytical analysis. Simulations are a numerical implementation of the stochastic dynamics expressed by the master equation, but they require a prior model for the scan matrix. Assuming a geometric hop model with its mean scan distance and the deamination efficiency as variable parameters, our prior simulations suggest a deamination efficiency range of 1–7% and average scanning distances of about 10 motifs (25). These conclusions are quite similar to the analytical analysis, which is reassuring, but there are fundamental conceptual and practical advantages to the analytical mathematical approach. Although the computer simulations also favored short scans with low deamination efficiencies, they were unable to rule out high deamination efficiencies coupled with long excursions, which also gave reasonable fits to the clonal mutation distribution data, as discussed in Ref. 25. The analytical theory eliminates this ambiguity because the scanning and catalysis are uncoupled. Another practical disadvantage of the simulations centers around the large joint scanning and catalysis parameter space that needs to be explored, requiring lengthy computer runs and statistical analyses. In contrast, the mathematical analysis shows that a two-point correlation for clonal mutations obtained at two time points is sufficient to determine scanning and deamination ranges independently and has enabled us to directly and unambiguously extract an intrinsic scanning dynamics of AID without an assumed model for the scan matrix W.

Our master equation model has focused exclusively on providing a general method to ascertain scanning dynamics and catalytic rates and efficiencies for enzymes that act on ssDNA. We have illustrated the model by analyzing the unfettered action of AID. However, when acting in B cells during class switch recombination and somatic hypermutation, AID is constrained to act during transcription by accessing ssDNA portions of a transcription bubble (18, 19, 37, 38). In the case of class switch recombination, there are stable R-loops present during transcription containing ∼1–2 kb of ssDNA (39) that AID might act on with relatively few constraints. However, during somatic hypermutation, the availability of ssDNA is likely to limited to small transcription bubbles, which are thought to be ∼7–10 nt. Our analysis of the most basic properties of AID may be relevant to transcription-dependent deamination during somatic hypermutation, at least from an Occam's razor perspective. A generic Ig variable region contains about 1.5–2 kb (15, 16). A transcription bubble moving at an optimal rate of ∼60–70 nt/s (40, 41) would speed past a motif in about 15–20 ms, which is far too rapid for AID to act. Perhaps a more likely scenario would be for AID to scan along the non-transcribed strand of a temporarily stalled transcription bubble. There are in vitro and in vivo data that support this possibility. In a T7 RNA polymerase in vitro transcription assay, AID-initiated C→T mutations occurring at adjacent motifs were greatly elevated over random movements (25, 38), and a similar enhancement of tandem mutations is observed in Ig variable regions in vivo (42, 43).

The bottom line from our current study is that when AID binds to one of its hottest motifs (AGC), it will catalyze about 3–5 deaminations for every 100 encounters, which is a remarkably low catalytic efficiency, yet one designed to ensure mutational diversity. More generally, studies on ssDNA-scanning enzymes are at a nascent stage, and this is an extremely important subject for in vitro experimental studies and provides a rich venue for mathematical modeling. Recent data implicate Apo3B in generating C to T mutations found in breast cancer (44). Expression of AID/Apobec proteins in yeast induces clusters of mutations similar to breast cancer mutation clusters with multiple mutations spaced one to several hundred nucleotides apart on the same DNA strands (45–47). AID/Apobec-induced mutation clusters most likely occur by C→U deaminations on transiently exposed ssDNA formed during double-strand breaks or damaged replication forks (46, 47). It is reasonable to anticipate that other APOBECs, such as Apo3A, Apo3F, and Apo3G, expressed in the “wrong place” at the “wrong time” are likely to act as unwelcome mutators and play a deleterious role in the initiation and promotion of cancer. The master equation model can be used as a benchmark method to identify the dynamic scanning and catalytic properties for the APOBEC family of enzymes.