Abstract
Humans can easily discriminate a randomly spaced from a regularly spaced visual pattern. Here, we demonstrate that observers can adapt to pattern randomness. Following their adaption to prolonged exposure to two-dimensional patterns with varying levels of physical randomness, observers judged the randomness of the pattern. Perceived randomness decreased (increased) following adaptation to high (low) physical randomness (Experiment 1). Adaptation to 22.5°-rotated adaptor stimuli did not cause a randomness aftereffect (Experiment 2), suggesting that positional variation is unlikely to be responsible for the pattern randomness perception. Moreover, the aftereffect was not selective to contrast polarity (Experiment 3) and was not affected by spatial jitter (Experiment 4). Last, the aftereffect was not affected by adaptor configuration (Experiment 5). Our data were consistent with a model assuming filter-rectify-filter processing for orientation inputs. Thus, we infer that neural processing for orientation grouping/segregation underlies the perception of pattern randomness.
The visual world is textured, and the visual system segregates an object from its background by detecting texture borders that are defined by orientation1,2,3,4,5, spatial frequency6,7,8,9,10,11, and motion12,13,14,15,16,17. Texture segregation is psychophysically explained by the filter-rectify-filter (FRF) process18,19,20,21,22,23. The FRF process involves three stages of processing (see Figure 1a). At the first stage, linear filters that are narrowband in terms of orientation and spatial frequency detect local luminance-defined orientation and spatial frequency. The outputs from the first-order filters are rectified (usually by half- or full-wave rectification) at the second stage. At the third stage, second-order filters that have larger receptive fields than the first-order filters sum the rectified outputs from the second stage, and if the second-order filters receive different rectified outputs, a texture border is detected.
Figure 1.
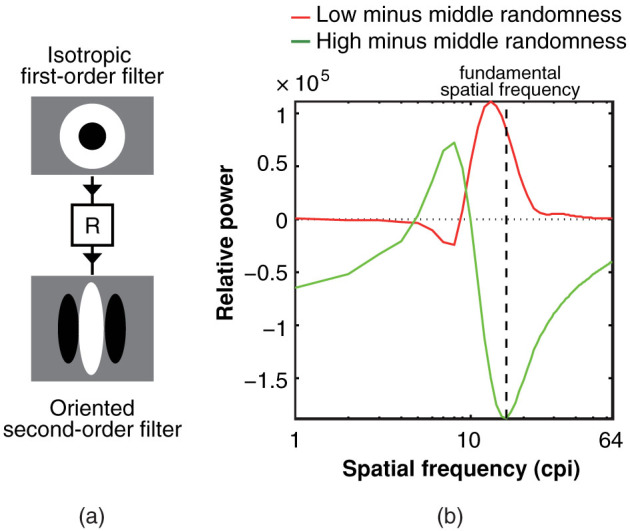
(a) The FRF process used to analyse the stimulus power. First, we convolved three types of dot patterns (patterns with low, middle, and high levels of randomness) with an isotropic first-order filter that was defined by the differences of a Gaussian (DoG) function (upper panel). The standard deviation of the centre region was three pixels, and that of the surrounding region was 4.5 pixels. The amplitude of the centre region was doubled. Second, the half-wave rectified outputs of the convolution were squared to calculate the spatial distribution of the power (middle panel). Third, the power distribution was convolved with the vertically oriented second-order filter (lower panel). The filter was defined by a sinusoidal grating that was windowed by a two-dimensional circular Gaussian function. The spatial frequency of the filter ranged from 1 to 64 cycles per image (cpi). (b) The differences in the second-order filter responses between the low- and middle-level randomness patterns (red curve) and between the high- and middle-level randomness patterns (green curve). The power at the stimulus fundamental spatial frequency of the periodic dot pattern was higher in the adaptor with a low level of randomness than in the adaptor with a middle level of randomness, but was lower in the adaptor with a high level of randomness than in the adaptor with a middle level of randomness because the FRF process is typically orientation-selective, and thus is more sensitive to a pattern with low randomness whose second-order orientation is narrow-band. Thus, the subtraction of the response peak intensity for the middle randomness pattern from the one for the low randomness pattern should be positive, while the subtraction for the middle randomness pattern from the one for the high randomness pattern should be negative. As such, the sign of the difference in the peak response intensity between adaptor and test stimuli at stimulus fundamental spatial frequencies would be a good predictor for the vector of the aftereffect.
Interestingly, a recent psychophysical study proposed that the FRF process operates in the perception of the regularity of a two-dimensional pattern24. Ouhnana et al. used a 7 × 7 grid of elements windowed by a circular aperture. Each grid consisted of elements of Gaussian blobs defined by luminance, difference of Gaussians, or random binary patterns, and these patterns were used as adaptor and test stimuli. Following 2.5 s of adaptation to a one- or two-adaptor pattern(s), two test and comparison pattern stimuli were presented simultaneously. Observers were asked to judge which pattern they perceived as more regular. The researchers reported that the human visual system could adapt to pattern regularity: after prolonged exposure to the regular adaptor stimuli, the appearance of less-regular test stimuli became more irregular (i.e., the regularity aftereffect), and this aftereffect transferred from first-order stimuli (Gaussian blobs) to second-order stimuli (difference of Gaussians and random binary patterns), and vice versa. According to Ouhnana et al. the FRF process of tuning to a second-order cardinal orientation has a spurious peak response at the second-order spatial frequency that corresponds to the fundamental spatial frequency of the periodic dot pattern stimulus when a regular pattern is the process input. By contrast, the process output exhibits no spurious peak at the frequency when a random pattern is input. Thus, the response peak intensity of the FRF process may determine the perceived regularity.
The present study was aimed at demonstrating that the human visual system can adapt to pattern randomness. Ouhnana et al. found that adaptation to pattern regularity is unidirectional; thus, the visual system might not adapt to pattern randomness. However, the researchers did not check the role of the sign of the difference in the response peak intensity between adaptor and test stimuli. Considering the function of the FRF process, it is possible that adaptation to pattern randomness also occurs (see Figure 1 for detail). In Experiment 1, we report that human observers can adapt to pattern randomness (demo can be found as a supplementary movie), and their performance can be explained in terms of the sign of the difference in the peak response intensity between adaptor and test stimuli.
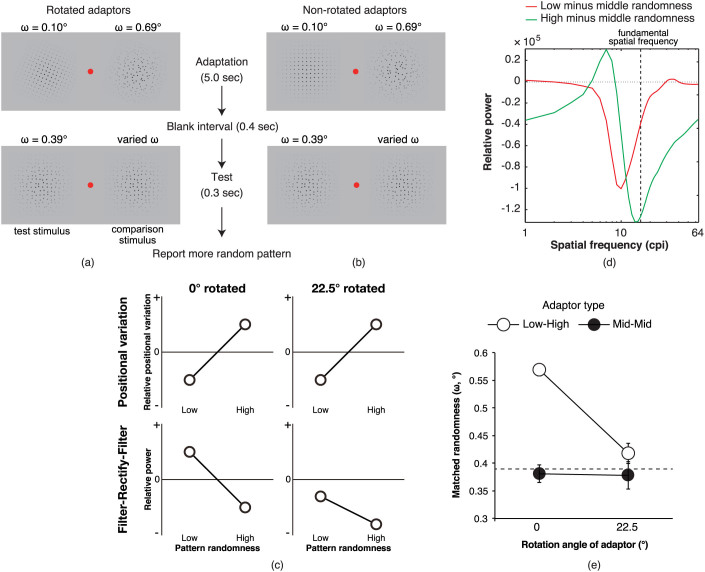
In Experiment 2, we examine whether models other than the FRF process, such as a model based on a relative positional relationship of dots (e.g., distance to the nearest neighbour; Dnn)25 or a model based on an autocorrelation function of patterns26, can explain an individual's adaptation to pattern randomness. We focused on the effect of the rotation of the adaptors on pattern regularity/randomness adaptation. Here, the ‘rotation’ means a change in orientation of a whole pattern (Figure 2a shows examples of a pattern), not a continuous rotational pattern motion. We considered an FRF process that consisted of an isotropic first-order filter defined by the differences of Gaussian function and a vertically oriented second-order filter defined by a sinusoidal grating that was windowed by a two-dimensional circular Gaussian function (Figure 1a). If the FRF process were involved in the pattern randomness aftereffect, the adaptation to rotated adaptors would not cause any aftereffects with non-rotated test stimuli because the FRF process adapting to the rotated pattern has a different orientation tuning to the FRF process for a non-rotated pattern. In Experiment 3, we examined whether the adaptation could occur independent of contrast polarity. Furthermore, to provide evidence on the dissociation of findings between current and previous studies (i.e., bidirectional vs. unidirectional aftereffect), we tested the effect of jittering on the pattern randomness aftereffect (Experiment 4). In some conditions in these experiments, we presented a control adaptor with middle randomness on the contralateral side of a critical adaptor having high randomness. In this situation, it was logically possible that the visual system might adapt to a weak regularity in the control adaptor without having any adaptation to randomness in the critical adaptor. Even under this scenario, a test stimulus that follows the critical adaptor with high randomness is judged to be more regular than a test stimulus that follows the control adaptor with middle randomness when the test stimuli have the same degree of randomness. In this way, with the paradigm having the two adaptors, we could not exclude the alternative interpretation that the visual system adapts to pattern regularity only24. To rule out the involvement of adaptation to a weak regularity in the control adaptor, in Experiment 5 we stopped using a control adaptor, and investigated whether the adaptation to pattern randomness was observed even when only a critical adaptor with high or low randomness was presented.
Figure 2.
(a, b) Schematic diagrams of how the stimuli were presented in (a) low-randomness and (b) high-randomness conditions. (c) The results of Experiment 1. Larger x and y values represent larger physical randomness of the adaptor stimulus and larger matched randomness of the test stimulus, respectively. The dashed line represents the physical randomness value of the test stimulus (i.e., with middle physical randomness) that was fixed through experiments. The error bars denote the standard errors of the means (n = 6).
Results
Observers underwent a two-alternative forced-choice task and were required to report subjectively which of a test and comparison stimulus was the more random pattern. The physical randomness of the test stimulus was fixed at a middle level (ω = 0.39°, ω: the range of uniform distribution for dot displacements in stimuli, see Method section for detail), whereas that of the comparison stimulus was varied by means of a staircase method with a ω range between 0.10° and 0.69°. Consequently, the randomness of the comparison stimulus was perceptually matched to that of the test stimulus, and hence larger matched randomness indicated relatively higher perceived randomness in the experiments that employed a dual adaptor method (Experiments 1–4). In Experiment 5, where a single adaptor method was used, larger matched randomness indicated higher perceived randomness of the test stimulus.
Experiment 1: Pattern randomness aftereffect
A one-way analysis of variance of the matched randomness with the physical randomness of the adaptor stimuli as a factor confirmed that the change in the matched randomness of the test stimulus was significant (F(2, 10) = 12.60, MSE = 0.260, p < 0.002; Figure 2c). Comparisons using Tukey's honestly significant difference method indicated that in the high-randomness condition the matched randomness of the test stimulus was significantly decreased by 0.074° of ω (p < 0.04), and in the low-randomness condition the matched randomness of the test stimulus was significantly increased by 0.070° of ω (p < 0.05). We calculated contrast values of the change in the matched randomness between conditions as [(ω of matched randomness – ω of physical middle randomness)/ω of physical middle randomness] * 100 (%). The calculated contrasts for high-, middle-, and low-randomness adaptors conditions were −18.7%, +0.3%, and +18.2%, respectively. These results are consistent with our prediction and suggest the existence of a strong pattern regularity aftereffect24 and a strong pattern randomness aftereffect.
Experiment 2: Rotating adaptors
Figure 3e shows the results of Experiment 2. A two-way analysis of variance on matched randomness with rotation (unrotated and 22.5° rotated) and type of adaptor stimuli (low-high and middle-middle) as factors confirmed a significant interaction between the factors (F(1, 3) = 55.90, MSE = 0.041, p < 0.005). Simple main effect tests indicated that in the low-high-type adaptor condition a significantly larger matched randomness of the test stimulus was obtained than in the middle-middle type condition when the pattern was not rotated (ω = 0.188°; F(1, 6) = 60.72, MSE = 0.121, p < 0.0003) but did not induce a stronger aftereffect when the pattern was rotated by 22.5° (ω = 0.040°; F(1, 6) = 2.74, MSE = 0.121, p > 0.14). Moreover, in the unrotated adaptor condition, a significantly larger matched randomness of the test stimulus was obtained than in the 22.5°-rotated adaptor condition when the low-high-type adaptor stimuli were used (ω = 0.151°; F(1, 6) = 86.65, MSE = 0.055, p < 0.0002). The high-low type adaptor in the unrotated condition induced a large change in the matched randomness of the test stimulus (a 45.3% increase), while the other conditions induced small changes (high-low-rotated: a 13.9% increase; middle-middle-unrotated: a 1.3% decrease; middle-middle-rotated: a 1.3% decrease). The large change in the high-low-unrotated condition, compared with the high and low conditions in Experiment 1, was due to simultaneous adaptation to the high and low adaptors in Experiment 2. Consistent with our prediction, the results showed that the rotated adaptor stimuli did not induce an aftereffect, suggesting that the peak response of the FRF process at stimulus fundamental spatial frequencies is a determinant in the perception of pattern regularity/randomness, not the positional variations of the dots.
Figure 3.
(a, b) Schematic diagrams for stimulus presentation in (a) rotated adaptor and (b) non-rotated adaptor conditions. (c) Models. The top two and bottom two panels show the possible outputs from the positional variation model and the filter-rectify-filter (FRF) model, respectively. The left two and right two panels show the possible outputs when the adaptor pattern is rotated by 0° and 22.5°, respectively. The zero on the vertical axis means a possible output value for the middle randomness pattern. A relative positional variation does not change even when the pattern is rotated (top right). Conversely, the relative power of outputs from an FRF process with vertical second-order filters decreases to negative values regardless of the adaptor's randomness when the pattern is rotated (bottom right). Thus, when the adaptor pattern is rotated, the positional variation model predicts an intact pattern randomness aftereffect but the FRF model predicts no aftereffect. (d) The differences in the second-order filter responses between the rotated low-randomness patterns and the non-rotated middle-randomness patterns (red curve) and between the rotated high-randomness patterns and non-rotated middle-randomness patterns (green curve). When the adaptors were rotated by 22.5°, the sign of the difference in the power between the patterns was negative for both pairs of adaptor-test stimuli. (e) The results of Experiment 2. Larger y values represent a larger matched randomness of the test stimulus. The dashed line represents the physical randomness value of the test stimulus (i.e., with middle physical randomness) that was fixed through experiments. The error bars denote the standard errors of the mean (n = 4).
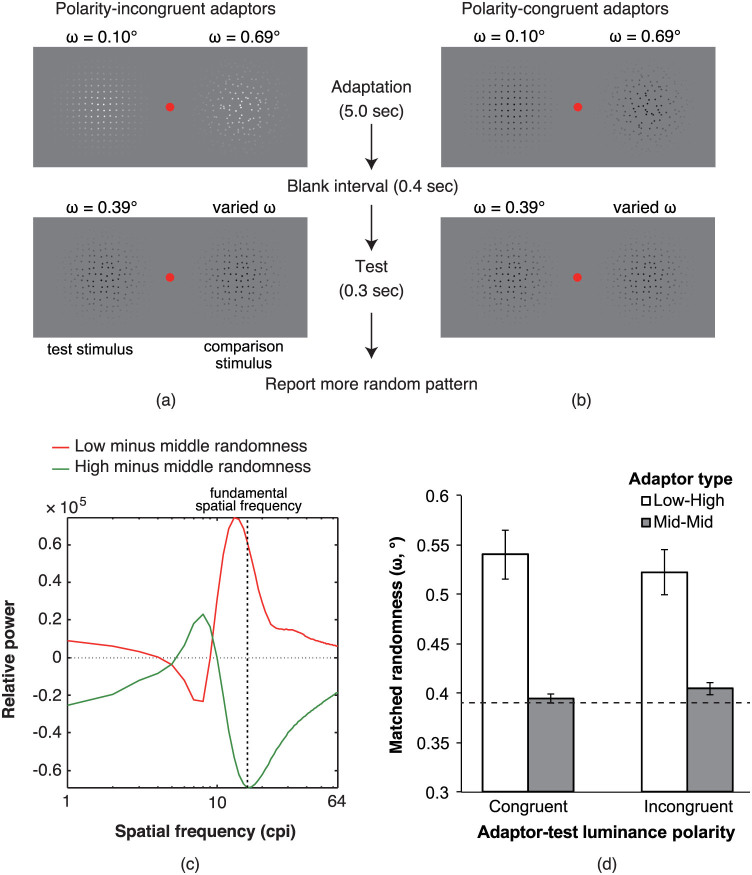
Experiment 3: Reversing contrast polarity between adaptors and test/comparison stimuli
Figure 4d shows the results of Experiment 3. The matched randomness was separately estimated in each of the black-black and white-white conditions and in each of the black-white and white-black conditions; the averaged matched randomness values calculated for each of the congruent and incongruent conditions were used. A two-way analysis of variance on the matched randomness of the test stimulus with the contrast polarity (congruent and incongruent with test stimuli) and type of adaptor stimuli (low-high and middle-middle) as factors showed a significant main effect of type only (F(1, 4) = 33.34, MSE = 0.271, p < 0.005). An individual paired t-test indicated that in the low-high-type adaptor condition a significantly larger matched randomness of the test stimulus was obtained than in the middle-middle-type adaptor condition, even when the contrast polarity of the adaptor and test stimuli was incongruent (ω = 0.118°; t(4) = 5.77, p < 0.005). The high-low type adaptors in both the congruent (a 37.9% increase) and incongruent conditions (a 33.3% increase) induced a large change in the matched randomness of the test stimulus, while the middle-middle type adaptors in the congruent (a 0.8% increase) and incongruent conditions (a 3.3% increase) induced small changes. Thus, the results demonstrated that the congruency of contrast polarity between the adaptor and test stimuli did not affect the magnitude of the aftereffect, suggesting that processing that is insensitive to contrast polarity is involved in the perception of pattern randomness. Such a mechanism is consistent with the idea that the FRF process is involved in the perception of pattern randomness.
Figure 4.
(a, b) Schematic diagrams for the stimulus presentation in (a) the polarity incongruent adaptor conditions and (b) the polarity congruent adaptor conditions. (c) The output of the filter analysis. The patterns with white and black dots were convolved with on- and off-centre filters, respectively. Regardless of the contrast polarity difference between the adaptor and test stimuli, the sign of the difference in the power of the filter responses between the low- and middle-randomness patterns was opposite to the one between the high- and middle-randomness patterns. (d) The results of Experiment 3. Larger y values represent a larger matched randomness of the test stimulus. The dashed line represents the physical randomness value of the test stimulus (i.e., with middle physical randomness) that was fixed through experiments. The error bars denote the standard errors of the mean (n = 5).
Experiment 4: Spatially jittering adaptors
Figure 5 shows the results of Experiment 4. The data obtained in this experiment with spatial jitter in the overall position of the adaptor stimuli are presented as the jitter condition. For comparison, the data of the high-randomness condition of Experiment 1 are presented and here renamed as the no-jitter condition. The individual data show that the matched randomness of the test stimulus in the jitter condition was comparable with that in the no-jitter condition. Moreover, the 95% confidence intervals of the individual data indicate that the matched randomness in the jitter condition was significantly lower than the 0.39° that was the physical randomness value of the test stimulus (YY: a 30.2% decrease; TD: a 34.9% decrease; TO: a 12.6% decrease), confirming that the pattern randomness aftereffect occurred for each observer. These results suggest that jittering the overall positions of the adaptor stimuli did not affect the pattern randomness aftereffect.
Figure 5. Individual data in Experiment 4.
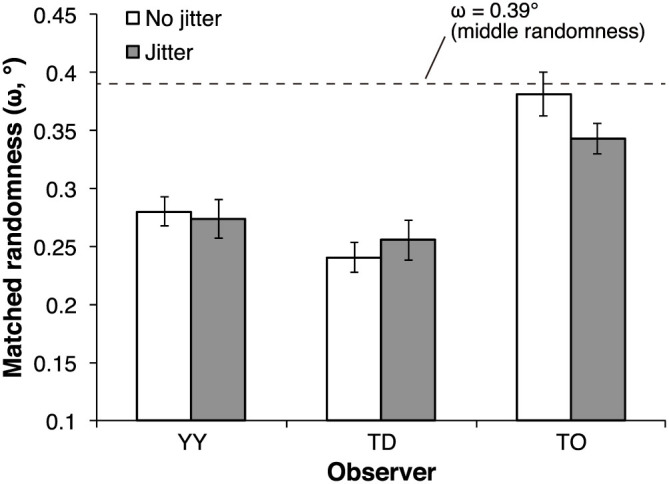
The dashed line represents the physical randomness value of the test stimulus (i.e., with middle physical randomness) that was fixed through experiments. The error bars denote 95% confidence intervals calculated on the basis of the psi method.
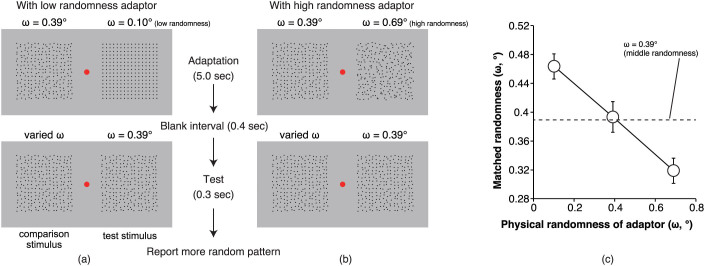
Experiment 5: Single adaptor
Figure 6 shows the results of Experiment 5. Both of the individual data commonly show that the matched randomness of the test stimulus changed depending on the physical randomness of the adaptor stimuli, as in Experiment 1. The 95% confidence intervals of the individual data indicate that the matched randomness in the low-randomness condition was significantly higher than the 0.39° that was the physical randomness value of the test stimulus (YY: a 47.1% increase; TD: a 48.8% increase). The matched randomness in the high-randomness condition was significantly lower than 0.39° (YY: a 24.6% decrease; TD: a 15.7% decrease). These results suggested that the pattern regularity and randomness aftereffects occurred significantly for each observer. Thus, our finding excluded the possibility that the dual adaptor method used in Experiments 1–4 caused the apparent increase in perceived randomness of the test stimulus.
Figure 6.
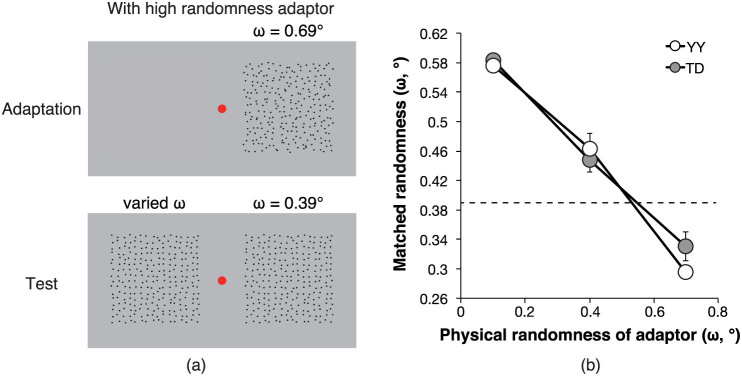
(a) The single adaptor method. (b) Individual data in Experiment 5. The dashed line represents the physical randomness value of the test stimulus (i.e., with middle physical randomness) that was fixed through experiments. The error bars denote 95% confidence intervals calculated on the basis of the psi method.
Discussion
The present study examined whether the human visual system could adapt to pattern randomness. In Experiment 1, we demonstrated that significant negative aftereffects in the perception of pattern randomness occurred after adaptation to both highly regular and highly random patterns. Then, in Experiment 2, we examined whether the adaptation to rotated patterns induced an aftereffect in the perception of pattern randomness. The results demonstrated that the non-rotated patterns significantly induced an aftereffect, whereas the rotated patterns did not, suggesting that the FRF process that a previous study suggested24 is responsible for pattern regularity/randomness perception, not the mechanism for detecting positional variation, such as Dnn25 or an autocorrelation function26. In Experiment 3, we also found that the adaptation to pattern randomness/regularity was insensitive to the luminance contrast of the dots between the adaptor and test stimuli. In Experiment 5, the single adaptor successfully induced the pattern randomness aftereffect. These results suggest that the human visual system can indeed encode pattern randomness.
We also observed large differences in the filter responses between the adaptor and test stimuli at frequencies lower than the stimulus fundamental spatial frequencies. One may argue that the difference in the filter responses at lower frequencies might also contribute to the perception of pattern randomness. However, this possibility is unlikely because the stimuli used in both Experiments 1 and 2 had a similar pattern of the difference at lower spatial frequencies, whereas in Experiment 1 only, the pattern randomness aftereffect occurred when there was a large difference between the filter responses at stimulus fundamental spatial frequencies. These results support the hypothesis that filter responses at stimulus fundamental spatial frequencies are responsible for the perception of pattern randomness.
The reason for the disparity between the results of this study, which observed both the pattern randomness and regularity aftereffects, and those of Ouhnana et al24. who observed only a unidirectional regularity aftereffect, is still unclear. This disparity may be due to the methodological differences between the studies. One of the prominent differences between the two studies was in the number of elements: we used a 16 × 16 grid, whereas Ouhnana et al. used a 7 × 7 grid. This latter condition may be insufficient to yield an ample difference in peak response at stimulus fundamental spatial frequencies in conditions of high randomness, which would prevent the occurrence of an aftereffect. Furthermore, in the study by Ouhnana et al. stimuli were jittered to avoid afterimages or positional adaptation. Thus, one may argue that this jitter may have disrupted the perception of randomness; however, the results of Experiment 4 suggest that jittering the overall positions of the adaptor stimuli does not affect the pattern randomness aftereffect. Moreover, it was possible that the difference in the adaptor configuration (single vs. dual adaptor method) was related to this discrepancy, but this possibility was also excluded in Experiment 5.
The pattern randomness aftereffect occurred even when the contrast polarity of the dots was reversed between the adaptor and test stimuli (Experiment 3). In this respect, the process responsible for the aftereffect should be insensitive to contrast polarity. To date, some data on the adaptation to texture patterns have been reported, but they are often selective to contrast polarity. For example, adaptations to the density of texture27,28 and global shape29 are sensitive to contrast polarity changes between adaptor and test stimuli. Recent studies have also suggested that the spatial integration of contrast or orientation is polarity selective30,31. By contrast, tilt aftereffects that are involved in gain control for the outputs of first-order orientation detectors are not selective to contrast polarity32,33. Taken together, we suggest that the perception of pattern randomness is rooted in the adaptation of polarity-independent orientation detectors that are located in a different processing stream than that of the spatial integration of first-order orientation. A previous study proposed that the FRF process can be selective of the phase of first-order filters, and that the subsequent outputs of the FRF processes are summed across the FRF process tuning to different first-order phases34. The processing involved in the subsequent summation of second-order orientation detectors may be responsible for the perception of pattern randomness.
Which neural sites are responsible for the perception of pattern randomness remains unclear. The inferotemporal cortex (IT) may represent the statistical properties of image information35. However, the neurons in that area are often selective to contrast polarity36,37. Thus, the IT neurons may not be responsible for the pattern randomness aftereffects that are not selective to contrast polarity. The neurons in the lateral occipital complex (LOC) are insensitive to contrast polarity in stimuli38 and generally subserve object recognition39. Furthermore, these neurons contribute to the spatial integration of orientation signals40,41. Because we assume that the FRF process relevant to pattern randomness aftereffects is not related to the spatial integration of first-order orientation, it is not clear whether LOC neurons can be considered neural sites that represent pattern randomness. A previous study found that VO1 and LO1 are responsible for the orientation processing of contrast modulation42. We suspect that these neural sites are responsible for the perception of pattern randomness. Future studies are warranted to uncover the neural and psychophysical mechanisms that underlie the perception of pattern randomness.
Methods
Experiment 1
In Experiment 1, we aimed to demonstrate an aftereffect following an adaptation to a random pattern that is beyond the aftereffect following the adaptation to regular patterns that was reported by Ouhnana et al24. Figure 2a and 2b represent schematic diagrams of how the stimuli were presented. We predicted that if the relative filter responses at stimulus fundamental spatial frequencies between adaptor and test stimuli were critical, the sign of the difference in the peak power should also alter the vector in the resultant aftereffect. By employing an FRF process in which a second-order orientation filter receives the powered outputs of an off-centre isotropic detector (Figure 1a), we found that at stimulus fundamental spatial frequencies, the difference in peak power between adaptor and test stimuli was positive when comparing a low-randomness adaptor and test stimulus (the red curve in Figure 1b) but was negative when comparing a high-randomness adaptor and test stimulus (the green curve in Figure 1b). If the visual system discriminates pattern randomness based on the filter responses at this second-order spatial-frequency, a bi-directional aftereffect should occur. In other words, a middle-randomness pattern will appear less random after adapting to a high-randomness pattern, and will appear more random after adapting to a low-randomness pattern.
Observers
Six observers (3 males, 3 females), including the authors (YY and MM), participated in Experiment 1. Apart from the authors, the observers were unaware of the purpose of the experiment, and all reported that they had normal or corrected-to-normal visual acuity. This and the subsequent experiments were conducted according to the principles laid down in the Declaration of Helsinki. Written informed consent was obtained from all participants except the authors after the nature and possible consequences of the study were explained to them. The ethics committee of Yamaguchi University approved the protocol.
Apparatus
Stimuli were presented on a linearised 21-inch CRT monitor (GDM-F520, Sony, Tokyo, Japan) with a resolution of 1024 × 768 pixels and a 100-Hz refresh rate. The presentation of stimuli and the collection of data were controlled by a computer (Mac Pro, Apple). The observer's visual field was fixed at a viewing distance of 45 cm using a chin-head rest, and the size information and visual angle described here were based on this viewing distance. The stimuli were generated by MATLAB (Mathworks Inc.) with the Psychtoolbox extensions.
Stimuli
Stimuli (see Figure 2a and 2b) consisted of a fixation point, two adaptor stimuli, and a test and comparison stimuli that were displayed on a grey background (60.78 cd/m2). The fixation point was a small red circle (CIE: 0.60/0.33, 18.47 cd/m2) with a radius of 0.49° and was presented in the centre of the display. The stimulus patterns consisted of two-dimensional dot patterns consisted of 256 (16 × 16) black dots with a radius of 0.05° (0.02 cd/m2) and a height and width of 12.54°. The distance between dot centres was 0.78°. The left and right adaptors (and the test and comparison stimuli) were centred at the left and right sides of the display, respectively, with an eccentricity of 9.80°. Within each pattern, the position of each dot was determined based on a continuous uniform probability density function with mean μ and range ω in x and y dimensions43:
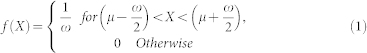 |
where X represents the position of each dot, μ represents a possible dot position when the dots were completely aligned on a grid, and ω determined the physical randomness of the pattern; a larger ω denotes a more physically random pattern. Patterns with low, middle, and high physical randomness were employed as the adaptor stimuli (ω = 0.10, 0.39, and 0.69°, respectively). Patterns with seven levels of physical randomness were employed as the comparison stimuli (ω = 0.10, 0.20, 0.30, 0.39, 0.49, 0.59, and 0.69°).
Procedure
The experiment was conducted in a darkened room. The observer initiated each trial by pressing the spacebar on a computer keyboard. The fixation point was presented throughout the experiment. Immediately after the spacebar was pressed, the adaptor stimuli were presented for 5.0 s (10.0 s in the first trial). One adaptor stimulus was always a pattern with middle-level randomness, and the other adaptor stimulus was a pattern with a low, middle, or high level of randomness. The presentation side of a pattern with each of the three levels of randomness was fixed in an experimental block and was counterbalanced across all observers. Next, a blank screen was shown for 0.4 s; subsequently, the test and comparison stimuli were presented for 0.3 s. After the stimulus presentation was finished, the observers were asked to judge which of the test and comparison stimuli was perceived to be more random in a two-alternative forced-choice fashion. The comparison stimulus presented at the location of the adaptor with a middle level of randomness was given a physical randomness (ω) manipulated by the Psi method44 using the Palamedes toolbox45 to estimate the point of subjective equality of the matched randomness for the test stimulus. The test stimulus, with a high or low level of randomness, was presented at the location of the adaptor, which was always given a middle level of randomness. Although the matched randomness here is a relative measure that actually shows a difference in appearance of the test and comparison stimuli, the adaptor stimuli with middle physical randomness was presented at the location of the comparison stimulus in all of the experimental blocks; therefore, we considered the larger matched randomness as the (relatively) higher perceived randomness of the test stimulus, compared with the comparison stimulus. The minimum step size was 0.10° of ω, and the measurements were stopped after 150 trials. No explicit feedback for the correctness of responses was provided. Each of the three levels of physical randomness of one adaptor stimulus was blocked, and the order of the blocks was randomised across observers.
Experiment 2
The purpose of this experiment was to rule out the possibility that the randomness aftereffect stemmed from the adaptation to relative positional variations among dots. Here, we employed rotated adaptors (Figure 3). If the visual system could adapt to the positional variations among dots, no difference in aftereffect magnitudes would be observed between the unrotated and 22.5°-rotated adaptors because the positional variations among dots were identical (Figure 3c, Top). However, if the FRF process could be adapted, a difference in aftereffect magnitudes would be observed for the reason described below (Figure 3c, Bottom). We analysed how the filter tuning to vertical orientation could respond to dot pattern stimuli rotated 22.5° clockwise (Figure 3a), and calculated differences in the change in peak power of the filter between 22.5°-rotated patterns with varying magnitudes of randomness and unrotated patterns with a middle randomness magnitude (Figure 3d). Interestingly, the sign of the peak response at stimulus fundamental spatial frequencies was negative between both the 22.5°-rotated adaptors with high/low physical randomness and the unrotated test stimulus. If the sign of the difference in peak powers at the fundamental spatial frequencies were the determinant of the aftereffect vector, the adaptation to the 22.5°-rotated pattern would not cause an aftereffect with the unrotated pattern because the adaptation to the rotated pattern would not change the peak response of the FRF process for the unrotated test stimulus at the fundamental spatial frequencies.
Observers
Four observers (1 male, 3 females), including one of the authors (YY), participated in Experiment 2. Apart from the author, the observers were unaware of the purpose of the experiment, and all reported that they had normal or corrected-to-normal visual acuity.
Apparatus, stimuli, and procedure
This experiment was identical to Experiment 1 except for the following aspects. Adaptor, test, and comparison stimuli were windowed by a two-dimensional, circular Gaussian function with a standard deviation of 3.54°. The adaptor stimuli were unrotated or rotated by 22.5° clockwise or anticlockwise, and the rotation direction was counterbalanced between observers. We did not rotate the stimuli by 45° because the two-dimensional Fourier amplitude spectrum of the unrotated stimuli clearly contained oblique components and we wanted to reduce the contamination of the oblique components between 45°-rotated and unrotated patterns. In the low-high condition, the physical randomness of one adaptor stimulus was fixed to be low (ω = 0.10°) and that of another adaptor stimulus was fixed to be high (ω = 0.69°). In the middle-middle condition, the physical randomness of both adaptor stimuli was fixed at a middle level (ω = 0.39°). Finally, in the low-high condition, the comparison stimulus following the adaptor with a high-level of randomness was given a physical randomness manipulated by the Psi method, whereas the test stimulus following the adaptor with a low-level randomness was given a middle-level randomness (ω = 0.39°). Thus, matched randomness represented the sum of the simultaneous adaptation effect by low- and high-physical randomness stimuli on the test and comparison stimuli, respectively. Hence, a larger matched randomness occurred when the degree of the negative aftereffect from one adaptor stimulus was larger than the degree of the positive aftereffect from the other adaptor stimulus (if any), and we considered this as a larger pattern randomness aftereffect.
Experiment 3
If the power of the orientation filters were the source of the aftereffect, a contrast polarity change between adaptor and test stimuli (Figure 4a) should not affect the magnitude of the aftereffect because the sign of the difference in the power at stimulus fundamental spatial frequencies is preserved, even when the contrast polarity between the adaptor stimulus and the test and comparison stimuli is reversed (Figure 4c).
Observers
Five observers (2 males, 3 females), including one of the authors (YY), participated in Experiment 3. Apart from the author, the observers were unaware of the purpose of the experiment, and all reported that they had normal or corrected-to-normal visual acuity.
Apparatus, stimuli, and procedure
This experiment was identical to Experiment 1 except in the following aspects. The background luminance was decreased to 40.69 cd/m2, and adaptor stimuli that consisted of white dots (81.64 cd/m2) were also generated. In the congruent condition (Figure 4b), the luminance of the dots was the same in the adaptor, test, and comparison stimuli (black-black or white-white). In the incongruent condition (Figure 4a), the luminance of the dots was different between the adaptor stimuli and the test and comparison stimuli (black-white or white-black). As in Experiment 2, the low-high and middle-middle conditions were employed.
Experiment 4
Experiment 4 was performed to test whether jittering the overall position of the adaptor stimuli disrupted adaptation to high-randomness patterns.
Observers
One of the authors (YY) and two observers (TD and TO) who were experienced in psychophysical experiments but unaware of the experimental hypothesis participated in this experiment, and all reported that they had normal or corrected-to-normal visual acuity.
Apparatus, stimuli, and procedure
Experiment 4 was identical to the high-randomness condition (ω = 0.69°) of Experiment 1 in the main text other than the following. Every 500 ms, the positions of the dots in the adaptor stimuli were refreshed, and the overall positions of the adaptor stimuli were displaced by 20′ in a random direction.
Experiment 5
We interpreted the previous results as indicating that the visual system adapts to pattern randomness. However, it is possible to argue that the results of Experiments 1–4 were due to artefacts based on the dual adaptor method used in those experiments. In the previous experiments, the middle-randomness adaptor was presented on the contralateral side of the high-randomness adaptor. We believe that the visual system adapted to randomness in the adaptor with high randomness. However, it was logically possible that under the dual-adaptor presentation, the visual system might adapt to a weak regularity in the middle randomness adaptor without having any adaptation to randomness in the high randomness adaptor. Even under this scenario, a test stimulus that follows the high-randomness adaptor is judged to be more regular than a test stimulus that follows the middle randomness adaptor when the test stimuli have the same degree of randomness. Thus, the previous results were still consistent with Ouhnana et al. suggesting that the visual system can adapt to pattern regularity, but not to pattern randomness. Therefore, we could not assert the existence of the adaptation to pattern randomness under the dual-adaptor method. To exclude the involvement of an adaptation to a weak regularity in the middle-randomness adaptor, in Experiment 5 we used a single adaptor method in which only one adaptor stimulus was presented.
Observers
One of the authors (YY) and one observer (TD), who were experienced in psychophysical experiments but unaware of the experimental hypothesis, participated in this experiment, and both reported that they had normal or corrected-to-normal visual acuity.
Apparatus, stimuli, and procedure
Experiment 5 was identical to Experiment 1 other than the following: in this experiment, the adaptor stimulus that always had a fixed physical randomness at the middle level (ω = 0.39°) was no longer presented.
Author Contributions
Y.Y., T.K. and M.M. designed the experiments, discussed the data, and wrote the paper. Y.Y. conducted the experiments. Y.Y. and T.K. analysed the data. M.M. supervised the project.
Supplementary Material
Supplementary Video
Supplementary Info
Acknowledgments
This work was supported by the Japan Society for the Promotion of Science KAKENHI (Grants-in-Aid for Scientific Research) Grant Numbers 21670004 and 25242058 to M.M.
References
- Beck J. Perceptual grouping produced by changes in orientation and shape. Science 154, 538–540 (1966). [DOI] [PubMed] [Google Scholar]
- Landy M. S. & Bergen J. R. Texture segregation and orientation gradient. Vis Res 31, 679–691 (1991). [DOI] [PubMed] [Google Scholar]
- Motoyoshi I. & Nishida S. Temporal resolution of orientation-based texture segregation. Vis Res 41, 2089–2105 (2001). [DOI] [PubMed] [Google Scholar]
- Nothdurft H. C. Orientation sensitivity and texture segmentation in patterns with different line orientation. Vis Res 25, 551–560 (1985). [DOI] [PubMed] [Google Scholar]
- Sagi D. & Julesz B. “Where” and “what” in vision. Science 228, 1217–1219 (1985). [DOI] [PubMed] [Google Scholar]
- Beck J., Sutter A. & Ivry R. Spatial frequency channels and perceptual grouping in texture segregation. Comput Vision Graph 37, 299–325 (1987). [Google Scholar]
- Bergen J. R. & Adelson E. H. Early vision and texture perception. Nature 333, 363–364 (1988). [DOI] [PubMed] [Google Scholar]
- Bovik A. C., Clark M. & Geisler W. S. Multichannel texture analysis using localized spatial filters. IEEE Trans Pattern Anal Mach Intell 12, 55–73 (1990). [Google Scholar]
- Fogel I. & Sagi D. Gabor filters as texture discriminator. Biol Cybern 61, 103–113 (1989). [Google Scholar]
- Joffe K. M. & Scialfa C. T. Texture segmentation as a function of eccentricity, spatial frequency and target size. Spatial Vision 9, 325–342 (1995). [DOI] [PubMed] [Google Scholar]
- Sutter A., Beck J. & Graham N. Contrast and spatial variables in texture segregation: testing a simple spatial-frequency channels model. Percept Psychophys 46, 312–332 (1989). [DOI] [PubMed] [Google Scholar]
- Braddick O. A short-range process in apparent motion. Vis Res 14, 519–527 (1974). [DOI] [PubMed] [Google Scholar]
- Kandil F. I. & Fahle M. Figure–ground segregation can rely on differences in motion direction. Vis Res 44, 3177–3182 (2004). [DOI] [PubMed] [Google Scholar]
- Lee S.-H. & Blake R. Visual form created solely from temporal structure. Science 284, 1165–1168 (1999). [DOI] [PubMed] [Google Scholar]
- Nakayama K. & Silverman G. H. Serial and parallel processing of visual feature conjunctions. Nature 320, 264–265 (1986). [DOI] [PubMed] [Google Scholar]
- Nothdurft H.-C. The role of features in preattentive vision: Comparison of orientation, motion and color cues. Vis Res 33, 1937–1958 (1993). [DOI] [PubMed] [Google Scholar]
- Takeuchi T., Yokosawa K. & De Valois K. K. Texture segregation by motion under low luminance levels. Vis Res 44, 157–166 (2004). [DOI] [PubMed] [Google Scholar]
- Chubb C. & Sperling G. Drift-balanced random stimuli: A general basis for studying non-Fourier motion perception. J Opt Soc Am A Opt Image Sci Vis 5, 1986–2007 (1988). [DOI] [PubMed] [Google Scholar]
- Dakin S. C., Williams C. B. & Hess R. F. The interaction of first- and second-order cues to orientation. Vis Res 39, 2867–2884 (1999). [DOI] [PubMed] [Google Scholar]
- Graham N., Beck J. & Sutter A. Nonlinear processes in spatial-frequency channel models of perceived texture segregation: Effects of sign and amount of contrast. Vis Res 32, 719–743 (1992). [DOI] [PubMed] [Google Scholar]
- Kawabe T. & Miura K. Surface segregation driven by orientation-defined junctions. Exp Brain Res 158, 391–395 (2004). [DOI] [PubMed] [Google Scholar]
- Kingdom F. A. A., Prins N. & Hayes A. Mechanism independence for texture-modulation detection is consistent with a filter-rectify-filter mechanism. Vis Neurosci 20, 65–76 (2003). [DOI] [PubMed] [Google Scholar]
- Malik J. & Perona P. Preattentive texture discrimination with early vision mechanisms. J Opt Soc Am A Opt Image Sci Vis 7, 923–932 (1990). [DOI] [PubMed] [Google Scholar]
- Ouhnana M., Bell J., Solomon J. A. & Kingdom F. A. A. Aftereffect of perceived regularity. J Vis 13(8):18, 1–13 (2013). [DOI] [PubMed] [Google Scholar]
- Ginsburg N. The organization of visual objects: randomness. Percept Mot Skills 85, 575–578 (1997). [DOI] [PubMed] [Google Scholar]
- Fujii K., Sugi S. & Ando Y. Textural properties corresponding to visual perception based on the correlation mechanism in the visual system. Psychol Res 67, 197–208 (2003). [DOI] [PubMed] [Google Scholar]
- Durgin F. H. & Huk A. C. Texture density aftereffects in the perception of artificial and natural textures. Vis Res 37, 3273–3282 (1997). [DOI] [PubMed] [Google Scholar]
- Tibber M. S., Greenwood J. A. & Dakin S. C. Number and density discrimination rely on a common metric: Similar psychophysical effects of size, contrast, and divided attention. J Vis 12(6):8, 1–19 (2012). [DOI] [PubMed] [Google Scholar]
- Bell J., Gheorghiu E., Hess R. F. & Kingdom F. A. A. Global shape processing involves a hierarchy of integration. Vis Res 51, 1760–1766 (2011). [DOI] [PubMed] [Google Scholar]
- Qian K., Kawabe T., Yamada Y. & Miura K. The role of orientation processing in the scintillating grid illusion. Atten Percept Psychophys 74, 1020–1032 (2012). [DOI] [PubMed] [Google Scholar]
- Sato H., Motoyoshi I. & Sato T. Polarity selectivity of spatial interactions in perceived contrast. J Vis 12(2):3, 1–10 (2012). [DOI] [PubMed] [Google Scholar]
- Magnussen S. & Kurtenbach W. A test for contrast-polarity selectivity in the tilt afltereffect. Perception 8, 523–528 (1979). [DOI] [PubMed] [Google Scholar]
- O'Shea R. P., Wilson R. G. & Duckett A. The effects of contrast reversal on the direct, indirect, and interocularly-transferred tilt aftereffect. NZ J Psychol 22, 94–100 (1993). [Google Scholar]
- Motoyoshi I. & Kingdom F. A. A. Differential roles of contrast polarity reveal two streams of second-order visual processing. Vis Res 47, 2047–2054 (2007). [DOI] [PubMed] [Google Scholar]
- Nishio A., Goda N. & Komatsu H. Neural selectivity and representation of gloss in the monkey inferior temporal cortex. J Neurosci 32, 10780–10793 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruizinga P. & Petkov N. Computational model of dot-pattern selective cells. Biol Cybern 83, 313–325 (2000). [DOI] [PubMed] [Google Scholar]
- Tanaka K., Saito H.-A., Fukada Y. & Moriya M. Coding visual images of objects in the inferotemporal cortex of the macaque monkey. J Neurophysiol 66, 170–189 (1991). [DOI] [PubMed] [Google Scholar]
- Murray S. O. & He S. Contrast invariance in the human lateral occipital complex depends on attention. Curr Biol 16, 606–611 (2006). [DOI] [PubMed] [Google Scholar]
- Grill-Spector K., Kourtzi Z. & Kanwisher N. The lateral occipital complex and its role in object recognition. Vis Res 41, 1409–1422 (2001). [DOI] [PubMed] [Google Scholar]
- Kourtzi Z., Tolias A. S., Altman C. F., Augath M. & Logothetis N. K. Integration of local features into global shapes: Monkey and human fMRI studies. Neuron 37, 333–346 (2003). [DOI] [PubMed] [Google Scholar]
- Lerner Y., Hendler T. & Malach R. Object-completion effects in the human lateral occipital complex. Cereb Cortex 12, 163–177 (2002). [DOI] [PubMed] [Google Scholar]
- Larsson J., Landy M. S. & Heeger D. J. Orientation-selective adaptation to first- and second-order patterns in human visual cortex. J Neurophysiol 95, 862–881 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan M. J., Mareschal I., Chubb C. & Solomon J. A. Perceived pattern regularity computed as a summary statistic: Implications for camouflage. Proc R Soc Lond B Biol Sci 279, 2754–2760 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kontsevich L. L. & Tyler C. W. Bayesian adaptive estimation of psychometric slope and threshold. Vis Res 39, 2729–2737 (1999). [DOI] [PubMed] [Google Scholar]
- Prins N. & Kingdom F. A. A. Palamedes: Matlab routines for analyzing psychophysical data. http://www.palamedestoolbox.org (2009). [Accessed 29 July 2013]. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Video
Supplementary Info