Abstract
Corneal biomechanics is an essential parameter for developing diagnostic and treatment methods of corneal-related diseases. It is widely accepted that corneal mechanical strength stems from the stroma's collagenous composition. However, more comprehensive insight into the mechanical properties within the stroma is needed to improve current corneal diagnostic and treatment techniques. The purpose of this study was to perform elasticity characterization of anterior and posterior stromal regions of human corneas using atomic force microscopy (AFM). Nine pairs of human whole globes were placed in 20% Dextran solution, cornea side down, to restore the corneal thickness to physiological levels (400-600μm). The epithelium and Bowman's membrane were removed from all eyes. Anterior stromal AFM elasticity testing was then performed on left (OS) eyes. Additional stroma was removed from right (OD) eyes to allow posterior stromal measurements at a depth of 50% of the original thickness. All experiments were performed with corneas submerged in 15% Dextran to maintain corneal hydration. The results of the study showed that the Young's modulus of elasticity of the anterior stroma (average: 281 ± 214kPa; range: 59-764kPa) was significantly higher than that of the posterior stroma (average: 89.5 ± 46.1kPa; range: 29-179kPa) (p=0.014). In addition, a linear relationship was found between the posterior stromal elasticity and anterior stromal elasticity (p=0.0428). On average, the elasticity of the posterior stroma is 39.3% of the anterior stroma. In summary, there appears to be an elasticity gradient within the corneal stroma, which should be considered in the design and development of corneal diagnostic and treatment methods to enhance efficacy.
Keywords: Atomic Force Microscopy, cornea, mechanical properties
1. Introduction
Corneal biomechanics have been shown to be relevant in the diagnosis and treatment of various corneal diseases. Corneal biomechanics provide insight into the structure of the cornea and its relation to corneal physiological function. Such knowledge allows the assessment of postoperative therapeutic methods like crosslinking for keratoconus and post-LASIK ectasia or phototherapeutic keratectomy (PTK) for granular corneal dystrophy. In addition, accurate corneal mechanical measurements are needed to avoid compliance mismatch in keratoprothesis, corneal onlay, and corneal inlay development (Ruberti et al, 2011; Kamiya et al, 2008; Pepose et al, 2007). Corneal biomechanics is also vital in determining accurate intraocular pressure measurements, which greatly influence effective diagnosis as well as risk and treatment management of glaucoma (Harada and Naoi, 2004; Brown et al, 2006).
Corneal mechanical strength and structural integrity stems from its collagen constituents found predominantly in the stroma (Dupps et al. 2006; DelMonte et al. 2011; Winkler et al. 2011). The structure of the collagen framework in the corneal stroma greatly influences corneal biomechanical and optical properties (Daxer et al. 1998; Winkler et al. 2011). Various studies have shown the existence of regional differences in collagen lamellar orientation across and throughout the thickness of human corneas, especially within the stroma (Kokott. 1938;Kamma-Lorger et al. 2010;Abahussin et al. 2009;Boote et al. 2005). The anterior stroma consists of thinner, more densely-packed interwoven collagen lamellae of random orientation with some connecting to Bowman's membrane, contributing to the anterior corneal mosaic formation and corneal curvature (DelMonte et al. 2011; Abahussin et al. 2009; Morishige et al. 2011; Kotecha, 2007; Bron, 1968; Bron et al. 1969; Bron et al. 1970; Komai et al. 1991; Freund et al. 1995; Bron, 2001). The posterior stroma contains thicker, more loosely-packed lamellae of limbus to limbus orientation and is a region of increased collagen lamellae order, hydration, and swelling properties (Freund et al. 1995; Bron, 2001; Patel et al. 1995; Turss et al. 1971; Muller et al. 2001).
With such depth-dependent structural differences within the stroma, corresponding biomechanical property differences between the distinct stromal regions should also be reflected. In fact, previous studies have shown such depth dependence of the corneal mechanical properties, despite different characterization techniques (Winkler et al. 2011; Randleman et al. 2008; Kohlhaas et al. 2006; Scarcelli et al. 2013). Although the numerical values of mechanical properties varied among the studies, all agreed that the mechanical properties of the anterior stroma are significantly distinct from that of the posterior stroma. The anterior stroma was found to be stiffer (Winkler et al. 2011; Kohlhaas et al. 2006; Scarcelli et al. 2012; Scarcelli et al. 2013) as well as have a greater adhesion force (Randleman et al. 2008) than the posterior stroma. Thus, the overall goal of this study is to build upon the previous findings of Kohlhaas et al (2006), Randleman et al (2008), Winkler et al (2011), and Scarcelli et al (2013) by investigating the localized effective compressive elastic modulus of the hydrated human stroma at different depths and determining a relationship between anterior and posterior stromal elasticity using Atomic Force Microscopy (AFM). AFM enables localized mechanical sample testing in aqueous solutions (Lal et al. 1994; Karrasch et al. 1994). Because of the low indentation depths applied perpendicular to the tissue plane of interest, AFM can independently characterize the distinct layers of the cornea and perform depth-dependent characterization studies. The application of AFM to mechanically characterize the corneal tissue is forthcoming, with recent studies including the elastic characterization of the human corneal basement membranes, Bowman's membrane and anterior stroma (Last et al. 2009; Last et al. 2012; Lombardo et al. 2012).
2. Materials and Methods
2.1 Atomic Force Microscope
Atomic force microscopy (AFM) can be used to determine the mechanical properties of a variety of biological samples through the principle of nanoindentation. AFM involves the use of a cantilever tip that probes a sample of interest, applying a small force (typically on the order of pN), and monitoring the cantilever deflection due to sample interaction with the use of laser that is focused onto the cantilever tip (Binnig et al. 1986). Although AFM is widely used in the field of cell mechanics, the use of AFM can be expanded to the tissue level. This can be achieved by the modification of standard AFM indenter tips with glass microspheres, thereby increasing the surface contact area to measure tissue mechanical responses rather than individual tissue components (Last et al. 2009). The AFM system used in these studies is a custom laboratory-made modification of the AFM design used for imaging (Last et al. 2009;Wojcikiewicz et al. 2003;Ziebarth et al. 2007;Ziebarth et al. 2011). Tipless AFM cantilevers (nominal spring constant: 4.5 N/m, NSC12 series, Mikromasch, San Jose, CA) were modified with glass microspheres (59-74μm diameter, 15926-100, Polysciences Inc.) by using a water-resistant two-part epoxy adhesive to attach a microsphere onto the cantilever with the aid of an inverted optical microscope (Carl Zeiss Stemi-2000C), allowing it to dry overnight, and then rinsing it in ethanol to remove excess epoxy from the tip. The modified tip was then calibrated to determine its spring constant using a reference force calibration cantilever (nominal spring constant: 10.4 N/m, CLFC-NOBO, Bruker, Camarillo, CA) manufactured specifically for the calibration of other probes. Using the reference cantilever calibration technique, the modified tip was used to probe both the tip and the base of the reference cantilever to obtain and record the resultant deflections (Sref and Shard, respectively) (Ohler, 2010). Using the acquired deflection values, the spring constant of the modified tip, k, is calculated from (Ohler, 2010):
where kref [N/m] is the spring constant of the reference cantilever, Sref [nm/V] is the measured deflection on the tip of the reference cantilever, Shard [nm/V] is the measured deflection on the base of the reference cantilever, L[m] is the length of the reference cantilever, and ΔL [m] is the offset distance of the modified tip from the end of the reference cantilever.
The modified cantilever tips were lowered onto the corneal samples using a piezoelectric mechanism (60μm maximal expansion, P-841.40, Physik Instrumente, Germany). In effect, the cantilever experiences a combination of indentation and deflection (bending) dependent on the sample softness: the harder the sample, the more the cantilever deflects and the less it indents the sample. Cantilever deflection corresponds to the force that the AFM probe tip exerts on the sample. Recorded cantilever deflection-indentation curves can be used to derive the sample's force-indentation curves, after factoring out the cantilever deflection on a hard surface and incorporating the measured spring constant. According to the Hertz contact mechanical model (Hertz, 1881), the force-indentation relation is a function of the effective Young's modulus of elasticity:
where F [N] is the measured force (N), E [N/m2] is Young's modulus (Pa), ν is Poisson's ratio (ν=0.49 for the cornea (Liu et al. 2005;Knox Cartwright et al. 2011;Cabrera Fernandez et al. 2005)), R [m] is the radius of the spherical indenter (m), and D is the measured indentation. The custom AFM system was calibrated with agarose gels of different concentrations for comparison to that seen in literature (Normand et al. 2000); the elasticity results obtained from the custom AFM system were an average of 1.5 times greater than the compressive elasticity results produced from the Instron machine used by Normand et al (2000).
2.2 Experimental protocol
Experiments were conducted on 9 pairs of human cadaver eyes (age range: 63-93 years old) retrieved from the Florida Lions Eye Bank (Miami, FL) with the average postmortem time of 7.1 ± 2.8 days (range: 3-11 days). The human eye globes arrived from the eye bank in sealed vials placed in Styrofoam containers filled with ice. Upon arrival in the laboratory, the corneal epithelium was removed using a cotton-tipped applicator and pachymetry measurements were taken to determine extent of corneal swelling. The whole globes were submerged in 20% Dextran solution, cornea side down, to restore corneal thickness to physiological levels (Swinger et al. 1985; Duffey et al. 1989; Borja et al. 2004). The whole globes remained in the 20% Dextran solution (20 grams of dextran in 100mL of PBS; D8821, avg. molecular weight: 64,000-76,000 g/mol, Sigma Aldrich, St. Louis, MO) for 24 hours in the refrigerator at 4°C. Pachymetry measurements were taken using an ultrasound pachymeter (DGH 55 Pachmate, DGH Technology Inc., Exton, PA) after 24 hours to ensure the restoration of the corneal thickness within the physiological range of 400-600μm. All human eyes were obtained and used in compliance with the guidelines of the Declaration of Helsinki for research involving the use of human tissue.
For this study, the left (OS) eyes were prepared for anterior stromal mechanical testing and the right (OD) eyes were prepared for posterior stromal mechanical testing. Using a 4mm surgical blade (Alcon), approximately 50μm of corneal tissue was removed from left eyes to expose the anterior stroma. Approximately 50% of the restored corneal thickness was removed from right eyes to expose the posterior stroma. Pachymetry measurements were taken incrementally to ensure accurate depth control. The cornea was excised within the sclera beyond the limbus and was mounted onto the base of a custom cornea holder. The holder is comprised of a spherical protrusion that has a radius of curvature matching that of the cornea. The cornea was secured onto the spherical base with the holder's anchoring top that contains a hole to expose the central region of cornea for mechanical testing (Figure 1). While in the holder, the cornea is submerged in 15% Dextran solution to maintain corneal hydration during mechanical testing with the custom-built AFM system (Figure 1).
Figure 1.
Custom Cornea Holder. Side View (Top) and Top View (Bottom) of the Human Cornea in Custom Corneal Holder for AFM Testing. A human cornea (stained with 0.4% trypan blue for illustration purposes) is placed in the custom corneal holder during AFM testing. A human cornea (stained with 0.4% trypan blue for illustration purposes) was excised within the sclera beyond the limbus and was mounted onto the base of a custom cornea holder. The holder is comprised of a spherical protrusion that has a radius of curvature matching that of the cornea. The cornea was secured onto the spherical base with the holder's anchoring top that contains a hole to expose the central region of cornea for mechanical testing. This holder enables sturdy anchoring of an intact cornea, maintenance of corneal curvature, and the filling of 15% Dextran solution for proper corneal hydration during AFM testing.
After each cornea was prepared as described above, the custom cornea holder containing the sample was placed under the AFM cantilever. The sample was positioned so that the modified cantilever tip was over the central portion of the sample. The modified tip was lowered until it was just touching the surface. This position was determined by the point when the reflected laser beam moves off the photodiode. The location of the cantilever on the sample was observed using the 10x microscope objective connected to the camera beneath the sample. This enabled the positioning of the cantilever above an area with no surface irregularities. The modified tip was then lowered using the piezoelectric control so that it was in contact with the tissue. The measurements were conducted using a cantilever approach and retraction speed of 15μm/s and a maximal indentation force of 1000V (<20nN). The voltage detected at the photodiode due to deflection of the cantilever was recorded as a function of piezoelectric displacement. These recordings were repeated at least 15 times per sample. All experiments were performed at room temperature. With the use of custom MATLAB programs, the indentation force-indentation depth curves were analyzed using the Hertz model for a spherical indenter and the effective Young's modulus of elasticity was determined. The accuracy of the curve fit was visually verified. After AFM testing, all corneal samples were placed in 10% buffered formalin (HT501128, Sigma-Aldrich, St. Louis, MO) and prepared for histology. Sections were taken through the corneas, and slides were prepared with these sections, which were stained with methylthionine.
3. Results
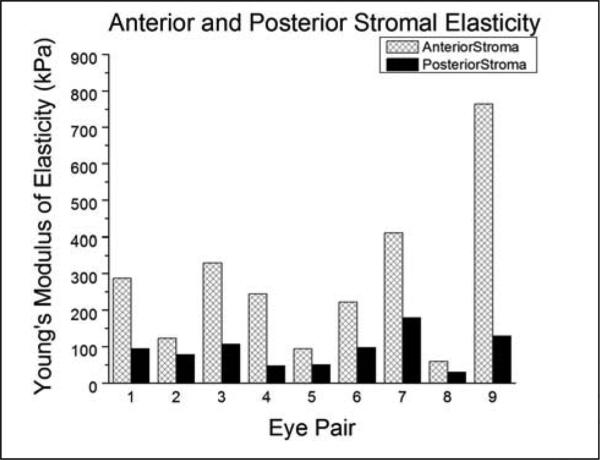
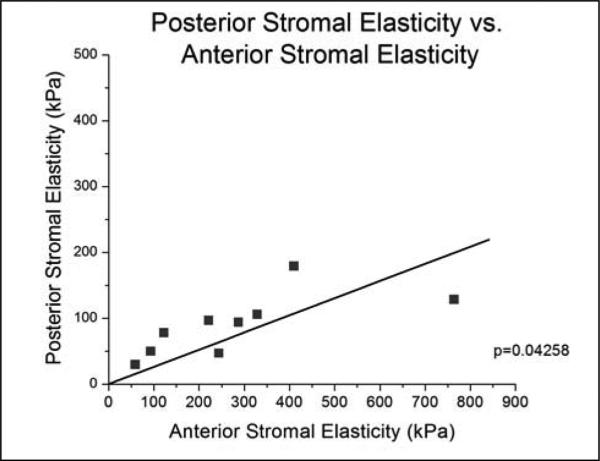
The effective Young's modulus of elasticity was 281 ± 214kPa (range: 59-764kPa) for the anterior stroma and 89.5 ± 46.1kPa (range: 29-179kPa) for the posterior stroma (Table 1). For each individual eye pair, the elastic modulus of the anterior stroma was consistently higher than its posterior stromal counterpart (Figure 2). A paired Student's t-test was performed to compare the anterior and posterior elasticity measurements and resulted in statistical significance (p=0.014). The posterior stromal elasticity exhibited stiffness that was, on average, 39.3% of the anterior stromal elasticity (range: 16.7 – 63.1%). Among the various fits performed, a linear relationship between the posterior stromal elasticity and the anterior stromal elasticity demonstrated to be most significant (p=0.0428), yielding a slope of 0.26 with zero intercept (Figure 3). The location of the measurements was confirmed using the histological sections.
Table 1.
Human Cornea Sample Information. The aae, post-mortem time, restored thickness, and Young's modulus of elasticity for each respective eye pair. The right (OS) eyes were used for anterior stromal elasticity testing and the left (OD) eyes were used for posterior stromal elasticity testing.
| Eye Pair | Age (years) | Post-Mortem Time (days) | Restored Thickness (μm) | Young's Modulus of Elasticity (kPa) (Average ± SD) | ||
|---|---|---|---|---|---|---|
| OS | OD | OS | OD | |||
| 1 | 63 | 7 | 562 | 433 | 287.5 ± 42.2 | 93.6 ± 11.2 |
| 2 | 66 | 11 | 531 | 534 | 122.7 ± 13.6 | 77.5 ± 8.2 |
| 3 | 67 | 7 | 535 | 585 | 328.9 ± 64.2 | 105.6 ± 31.2 |
| 4 | 72 | 3 | 493 | 539 | 764.0 ± 67.6 | 128.2 ± 18.7 |
| 5 | 75 | 6 | 588 | 508 | 243.9 ± 16.9 | 46.7 ± 3.9 |
| 6 | 84 | 4 | 451 | 499 | 93.4 ± 14.1 | 49.6 ± 6.9 |
| 7 | 86 | 11 | 590 | 543 | 221.7 ± 52.1 | 96.3 ± 11.8 |
| 8 | 89 | 9 | 402 | 523 | 395.7 ± 51.4 | 178.9 ± 13.6 |
| 9 | 93 | 6 | 450 | 493 | 59.3 ± 8.7 | 29.2 ± 3.1 |
Values for the modulus of elasticity are average ± standard deviation.
Figure 2.
Bar Graph of Anterior Stromal Elasticity and Posterior Stromal Elasticity. A bar graph comparing the Young's modulus of elasticity of the anterior stroma and posterior stroma for each respective eye pair is shown. Right eyes were subjected to anterior stromal elasticity testing and left eyes were subjected to posterior stromal elasticity testing using atomic force microscopy.
Figure 3.
Linear Regression of Posterior Stromal Young's Modulus of Elasticity vs. Anterior Stromal Young's Modulus of Elasticity. This graph demonstrates a significant linear relationship between the elasticity of the posterior stroma and anterior stroma.
4. Discussion
A custom-built AFM for nanoindentation measurements was used to independently quantify the mechanical properties of the anterior and posterior corneal stroma. Experiments were performed on fully hydrated corneal samples restored to the physiological corneal thickness range of 400-600μm. The relationship between anterior and posterior stromal elasticity was determined to be linear. Results of this study revealed that the effective posterior stromal elasticity is approximately 39.3% of its anterior stromal counterpart.
Nanoindentation is intended to provide mechanical measurements of materials of interest through the application of ultrasmall forces perpendicular to the sample plane of interest and measurement of the resultant sample indentation. Providing a relationship between applied force and sample indentation, the Hertz model has become a popular contact mechanical model to derive a sample's Young's modulus when using spherical indenters. The Hertz model assumes that the sample of interest is of a homogeneous, isotropic, linearly elastic nature with an infinite sample thickness and infinitesimal deformations (Last et al. 2012;Last et al. 2010;Li et al. 2008;Costa et al. 1999). However, this is not the case for soft tissues, such as the cornea, which are heterogeneous, viscoelastic, and anisotropic. Therefore, when applied to soft tissue samples, the Hertz model can only provide a linear elastic approximation. Because of this, the results of this study reflect the effective elastic properties of the anterior and posterior corneal stroma only relative to one another, as opposed to signifying one “absolute” Young's modulus of the both stromal regions, respectively, due to the tissue's anisotropic and nonlinear nature (Whitcomb et al. 2011).
Commercially available AFM cantilever tips are typically less than 50nm in diameter, and are therefore limited to mechanical characterization of individual tissue constituents. To measure tissue-level mechanical properties of soft tissues using indentation testing, it has been determined that a contact area greater than 50μm in diameter is required (Ebenstein et al. 2006; Ebenstein et al. 2004). With the intent of characterizing at the tissue-level rather than at the nanoscale level, this current study used AFM cantilevers modified with glass microspheres (average diameter 67.6μm) to measure the elasticity of anterior and posterior stromal layers. The use of these modified cantilevers increases the surface contact area with the sample thereby enabling networks of the stromal tissue microstructure to be mechanically probed rather than individual collagen components of the stroma.
Accurate determination of the cantilever's spring constant is of particular significance when using cantilevers with modified tips. The value of the cantilever's spring constant greatly influences the force measurements retrieved and consequent outcome of elasticity values obtained. When a microsphere is attached to an AFM cantilever, its weight coupled with the application of epoxy glue to adhere it alters the nominal spring constant prescribed to the cantilever, producing further stiffening. For this reason, it is important to calibrate the modified cantilever rather than just assume the spring constant to be equivalent to the nominal spring constant of the unmodified cantilever. Using the reference cantilever calibration technique (Ohler, 2010), it was found that the spring constant of the modified AFM tips was about 1.5 times stiffer than the unmodified cantilever's nominal spring constant.
The technique of manually removing the Bowman's membrane and underlying stromal layers to access the respective anterior and posterior stroma, using a surgical blade, stemmed from the manual delamination technique used in Descemet's Stripping Endothelial Keratoplasty and Deep Lamellar Keratoplasty surgeries (Stoiber et al. 2004; Marchini et al. 2006). Ophthalmologists commonly use either spatula or blunted surgical instrument to gently remove stromal layers. Although the femtosecond laser is the recent technology for creating excisions within the cornea, the effect of its high-pulse energies on corneal biomechanical properties is not certain. For this reason, the femtosecond laser was not used in this study.
The accuracy of biomechanical measurements obtained from post-mortem corneas depend strongly upon the tissue's state of hydration (Borja et al. 2004). The donor corneas retrieved from the eye bank were in an edematous state with thicknesses above the normal physiological levels. Performing mechanical characterization testing on such edematous corneas would provide biomechanical results influenced by the high water content and not give an accurate measure of in-situ corneal responses. For this reason, Dextran solution was used to restore the corneas to their normal thickness range of 400-600μm. Dextran has been extensively studied in the area of post-mortem corneal preparation and hydration for experimental studies (Swinger et al. 1985; Duffey et al. 1989; Borja et al. 2004;Hamaoui et al. 2001;Terry et al. 1994). Based on the studies of Hamaoui et al (2001), it was noted that dextran solutions of 20% proved most effective in bringing edematous corneas back to normal in vivo thickness ranges and that 15% effectively maintained corneal hydration during experimentation. To validate our use of 15% Dextran to maintain corneal hydration in this study, we performed time-lapse experiments using optical coherence tomography (OCT). Once the normal in vivo thickness was restored, corneal thickness was maintained for at least 2 hours (longer than needed for AFM testing) for the cases where: (1) Bowman's membrane was intact and (2) Bowman's membrane was removed to expose the stromal layer. For both cases, there were no significant distinctions observed in the swelling of the anterior and posterior stromal regions. As a result, the use of 15% Dextran is an effective protocol to maintain appropriate corneal hydration levels during experimentation.
Although being the most appropriate eye model for this study, the use of human donor corneas introduces limitations that cannot be controlled by the researchers. One general issue concerning the use of human donor eyes in ex-vivo studies is the limited availability of tissue, which restricts the present study's sample age range and size. In addition, medications that the donor was taking or diseases such as diabetes and glaucoma could impact the measurements obtained. Another important issue associated with using donor corneas, especially in regards to biomechanical characterization, is the eye's post-mortem time because it can also influence the results of biomechanical measurements. Although there was no significant relationship between measured Young's modulus of elasticity and postmortem time, factors contributing to the varying post-mortem time of eyes in this present study include the unpredictable retrieval time between a donor's death and arrival at the eye bank (which can take between 1-5 days) and the corneal 15% dextran dehydration protocol for corneal physiological thickness restoration, which requires an additional 24 hours. However, despite the varied postmortem time, the anterior and posterior stromal elasticity gradient remains independent of the post-mortem time.
Separate characterization of the anterior and posterior stroma has been previously investigated by Randleman et al (2008), Kohlhaas et al (2006), Scarcelli et al (2013), and Winkler et al (2011) using adhesion tensile stretching, tensile stretching, Brillouin microscopy, and indentation testing, respectively. The results of our study demonstrate the same qualitative trend found by these previous studies, where the anterior stroma elastic modulus was significantly higher than that of the posterior stroma. Such a mechanical distinction within the stroma is linked to the structural changes observed by its layered collagen networks. The anterior stromal region's relatively high elastic modulus values correspond to this region's densely compacted and interwoven collagen networks. Conversely, the lower elastic moduli results of the posterior stromal region reflect the loosely-connected collagen lamellae of this area. The depth-dependent change of stromal mechanical elasticity from anteriorly high to posteriorly low suggests the existence of a biomechanical gradient within the human stroma that is linked to its gradual change of structural collagen features. However, the quantitative values observed in Randleman et al (2008), Kohlhaas et al (2006), and Scarcelli et al (2013) are incomparable to that of the this present study; Randleman et al (2008) measured the stroma's adhesion force, Kohlhaas et al (2006) measured the stroma's tangential elastic modulus rather than sagittal, and the Brillouin modulus of Scarcelli et al (2013) lacks an established relation to the standard Young's modulus. The studies of Winkler et al (2011) and Last et al (2012) used a similar characterization technique as that used in this study; however the quantitative results of our study are different than what was measured in these studies due to hydration, postmortem time, and the depth measured in the cornea.
In summary, it was found that the effective Young's modulus of the anterior stromal region is consistently higher than that of the posterior stromal region. In addition, there is a linear relationship between the anterior and posterior stromal elasticity, with the posterior stroma approximately 39.3% as stiff as the anterior stroma. These results suggest that a biomechanical elasticity gradient exists within the stroma. AFM proves to be a reliable characterization technique for tissue applications, enabling the procurement of localized mechanical sample testing of fully hydrated samples.
Highlights.
We measured the elasticity of the human anterior and posterior stroma using AFM.
The anterior stroma is significantly stiffer than the posterior stroma.
A linear relationship between anterior and posterior stromal elasticity exists.
On average, the elasticity of the posterior stroma is 39.3% of the anterior stroma.
Acknowledgements
Donor human eyes were provided by the Florida Lions Eye Bank. The optical coherence tomography system used in the time lapse experiments was courtesy of Jean-Marie Parel, PhD and the Ophthalmic Biophysics Center of Bascom Palmer Eye Institute. Corneal histology was provided by Magda Celdran of Bascom Palmer Eye Institute and analyzed by Michael Lorenzo.
Grant support NIH Initiative for Maximizing Student Diversity Graduate Fellowship (JD); NIH National Research Service Award Individual Predoctoral Fellowship (1F31EY021714-01, JD); UNCF/MERCK Graduate Science Dissertation Fellowship (JD); American Federation for Aging Research (NMZ).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
The authors do not have any proprietary or financial interest in any of the devices presented.
Presented in part at the Association for Research in Vision and Ophthalmology 2011 meeting.
References
- Abahussin M, Hayes S, Knox Cartwright NE, Kamma-Lorger CS, Khan Y, Marshall J, Meek KM. 3D Collagen Orientation Study of the Human Cornea Using X-ray Diffraction and Femtosecond Laser Technology. Invest Ophthalmol Vis Sci. 2009;50:5159–5164. doi: 10.1167/iovs.09-3669. [DOI] [PubMed] [Google Scholar]
- Binnig G, Quate CF, Gerber C. Atomic force microscope. Phys. Rev. Lett. 1986;56:930–933. doi: 10.1103/PhysRevLett.56.930. [DOI] [PubMed] [Google Scholar]
- Boote C, Dennis S, Huang Y, Quantock AJ, Meek KM. Lamellar orientation in human cornea in relation to mechanical properties. J. Struct. Biol. 2005;149:1–6. doi: 10.1016/j.jsb.2004.08.009. [DOI] [PubMed] [Google Scholar]
- Borja D, Manns F, Lamar P, Rosen A, Fernandez V, Parel JM. Preparation and hydration control of corneal tissue strips for experimental use. Cornea. 2004;23:61–66. doi: 10.1097/00003226-200401000-00010. [DOI] [PubMed] [Google Scholar]
- Bron AJ. Anterior corneal mosaic. Br. J. Ophthalmol. 1968;52:659–669. doi: 10.1136/bjo.52.9.659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bron AJ, Tripathi RC. Anterior corneal mosaic. Further observations. Br. J. Ophthalmol. 1969;53:760–764. doi: 10.1136/bjo.53.11.760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bron AJ, Tripathi RC. The anterior corneal mosaic. Br. J. Physiol. Opt. 1970;25:8–13. [PubMed] [Google Scholar]
- Bron AJ. The architecture of the corneal stroma. Br J Ophthalmol. 2001;85:379–381. doi: 10.1136/bjo.85.4.379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown KE, Congdon NG. Corneal structure and biomechanics: impact on the diagnosis and management of glaucoma. Curr. Opin. Ophthalmol. 2006;17:338–343. doi: 10.1097/01.icu.0000233951.01971.5b. [DOI] [PubMed] [Google Scholar]
- Cabrera Fernandez D, Niazy AM, Kurtz RM, Djotyan GP, Juhasz T. Finite element analysis applied to cornea reshaping. J. Biomed. Opt. 2005;10:064018. doi: 10.1117/1.2136149. [DOI] [PubMed] [Google Scholar]
- Costa KD, Yin FC. Analysis of indentation: implications for measuring mechanical properties with atomic force microscopy. J. Biomech. Eng. 1999;121:462–471. doi: 10.1115/1.2835074. [DOI] [PubMed] [Google Scholar]
- Daxer A, Misof K, Grabner B, Ettl A, Fratzl P. Collagen fibrils in the human corneal stroma: structure and aging. Invest. Ophthalmol. Vis. Sci. 1998;39:644–648. [PubMed] [Google Scholar]
- DelMonte DW, Kim T. Anatomy and physiology of the cornea. J Cataract Refract Surg. 2011;37:588–598. doi: 10.1016/j.jcrs.2010.12.037. [DOI] [PubMed] [Google Scholar]
- Duffey RJ, Tchah H, Lindstrom RL. Human cadaver corneal thinning for experimental refractive surgery. Refract. Corneal Surg. 1989;5:41–42. [PubMed] [Google Scholar]
- Dupps WJ, Jr, Wilson SE. Biomechanics and wound healing in the cornea. Exp. Eye Res. 2006;83:709–720. doi: 10.1016/j.exer.2006.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebenstein DM, Pruitt LA. Nanoindentation of soft hydrated materials for application to vascular tissues. J. Biomed. Mater. Res. A. 2004;69:222–232. doi: 10.1002/jbm.a.20096. [DOI] [PubMed] [Google Scholar]
- Ebenstein DM, Pruitt LA. Nanoindentation of biological materials. Nano Today. 2006;1:26–33. [Google Scholar]
- Freund DE, McCally RL, Farrell RA, Cristol SM, L'Hernault NL, Edelhauser HF. Ultrastructure in anterior and posterior stroma of perfused human and rabbit corneas. Relation to transparency. Invest. Ophthalmol. Vis. Sci. 1995;36:1508–1523. [PubMed] [Google Scholar]
- Hamaoui M, Tahi H, Chapon P, Duchesne B, Fantes F, Feuer W, Parel J. Corneal Preparation of Eye Bank Eyes for Experimental Surgery. Cornea. 2001;20:317–20. doi: 10.1097/00003226-200104000-00015. [DOI] [PubMed] [Google Scholar]
- Harada Y, Naoi N. Corneal elasticity as a measure of intra-ocular pressure: a controlled clinical examination. Kobe J. Med. Sci. 2004;50:141–152. [PubMed] [Google Scholar]
- Hertz H. Uber die Beruhrung Fester Elastischer Korper (On the Contact of Elastic Solids). J. Reine Angew. Math. 1881;92:156. [Google Scholar]
- Kamiya K, Shimizu K, Ohmoto F. The changes in corneal biomechanical parameters after phototherapeutic keratectomy in eyes with granular corneal dystrophy. Eye. 2008;23:1790–1795. doi: 10.1038/eye.2008.373. [DOI] [PubMed] [Google Scholar]
- Kamma-Lorger CS, Boote C, Hayes S, Moger J, Burghammer M, Knupp C, Quantock AJ, Sorensen T, Di Cola E, White N, Young RD, Meek KM. Collagen and mature elastic fibre organisation as a function of depth in the human cornea and limbus. J. Struct. Biol. 2010;169:424–430. doi: 10.1016/j.jsb.2009.11.004. [DOI] [PubMed] [Google Scholar]
- Karrasch S, Hegerl R, Hoh JH, Baumeister W, Engel A. Atomic force microscopy produces faithful high-resolution images of protein surfaces in an aqueous environment. Proceedings of the National Academy of Sciences. 1994;91:836–838. doi: 10.1073/pnas.91.3.836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knox Cartwright NE, Tyrer JR, Marshall J. Age-related differences in the elasticity of the human cornea. Invest. Ophthalmol. Vis. Sci. 2011;52:4324–4329. doi: 10.1167/iovs.09-4798. [DOI] [PubMed] [Google Scholar]
- Kohlhaas M, Spoerl E, Schilde T, Unger G, Wittig C, Pillunat LE. Biomechanical evidence of the distribution of cross-links in corneas treated with riboflavin and ultraviolet A light. J. Cataract Refract. Surg. 2006;32:279–283. doi: 10.1016/j.jcrs.2005.12.092. [DOI] [PubMed] [Google Scholar]
- Kokott W. Über mechanisch-funktionelle Strukturen des Auges. Graef Arch Clin Exp. 1938;138:424. [Google Scholar]
- Komai Y, Ushiki T. The three-dimensional organization of collagen fibrils in the human cornea and sclera. Invest Ophthalmol Vis Sci. 1991;32:2244–2258. [PubMed] [Google Scholar]
- Kotecha A. What Biomechanical Properties of the Cornea Are Relevant for the Clinician? Surv. Ophthalmol. 2007;52:S109–S114. doi: 10.1016/j.survophthal.2007.08.004. [DOI] [PubMed] [Google Scholar]
- Lal R, John SA. Biological applications of atomic force microscopy. Am J Physiol-Cell Ph. 1994;266:C1–C21. doi: 10.1152/ajpcell.1994.266.1.C1. [DOI] [PubMed] [Google Scholar]
- Last JA, Liliensiek SJ, Nealey PF, Murphy CJ. Determining the mechanical properties of human corneal basement membranes with atomic force microscopy. J. Struct. Biol. 2009;167:19–24. doi: 10.1016/j.jsb.2009.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Last JA, Russell P, Nealey PF, Murphy CJ. The Applications of Atomic Force Microscopy to Vision Science. Invest Ophthalmol Vis Sci. 2010;51:6083–6094. doi: 10.1167/iovs.10-5470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Last JA, Thomasy SM, Croasdale CR, Russell P, Murphy CJ. Compliance profile of the human cornea as measured by atomic force microscopy. Micron. 2012;43:1293–8. doi: 10.1016/j.micron.2012.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li QS, Lee GYH, Ong CN, Lim CT. AFM indentation study of breast cancer cells. Biochem. Biophys. Res. Commun. 2008;374:609–613. doi: 10.1016/j.bbrc.2008.07.078. [DOI] [PubMed] [Google Scholar]
- Liu J, Roberts CJ. Influence of corneal biomechanical properties on intraocular pressure measurement: Quantitative analysis. J Cataract Refract Surg. 2005;31:146–155. doi: 10.1016/j.jcrs.2004.09.031. [DOI] [PubMed] [Google Scholar]
- Lombardo M, Lombardo G, Carbone G, De Santo MP, Barberi R, Serrao S. Biomechanics of the Anterior Human Corneal Tissue Investigated with Atomic Force Microscopy. Invest Ophthalmol Vis Sci. 2012;53:1050–1057. doi: 10.1167/iovs.11-8720. [DOI] [PubMed] [Google Scholar]
- Marchini G, Mastropasqua L, Pedrotti E, Nubile M, Ciancaglini M, Sbabo A. Deep lamellar keratoplasty by intracorneal dissection: a prospective clinical and confocal microscopic study. Ophthalmology. 2006;113:1289–1300. doi: 10.1016/j.ophtha.2006.01.071. [DOI] [PubMed] [Google Scholar]
- Morishige N, Takagi Y, Chikama T, Takahara A, Nishida T. Three-dimensional analysis of collagen lamellae in the anterior stroma of the human cornea visualized by second harmonic generation imaging microscopy. Invest. Ophthalmol. Vis. Sci. 2011;52:911–915. doi: 10.1167/iovs.10-5657. [DOI] [PubMed] [Google Scholar]
- Müller LJ, Pels E, Vrensen GFJM. The specific architecture of the anterior stroma accounts for maintenance of corneal curvature. Br J Ophthalmol. 2001;85:437–443. doi: 10.1136/bjo.85.4.437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Normand V, Lootens DL, Amici E, Plucknett KP, Aymard P. New insight into agarose gel mechanical properties. Biomacromolecules. 2000;1:730–738. doi: 10.1021/bm005583j. [DOI] [PubMed] [Google Scholar]
- Ohler B. Practical Advice on the Determination of Cantilever Spring Constants. [Feb 5, 2013];Veeco Application Note. 2010 http://nanoscaleworld.brukeraxs.com/nanoscaleworld/media/p/143.aspx.
- Patel S, Marshall J, Fitzke FW., 3rd Refractive index of the human corneal epithelium and stroma. J. Refract. Surg. 1995;11:100–105. doi: 10.3928/1081-597X-19950301-09. [DOI] [PubMed] [Google Scholar]
- Pepose JS, Feigenbaum SK, Qazi MA, Sanderson JP, Roberts CJ. Changes in Corneal Biomechanics and Intraocular Pressure Following LASIK Using Static, Dynamic, and Noncontact Tonometry. Am. J. Ophthalmol. 2007;143:39–47. e1. doi: 10.1016/j.ajo.2006.09.036. [DOI] [PubMed] [Google Scholar]
- Randleman JB, Dawson DG, Grossniklaus HE, McCarey BE, Edelhauser HF. Depth-dependent cohesive tensile strength in human donor corneas: implications for refractive surgery. J. Refract. Surg. 2008;24:S85–9. doi: 10.3928/1081597X-20080101-15. [DOI] [PubMed] [Google Scholar]
- Ruberti JW, Sinha Roy A, Roberts CJ. Corneal Biomechanics and Biomaterials. Annu. Rev. Biomed. Eng. 2010;13:269–95. doi: 10.1146/annurev-bioeng-070909-105243. [DOI] [PubMed] [Google Scholar]
- Scarcelli G, Pineda R, Yun S. Brillouin optical microscopy for corneal biomechanics. Invest Ophthalmol Vis Sci. 2012;53:185–190. doi: 10.1167/iovs.11-8281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scarcelli G, Kling S, Quijano E, Pineda R, Marcos S, Yun S. Brillouin microscopy of collagen crosslinking: noncontact depth-dependent analysis of corneal elastic modulus. Invest Ophthalmol Vis Sci. 2013;54:1418–1425. doi: 10.1167/iovs.12-11387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoiber J, Fernandez V, Kaminski S, Lamar PD, Dubovy S, Alfonso E, Parel JM. Biological response to a supraDescemetic synthetic cornea in rabbits. Arch. Ophthalmol. 2004;122:1850–1855. doi: 10.1001/archopht.122.12.1850. [DOI] [PubMed] [Google Scholar]
- Swinger CA, Kornmehl EW. Dehydration of post-mortem eyes for practice and experimental surgery. Ophthalmic Surg. 1985;16:182–183. [PubMed] [Google Scholar]
- Terry MA, Ousley PJ, Zjhra ML. Hydration changes in cadaver eyes prepared for practice and experimental surgery. Arch. Ophthalmol. 1994;112:538–543. doi: 10.1001/archopht.1994.01090160118031. [DOI] [PubMed] [Google Scholar]
- Turss R, Friend J, Reim M, Dohlman CH. Glucose Concentration and Hydration of the Corneal Stroma. Ophthal Res. 1971;2:253–260. [Google Scholar]
- Whitcomb JE, Amini R, Simha NK, Barocas VH. Anterior–posterior asymmetry in iris mechanics measured by indentation. Exp. Eye Res. 2011;93:475–481. doi: 10.1016/j.exer.2011.06.009. [DOI] [PubMed] [Google Scholar]
- Winkler M, Chai D, Kriling S, Nien CJ, Brown DJ, Jester B, Juhasz T, Jester JV. Nonlinear optical macroscopic assessment of 3-d corneal collagen organization and axial biomechanics. Invest. Ophthalmol. Vis. Sci. 2011;52:8818–8827. doi: 10.1167/iovs.11-8070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wojcikiewicz EP, Zhang X, Chen A, Moy VT. Contributions of molecular binding events and cellular compliance to the modulation of leukocyte adhesion. J. Cell. Sci. 2003;116:2531–2539. doi: 10.1242/jcs.00465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziebarth NM, Wojcikiewicz EP, Manns F, Moy VT, Parel JM. Atomic force microscopy measurements of lens elasticity in monkey eyes. Mol. Vis. 2007;13:504–510. [PMC free article] [PubMed] [Google Scholar]
- Ziebarth NM, Arrieta E, Feuer WJ, Moy VT, Manns F, Parel J. Primate lens capsule elasticity assessed using Atomic Force Microscopy. Exp. Eye Res. 2011;92:490–494. doi: 10.1016/j.exer.2011.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]