Computational methods for constructing protein structure models from 3D electron microscopy maps

Abstract

Protein structure determination by cryo-electron microscopy (EM) has made significant progress in the past decades. Resolutions of EM maps have been improving as evidenced by recently reported structures that are solved at high resolutions close to 3 Å. Computational methods play a key role in interpreting EM data. Among many computational procedures applied to an EM map to obtain protein structure information, in this article we focus on reviewing computational methods that model protein three-dimensional (3D) structures from a 3D EM density map that is constructed from two-dimensional (2D) maps. The computational methods we discuss range from de novo methods, which identify structural elements in an EM map, to structure fitting methods, where known high resolution structures are fit into a low-resolution EM map. A list of available computational tools is also provided.

Introduction

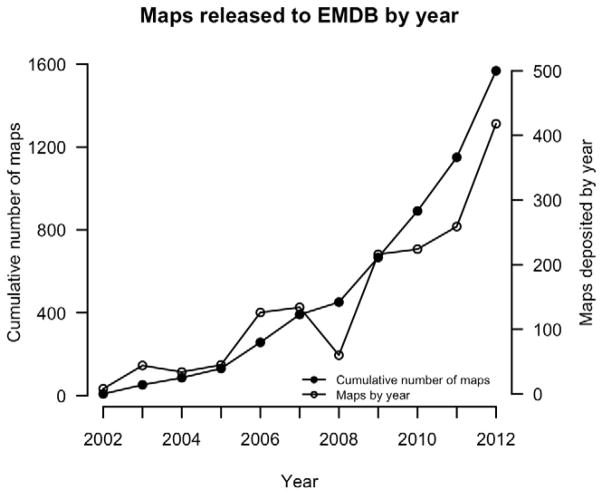
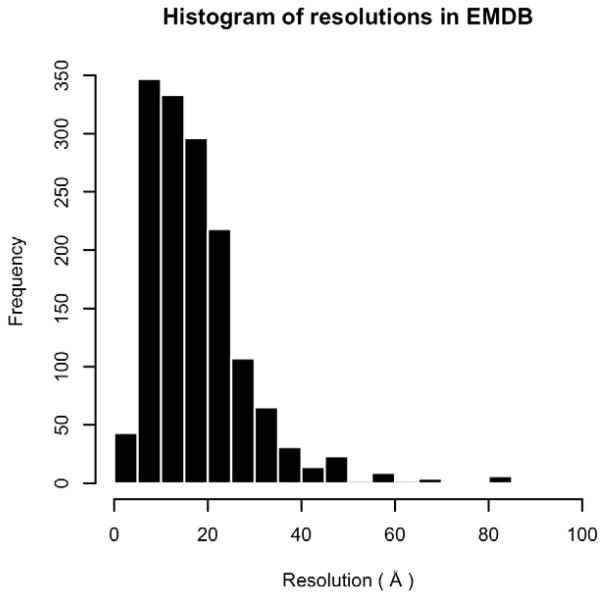
Electron density maps from cryo-electron microscopy (cryo-EM) have been used to model macromolecular structures for almost two decades (Volkmann et al., 2000; Ludtke et al., 2004; Mitra et al., 2005). Each step in structure determination by cryo-EM has steadily improved, allowing scientists to determine structures with higher resolutions (Rossmann et al., 2005). The number of structures solved by EM is also increasing, resulting in over 1,600 EM maps available in the EM Data Bank (EMDB) (Lawson et al., 2011) (Figure 1). The entries in EMDB include many important biological macromolecules, such as GroEL and virus capsids (Zhou, 2008). As shown in Figure 2, resolutions of the EM maps in EMDB range from 3.1 Å to ~9 nanometers. It has been reported recently that the resolution of structures determined by EM is approaching those determined by X-ray crystallography (Zhang et al., 2008).

Figure 1.

The growth in the number of EM Maps in the Electron Microscopy Data Bank. The total number of entries at each year (horizontal axis), starting in 2002, is shown as a continuous line with filled circles as markers (left vertical axis). Additionally, a continuous line with unfilled circles shows the number of entries deposited each year (right vertical axis).

Figure 2.

Distribution of EM map resolutions in the EMDB. Entries are eliminated if the resolution is not provided.

The structure determination by cryo-EM involves several stages as overviewed in Figure 3. Once 2D density maps are obtained by single particle cryo-EM for a sample of macromolecules, they are subjected to computational image processing, refinement, and 3D structure reconstruction. A 3D density map is constructed from individual 2D maps that capture different poses in the sample. Different 2D views of the same pose can be grouped together to form clusters that putatively represent the same molecular orientation. If a considerable degree of structural heterogeneity is present in the sample, finding common features to group the 2D projections into clusters becomes more challenging, and the quality of the clusters directly impacts the resolution of the reconstruction (Förster and Villa, 2010). Several experimental steps in the process, such as the centrifugation and the freeze-and-thaw steps, are crucial for obtaining samples that contain structurally homogeneous particles. While homogeneity in the sample can create higher resolution maps, the ability to handle heterogeneous samples is one of the advantages that cryo-EM has over other structural determination techniques such as X-ray crystallography and NMR spectroscopy. Other factors that influence the quality of the 3D map include electron beam alignment, compensating for specimen drift, and making corrections for defocusing. An iterative refinement process can be applied for 2D map alignment that considers these factors.

Figure 3.

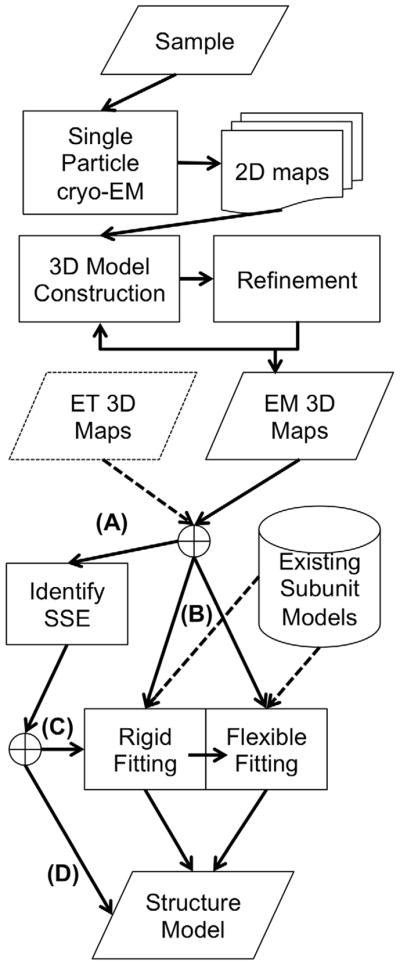
Steps involved in constructing structure models of proteins from an EM map. The first steps involve experiments such as sample preparation and single-particle cryo-EM data collection. Once a 3D EM map is constructed, computational methods are applied to build structural models, which range from determining secondary structure elements to rigid-fitting and flexible fitting approaches. (A) α-helices start to be identifiable in an EM map if its resolution is 10 Å or higher and they can be clearly identified at 6 Å resolution, while β-sheets can be identified in a map at around 5 Å. To follow this route in the diagram the input EM maps should meet the resolution. (B) In order to perform structural fitting to a map the user needs to have atomic-detailed models of the subunits to fit. These can come either from X-ray, NMR spectroscopy, or computational modeling. (C) Some methods use the identified SSEs as input to their rigid fitting algorithm. (D) Coarse-grain models that provide only a backbone trace can be directly derived from identified SSEs in the EM map.

Electrons can cause radiation damage to biological samples and thus impacts the attainable resolution. Low-contrast images and challenging signal-to-noise ratios are the main problem that computational methods have to deal with in terms of image processing (Chiu et al., 2005). Ruprecht and Nield (Ruprecht and Nield, 2001), as well as Zhou more recently (Zhou, 2008, 2011), have presented in-depth discussions about the factors that contribute to higher quality EM maps. A high-resolution map is a requirement for constructing a high-quality atomic-level model.

Once a 3D electron density map has been determined, different types of computational methods can be applied to obtain the 3D structure information of biological macromolecules. The effectiveness and types of methods used depend on the density map resolution or additional information available for the macromolecules being studied. The aim of the methods ranges from the identification of secondary structure elements to the modeling of full-atom structures (Fabiola and Chapman, 2005; Topf and Sali, 2005; Lindert, Stewart, et al., 2009; Beck et al., 2011).

In this review, we focus on discussing of computational methods and tools used for constructing 3D structure models from a 3D EM map (the bottom half in Figure 3). First, we describe methods to identify local structures, particularly secondary structures in a 3D EM density map, without assuming the availability of an atomic-detailed protein structure to fit in. The following three sections analyze methods for fitting atomic-detailed structures of proteins to an EM map. We begin with analyzing different scoring functions that evaluate the quality of a fit. Then, we explain the main characteristics of methods for fitting high-resolution structures into an EM map that do not explicitly consider protein flexibility (rigid fitting). What follows is a discussion on methods that account for protein structure flexibility in structure fitting (flexible fitting). While some of the methods clearly belong to one of the aforementioned sections, readers should note that the classification of methods is not always clear-cut because they have multiple components that belong to different classifications. Finally, in the last section, we discuss examples of actual applications using these methods.

Identification of secondary structure elements in an EM map

If the resolution of an EM map is below 10 Å, the secondary structures of proteins can be identified in the map (Beck et al., 2012). Normally α-helices start to be identified in a map at a 10 Å resolution and can be clearly characterized at a 6 Å resolution, while β-sheets can be identified at a resolution of 5 Å (Baker et al., 2012). Most methods mask out low-density regions in an EM map and search for secondary structure features in the remaining regions. Once secondary structures are identified, amino acid sequences can be mapped to those regions (Chiu et al., 2002).

One of the earlier methods, Helixhunter, examines groups of voxels (segments) to determine if they have helix-like features, which are quantified by correlation functions and tensor matrices around the regions (Jiang et al., 2001). The algorithm first masks out low density regions to eliminate non-helical density regions in a map. Further, it computes cross-correlation of each identified region with a prototypical helix located in various angles to identify plausible helix regions in the map. Then, a 3×3 second moment tensor is computed for each plausible helix region, for which eigen-analysis is performed to identify three eigenvectors and eigenvalues. If the largest eigenvalue is considerably larger and the other two values and if the latter two are less than 3 Å, the region is considered as a helix. Once an α-helix is identified, it can be represented in coarse-grained tubular fashion or an existing atomic-detailed structure of helix can be fit in it. The same ideas to recognize helices were implemented as the first stage in EMatch (Dror et al., 2007).

Transmembrane (TM) helix bundles were identified in a similar way in an EM map (Enosh et al., 2004). For fitting TM helices additional information such as endpoints and connectivity of TM helices can be used as constraints.

Sheetminer focuses on identifying β-sheets in an EM map (Kong and Ma, 2003). The method first classifies voxels into core or surface voxels and computes slices of density regions that are less thick and more continuous than typical α-helical regions. The method computes the proportion of amino acid residues that are predicted to be in β-regions. While Sheetminer outputs clusters of voxels that are presumed to be β–sheets, an extension called Sheettracer refines the output from Sheetminer and identifies individual β-strands in the β-sheets (Kong et al., 2004). To do so, it first identifies backbone voxels by looking for high-density regions through local peak filtering. Then, it analyzes the distribution of the voxels to determine if it is linear, as would be expected for strands. This is followed by a clustering step to separate voxels into different strands. At the end, a pseudo-Cα trace is output by the method.

SSEhunter identifies both α helices and β-strands in an EM density map (Baker et al., 2007). The algorithm first identifies pseudo-atoms in the density map, which are points with locally high-density values. Then, α helices and β strands are assigned to the EM map based on several features including geometrical features of high-density regions and the characteristic distribution of pseudo-atoms relative to high-density regions in the EM map. This algorithm along with the companion tool, SSEbuilder, are provided as a part of the EMAN2 software suite (Tang et al., 2007). Gorgon, an interactive modeling toolkit (Baker et al., 2010, 2012), also integrates SSEbuilder.

A more recent approach, SSELearner, uses a support vector machine (SVM) to classify voxels into both α-helices and β-sheets (Si et al., 2012). The SVM is trained to recognize features of voxels that are specific to α-helices and β-sheets using a known dataset of high-resolution structures mapped on EM maps. The features used are similar to those mentioned above, namely, tensor gradients and eigenvalues of electron density, which characterize if the neighbor densities have a tubular shape or a flat one, as well as the thickness of the regions. SSELearner classifies all voxels into three categories: α-helices, β-sheets, or neither of them.

Pathwalking (Baker et al., 2012) also starts with identifying pseudo-atoms in an EM map that are assumed to be Cα atoms. Then, the pseudo-atoms are connected by an algorithm to solve the traveling salesman problem imposing restrictions that reflect topological characteristics of a protein main-chain (e.g. main chain atoms have at least two neighbors along its sequence). Finally, the primary sequence is threaded on to the model automatically.

To obtain the overall fold of a protein, identified secondary structures need to be connected. In EM-Fold, an extension to the Rosetta protein structure modeling program (Leaver-Fay et al., 2011), α-helices are identified using combined predictions that come from the density map and the protein primary sequence. Identified α-helices are later connected with loops. Rosetta also rebuilds side chains for a reconstructed main-chain trace. (Lindert, Staritzbichler, et al., 2009).

In summary, secondary structure identification methods in an EM map rely on the distinct geometric characteristics present in EM maps. Thus, a sufficiently high resolution (lower than 10Å) is required to distinguish these features. While earlier methods focused on α helices, more recent methods have the capability of identifying both α helices and β sheets. To build a full structure model, identified SSEs need to be connected with loops. Identified SSEs can also be used as clues to identify overall folds as will be mentioned in later sections.

Scoring quality-of-fit

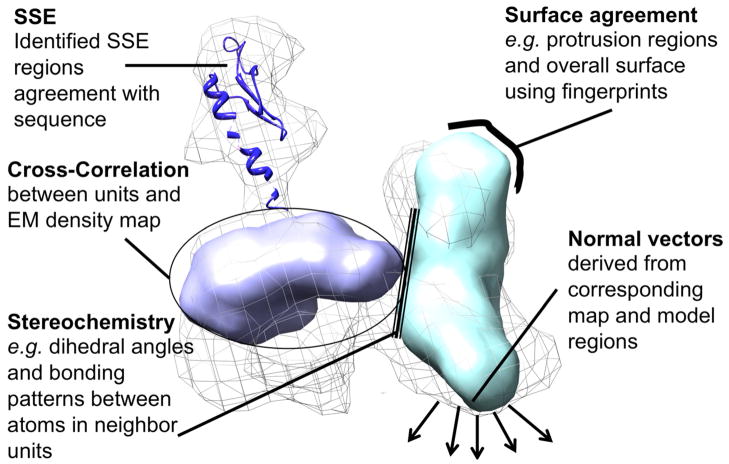
There are often cases where high-resolution structures of component molecules have been solved and are available along with an EM map of the entire complex structure. In such cases, one of the main computational tasks is to identify locations in the EM map where the individual high-resolution structures fit. Two aspects must be considered to find these locations: sampling of the conformational space and assessing the goodness-of-fit of high-resolution structures to the EM map. In this section we address scoring terms that evaluate the goodness-of-fit. Figure 4 presents a general classification of the scoring features used by the methods in this article.

Figure 4.

Graphical summary of different scoring terms used in the EM fitting process.

Correlation of electron densities

The objective of rigid fitting methods is to identify the best positioning of protein models in an EM map so that their electron densities match well (Rossmann, 2000). Among a number of metrics proposed that quantify the agreement of electron density of an EM map and a protein model, cross-correlation is the most commonly used scoring term (Rossmann et al., 2001). The cross-correlation coefficient between the electron density of a protein model structure and the region of the EM map where the subunit is aligned to is defined as follows:

$$CC=\frac{{\displaystyle \sum _{i=1}}({\rho }_{1i}-{\overline{\rho }}_1)({\rho }_{2i}-{\overline{\rho }}_2)}{\sqrt{{\displaystyle \sum _{i=1}}{({\rho }_{1i}-{\overline{\rho }}_1)}^2}\sqrt{{\displaystyle \sum _{i=1}}{({\rho }_{2i}-{\overline{\rho }}_2)}^2}},$$ (1)

where ρ_1i and ρ_2i are electron densities of voxels at position i from the component protein and a region in an EM map, respectively. The electron densities for the component protein are obtained by simulation of the density map from the atomic structure of the components.

Wu et al. applied different weights for densities in surface and core regions when computing the cross-correlation (Wu et al., 2003). In this approach each voxel in an EM map is assigned a weight named the core index value, which has a high value for core regions and a small value for surface regions. The rationale behind this idea is that interactions between different subunits can affect electron densities at surface regions while densities at core regions are expected to stay at a similar value upon subunit interactions. The procedure has been implemented as part of CHARMM (Brooks et al., 2009).

More recently, Flex-EM (Topf et al., 2008) added two more scoring terms that are linearly combined with a cross-correlation function. The first term is a sum of harmonic terms of chemical bonds, bond angles, and dihedral angles of atoms from more than one rigid body to be docked. Since input structures are often fragments of a protein chain, it is necessary to have a scoring term that checks stereo chemical properties of fitted structures. The second term introduced is a van der Waals term for evaluating non-bonded atom interactions between atom pairs from different rigid units.

Alternatives to the correlation function

There are several alternatives to cross-correlation that quantify the quality of fit between structures and EM maps (Vasishtan and Topf, 2011). One such example is mutual information:

$$I(X;Y)=\sum _{x\in X}\sum _{y\in Y}p(x,y)log\frac{p(x,y)}{p(x)p(y)}$$ (2)

Here, X and Y correspond to the density values in voxels of two compared density maps while p(x) and p(y) are the fraction of voxels with densities equal to x and y.

Another scoring term uses normal vectors of two densities, which captures the shape of isosurfaces (Ceulemans and Russell, 2004). Normal vectors are calculated at voxels on the isosurface of a predefined density range in EM maps. The vectors in the original map and the fitted structure are compared against each other using a matching score that averages the corresponding vector angles:

$$NV=\frac{1}{n}\sum _{i\in V}\frac{{\overrightarrow{N}}_i^T\times {\overrightarrow{N}}_i^P}{\left|{\overrightarrow{N}}_i^T\right|\left|{\overrightarrow{N}}_i^P\right|}$$ (3)

In the equation, n is the number of normal vectors calculated for voxels, T indicates that the vector is from the target EM map while P indicates that the vector is from the probe (protein) map taken from the corresponding point i, and N⃗ are normal vectors. The computational cost for this normal vector-based score is smaller than the correlation function since the representation of EM maps to be compared with is reduced in the form of isosurfaces. In the 3SOM program (Ceulemans and Russell, 2004) the optimal superimposition of two isosurfaces from two EM maps is identified using the normal vector-based score, which is followed by refinement using the cross-correlation score (Eqn. 1).

Zhang et al. reduced a fitting procedure of multiple structures to an EM map to a point set matching problem that takes the geometric architecture of the point distributions and the consistency of their density values into account (Zhang et al., 2010). For the registration of the point sets, an efficient mathematical algorithm called Integer quadratic programming (IQP) was applied. Matching of point sets was scored by considering matching of density of points and distance of pairs of matched points.

It is also possible to use surface representations that implicitly describe the overall molecular shape as an approximation using mixtures of Gaussian functions (Kawabata, 2008).. One of the main advantages of this approach is that it has a lower computational cost and is suitable for capturing global structural features of protein complexes.

Our group has shown that the 3D Zernike descriptors (3DZD), a mathematical series expansion of a 3D function, is effective for fast comparison of isosurfaces derived from EM density maps (Sael and Kihara, 2010). 3DZD represents a 3D object (isosurface of an EM density map) compactly as a vector of coefficient values of the series expansion in a rotationally invariant fashion. It was shown that the 3DZD is versatile and efficient for representing shapes of biomolecules, proteins, protein complexes, and small chemical ligand molecules, as well as EM maps (Kihara et al., 2011). In our work, we showed that the isosurface representation by 3DZD can distinguish EM maps of protein structures of the same fold even at 15 Å resolution (Sael and Kihara, 2010). A similar work has been performed that uses 3DZD for describing EM maps (Yin and Dokholyan, 2011).

A detailed comparison between several scoring methods was performed using 4 experimental and 16 simulated 3D density maps with resolutions between 6 and 23 Å (Vasishtan and Topf, 2011). The study compared seven different scoring functions including cross-correlation, Laplacian-filtered cross-correlation, the envelope score, which considers overlap between an EM map and a simulated EM map of a component, mutual information, the normal vector score, and the Chamfer distance, which is a well-established pattern matching score used frequently in computer vision. The performance of the scoring functions was evaluated in terms of the Spearman correlation coefficient between the scores and the RMSD of the pose to the ideal position of the fitted structures. All of the scoring functions were comparable and accurate when maps were between 6 and 10 Å. Overall, cross-correlation performed as one of the best scoring methods. For low-resolution maps at sub-nano-meter resolution, Laplacian-filtered cross-correlation and mutual information performed well. It would be worthwhile to note that the envelope score is an order of magnitude faster to calculate.

To summarize this section, cross-correlation is the most commonly used scoring term for evaluating the goodness-of-fit of high-resolution structures and an EM map. There are several variants of the cross-correlation function and other scoring functions proposed in literature. There is still room for improving the scoring function by using or combining alternative functions with cross-correlation, particularly for speeding up the computational time or for dealing with EM maps with a low-resolution (e.g. over 10 Å).

Rigid fitting methods

If high-resolution structures of component proteins are available, they need to be assembled together within an EM map. Although proteins are intrinsically flexible and their conformations in a complex may differ from their isolated state, treating their structure as a rigid body would be a reasonable approximation. This is called rigid fitting. It can be described as a six-dimensional optimization problem where the optimal translation for three directions (x, y, z) and three rotation angles are sought for fitting each component protein structure into an EM map so that their electron densities have a good agreement. Two important factors in rigid fitting are how to evaluate goodness-of-fit (scoring) and how to search poses of protein structures in an EM map. The choice of the scoring is intertwined with how the electron densities of protein structures and an EM map are represented. One of the first approaches for automated fitting was EMfit (Rossmann et al., 2001). In this method the fitting procedure starts by placing the center of an X-ray crystallographically-determined protein structure manually at a predefined region, which can be determined by biological knowledge of the protein complex and also by analyzing the symmetry of the density map, if the complex is known to be symmetrical. Next, a rotational and translational search is performed with a predetermined interval to refine the positioning of the high-resolution protein structure. EMfit uses the cross-correlation of EM densities as one of the scoring terms associated with several other terms including the sum of densities at atomic sites, the lack of atoms in negative or low density, and the absence of atom clashes. In what follows, first we discuss several notable scoring terms and then review conformation search algorithms used in published works.

Situs uses an efficient representation of local electron density called codebook vectors (Wriggers et al., 1999; Wriggers and Birmanns, 2001). The codebook vector is a vector of local densities around cluster centroids in an EM map. The vectors enable fast density comparisons without explicit map superimposition.

An alternative class of scores considers the 3D shape or edge information of electron densities in EM maps. The Colores algorithm uses the surface contour computed with a Laplacian filter that enhances the 3D edge information of an EM map (Chacón and Wriggers, 2002). As also concluded by Vasishtan and Topf (2011), the Laplacian filter is effective for rigid fitting particularly when the resolution of the EM map is relatively low (~20 Å or lower). This method is also included as part of the Situs package (Wriggers, 2012). Gmfit uses a further coarse-grained representation of EM maps that enables faster fitting with atomic structures (Kawabata, 2008). It represents an EM map and atomic structures as Gaussian mixture models, which approximate the shape of a density map by a combination of several Gaussian functions. The Gaussian mixture model can analytically provide an integral of a product of two distribution functions as a goodness-of-fit. Because of the speed, the method is particularly effective for fitting multiple subunits into an EM map. Along a similar line, our group has used the 3DZD for representing the shape of EM maps in the EMLZerD algorithm (Esquivel-Rodríguez and Kihara, 2012). EMLZerD fits multiple high-resolution structures into an EM map. It first uses a multiple protein-protein docking method, Multi-LZerD (Esquivel-Rodríguez et al., 2012), to generate a couple hundred candidate models of the protein complex. Then, each candidate model is compared with an EM map, using their 3DZD shape profiles, to select the best-fitted models. Since the representation of the 3DZD becomes a simple vector of coefficients, it efficiently compares the shapes by computing the Euclidean distance between them.

Next, we discuss search methods for poses of high-resolution structures in EM maps. Visual modeling tools can be used for rigid fitting. A widely used program, Chimera (Pettersen et al., 2004), provides functionality for users to place a high-resolution structure in an EM map in a graphical user interface. Then the “Fit in Map” tool can perform local optimization of the pose, which is guided by the cross-correlation. Coot (Emsley et al., 2010) also provides visual modeling functionality.

As mentioned above, in principle a six dimensional search needs to be performed to find a correct pose of a structure in an EM map. The search can be made faster by using Fast Fourier Transforms as implemented in Colores map (Chacón and Wriggers, 2002). The search for the rotational space can be accelerated by applying spherical harmonics (Garzón et al., 2007). The approach, named ADP_EM, reports that it runs 1 to 2 orders of magnitude faster than Colores in their benchmark study. An alternative to an exhaustive search for poses of structures is Monte Carlo stochastic sampling as implemented in Bsoft (Heymann and Belnap, 2007). Bsoft is a comprehensive toolbox of computational methods for electron micrographs and image processing. MultiFit (Lasker et al., 2009, 2010; Tjioe et al., 2011), a multi-body fitting method, uses a divide-and-conquer approach for searching spaces discretized using Mod-EM (Topf et al., 2005). BCL::EM-Fit (Woetzel et al., 2011) applies geometric hashing in the pose search. Local points of EM maps are characterized by the density and the gradient around them, which are stored and compared with points in a high-resolution structure to find local matches. The initial matches found by geometric hashing are subject to local optimization with a Monte Carlo simulated annealing protocol. In the case of fitting multiple protein units into an EM map, it is very helpful if we can segment the EM map to roughly identify where each unit is located. In the algorithm by Pintilie et al., an EM map is segmented into local regions using the immersive watershed algorithm, an image processing algorithm that highlights salient features in the map (Pintilie et al., 2010).

Lastly in this section, we introduce methods that build secondary structures and main-chain conformations of proteins in EM density maps. Foldhunter compares the structural motifs found in an EM map against existing structures in the Protein Data Bank (PDB) (Jiang et al., 2001). Foldhunter can identify a substructure of a protein at a specific part of the EM map. The candidate structures fitted are ranked by their correlation coefficient with respect to the EM map. Foldhunter as well as Helixhunter are available as part of EMAN2 (Tang et al., 2007). EMatch (Dror et al., 2007) also has a stage that performs fold recognition and fitting. Pairs of non-linear SSE segments are used for finding existing structures in a protein structure database. The agreement of electron densities can also be applied for improving protein structure modeling. Mod-EM (Topf et al., 2005) and Moulder-EM (Topf et al., 2006) fit protein structure models into an EM map. These two tools are built with a comparative modeling tool, MODELLER (Sali and Blundell, 1993). It was shown in the papers that the cross-correlation term was able to identify near native structure models from many other models generated from alternative target-template alignments.

To summarize this section, the two main factors for rigid fitting are the efficient sampling of protein structure poses fitted in an EM map and scoring functions to evaluate goodness-of-fit. The exhaustive search is sped up by computational techniques such as Fast Fourier Transform and spherical harmonics. Other searching algorithms, including geometric hashing and stochastic sampling are also explored. In terms of scoring, a small number of works have been done that use scoring terms other than cross-correlation. However, it is important to note that several methods pointed out the importance of surface comparison methods. Rigid fitting is a first step in a larger protocol that performs flexible refinement after an initial coarse-grained fitting of structures.

Flexible fitting methods

Proteins are intrinsically flexible molecule. They will change conformations from their isolated states for which their high-resolution structures are usually solved to the states when they interact with other subunits in a complex. In this section we review methods that explicitly consider alternative conformations of proteins in a structure fitting process. The proposed methods vary in their approaches to sample alternative conformations and levels of flexibility to be considered, which range from the atomic level to residue and segment levels.

One of the first work is real-space refinement of protein structures fitted in an EM map using a method, RSRef (Chapman, 1995), which was originally developed for high-resolution crystallographic analysis (Chen et al., 2001). RSRef calculates the partial derivative of the fit to the EM map and the agreement with standard stereochemical restraints. It uses conjugate gradient descent to optimize the atomic positions of proteins. A conventional molecular dynamics (MD) simulation has also been used to handle protein flexibility. The molecular dynamics flexible fitting method (MDFF) extends a conventional MD potential by adding two new terms: one that drives atoms towards regions of appropriate electron density in an EM map and another term that preserves the secondary structures by constraining dihedral angles and interatomic distances (Trabuco et al., 2008, 2009). To deal with the case that a protein complex is symmetric, an extended version of MDFF (called symmetry-restrained MDFF) incorporates a term that examines the deviation of subunit positions in a model from a perfectly symmetrical complex (Chan et al., 2011, 2012). There are also methods that add a cross-correlation term to the potential that guides MD trajectories to have a larger correlation (Orzechowski and Tama, 2008; Grubisic et al., 2010). The correlation term is expressed as k(1 – cc), where k is a constant and cc is the correlation coefficient between the EM density map and a fitted structure.

Compared to the MD-based approaches, Flex-EM performs more coarse-grained optimization of fitting (Topf et al., 2008). It has three stages of the optimization. In the first stage, rigid fitting of proteins or domains is performed to optimize the cross-correlation with the EM map. Then, the second stage performs conjugate gradient optimization of each protein or domain using three scoring terms: the cross-correlation and two terms for stereochemistry and atom-atom contacts. In the third stage, positions of secondary structure elements are refined with a simulated annealing rigid-body MD protocol. RIBFIND, an extension of Flex-EM, determines groups of secondary structure elements as rigid bodies and moves them as clusters in the third stage of Flex-EM (Pandurangan and Topf, 2012a, 2012b). Identifying rigid-bodies helps the optimization by limiting the conformational degree of freedom and preventing it from being trapped in local minima. The Rosetta protein structure prediction package has also been extended to include a scoring term that takes into account density correlations between a structure model and an EM map (DiMaio et al., 2009). The scoring term is the negative log-likelihood that a particular correlation occurs by chance, assuming they follow a Gaussian distribution. FRODA uses geometric constraints based on clusters of atoms within the biomolecule that can be considered as rigid regions, e.g. secondary structure elements (Jolley et al., 2008). It uses a Monte Carlo (MC) algorithm in which motion of rigid clusters is simulated by rotation about bonds and avoiding steric clashes. The goodness-of-fit to an EM map is evaluated by the cross-correlation. EM-IMO is targeted for refining user-specified segments (secondary structure elements) (Zhu et al., 2010). Specified segments are handled as rigid bodies, which are refined to improve the cross-correlation and an atom contact score. At the last step, MDFF simulation was employed for an atom-level refinement.

A number of works have used normal mode analysis (NMA), particularly on elastic network models (ENM) (Bahar et al., 1997) as a source of protein flexibility. NMA (Hinsen, 1998; Skjaerven et al., 2009) uses harmonic potentials to approximate potential functions and identifies flexible regions and the principal motion directions of atoms or residues. It is shown that a few low frequency normal modes are relevant to biological functions such as transitions between open and closed conformations (Tama and Sanejouand, 2001; Krebs et al., 2002), although limitations of the approach have been discussed (Ma, 2005).

ENM can use different coarse-grained structure representations, for example, some methods use a residue-based representation where Cα atoms of amino acids are represented as beads while others represent atoms with beads. Typically beads are connected by an edge if they are closer than a distance threshold and a harmonic potential is defined between them. These models are simple and thus have an advantage that they can explore a large conformational space (Bahar et al., 2010).

Most of the flexible fitting methods that use NMA on ENM iteratively modify structures and optimize the fit between them and an EM density map. NMFF (Normal Mode Flexible Fitting) is one of the first methods to use ENM. It uses normal modes to deform the initial structure to create several candidate structures and then identify the structure that has the highest correlation with respect to the EM density map (Tama et al., 2004a, 2004b). NORMA uses elNémo (Suhre and Sanejouand, 2004) to compute NMA of ENM for structures to be fitted to an EM map. It can also consider the symmetry of complexes (Suhre et al., 2006). A method proposed by Zheng uses two beads to represent each residue, one at the Cα atom and another one at the center of mass of side-chain atoms. This representation better captures local motions along with global motions of proteins (Zheng, 2011).

ENM can be also used for atom-level refinement by representing atoms rather than amino acid residues with beads. DireX (Wang and Schröder, 2012) combines a variant of ENM, named Deformable Elastic Network (DEN) (Schröder et al., 2007), with a conformational sampling algorithm, CONCOORD (De Groot et al., 1997) for refining structures that fit to an EM map. DEN updates equilibrium distances between atoms after each iteration of the refinement. The advantage of this approach is that the method is able to change the flexibility at different positions of a protein chain. Conformations of flexible regions are sampled while other parts are kept close to the original conformation. After applying moves by DEN, the atoms of the structure are moved to have better fit with respect to the EM map, then, stereochemistry of the structure is optimized with CONCOORD. This procedure is applied iteratively. Another refinement method, YUP.SCX, uses a Gaussian Network model (GNM) that connect neighboring atoms within predefined cutoff lengths (Tan et al., 2008). To aim for fine refinement of a structure, different cutoff values are used for different atom types. The object function to be optimized consists of three terms, a term that keeps the structure within the EM map, the GNM-based term, and a scoring term that restrains the protein stereochemistry of the structure. Simulated annealing is used as the optimization method.

Protein flexibility information can also be obtained from sources other than dynamics computations. S-flexfit (Velazquez-Muriel and Carazo, 2007) uses structure variations observed in proteins of the same superfamily in the CATH protein structure classification database (Pearl et al., 2003).

Recently Levitt and his colleagues proposed a structure refinement protocol for protein conformations by comparing them to two dimensional (2D) EM maps rather than to a reconstructed 3D map (Zhang et al., 2012). By directly comparing against 2D maps and bypassing the construction of 3D maps, it is possible to better consider the structural heterogeneity and different orientations of the molecules. The method clusters 2D maps into 100 groups, each of which is a 2D view of a protein in a different conformation and orientation. The protein structure is projected onto each 2D average image of clusters to determine its most probable orientation. Then, starting from the initial structure, conformations are constructed by a MC procedure, which are projected onto a 2D space and compared against the 2D average map to quantify their agreement. In the MC simulation, the number of degrees of freedom of the structure is reduced so that largely different conformations can also be sampled efficiently.

To summarize this section, flexible fitting is aimed at considering alternative conformations of proteins that would provide better quality in fitting their structures to EM density maps. Flexibility information can be obtained by computational simulations that range from MD to more coarse-grained methods, such as ENM as well as those which move segments and rigid domains, and thus can sample larger conformational changes. Methods also exist that consider flexibility in multiple resolutions in a hierarchical or iterative fashion. Different methods may yield different structures but it has been suggested that taking consensus models computed by different methods can improve the model accuracy (Ahmed et al., 2012).

Actual scenarios of structural modeling

In this section we discuss actual examples of applications of computational tools to construct atomic models from 3D EM maps. The first example is the construction of an atomic model of a group II chaperonin from Methanococcus maripaludis (Mm-cpn) (Baker et al., 2010). In that study, after the 3D density map was determined, the authors first segmented the map to identify locations of single protein subunits. Then, SSEHunter and SSEBuilder were used to identify secondary structure features in the map. Next, a sequence similarity search including PSI-BLAST was performed (Altschul et al., 1997) against the PDB to find known tertiary structures of the protein or its structural homologs, which could be used for template structures for homology modeling. In the case of Mm-cpn, a homology model was constructed using SWISS-MODEL (Arnold et al., 2006; Kiefer et al., 2009). Then, the homology model was fit to the EM map using Foldhunter and Cα atoms of missing residues were filled in with HelixEditor and LoopEditor.

Unlike the study of Mm-cpn, there are situations that the structure of the protein has not been solved or cannot be modeled due to the lack of structures of its homologs. In such cases, the predicted secondary structures of the protein by using programs such as PSIPRED (McGuffin et al., 2000) can be corresponded with identified secondary structure regions in the EM map. Subsequently, Cα atoms can be placed in the map by assigning helices and strands/loops in the map using Helix Editor and Loop Editor functions in Gorgon.

Coming back to the case of Mm-cpn, after all the Cα atom positions were assigned, they were then adjusted such that reasonable Cα-Cα distances and angles were maintained. The full atomic model was constructed from the Cα model with SABBAC (Maupetit et al., 2006). The side-chain positions were optimized using the Rotamer option in Coot and outliers of atom positions in the Ramachandran plot were fixed. Lastly the models were fit back to the density map.

In a study on the structure determination of the 26S proteasome holocomplex, the complex was assembled by an integrated approach that consists of EM, high-resolution structures from X–ray crystallography, cross-linking, and protein-protein interaction data (Lasker et al., 2012). The authors first discretized a 8.4 Å resolution cryo-EM map into a graph of 238 nodes where the nodes were the density map regions and edges indicated neighboring regions. Similarly protein subunits were also represented in a coarse-grained fashion using beads of approximately 50-residue fragments. Then, the possible locations of subunits were assigned such that the assignment is consistent with available subunit shape, protein-protein interaction, cross-linking, and localization data. For a part of the map, MultiFit (Lasker et al., 2010), which assigns high-resolution structures to nodes in the graph in the EM map, was employed. In the refinement step, flexible fitting using MDFF was performed to fit atomic models.

As illustrated in the two actual structure determination studies above, a series of tools are needed to build a complex model from a 3D EM map. Table 1 provides links to the tools reviewed in this article with websites or code releases.

Table 1.

Availability of tools for structural modeling with 3D EM maps

Method Name	Availability (Web URL)	Description
Chimera	www.cgl.ucsf.edu/chimera	Visual modeling program that contains tools for EM fitting, segmentation and related features
Coot	www.biop.ox.ac.uk/coot	Visual macromolecular model building, model completion and validation
Situs/colores	situs.biomachina.org	Rigid fitting, included as part of the Situs package
EMFit	bilbo.bio.purdue.edu/~viruswww/Rossmann_home/softwares/emfit.php	Correlation-based rigid fitting
ADP_EM	sbg.cib.csic.es/Software/ADP_EM	Rigid and flexible fitting, optimized by using spherical harmonics to search the rotational space
MODELLER/Mod-EM	www.salilab.org/modeller	Mainly for comparative (homology) modeling. Mod-EM is an extension used for fitting
Gmfit	strcomp.protein.osaka-u.ac.jp/gmfit	Rigid fitting based on Gaussian Mixture Models
3SOM	www.russelllab.org/3SOM	Rigid fitting based on surface overlap
MultiFit	www.cgl.ucsf.edu/chimera/docs/ContributedSoftware/multifit/multifit.html	Rigid fitting of multiple components that adds shape-based terms
BCL::EM-Fit	meilerlab.org	Rigid fitting based on geometric hashing
Gorgon and Pathwalking	gorgon.wustl.edu	Structure modeling secondary structure prediction and fitting
EMatch	bioinfo3d.cs.tau.ac.il/EMatch	Fold recognition (in its initial stages) and rigid fitting
SSEhunter SSEbuilder Helixhunter Foldhunter	blake.bcm.edu/emanwiki	These methods are included as part of EMAN2. Foldhunter performs rigid fitting while the other three methods deal with SSE identification
Rosetta/EM-Fold	meilerlab.org	Alpha-helix identification and modeling implemented as an extension in the Rosetta prediction and modeling package.
EM-IMO	wiki.c2b2.columbia.edu/honiglab_public/index.php/Software:cryoEM	Homology modeling refinement using EM maps as constraints.
Flex-EM/RIBFIND	salilab.org/Flex-EM ribfind.ismb.lon.ac.uk	Flex-EM is a correlation-based flexible fitting method with MD refinement. RIBFIND is an extension included in Flex-EM that helps identify rigid bodies in structures
MDFF	www.ks.uiuc.edu/Research/mdff	Extension to molecular dynamics to perform flexible fitting
DireX	www.schroderlab.org/software/direx/index.html	Flexible fitting using deformable elastic networks
NORMA	elnemo.org/NORMA	Flexible fitting that considers symmetry. Is uses elNémo for computing protein flexibility.
S-flexfit	biocomp.cnb.csic.es/Sflexfit	Flexible fitting using structural variation in superfamilies
FRODA	flexweb.asu.edu	Flexible fitting with constrained geometric simulations

This table only lists programs that are available on the Internet. They are mentioned in the text.

Discussion

We have reviewed computational methods for building protein structure models from a 3D EM map. While the resolution of EM maps has been improved over the years to observe medium to high resolution models (3–8 Å) more frequently, it is still common to see new structures solved at over 10 Å deposited in the EMDB. Thus, different proper computational approaches need to be developed and used depending on resolutions of EM maps as well as the availability of other information such as high-resolution structures of protein subunits, or symmetry of the target protein complex.

Although 3D EM map data have been accumulated in the EMDB at an increasing pace (Fig. 1), it is still more than one order of magnitude lower than what is available in the PDB. Moreover, only about one third of the EM maps in the EMDB are associated with high-resolution structures in the PDB. As the number of EM data grows, more methods based on bioinformatics or machine-learning techniques will arise. The increase in the number of fitted structures into EM maps will greatly benefit the method development because they can be used to compute more accurate parameters of methods and also as the ground truth for method validation.

Structure determination by cryo-EM hybrid approaches requires many steps in both experiments and computational methods. Therefore, advances in this field require not only improvement of individual methods and tools but also protocols that apply these individual methods. It would be worth mentioning that advances of methods in protein bioinformatics fields including template-based structure modeling (Qu et al., 2009; Chen and Kihara, 2011), protein-protein docking (Venkatraman et al., 2009; Moreira et al., 2010; Esquivel-Rodríguez et al., 2012), structure refinement (Kolinski et al., 2001; Raval et al., 2012), and model quality assessment (Kihara et al., 2009; Yang et al., 2010) will contribute to the improvement of structure modeling for EM maps.

ABBREVIATIONS

3DZD

3D Zernike descriptor

CATH

Class, Architecture, Topology, Homologous superfamily. Acronym for the CATH protein structure database

DEN

Deformable Elastic Network

EM

Electron Microscopy

EMDB

Electron Microscopy DataBank

ENM

Elastic Network Model

MC

Monte Carlo

MD

Molecular Dynamics

MDFF

Molecular Dynamics Flexible Fitting

NMA

Normal Mode Analysis

NMFF

Normal Mode Flexible Fitting

NMR

Nuclear Magnetic Resonance

PDB

Protein Data Bank

RMSD

Root Mean Square Deviation

SVM

Support Vector Machine