Abstract
Accurate prediction of brain dysfunction caused by disease or injury requires the quantification of resultant neural connectivity changes compared with the normal state. There are many methods with which to assess anatomical changes in structural or diffusion magnetic resonance imaging, but most overlook the topology of white matter (WM) connections that make up the healthy brain network. Here, a new neuroimaging software pipeline called the Network Modification (NeMo) Tool is presented that associates alterations in WM integrity with expected changes in neural connectivity between gray matter regions. The NeMo Tool uses a large reference set of healthy tractograms to assess implied network changes arising from a particular pattern of WM alteration on a region- and network-wise level. In this way, WM integrity changes can be extrapolated to the cortices and deep brain nuclei, enabling assessment of functional and cognitive alterations. Unlike current techniques that assess network dysfunction, the NeMo tool does not require tractography in pathological brains for which the algorithms may be unreliable or diffusion data are unavailable. The versatility of the NeMo Tool is demonstrated by applying it to data from patients with Alzheimer's disease, fronto-temporal dementia, normal pressure hydrocephalus, and mild traumatic brain injury. This tool fills a gap in the quantitative neuroimaging field by enabling an investigation of morphological and functional implications of changes in structural WM integrity.
Key words: altered brain connectivity, brain networks, fiber tracking, neurodegenerative disorder, traumatic brain injury
Introduction
Disruption in the brain's structural network of white matter (WM) pathways occurs in many diseases and disorders, including multiple sclerosis (Kutzelnigg et al., 2005), trauma (Kinnunen et al., 2011), tumor (Yen et al., 2009), normal pressure hydrocephalus (NPH) (Hattori et al., 2012), addiction (Schulte et al., 2012), and neurodegeneration (Zhang et al., 2009). Across and within most of these conditions, there is great variation in the extent and type of physical and cognitive dysfunction that occurs (Chen et al., 2000; Røe et al., 2009). Some of this variation in dysfunction is likely due to differences in the size and location of pathology as well as differences in its effect on the structural brain network (Alstott et al., 2009; Johansen-Berg, 2010; Kuceyeski et al., 2011; Lipton et al., 2012). This complexity is one of the reasons that a neurological assessment of cognitive and functional alterations secondary to WM pathology have hitherto been challenging to quantify, let alone predict. Although there exist a panoply of neuroimaging analysis tools for assessment of morphological and microstructural changes, a few enable a systematic quantification of the network effects, and those that do require diffusion imaging and tractography to be performed in patient populations.
Filling this important gap requires mathematical encoding of the expectation that focal or diffuse alterations of WM integrity have distal consequences at the terminating gray matter (GM) regions. We, thus, present a software pipeline called the Network Modification (NeMo) Tool that takes a map of alterations (either positive or negative) of a brain's WM characteristics and determines the changes to implied whole-brain inter-regional fiber connectivity. Our tool allows a user to project WM injury to the cortices and deep brain nuclei, which then enables the assessment of region-specific functional and cognitive alterations. Global changes to the network are assessed by the NeMo Tool via graph theoretic metrics, a technique that has become popular in brain network analysis (Achard et al., 2006; Bullmore and Sporns, 2009; Sporns and Zwi, 2004). In contrast to existing methods, our tool can directly assess the effect of a given pattern of WM alteration on whole-brain network properties, incorporating the size, severity, and location of WM lesions without having to perform tractography in pathological brains. Whether or not to perform tractography in diseased patients is still an open question, and there will be neurological scenarios that necessitate tractography in patients. Our approach provides a convenient tool in other scenarios, for example, in cases where practitioners are uncomfortable or unable to do tractography in their subjects or when diffusion data do not exist.
The type of connectivity analysis provided by the NeMo Tool represents one of the first steps in predicting executive and behavior-specific changes that may occur due to a certain pattern of WM integrity alterations in various disorders. More importantly, network-based metrics that capture the systemic effects of pathology are more likely to be attuned to the level of disability or recovery after an onset of disease or injury than deductions based on anatomical changes in specific structures. To this end, the NeMo Tool provides measures of global network modifications that can be used to create biomarkers for prognosis, monitoring of disease progression or recovery, and, possibly, subsequent development of rehabilitation programs which optimize outcomes.
The first step in the NeMo Tool pipeline is to superimpose user-defined WM alteration masks onto the Tractogram Reference Set (TRS) that consists of a large number of tractograms from normal subjects. For each tractogram, the NeMo Tool finds the tracts that pass through areas in the WM alteration mask and records the GM regions they connect. The output of this tool consists of (1) the Change in Connectivity (ChaCo) metric, defined for each cortical/subcortical GM region in a particular atlas, which gives the amount of increase or decrease in that region's connection to the rest of the network and (2) overall network changes as measured by summary graph metrics.
A primary advantage of the NeMo Tool is the capacity to provide dis/hyper-connectivity analysis without having to perform tractography in normal or abnormal subjects. Tractography is an active area of research that requires some expertise to perform, and the NeMo Tool enables researchers and clinicians to investigate changes in brain connectivity without having to implement these rather complex tools. Thus far, most analyses of brain network connectivity changes have depended on tractography performed in brains affected by a disease, injury, or aging. It is not known whether these methods, which are sensitive to noise, can yield reliable connectivity information in abnormal brains (Pagani et al., 2007; Pierpaoli et al., 2001; Wheeler-Kingshott and Cercignani, 2009). For example, in a previous study of mild traumatic brain injury (TBI), connectivity metrics based on tractography in healthy normal individuals yielded functionally meaningful correlations with behavioral data, whereas those derived directly from patients did not (Kuceyeski et al., 2011). The NeMo Tool's use of a large collection of tractograms from healthy subjects to project the location of integrity changes in patients may better capture pathological connectivity changes than by performing tractography directly in those populations. Other advantages of the NeMo Tool include its ease of use; a mask of brain changes from an individual or group is all that is required as input. It can be used in retrospective studies in which diffusion images do not exist or in studies in which the diffusion data cannot be acquired, such as in patients for whom long sessions of magnetic resonance imaging (MRI) are untenable.
The purpose of this article is to introduce the NeMo Tool and demonstrate its functionality by applying it to a variety of patient image data to show both novel findings and an interesting comparison with existing knowledge. We explore three different and unique disease datasets: (1) Alzheimers (AD) and frontotemporal dementia (FTD) data from a previous study (Kuceyeski et al., 2012); (2) a single NPH subject whose WM alteration masks are two hand-drawn binary regions of interest (ROI) denoting abnormal WM hyperintensities; and (3) WM alteration maps from individuals with chronic-stage mild TBI showing both losses and gains in apparent WM fiber integrity. In all cases, the unique strength of the proposed tool in unraveling the WM–GM relationship was established.
Previous work
Pathologic brain changes can be measured by structural, diffusion, or functional MRI and assessed with voxel-based morphometry (VBM) (Ashburner and Friston, 2000), deformation-based morphometry (DBM) (Chung et al., 2001), tract-based spatial statistics (TBSS) (Smith et al., 2006), MR volumetrics (Fischl and Dale, 2000; Ad-Dab'bagh et al., 2006; Friston et al., 2006; Woolrich et al., 2009), functional magnetic resonance imaging activation analysis (Cox, 1996), and so on. Recently, an exploration of the cortical and subcortical WM connectivity network has become an area of wide interest due to two developments: the rise of diffusion imaging that can measure WM structures in vivo (Assaf and Pasternak, 2008) and the application of complex network analysis (Barabási, 2009; Przulj, 2004; Strogatz, 2001) to the observed WM structural network (Bullmore and Sporns, 2009; Raj and Chen, 2011; Sporns et al., 2004; Sporns and Zwi, 2004).
The integrity of WM tracts is essential to the quality of the signal transmitted through these connections and may influence cognitive or physical behaviors that depend on these connections (Fields, 2008; Johansen-Berg, 2010). Although atlases that parcellate WM tissue into anatomically coherent regions (i.e., fiber bundles) have been created based on existing knowledge of their trajectories and connections to GM regions (Hua et al., 2008; Oishi et al., 2009; Wakana et al., 2004), these atlases do not allow a quantitative analysis of GM connectivity disruption at the regional or global level. A few studies have linked increases in the integrity of specific WM pathways to behavioral improvement (Johansen-Berg et al., 2010; Scholz et al., 2009). Conversely, other studies have assessed how decreases in the integrity of WM pathways relate to dysfunction in stroke (Mukherjee, 2005), aging (Pfefferbaum et al., 2005), mild TBI (Niogi et al., 2008), and multiple sclerosis (Charil et al., 2003; Vellinga et al., 2009; Wilson et al., 2003). Yet other studies have focused on changes to the overall network in various states, including aging (Wen et al., 2011) and disorders such as schizophrenia (Bassett et al., 2008; Zalesky et al., 2010), AD (He et al., 2009; Lo et al., 2010), and stroke (Chen et al., 2000; Crofts et al., 2011; Nazzal et al., 2009). There are methods that can be used to detect local as well as global connectivity changes in pathological brains. Rubinov and Sporns (2010) developed a toolbox within Matlab to enable analysis via graph theoretical metrics on functional and structural brain networks, while Irimia et al. (2012) developed a way to construct and visualize connectivity networks and applied it to three cases of TBI individuals. In another interesting use of tractography to infer connectivity changes, Pannek et al. (2011) compared average path length maps in normal and severe TBI cases.
The present work builds on our own previous work on WM connectivity importance maps, which demonstrated the use of network-centric methods applied to WM lesion maps (Kuceyeski et al., 2011), as well as another recent work that modeled disease propagation as a diffusion process on the normal brain connectivity network (Raj et al., 2012). The utility of the present approach is substantiated by our earlier investigation of implied loss of connectivity in the cortex due to loss of WM integrity in AD and FTD (Kuceyeski et al., 2012b) and preferential disruption in the brain's reward processing sub-network in alcohol-dependent individuals (Kuceyeski et al., 2012a). The NeMo Tool incorporates these early investigations, and formalizes them within a fully executable software pipeline with expanded capabilities. Compared with an earlier work, this tool (1) allows both positive and negative WM alterations with the capability of indicating WM integrity gains due to network rewiring post-injury or disease onset; (2) has greatly reduced population bias by establishing a reference set of data with a larger number of normal subjects; (3) integrates tractograms from individual subjects into common Montreal Neurological Institute (MNI) space, allowing for more reliable tract inference and minimization of coregistration errors, while speeding up and simplifying calculations; and (4) features various outputs, including surface and “glass brain” renderings and graph-theoretic statistics.
Materials and Methods
The TRS
The TRS is a large collection of sets of streamlines that represent WM fiber tracts of a normal individual cohort. The TRS constitutes the database with which the NeMo Tool examines the effects of the user-defined WM alteration mask. The streamlines in the TRS were created first in diffusion space and then transformed into common MNI space. This study's normal subject data were collected jointly by Weill Cornell Medical College and the Brain Trauma Foundation. Seventy-three healthy subjects (40 men, 33 women, 30.2±6.7 years) were used to create the normative connectivity information in the form of tractograms. The conditions for exclusion were pregnancy, a history of neurological or psychiatric diagnosis, seizure, or drug or alcohol abuse. T1-weighted structural and diffusion-weighted MR images were collected on a 3 T GE Signa EXCITE scanner (GE Healthcare, Waukesha, WI). The High Angular Resolution Diffusion Images data were acquired with 55 isotropically distributed diffusion-encoding directions at b=1000 sec/mm2 and one at b=0 sec/mm2, from 72 1.8-mm thick interleaved slices (no slice gap) and 128×128 matrix size, zero-filled during reconstruction to 256×256, with a field of view (FOV) of 230 mm2. The structural scan was an axial threedimensional inversion-recovery fast spoiled gradient-recalled echo sequence ((echo time [ET]=1.5 msec, repetition time [TR]=6.3 msec, inversion time [TI]=400 msec) flip angle of 15°) with a 256×256 matrix over a 230 mm2 FOV and 156 1.0-mm contiguous partitions. The diffusion images were corrected for eddy current and motion artifacts using FMRIB Software Library (FSL) (Smith et al., 2004).
The T1 images were processed by first segmenting the tissue into cerebrospinal fluid, WM and GM. The GM segment was subsequently parcellated into 116 different ROIs using the Automated Anatomical Labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002). The AAL atlas is widely used and has a moderate number of discrete GM ROIs, but other atlases may be more desirable by the user. The analyses in this work were done using the 116-region atlas, but an 86 region atlas that corresponds to the FreeSurfer ROIs is also available in the NeMo Tool. The parcellated GM was then linearly transformed and resampled to diffusion image space for use in tractography. Briefly, the surface voxels of the parcellated cortical and subcortical structures were used to seed the tracts. Proposed and validated in Iturria-Medina and colleagues (2005), the tractography algorithm implemented here incorporates tissue classification probability and orientation distribution information in a Bayesian manner. A tract terminated when the algorithm reached the boundary of an image volume, the edge of a GM region, a voxel not in the gray or WM masks, or when the angle between subsequent steps exceeded π/3. This analysis was done using the eighth version of Statistical Parametric Mapping (SPM), (Friston et al., 2006), a software package within Matlab R2009a (The Mathworks, Inc., Natick, MA), and the Individual-Based Atlas toolbox (Alemán-Gómez et al., 2005) within SPM. Further details of the image processing and tractography method are given in a previous publication (Kuceyeski et al., 2011).
To transform the streamlines into MNI space, we first applied the inverse of the linear transformation to map the diffusion space streamlines to their corresponding position in T1 space. Next, the 12-parameter non-affine transform that coregistered each subject's T1 image to the MNI T1 atlas was found using the normalize function within SPM (Friston et al., 2006). The coefficients of the deformation field that correspond to this transform were defined for each voxel center; so, they were interpolated to be applied to points not at the center of a voxel. The tri-linearly interpolated coefficients were applied on a point-by-point basis to the T1-space streamline, providing the corresponding streamline in MNI space. For the details of the validation of the tractogram normalization (see Supplementary Data S1; Supplementary Data are available online at www.liebertpub.com/brain).
Once the WM tracts were mapped and the connectivity of different regions in the brain were determined, the results were represented by a graph, which was analyzed using available graph theoretical methods (see Gondran and Minoux, 1984). A graph G=(R, C) is defined by a set of vertices R that are linked pairwise by edges C. The edges can be assigned a capacity or weight cij that describes the strength of connection between any two vertices i and j. A graph can also be represented by a matrix c whose element in the ith column and the jth row is the edge weight cij. In the graph that represents brain connections, the vertices of the original graph are GM regions and the edges are their connections via WM tracts. The connectivity between regions can be summarized in different ways, including probability of connection or the amount of WM tissue connecting any two regions. For each tractogram in the TRS, the weights cij of the corresponding graph were integer values greater than zero that were simply a count of the number of WM tracts between regions i and j. Finally, the characteristics of each connectivity network in the TRS can be summarized using metrics, including degree, characteristic path length, efficiency, betweenness centrality, and clustering coefficient.
The NeMo tool
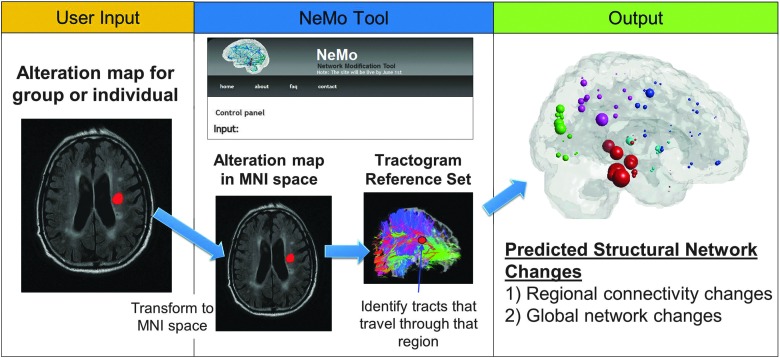
The NeMo Tool, freely available at http://ideal-cornell.com/index.php/research/brain-tools, quantifies disease- or injury-related neural connectivity changes by predicting the effects of a hypothetical lesion (or other changes) to specific WM tracts among the normal subjects in the TRS. The workflow of the NeMo Tool, including a screenshot of the user interface, is summarized in Figure 1. In the following text, we describe the user input to and output of the NeMo Tool.
FIG. 1.
The Network Modification (NeMo) tool workflow. The user inputs a mask of white matter (WM) pathology/alteration, which is then transformed into MNI space if needed using Statistical Parametric Mapping's non-linear normalization routine. The Tractogram Reference Set (TRS) is searched for streamlines traveling through areas with altered WM integrity. Two outputs are generated: (1) the regional connectivity changes in the form of the weighted proportion of tracts connecting to a region which travel through the alteration mask, that is, Change in Connectivity (ChaCo) scores, and (2) the global network changes in the form of metrics on the connectivity network matrices corresponding to that alteration mask. The top of the middle panel provides a snapshot of the online version of the NeMo Tool.
The NeMo Tool takes a mask of WM alterations as input from the user and searches the TRS for streamlines passing through this mask. The user input mask is a representation of a brain volume that indicates either the state (binary) or the progression (continuous) of disease or injury from a single subject or a population. The values of the mask can be between −1 and 1, indicating WM integrity decreases or increases, respectively. This mask is not created within the NeMo Tool, but rather should be provided by the user. The mask can be generated from existing image processing tools such as FSL (Smith et al., 2004) or SPM (Friston et al., 2006). For example, the mask could indicate areas of WM hyperintensity, increases or decreases from normal values of diffusion summary statistics such as fractional anisotropy (FA), longitudinal diffusivity (LD), or radial diffusivity (RD), or even contain a hand-drawn ROI. The alteration mask can either be uploaded in MNI space or supplied with an accompanying structural MRI that can be used for MNI space normalization. Depending on the sparsity of the alteration mask, the NeMo calculation can take from under an hour up to several hours, as tested on a Linux desktop computer with 12 GB of RAM and six 3.33 GHz Intel Core i7 processors.
The NeMo Tool outputs two separate summaries of network connectivity alteration: (1) the ChaCo score defined for each GM region and (2) changes in overall network summary statistics. The ChaCo score for each ROI is calculated via the following process:
All of the streamlines which connect to that ROI are identified and assigned a weight of zero.
The non-zero values in the WM alteration mask that a streamline passes through are collected, and that streamline's weight is reassigned by taking the minimum of these values. If a streamline passes through only zero entries, its weight remains at zero.
The ChaCo score for that ROI is then calculated by taking the sum of the streamline weights and dividing by the number of tracts connecting to it to ensure normalization and enable a comparison between regions.
The ChaCo score parallels measures of differences in connection density that are derived using tractograpy in pathological brains. It can be thought of as a weighted proportion of altered tracts; for example, if the alteration mask is binary and negative, then the resulting score is negative one times the proportion of tracts passing through “injured” WM areas which connect to that ROI. Other ways of streamline weight assignment may be more appropriate depending on the situation (see section “Limitations”).
In the second output of the NeMo Tool, overall network changes as compared with the intact brain network are characterized by graph theoretic metrics. As stated in the previous section, the edge weights cij for the networks of each normal individual in the TRS were calculated by counting the number of streamlines between ROI pairs. This process was identical to assigning each streamline a weight of 1 and taking the sum of these weights. For the network resulting from a given WM alteration mask, edge weights cij between the ROI pair i and j are calculated via the following process:
All the streamlines connecting ROIs i and j are collected and assigned a default weight of 1.
The non-zero values in the WM alteration mask which a streamline passes through are collected, and that streamline's weight is reassigned by taking the minimum of these values and adding 1. If a streamline passes through only zero entries in the WM alteration mask, its weight remains at 1. If a streamline passes through a voxel marked as “injured,” its weight is less than 1 (0 when the alteration mask is binary and negative).
The weights of all the streamlines connecting i and j are then summed and entered into the altered brain network matrix as edge cij.
The altered network is constructed by repeating this process for each ROI pair.
For a given WM alteration mask, the ChaCo scores and summary network metrics are calculated for each subject in the TRS. The averages of the ChaCo scores and summary network metrics represent the expected connectivity changes caused by the specified WM alterations. However, there are normal variations in WM architecture across individuals that may influence the NeMo Tool's results. In addition to population variance, there is noise introduced from the tractography algorithm itself. The influence of these sources of noise can be estimated by examining the range of the ChaCo scores and summary network metrics across subjects in the TRS for the same WM alteration mask. The bottom panels of Figures 3 and 5 illustrate the distribution of the ChaCo scores for the AD and FTD masks using a boxplot that is color coded by regional membership (frontal=blue, parietal=pink, occipital=green, temporal=red, subcortical=cyan, and cerebellar=yellow). Wilcox signed-rank tests with Bonferroni correction are performed on the distributions of ChaCo scores to test whether they are significantly different from zero (colored boxes) or not (black boxes). The reporting of variance information is an important aspect of our tool, as it gives the user the ability to assess the level of confidence in the estimation of disconnection. For a WM alteration mask with uniform zero values (a trivial alteration mask representing a “normal” subject by definition), the ChaCo scores are zero with zero variance, while summary network metrics replicate those for each subject in the TRS, representing variations within a normal population.
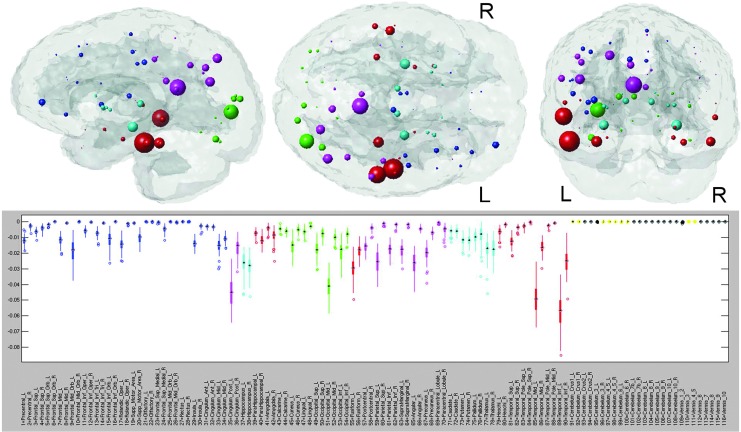
FIG. 3.
NeMo results for Alzheimer's disease (AD). The glassbrain visualization displays each of the 116 regions' centroids as a sphere (color coded by regional membership) whose size corresponds to the mean ChaCo of that region (larger spheres indicate more negative ChaCo). The boxplot in the bottom panel shows the distribution of ChaCo scores across the 73 subjects in the TRS for each of the 116 regions (color coded by regional membership), to demonstrate the influence of the normal variation of WM architecture on the results. If a region's boxplot has a smaller range, greater confidence can be assigned to the disconnection estimates than can be assigned to regions with a higher variation. The black boxplots denote those regions whose ChaCo distributions are not significantly different from zero.
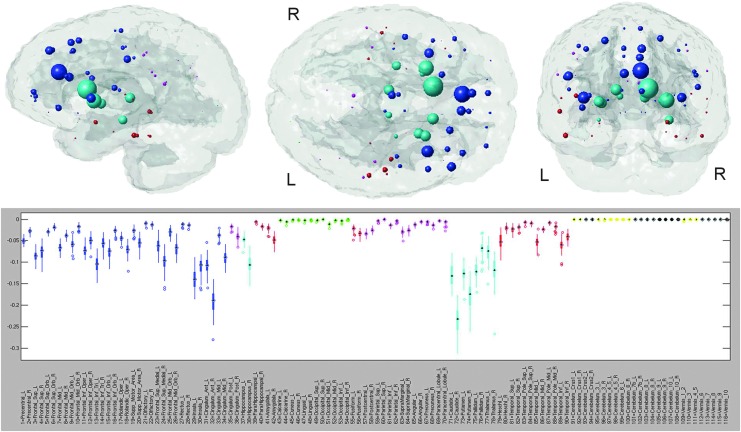
FIG. 5.
NeMo results for frontotemporal dementia. The glassbrain visualization displays each of the 116 regions' centroids as a sphere (color coded by regional membership) whose size corresponds to the ChaCo of that region (larger spheres indicate more negative ChaCo). The boxplot in the bottom panel shows the distribution of ChaCo scores across the 73 subjects in the TRS for each of the 116 regions (color coded by regional membership), to demonstrate the influence of the normal variation of WM architecture on the results. If a region's boxplot has a smaller range, greater confidence can be assigned to the disconnection estimates than can be assigned to regions with a higher variation. The black boxplots denote those regions whose ChaCo distributions are not significantly different from zero.
The mean results of the NeMo analysis can be displayed in various ways. The top panel of Figures 4 and 5 shows one possible mode of display called the “glassbrain” which conveys the ChaCo scores by the size and location of spheres that are color coded by regional membership using the same scheme as the boxplots and centered at each GM region. Alternatively, the user can display the ChaCo scores as a color on the surface of each GM region as in Figure 7, called the “gummibrain,” with red, yellow, and green indicating decreases, no change, and increases in connectivity, respectively. The gummibrain visualization is suitable for showing the results from WM alteration masks with positive and negative values, as the colored surfaces can illustrate the positive and negative changes in connectivity. As preliminary validation of the NeMo Tool, we created two binary WM alteration masks that “removed” the splenium of the corpus callosum and the superior longitudinal fasciculus, and checked that proper GM regions were identified for a particular WM lesion (Supplementary Data S2).
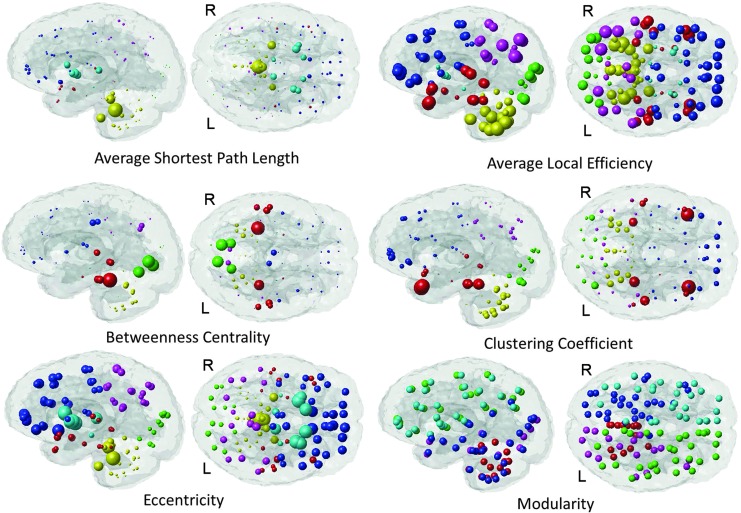
FIG. 4.
Local properties of the altered AD network. The values of these local network properties (average shortest path length, average local efficiency, betweenness centrality, clustering coefficient, eccentricity, and modularity) are communicated via the radius of the sphere. Color denotes regional membership except for the modularity plot in which color denotes cluster assignment.
FIG. 7.
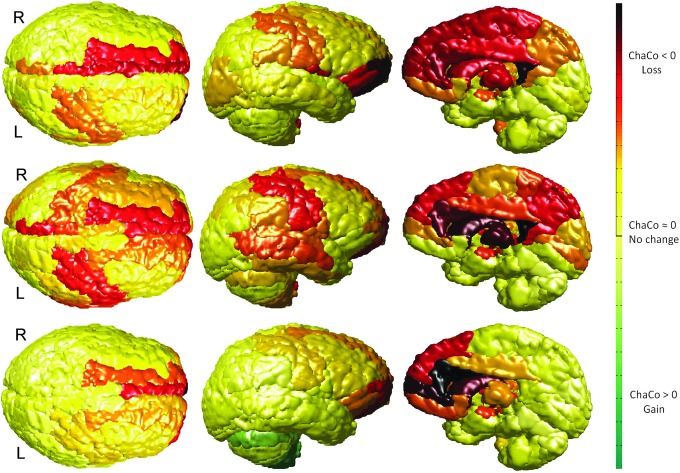
Gummibrain visualization of the ChaCo scores for three mild TBI patients. The ChaCo score of each region is that region's color, where losses are represented in red, no changes in yellow, and gains in green.
Application to various disorders
AD/FTD/normal control data
This set of data was the same as was used in Zhang and colleagues (2009) and Kuceyeski and colleagues (2012b); here, they were re-processed using the NeMo Tool. The details of the image processing can be found in the latter publication. In short, a group-wise comparison of the diffusion summary statistics of FA, LD, and RD was computed for AD versus age-matched cognitively normal controls (CN) and FTD versus CN, resulting in two sets of three t-maps. The t-maps were thresholded utilizing a significance level of p=0.05 (with adjustment for multiple comparisons performed using voxel-wise false discovery rate (FDR) method (Genovese et al., 2002) to find areas of significant WM integrity loss. The union of the three binary masks was taken, resulting in a WM alteration mask in MNI space for input to the NeMo Tool.
NPH
T2 fluid-attenuated inversion recovery MRI data were acquired at Weill Cornell Medical College for a subject with probable NPH on a 3 T GE system sequence (TE=9500 msec, TR=144 msec, and TI=2250 msec) with a 320×192 matrix over a 220 mm2 FOV and 3.0-mm slice thickness. These images were used by a board certified neurologist and co-author to identify binary peri-ventricular WM hyperintensity masks for input to the NeMo Tool. Two masks were made, one with an anterior locus and the other with a posterior locus, in order to separately investigate their possible effects.
TBI
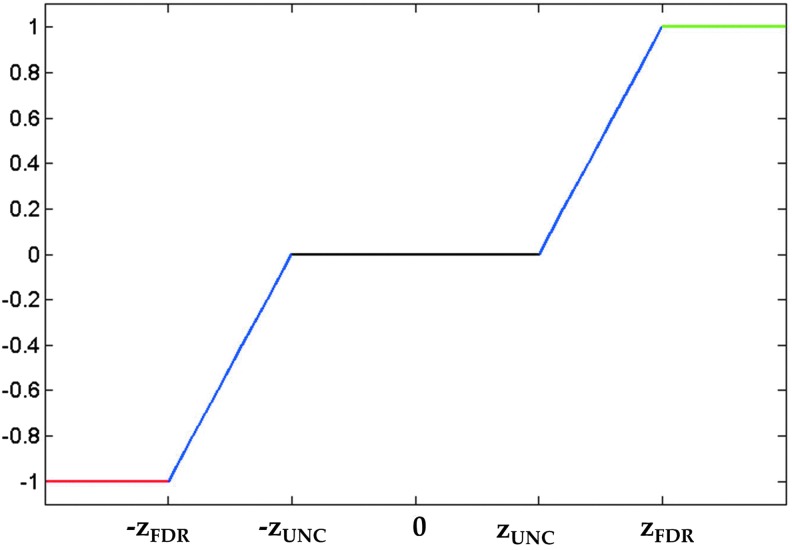
The mild TBI data were collected jointly by the Weill Cornell Medical College and the Brain Trauma Foundation. Diffusion images were collected from 28 subjects (17 men, 11 women, 36.5±11.8 years) with identical acquisition parameters as those for CN in the TRS and were post-processed in the same way. Each T1 image was downsampled into diffusion space and transformed into MNI space via a 12-parameter non-affine transformation (found using SPM). This transformation was then applied to the FA maps using trilinear interpolation, and each patient's voxel-wise z-map was calculated using the mean and standard deviations of the FA map from the 73 CN in the TRS. Once the z-maps were found, the WM alteration masks were created using the piece-wise continuous function, illustrated in Figure 2:
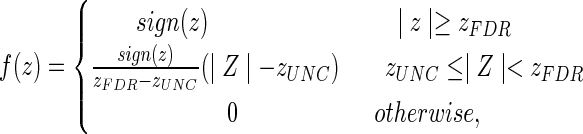 |
FIG. 2.
Step-wise continuous function for converting voxel-wise z-scores of fractional anisotropy into WM alteration masks for the mild traumatic brain injury (TBI) patient data.
where zUNC was the z-value corresponding to the uncorrected significance level, and zFDR was the z-value corresponding to the group-wise FDR corrected significance level. The value of zUNC (here±2.576, corresponding to α=0.005) can be adjusted to ensure a sufficient noise exclusion (Supplementary Data S3) and a reduced computation time. It should be emphasized that in all of these analyses, including TBI, the WM alteration masks were generated to represent deviations from the normal population and not change over time.
Results
Application to various disorders
AD and FTD
The ChaCo results derived from the single WM alteration mask for the AD population are given in Figure 3. The “glassbrain” (top row) shows the mean ChaCo scores over the 73 normal subjects in the TRS. To assess the influence of algorithmic and normal population variance in the ChaCo results, we create boxplots (bottom row) that illustrate the distribution of the ChaCo scores across the normal subjects in the TRS. The areas with largest implied connectivity losses include the temporal regions, hippocampi and posterior cingulate, as well as some parietal and occipital regions, with the left containing more disconnections than the right (see Table in Supplemental Data S4). Figure 4 displays various network properties of each node in the altered AD network, including average shortest path length, efficiency, clustering coefficient, eccentricity, and modularity. The color in all the subfigures denotes regional membership, except the modularity plot in which color denotes membership in a cluster. The results for the WM alteration mask for the FTD population are illustrated in Figure 5. The areas with largest implied connectivity losses are mostly the frontal and subcortical regions (insula, bilateral putamen, caudate nucleus, pallidum, thalamus, and hippocampus), anterior and middle cingulatecortices, and some temporal regions. Cerebellar regions (in yellow in the boxplot) are very close to zero in both groups.
NPH
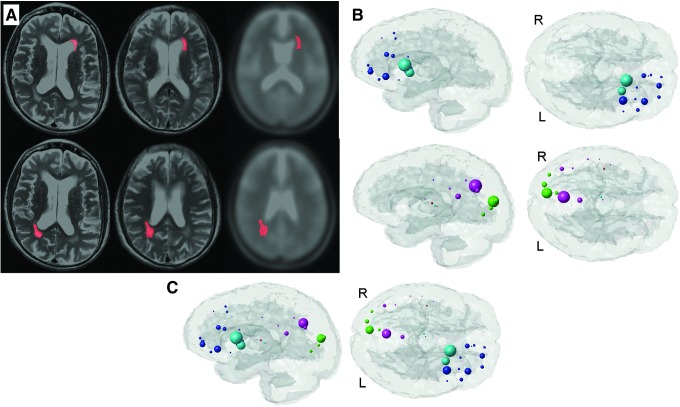
Figure 6A displays the normalization process for the anterior (top row) and posterior (bottom row) masks. The left column is the lesion in patient space superimposed on the patient's scan, the middle column is the lesion in MNI space superimposed on the normalized patient scan, and the right column is the lesion in MNI space superimposed on the template scan. The corresponding mean ChaCo scores are given in Figure 6B for the anterior (top) and posterior (bottom) masks. The anterior pathology mask (top row) implicates losses in connectivity in the subcortical regions of the left caudate and putamen and frontal areas, including left insula, frontal inferior, and superior orbital gyri. The posterior mask (bottom row) implicates highest disruption in the right cuneus and precuneus. Since the glassbrain visualization shows the ChaCo scores with a relative scale that is consistent only within the plot, the effects of the two different alteration masks cannot be directly compared in these figures. The mean ChaCo scores from the two alteration masks are plotted together in Figure 6C to show the relative contribution of the anterior and posterior masks.
FIG. 6.
NeMo results for normal pressure hydrocephalus. (A) Illustrates the normalization process for the anterior (top row) and posterior (bottom row) hand-drawn regions of interest masks that indicate peri-ventricular WM hyperintensities. The left column is the lesion in original patient space superimposed on the patient's scan, the middle column is the lesion in MNI space superimposed on the normalized patient scan, and the right column is the lesion in MNI space superimposed on the template scan. The corresponding ChaCo scores are given in (B) for the anterior (top) and posterior (bottom) masks. Each of the 116 regions' centroids are a sphere (color coded by regional membership) whose size corresponds to the ChaCo of that region (larger spheres indicate more negative scores). (C) Shows the two masks' results in the same brain as to illustrate their inter-relationship.
TBI
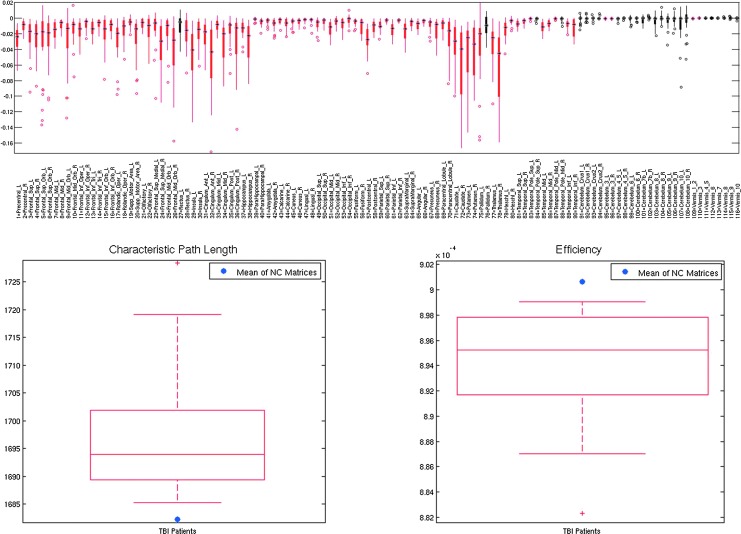
Figure 7 shows the mean ChaCo scores via the gummibrain visualization for three representative mild TBI patients, with decreases in connectivity shown in red (dark red=1, yellow=0) and increases in green (dark green=1, yellow=0). The top panel of Figure 8 shows the distribution of the mean ChaCo scores per region for each of the 28 TBI subjects; regions with negative group-mean changes in connectivity are in red while changes that are not significantly different from zero are in black. The bottom two panels in Figure 8 show global network properties of the TBI subjects, indicating a change from the mean of the CN given in blue.
FIG. 8.
NeMo results for mild TBI. The top panel shows the boxplot of the ChaCo scores of the 28 mild TBI individuals, with significant average population losses in connectivity given in red and non-significant changes in black. The bottom panels show characteristic path length and efficiency for the mild TBI individuals with the red boxplot and the mean of these metrics from the normal population with the single blue point.
High levels of potential disconnection were found in the frontal and subcortical areas (Fig. 8, top). The subcortical areas had the most negative ChaCo scores in this TBI population, including the bilateral caudate, putamen, thalami, right hippocampus, and left pallidum. Particularly negative in the frontal lobes are the left insula, right cingulate regions, middle and superior frontal orbital, and superior frontal gyri. Some areas of the parietal lobe also appeared to have moderate potential disconnection, including the right posterior cingulate and left postcentral gyri. The WM alteration masks in some patients predicted small but significant implied increases in connectivity in areas of the cerebellum. On a population level, these were deemed not statistically different from zero (see Fig. 8). The spread in the ChaCo scores shows the extent of between-individual variations in implied GM connectivity changes associated with variations of WM changes in the TBI subjects.
Discussion and Conclusions
The NeMo Tool is a novel, automatic, spatially unbiased, region- and network-based approach that will enable researchers to examine the potential influence of particular patterns of tissue damage or rewiring on the brain's structural connectivity network with the eventual goal of predicting concurrent behavioral outcomes. Although quantitative tractography in patients is commonly reported in the literature, the practice needs to be scrutinized because of the increased noise associated with pathological data (Kuceyeski et al., 2011; Pagani et al., 2007; Pierpaoli et al., 2001; Wheeler-Kingshott and Cercignani, 2009). On the other hand, the problem can be avoided altogether. In our approach, voxels associated with pathology or changes are projected directly onto normal anatomy, from which connectivity changes are inferred. This tool may improve many facets of patient care across a variety of diseases, including prognosis, diagnosis, disease progression monitoring, and rehabilitation planning. The examples given in this article represent only a few of the tool's wide range of possible applications.
Interpretation of the NeMo results
The functionality of the NeMo Tool was demonstrated by applying it to four disease/injury states (AD, FTD, NPH, and TBI) with various data arrangements (single subjects/groups) and different methods for creating the WM alteration masks. The flexibility of the NeMo Tool enables creation of alteration masks using other methods such as VBM, DBM, and TBSS as well.
AD and FTD
The results shown here generally agreed with the pathology of both AD (hippocampi, temporal, and posterior cingulate structures) and FTD (orbito-frontal, anterior cingulate, and subcortical structures). The variance in the ChaCo scores across individuals in the TRS (as shown with the boxplots, Figs. 3 and 5) suggests there is some influence of normal population differences and/or algorithmic variance in the NeMo Tool results.
NPH subject
NPH is frequently associated with periventricular T1 hyperintensities that can be reversed by shunt treatment. After creating the hand-drawn ROIs outlining these periventricular WM abnormalities, the images were normalized to MNI space. The ventricles in the NPH subject were quite large; so, there were some small differences in the relative location of the masks but overall, the quality of the normalization was deemed acceptable. Since the NeMo Tool reports results as distributions over a population of CN, small differences in ROI location should not unduly influence the results. The NeMo results indicated that the fiber tracts passing through these regions connect to cortical and subcortical structures which have been implicated as loci of abnormal brain function in NPH (Akiguchi et al., 2008; Gleichgerrcht et al., 2009; Otani et al., 2004; Saito et al., 2011). Both the anterior and posterior masks showed reduced connections only ipsi-laterally. While this observation may reflect an actual change in connectivity, the lack of cross-hemispheric connections could also be a by-product of the probabilistic tractography that emphasizes shorter u-fibers and has trouble reproducing long-range connections which are contained in the corpus callosum. Since the posterior lesion mask is proximal to the cortex, the ChaCo metric might have been influenced largely by u-fibers. When the results from the anterior and posterior masks were plotted together, the posterior regions showed only slightly lower disconnection measures than the anterior regions. This comparison sheds light on the relative contribution of anterior and posterior pathologies to functional changes.
TBI subjects
In agreement with the etiology of the pathology, the ChaCo scores varied widely from individual to individual within TBI (as shown in the boxplots of the top panel of Fig. 8). In general, however, the regions the NeMo Tool reported as having high implied disconnection included those associated with executive functioning and memory. The precentral gyrus, which includes the frontal eye field, was another region with high disconnection. These observations agree with symptoms classically associated with mild TBI, namely attention and memory. In particular, some of these regions agree with those found to correlate with attention measures in Fan and colleagues (2005). The global network metrics of the TBI subjects varied from the normal population as expected, with increases in characteristic path length and decreases in efficiency (bottom panel of Fig. 8). The global network metrics also varied widely in this population, providing potential for exploring correlations to cognitive measurements.
Limitations
The NeMo methodology is susceptible to errors introduced at different levels of analysis, including image acquisition and tractography. The diffusion acquisition resolution of 1.8 mm iso-voxel may be insufficient to capture small fiber tracts in the brain, especially u-fibers that are adjacent to GM. Drawbacks in tractography include difficulties in handling crossing or kissing fibers, which was somewhat corrected here with the use of probabilistic tractography. Nevertheless, probabilistic tractography has difficulty in reconstructing long-range fiber connections and assigns higher probabilities to shorter streamlines, which can exaggerate the number of WM tracts adjacent to GM. Subcortical regions are particularly susceptible to these effects, as they tend to be smaller in volume and have complex adjacent WM structure. The effects of some of these limitations on the NeMo Tool can be demonstrated with hand-drawn masks that remove gross WM structures (Supplemental Data S2). The accuracy of the NeMo Tool will improve as better tractography methods become available. Another way in which we attempted to reduce the influence of data and algorithm error in the NeMo Tool was the use of global network metrics, which have been shown to be less susceptible to sources of error than individual measures of region-to-region connectivity (Vaessen et al., 2010).
When analyzing the TBI cohort, we chose to assign streamline weights based on the minimum value of nonzero entries in the WM alteration mask that a particular streamline encounters within its length. This “bottleneck” approach seems intuitive for streamlines that go through damaged tissue, as axons will only be as functional as their most damaged section. For tracts that pass through WM areas with both normal and increased integrity, we estimated their increase in functionality to be limited by the smallest increase in the structural integrity. This method assumes that normal tissues are equipped to handle transmission of signals with fidelity higher than ordinary. Alternative approaches may include taking the average of the values of the WM alteration mask over the entire streamline. Various methods of assigning streamline weights may be tested with further studies.
The normal population variation in WM connectivity architecture has not been quantified and may be large. This population variance can be estimated by analyzing the ChaCo scores and network metrics across the normal individuals in the TRS. We postulate that these variations reflect individuals' susceptibility to alterations of WM integrity in specific locations and that this susceptibility is related to the functional outcome for the individual, the validation of which awaits further studies.
Coregistering individual brains that have anatomical abnormalities to a common space is a well-known and difficult problem, especially if that brain has a gross abnormality or has advanced aging effects. For the examples in this article, all the coregistrations were checked visually and deemed acceptable. Quality control steps will be in place within the NeMo Tool; so, the user can check that the coregistration is acceptable. In cases of severely atrophied or deformed brains, SPM's coregistration routine may prove inadequate. If the need arises, it will be possible to implement an option within the NeMo Tool to use more sophisticated normalization routines such as SPM's DARTEL or FSL.
Supplementary Material
Acknowledgments
The data processing, analysis and NeMo Tool creation and validation were supported by a Leon Levy Foundation Neuroscience Fellowship as well as the following National Institutes of Health grants: F32 EB012404-01, P41 RR023953-02, P41 RR023953-02S1, and R21 EB008138-02. The normative data used in the TRS and the TBI patient data were collected and maintained with support from the Department of Defense grants W81XWH-08-1-0646 and W81XWH-08-2-0177, and a James S. McDonnell Foundation grant for the Cognitive Neurobiological Research Consortium in Traumatic Brain Injury. The NPH portion of this study was supported by The Leon Levy Foundation. The authors thank Dr. Bruce Miller and NIH grants P01 AG19724 and P50 AG1657303-75271 for sharing data and Eve LoCastro for help in creating the Tractogram Reference Set. They also thank Xiaobo Shen for his help in packaging and publishing the NeMo Tool and Eve LoCastro for adapting her Brainography visualization software for use within the NeMo Tool.
Author Disclosure Statement
No competing financial interests exist.
References
- Achard S, et al. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J Neurosci. 2006;26:63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akiguchi I, et al. Shunt-responsive parkinsonism and reversible white matter lesions in patients with idiopathic NPH. J Neurol. 2008;255:1392–1399. doi: 10.1007/s00415-008-0928-1. [DOI] [PubMed] [Google Scholar]
- Alemán-Gómez Y. Melie-García L. Valdés-Hernandez P. IBASPM: toolbox for automatic parcellation of brain structures. Presented at the 12th Annual Meeting of the Organization for Human Brain Mapping; Florence, Italy. 2005. [Google Scholar]
- Alstott J, et al. Modeling the impact of lesions in the human brain. PLoS Comput Biol. 2009;5:e1000408. doi: 10.1371/journal.pcbi.1000408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner J. Friston KJ. Voxel-based morphometry—the methods. NeuroImage. 2000;11(6 Pt 1):805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- Assaf Y. Pasternak O. Diffusion tensor imaging (DTI)-based white matter mapping in brain research: a review. J Mol Neurosci. 2008;34:51–61. doi: 10.1007/s12031-007-0029-0. [DOI] [PubMed] [Google Scholar]
- Barabási AL. Scale-free networks: a decade and beyond. Science. 2009;325:412–413. doi: 10.1126/science.1173299. [DOI] [PubMed] [Google Scholar]
- Bassett DS, et al. Hierarchical organization of human cortical networks in health and schizophrenia. J Neurosci. 2008;28:9239–9248. doi: 10.1523/JNEUROSCI.1929-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E. Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Charil A, et al. Statistical mapping analysis of lesion location and neurological disability in multiple sclerosis: application to 452 patient data sets. NeuroImage. 2003;19:532–544. doi: 10.1016/s1053-8119(03)00117-4. [DOI] [PubMed] [Google Scholar]
- Chen CL, et al. Brain lesion size and location: effects on motor recovery and functional outcome in stroke patients. Arch Phys Med Rehabil. 2000;81:447–452. doi: 10.1053/mr.2000.3837. [DOI] [PubMed] [Google Scholar]
- Chung MK, et al. A unified statistical approach to deformation-based morphometry. NeuroImage. 2001;14:595–606. doi: 10.1006/nimg.2001.0862. [DOI] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Crofts J, et al. Network analysis detects changes in the contralesional hemisphere following stroke. NeuroImage. 2011;54:161–169. doi: 10.1016/j.neuroimage.2010.08.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B. Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci U S A. 2000;97:11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, et al. The activation of attentional networks. NeuroImage. 2005;26:471–479. doi: 10.1016/j.neuroimage.2005.02.004. [DOI] [PubMed] [Google Scholar]
- Fields RD. White matter in learning, cognition and psychiatric disorders. Trends Neurosci. 2008;31:361–370. doi: 10.1016/j.tins.2008.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, et al. Burlington, MA: Academic Press; 2006. Statistical Parametric Mapping: The Analysis of Functional Brain Images. [Google Scholar]
- Genovese CR. Lazar NA. Nichols T. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. NeuroImage. 2002;15:870–878. doi: 10.1006/nimg.2001.1037. [DOI] [PubMed] [Google Scholar]
- Gleichgerrcht E, et al. Executive function improvement in normal pressure hydrocephalus following shunt surgery. Behav Neurol. 2009;21:181–185. doi: 10.3233/BEN-2009-0249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gondran M. Minoux M. New York, NY: John Wiley and Sons; 1984. Graphs and Algorithms (Discreet Mathematics Series: 1-484) [Google Scholar]
- Hattori T, et al. White matter alteration in idiopathic normal pressure hydrocephalus: tract-based spatial statistics study. Am J Neuroradiol. 2012;33:97–103. doi: 10.3174/ajnr.A2706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, et al. Neuronal networks in Alzheimer's disease. Neuroscientist. 2009;15:333–350. doi: 10.1177/1073858409334423. [DOI] [PubMed] [Google Scholar]
- Hua K, et al. Tract probability maps in stereotaxic spaces: analyses of white matter anatomy and tract-specific quantification. NeuroImage. 2008;39:336–347. doi: 10.1016/j.neuroimage.2007.07.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irimia A, et al. Patient-tailored connectomics visualization for the assessment of white matter atrophy in traumatic brain injury. Front Neurol. 2012;3:10. doi: 10.3389/fneur.2012.00010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iturria-Medina Y, et al. Bayesian formulation for fiber tracking. Presented at the 11th Annual Meeting of the Organization for Human Brain Mapping; Toronto, Canada. NeuroImage. 2005. p. 26. [Google Scholar]
- Ad-Dab'bagh Y. Lyttelton O. Muehlboeck JS. Lepage C. Einarson D. Mok K. Ivanov O, et al. The CIVET Image-Processing Environment: A Fully Automated Comprehensive Pipeline for Anatomical Neuroimaging Research. In: Corbetta M, editor. Proceedings of the 12th Annual Meeting of the Organization for Human Brain Mapping; Florence, Italy. 2006. [Google Scholar]
- Johansen-Berg H. Behavioural relevance of variation in white matter microstructure. Curr Opin Neurol. 2010;23:351–358. doi: 10.1097/WCO.0b013e32833b7631. [DOI] [PubMed] [Google Scholar]
- Johansen-Berg H. Scholz J. Stagg CJ. Relevance of structural brain connectivity to learning and recovery from stroke. Front Syst Neurosci. 2010;4:146. doi: 10.3389/fnsys.2010.00146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinnunen KM, et al. White matter damage and cognitive impairment after traumatic brain injury. Brain. 2011;134(Pt 2):449–463. doi: 10.1093/brain/awq347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuceyeski A, et al. The generation and validation of white matter connectivity importance maps. NeuroImage. 2011;58:109–121. doi: 10.1016/j.neuroimage.2011.05.087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuceyeski A. Meyerhoff DJ, et al. Loss in connectivity among regions of the brain reward system in alcohol dependence. Hum Brain Mapp. 2012a doi: 10.1002/hbm.22132. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuceyeski A. Zhang Y. Raj A. Linking white matter integrity loss to associated cortical regions using structural connectivity information in Alzheimer's disease and fronto-temporal dementia: the Loss in Connectivity (LoCo) score. NeuroImage. 2012b;61:1311–1323. doi: 10.1016/j.neuroimage.2012.03.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutzelnigg A, et al. Cortical demyelination and diffuse white matter injury in multiple sclerosis. Brain. 2005;128(Pt 11):2705–2712. doi: 10.1093/brain/awh641. [DOI] [PubMed] [Google Scholar]
- Lipton ML, et al. Robust detection of traumatic axonal injury in individual mild traumatic brain injury patients: intersubject variation, change over time and bidirectional changes in anisotropy. Brain Imaging Behav. 2012;6:329–342. doi: 10.1007/s11682-012-9175-2. [DOI] [PubMed] [Google Scholar]
- Lo C-Y, et al. Diffusion tensor tractography reveals abnormal topological organization in structural cortical networks in Alzheimer's disease. J Neurosci. 2010;30:16876–16885. doi: 10.1523/JNEUROSCI.4136-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee P. Diffusion tensor imaging and fiber tractography in acute stroke. Neuroimaging Clin North Am. 2005;15:655–665, xii. doi: 10.1016/j.nic.2005.08.010. [DOI] [PubMed] [Google Scholar]
- Nazzal ME, et al. Acute ischemic stroke: relationship of brain lesion location and functional outcome. Disabil Rehabil. 2009;31:1501–1506. doi: 10.1080/09638280802627702. [DOI] [PubMed] [Google Scholar]
- Niogi SN, et al. Structural dissociation of attentional control and memory in adults with and without mild traumatic brain injury. Brain. 2008;131(Pt 12):3209–3221. doi: 10.1093/brain/awn247. [DOI] [PubMed] [Google Scholar]
- Oishi K, et al. Atlas-based whole brain white matter analysis using large deformation diffeomorphic metric mapping: application to normal elderly and Alzheimer's disease participants. NeuroImage. 2009;46:486–499. doi: 10.1016/j.neuroimage.2009.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otani N, et al. Normal pressure hydrocephalus manifesting as transient prosopagnosia, topographical disorientation, and visual objective agnosia. J Clin Neurosci. 2004;11:313–317. doi: 10.1016/j.jocn.2003.02.014. [DOI] [PubMed] [Google Scholar]
- Pagani E, et al. Diffusion MR imaging in multiple sclerosis: technical aspects and challenges. Am J Neuroradiol. 2007;28:411–420. [PMC free article] [PubMed] [Google Scholar]
- Pannek K, et al. The average pathlength map: a diffusion MRI tractography-derived index for studying brain pathology. NeuroImage. 2011;55:133–141. doi: 10.1016/j.neuroimage.2010.12.010. [DOI] [PubMed] [Google Scholar]
- Pfefferbaum A. Adalsteinsson E. Sullivan EV. Frontal circuitry degradation marks healthy adult aging: evidence from diffusion tensor imaging. NeuroImage. 2005;26:891–899. doi: 10.1016/j.neuroimage.2005.02.034. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C, et al. Water diffusion changes in Wallerian degeneration and their dependence on white matter architecture. NeuroImage. 2001;13(6 Pt 1):1174–1185. doi: 10.1006/nimg.2001.0765. [DOI] [PubMed] [Google Scholar]
- Przulj N. Graph theory approaches to protein interaction data analysis I. In: Jurisica I, editor; Wigle D, editor. Knowledge Discovery in Proteomics. Boca Raton, FL: CRC Press Taylor & Francis Group; 2004. [Google Scholar]
- Raj A. Chen Y. The wiring economy principle: connectivity determines anatomy in the human brain. PLoS ONE. 2011;6:11. doi: 10.1371/journal.pone.0014832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj A. Kuceyeski A. Weiner M. A network diffusion model of disease progression in dementia. Neuron. 2012;73:1204–1215. doi: 10.1016/j.neuron.2011.12.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Røe C, et al. Post-concussion symptoms after mild traumatic brain injury: influence of demographic factors and injury severity in a 1-year cohort study. Disability Rehabil. 2009;31:1235–1243. doi: 10.1080/09638280802532720. [DOI] [PubMed] [Google Scholar]
- Rubinov M. Sporns O. Complex network measures of brain connectivity: uses and interpretations. NeuroImage. 2010;52:1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- Saito M, et al. Cognitive profile of idiopathic normal pressure hydrocephalus. Dement Geriatr Cogn Dis Extra. 2011;1:202–211. doi: 10.1159/000328924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholz J, et al. Training induces changes in white-matter architecture. Nature Neurosci. 2009;12:1370–1371. doi: 10.1038/nn.2412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schulte T, et al. How acute and chronic alcohol consumption affects brain networks: insights from multimodal neuroimaging. Alcohol Clin Exp Res. 2012;36:2017–2027. doi: 10.1111/j.1530-0277.2012.01831.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, et al. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23(Suppl 1):S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Smith SM, et al. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. NeuroImage. 2006;31:1487–1505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
- Sporns O, et al. Organization, development and function of complex brain networks. Trends Cogn Sci. 2004;8:418–425. doi: 10.1016/j.tics.2004.07.008. [DOI] [PubMed] [Google Scholar]
- Sporns O. Zwi J. The small world of the cerebral cortex. Neuroinformatics. 2004;2:145–162. doi: 10.1385/NI:2:2:145. [DOI] [PubMed] [Google Scholar]
- Strogatz SH. Exploring complex networks. Nature. 2001;410:268–276. doi: 10.1038/35065725. [DOI] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage. 2002;15:273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- Vaessen MJ, et al. The effect and reproducibility of different clinical DTI gradient sets on small world brain connectivity measures. NeuroImage. 2010;51:1106–1116. doi: 10.1016/j.neuroimage.2010.03.011. [DOI] [PubMed] [Google Scholar]
- Vellinga MM, et al. Clinical correlations of brain lesion distribution in multiple sclerosis. J Magn Reson Imaging. 2009;29:768–773. doi: 10.1002/jmri.21679. [DOI] [PubMed] [Google Scholar]
- Wakana S, et al. Fiber tract-based atlas of human white matter anatomy. Radiology. 2004;230:77–87. doi: 10.1148/radiol.2301021640. [DOI] [PubMed] [Google Scholar]
- Wen W, et al. Discrete neuroanatomical networks are associated with specific cognitive abilities in old age. J Neurosci. 2011;31:1204–1212. doi: 10.1523/JNEUROSCI.4085-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheeler-Kingshott CAM. Cercignani M. About “axial” and “radial” diffusivities. Magn Reson Med. 2009;61:1255–1260. doi: 10.1002/mrm.21965. [DOI] [PubMed] [Google Scholar]
- Wilson M, et al. Pyramidal tract mapping by diffusion tensor magnetic resonance imaging in multiple sclerosis: improving correlations with disability. J Neurol Neurosurg Psychiatry. 2003;74:203–207. doi: 10.1136/jnnp.74.2.203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolrich MW, et al. Bayesian analysis of neuroimaging data in FSL. NeuroImage. 2009;45(1 Suppl):S173–S186. doi: 10.1016/j.neuroimage.2008.10.055. [DOI] [PubMed] [Google Scholar]
- Yen PS, et al. White matter tract involvement in brain tumors: a diffusion tensor imaging analysis. Surg Neurol. 2009;72:464–469. doi: 10.1016/j.surneu.2009.05.008. discussion 469. [DOI] [PubMed] [Google Scholar]
- Zalesky A. Fornito A. Bullmore ET. Network-based statistic: identifying differences in brain networks. NeuroImage. 2010;53:1197–1207. doi: 10.1016/j.neuroimage.2010.06.041. [DOI] [PubMed] [Google Scholar]
- Zhang Y, et al. White matter damage in frontotemporal dementia and Alzheimer's disease measured by diffusion MRI. Brain. 2009;132(Pt 9):2579–2592. doi: 10.1093/brain/awp071. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.