4Pi fluorescence detection and 3D particle localization with a single objective

Abstract

Coherent detection through two opposing objectives (4Pi configuration) improves the precision of three-dimensional (3D) single-molecule localization substantially along the axial direction, but suffers from instrument complexity and maintenance difficulty. To address these issues, we have realized 4Pi fluorescence detection by sandwiching the sample between the objective and a mirror, and create interference of direct incidence and mirror-reflected signal at the camera with a spatial light modulator. Multifocal imaging using this single-objective mirror interference scheme offers improvement in the axial localization similar to the traditional 4Pi method. We have also devised several PSF engineering schemes to enable 3D localization with a single emitter image, offering better axial precision than normal single-objective localization methods such as astigmatic imaging.

Introduction

Many super-resolution microscopy and single-particle tracking methods rely on precise single-molecule and single-particle localization in three dimensions. Such 3D localization is commonly performed on a wide-field fluorescence microscope by defocusing [1, 2], imaging at multiple focal planes [3–7], the introduction of astigmatic aberration [8–10], or Point Spread Function (PSF) engineering [11–18]. All these methods rely on the 3D shape of the PSF. However, for typical numerical apertures (NA) the PSF of a single objective decays about 2.5 times as slow in the axial direction as in the lateral direction, because the axial PSF length scales with 1/NA² and the lateral width with 1/NA. Correspondingly, the axial localization precision is worse than lateral precision by a factor of approximately 2.5 [19–22]. 4Pi fluorescence detection has been employed to improve the axial localization precision [23, 24]. In these cases, the sample is sandwiched between two opposing objectives. The fluorescence signal collected by these two objectives is brought back together to interfere at the camera plane. The resulted 4Pi PSF is approximately a superposition of the regular PSF and a plane wave interference pattern along the axial direction, which introduces more information for axial localization [25–27]. The major drawback, however, is that the two interference arms, each > 10 cm long, need to be maintained with sub-wavelength-scale stability. This stability requirement demands complex instrumentation and intricate maintenance, thus limiting the application of 4Pi microscopy in everyday biological research.

We propose a 3D localization method that is simple in usability, but still achieves high axial precision. Similar to several other fluorescence self-interference [28–30] and optical trapping techniques [31, 32], our method is based on a single-objective 4Pi configuration that sandwiches the sample between the objective and a mirror. This configuration was initially developed to interfere the excitation light for isotropic laser focusing in confocal microscopy [33, 34] and also proposed to improve the axial resolution of Stimulated Emission Depletion (STED) microscopy [35]. Different from these cases, our method deals with the fluorescence emission instead of the excitation light. We establish 4Pi fluorescence detection by generating the two interference paths from the direct image and mirror image of the emitter. These two paths share almost all optical components except for the micrometer-scale distance between the emitter and the mirror. Therefore, this single-objective design greatly simplifies the setup and provides high interference stability.

2. Theory and simulations

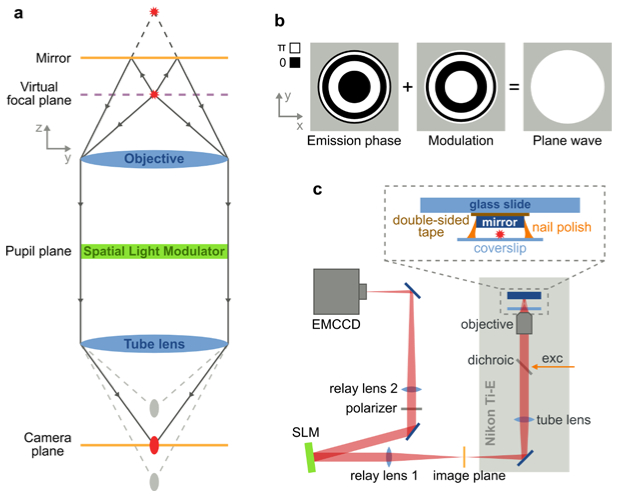
When imaging a single emitter in front of a mirror, a microscope generates two images along the optical axis: the emitter image and the mirror image (see Fig. 1(a) ). If the objective is focused on the mirror, the emitter image is in front of the camera plane whereas the mirror image is behind. To establish interference at the camera plane, both images need to be in focus. This condition can be achieved by introducing a phase-only Spatial Light Modulator (SLM) in the pupil plane of the imaging path [33]. For an emitter at a given distance from the mirror, we can calculate the phase of the emission in the pupil plane and apply a SLM phase modulation with its exact negative result (Fig. 1(b)). This modulation results in a plane wave that will be focused at the camera plane, effectively creating a virtual focal plane. Changing the modulation according to the emitter-mirror distance adjusts the virtual focal plane without any physical movement.

Fig. 1.

Schematic of 4Pi detection with a single-objective and the experimental setup. (a) A fluorophore and its reflection (red stars) are imaged by an infinity corrected microscope (blue), which generates an image and a mirror image of the fluorophore along the optical axis (gray ellipses). Phase modulation in the pupil plane with an SLM (green) can overlay the two images (red ellipse) at the camera plane (orange), creating a virtual focal plane (violet) at the fluorophore position. (b) The emission phase of a fluorophore in front of a mirror at the pupil plane are concentric rings of either 0 or π and is strongly dependent on the distance between fluorophore and mirror. Modulation of this phase with its exact opposite (middle) results in a plane wave (right), which is focused at the camera plane. (c) The experimental setup is based on a Nikon Ti-U microscope with a custom excitation path and a relayed emission path. The SLM is located at the Fourier plane of relay lens 1. The sample is sandwiched between the coverglass and a mirror.

To test the feasibility of the proposed single-objective interference setup, we simulated 3D PSFs of the following wide-field microscope setups: conventional, single-objective interference detection and dual-objective 4Pi detection. The simulations are based on the imaging model described by Hanser et al [36]. The PSFs are computed from theoretical pupil functions via a Fast Fourier Transform:

$$\mathrm{PSF}\left(x,y,z\right)={\left|\mathrm{FFT}\left\{\text{P}\left(k_x,k_y\right)\times \exp \left[2\pi i\cdot k_z\left(k_x,k_y\right)\cdot z\right]\right\}\right|}^2$$ (1)

where x, y and z are real space coordinates, k_x, k_y and k_z the corresponding Fourier space coordinates, and P(k_x, k_y) the complex, numerical aperture limited pupil function. Furthermore, k_z (k_x, k_y) = [(n/λ)² – (k_x² + k_y²)]^1/2, where n is the refractive index and λ the wavelength. The pupil plane for a conventional microscope is a plane wave with constant amplitude and phase. The single-objective interference pupil functions are computed by adding two defocused pupil functions, with a π phase delay added to the one corresponding to the mirror image. To simulate a dual-objective 4Pi PSF, we summed two conventional complex PSFs before taking the absolute square, with one of them flipped along the optical axis. The wavelength, refractive index and numerical aperture for all simulations were 690 nm, 1.33 and 1.27, respectively, matching our experimental setup.

To quantify the theoretical localization precision of the various schemes that we have developed, we used the Cramer-Rao Lower Bound (CRLB) criterion [19, 21, 22, 37–39]. We compared the CRLBs of the proposed 3D localizations schemes with astigmatic, biplane and 4Pi detection. The CRLBs were calculated from simulated PSFs for imaging with a pixelated detector and Poisson distributed noise as described by Ober et al. [37]. We modified the pupil function of a conventional microscope with an astigmatic phase mask (Zernike mode (2,2)) for astigmatic 3D localization and simulated the dual-objective 4Pi localization scheme with four phase delays as described by Aquino et al [24]. The CRLB is defined as the standard deviation of an unbiased estimator for the 3D location of a molecule, given a specific PSF. The standard deviations for the x, y and z position of a molecule are the inverse square roots of their corresponding diagonal elements in the Fisher Information matrix:

$${\text{CRLB}}_{\theta }\left(z\right)={\left\{{{\displaystyle \sum _{x,y}\frac{1}{\text{PSF}\left(x,y,z\right)+b}\left[\frac{\partial \text{PSF}\left(x,y,z\right)}{\partial \theta }\right]}}^2\right\}}^{-\frac{1}{2}},\begin{array}{cc}& \end{array}\theta =x,y,z$$ (2)

where b is the average background per pixel per frame. The CRLB for a multi-focal plane setup is calculated by summing the Fisher Information matrices of all planes before taking the inverse square root of the diagonal elements [6].

3. Experimental setup

We verified our simulations on an experimental setup (Fig. 1(c)) based on a commercial Nikon Ti-U microscope body with excitation from a 642 nm diode laser (CUBE-640-100C, Coherent) and a 60 × , 1.27 NA water immersion objective (Nikon). The fluorescence signal was separated from the excitation light using a dichroic mirror (T660LPXR, Chroma) and a band-pass filter (ET705/72m, Chroma). The image plane was relayed with a 150 mm and 300 mm lens onto a back-illuminated EMCCD camera (iXon + DU-897-BV, Andor). A 512 × 512 pixel phase-only SLM (HSPDMP512-640-750-PCIe, Boulder Nonlinear Systems) was placed at the Fourier plane after the 150 mm relay lens. A linear polarizer in the emission path filtered out the polarization that cannot be modulated by the SLM. We imaged 100 nm fluorescent beads (TetraSpeck, Invitrogen), mounted in aqueous solution on a coverslip. An economic Ø1/2” silver mirror (ME05-P01, Thorlabs) was dropped on top of the coverslip and mounted with nail polish, resulting in a distance of 1-2 µm between beads and mirror.

The axial dimension of our single-objective interference results represent virtual focusing by phase modulation, whereas that of conventional detection results represents physical refocusing by a piezoelectric stage (Nano-LPS 100, Mad City Labs).

To correct aberrations in the imaging optics, we applied the negative of phase retrieved pupil functions [40, 41] to the SLM before adding any modulation for interference detection.

4. Results

The simulations of single-objective interference PSFs show a 4Pi-like PSF, which has enhanced axial information (steeper slope) than conventional non-interferometric PSFs (Fig. 2(a) -2(d)). We imaged fluorescent beads in front of a mirror with a single-objective interference setup to verify the 4Pi-like PSF experimentally (Fig. 2(e)-2(g)). In the axial direction, the single-objective interference PSF shows similar intensity oscillations as the dual-objective 4Pi PSF. The difference is a slight asymmetry, with the peaks on the mirror side higher than those on the coverglass side. This asymmetry appears when the emitter-mirror distance is close to the PSF length, and vanishes for larger emitter-mirror distances.

Fig. 2.

Simulated and experimental PSFs of a conventional (a, e), single-objective interference (b, f) and dual-objective 4Pi (c) microscopes and their axial intensity profile (d, g). Experimental PSFs show an axial scan of a 100 nm fluorescent bead at 1.04 µm distance to a mirror. The simulations show the axial scan of a point source at the same position.

For single-particle and single-molecule localization, only one lateral slice of the single-objective interference PSF is insufficient, because it cannot decouple the intensity change along the z axis of the PSF from the intrinsic intensity variability of emitters. For example, the mirror reflection of the excitation light could interfere with the direct incidence, causing the excitation intensity to vary at different distances to the mirror [30]. Previous dual-objective interference systems split the fluorescence signal into multiple paths and acquired interference images with 3-4 different phase delays at the same time [23, 24]. In this way, the emitter’s axial position can be determined from the relative intensities of these images. A similar strategy can be used in our single-objective interference approach. The conceptually most straightforward way is to split the fluorescence signal into four different light paths, each modulated at a different virtual focal plane. With these four virtual planes separated by 1/4 of the axial intensity oscillation period in the interference PSF (Fig. 3(a) ), the relative intensity of the four images uniquely defines the z position of the emitter within an oscillation period. The beam splitting can be based on polarization so that 100% of the photons are utilized. To reduce the cost, the system can also be designed to use the four quadrants of the same SLM for modulation and the four quadrants of the same camera for detection. Similar to the dual-objective 4Pi case, intensity-only analysis cannot specify which oscillation period the emitter is located in [23]. This issue has been resolved by analyzing the shape of the emitter image, such as its higher order moments [24].

Fig. 3.

Simulations and experiments of the proposed four plane mirror interference setup and interference PSF engineering. The phase modulations at the pupil plane are shown on top. Below are simulated and measured lateral slices of the respective PSFs at five axial positions. (a) In this proposed setup the emission is split into four paths, each with a different focal plane modulation, and imaged separately. (b) The modulation is split into four quadrants with the quadrants in horizontal direction encoding a different virtual focal plane than the quadrants in vertical direction. (c) The modulation encodes for a virtual focal plane for each radial angle in a ramp with a span of one emission wavelength. (d) Three virtual focal planes are superimposed with a phase tilt so that the images are shifted laterally. The modulation is a random mix of the three tilted focal planes.

To further simplify the setup, we demonstrate here several ways to encode multiple virtual focal planes in the same modulation pattern. Figure 3(b)-3(d) shows three possible modulation patterns: (1) The modulation pattern is split into four quadrants, with the two quadrants along the horizontal direction modulating for one focal plane and the two along the vertical direction for a different focal plane separated by 172.5 nm; (2) The modulation pattern along the radial direction ramps continuously from a focal plane of 695 nm to 1385 nm; and (3) Three modulation patterns corresponding to virtual focal planes of 937, 1040 and 1143 nm are superimposed with linear phase ramps that shift the images by 440 nm, and then randomly mixed pixel-by-pixel. Both the simulated and experimental measured PSF are shown.

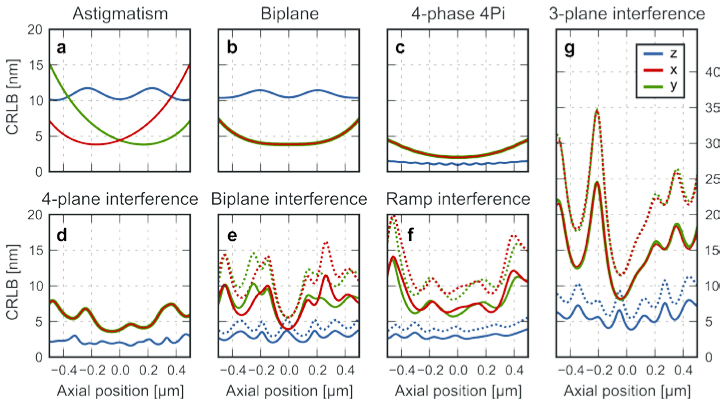
We computed the theoretical 3D localization precision as Cramer-Rao Lower Bounds for each proposed engineered PSF and the multi-focal plane imaging as well as for dual-objective four-phase 4Pi detection, biplane detection and astigmatic PSFs (Fig. 4 ). We simulated 3000 collected signal photons in the pupil plane of each objective (6000 for mirror detection) and 50 background photons per pixel in the image plane (100 for 4Pi and mirror detection). The simulations for the engineered PSFs (Fig. 4(e)-4(g)) are shown with either 100% of the photons or by taking the 50% photons loss into account that arises from the polarization sensitivity of currently available SLMs.

Fig. 4.

Simulated CRLBs (standard deviation) for (a) astigmatic, (b) conventional biplane, (c) four-phase dual-objective 4Pi, (d) four plane single-objective interference and (e, f, g) PSF engineered particle localization. The simulation for astigmatic imaging introduced a 340 nm offset between the x and y focal planes. The detection planes for conventional biplane imaging are simulated 380 nm apart. These separations were chosen for the most uniform z localization precision across the entire range. The simulation conditions for (d-g) are identical to those in Fig. 3a-d, except for that (g) used an image shift of 772 nm instead of 440 nm, which gives better CRLB. For the PSF engineered cases, we plotted the CRLB for 50% (dashed) and 100% (solid) photon recovery, representing a polarization dependent and a polarization independent SLM, respectively.

The simulations show that all single-objective interference setups have substantially better axial localization precision compared to single-objective astigmatic and biplane imaging. In fact, both the four plane interference setup and our three PSF engineering schemes give a better axial localization precision than the lateral precision, resembling the key characteristic of dual-objective 4Pi microscopes. The four-plane interference setup has the best overall localization precision among the simulated single-objective interference setups, and exhibits an almost uniform 3D localization precision in the simulated 1 µm axial range.

We note that the localization precision is substantially worse in the triple plane interference case (Fig. 4(g)), because we used the random mixing approach to create the three separate images. This approach is straightforward, but the photon efficiency per image scales with 1/N², where N is the number of part-images. An optimal photon efficiency of 1/N can be achieved by computer-aided optimization of the modulation [42], which has been demonstrated for the holographic generation of multiple optical traps [32].

4. Discussions and conclusion

We propose a method for 3D molecule localization that is superior in axial precision over ordinary single-objective 3D localization methods and easier to use than dual-objective 4Pi detection. We have generated a 4Pi-like PSF by sandwiching the sample between an objective and a mirror, which significantly reduces the complications of a dual-objective 4Pi microscope. In fact, we were able to build our system using a commercial inverted microscope frame.

Despite the simplicity, our mirror interference method still has two limitations. First, it has a limited depth range. The 4Pi-like PSF can be produced only if the molecule is at least one wavelength away from the mirror. Otherwise, parts of the 4Pi-like PSF are disturbed by the mirror reflection. On the other hand, if the emitter-mirror distance is larger than ~2.5 µm, we have observed a much reduced intensity oscillation along the axial direction in the virtually refocused PSF. This effect likely arises when the length difference between the direct and reflected optical paths is approaching the coherence length of fluorescence, typically a few micrometers. Therefore, fluorescent probes with narrower emission wavelength range such as quantum dots and lanthanide nanoparticles could extend this maximal depth. In addition, in the proposed four-plane setup, one could split imaging paths by wavelength [24], thereby increasing the fluorescence coherence length.

The second limitation is the lower photon recovery compared to a traditional 4Pi microscope. An ideal 4Pi microscope doubles the number of photons collected from the fluorophore in the image plane, whereas the simulated refocused interference image contains about 1.7 times as many photons as either the direct image or the mirror image by itself. Generally, when the emitter-mirror distance is larger than the wavelength, this photon gain factor oscillates between 1.4 and 1.9 depending on the emitter-mirror distance, and converges to 1.62 when the emitter is far away from the mirror. The remaining photons are distributed in two dim foci before and after the camera plane. This effect arises because the modulation pattern resembles a binary phase Fresnel lens, which has limited diffraction efficiency [43]. Our experimental photon recovery is lower than the simulation, possibly due to the fluorescence coherence length issue, which results in imperfect constructive interference. In addition, the polarization sensitivity of the SLM could further reduce the light collection efficiency by a factor of two, although this issue can be solved by developing a polarization independent SLM, replacing the SLM with a transmissive phase plate [14, 16], or by splitting and modulating the two polarizations of fluorescence emission separately [13], as in our 4-plane interference scheme.

Despite these limitations, the implementation of the proposed single-objective interference setup and further experimental improvements can make this method valuable and complementary to existing 3D molecule localization methods. In particular, single-objective interference detection can be favorable for applications where high axial localization precision is more important than lateral.