Bright broadband coherent fiber sources emitting strongly blue-shifted resonant dispersive wave pulses

Abstract

We predict and realize the targeted wavelength conversion from the 1550-nm band of a fs Er:fiber laser to an isolated band inside 370-850 nm, corresponding to a blue-shift of 700-1180 nm. The conversion utilizes resonant dispersive wave generation in widely available optical fibers with good efficiency (~7%). The converted band has a large pulse energy (~1 nJ), high spectral brightness (~1 mW/nm), and broad Gaussian-like spectrum compressible to clean transform-limited ~17 fs pulses. The corresponding coherent fiber sources open up portable applications of optical parametric oscillators and dual-output synchronized ultrafast lasers.

1. Introduction

The coupling of a pulsed pump laser into a (longitudinally) uniform optical fiber has allowed nonlinear conversion of pump wavelengths into wavelengths that are difficult to access, while the pursuit of various favorable conditions has advanced our basic understanding of soliton and dispersive wave dynamics. Noticeably, the 1999 discovery of Ti:sapphire oscillator-induced octave-spanning continuum [1] stimulated the theoretical tools of reduced Maxwell’s equations, which attributed this phenomenon to the fission of higher-order solitons into red-shifted fundamental solitons and their blue-shifted phase-matched dispersive waves [2]. The unusual prediction that long pump pulses are advantageous over short (fs) ones for uniform spectral broadening has led to the combination of a ps Yb:fiber master-oscillator-power-amplifier (MOPA) with a dispersion-engineered photonic crystal fiber (PCF) [3]. In this platform, however, the simple soliton-dispersive-wave picture must incorporate a pulse trapping mechanism to synchronize the blue and red expansions of the continuum [4]. This condition achieves broad spectrum and high spectral brightness, but at the cost of temporal coherence due to high soliton order (N) modulation instability [5]. A complementary translation to a fs Er:fiber platform using specifically Ge-doped fibers has lowered the soliton order (improved the coherence) [6]. Despite its narrower bandwidth and lower spectral brightness (Table 1 ), this platform allows few-cycle pulse compression and single-cycle pulse synthesis. Taking advantage of all-fiber pumps, the ps Yb:fiber platform [3] and the fs Er:fiber platform [6] have become arguably the most popular techniques for fiber continuum generation. Motivated by a recently developed platform that produces energetic deep-UV pulses [7], we extend the coherent spectral coverage of the fs Er:fiber platform to the UV-visible-near-IR region (Table 1), corresponding to the popular optical frequency references and electronic transitions of absorptive or fluorescent molecules. We envision that this blue-extended fs Er:fiber platform would bring numerous techniques of ultrafast electronic spectroscopy, frequency metrology, femtobiology, and nonlinear biomedical imaging [8] out of optical laboratories and into real-world applications.

Table 1. Representative platforms for broadband fiber nonlinear wavelength conversion.

Platform	Ultrafast pump laser (typical specifications)	Nonlinear fiber(s) (typical λZDW and fiber length)	Soliton order N	Spectral coverage (nm)	Spectral brightness (mW/nm)	Coherence
[1]	Ti:sapphire oscillator (800 nm, 80 MHz, 100 fs)	Nonlinear PCFs (750-800 nm, 10 cm)	~100	400-1600	0.1	Moderate or low
[3]	Yb:fiber MOPA (1050 nm, 50 MHz, 5 ps)	Specific PCF (1000 nm, 2 m)	>500	400-2000	2	low
[6]	Er:fiber MOPA (1550 nm, 50 MHz, 80 fs)	Ge-doped fibers (1300-1400 nm, 5 cm)	~6	850-1400, 1600-2000	0.1	High
[7]	Ti:sapphire amplifier (800 nm, 1 kHz, 30 fs)	Ar-filled hollow-core fiber (700 nm, 20 cm)	8.6	200-320	0.01	No data
This study	Er:fiber MOPA (1550 nm, 50 MHz, 80 fs)	Low-nonlinearity fibers (890-1313 nm, 9 cm)	<6	378-850	0.5-2 in the visible	High

The ~1550-nm wavelength of an Er:fiber laser has not been converted to the UV-visible region in the fundamental mode of a uniform silica-based fiber, possibly due to the large (optical) frequency up-conversion ratio equivalent to third (or fourth) harmonic generation. However, the 800-nm μJ pulses from a Ti:sapphire amplifier have been successfully converted to deep-UV (down to 200 nm) dispersive waves in an Ar-filled hollow-core fiber with surprisingly high efficiencies (~7%) (Table 1) [7]. Also, this effect has not only been explained by the reduced Maxwell’s equations [2], but also equally well by the generalized nonlinear Schrödinger equation (GNLSE) under the slowly varying envelope approximation [5], indicating that complex theoretical models may not be necessary in sub-cycle regime modeling [7]. Moreover, the large frequency up-conversion ratio has been attributed to the nonlinear symmetry breaking intrinsic to dispersion wave generation [9], and is thus not restricted to the Ar-filled fiber. It is therefore of high interest to explore relatively simple GNLSE models using lower energy pump pulses and more common solid-core fibers, and to predict if biased spectral transformation toward the high frequency end could be realized in the compact fs Er:fiber platform.

2. Theory

The fibers under investigation consist of a large mode-area PCF (LMA-8, NKT Photonics A/S), and another PCF with a smaller core (NL-3.3-890-02, Thorlabs Inc.). The LMA-8 belongs to a class of PCFs fully characterized by only two cross-sectional parameters, i.e., hole-to-hole distance Λ and hole diameter d, whereas the NL-3.3-890-02 has a very high air-filling fraction (>88%) and therefore a slightly more complex structure. For both fibers, however, the dispersion curve, zero-dispersion wavelength (λ_ZDW), and effective area may easily be calculated by e.g. the plane-wave method (Table 2 ). The pump pulses are assumed to be 1550-nm unchirped 80-fs (FWHM) 50-MHz Gaussian pulses, which approximate those of the fs Er:fiber platform [6]. A 9-cm LMA-8 (NL-3.3-890-02) fiber is pumped by an input pulse energy of 23.4-nJ (9-nJ), corresponding to a soliton order of N = 4.9 (N = 6.1) (Table 2). Given these data, we solve a fairly “standard” GNLSE using the general formalism of a recent study [10].

Table 2. Observed bright RDW with Gaussian-like spectra from commercial PCFs (NKT Photonics A/S) and standard fiber (SMF-28) pumped by approximated 1550-nm 80-fs (FWHM) unchirped Gaussian pulses.

Fiber	SMF-28	ESM-12B	LMA-10	LMA-8	LMA-5	NL-4.0-1005	NL-3.7-975	NL-3.2-945	NL-3.3-890-02
Λ (μm)	N.A.	8.0	6.6	5.6	3.2	2.7	2.6	2.1	3.2
d/Λ	N.A.	0.46	0.46	0.46	0.46	0.50	0.52	0.49	N.A.
λZDW (nm)	1313	1205	1181	1157	1052	1005	975	945	890
β2@1550 nm (fs2/cm)	200	393	438	486	689	805	956	1020	1147
Mode field diameter @1550 nm (μm)	10.5	10.5	9.2	7.7	4.9	3.8	3.2	2.9	2.5
γ @1550 nm (W−1km-1)	1.12	1.12	1.46	2.1	5.3	8.6	12.1	14.7	19.8
Input pulse energy (nJ)	23.8	32.8	32.5	23.4	14.8	11.2	9.5	7.2	5.8
Soliton order N	5.6	4.8	5.1	4.9	5.2	5.4	5.4	5.0	4.9
Soliton fission length (cm)	1.8	1.1	0.92	0.86	0.57	0.48	0.40	0.40	0.36
RDW pulse energy (nJ)	1.9	2.3	2.3	1.7	1.1	0.76	0.49	0.28	0.02
RDW central wavelength (nm)	825	690	665	620	507	471	452	436	378
RDW FWHM bandwidth (nm)	43	40	42	43	40	42	41	28	12

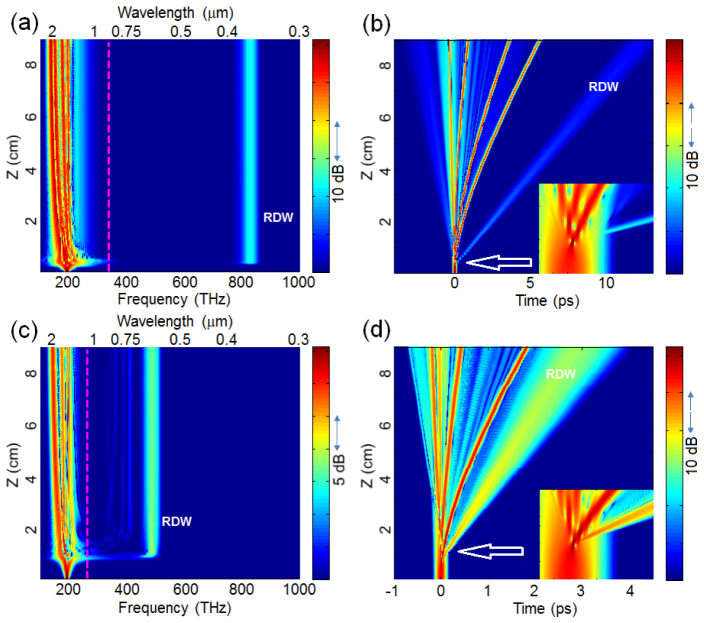
In comparison to [7], the calculated spectral broadening in Figs. 1(a) -1(d) exhibits similar dispersion wave generation with no influence (blue-shift) from the pulse trapping [4]. For the LMA-8 (NL-3.3-890-02) fiber, the dispersive wave emits at 604 nm (360 nm), and diverts ~8% (0.1%) of energy from the input pump pulse. These are extraordinary results because comparable conversion efficiency and frequency up-conversion ratio are obtained at 50 times lower pump pulse energies than those reported previously [7]. The NL-3.3-890-02 case [Fig. 1(a)] sets a record frequency up-conversion ratio (>4) for solid-core fibers, which easily surpasses that of the pulse-trapping expanded continuum generation (<3) [3]. The cascading processes of the latter have been widely believed to provide the largest blue extension.

Fig. 1.

Calculated spectral (a, c) and temporal (b, d) evolution of a transform-limited 80-fs (FWHM) Gaussian pulse along a 9-cm NL-3.3-890-02 fiber with 9-nJ input pulse energy (a, b), and a 9-cm LMA-8 fiber with 23.4-nJ input pulse energy (c, d). The dashed lines in the spectral domain separate the normal (short wavelengths) and anomalous (long wavelengths) dispersion regimes, while the insets in the temporal domain are magnified images showing RDW generation at maximum input pulse compression.

Of more practical interest is the dispersive wave generated in the LMA-8 fiber, which retains a “resonant” nature at surprisingly high average power of ~100 mW (pulse energy of ~2 nJ). The characteristic features of a resonant dispersion wave (RDW) include: (1) sudden and complete generation within a short (a few mm) fiber segment corresponding to maximum input pulse compression [7, 11]; (2) isolated Gaussian-like spectrum far from the pump spectrum, with no non-specific continuum features in between [12]; and (3) a central wavelength dictated by a nonlinear-phase-corrected phase-matching condition [2, 12, 13]. While the former two are confirmed in Figs. 1(c), 1(d), the third feature can be verified by reproducing the resonant wavelength of 604 nm (within 5 nm) with the phase-matching condition. The RDW generation was predicted in 1986 [14], and was often termed as “Cherenkov radiation” [15] in the literature. Visible RDW has only been observed in highly nonlinear fibers, and has been limited to an average power of a few mW [11–13, 16], beyond which a dramatic spectral transformation toward continuum generation occurs at rather short (10 cm) fiber lengths [17]. Thus, the prediction of this high power continuum-free visible RDW in a low-nonlinearity fiber is unusual. Another unexpected aspect is the enlarged RDW bandwidth over the pump bandwidth to support sub-20-fs pulse compression (see below). Previously reported broadband RDW has demanded ultrashort 10-fs pumping [13] or fiber tapering [18].

The above modeling has predicted an overlooked but practically useful operation regime of the fs Er:fiber platform, which has long been restricted to the Ge-doped fibers [6]. By simply increasing the pump pulse energy above 24 nJ, this platform would have benefited from the well-established PCF technologies [19].

3. Experiment

The existing fs Er:fiber lasers rarely generate >10 nJ pulses, in sharp contrast to their more matured Yb fiber laser counterparts [20]. The state-of-the-art Er:fiber system employing an Er/Yb co-doping technique produces 16-nJ 450-fs compressed pulses [21], which are inadequate for generating the intended RDW. Here we adopt a similar all-fiber MOPA design based on a passively mode-locked Er:fiber oscillator (Fig. 2 ). Critical improvements over [21] include: (1) shortened pulse duration of ~80-fs (FWHM) [Fig. 3(a) ] and increased pulse energy of 46 nJ at 50-MHz (2.3 W average power), despite the self-phase modulation-induced spectral distortion [Fig. 3(b)]; (2) all-polarization-maintaining single-mode fibers and components for polarized output and environmental stability; and (3) commercialized setup (Mendocino FPL-05C, Calmar Laser, Inc.) consisting of an air-cooled laser box (48x50x18 cm, controller included), a 0.5-m delivery fiber, and a compact (4x4x18 cm) laser head of free-space compressor (Fig. 2). The laser head and the fiber-pumping apparatus [12] are mounted on a small optical breadboard (40x30 cm), which can be moved to a wheeled cart where the laser box can be rack mounted, making the whole system portable. Optimized aspheric lenses allow 60-85% coupling efficiency of pump pulse energy to one of several 9-cm cleaved fibers, with progressively varying core diameter and dispersion (Table 2).

Fig. 2.

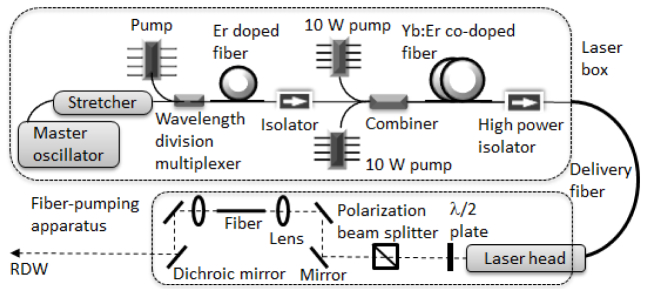
Portable RDW fiber source consisting of a rack-mounted laser box, a delivery fiber, and a fiber-pumping apparatus on an optical breadboard.

Fig. 3.

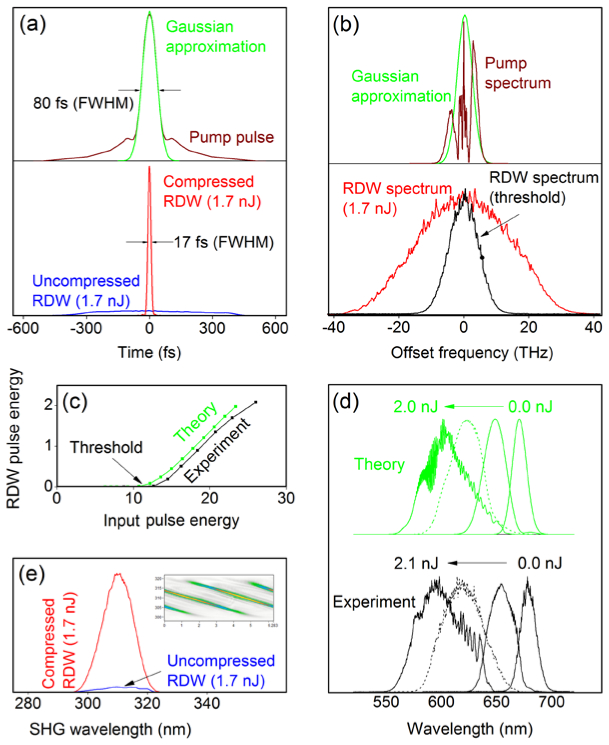
Properties of RDW from a 9-cm LMA-8 fiber. (a) Temporal profiles of pump pulse (brown, top panel), approximated 80-fs Gaussian pulse (green, top panel), uncompressed (blue, bottom panel) and compressed (red, bottom panel) 1.7-nJ RDW pulse; (b) Spectra of pump pulse centered at 1550 nm (brown, top panel), approximated 80-fs Gaussian pulse (green, top panel), 1.7-nJ RDW pulse centered at 620 nm (red, bottom panel), and threshold RDW pulse centered at 679 nm (black, bottom panel); (c) Observed (black) and GNLSE-modeled (green) relations of RDW pulse energy vs. input pulse energy; (d) Observed (black) and GNLSE-modeled (green) RDW spectra at several RDW pulse energies; (e) Second harmonic generation (SHG) signal spectra of uncompressed (blue) and compressed (red) 1.7-nJ RDW pulses. Inset: MIIPS trace of compressed 1.7-nJ RDW pulse.

Indeed, the red RDW emission in the LMA-8 fiber is visibly detected when the input pulse energy (measured as fiber output pulse energy assuming zero transmission loss) reaches a threshold [12]. Beyond that, the pulse energy of the RDW increases with the input pulse energy according to a conversion efficiency of ~7% [Fig. 3(c)]. With increasing pulse energy, the RDW spectrum undergoes a blue-shift and broadening, but retains its Gaussian-like spectrum, until it is finally disrupted by an interference-like effect [Fig. 3(d)]. By approximating the pump pulses with 80-fs (FWHM) Gaussian pulses in Figs. 3(a) and 3(b), the GNLSE model quantitatively reproduces the observed power-dependent RDW pulse energy and spectrum in Figs. 3(c) and 3(d), confirming the predicted 100-mW-level (~2 nJ) RDW [Fig. 1(c)]. The progressive evolution of a Gaussian-like spectrum in Fig. 3(d) results in broad wavelength tuning (595-670 nm) and pedestal-free 17-fs pulse compression (see below). Interestingly, the optical fiber cleans up and shortens the complex input (fiber laser) pulses through a blue-shifted wavelength conversion in Figs. 3(a) and 3(b), in contrast to the widely recognized and used red-shifted soliton generation.

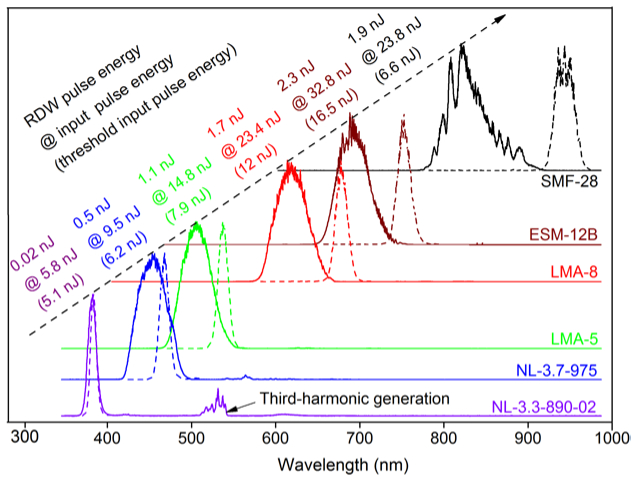
Other PCFs, along with the standard telecommunication fiber (SMF-28), produce RDWs throughout 370-850 nm with comparable conversion efficiencies (Fig. 4 ), presumably due to different dispersion and nonlinearity properties. The RDW from each PCF undergoes a large (>700 nm) blue-shift from the pump wavelength, retains the Gaussian-like spectrum before the interference-like disruption, and aligns itself with the input pulse in polarization with an extinction ratio of >25 dB. Thus, the RDW generated from a polarization-maintaining PCF (LMA-5-PM) approximates that from its non-polarization-maintaining counterpart (LMA-5) (Table 2), if the input polarization is aligned with a principal axis of the fiber. The RDW from the SMF-28 fiber is similarly polarized, but suffers spectral distortion even at the threshold, possibly due to the solitonic interaction before the pulse trapping [13]. The predicted RDW in NL-3.3-890-02 with >4 frequency up-conversion ratio [Fig. 1(a)] is also confirmed, although at somewhat longer wavelength (378 nm) and lower input pulse energy (~5.8 nJ) (Fig. 4). The discrepancies may be attributed to the combined effects of fiber dispersion inaccuracy, pump pulse uncertainty, and Raman-induced fiber transmission loss (estimated to be ~2 nJ for the 9 nJ input pulse energy). Even so, the sub-cycle regime GNLSE modeling predicts this unexpected phenomenon reasonably well. Higher energy input pulses would be preferentially converted to an intermodal third-harmonic band (Fig. 4), not the RDW.

Fig. 4.

RDW spectra at threshold input pulse energies (broken curves) and higher input pulse energies (solid curves) from a series of 9-cm fibers, along with RDW pulse energies at the higher input pulse energies.

Finally, we evaluate the coherence of the RDW source. Typical fs-induced fiber supercontinuum [1] has insufficient coherence for transform-limited pulse compression, even though the full phase compensation of a spatial light modulator-based 4f pulse shaper is employed [22]. Thus, this pulse compression is usually conducted on the supercontinuum generated completely in a normal dispersion regime of the fiber [23, 24], using techniques such as the multiphoton intrapulse interference phase scan (MIIPS) [25]. By the use of a MIIPS-assisted 4f pulse shaper (FemtoJock, Biophotonics Solutions Inc.), we achieve high quality transform-limited compression of the 1.7-nJ RDW from the LMA-8 fiber in Fig. 3(a) and 3(b) as that reported previously [23, 24], as indicated by the 15-fold increase of the second-harmonic signal after compression and the straight parallel MIIPS traces free of non-specific components [Fig. 3(e)] [25]. The compressed RDW is a clean 17-fs (FWHM) pulse [Fig. 3(a), bottom panel], corresponding to an 8-cycle pulse at 620 nm. Because the chirp of the RDW pulse is largely linear, a simple linear compressor would lead to 25-fs (FWHM) compression. Similar compressibility is generally applicable to other RDW pulse energies or the RDWs from other fibers (including SMF-28). However, the interference-like disruption appears to negatively impact the compression quality, and is therefore avoided by operating at low soliton orders of N<6 (Table 2).

4. Discussions and perspectives

The above compression results reinforces the high coherence of RDW that has been demonstrated using alternative techniques such as spectral interferometry [18] (or prism-pair pulse compression [6]), and has been directly linked to the low optical amplitude [18] (or phase [6]) noise at low soliton orders of N<10 (Table 1) [5]. Thus, our RDW fiber source operated at N<6 approximates a solid-state optical parametric oscillator (OPO) in spectrum shape, polarization, pulse energy, average power, and coherence (or optical noise), except for a (perhaps more desirable) broader bandwidth or shorter pulse duration. In comparison to the fs Yb:fiber platform [16], the Er platform has the advantage that anomalous dispersion at the pump wavelength can be achieved in large-core fibers (Table 2), thus facilitating RDW power scaling and simplifying the cascaded fusion splicing [26] to build more robust all-fiber RDW sources [16]. By the use of a higher repetition rate (~250 MHz) fs Er:fiber master oscillator (Fig. 2) widely used in fiber frequency comb sources, the RDW power may be further increased. Our prototypical RDW source has been operated outside of the optical laboratory and has shown strong resistance to mechanical and thermal disturbances. This combination of reliability, simplicity, compactness, and cost effectiveness is difficult, if not impossible, to realize in OPO-type solid-state lasers. The integration of the existing fs Er:fiber platform and its well-documented branched configuration [6] into this RDW source should facilitate various (portable) ultrafast applications that demand two synchronized pulse chains with broad spectral coverage. Strongly blue-shifted (>700 nm) RDW sources may also be built upon Tm or other rare-earth-doped fiber technologies for extended spectral coverage.