Abstract
Previous research has found a relationship between individual differences in children’s precision when nonverbally approximating quantities and their school mathematics performance. School mathematics performance emerges from both informal (e.g., counting) and formal (e.g., knowledge of mathematics facts) abilities. It remains unknown whether approximation precision relates to both of these types of mathematics abilities. In the present study we assessed the precision of numerical approximation in 85 3- to 7-year-old children four times over a span of two years. Additionally, at the last time point, we tested children’s informal and formal mathematics abilities using the Test of Early Mathematics Ability (TEMA-3; Ginsburg & Baroody, 2003). We found that children’s numerical approximation precision correlated with and predicted their informal, but not formal, mathematics abilities when controlling for age and IQ. These results add to our growing understanding of the relationship between an unlearned, non-symbolic system of quantity representation and the system of mathematical reasoning that children come to master through instruction.
Keywords: Approximate Number System (ANS), informal math, formal math, individual differences
To succeed in school mathematics, children need to master a variety of skills. These skills include informal mathematics abilities such as numbering and counting, comparing numbers to determine which is more or less, and calculating the answers to simple arithmetic problems using tokens or fingers (Ginsburg & Baroody, 2003; Jordan, Kaplan, Ramineni, & Locuniak, 2009; National Mathematics Advisory Panel, 2008). These skills also include formal, school-taught abilities, which require adherence to the formal conventions of mathematics and include, for example, the ability to read and write Arabic numerals, understanding of the place value system, and the ability to recall memorized addition, subtraction, and multiplication facts (Ginsburg & Baroody, 2003; Jordan et al., 2009; National Mathematics Advisory Panel, 2008).
In addition to these informal and formal mathematics skills, all of which typically require thinking about or manipulating number symbols (e.g., number words or digits), children also have access to a non-symbolic, pre-linguistic system of numerical representation. This system can be used to approximate numerical quantities, compare approximate numerical representations, and perform approximate arithmetic operations including addition and subtraction (Barth, La Mont, Lipton, & Spelke, 2005; Dehaene, 1992; Feigenson, Dehaene, & Spelke, 2004). This Approximate Number System (ANS) is present in humans from birth onwards (Halberda, Ly, Willmer, Naiman, & Germine, 2012; Izard, Sann, Spelke, & Streri, 2009) and has been demonstrated in a variety of non-human animals (Brannon & Merritt, 2011). A hallmark feature of the ANS is that the imprecision in its representations increases as numerosity grows. As a consequence, the discriminability between two approximate number representations is determined by the ratio between them, not by their absolute difference (such performance is also commonly described as adhering to Weber’s Law). Although ANS representations remain noisy and imprecise throughout the lifespan (Halberda et al., 2012), numerous studies have found that the precision of ANS representations increases with age (Halberda & Feigenson, 2008; Halberda et al., 2012; Libertus & Brannon, 2010; Xu & Spelke, 2000). Even so, there are large differences in ANS precision between individuals of similar age. These individual differences are already present and stable in infancy (Libertus & Brannon, 2010; Libertus, Brannon, & Woldorff, 2011) and can be found across the entire lifespan (Halberda et al., 2012).
Previous research has revealed a small but stable relationship between these individual differences in ANS precision and mathematics performance in both children and adults (for review, see Feigenson, Libertus, & Halberda, 2013). For example, Halberda and colleagues (2008) found that students’ mathematics abilities from kindergarten through sixth grade (measured using standardized math assessments) significantly correlated with their ANS precision measured at age 14. Importantly, this relationship remained robust even when controlling for other cognitive abilities such as general intelligence, visuo-spatial skills, and working memory, thereby suggesting a fairly specific relationship between the ANS and mathematics ability. Furthermore, recent studies showed that ANS precision and mathematics performance are already linked in preschool-aged children, before the onset of rigorous mathematics instruction (Libertus, Feigenson, & Halberda, 2011), and that ANS precision measured in preschool predicts later mathematics performance (Libertus, Feigenson, & Halberda, 2013; Mazzocco, Feigenson, & Halberda, 2011). Finally, this link appears to persist even into adulthood (Halberda et al., 2012; Libertus, Odic, & Halberda, 2012).
While it is still unclear what mechanisms may support a link between ANS precision and mathematics abilities, several possibilities have been raised. One is that the link may reside in children’s intuitive arithmetic operations (Gilmore, McCarthy, & Spelke, 2007, 2010). Another possibility is that it is created through a mapping between the ordinal relations of the ANS and ordinal relations among number symbols (Lyons & Beilock, 2011). Finally, it may arise during the acquisition of number symbol meanings and during online access of those meanings (De Smedt, Verschaffel, & Ghesquiere, 2009; Holloway & Ansari, 2009; Rousselle & Noel, 2007; Sasanguie, De Smedt, Defever, & Reynvoet, 2011).
An important step toward evaluating these possibilities is obtaining a clearer characterization of the specific mathematical abilities that are linked to ANS precision. In particular, the relationship between ANS precision and formal and informal mathematical abilities has yet to be elucidated. As described above, mathematics has often been conceived as including both formal and informal concepts and skills (e.g., Baroody, 1987; Raman, 2002) and this distinction between formal and informal mathematical abilities has played an important role in investigations of mathematical learning impairments (Mazzocco & Thompson, 2005; Russell & Ginsburg, 1984). This raises the question of whether ANS precision relates only to informal mathematical abilities, only to formal abilities, or some combination of the two. At present, no research has examined the extent to which formal versus informal mathematical abilities relate to the precision of the ANS.
Additionally, we note that alongside the many studies documenting a relationship between ANS precision and mathematical ability, several studies have failed to find such a link (Castronovo & Göbel, 2012; Price, Palmer, Battista, & Ansari, 2012) or have found a link in children but not in adults (Inglis, Attridge, Batchelor, & Gilmore, 2011). Although there are several possible sources for this discrepency, including the size of the tested population and the tasks used to measure the ANS, the extent to which tests of mathematical abilities tap formal versus informal mathematical knowledge might also contribute.
To date, the relationship between the ANS and different types of mathematical abilities has not been systematically investigated. One study by Desoete and colleagues (2010) found that kindergarteners’ non-symbolic number comparison skills predicted their calculation skills in grade 1, but not grade 2, and predicted their fact retrieval skills in both grades. This is suggestive that ANS representations may influence formal mathematical abilities. However, the non-symbolic number comparison task used by Desoete and colleagues only included six questions, several of which contained arrays of dots with numbers less than four. Many studies suggest that such small arrays often activate non-numerical representations of individual objects (see Feigenson et al., 2004); hence understanding the relationship between numerical approximation ability and formal mathematics ability requires further exploration with more numerous and varied test items.
In the present study, we asked whether children’s ANS precision relates to and predicts their informal and formal mathematics abilities as assessed by the Test of Early Mathematics Ability (TEMA-3; Ginsburg & Baroody, 2003). To this end, we assessed children’s ANS precision four times over the course of two years and also assessed their informal and formal mathematics abilities during the final testing session.
Method
Participants
Eighty-five children (39 females, average age at Time 1 = 4.15 years, SD = 0.66) who were recruited as part of a larger, longitudinal study on children’s mathematics and language development contributed data to this study (see Libertus, Feigenson, et al., 2011; Libertus et al., 2013, for results from other aspects of the study). Data from eight of these children were not included in the analyses of performance from Time 1 due to inability to complete the task (n = 3), external interference (n = 2), language problems (n = 1), or absence from the preschool at the assigned day of testing (n = 2). Data from six children were not included in the analysis of performance from Time 2 because they were unavailable to complete the testing session at this time (n = 5) or because of equipment failure (n = 1). Data from five of these children were excluded from the analyses of performance from Time 3 because the children were unavailable to complete the testing session at this time. Finally, data from nine children were not included in the analyses of performance from Time 4 because children were unable to pay attention during a majority of the testing session. This means that sample sizes varied across our analyses depending on whether a child contributed data at a particular time point. The average delay between Time 1 and Time 2 was 208.36 days (SD = 49.25), between Time 2 and Time 3 it was 190.52 days (SD = 49.58), and between Time 3 and Time 4 it was 271.34 days (SD = 40.34).
Most children came from families of middle to high socio-economic status. The IQ of the children in our sample was assessed at Time 3 and was found to be more than one standard deviation above the expected mean (M = 121.10, SD = 20.20). Parents of all children provided informed written consent prior to their child’s participation, and children provided verbal assent before each assessment. All children received a small gift (e.g., a small toy or book) to thank them for their participation after each testing session.
Materials
ANS precision task
To measure the precision of children’s Approximate Number System (ANS) for visual arrays at each time point, we administered a version of Panamath (the Psychophysical Assessment of Number-sense Acuity; Halberda & Ly, in preparation) – a non-symbolic numerical comparison task (Halberda et al., 2008; Libertus, Feigenson, et al., 2011). Children were told that the cartoon character Grover had a box of blue balls and the character Big Bird had a box of yellow balls, and then were shown arrays of spatially separated blue and yellow dots on a 13-inch laptop screen. Children were asked to indicate who had more balls (i.e., whether more of the dots were blue or more of the dots were yellow). The experimenter initiated each trial when the child appeared to be attentive. Each stimulus array of blue and yellow balls was visible for 2000 ms and was followed by a blank screen that remained until children gave a verbal response (e.g., “yellow”). The experimenter immediately pressed the corresponding key on an external keyboard (e.g., “y” for “yellow”). Two different sounds provided feedback throughout the experiment: a high-pitched tone indicated a correct answer and a low-pitched tone indicated an incorrect answer. Children were familiarized to these sounds on six practice trials during which the experimenter provided additional verbal feedback to ensure that children understood the task and were motivated to participate.
Following these practice trials, children completed a given number of test trials. The number of test trials varied across the four time points, and was adjusted depending on the duration of each testing session. In addition, we presented children with different numerical ratio discriminations across the four time points to ensure adequate task difficulty for all children. At Time 1 and 2, 60 test trials were presented. On each of these, the presented numerosities were drawn randomly from one of four numerical ratio bins: 1.17, 1.33, 1.5, and 2.0 (with the absolute number of dots in each collection varying between 4 and 15, such that a trial with e.g., 5 yellow versus 10 blue dots would go into the 2.0-ratio bin). At Time 3, 64 test trials were presented and the number of dots in each collection ranged from 5 to 22, with test numerosities drawn randomly from one of four numerical ratio bins: 1.14, 1.17, 1.5, and 2.5. At Time 4, 42 test trials were presented and the number of dots in each collection ranged from 5 to 21, with test numerosities drawn randomly from one of seven numerical ratio bins: 1.11, 1.14, 1.17, 1.25, 1.5, 2.0, and 3.0. At all time points, on half of the trials the yellow dots were more numerous and on the other half the blue dots were more numerous. Orthogonally, the dots in each array also varied in size in order to discourage children from using dot size as a cue. The default radius of the dots was 60 pixels and the maximum variability in size between the dots was +/−35%. On half of the trials the two arrays were equated for individual dot size (i.e., the average size of the dots in each collection was equal). On the other half of the trials, the cumulative surface area of the blue dots and the yellow dots was equated.
Standardized mathematics assessment
To assess informal and formal mathematics abilities, at Time 4 we administered Form A of the Test of Early Mathematics Ability (TEMA-3; Ginsburg & Baroody, 2003). The TEMA-3 is comprised of 72 items, divided into two broad categories. One category tests informal mathematical abilities such as numbering skills (e.g., verbally counting the number of objects on a page), number-comparison facility (e.g., determining which of two spoken number words is larger), informal calculation (e.g., solving word problems with the aid of tokens or fingers), and informal number concepts (e.g., the cardinality principle, i.e., knowing that the last number in a count sequence is the number of items in the set). The other TEMA-3 category tests formal mathematical abilities such as numeral literacy (e.g., reading and writing Arabic numerals), mastery of number facts (e.g., retrieving addition, subtraction, and multiplication facts), calculation skills (e.g., solving mental and written addition and subtraction problems), and number concepts (e.g., answering how many tens are in one hundred). The administration of the TEMA-3 followed the standardized procedure, i.e., testing started with an item that was determined by the child’s age, and stopped after the child answered incorrectly on five consecutive items. Items before the age-defined starting point were only administered if the child did not succeed on five consecutive items between the starting and stopping points. The TEMA-3 has been normed for children between the ages of 3 years 0 months and 8 years 11 months.
Procedure
At Times 1-3, approximately half of the children were tested in a quiet room at their preschools and the other half were tested in a quiet room in the laboratory. At Time 4, 78 children were tested in a quiet area of their own homes and 7 children were tested in a quiet room in the laboratory1. All tasks were administered as part of a larger assessment of children’s math, language, and general cognitive development. At Time 4, for half of the children, the standardized mathematics assessment was administered prior to the ANS precision task; for the other half, it was administered immediately following the ANS precision task. It took children about 5-15 minutes to complete the ANS task at each time point and 20-30 minutes to complete the standardized mathematics assessment at Time 4.
Results
Data analysis
ANS precision task
Within each time point, children received identical trials. Therefore, we used average accuracy (percent correct) across all trials as a measure of children’s ANS precision at each time point. We used accuracy instead of Weber fraction because estimates of individual Weber fractions, especially at the youngest ages, are quite volatile and noisy (Libertus, Feigenson, et al., 2011). Data from two children at Time 3 and two other children at Time 4 were excluded because their average accuracies were more than three standard deviations below the group average. Preliminary analyses revealed no significant differences in accuracy for trials in which individual dot size was equated compared to trials in which cumulative surface area was equated when age was controlled for at any of the time points (all Fs < 2.17, ps > 0.14). Thus, we collapsed our analyses across both trial types. The Spearman-Brown corrected split-half reliabilities for the ANS task ranged from 0.65 to 0.72 across the four time points.
Standardized mathematics assessment
To measure children’s informal versus formal mathematics abilities, we used the item categorization given in the TEMA-3 Examiner’s Manual (Ginsburg & Baroody, 2003). The standardized administration of the TEMA-3 requires starting and ending at different items in the test sequence depending on children’s age and performance. To account for the resulting difference in the total number of items and the number of informal versus formal math items administered to each child, we averaged children’s scores (with children receiving a 0 or 1 for each administered item) and multiplied these averages by 100 to create separate percentage scores for informal and formal mathematics skills categories. This resulted in an average informal math score and an average formal math score for each child. Importantly, because children start at different points according to their age, the resulting informal and formal math scores are, in practice, roughly controlled for age at time of testing. The average inter-item correlation for all administered TEMA-3 items was 0.99 (Cronbach’s alpha). For informal math scores, Cronbach’s alpha was 0.98, and for formal math scores it was 0.97.
Relationship between informal and formal mathematics abilities and ANS precision
Descriptive statistics for ANS precision estimates at each time point are given in Table 1. Children completed an average of 18.58 (SD = 4.52) TEMA-3 items that were categorized as assessing informal mathematics abilities, and an average of 11.53 (SD = 7.64) TEMA-3 items that were categorized as assessing formal mathematics abilities. Children answered correctly on an average of 68.42% (SD = 14.60%) of the informal mathematics ability items on the TEMA-3 and 45.46% (SD = 17.74%) of the formal mathematics ability items.
Table 1.
Descriptive statistics for ANS precision at each time point
| Time point | Mean age in years (SD) |
N | Mean ANS % correct (SD) |
|---|---|---|---|
| Time 1 | 4.15 (0.66) | 77 | 66.08 (14.30) |
| Time 2 | 4.77 (0.68) | 79 | 76.31 (13.50) |
| Time 3 | 5.26 (0.68) | 78 | 83.81 (6.24) |
| Time 4 | 5.99 (0.70) | 74 | 85.19 (7.25) |
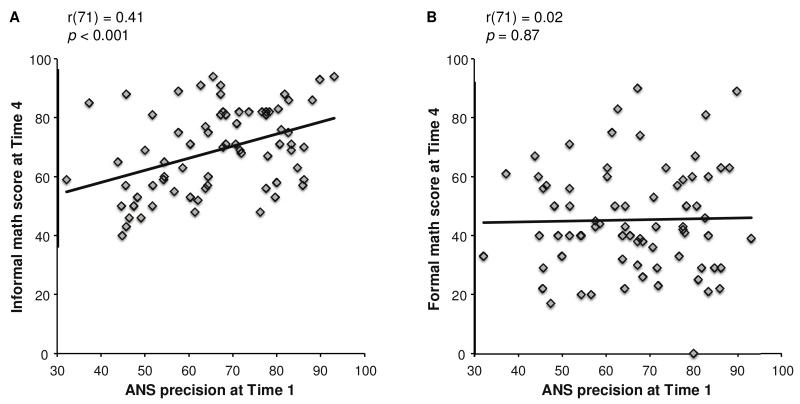
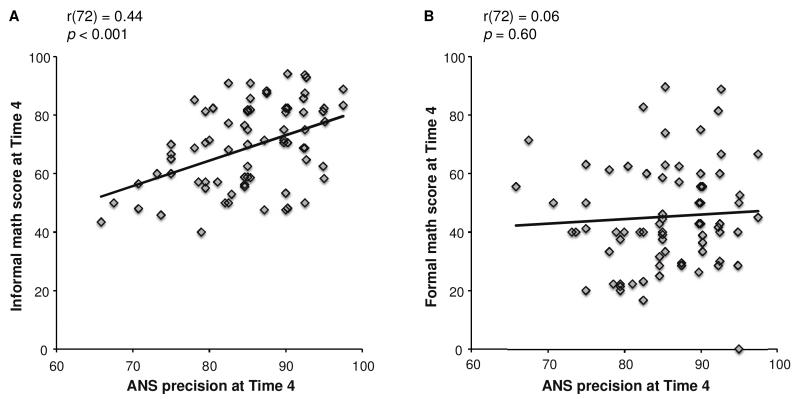
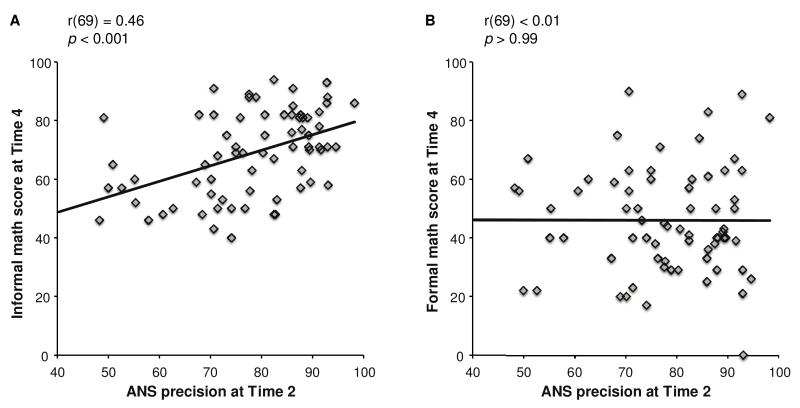
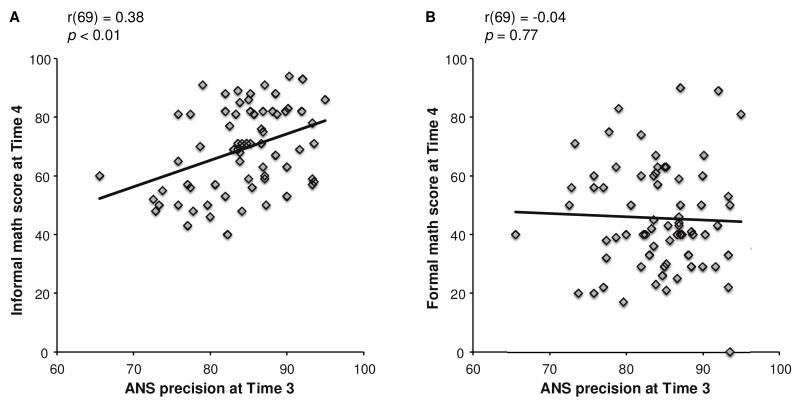
To assess the relationship between children’s ANS precision and their informal and formal mathematics abilities, we correlated children’s accuracy on the ANS precision task at Times 1-4 with their informal and formal mathematics ability scores. As shown in Figures 1-4, we found that informal mathematics ability scores (measured at Time 4) were significantly correlated with ANS precision at each of the four time points (all rs > 0.38, all ps < 0.01). In contrast, formal mathematics ability scores were never correlated with ANS precision (all rs < 0.07, all ps > 0.59). A direct comparison using Fisher’s r-to-z transformation showed a significant difference in the correlation coefficients for informal and formal math scores with ANS respectively at all four time points (all Zs > 2.59, all ps < 0.01).
Figure 1.
Scatterplots of ANS precision at Time 1 and informal (A) and formal (B) mathematics abilities measured on the TEMA-3 at Time 4. There is a significant link between ANS precision at Time 1 and informal but not formal math scores at Time 4.
Figure 4.
Scatterplots of ANS precision at Time 4 and informal (A) and formal (B) mathematics abilities measured on the TEMA-3 at Time 4. There is a significant link between ANS precision and informal but not formal math scores at Time 4.
To confirm the specificity of the link between ANS and informal mathematical abilities, we conducted further multiple linear regression analyses for each time point in which ANS precision, age at the time of testing, an interaction term between ANS precision and age, and IQ were entered at the same time as potential predictors of informal TEMA scores. We first normalized age and accuracy on the ANS precision task to avoid problems with multicollinearity in our calculations of the interaction term for each time point. As can be seen in Table 2, except for at Time 1, ANS precision always remained a unique significant predictor of informal math scores even when controlling for age, an interaction between age and ANS precision, and IQ.
Table 2.
Summary of multiple linear regression analyses for variables at Time 1 – Time 4 predicting informal math scores at Time 4. Standardized beta values and associated statistical results are shown for each variable at each time point.
| Time | Variable | std beta | t | p-value |
|---|---|---|---|---|
| Time 1 | ANS precision | .20 | 1.54 | .13 |
| Age | .37 | 2.76 | <.01 | |
| ANS × Age | .05 | 0.41 | .68 | |
| IQ | .21 | 1.95 | .06 | |
| Time 2 | ANS precision | .27 | 2.31 | . 02 |
| Age | .37 | 3.13 | <.01 | |
| ANS × Age | −.05 | −0.45 | .65 | |
| IQ | .21 | 2.09 | .04 | |
| Time 3 | ANS precision | .28 | 2.59 | .01 |
| Age | .43 | 4.11 | <.001 | |
| ANS × Age | .01 | 0.07 | .95 | |
| IQ | .15 | 1.46 | .15 | |
| Time 4 | ANS precision | .34 | 3.67 | <.001 |
| Age | .51 | 5.45 | <.001 | |
| ANS × Age | .15 | 1.67 | .10 | |
| IQ | .16 | 1.70 | .09 |
Lastly, informal and formal mathematics ability scores were not significantly correlated with each other (R = 0.15, p = 0.20).
Discussion
The present investigation adds to our understanding of the relationship between the unlearned ability to approximate quantities and the mathematics that children acquire via instruction. Here we found that children’s ability to approximate numbers of visual items correlated with and predicted their overall informal mathematics abilities (such as their ability to count and to solve simple arithmetic problems using tokens or fingers) over a span of up to two years (the longest time span assessed in the current study). Importantly, this association remained significant even when controlling for age at the time of testing, the interaction between age and ANS precision, and IQ. Greater accuracy when performing numerical estimations was associated with better informal mathematics abilities. In contrast, formal mathematics abilities (such as the ability to demonstrate understanding of the place value system and to recall basic addition, subtraction, and multiplication facts) were never linked to children’s ANS precision at any time point in our sample.
These findings suggest that the ANS may be particularly important for certain mathematical skills over others. In particular, the ANS may help children to master the verbal count system, to understand the ordered relationship between numerical symbols, and to link arithmetic problems to physical representations of numbers. In contrast, our results suggest that the ANS may be less important for mastering formal mathematical conventions such as the ability to understand the place value system and to recall basic number facts. Our results thereby integrate well with accounts suggesting that the mapping between non-symbolic ANS representations and formal number symbols may be a crucial link mediating the relationship between ANS precision and mathematics abilities (Holloway & Ansari, 2009; Lyons & Beilock, 2011).
While our results provide evidence for a link between ANS precision and informal mathematics abilities, there are important limitations that should be addressed in future studies. First, the distinction between informal and formal mathematics abilities is still a very coarse one, and future studies should investigate the subcategories within each set of abilities more closely. Unfortunately, we were unable to perform this finer-grained analysis in the present study due to the way in which the TEMA-3 is typically administered. Standard TEMA-3 administration results in children being tested on different numbers of items from each subcategory. This imbalance, and the relatively small number of items from certain subcategories, makes it difficult to draw conclusions regarding the link between ANS precision and individual subcategories of informal and formal math abilities. Future studies could use tasks that give participants equal numbers of items across all subcategories of math abilities. Related to this goal, it is worth noting that we did not find a significant association between children’s informal and formal math abilities on the TEMA-3. This lack of an association should be further investigated and extended to the different subcategories in order to shed light on the interrelations between the different subcategories of early mathematics abilities.
In addition, we note that the link between informal versus formal mathematical abilities and the ANS may change over developmental time. Previous studies have found a small but significant link between school mathematics ability and ANS precision in older children and adults (DeWind & Brannon, 2012; Halberda et al., 2012; Libertus et al., 2012; Lourenco, Bonny, Fernandez, & Rao, 2012). The assessments used to measure mathematics ability in these samples included many items that required formal mathematics abilities of the kind administered in the present study, and few if any informal items. The finding that performance on these tasks, comprised mostly of formal math items, correlated with ANS precision raises the possibility that, with age and experience, formal mathematical abilities also become linked to the ANS. Further study with a wider range of age groups is needed to investigate this possibility, as well as to ask whether there are also differences between various aspects of formal mathematics ability (e.g. fractions, geometry, algebra, calculus etc.) and their link to the ANS. Finally, our sample was comprised of children with above-average intelligence from mostly middle- and upper-class backgrounds. Further studies are needed to test whether the effects observed in the present study generalize to a more diverse population.
In sum, we found that the precision of 3- to 7-year-old children’s Approximate Number System (ANS), measured repeatedly over the course of two years, correlated with and predicted children’s informal, but not formal, mathematics abilities even when controlling for age at the time of testing, the interaction between age and ANS precision, and IQ. Future studies are necessary to replicate and extend these findings to more clearly delineate the relationship between ANS precision and subcategories of informal and formal mathematical abilities across developmental time. Such work will be a needed step on the path towards describing the mechanism that links the ANS with mathematical thought.
Highlights.
We tested ANS precision and informal and formal math ability of 3-7-year-olds.
ANS precision correlated with and predicted informal math ability over 2 years.
ANS precision did not correlate with or predict formal math ability.
Correlations remained significant even when controlling for age and IQ.
Figure 2.
Scatterplots of ANS precision at Time 2 and informal (A) and formal (B) mathematics abilities measured on the TEMA-3 at Time 4. There is a significant link between ANS precision at Time 2 and informal but not formal math scores at Time 4.
Figure 3.
Scatterplots of ANS precision at Time 3 and informal (A) and formal (B) mathematics abilities measured on the TEMA-3 at Time 4. There is a significant link between ANS precision at Time 3 and informal but not formal math scores at Time 4.
Acknowledgements
We thank Andrea Stevenson, Selin Zeytinoglu, Stephanie Caronna, Misti Jeffers, and Ruxue Shao for help with testing participants, and all families and children for their participation. This research was supported by NICHD grant R01 HD057258 to LF and JH. Creation of the Panamath software was supported by NSF grant DRL0937675 to JH.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Omitting the children tested in the laboratory from our analyses did not alter the pattern of results. Thus, we included all children in the results reported here.
References
- Baroody AJ. Children’s Mathematical Thinking. A Developmental Framework for Preschool, Primary, and Special Education Teachers. Teachers College Press; New York: 1987. [Google Scholar]
- Barth H, La Mont K, Lipton J, Spelke ES. Abstract number and arithmetic in preschool children. Proc Natl Acad Sci U S A. 2005;102(39):14116–14121. doi: 10.1073/pnas.0505512102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brannon EM, Merritt DJ. Evolutionary foundations of the Approximate Number System. In: Dehaene S, Brannon EM, editors. Space, Time, and Number in the Brain: searching for the foundations of mathematical thought. Academic Press; London, UK: 2011. [Google Scholar]
- Castronovo J, Göbel SM. Impact of High Mathematics Education on the Number Sense. PLoS One. 2012;7:e33832. doi: 10.1371/journal.pone.0033832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Smedt B, Verschaffel L, Ghesquiere P. The predictive value of numerical magnitude comparison for individual differences in mathematics achievement. Journal of Experimental Child Psychology. 2009;103(4):469–479. doi: 10.1016/j.jecp.2009.01.010. [DOI] [PubMed] [Google Scholar]
- Dehaene S. Varieties of numerical abilities. Cognition. 1992;44(1-2):1–42. doi: 10.1016/0010-0277(92)90049-n. [DOI] [PubMed] [Google Scholar]
- Desoete A, Ceulemans A, De Weerdt F, Pieters S. Can we predict mathematical learning disabilities from symbolic and non-symbolic comparison tasks in kindergarten? Findings from a longitudinal study. Br J Educ Psychol. 2010 doi: 10.1348/2044-8279.002002. DOI:10.1348/2044-8279.002002. [DOI] [PubMed] [Google Scholar]
- DeWind NK, Brannon EM. Malleability of the approximate number system: effects of feedback and training. Frontiers in Human Neuroscience. 2012;6(68) doi: 10.3389/fnhum.2012.00068. doi:10.3389/fnhum.2012.00068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences. 2004;8(7):307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Libertus ME, Halberda J. Links between the intuitive sense of number and formal mathematics ability. Child Development Perspectives. 2013;7(2):74–79. doi: 10.1111/cdep.12019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmore CK, McCarthy SE, Spelke ES. Symbolic arithmetic knowledge without instruction. Nature. 2007;447(7144):589–591. doi: 10.1038/nature05850. [DOI] [PubMed] [Google Scholar]
- Gilmore CK, McCarthy SE, Spelke ES. Non-symbolic arithmetic abilities and mathematics achievement in the first year of formal schooling. Cognition. 2010;115(3):394–406. doi: 10.1016/j.cognition.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ginsburg HP, Baroody AJ. Test of Early Mathematics Ability. Third Edition Pro Ed; Austin, Texas: 2003. [Google Scholar]
- Halberda J, Feigenson L. Developmental change in the acuity of the ‘number sense’: The approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Developmental Psychology. 2008;44(5):1457–1465. doi: 10.1037/a0012682. [DOI] [PubMed] [Google Scholar]
- Halberda J, Ly R. Panamath: The Psychophysical Assessment of Number-sense Acuity. in preparation. [Google Scholar]
- Halberda J, Ly R, Willmer J, Naiman D, Germine L. Number sense across the lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences, Early Edition. 2012 doi: 10.1073/pnas.1200196109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberda J, Mazzocco MM, Feigenson L. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008;455(7213):665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Mapping numerical magnitudes onto symbols: The numerical distance effect and individual differences in children’s mathematics achievement. Journal of Experimental Child Psychology. 2009;103(1):17–29. doi: 10.1016/j.jecp.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Inglis M, Attridge N, Batchelor S, Gilmore C. Non-verbal number acuity correlates with symbolic mathematics achievement: But only in children. Psychonomic Bulletin & Review. 2011 doi: 10.3758/s13423-011-0154-1. DOI 10.3758/s13423-011-0154-1. [DOI] [PubMed] [Google Scholar]
- Izard V, Sann C, Spelke ES, Streri A. Newborn infants perceive abstract numbers. Proc Natl Acad Sci U S A. 2009;106(25):10382–10385. doi: 10.1073/pnas.0812142106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Kaplan D, Ramineni C, Locuniak MN. Early math matters: kindergarten number competence and later mathematics outcomes. Dev Psychol. 2009;45(3):850–867. doi: 10.1037/a0014939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Brannon EM. Stable individual differences in number discrimination in infancy. Developmental Science. 2010;13(6):900–906. doi: 10.1111/j.1467-7687.2009.00948.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Brannon EM, Woldorff M. Parallels in Stimulus-Driven Oscillatory Brain Responses to Numerosity Changes in Adults and Seven-Month-Old Infants. Developmental Neuropsychology. 2011;36(6):651–667. doi: 10.1080/87565641.2010.549883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Feigenson L, Halberda J. Preschool Acuity of the Approximate Number System Correlates with School Math Ability. Developmental Science. 2011;14(6):1292–1300. doi: 10.1111/j.1467-7687.2011.01080.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Feigenson L, Halberda J. Is Approximate Number Precision a Stable Predictor of Math Ability? Learning and Individual Differences. 2013;25:126–133. doi: 10.1016/j.lindif.2013.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Odic D, Halberda J. Intuitive sense of number correlates with math scores on college-entrance examination. Acta Psychologica. 2012;141:373–379. doi: 10.1016/j.actpsy.2012.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lourenco SF, Bonny JW, Fernandez EP, Rao S. Nonsymbolic number and cumulative area representations contribute shared and unique variance to symbolic math competence. Proceedings of the National Academy of Sciences. 2012;109(46):18737–18742. doi: 10.1073/pnas.1207212109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyons IM, Beilock SL. Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition. 2011;121(2):256–261. doi: 10.1016/j.cognition.2011.07.009. [DOI] [PubMed] [Google Scholar]
- Mazzocco MM, Feigenson L, Halberda J. Preschoolers’ precision of the approximate number system predicts later school mathematics performance. PLoS One. 2011;6(9):e23749. doi: 10.1371/journal.pone.0023749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzocco MM, Thompson RE. Kindergarten Predictors of Math Learning Disability. Learning Disabilities Research & Practice. 2005;20:142–155. doi: 10.1111/j.1540-5826.2005.00129.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Mathematics Advisory Panel . Foundations for Success: The Final Report of the National Mathematics Advisory Panel. U.S. Department of Education; Washington, DC: 2008. [Google Scholar]
- Price GR, Palmer D, Battista C, Ansari D. Nonsymbolic numerical magnitude comparison: Reliability and validity of different task variants and outcome measures, and their relationship to arithmetic achievement in adults. Acta Psychologica. 2012;140:50–57. doi: 10.1016/j.actpsy.2012.02.008. [DOI] [PubMed] [Google Scholar]
- Raman M. Coordinating informal and formal aspects of mathematics: student behavior and textbook messages. Journal of Mathematical Behavior. 2002;21(2):135–150. [Google Scholar]
- Rousselle L, Noel MP. Basic numerical skills in children with mathematics learning disabilities: A comparison of symbolic vs non-symbolic number magnitude processing. Cognition. 2007;102(3):361–395. doi: 10.1016/j.cognition.2006.01.005. [DOI] [PubMed] [Google Scholar]
- Russell RL, Ginsburg HP. Cognitive analysis of children’s mathematics difficulties. Cognition and Instruction. 1984;1:217–244. [Google Scholar]
- Sasanguie D, De Smedt B, Defever E, Reynvoet B. Association between basic numerical abilities and mathematics achievement. Brit Jour Dev Psych. 2011 doi: 10.1111/j.2044-835X.2011.02048.x. DOI:10.1111/j.2044-835X.2011.02048.x. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74(1):B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]