Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 Aug 29;4(18):3104–3109. doi: 10.1021/jz4014079

Detailed Examination of a Single Conduction Event in a Potassium Channel

Philip W Fowler 1, Oliver Beckstein 1, Enrique Abad 1, Mark S P Sansom 1,*
PMCID: PMC3797101  PMID: 24143269

Abstract

graphic file with name jz-2013-014079_0006.jpg

Although extensively studied, it has proved difficult to describe in detail how potassium ion channels conduct cations and water. We present a computational study that, by using stratified umbrella sampling, examines nearly an entire conduction event of the Kv1.2/2.1 paddle chimera and thereby identifies the expected stable configurations of ions and waters in the selectivity filter of the channel. We describe in detail the motions of the ions and waters during a conduction event, focusing on how waters and ions enter the filter, the rotation of water molecules inside the filter, and how potassium ions are coordinated as they move from a water to a protein environment. Finally, we analyze the small conformational changes undergone by the protein, showing that the stable configurations are most similar to the experimental crystal structure.

Ion channels are proteins that control the flow of ions across polarized cell membranes. The voltage-gated sodium (Nav) and potassium (Kv) channels are central to the generation of action potentials and hence are of tremendous physiological importance.1 Both families of channels have been extensively studied thanks to the exquisite sensitivity of single-channel electrophysiology and recent successes in elucidating atomic-resolution structures by X-ray diffraction.

Long et al.2 elucidated the structure of the tetrameric Kv1.2/2.1 paddle chimera (Kvchim - Figure 1A), which is functionally similar to Shaker, the canonical voltage-gated potassium ion channel.3 The central pore domain, common to all potassium channels, is surrounded by four voltage-sensing domains. The pore-lining helices are kinked, opening the intracellular gate wide enough that it is thought to be open.2,4

Figure 1.

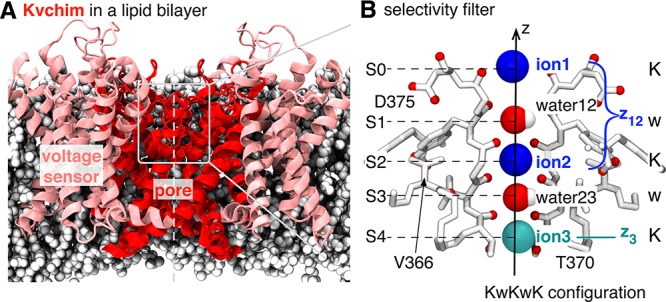
Figure 1

Open in a new tab

(A) Structure of the chimeric voltage-gated potassium ion channel Kvchim.2 It is a homotetramer, with each monomer contributing a peripheral voltage sensor (pink) and one-quarter of the central pore domain (red). The narrowest part of the pore, the selectivity filter, is delineated by a light gray box. (B) Detailed image of the selectivity filter. Three potassium ions are labeled ion1, ion2 (both in blue), and ion3 (cyan).11 The displacement along the pore axis, z, of the center of mass of the top two ions is denoted by z12, while the displacement of the lower ion is denoted by z3. We shall describe the configuration of the selectivity filter by a string of letters that denote the species present in each binding site, from S0 (left) to S4 (right), with the cavity species, where appropriate, given in parentheses. The configuration shown is KwKwK.

The extracellular third of the pore forms a narrow constriction, the selectivity filter (Figure 1B), made from four loops each with the highly conserved sequence TVGYG, one from each monomer. The loops are arranged so that the backbone carbonyl oxygens point toward the pore axis, creating a series of octahedral cages (labeled S0–S4) that can coordinate a cation or a water molecule. The selectivity filter is sufficiently narrow that potassium ions must dehydrate to enter and can only move through in single-file.5 The prevailing view is that inside the filter there is always a single water (w) between each ion (K), leading to what we call the KwK mechanism.6 The energetics so are finely tuned that sodium ions are excluded, yet over half a billion of potassium ions can pass through per second. Immediately below the selectivity filter is the central cavity, which contains water molecules and cations,7 and in the Kvchim structure this is contiguous with the intracellular medium.

How can we examine the conduction of potassium ions by Kvchim in atomistic detail? This is difficult to do by experiment alone because the process of conduction is fast and occurs in a confined, highly optimized space that is very sensitive to perturbation8 and there is no experimental technique with the sufficient spatial and temporal resolution to resolve a single selectivity filter. Computer simulation can complement experiment provided one is careful to validate the results. Molecular dynamics simulations have been used to study different aspects of the behavior of potassium ion channels, including how potassium ions and water move through the selectivity filter.9 One defines several collective variables so that the conduction process can be followed; these are usually the displacements of the ions and waters along the pore axis. Although a fast process, the energetic barriers are sufficiently high that biased simulations methods have typically been applied.10 These methods apply forces to the ions and waters to ensure that the required region of collective variable space is sampled. A multidimensional potential of mean force (PMF) contains a considerable amount of information; for example, stable configurations of the selectivity filter can be identified. Bernèche and Roux11 used this approach to examine the conduction of potassium through the selectivity filter of the first, low-resolution structure of KcsA.12 Other potassium and related channels have been studied, including KirBac1.1,13,14 Kv1.2,15,16 the high-resolution structure of KcsA,17 NaK,18 and sodium channels.19,20 The sensitivity and reproducibility of conduction PMFs have been examined.21 More recently, computer power has increased to the point at which it has become possible to simulate multiple conduction events by “brute force” simulations if very high electric fields are applied.22−25 Although such unbiased simulations are intuitively appealing, it perhaps remains more efficient and informative to use biased approaches to investigate conduction. From the resulting PMFs one can, in theory, (i) make a direct connection to analytical and hierarchical theories and thereby calculate the conductance of the channel and (ii) examine a conduction event in more detail. We discuss the feasibility of the former in another paper.21

We instead examine the net permeation of a single potassium ion through the Kv1.2/2.1 paddle chimeric channel. Not only do we study the energetics but we also study conduction from the perspective of the permeating species and determine how the conformation of the selectivity filter and its surrounding residues change during a conduction event.

We simulated only the pore domain of the Kvchim paddle chimaera.2 This is reasonable because it has been shown that the pores of unrelated K channels can be spliced into a Kv channel, suggesting that Kv channels are modular in nature.26 We placed potassium ions and waters at alternate sites within the selectivity filter, and a third potassium ion (ion3) was placed in the central cavity below the selectivity filter. The resulting structure was embedded in a lipid bilayer and equilibrated using classical molecular dynamics.

The positions of the permeant species, and hence the configuration of the selectivity filter, was followed using the same collective variables as previous studies.11,21 Harmonic potentials were then separately applied to the center of mass of the two ions in the filter (ion12, z12) and the incoming ion (ion3, z3). By running 125 × 0.5 ns simulations, each with the harmonic potentials centered on a different value of (z12,z3), we were able to sample nearly an entire conduction event using stratified umbrella sampling. Three independent sets of umbrella simulations were run, making a total of 375 simulations.

Because we have implicitly assumed that there is always a water between any two potassium ions in the selectivity filter, we checked whether this was true for all umbrella simulations. The water between the two potassiums in the selectivity filter occasionally managed to squeeze past one of the ions.21 This occurred in 8% of frames (Figure S1 and Table S1 in the Supporting Information). All of these frames were removed, thereby ensuring our simulations followed the KwK mechanism. This process reduced the overlap in certain regions of (z12,z3) coordinate space, preventing us from calculating the three separate PMFs. Instead we combined all data to ensure adequate sampling of (z12,z3) space and calculated a single 2D PMF. We explicitly determined when the 2D PMFs were converged and, after discarding that portion of the data, estimated the correlation time and thereby calculated the errors (Figures S2–S4 in the Supporting Information).

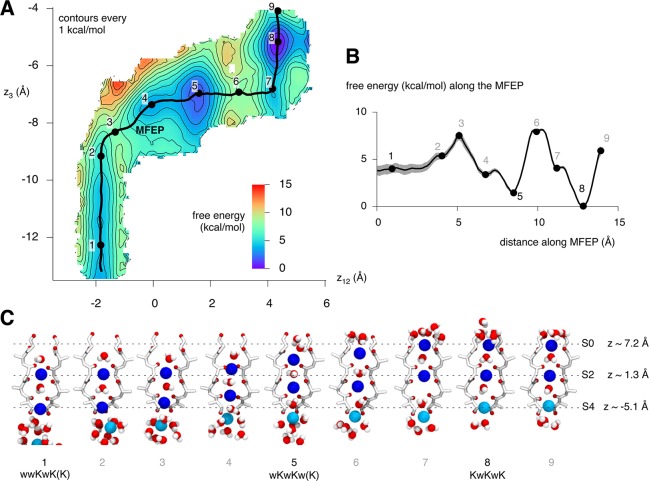
The final result is a complex landscape with several minima (Figure 2) corresponding to the expected stable configurations of the selectivity filter: wwKwK(K), wKwKw(K), and KwKwK. The landscape suggests that the KwKwK configuration is more stable than the wwKwK(K) configuration by 4.0 ± 0.5 kcal/mol (Table S2 in the Supporting Information). Using shorter umbrella simulations, we have previously identified the same stable configurations and estimated that the KwKwK configuration is more stable than the wKwKw(K) configuration by 5–8 kcal/mol.21

Figure 2.

Figure 2

Open in a new tab

(A) Final converged average 2D PMF for the KwK mechanism. The MFEP is drawn as a black line and nine points are labeled – these points will be referred to in subsequent panels and figures. Contours are drawn every 1 kcal/mol. (B) Free energy along the MFEP. This more clearly shows the minima and maxima. These are labeled as above, and the estimated error is indicated. (C) Representative snapshots of the selectivity filter at each of the nine points. The same coloring scheme is used as in Figure 1. Any waters close to a potassium ion are also rendered, and for clarity only two monomers are shown. Points 1, 5, and 8 correspond to the wwKwK(K), wKwKw(K), and KwKwK configurations of the selectivity filter.

To validate the above 2D PMF, we calculated the free energy required to move a potassium ion from the cavity into the S0 site, ΔGcavity→S0 (and vice versa), using thermodynamic integration (Figure S5 in the Supporting Information), resulting in ΔGcavity→S0 = 8.6 ± 0.2 kcal/mol and ΔGS0→cavity = −8.1 ± 0.2 kcal/mol. The forward and reverse calculations therefore agree with one another to within the estimated error and confirm that the three-ion configuration (KwKwK) is indeed more favorable than the wwKwK(K) configuration. The difference between the above values and our previous estimate derived from the 2D PMF could be because the two free energies are not directly comparable, or it may indicate that one or both calculations are, despite the results of our analyses, not yet converged. We conclude that the three-ion configuration (KwKwK) is more favorable than the wwKwK(K) configuration by 4–8 kcal/mol and is the most stable configuration of the selectivity filter.

The minimum free-energy path (MFEP) represents the most probable conduction mechanism (Figure 2). It has three major minima (points 1, 5, and 8) corresponding to the wwKwK(K), wKwKw(K), and KwKwK configurations of the selectivity filter, two barriers (points 3 and 6), and three possible intermediates (points 2, 4, and 7) (Table S2 in the Supporting Information). The depth of two of the possible intermediates is less than the estimated error so should be ignored. Only the configuration (point 4) can be considered to be metastable. Here both ion1 and ion2 appear to be in the process of moving between sites and are held in the plane of carbonyl oxygens. The heights of the barriers are in the range 3.5–7.9 kcal/mol (Table S3 in the Supporting Information) and seem rather too high to match the experimental order of magnitude of conductance properties for this channel in the framework of standard electrodiffusion theory. These barrier heights are consistent with a previous study21 where we methodically examined the reproducibility and sensitivity to changes in the force field of such 2D PMFs. The potential reasons for this lack of agreement are extensively debated in that paper.

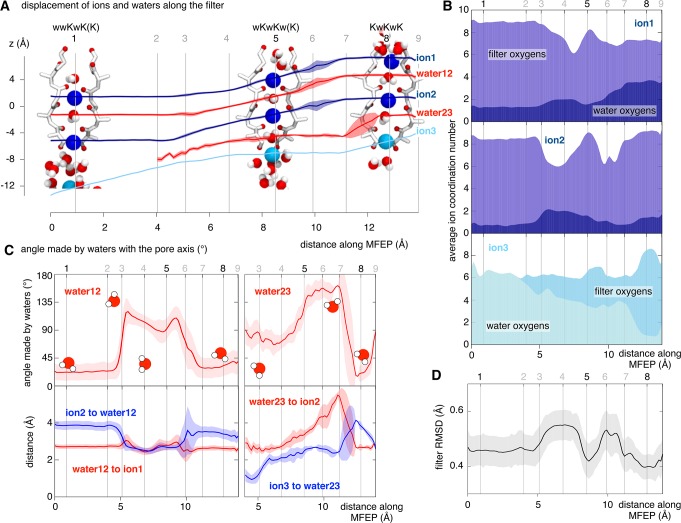
In the remainder of this letter we shall examine in detail a single conduction event. Let us start with a solvated potassium ion (ion3) in the central cavity and two potassium ions (ion1 and ion2) bound at S2 and S4, with water molecules at S1 and S3. As ion3 approaches and enters the selectivity filter the average water persistence time (i.e., how long a water molecule stays within its solvation shell) increases (Figure 3A, B). Log–linear histograms of the water persistence times as a function of z3 (Figure 3C) show that when ion3 is in the central cavity (−12 < z3 ≤ −13 Å) the solvating waters rapidly exchange with bulk, leading to an approximately exponential distribution in the water persistence times. As ion3 approaches Thr370, waters spends longer and longer between the ion and the bottom of the selectivity filter. Eventually, when ion3 is directly below S4 (−6 < z3 ≤ −7 Å), the water above it (water23) sporadically coordinates ion3 for the entire trajectory (400 ps).

Figure 3.

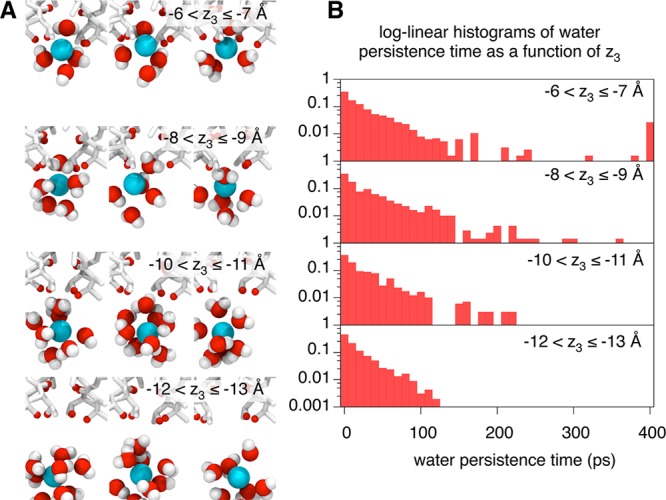
Figure 3

Open in a new tab

As ion3 approaches S4 from the central cavity, the persistence time of its coordinating waters increases. (A) Illustrative snapshots showing this process. (B) Four log–linear distributions demonstrate that when ion3 is far below S4 the coordinating waters rapidly exchange with other waters in the central cavity and hence the persistence time is <140 ps. But as ion3 comes closer to the hydroxyl side chains of Thr370 that define the entrance to the filter, some waters persist for longer and longer until, when in the region −6 < z3 ≤ −7 Å, several waters persist for the entire equilibrated region of the trajectory (400 ps).

The nonlinear increase in the water persistence time along the pore axis strongly suggests that the entry of permeating species into the selectivity filter is a complex process and there is no clear boundary, one side of which a water is ‘outside’ the filter and the other it is ‘inside’ the filter. Instead there are wide regions at the base of the filter (and probably also at the top) where the water is transitioning from being ‘outside’ to being ‘inside’. It is therefore incorrect to consider the selectivity filter as a hollow cylinder and the ions and waters as hard spheres.21 Likewise, our observation that waters can occasionally squeeze past ions in the selectivity filter suggests that even when definitely inside the filter the persistence time for waters is long but not infinite.

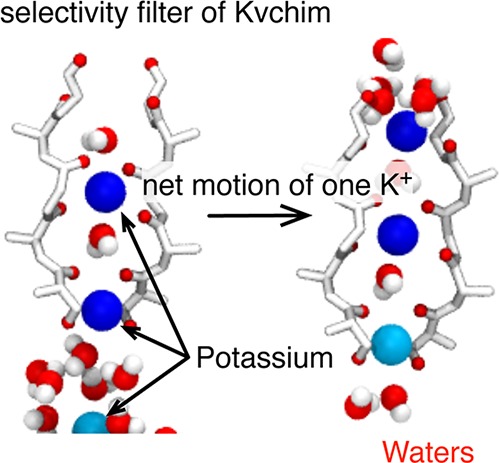
As ion3 approaches the hydroxyl side chains of Thr370, all of the species in the filter move up one site in a concerted manner (‘knock-on’), and a water then enters site S4 (points 3–4, Figure 4A). A second ‘knock-on’ event (points 6–7) then occurs and ion3 enters the filter, leading to the KwKwK configuration.

Figure 4.

Figure 4

Open in a new tab

Detailed look at a conduction event. (A) Average displacement of the conducting species along the minimum free energy path (MFEP). The nine points labeled correspond to those in Figure 2. The position of water23 is not well-defined until it enters the filter, which is assumed to occur after point 2. (B) Examining the ion coordination numbers ion shows that ions 1 and 2 are coordinated by oxygens from both the protein and water, with the former dominating, leading to coordination numbers in the region 6–9. Lower values occur outside of stable configurations. Ion3 is initially entirely coordinated by water, but there is a gradual increase in the amount of coordination provided by the protein as it approaches S4 from the central cavity. (C) Average angles of the intervening waters along the MFEP. Also shown are the distances between the waters and ions within the selectivity filter. (D) ) Examining the RMSD of the filter along the MFEP shows how the selectivity filter is most similar to the crystal structure when ions and waters are stably bound (points 1, 5, and 8). The RMSD is calculated relative to the crystal structure of Kvchim2 and compares the backbone heavy atoms (Cα, C, N, O) as well as the Cβ atoms of the entire selectivity filter (the sequence TVGYG).

The optimum coordination number of a potassium ion is 6–9.27 During conduction the coordination numbers of ion1 and ion2 are 8–9, except during both knock-on events when they are reduced. The coordination number of ion1 remains low (∼7) after the second knock-on event as it is in S0, which has only four carbonyl oxygens coordinating the cation with the remainder of the coordinating oxygens coming from water molecules. The incoming ion, ion3, is initially solvated by waters in the central cavity, but as it approaches Thr370 there is a gradual substitution of water oxygens by protein oxygens until ion3 is fully stabilized in site S4 and the filter achieves the KwKwK configuration (point 8). The coordination number of ion3 remains stable at 6–7 until ion3 enters the selectivity filter, whereupon it increases to 7–9, consistent with that experienced by ion2 at the start of the MFEP.

A water molecule trapped between two potassium ions can coordinate only one ion at a time. This is seen in the average angles made by the two waters in the filter (Figure 4C). With ion3 in the central cavity, water12 is orientated (∼20°) to solvate ion1, which is above it in site S2. This is energetically favorable because ion2, which is below the water in site S4, can be solvated by waters from the central cavity, whereas ion1 cannot. As a result the average distance between ion1 and water12 is less than the distance between ion2 and water12. During the first ‘knock-on’, ions1 and 2 and water12 get squeezed together and water12 adopts an average angle of ∼90°, presumably indicating that it coordinates both ions equally. Water23 now enters the selectivity filter and rotates (∼150°) during the second knock-on to coordinate ion3 as it subsequently enters the filter. Water12 then starts to rotate back to ∼20° (points 5–6), so it is once again coordinating ion1 (in S0), again resulting in the distance between ion2 and water12 increasing. During this movement the distance between water23 and ion3 starts to increase until (point 7) water23 suddenly moves to coordinate ion2 rather than ion3 by simultaneously rotating (∼20°) and moving up in the filter. The stable KwKwK configuration is thereby attained with both ‘trapped’ waters coordinating the ions above them in the selectivity filter. Because each water is an electrical dipole the external electric field could affect these rotations in subtle ways.

The selectivity filter subtly changes conformation during the conduction event, as shown by the root-mean-square deviation (RMSD) of the selectivity filter (Figure 4D and Figure S6 in the Supporting Information). The RMSD is smallest when the filter is in one of the stable configurations, suggesting that, as we might expect, the crystal structure is a spatial average of proteins with stable configurations of their selectivity filters.2 To probe how the selectivity filter changes conformation, we measured the distances between the opposing oxygens that line the filter28 and the backbone dihedral angles (Figure S7 in the Supporting Information). The opposing oxygen distances show how the filter has to first open slightly at Thr370 and then close to ‘swallow’ first water23 (points 3–5) and then ion3 (points 6–8). There is no clear correlation between any single dihedral angle and the individual opposing oxygen distances, suggesting that the ‘swallowing’ effect observed is driven by multiple small changes in dihedral angles along the backbone of the selectivity filter.

All K channels have a network of hydrogen bonds around the selectivity filter (Figure S8 in the Supporting Information). For example in Kvchim, Ser367 can form a hydrogen bond with both the backbone carbonyl of Tyr363 and the hydroxyl group of Tyr373. It has been shown that mutating either tryptophan or the residue equivalent to Ser367 (a threonine) in the Shaker channel prevents expression,8 consistent with the hypothesis that these interactions help stabilize the selectivity filter. The propensity of all hydrogen bonds investigated remained approximately constant during the conduction event, and there was no correlation between the fluctuations and the movement of the conducting species, further suggesting that these hydrogen bonds simply stabilize the selectivity filter.

In conclusion, we have calculated a 2D PMF characterizing nearly an entire conduction event through the selectivity filter of the Kv1.2/2.1 chimeric voltage-gated channel, assuming the KwK mechanism is correct. This identifies the expected stable configurations of the selectivity filter (wwKwK(K), wKwKw(K), and KwKwK; Figure 2). We have described in detail the motions of the ions and waters during two ‘knock-on’ events, have shown how the filter is able to smooth the transition of a potassium ion from water into the narrow constriction of the selectivity filter, and have investigated the small conformational changes that occur during a conduction event. This is the first study to combine in this fashion the calculation of PMFs with detailed structural analysis.

Acknowledgments

This work was funded by the Wellcome Trust through programme grants 083547/Z/07/Z and 092970/Z/10/Z. We thank the Oxford Supercomputing Centre and the U.K. National Grid Service for computer time. We are grateful to the EPSRC, who, through the Complementary Capability Computing Initiative (grant EP/G042659/1), provided access to the HPCx supercomputer. E.A. gratefully acknowledges additional financial support by the Wiener Anspach foundation in the early stages of this work as well as support by the Ministerio de Ciencia y Tecnologia (Spain) through Grant No. FIS2010-16587 (partially financed by FEDER funds) and by the Junta de Extremadura through Grant No. GRU10158

Supporting Information Available

Computational details and the simulations and their analysis. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

† O.B.: Department of Physics, Arizona State University, USA.

Author Present Address

‡ E.A.: Departamento de Física Aplicada, Centro Universitario de Mérida, Universidad de Extremadura, Mérida, Spain.

The authors declare no competing financial interest.

Supplementary Material

jz4014079_si_001.pdf (4.2MB, pdf)

References

  1. Hille B.Ion Channels of Excitable Membranes, 3rd ed.; Sinauer Associates, Inc: Sunderland, MA, 2001. [Google Scholar]
  2. Long S. B.; Tao X.; Campbell E. B.; MacKinnon R. Atomic Structure of a Voltage-Dependent K+ Channel in a Lipid Membrane-Like Environment. Nature 2007, 450, 376–382. [DOI] [PubMed] [Google Scholar]
  3. Tao X.; MacKinnon R. Functional Analysis of Kv1.2 and Paddle Chimera Kv Channels in Planar Lipid Bilayers. J. Mol. Biol. 2008, 382, 24–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Fowler P. W.; Sansom M. S. P. The Pore of Voltage-Gated Potassium Ion Channels Is Strained When Closed. Nat. Commun. 2013, 4, 1872. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Hodgkin A. L.; Keynes R. D. The Potassium Permeability of a Giant Nerve Fibre. J. Physiol. 1955, 128, 61–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Zhou Y.; MacKinnon R. The Occupancy of Ions in the K+ Selectivity Filter: Charge Balance and Coupling of Ion Binding to a Protein Conformational Change Underlie High Conduction Rates. J. Mol. Biol. 2003, 333, 965–975. [DOI] [PubMed] [Google Scholar]
  7. Zhou Y.; Morais-Cabral J. H.; Kaufman A.; MacKinnon R. Chemistry of Ion Coordination and Hydration Revealed by a K+ Channel-Fab Complex At 2.0 Å Resolution. Nature 2001, 414, 43–48. [DOI] [PubMed] [Google Scholar]
  8. Yifrach O.; MacKinnon R. Energetics of Pore Opening in a Voltage-Gated K+ Channel. Cell 2002, 111, 231–9. [DOI] [PubMed] [Google Scholar]
  9. Maffeo C.; Bhattacharya S.; Yoo J.; Wells D.; Aksimentiev A. Modeling and Simulation of Ion Channels. Chem. Rev. 2012, 112, 6250–6284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Tai K.; Fowler P. W.; Mokrab Y.; Stansfeld P.; Sansom M. S. P. In Methods in Cell Nano Biology, 1st ed.; Jena B. P., Ed.; Elsevier B.V.: Boston, 2008; Vol. 90, Chapter 12, pp 233–265. [DOI] [PubMed] [Google Scholar]
  11. Bernèche S.; Roux B. Energetics of Ion Conduction Through the K+ Channel. Nature 2001, 414, 73–7. [DOI] [PubMed] [Google Scholar]
  12. Doyle D.; Cabral J.; Pfuetzner R.; Kuo A.; Gulbis J. M.; Cohen S. L.; Chait B. T.; MacKinnon R. The Structure of the Potassium Channel: Molecular Basis of K+ Conduction and Selectivity. Science 1998, 280, 69–77. [DOI] [PubMed] [Google Scholar]
  13. Domene C.; Klein M. L.; Branduardi D.; Gervasio F. L.; Parrinello M. Conformational Changes and Gating at the Selectivity Filter of Potassium Channels. J. Am. Chem. Soc. 2008, 130, 9474–9480. [DOI] [PubMed] [Google Scholar]
  14. Furini S.; Domene C. Atypical Mechanism of Conduction in Potassium Channels. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 16074–16077. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Treptow W.; Tarek M. K+ Conduction in the Selectivity Filter of Potassium Channels Is Monitored by the Charge Distribution Along Their Sequence. Biophys. J. 2006, 91, L81–L83. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Bastug T.; Kuyucak S. Comparative Study of the Energetics of Ion Permeation in Kv1.2 and KcsA Potassium Channels. Biophys. J. 2011, 100, 629–636. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Egwolf B.; Roux B. Ion Selectivity of the KcsA Channel: A Perspective from Multi-Ion Free Energy Landscapes. J. Mol. Biol. 2010, 401, 831–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Furini S.; Domene C. Gating at the Selectivity Filter of Ion Channels that Conduct Na+ and K+ Ions. Biophys. J. 2011, 101, 1623–1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Corry B. Na+/Ca2+ Selectivity in the Bacterial Voltage-Gated Sodium Channel NavAb. PeerJ 2013, 1, e16. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Furini S.; Domene C. On Conduction in a Bacterial Sodium Channel. PLoS Comput. Biol. 2012, 8, e1002476. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Fowler P. W.; Abad E.; Beckstein O.; Sansom M. S. P.. Energetics of Multi-Ion Conduction Pathways in Potassium Ion Channels. J. Chem. Theor. Comput. 2013, submitted [DOI] [PMC free article] [PubMed]
  22. Khalili-Araghi F.; Tajkhorshid E.; Schulten K. Dynamics of K+ Ion Conduction Through Kv1.2. Biophys. J. 2006, 91, L72–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jensen M. O.; Borhani D. W.; Lindorff-Larsen K.; Maragakis P.; Jogini V.; Eastwood M. P.; Dror R. O.; Shaw D. E. Principles of Conduction and Hydrophobic Gating in K+ Channels. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 5833–5838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Jensen M. O.; Jogini V.; Borhani D. W.; Leffler A. E.; Dror R. O.; Shaw D. E. Mechanism of Voltage Gating in Potassium Channels. Science 2012, 336, 229–233. [DOI] [PubMed] [Google Scholar]
  25. Jensen M. O.; Jogini V.; Eastwood M. P.; Shaw D. E. Atomic-Level Simulation of Current-Voltage Relationships in Single-File Ion Channels. J. Gen. Physiol. 2013, 141, 619–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lu Z.; Klem A. M.; Ramu Y. Ion Conduction Pore Is Conserved Among Potassium Channels. Nature 2001, 413, 809–813. [DOI] [PubMed] [Google Scholar]
  27. Bostick D. L.; Brooks C. L. Selectivity in K+ Channels Is Due to Topological Control of the Permeant Ion’s Coordinated State. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 9260–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Fowler P. W.; Tai K.; Sansom M. S. P. The Selectivity of K+ Ion Channels: Testing the Hypotheses. Biophys. J. 2008, 95, 5062–72. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz4014079_si_001.pdf (4.2MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES