Skip to main content
NCBI home page
Oxford University Press logoLink to Oxford University Press
. 2013 Oct 9;21(4):430–448. doi: 10.1093/pan/mpt016

Dynamic Network Logistic Regression: A Logistic Choice Analysis of Inter- and Intra-Group Blog Citation Dynamics in the 2004 US Presidential Election

Zack W Almquist 1,✉, Carter T Butts 2,✉
PMCID: PMC3797130  PMID: 24143060

Abstract

Methods for analysis of network dynamics have seen great progress in the past decade. This article shows how Dynamic Network Logistic Regression techniques (a special case of the Temporal Exponential Random Graph Models) can be used to implement decision theoretic models for network dynamics in a panel data context. We also provide practical heuristics for model building and assessment. We illustrate the power of these techniques by applying them to a dynamic blog network sampled during the 2004 US presidential election cycle. This is a particularly interesting case because it marks the debut of Internet-based media such as blogs and social networking web sites as institutionally recognized features of the American political landscape. Using a longitudinal sample of all Democratic National Convention/Republican National Convention–designated blog citation networks, we are able to test the influence of various strategic, institutional, and balance-theoretic mechanisms as well as exogenous factors such as seasonality and political events on the propensity of blogs to cite one another over time. Using a combination of deviance-based model selection criteria and simulation-based model adequacy tests, we identify the combination of processes that best characterizes the choice behavior of the contending blogs.

1 Introduction

Methods for analysis of dynamic network data have seen great progress over the past decade. This article applies Dynamic Network Logistic Regression (DNR)—a simple family of models for network panel data—and a special case of the Temporal Exponential-Family Random Graph Model (TERGM) family—to a temporally evolving network of blog interaction data to illustrate four methodological contributions: (1) a decision-theoretic framework for hypothesis testing and interpretation; (2) an example of how to build hypotheses in this framework; (3) model selection and assessment procedures for this model family; and (4) comparison of a DNR model to a more general TERG model with simultaneous dependence.

The 2004 US presidential election cycle marked the debut of Internet-based media such as blogs and social networking web sites as institutionally recognized features of the American political landscape. Particularly significant was the credentialing of selected blogs as officially designated media sources for purposes of covering the major political party conventions, an act which gave particular legitimacy to two contending groups of partisan blogs (one credentialed for the Republican National Convention [RNC] and the other for the Democratic National Convention [DNC]). In the months that followed, these blogs served as significant foci for online journalistic, promotional, fund-raising, and organizing activities relating to the 2004 election.

In this study, we employ a dynamic logistic choice model to study the dynamics of interaction within and between these two groups of political blogs. Using a longitudinal sample of all DNC- and RNC-designated blog citation networks (sampled at six-hour intervals for approximately four months) from Butts and Cross (2009), we are able to test for the influence of various strategic, institutional, and balance-theoretic mechanisms—as well as exogenous factors such as seasonality and political events—on the propensity of blogs to cite (i.e., hyperlink to) one another over time. Capitalizing on the temporal resolution of our data, we utilize an autoregressive network regression framework to carry out inference for a logistic choice process closely related to the actor-oriented framework of Snijders (2001).

This article is structured as follows. We begin by providing some general background from the relevant social science and social network literatures, with a particular focus on the role of political blogs during the study period. This is followed by a description of the study data, and an overview of our modeling approach. The latter includes both a discussion of the general assumptions behind the modeling of blog evolution as a dynamic decision process, and a treatment of the factors potentially shaping actors’ payoffs. We follow this with a discussion of our implementation and inferential framework, data analysis, and findings. Finally, we conclude with a discussion of the implications of our results for our understanding of the social mechanisms shaping contentious groups in the online environment.

2 Background

In recent years, the online world has generated a diverse array of new media for social interaction (Wellman 2001), one of the most successful of which is the weblog (or “blog”). Although a relatively obscure medium for many years, the growing popularity of blogs as a means for information dissemination, coordination, and political organization through the early to mid-2000s eventually led to their recognition of and adoption by established institutions. A key landmark in this process was the 2004 US presidential election cycle, in which the DNC and RNC first granted press credentials to selected bloggers for coverage of their national political conventions (Adamic and Glance 2005; Howard 2005; Rainie, Cornfield, and Horrigan 2005; Butts and Cross 2009). This institutionalized legitimation by the major US political parties constituted a de facto recognition of the role of blogs (and the online community more broadly) as a durable element of the political landscape, and arguably marked the debut of the “new media” as a force in electoral politics.

The impact of blogs first gained institutional attention in the US political sphere in the early phases of the 2004 US electoral cycle, when Democratic presidential candidate and Vermont Governor Howard Dean rose to prominence partially as a result of his extensive use of online organizing to compensate for limited conventional resources in garnering media attention and raising funds (Ammori 2005; Kerbel and Bloom 2005). Dean’s success in utilizing online interaction to mobilize a widely dispersed base of supporters was quickly noted by political observers, and (despite his loss of the Democratic nomination to Senator John Kerry) paved the way for other politicians to incorporate online media into their political campaigns (Cone 2003). Indeed, by the end of the 2004 electoral cycle blogs and other online resources had been adopted by a number of presidential contenders, and (via actions such as the above-mentioned credentialing of bloggers as members of the press) by the major US political parties themselves. These and further developments in the historical evolution of the online environment over the past decade have set the stage for academic, governmental, nonprofit, and for-profit interest in blogs and other new media, particularly in political contexts (Drezner and Farrell 2008).

With respect to the role played by blogs per se, Woodly (2008) demonstrates that blogs are actively used in mobilizing opinions, setting agendas, and generally influencing the elite members of the political parties. His work demonstrates that the interactions between political blogs are a particularly important dimension of this phenomenon. Because a distinctive feature of blogs is their combination of commentary on current events with hypertext references to primary or secondary information sources, the constantly evolving network of citations between blogs is at least as significant (e.g., from an information search standpoint) as the content of the individual blogs themselves. Within this network of references, blog authors (or “bloggers”) have become a new form of journalist, in some cases with similar information access and responsibilities to practitioners within traditional media outlets (Wall 2005). As the importance of this medium has continued to increase in recent years, its growth in size and elaboration has made its study both relevant and difficult. We thus focus our attention on the initial “watershed” period of the 2004 US presidential election, when the role of blogs as legitimated media entities was just beginning to crystallize. In particular, our attention centers on the interactions among the relatively small number of blogs credentialed for the major-party political conventions, as they jockeyed to promote their issues, candidates, and arguably themselves in the midst of a rapidly changing political and technological landscape. As players with some institutional recognition but little control from established political actors, these blogs provide an early example of a phenomenon that has become increasingly common throughout the developed world.

3 Data

The data used in this article are a dynamic inter- and intra-group blog citation network collected by Butts and Cross (2009), consisting of interactions among all blogs credentialed by the DNC or RNC for their respective 2004 conventions. Specifically, the set of actors (or vertex set) for this network consists of thirty-four DNC and fourteen RNC credentialed blogs (with one blog credentialed by both groups) providing a combined network of forty-seven nodes observed over a 121-day period (for a temporal snapshot of this network, see Fig. 1). Network data were obtained by automatically querying the main page of each blog at six-hour intervals starting at midnight, Pacific time. The period of observation for this study begins on July 22, 2004 (shortly before the DNC convention), and ends November 19, 2004 (shortly after the presidential election), leading to a total of 484 time points. At each time point, the collected data consist of the network of URLs linking the main page of one blog to any page within another; that is, there is an edge from blog i to blog j at time t if a link to blog j appears on the main page of i at time t. We may conceive of these data as an adjacency array, A, such that Inline graphic if i cites (i.e., links to) j at time t, and 0 otherwise. For purposes of this study, we ignore self-citations (i.e., internal links from a blog to itself).1

Fig. 1.

Fig. 1

Open in a new tab

Fifteen time points for the RNC/DNC credentialled blog citation network. White (blue) nodes represent DNC, black (red) represents RNC, and grey (purple) node is credentialled by both the RNC and DNC. Time is labeled [Year.Month.Day.Hour].

In addition to the evolving blog network, Butts and Cross (2009) provide a timeline of major events during the campaign cycle, dividing the 121-day period into a series of “epochs” based on salient activities such as the RNC and DNC conventions, the televised presidential debates, and the election itself (Table 1). In an analysis of volatility within the RNC and DNC networks (taken separately), Butts and Cross (2009) find that these campaign events are related to the pace of change within the network (along with daily and weekly seasonal effects). As such, we include these temporal effects as covariates in our analyses (as described below).

Table 1.

Epochs in the 2004 election cycle from Butts and Cross (2009)

Epoch Description Start time End time Time points
PreCon Start of window to DNC Convention 7/22, 00:00 7/25, 18:00 16
DNCCon DNC Convention 7/26, 00:00 7/29, 18:00 16
InterCon End of DNC Convention to start of RNC Convention 7/30, 00:00 8/29, 18:00 124
RNCCon RNC Convention 8/30, 00:00 9/2, 18:00 16
PreDeb End of RNC Convention to first presidential debate 9/3, 00:00 9/20, 12:00 71
Deb First presidential debate to last presidential debate 9/20, 18:00 10/14, 18:00 93
PreElec Post last presidential debate to Election Day 10/14, 00:00 11/1, 18:00 76
Elec Election Day 11/2, 00:00 11/2, 18:00 4
PostElec Post election to end of window 11/3, 00:00 11/19, 18:00 67
Open in a new tab

4 Network Evolution as a Decision Process

Blogs of the type studied here are the deliberately constructed and maintained products of individuals, or small groups thereof. Moreover, those blogs credentialed during the 2004 electoral cycle represented a small “elite” circle of especially active authors, whose blogs centered on coverage of politics and current events. As such, it is reasonable to consider modeling the evolving blog network as arising from a dynamic decision process, in which blog authors select those to whom they link in response to context and past history. This approach has been most fully developed by Snijders (1996), Snijders and Van Duijn (1997), and Snijders (2001), who posit an “actor-oriented” model in which network members change their relationships via a latent continuous-time choice process. We here employ a somewhat simpler version of this general scheme, which represents network evolution as a discrete time logistic choice process (McFadden 1974, 1976). Although requiring somewhat stricter assumptions on decision simultaneity, this variant facilitates the accommodation of complex backward-looking behavior, and scales more easily to larger data sets.

Although the inferential aspects of this framework will be described in Section 5, we begin here by presenting the model from a behavioral point of view. First, we review the notion of edge updating as a logistic choice process (Snijders 2001), with a specific emphasis on its interpretation in the present case. As a revealed preference model, the logistic choice framework requires a parametric utility function; thus, we follow our initial discussion with a consideration of the payoff elements that may be expected to enter into blog authors’ decision-making processes, as they decide to whom they will or will not link. These payoff elements will form the core building blocks for our analysis of the evolving blog network.

4.1 Edge Updating as Logistic Choice

At its crudest level, a blog is a web page with dynamically updated links to other online resources. The core decision facing a blog author, then, is that of the other sites to which he or she should link, and (conversely) the links that can be removed (directly, or by allowing them to “expire” by no longer being shown on the blog’s front page). Such citations can be controlled on an individual basis, and are limited only by attentional and/or energetic costs: there is in principle no effective limit on the number of citations that can be maintained, and no barrier to adding or removing citations when desired. At the same time, adding or removing links requires attention and effort on the part of the author, and is thus the result of deliberate action (as opposed, e.g., to the accidental, incidental, or automatic behaviors that are of considerable importance in face-to-face settings [Goffman 1959]). Blog authors—particularly active ones, such as those represented in this sample—can and do spend considerable time monitoring their environment, and may thus be expected to be aware of and react to the actions of salient alters; moreover, recent citation history is relatively easily discovered in this environment, potentially facilitating the use of backward-looking strategies. On the other hand, the complexity and dynamic nature of the online environment make prediction difficult, suggesting a very limited capacity for forward-looking behavior.

Taken together, the above considerations suggest the following propositions as a reasonable starting point for modeling the evolution of the blog network. For simplicity of discussion, we will refer to the “blog” as the unit of decision making, and the links or citations from one blog to another as “edges” within the associated network.2

  1. The state of outgoing edges at each observation of the blog network is assumed to result from the choices of the sending blog.

  2. Each blog in the network may send an edge to any number of other blogs in the network at any time.

  3. The decision of a given blog regarding the state of a given edge is made myopically, and in isolation (i.e., the decision is considered on its own terms, without factoring in the effects of other decisions that might be made simultaneously).

  4. The decision of a given blog regarding the state of a given edge may depend upon the past history of the blog network, or of the current external context (e.g., time of day, electoral cycle events).

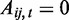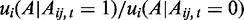Subject to the above, we further presume that blog citation behavior follows a weakly consistent pattern of preferences, in the sense that there exists a utility function, u, such that for the two alternative states Inline graphic and Inline graphic, the odds that i will choose Inline graphic are strictly increasing in Inline graphic. Such a pattern of behavior is typically referred to as a stochastic choice process, and can be viewed as a form of bounded rationality. Although many stochastic choice models exist, we here use the common logistic choice model. In the present case, this amounts to the assumption that

graphic file with name mpt016m1.jpg (1)

or, equivalently, that

graphic file with name mpt016m2.jpg (2)

That is, the log-odds that i will choose to cite j at time t is equal to the utility difference associated with sending (versus not sending) an edge. Where the utility of one option is substantially greater than the other, then, actor behavior is nearly deterministic: the utility-increasing choice is selected with very high probability. As the actor approaches indifference, however, choice behavior becomes increasingly random (an effect interpretable either as difficulty in determining the preferable option or as reflecting the influence of various small, idiosyncratic payoffs). When the actor is entirely indifferent between citing and not citing another, the choice becomes fully arbitrary (i.e., a coin flip).

To put this scheme into practice, we must make some further assumptions regarding the nature of the utility function. From our list of propositions, we have assumed that decisions are made myopically, depending on the past (and on general context), but not on simultaneous or future decisions. As such, we require that u depend upon the network history, A, only through its prior states, and through the conjecturally perturbed state associated with a single decision (i.e., for the Inline graphic decision, ui may depend upon Inline graphic where Inline graphic, and on Inline graphic such that Inline graphic for all Inline graphic). u may also depend upon t, and on exogenous covariates (denoted by X). Finally, we will assume in general that u can be written as a sum of linearly separable payoff elements, s, such that Inline graphic. Intuitively, s expresses the factors potentially driving i’s behavior, whereas the parameter vector θ expresses the direction and magnitude of the effect these factors have on the propensity to send or refrain from sending a tie.

As a model of boundedly rational dynamics, the logistic choice framework is quite general: a wide range of factors can potentially enter into the utility function, and the choice of possible candidates must be made based on substantive considerations. With that in mind, we now turn to a consideration of the payoff elements that may plausibly drive behavior within the blog network.

4.2 Potential Payoff Elements

We apply three core hypotheses to the construction of the potential payoff elements that might influence this network. The first hypothesis is built around the long-standing notion of preferential mixing (McPherson, Smith-Lovin, and Cook 2001) (e.g., homophily); the second set of hypotheses center around balance theory (Cartwright and Harary 1956; Heider 1958) and its predictions for interaction between two opposing groups; and the last set of hypotheses are constructed via the natural cyclic rhythms of modern society (Shumway and Stoffer 2006).

The sampling frame employed by Butts and Cross (2009) guarantees two distinct groups, specifically DNC-designated blogs and RNC-designated blogs. In this context, these groups represent two contentious factions competing for very real and tangible stakes in the US political arena (see Drezner and Farrell 2008, etc.). We may view these two groups as halves of an adversarial relationship (Hargittai, Gallo, and Kane 2008), and in doing so may further characterize their interaction through the lens of balance-theoretic notions (Cartwright and Harary 1956; Heider 1958). This allows us to test different influences of dynamic notions of balance: Is a DNC blog more likely to cite another DNC blog? Is a DNC blog citing an RNC blog less likely to cite an RNC blog at the next time step? and so forth. In this article, we will assume that blogs designated by the DNC represent a cohesive group, blogs designated by the RNC represent a cohesive group, and the interaction between the two groups represents a negative relation.

4.2.1 Mixing

In the social network literature, a priori group partitioning in the model and group interaction is often known as mixing or nonrandom mixing. Hargittai, Gallo, and Kane (2008) hypothesize that bloggers cluster ideologically and thus will only link to other blogs with the same ideology. We may re-express this hypothesis as a type of assortative mixing process where blogs have an almost exclusive propensity to cite within-group and not across-group.

A counter-hypothesis arises from our a priori grouping of nodes along political lines, and the assumption that these two parties represent competing organizations. A reasonable assumption, given our population, is that between-group citations represent a negative relation, such that if a blog from the DNC cites a blog from the RNC it is an action performed to criticize or refute a claim made by the RNC (and vice versa). Under this assumption, it is natural to hypothesize that cross-group mixing reflects rivalry, and that the rate of such citations during the study period will be high. At the extreme limit in which blog citations are being primarily deployed to damage opponents rather than to boost allies, such cross-group citations should dominate within-group citations.

Thus, we propose two contending hypotheses for mixing:

Mixing Hypothesis 1: Bloggers prefer to support allies

Ceteris paribus, in-group ties will have significantly higher payoffs than cross-group ties.

Mixing Hypothesis 2: Bloggers prefer to attack opponents

Ceteris paribus, cross-group ties will have significantly higher payoffs than in-group ties.

4.2.2 Balance-theoretic influences

Cartwright and Harary (1956) introduced the concept of structural balance based on Heider’s (1958) theory of cognitive balance, which suggests a number of possible mechanisms that could plausibly affect actors’ choices regarding the formation or dissolution of ties in a contentious environment. Heider’s theory stems from Gestalt psychology, and posits that individuals attempt to maintain a specific set of consistency conditions among the valances they associate with individuals, objects, and relations (these collectively constituting a state called balance). Violations of balance are posited to be aversive, with actors attempting to resolve the violations by some combination of changed subjective perceptions (e.g., re-evaluating a positive association as a negative one) and objective changes to their environment (e.g., dissolving a positive relationship with a negatively viewed alter). In structural balance theory (BT), it is standard to make the additional assumptions that (1) there is a consensus view of the valance associated with particular objects or relations by each individual (e.g., there is agreement by all parties about whether a given tie is positive or negative), and (2) that effective resolution of imbalance occurs only through manifest actions (generally, tie formation, dissolution, or valance change).

Although we cannot directly measure the valance of citations in our network, both the nature of the milieux and the authors’ inspection of blog content suggest that links among bloggers with common party affiliation are generally positive in nature, and those crossing party lines are generally negative. Given the highly visible, institutionalized nature of blog party affiliations and the very public nature of bloggers’ interactions during the period, it is also reasonable to assume a high level of consensus among the actors involved regarding link valance. Given these assumptions, we may propose four hypotheses regarding actors’ link utilities based on structural balance (BT 1–4):

BT Hypothesis 1: Ally of an ally (in-group two paths)

 We hypothesize that the presence of an Inline graphic two path will, ceteris paribus, increase i’s utility for linking to k when i, j, and k have the same party affiliation. This follows from the BT prediction that a positive Inline graphic interaction associated with a positive Inline graphic interaction should lead to a positive Inline graphic evaluation, and increase the motivation for i to direct positive action toward k.

BT Hypothesis 2: Opponent of an ally/opponent of an opponent (cross-group two paths)

 We hypothesize that the presence of an Inline graphic two path will, ceteris paribus, increase i’s utility for linking to k when i has the same party affiliation as exactly one of j and k, with the other belonging to the opposing party. This follows from BT predictions under two scenarios:

  • If i and j are allies and k a mutual opponent, a positive Inline graphic interaction associated with a negative Inline graphic interaction should lead to a negative Inline graphic evaluation, and increase the motivation for i to direct negative action toward k. (By assumption, cross-group links are negative.)

  • If i and k are allies and j a mutual opponent, a negative Inline graphic interaction associated with a negative Inline graphic interaction should lead to a positive Inline graphic evaluation, and increase the motivation for i to direct positive action toward k. (By assumption, within-group links are positive.)

BT Hypothesis 3: Reciprocity (ally)

 We hypothesize that the presence of a Inline graphic edge will, ceteris paribus, increase i’s utility for linking to j when i and j have the same party affiliation. This follows from the BT prediction that a positive Inline graphic interaction will lead to a positive Inline graphic evaluation, and increase the motivation for i to direct positive action toward j.

BT Hypothesis 4: Reciprocity (hostile)

 We hypothesize that the presence of a Inline graphic edge will, ceteris paribus, increase i’s utility for linking to j when i and j have the opposite party affiliation. This follows from the BT prediction that a negative Inline graphic interaction will lead to a negative Inline graphic evaluation, and increase the motivation for i to direct negative action toward j.

We note that whereas, for example, within-group and between-group reciprocity are both predicted by BT under our assumptions, the specific mechanisms posited (e.g., mutual positivity versus mutual negativity) are nonidentical. If, for example, within-group ties are not viewed as strongly positive (or, variously, between-group ties are not viewed as strongly negative) by the bloggers, balance-theoretic mechanisms may encourage reciprocity or closure in some contexts but not others. By testing these hypotheses independently, we retain the ability to distinguish between balance-theoretic effects involving in-group and out-group ties.

4.2.3 Context and seasonality

Networks tend to have certain basic structural characteristics which should be accounted for in any network analysis (e.g., sender and receiver effects; Wasserman and Faust [1994]).

In a time-series context, it is known that there are certain seasonal and period effects that occur in any temporally collected data (Shumway and Stoffer 2006). Common seasonal effects in behavioral data collected within developed societies include daily and hourly effects (e.g., Monday, Tuesday, etc., and midnight versus midday). Below, we posit several temporally motivated hypotheses, which take into account the interaction between structural properties of the network under question and the daily fluctuations of human interaction, such as a differential propensity to update one’s links (an effortful procedure) over the course of the day.

Seasonality Hypothesis 1

 Butts and Cross (2009) found that the volatility of the blog networks changes with time of day, day of week, and period in the electoral cycle. Translating their notion of “volatility” into the present modeling framework, we posit that the degree of inertia in network structure (i.e., the lag effect) will vary systematically with time.

Seasonality Hypothesis 2

 We suspect that overall propensity to send links will vary over time. We argue that ego’s linking to others involves a search process, and is consumptive of attentional/energetic resources. Resource availability varies over time, and with it perhaps the total number of links maintained by each blog.

Seasonality Hypothesis 3

 We propose that behavioral factors might change with time and context. Specifically, we hypothesize a mechanism of selective salience, in which the propensity to create ties within or across groups increases during important events in the election cycle (Table 1).

5 Methodology

This work employs the DNR methodology elaborated by Almquist and Butts (Forthcoming) for large dynamic data sets, which builds on the Exponential-Family Random Graph (Holland and Leinhardt 1981a, 1981b; Strauss and Ikeda 1990; Snijders et al. 2006; Butts 2008a; Cranmer and Desmarais 2011), TERGs (Robins and Pattison 2001; Hanneke, Fu, and Xing 2010; Desmarais and Cranmer 2011; Desmarais and Cranmer 2012), and network regression (Krackhardt 1987a, 1987b, 1988) literatures. This model family is particularly appealing in our context because it is very natural to model citation dynamics as a binary choice process, and this framework allows us to explore the mechanisms that predict whether one blogger chooses to cite another blogger.

We begin by discussing the necessary statistical details needed to connect our inferential framework with our theoretical framework. We then follow this discussion with the operationalized version of the mechanisms discussed in Section 4.2.

5.1 Inferential Framework: DNR

A standard inferential framework for network analysis is that of Exponential-Family Random Graph Modeling (ERGMs) (Holland and Leinhardt 1981a; Cranmer and Desmarais 2011, etc.). Sometimes misconstrued as referring to a narrow class of models, the ERGM framework is better understood as a general approach to the representation of statistical models for network data. In the case of networks on a fixed set of individuals, we may write the likelihood of observing a given network in exponential family form as

graphic file with name mpt016m3.jpg (3)

where A is a random network (represented by its adjacency matrix) on n nodes, drawn from some set 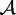Inline graphic of potentially observable networks. (In the present context, 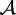Inline graphic is the set of all directed networks on the set of RNC and DNC blogs.) X is then a set of covariates, θ is a vector of real-valued parameters, t is a vector of graph statistics on a and X (e.g., structural properties and covariate effects), and Inline graphic is an indicator function that returns 1 if a is in the set of potentially observable graphs, and 0 otherwise. Inline graphic is simply the sum of the numerator over all observable networks; a normalizing factor, Inline graphic, ensures that the total probability of all potentially observable graphs sums to 1.

In the dynamic context, temporal ERGMs (TERGMs) extend the above by modeling each point in a network time series in ERGM form. Almquist and Butts (Forthcoming) demonstrate that if one assumes the network only depends upon the past history and/or on exogenous factors (i.e., the covariate set X), one can show that the above model form simplifies to logistic network regression. Drawing on ERG theory, they show that this allows us to write the conditional log-odds of an edge in logistic form; that is,

graphic file with name mpt016m4.jpg (4)

In Section 4, we introduced the notation and theory of a dynamic logistic choice model. Under the assumptions of a logistic choice framework (equations (1) and (2)) and the independence assumptions of Section 4.1, it is clear that in our case the logistic choice model is indeed dynamic logistic network regression, where the inferred parameters represent the weights each blogger places on the elements of his or her payoff function (i.e., utilities). Thus, we can implement our decision theoretic model for blog dynamics by expressing our hypothesized mechanisms (payoff function components) in terms of model statistics (t), and fitting the resulting lagged-logistic regression model to estimate the unknown components of the utility function.

5.2 The Dynamic Decision Model

To operationalize our boundedly rational choice model of blog network dynamics, we must express our hypothesized mechanisms in terms of statistics that measure the inputs to each actor’s payoff function. Here, we consider each group of mechanisms, and discuss how they are implemented within the model.

5.2.1 Mixing terms

Methods for modeling nonrandom mixing have been known for some time; for our purposes, we employ a method similar to Morris (1991), and use a type of block model to represent the two groups (see Wasserman and Faust [1994] for a full review of the literature on block modeling). In doing so, we impose four parameters on the model: one parameter for each group’s internal interactions, and one parameter for each group’s tendency to send ties to the other. (Note that, since this is a directed network, RNC → DNC is different than DNC → RNC.) We assume these two groups represent competing organizations and thus expect to see a higher propensity for within-group citation than between-group citation.

The mixing terms are modeled as a block matrix, such that the model contains a variable for the number of edges in each of the four categories: DNC → DNC edges, RNC → RNC edges, DNC → RNC edges, and RNC → DNC edges. This set of terms is jointly identifiable, taking the place of the standard edge (count of the number of edges in the model) or density (number of edges divided by the total number of possible edges) terms frequently encountered in ERG models (Goodreau et al. 2008).

Expressed in the language of mixing terms, our competing interaction hypotheses can be restated as follows:

Mixing Hypothesis 1

 The weights of the in-group effects will be large and positive and cross-group effects will be small or negative; that is, the model will favor in-group but not cross-group mixing.

Mixing Hypothesis 2

 The weights of the in-group effects will be smaller than the cross-group effects; that is, the model will favor cross-group mixing.

5.2.2 Heiderian terms

Balance Theory is naturally testable in a dynamic network context and may be constructed from classic network decompositions such as two-stars and reciprocal links (see Wasserman and Faust 1994). Our balance-theoretic hypotheses can then be restated in operational terms as follows:

BT Hypothesis 1: Ally of an ally (in-group two paths)

 A count of the number of in-group two paths from i to k is employed as a predictor of the Inline graphic edge in the subsequent time period. We expect the weight on this term to be positive and significant.

BT Hypothesis 2: Opponent of an ally/opponent of an opponent (cross-group two paths)

 A count of the number of cross-group two paths from i to k is employed as a predictor of the Inline graphic edge in the subsequent time period. We expect the weight on this term to be positive and significant.

BT Hypotheses 3 and 4 Reciprocity (friendly/hostile)

 Indicators for Inline graphic edges are employed as predictors of the Inline graphic edge in the subsequent time period; distinct parameters are employed for in-group versus cross-group edges. We expect these terms to have positive signs.

5.3 Network Effects and Seasonality

It is often hypothesized that structural factors may increase or decrease the payoffs associated with edge formation. Two oft-studied structural effects are those of alter indegree and outdegree (this is sometimes known as preferential attachment; see Merton [1968]). We also include a clique comembership term to account for potential clustering effects3 (see, e.g., Wasserman and Faust 1994). As these mechanisms require actors to attend to broader events in the social network, we posited above that we might expect the nature of these effects to change dynamically with the time of day. This may be interpreted as an interaction effect between the seasonality dummy and the structural parameters. Below, we will discuss the details of the seasonality terms employed in this article.

5.3.1 History and seasonality

The effects of past interaction history and seasonality are hypothesized to act as follows:

Seasonality Hypothesis 1

 There will be substantive and large inertial effect; that is, the lag term will be large and significant.

Seasonality Hypothesis 2

 We test the hypothesis that the overall propensity to send links will vary over time via an interaction between hourly fixed effects and receiver effect and hourly fixed effects and the inertia term. We expect these to be important terms in the model, to be large and significant.

Seasonality Hypothesis 3

 We test the “selective salience” hypothesis with nine period effects; specifically, we expect there to be increase in activity during PreCon, DNCCon, RNCCon, Deb, Elec and decrease in activity during InterCon, PreDeb, PreElec, and PostElec (see Table 1 for details).

To model hourly seasonality, we employ three dummy variables for each hour (06, 12, and 18 in the day, with hour 0 as the reference group (Inline graphic).

To model weekly seasonality, we employ techniques from Harmonic Regression (Shumway and Stoffer 2006).4 This amounts to assuming the influence of a given week in a month is periodic (see Section 6.2 for more details).

5.4 Computational Considerations

All code for this article was written and executed in the R environment (R Development Core Team 2010). Although one advantage of the logistic framework is that one can implement it with standard statistical software such as R, STATA, SPSS, etc., for small networks, scalability usually requires a special-purpose implementation. Naive implementation of the logistic form simply involves vectorizing the adjacency matrix at each time point; this vector will grow with N2, however, often becoming larger than most stand-alone logistic regression functions are capable of handling. In order to manage this difficulty, we take advantage of the additive nature of the log-likelihood, decomposing it into a series of manageable chunks and then optimizing the combined values using trust-region methods (Geyer 2009) in order to obtain the maximum log-likelihood parameter estimates. All sufficient statistics are either built directly or employ modifications of the tools made available in the R package sna (Butts 2008b).5

6 Analysis

We begin by employing standard model selection techniques (selection by Bayesian information criterion [BIC]) and adequacy selection to determine the mechanisms that appear to be active in shaping actors’ choice processes; after identifying the relevant mechanisms, we examine the parameters of the best-fitting model to interpret the implied utility function. A natural way to begin our analysis is to first construct a simple, baseline model which contains only the mixing terms and seasonal effects (Model 1). We then add a single lag term (Model 2), followed by network control effects (Model 3). Next, we add in the Heiderian mechanisms (Model 4); finally, we add in period effects (Model 5), and hourly interaction terms with sender and inertia (Model 5). The parameter estimates and BIC scores for each of these models may be found in Table 2.

Table 2.

Five models for dynamic logistic choice of inter- and intra-group blog citation networks in the 2004 US presidential election ordered by BIC

Model 1 Model 2 Model 3 Model 4 Model 5
BIC 598094.826 42209.8184 41863.9425 41246.5485 40310.1217
DNC −1.7960* −5.8729* −5.9459* −6.0266* −4.5198*
RNC −0.9401* −4.0849* −4.1857* −4.4320* −3.2081*
DNC → RNC −3.9527* −6.9714* −6.9960* −6.9992* −5.4081*
RNC → DNC −3.3602* −5.2977* −5.4960* −5.7088* −4.5039*
Inline graphic 10.8933* 10.7390* 10.4363* 10.3164*
Cluster 0.3402*
Receiver 0.0633* 0.0353* 0.0470*
Sender −0.0523* −0.0321* −0.0231*
Group-2-Path 0.2165* 0.2125*
Cross-Group-2-Path 0.5393* 0.3316*
Group-Reciprocity −0.5401* −0.5108*
Between-Group-Reciprocity 0.3752 0.6299*
Inline graphic 0.0016 0.0604* 0.0580* 0.0525* 0.1048*
Inline graphic 0.0363* 0.1593* 0.1450* 0.1228* −0.1584*
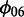Inline graphic −0.0933* −0.5516* −0.5128* −0.4488* −0.1209*
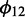Inline graphic −0.0922* −0.5899* −0.5507* −0.4841* −0.3459*
Inline graphic −0.0936* −0.6887* −0.6496* −0.5791* −0.4670*
Receiver Inline graphic −0.1169*
Receiver Inline graphic −0.1826*
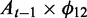Receiver Inline graphic −0.1102
Inline graphic 0.2045*
Inline graphic −0.2980*
Inline graphic 0.0704
DNCCon −1.9237*
InterCon −1.9549*
RNCCon −1.9511*
PreDeb −1.8196*
Deb −1.8898*
PreElec −1.9294*
Elec −2.4212*
PostElec −1.9480*
Open in a new tab

Notes. Significant at “*” 0.05 p-value level under a z-test unless otherwise specified. Inline graphic represent daily effects and Inline graphic represent hourly effects.

6.1 Model Adequacy Check

We start by employing the BIC model selection criterion (Schwarz 1978) to evaluate competing models, where the model with the lowest BIC is chosen as the preferred model. The relative performance of our candidate models provides us with the first evidence regarding our hypotheses: if a given effect does not appear in the preferred model, then the data suggest that the associated mechanism is not influential in the actors’ choice processes. Hypothesized effects not found in the best-fitting model are thus rejected.

Although likelihood-based model selection criteria such as the BIC are effective in evaluating the relative performance of competing models within a specified set, they do not evaluate the adequacy of the selected model in substantive terms. To verify that our selected model is adequately able to reproduce the basic features of our data set, we follow model selection with simulation-based adequacy assessment (Hunter, Goodreau, and Handcock 2008; Almquist and Butts Forthcoming). The method employed is as follows. First, we choose a set of Graph Level Indices (GLI) (Anderson, Butts, and Carley 1999) capturing various structural features of the blog networks. Given this set of network measures, we use the best-fitting model at each time step to simulate (forecast) the blog network to be observed at the next time step. The distribution of the network properties under the predicted networks are then compared with the values actually observed. Although we do not expect to perfectly forecast network evolution, we expect our model to produce predictions which are generally compatible with the evolving data.

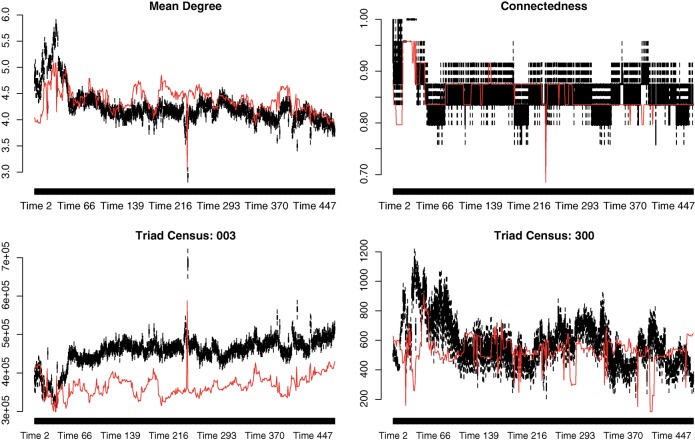
For present purposes, we evaluate model performance with respect to the following graph-level indices: density (known to be a very important graph statistic; see Wasserman and Faust [1994]); Krackhardt’s connectedness index (a measure of reachability and to what extent information might flow through the network; see Krackhardt [1994]); mean indegree (receiver) and mean outdegree (sender) (a common graph statistic, involved in theories of preferential attachment [receiver] and expansiveness [sender]; see Wasserman and Faust [1994]); the “null” or “empty” triad (designated as type 003 in Holland and Leinhardt’s typology a measure of isolates or actors not engaged in a given period, Fig. 2; see Wasserman and Faust [1994]); and finally the number of triangles or cliques (the complete triad, 300 in Holland and Leinhardt’s typology, an indicator of clustering or local interaction, Fig. 2; see Wasserman and Faust [1994]). The realized and forecast values for these statistics are shown in Fig. 3.

Fig. 2.

Fig. 2

Open in a new tab

Leinhardt’s typology of the triad isomorphism classes labeled by the number of Mutual, Asymmetric, and Null dyads within the triad and letters represent orientation (this is referred to as the MAN labeling). See Wasserman and Faust (1994, 564–9) for full details.

Fig. 3.

Fig. 3

Open in a new tab

Graph-level index comparison for one-step one-lag network logistic regression for Model 5 with hundred simulations at each time point.

We can see from Fig. 3 that Model 5 is very effective in capturing the basic trend for density, mean indegree/outdegree, triangles, and connectedness (Fig. 3 and Table 2), with observed values generally close to or within the forecast interval. The model forecast for null triads also tracks the trend, although the predicted value is somewhat higher than the observed. Overall, the adequacy checks suggest that the model captures the main features of the blog dynamics, and we therefore move forward with our analysis.

6.2 Findings

Parameter estimates for Model 5 are shown in Table 2. It is important when interpreting the parameters of Model 5 to recall that many effects are necessarily simultaneous, and should be viewed as a group. Take, for example, the mixing terms: although two of the mixing terms are negative, they cannot be interpreted without taking into account the lag term, which is larger than any one of the mixing terms and positive. Thus, although citation is costly in general, there is still a net tendency to cite those one has cited in the previous time step. We see that the base propensity for within-group blog-to-blog citation is higher for the RNC than DNC, and that the two groups are about equally likely to send cross-group ties (on an edgewise basis).

In terms of our hypotheses, we confirm Mixing Hypothesis 1 that within-group linking is more likely than between-group linking and refute Mixing Hypothesis 2 (positing the opposite). The two groups have similar levels of between-group linking. Payoffs to in-group citations are higher than cross-group citations; note that this is less true for the RNC on a per-tie basis, with the likelihood of interaction increasing from 0.01 to 0.04 for DNC and RNC, respectively. Since there are more DNC than RNC blogs, this may reflect the lower substitutability of RNC blogs than their DNC counterparts.

We confirm our balance-theoretic hypotheses of ally-of-ally and opponent-of-ally/opponent-of-opponent connections; two-path embeddedness acts as a citation incentive both within and across groups (Table 2: Group-2-Path, Cross-Group-2-Path), in line with what would be expected from the structural balance. In contrast with this result, we find that reciprocity does not follow a classic balance-theoretic pattern. Ceteris paribus, incoming ties from one’s own allies tend to reduce the propensity of a returning citation, whereas those of one’s opponents increase this propensity (Table 2: Group-Reciprocity, and Between-Group-Reciprocity; with an increased likelihood of interaction from 0.38 to 0.652, significantly different under a z-test). Although the former result is inconsistent with a positive, exchange-theoretic notion of citation, this is compatible with the notion that (1) citation within groups is redundant (or event deferential), and hence poorly reciprocated, whereas (2) citation between groups tends to take the form of critique or conflict, in which “returning fire” is highly incentivized. This finding underscores the importance of considering group or institutional context when theorizing the nature and role of reciprocating mechanisms.

We confirm Seasonality Hypothesis 1, finding that inertia is a strong and persistent effect in this network. To interpret the baseline payoff effects of the seasonal components and their interaction effects, we have plotted the hourly and weekly baseline (Figs. 4 and 5). Figure 4 demonstrates that the baseline propensity to form an edge evolves in a systematic and periodic fashion as a superposition of daily and weekly cycles. The propensity to form ties to others is highest at the start of the day, and declines as the day goes on; the effect also builds and recedes during the week, and is at its lowest during the weekend. Figure 5 allows us to see how other mechanisms interact with daily seasonality: inertia is at its highest in the early/mid-morning, and in the early evening. Sensitivity to others’ popularity is at its highest at night (when tie formation tendencies are also their strongest); this suggests that bloggers’ activities do not reflect a uniform pattern of behavior, but instead show a pattern of attention shift tied to daily and weekly activity patterns. The specific pattern observed is consistent with an “information processing cycle,” in which actors begin the day by reactively posting ties to other blogs widely attended to by peers, then shift into a period of media consumption (and low posting activity), a period of link purging and posting ties to new primary sources (rather than other blogs), and finally a period of quiescence before the cycle begins anew. This regular shift in the nature of activity leads to a network that does not evolve in a uniform, even manner, but that instead “pulses” as new information is drawn in, old ties are removed, and new ties are formed in response to the day’s events. Such a pattern is a marked departure from the temporally uniform behavior assumed by most current models of group dynamics.

Fig. 4.

Fig. 4

Open in a new tab

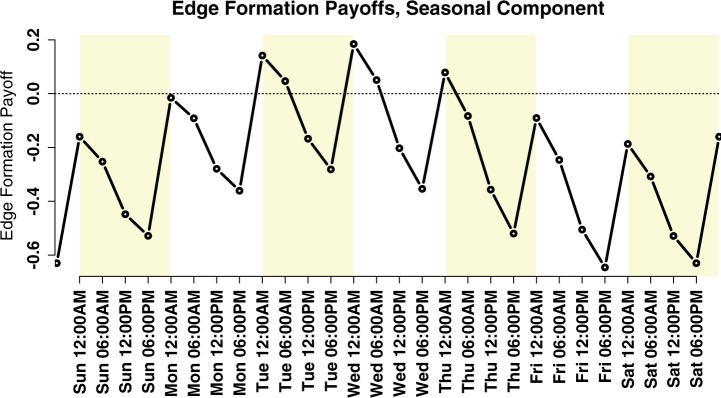
Visualization of the baseline edge formation payoffs by over one week.

Fig. 5.

Fig. 5

Open in a new tab

Visualization of the interaction edge formation payoff effects over a twenty-four-hour period.

Finally, we obtain mixed results for the Selective Salience Hypothesis (recalling that we have to interpret the associated terms in relation to the lag term). We see that the propensity to form ties is greatest during the PreCon and DNCCon periods, being generally stable during much of the rest of the electoral cycle (the exception being election day, when there is a noticeable decrease in edge creation). We thus see little to no evidence of “important” events fostering edge indication, and some suggestion that very important events (e.g., the election) may reduce citations within the blog network. Interpreted in terms of the “information processing cycle” described above, this may reflect increasing emphasis during such periods on attention to external sources, and a concomitant reduction in intra-network activity.

7 DNR Compared to TERGMs with Dependence

A common critique of conditional logistic analysis is that the conditional independence assumptions required fail to capture important dependence within actors. To this end, we compared the best-fitting DNR model to a full TERGM with all the terms in the DNR plus four standard ERGM terms commonly used in the social network literature. The TERG model we use for comparison with the best-fitting DNR model includes effects for Geometrically Weighted Indegree, Geometrically Weighted Outdegree, Geometrically Weighted Shared Partners, and a three-cycle term (Snijders et al. 2006; Robins et al. 2007; Goodreau, Kitts, and Morris 2009). To fit the full TERG model, we use the bootstrap pseudo-likelihood approach suggested by Cranmer and Desmarais (2011) and Handcock et al. (2008) for computing the sufficient statistics and performing the one-step-ahead prediction/simulation.6 We compare the one-step-ahead prediction for the four statistics proposed in Section 6.1 (Fig. 3) for the DNR model to the full TERG model (Fig. 6). The prediction results are strikingly similar; however, the DNR model performs slightly better for mean degree, and we fail to attain a boost in the count of three cliques (Triad Census: 300) that we might expect to obtain via full TERG modeling. Our results suggest that while modeling dependence may be important for many social network models, especially in the static case, it is not so obvious that the gains in estimation/simulation/prediction for the temporal models are always justified, given the added complexity in estimation and interpretation of a TERGM with simultaneous dependence. Indeed, the poorer predictive performance of the dependence model in this case suggests that researchers should avoid employing models with conditional dependence terms without first checking them against a conditionally independent baseline. Although this caution is contrary to the usual intuition that the introduction of dependence terms will lead to superior performance, our experience is not unprecedented. Notably, Franzese, Hays, and Kachi (2012) showed that the logit model performed better in prediction for dynamic network analysis when compared with the Actor Oriented Models for many cases of interest. Determining when and where dependence terms are called for is clearly an important problem for further research.

Fig. 6.

Fig. 6

Open in a new tab

Graph-level index comparison for one-step one-lag TERGM with a hundred simulations at each time point.

8 Discussion and Conclusion

In this work, we have modeled the evolution of an online political interaction network as a logistic choice process, treating blog authors as boundedly rational actors engaged in choices regarding their outgoing citations (a discrete-time analog of Snijders [2001]). To implement this model, we have employed a type of lagged logistic network regression (see Almquist and Butts Forthcoming) that arises as a natural consequence of our assumed decision-making process. Drawing on existing ideas from the group behavior literature, we have identified a number of candidate mechanisms of potential relevance to the choice process. By fitting our decision model to the observed network data, we have been able to determine which of these mechanisms do, in fact, seem to influence individual choices, and to determine the nature of the influences in question. The result provides us with a composite picture of social behavior that, although familiar in many respects, highlights the need for a deeper conceptualization of the role of context effects—particularly temporal context—on group dynamics.

Among the anticipated findings, we see that our two groups of respective allies (the RNC and DNC credentialed blogs) have a greater propensity for in-group citation than between-group citation (consistent with Hargittai, Gallo, and Kane [2008]). We also find a tendency toward triadic closure within groups (the “ally of an ally” mechanism), as expected on balance-theoretic grounds. Interestingly, triadic closure is also observed across groups, an effect predicted by balance theory only where cross-group ties carry negative valance. On the other hand, reciprocity dynamics behave quite differently than balance would suggest: although bloggers reciprocate ties from opponents, they tend not to reciprocate ties from allies, as would be the case if within-group ties had uniformly positive implications. A potential resolution of these otherwise puzzling effects can be found in the differing nature of within-group and cross-group interaction. Cross-group interaction in our setting is generally rivalrous, and reciprocity generally an act of self-defense (with the “ally-of-an-opponent” akin to an act of “piling on” to an opponent attacked by an ally). On the other hand, within-group citation appears to have a more functional role, and may reflect an underlying hierarchy of information dissemination (accounting for both lower reciprocity and a tendency toward transitive closure). Fundamentally, our findings are consistent with the observation that the social meaning of a tie is dependent on group and/or institutional context, and that the dynamics of network evolution are sensitive to these distinctions. Developing a richer set of theoretical propositions to predict precisely when, and how, these distinctions will be made would seem to be an important topic for future work.

An even more basic lesson of our findings, however, is that individual behavior and group dynamics are not uniform, but governed by regular cycles that affect both the nature and extent of activity. Although we are used to thinking of nonhuman animals as being governed by diurnal and seasonal cycles, social scientists have been slow to recognize the role of cyclic influences on choice behavior and the dynamics of interaction. Although theorists as wide ranging as Sorokin (1957), Mayhew (1980), and Elder (1974) have argued for greater attention to the role of temporal and environmental context as determinants of social outcomes, these calls are at best poorly reflected in current social science research. Our findings suggest the seriousness of this gap: without considering temporal context, one is at a loss to account not only for individual choices, but for the evolution of the social system as a whole. To the extent that phenomena such as the “information processing cycle” posited here hold in other settings, omission of seasonal effects likewise hinders our ability to understand the functional characteristics of social systems, and thus to anticipate the effects of planned or unplanned interventions. Even online, the physical realities of daily life and the institutional settings in which persons and groups are embedded provide a powerful and dynamic influence on social evolution.

Funding

This work was supported in part by Office of Naval Research (ONR) award (# N00014-08-1-1015), National Science Foundation (NSF) awards (# BCS-0827027, # SES-1260798, and # OIA-1028394), and National Institute of Health (NIH)/National Institute of Child Health & Human Development (NICHD) award (# 1R01HD068395-01).

Acknowledgments

Authors’ note: The authors would like to thank the participants and organizers in the QMSS 2 Conference on Power, Decision Making, and Social Networks, University College, Dublin, Ireland; and the participants and organizers of the 4th Annual Political Networks Conference, University of Michigan (where this work won a best methodology poster award). The authors would also like to thank the anonymous reviewers for their kind and helpful suggestions. Finally, the authors would like to mention that the data and code are available at Almquist and Butts (2013a).

Footnotes

2Note that this could be further extended as a two-step decision process; that is, a blogger first decides whether to blog and second proceeds to make a decision as to who to link to, if anyone. Further, Almquist and Butts (Forthcoming) suggest an analytic framework in which this two-stage logistic choice process could be embedded; however, in the case observed in this article the bloggers are extremely active. There are only ten time points (out of 484) where not every blogger observed is posting, and of those only one time point where more than a single blogger is not posting. It is worth pointing out that in this framework it is possible to have isolates (i.e., individuals who blog, but do not cite any other blogs).

3For algorithmic details, see Eppstein, Löffler, and Strash (2010).

4Equation (5) is used to model daily seasonality (days within the week). We assume a classic “signal in noise” with a hidden periodic signal. If we assume there is a single sinusoid, we can model the weekly cycles as follows:
graphic file with name mpt016um1.jpg
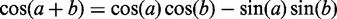Using the classic trigonometric formula Inline graphic, we can derive the terms we place in the model (equation (5)):
graphic file with name mpt016m5.jpg (5)

6Because pseudo-likelihood methods do not have an agreed-upon model selection criterion (Cranmer and Desmarais 2011)—that is, we cannot assess model fit using information-theoretic parametric measures of fit such as the BIC or Akaike information criterion (AIC)—we chose our model based first on preferred sufficient statistics used in the literature, and second that each of the terms was statistically significant.

References

  1. Adamic Lada A, Glance Natalie . 2005. The political blogosphere and the 2004 U.S. election: Divided they blog. Proceedings of the 3rd international workshop on link discovery. LinkKDD ’05 New York, USA: ACM, 36–43. [Google Scholar]
  2. Almquist Zack W, Butts Carter T. 2013a. Replication data for: Dynamic Network Logistic Regression: A logistic choice analysis of inter- and intra-group blog citation dynamics in the 2004 US presidential election. http://hdl.handle.net/1902.1/21916 IQSS Dataverse Network [Distributor] V1 [Version] (accessed September 2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Almquist Zack W, Butts Carter T. Logistic Network Regression for scalable analysis of networks with joint edge/vertex dynamics. Sociological Methodology. Forthcoming doi: 10.1177/0081175013520159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Ammori Marvin. A shadow government: Private regulation, free speech, and lessons from the Sinclair blogstorm. 2005. http://www.mttlr.org/voltwelve/ammori.pdf.
  5. Anderson Brigham S, Butts Carter T, Carley Kathleen. The interaction of size and density with graph-level indices. Social Networks. 1999;21:239–67. [Google Scholar]
  6. Butts Carter T. Social network analysis: A methodological introduction. Asian Journal of Social Psychology. 2008a;11:13–41. [Google Scholar]
  7. Butts Carter T. Social Network Analysis with SNA. Journal of Statistical Software. 2008b;24:1–51. doi: 10.18637/jss.v024.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Butts Carter T, Cross B Remy. Change and external events in computer-mediated citation networks: English language weblogs and the 2004 U.S. electoral cycle. Journal of Social Structure. 2009;10:1–29. [Google Scholar]
  9. Cartwright Dorwin, Harary Frank. Structural balance: A generalization of Heider’s theory. Psychological Review. 1956;63:277–93. doi: 10.1037/h0046049. [DOI] [PubMed] [Google Scholar]
  10. Cone Edward. The marketing of the president 2004. Baseline Magazine. 2003 [Google Scholar]
  11. Cranmer Skyler J, Desmarais Bruce A. Inferential network analysis with exponential random graph models. Political Analysis. 2011;19:66–86. [Google Scholar]
  12. Desmarais B A, Cranmer S J. Statistical mechanics of networks: Estimation and uncertainty. Physica A: Statistical Mechanics and Its Applications. 2012;391:1865–76. [Google Scholar]
  13. Desmarais Bruce A, Cranmer Skyler J. IEEE Computer Society; 2011. Forecasting the locational dynamics of transnational terrorism: A network analytic approach. Proceedings of the European Intelligence and Security Informatics Conference (EISIC) [Google Scholar]
  14. Drezner Daniel W, Farrell Henry. Blogs, politics, and power: A special issue of Public Choice. Public Choice. 2008;134:1–13. [Google Scholar]
  15. Elder Glen H. Children of the Great Depression: Social change in life experience. Chicago: University of Chicago Press; 1974. [Google Scholar]
  16. Eppstein David, Löffler Maarten, Strash Darren. Listing all maximal cliques in sparse graphs in near-optimal time. In: Kyung-Yong Chwa Otfried Cheong,, Park Kunsoo., editors. Algorithms and computation. 2010. Vol. 6506 of Lecture Notes in Computer Science, 403–14. Berlin, Heidelberg: Springer. [Google Scholar]
  17. Franzese Robert J, Jr, Hays Jude C, Kachi Aya. Modeling history dependence in network-behavior coevolution. Political Analysis. 2012;20:175–90. [Google Scholar]
  18. Geyer Charles J. Trust: Trust region optimization. 2009. R package version 0.1-2. http://www.stat.umn.edu/geyer/trust/ (accessed September 2012) [Google Scholar]
  19. Goffman Erving. Presentation of self in everyday life. Garden City, NY: Doubleday Anchor Books; 1959. [Google Scholar]
  20. Goodreau Stephen M, Kitts James A, Morris Martina. Birds of a feather, or friend of a friend? Using exponential random graph models to investigate adolescent social networks. Demography. 2009;46:103–25. doi: 10.1353/dem.0.0045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Goodreau Steven M, Handcock Mark S, Hunter David R, Butts Carter T, Morris Martina. A statnet tutorial. Journal of Statistical Software. 2008;24:1–26. [PMC free article] [PubMed] [Google Scholar]
  22. Handcock Mark S, Hunter David R, Butts Carter T, Goodreau Steven M, Morris Martina. statnet: Software tools for the representation, visualization, analysis and simulation of network data. Journal of Statistical Software. 2008;24:1–11. doi: 10.18637/jss.v024.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hanneke Steve, Fu Wenjie, Xing Eric P. Discrete temporal models of social networks. Electronic Journal of Statistics. 2010;4:585–605. [Google Scholar]
  24. Hargittai Eszter, Gallo Jason, Kane Mathew. Cross-ideological discussions among conservative and liberal bloggers. Public Choice. 2008;134:67–86. [Google Scholar]
  25. Heider Fritz. The psychology of interpersonal relations. Hillsdale, London: Lawrence Erlbaum Associates, Publishers; 1958. [Google Scholar]
  26. Holland Paul W, Leinhardt Samuel. An exponential family of probability distributions for directed graphs. Journal of the American Statistical Association. 1981a;76:33–50. [Google Scholar]
  27. Holland Paul W, Leinhardt Samuel. An exponential family of probability distributions for directed graphs: Rejoinder. Journal of the American Statistical Association. 1981b;76:62–65. [Google Scholar]
  28. Howard Philip N. Deep democracy, thin citizenship: The impact of digital media in political campaign strategy. Annals of the America Academy of Political and Social Sciences. 2005;597:153–70. [Google Scholar]
  29. Hunter David R, Goodreau Steven M, Handcock Mark S. Goodness of fit of social network models. Journal of the American Statistical Association. 2008;103:248–58. [Google Scholar]
  30. Kerbel Mathew R, David Bloom Joel. Blog for America and civic involvement. Harvard International Journal of Press/Politics. 2005;10:3–27. [Google Scholar]
  31. Krackhardt David. Cognitive social structures. Social Networks. 1987a;9:109–34. [Google Scholar]
  32. Krackhardt David. QAP partialling as a test of spuriousness. Social Networks. 1987b;9:171–86. [Google Scholar]
  33. Krackhardt David. Predicting with networks: Nonparametric multiple regression analyses of dyadic data. Social Networks. 1988;10:359–82. [Google Scholar]
  34. Krackhardt David. Graph theoretical dimensions of informal organizations. In: Carley Kathleen M, Prietula Michael J., editors. Computational organization theory. Hillsdale, NJ: Lawrence Erlbaum Associates; 1994. pp. 89–111. [Google Scholar]
  35. Mayhew Bruce H. Structuralism versus individualism: Part I, shadowboxing in the dark. Social Forces. 1980;59:335–75. [Google Scholar]
  36. McFadden Daniel. Conditional logit analysis of qualitative choice behavior. In: Zarembka Paul., editor. Frontiers in Econometrics. New York: Academic Press; 1974. pp. 105–42. [Google Scholar]
  37. McFadden Daniel. The Mathematical Theory of demand models. In: Stopher Peter R, Meyburg Arnim H., editors. Behavioral travel-demand models. Lexington, MA: Lexington Books; 1976. [Google Scholar]
  38. McPherson Miller, Smith-Lovin Lynn, Cook James M. Birds of a feather: Homophily in social networks. Annual Review of Sociology. 2001;27:415–44. [Google Scholar]
  39. Merton Robert K. The Matthew effect in science. Science. 1968;159:56–63. [PubMed] [Google Scholar]
  40. Morris Martina. A log-linear modeling framework for selective mixing. Mathematical Biosciences. 1991;107:349–77. doi: 10.1016/0025-5564(91)90014-a. [DOI] [PubMed] [Google Scholar]
  41. R Development Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2010. Vienna, Austria: R Foundation for Statistical Computing. http://www.R-project.org (accessed September 2012) [Google Scholar]
  42. Rainie Lee, Cornfield Michael, Horrigan John. Washington, DC; 2005. The Internet and campaign 2004. Technical Report. The Pew Research Center for the People and the Press: Internet and American Life Project. [Google Scholar]
  43. Robins Garry, Pattison Philippa. Random graph models for temporal processes in social networks. Journal of Mathematical Sociology. 2001;25:5–41. [Google Scholar]
  44. Robins Garry, Pattison Pip, Kalish Yuval, Lusher Dean. An introduction to exponential random graph (p*) models for social networks. Social Networks. 2007;29:173–91. [Google Scholar]
  45. Schwarz Gideon E. Estimating the dimension of a model. Annals of Statistics. 1978;6:461–4. [Google Scholar]
  46. Shumway Robert H, Stoffer David S. Time series analysis and its applications. 2nd ed. New York: Springer; 2006. [Google Scholar]
  47. Snijders Tom A B. Stochastic actor-oriented models for network change. Journal of Mathematical Sociology. 1996;21:149–72. [Google Scholar]
  48. Snijders Tom A B. The statistical evaluation of social network dynamics. In: Sobel M E, Becker M P, editors. Sociological methodology. Boston; London: Basil Blackwell; 2001. pp. 361–95. [Google Scholar]
  49. Snijders Tom A B, Duijn M A J Van. Simulation for statistical inference in dynamic network models. In: Conte R, Hegselmann R, Terna P, editors. Simulating social phenomena. Berlin: Springer; 1997. pp. 493–512. [Google Scholar]
  50. Snijders Tom A B, Pattison Philippa E, Robins Garry L, Handcock Mark S. New specifications for exponential random graph models. Sociological Methodology. 2006;36:99–153. [Google Scholar]
  51. Sorokin Pitrim A. Social and cultural dynamics. Boston, MA: Porter Sargent; 1957. [Google Scholar]
  52. Strauss David, Ikeda Michael. Psuedolikelihood estimation for social networks. Journal of the American Statistical Association. 1990;85:204–12. [Google Scholar]
  53. Wall Melissa. Blogs of war. Journalism. 2005;6:153–72. [Google Scholar]
  54. Wasserman Stanley, Faust Katherine. Social network analysis: Methods and applications. New York: Cambridge University Press; 1994. [Google Scholar]
  55. Wellman Barry. Computer networks as social networks. Science. 2001;293:2031–4. doi: 10.1126/science.1065547. [DOI] [PubMed] [Google Scholar]
  56. Woodly Deva. New competencies in democratic communication? Blogs, agenda setting, and political participation. Public Choice. 2008;134:109–23. [Google Scholar]

Articles from Political Analysis are provided here courtesy of Oxford University Press

RESOURCES