Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Oct 15.
Published in final edited form as: Psychol Sci. 2013 Aug 6;24(10):2013–2019. doi: 10.1177/0956797613482944

Training the Approximate Number System Improves Math Proficiency

Joonkoo Park 1, Elizabeth M Brannon 1,2
PMCID: PMC3797151  NIHMSID: NIHMS460715  PMID: 23921769

Abstract

Humans share with nonhuman animals an approximate number system (ANS) that permits estimation and rough calculation of number without symbols. Recent studies show a correlation between the acuity of the ANS and symbolic math performance throughout development and into adulthood, suggesting that the ANS may serve as a cognitive foundation for the uniquely human capacity for symbolic mathematics. Such a proposition leads to the untested prediction that training aimed at improving ANS performance will transfer to improvement in symbolic mathematics. Here, in two experiments, we show that ANS training on approximate addition and subtraction of arrays of dots, selectively improves symbolic addition and subtraction. This finding strongly supports the hypothesis that complex math skills are fundamentally linked to rudimentary preverbal quantitative abilities, provides the first direct evidence that ANS and symbolic math may be causally related, and raises the possibility that interventions aimed at the ANS could benefit children and adults who struggle with math.

Keywords: Number comprehension, mathematical ability

Introduction

Symbolic arithmetic is unique to humans. In literate societies, people learn symbolic arithmetic in school and continue to rely on basic symbolic calculations throughout life for essential activities like grocery shopping, tracking finances, and managing time. Yet, we are also equipped with an approximate number system (ANS) which allows us to represent number as imprecise noisy mental magnitudes without verbal counting or numerical symbols (Dehaene, 1999; Feigenson, Dehaene, & Spelke, 2004). The ANS is shared with other species and emerges early in human development (e.g., Libertus & Brannon, 2010; Wynn, 1998; Xu & Spelke, 2000). Its precision, the degree to which one numerosity or cardinal value of a set of items can be discriminated from another numerosity, gradually increases from infancy to adulthood (Halberda & Feigenson, 2008; Libertus & Brannon, 2010; Wynn, 1998; Xu & Spelke, 2000).

Several pieces of evidence suggest that the ANS is a cognitive foundation for higher-level symbolic mathematics (Dehaene, 1992; Feigenson et al., 2004; Gallistel & Gelman, 1992; Piazza, 2010). First, ANS acuity, typically measured by requiring participants to choose the numerically larger of two dot arrays, correlates with measures of symbolic mathematics both in adults and in children (e.g., DeWind & Brannon, 2012; Halberda, Ly, Wilmer, Naiman, & Germine, 2012; Halberda, Mazzocco, & Feigenson, 2008; Lyons & Beilock, 2011). Second, ANS acuity in preschool and kindergarten children predicts their performance on math achievement assays 2 months to 2 years later (Gilmore, McCarthy, & Spelke, 2010; Mazzocco, Feigenson, & Halberda, 2011b). Third, children with developmental dyscalculia, severe difficulties in symbolic mathematics, have lower numerical acuity compared to typically achieving children (Mazzocco, Feigenson, & Halberda, 2011a; Piazza et al., 2010).

If the ANS is a cognitive basis for symbolic math, then training that improves ANS precision should transfer to improvements in symbolic mathematics. Testing this hypothesis is important because it may provide critical support to the theoretical claims about the foundational role of the ANS and may also have practical implications for interventions aimed to improve math disability. Here, in two experiments, we ask whether performance on a non-symbolic arithmetic task that requires mentally manipulating ANS representations can be improved over multiple days of training, and more importantly whether enhancing ANS-based arithmetic improves symbolic arithmetic.

Experiment 1

Methods

We used a training study with a pre- and post-test design to assess whether performance on a non-symbolic arithmetic task would improve over repeated testing and whether improvement would transfer to symbolic arithmetic. We provide a brief overview of the methods here, with additional details about the study participants, tasks, and procedures in the Supplemental Online Material.

Adult participants (N=26) were trained over ten sessions to add or subtract large quantities of visually presented dot arrays without counting. Previous studies have shown that adults and children with no training on formal arithmetic are capable of approximate addition and subtraction (Barth et al., 2006; Barth, La Mont, Lipton, & Spelke, 2005; Knops, Viarouge, & Dehaene, 2009) and that performance on this task predicts symbolic math skills (Gilmore et al., 2010). On each trial of this non-symbolic approximate arithmetic training task, participants viewed an addition or subtraction animation of dot arrays ranging from 9 to 36 dots (Movie S1 in the Supplemental Online Material). On half of the trials, participants were cued to indicate whether the sum or difference was more or less than a third dot array. On the other half, they were cued to choose which of two arrays matched the sum or difference. These two trial types were used to keep participants engaged and to discourage task-specific strategies while leaving the core mental computation of adding and subtracting common in both conditions. The difficulty of the task was manipulated by varying the numerical distance between the correct answer and the alternative option in log-base2 scale (hence referred to as the log difference), and was titrated over the course of training to maintain accuracy between 70% and 85%.

To assess whether ANS-based training transfers to improvements in symbolic math, we gave all participants a set of multi-digit addition and subtraction problems both before the first training session and after the tenth training session. In this computerized self-paced symbolic math test, participants solved as many problems as possible within two 5-minute blocks. The same subjects were also given a multiple-choice vocabulary assay, which served as a control task in the pre- and post-test sessions. A second independent group of age-matched control subjects (N=26) were given the same pre- and post- symbolic math and vocabulary tests but were not given the intervening ANS-based training sessions.

Results and Discussions

Over the course of the ten training sessions, participants showed substantial improvement on the approximate arithmetic training task as indicated by a decrease in the log difference level (Fig. 1A). After the first session, participants on average were able to solve this task with 70-85% accuracy when the ratio between the correct answer and the alternative option was approximately 1:2 (log difference level of 0.95). After the tenth session, they were able to perform at the same accuracy when the ratio was approximately 2:3 (log difference of 0.60). This improvement in log difference level could be captured by significant linear (F1,24 = 39.52, p < 0.001) and quadratic (F1,24 = 51.91, p < 0.001) contrasts in a repeated-measures ANOVA.

Figure 1.

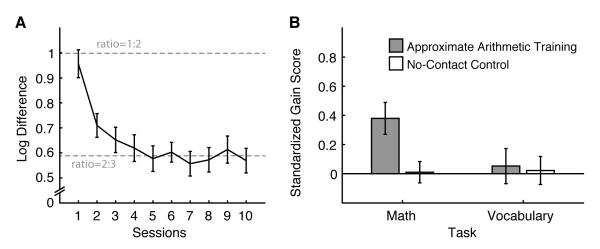
Figure 1

Open in a new tab

Training and transfer effects in Experiment 1. A. Improvement in non-symbolic approximate arithmetic performance over ten sessions. The vertical axis indicates the numerical distance between the correct answer and the alternative in a log scale. As participants progressed, they required more difficult comparisons to maintain 70-85% accuracy as indicated by lower log difference values. Solving a 1:2 ratio is equivalent to solving a log difference value of 1. A 2:3 ratio is roughly equivalent to a log difference value of 0.59. B. The standardized gain scores for symbolic math and vocabulary. Positive gain scores indicate better post-test compared to pre-test scores. On average, ANS training group solved 9.3 more problems correctly and the control group solved 0.3 more problems correctly after training. Error bar represents the standard error of the mean.

More importantly, the approximate arithmetic training resulted in a substantial improvement in symbolic math performance (Fig. 1B). The standardized gain score in math, defined by the post-test minus the pre-test performance measures divided by the standard deviation of the pre-test measures, was significantly greater in the training group compared to the control group which did not undergo the training (F1,50 = 7.87, p = 0.007, η2 = 0.136). These results suggest that improvement in non-symbolic arithmetic training transferred to improvement in symbolic arithmetic and that this improvement cannot be attributed to repeated testing on the symbolic math assay or familiarization with the test environment. Furthermore, neither the training nor the control group showed a gain score in vocabulary (F1,50 = 0.03, p = 0.875), which suggests that the improvement in math performance was selective.

A final analysis revealed that these results could not be explained by pre-existing individual differences between the training group and the control group in math or vocabulary scores. The same data were analyzed using ANCOVA on the post-test scores with pre-test scores as a covariate to control for any possible systematic bias between the two groups. In the math score, there was a significant effect of group (F1,48 = 5.93, p = 0.019) while the group-by-test score interaction was negligible (F1,48 = 0.04, p = 0.846). Again, this pattern was not observed in the vocabulary score which showed no differences in group (F1,48 = 0.00, p = 0.964) or the group-by-test score interaction (F1,48 = 1.58, p = 0.215).

These results show that improvement in an ANS-based non-symbolic approximate arithmetic training task over multiple sessions transfers to selective improvements in symbolic math. While these results are promising, the participants in the control group did not undergo any training, so it is possible that the training group participants could have improved in symbolic math skills as a result of mere increased confidence or willingness to expend more effort (i.e., placebo effects) (Jolles & Crone, 2012; Shipstead, Redick, & Engle, 2012). Experiment 2 addresses these concerns.

Experiment 2

Experiment 2 was designed to replicate and extend our findings in Experiment 1. First, to account for a possible placebo effect, we included a training group that was given general world knowledge training over multiple sessions. Second, we aimed to test the relative efficacy of the ANS-based training compared to other training based on symbolic numerical associations. A previous study by Lyons & Beilock (2011) showed that the capacity to accept or reject triads of Arabic numerals as being in the correct or incorrect order is a strong predictor of symbolic arithmetic performance and accounts for more variance than ANS acuity. This finding suggests that efficient processing of the relations among numerical symbols may be a critical factor in mathematical competence (Lyons & Beilock, 2011; Nieder, 2009). A third condition was therefore included to test whether numerical symbol order training improves symbolic math and to compare the relative efficacy of ANS training and numeral ordering training on improving symbolic math skills.

Methods

A new group of participants was recruited. During the pre and post-test sessions, participants received the symbolic math test and vocabulary test used in Experiment 1 as well as the numerical order judgment test similar to the one used in Lyons & Beilock (2011). They were then randomly assigned to the Approximate Arithmetic (AA) training group (N=16), the Numeral Ordering (NO) training group (N=14), or the Knowledge Training (KT) group (N=16). The AA group was trained with the non-symbolic approximate arithmetic task similar to the one described in Experiment 1. The NO group was trained with a task that required ordering sets of three Arabic numerals. Participants viewed triads of randomly ordered Arabic numerals that moved across the screen from one side to another (Movie S2 in the Supplemental Online Material). A mouse click on a triad changed the position of the three numbers. The task was to click on the triads until they were in an ascending (or descending) order before they disappeared off the screen. The difficulty of the task was manipulated by varying the speed of the triads traversing the screen (hence referred to as the item speed), and was titrated over the course of training to maintain accuracy between 80% and 90%. The KT group solved general world knowledge questions. Based on the results from Experiment 1, we conducted six rather than ten training sessions. See Supplemental Online Materials for details about the experimental methods.

Results and Discussions

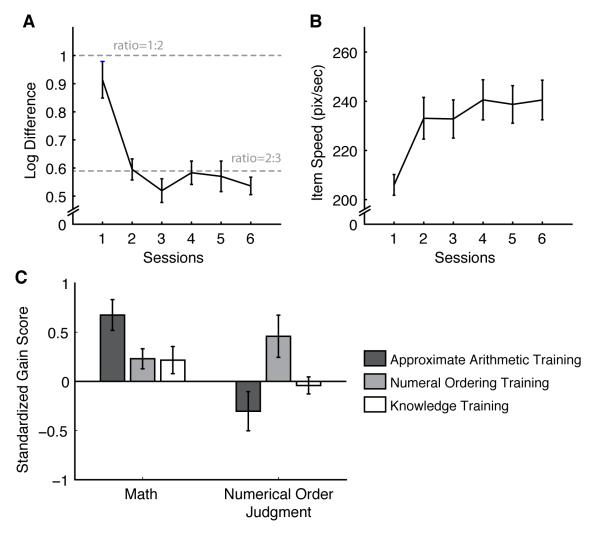
As in Experiment 1, there was substantial improvement on the non-symbolic approximate arithmetic task (Fig. 2A), with a significant decrease in the mean log difference level from 0.91 to 0.54 (linear effect in a repeated-measures ANOVA, F1,15 = 24.33, p < 0.001; quadratic effect, F1,15 = 20.85, p < 0.001). This means that participants’ ability to reliably solve the approximate arithmetic problems improved from solving a ratio close to 5:9 to a ratio close to 5:7. The NO training also showed substantial improvement (Fig. 2B), as indicated by a significant increase in the item speed from 206 to 240 pixels per second over the course of six sessions (linear effect in a repeated-measures ANOVA, F1,13 = 24.55, p < 0.001; quadratic effect, F1,13 = 19.21, p < 0.001).

Figure 2.

Figure 2

Open in a new tab

Training and transfer effects in Experiment 2. A. Improvement in non-symbolic approximate arithmetic training. B. Improvement in numeral ordering training. Item speed refers to the speed of each triad of Arabic numerals traversing the screen, while the task was to make the triads in an ascending or descending order before they disappeared off the screen. C. The standardized gain scores for symbolic math and accuracy in the numerical order judgment task. In the symbolic math problems, the AA group solved 15.4 more problems correctly on average, the NO group solved 5.1 more problems correctly, the KT group 5.0 more problems correctly after training.

To assess the transfer effects, we compared the standardized gain scores in symbolic math performance across the three training groups using one-way analysis of variance (ANOVA). As shown in Figure 2C, this analysis revealed significant differences on the math gain scores across the training groups (F2,43 = 3.728, p = 0.032, η2 = 0.148), which was driven by greater math improvement after the AA training compared to the NO training (t28 = 2.313, p = 0.028) and the KT (t30 = 2.199, p = 0.036). Interestingly, the NO training was no more effective than KT training in yielding symbolic math improvement (t28 = 0.074, p = 0.942). As in Experiment 1, these results could not be explained by pre-existing individual differences between the two training groups in math or vocabulary scores. The ANCOVA results showed a significant effect of group (F2,40 = 3.68, p = 0.034) in the math score while the group-by-test score interaction was negligible (F2,40 = 0.95, p = 0.397).

This improvement in symbolic math after the AA training seems to have been facilitated by the increase in participant’s speed to solve symbolic arithmetic problems. When the same analysis was performed using standardized gain score of the total number of problems attempted rather than total number of problems correctly solved, the gain score in the AA group still tended to be greater than the gain score in the KT group (t30= 2.324, p = 0.027) and the NO group (t28= 1.930, p = 0.064).

As shown in Figure 2C, ANOVA on the standardized gain scores in the accuracy of the numerical order judgment test (Lyons & Beilock, 2011) revealed significant differences in the three training groups (F2,43 = 4.854, p = 0.013, η2 = 0.184). This difference was driven by greater improvement after NO training compared to AA (t28 = 2.612, p = 0.014) and KT (t30 = 2.268, p = 0.031) training. In contrast there was little difference between the groups in the gain scores in vocabulary (F2,43 = 1.983, p = 0.150) or in the reaction time of the numerical order judgment task (F2,43 = 2.868, p = 0.068).

These results indicate that symbolic math improvement after the AA training cannot be attributed to a placebo effect. Moreover, this ANS-based training showed a much more prominent transfer effect than training designed to facilitate symbolic numerical associations (i.e., NO training). Despite the lack of transfer to symbolic arithmetic after NO training, consistent with Lyons & Beilock (2011) symbolic math scores were correlated with reaction time (r44 = −0.379, p = 0.009) and marginally correlated with accuracy (r44 = 0.285, p = 0.055) in the numerical order judgment task at pre-test.

Discussion

We demonstrated that training on a non-symbolic approximate arithmetic task improves performance over six to ten sessions of repeated training and that this improvement transfers to symbolic arithmetic performance. Furthermore, the amount of improvement in symbolic math was beyond the improvement observed from the passive control group and two other training conditions designed to improve world knowledge and symbolic numerical associations.

The current findings are novel and significant in several respects. First, participants showed significant improvement in an ANS-based approximate arithmetic task over multiple sessions of training. Another attempt to improve ANS performance using a numerical comparison task (rather than approximate arithmetic) showed little change in performance (DeWind & Brannon, 2012). Due to multiple differences in the paradigms, it is not possible to directly compare the two results. Nevertheless, we speculate that the difference is primarily due to differences between numerical comparison and approximate arithmetic. Alternatively, the current training program may have been more engaging due to two distinct trial types and the titration procedure which kept the task challenging. Findings from other training studies suggest that minimizing task-specific strategies and inducing active engagement via adaptive game-like paradigms may be critical for a training program (Jolles & Crone, 2012; Morrison & Chein, 2011). This adaptive and challenging design may have allowed participants to continue to improve.

Second, there was a striking transfer from our approximate addition and subtraction task which young children and even monkeys can perform (Barth et al., 2005; Cantlon & Brannon, 2007) to a symbolic math test which taps a uniquely human ability. Interestingly, this ANS-based training yielded much greater improvement in math compared to numeral ordering training which was aimed at facilitating associations between numerical symbols (see Fig. 2C). The relative efficacy of the AA training compared to the NO training in yielding a transfer effect in symbolic math performance is particularly noteworthy given a) the two tasks showed comparable improvements over training (see Figs. 2A and 2B), and b) the numerical order judgment ability is highly correlated with symbolic math performance (Lyons & Beilock, 2011). These patterns suggest that approximate arithmetic training has a specific transfer effect on symbolic math at least within the context of our study. These results strongly corroborate the proposition that non-symbolic arithmetic ability and symbolic mathematics share cognitive foundations. The current results go beyond the prior demonstrations of correlations between ANS and symbolic math and provide the first direct evidence that ANS may be causally influencing symbolic math.

Third, this demonstrated link between training on approximate arithmetic and symbolic mathematics suggests important directions for interventions aimed to improve math disability (Kucian et al., 2011; Räsänen, Salminen, Wilson, Aunio, & Dehaene, 2009; Wilson, Revkin, Cohen, Cohen, & Dehaene, 2006). For example, it may be possible to train at-risk children with low numerical competence even before their acquisition of symbolic number knowledge and expect improved symbolic math fluency later in development.

Future studies should explore the underlying cognitive mechanisms for this transfer effect. Why might improving the ANS-based approximate arithmetic yield benefits for symbolic mathematics? One possibility is that training on the non-symbolic arithmetic task may have a domain-specific effect on number representations. The ANS can be characterized as values represented as Gaussian distributions with means located along a mental number line. With increasing magnitude on the mental number line, there is greater overlap between values either due to logarithmic spacing or increasing spread of the Gaussian distributions (Feigenson et al., 2004; Gallistel & Gelman, 2000). An exciting possibility is that improvement in the non-symbolic approximate arithmetic task actually reflects a sharpening in the Gaussian distributions for each numerosity. Symbolic arithmetic may then benefit from increasing precision in the ANS representations that are mapped onto symbols and automatically retrieved.

Another possibility, although not mutually exclusive with the first case, is that the training and transfer effects in the current study reflect facilitations in cognitive processes related to addition and subtraction. For example, previous studies have suggested that approximate addition and subtraction may involve shifting of attention as if one is moving quantities along a mental number line (Knops et al., 2009; McCrink, Dehaene, & Dehaene-Lambertz, 2007). By this account, repeated training on non-symbolic arithmetic may yield improvements in visual attention or spatial working memory, a critical cognitive basis of symbolic arithmetic (see Raghubar, Barnes, & Hecht, 2010 for a recent review). Therefore, improvements in visuospatial processing required for addition and subtraction during the ANS-based training may in turn benefit symbolic arithmetic.

In sum, we provide the first evidence that ANS training improves symbolic arithmetic. This transfer effect, reliably demonstrated in two experiments, suggests that our evolutionarily and developmentally primitive nonverbal number sense, including the internal representation of approximate numbers and their operations, provides a critical foundation for uniquely human symbolic mathematics and may indicate new interventions for math educators.

Supplementary Material

Movie S1

Movie S1. Animation showing examples of non-symbolic arithmetic training trials. Participants responded with mouse clicks, but for technical reasons, mouse movement and clicks are not depicted in the movie. The text indicating the trial types was not shown to the participants and is only there for illustrative purposes.

Download video file (323.1KB, mov)
Movie S2

Movie S2. Animation showing examples of the numeral ordering training trials at different item speeds. Participants responded with mouse clicks, but for technical reasons, mouse movement and clicks are not depicted in the movie. The text indicating the item speed was not shown to the participants and is only there for illustrative purposes.

Download video file (1,008.3KB, mov)
Supplementary Materials

Acknowledgement

We thank Deborah Moon and Rachel Roberts for their assistance in data collection. This study was supported by the James McDonnell Scholar Award and NIH RO1 HD059108 to EMB and Duke Fundamental and Translational Neuroscience Postdoctoral Fellowship to JP.

References

  1. Barth H, La Mont K, Lipton J, Dehaene S, Kanwisher N, Spelke E. Non-symbolic arithmetic in adults and young children. Cognition. 2006;98(3):199–222. doi: 10.1016/j.cognition.2004.09.011. [DOI] [PubMed] [Google Scholar]
  2. Barth H, La Mont K, Lipton J, Spelke ES. Abstract number and arithmetic in preschool children. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(39):14116–14121. doi: 10.1073/pnas.0505512102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Cantlon JF, Brannon EM. Basic Math in Monkeys and College Students. PLoS Biol. 2007;5(12):e328. doi: 10.1371/journal.pbio.0050328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Dehaene S. Varieties of numerical abilities. Cognition. 1992;44(1,Äì2):1–42. doi: 10.1016/0010-0277(92)90049-n. [DOI] [PubMed] [Google Scholar]
  5. Dehaene S. The Number Sense: How the Mind Creates Mathematics. Oxford University Press; 1999. [Google Scholar]
  6. DeWind NK, Brannon EM. Malleability of the approximate number system: effects of feedback and training. Frontiers in human neuroscience. 2012;6 doi: 10.3389/fnhum.2012.00068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in cognitive sciences. 2004;8(7):307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
  8. Gallistel CR, Gelman R. Preverbal and verbal counting and computation. Cognition. 1992;44(1-2):43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
  9. Gallistel CR, Gelman R. Non-verbal numerical cognition: from reals to integers. Trends in cognitive sciences. 2000;4(2):59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
  10. Gilmore CK, McCarthy SE, Spelke ES. Non-symbolic arithmetic abilities and mathematics achievement in the first year of formal schooling. Cognition. 2010;115(3):394–406. doi: 10.1016/j.cognition.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Halberda J, Feigenson L. Developmental change in the acuity of the “Number Sense”: The Approximate Number System in 3-, 4-, 5-, and 6-year-olds and adults. Developmental psychology. 2008;44(5):1457–1465. doi: 10.1037/a0012682. [DOI] [PubMed] [Google Scholar]
  12. Halberda J, Ly R, Wilmer JB, Naiman DQ, Germine L. Number sense across the lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences. 2012 doi: 10.1073/pnas.1200196109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Halberda J, Mazzocco MM, Feigenson L. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008;455(7213):665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
  14. Jolles DD, Crone EA. Training the developing brain: a neurocognitive perspective. Frontiers in human neuroscience. 2012;6:76. doi: 10.3389/fnhum.2012.00076. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Knops A, Viarouge A, Dehaene S. Dynamic representations underlying symbolic and nonsymbolic calculation: evidence from the operational momentum effect. Attention, perception & psychophysics. 2009;71(4):803–821. doi: 10.3758/APP.71.4.803. [DOI] [PubMed] [Google Scholar]
  16. Kucian K, Grond U, Rotzer S, Henzi B, Schonmann C, Plangger F, et al. Mental number line training in children with developmental dyscalculia. NeuroImage. 2011;57(3):782–795. doi: 10.1016/j.neuroimage.2011.01.070. [DOI] [PubMed] [Google Scholar]
  17. Libertus ME, Brannon EM. Stable individual differences in number discrimination in infancy. Developmental science. 2010;13(6):900–906. doi: 10.1111/j.1467-7687.2009.00948.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Lyons IM, Beilock SL. Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition. 2011;121(2):256–261. doi: 10.1016/j.cognition.2011.07.009. [DOI] [PubMed] [Google Scholar]
  19. Mazzocco MMM, Feigenson L, Halberda J. Impaired Acuity of the Approximate Number System Underlies Mathematical Learning Disability (Dyscalculia) Child Development. 2011a;82(4):1224–1237. doi: 10.1111/j.1467-8624.2011.01608.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Mazzocco MMM, Feigenson L, Halberda J. Preschoolers’ Precision of the Approximate Number System Predicts Later School Mathematics Performance. PLoS ONE. 2011b;6(9):1–8. doi: 10.1371/journal.pone.0023749. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. McCrink K, Dehaene S, Dehaene-Lambertz G. Moving along the number line: Operational momentum in nonsymbolic arithmetic. Attention, Perception and Psychophysics (pre-2011) 2007;69(8):1324–1333. doi: 10.3758/bf03192949. [DOI] [PubMed] [Google Scholar]
  22. Morrison AB, Chein JM. Does working memory training work? The promise and challenges of enhancing cognition by training working memory. Psychonomic bulletin & review. 2011;18(1):46–60. doi: 10.3758/s13423-010-0034-0. [DOI] [PubMed] [Google Scholar]
  23. Nieder A. Prefrontal cortex and the evolution of symbolic reference. Current Opinion in Neurobiology. 2009;19(1):99–108. doi: 10.1016/j.conb.2009.04.008. [DOI] [PubMed] [Google Scholar]
  24. Piazza M. Neurocognitive start-up tools for symbolic number representations. Trends in cognitive sciences. 2010;14(12):542–551. doi: 10.1016/j.tics.2010.09.008. [DOI] [PubMed] [Google Scholar]
  25. Piazza M, Facoetti A, Trussardi AN, Berteletti I, Conte S, Lucangeli D, et al. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition. 2010;116(1):33–41. doi: 10.1016/j.cognition.2010.03.012. [DOI] [PubMed] [Google Scholar]
  26. Raghubar KP, Barnes MA, Hecht SA. Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches. Learning and Individual Differences. 2010;20(2):110–122. [Google Scholar]
  27. Räsänen P, Salminen J, Wilson AJ, Aunio P, Dehaene S. Computer-assisted intervention for children with low numeracy skills. Cognitive Development. 2009;24(4):450–472. [Google Scholar]
  28. Shipstead Z, Redick TS, Engle RW. Is working memory training effective? Psychological Bulletin. 2012;138(4):628–654. doi: 10.1037/a0027473. [DOI] [PubMed] [Google Scholar]
  29. Wilson AJ, Revkin SK, Cohen D, Cohen L, Dehaene S. An open trial assessment of “The Number Race”, an adaptive computer game for remediation of dyscalculia. Behavioral and brain functions : BBF. 2006;2:20. doi: 10.1186/1744-9081-2-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Wynn K. Psychological foundations of number: numerical competence in human infants. Trends in cognitive sciences. 1998;2(8):296–303. doi: 10.1016/s1364-6613(98)01203-0. [DOI] [PubMed] [Google Scholar]
  31. Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74(1):B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Movie S1

Movie S1. Animation showing examples of non-symbolic arithmetic training trials. Participants responded with mouse clicks, but for technical reasons, mouse movement and clicks are not depicted in the movie. The text indicating the trial types was not shown to the participants and is only there for illustrative purposes.

Download video file (323.1KB, mov)
Movie S2

Movie S2. Animation showing examples of the numeral ordering training trials at different item speeds. Participants responded with mouse clicks, but for technical reasons, mouse movement and clicks are not depicted in the movie. The text indicating the item speed was not shown to the participants and is only there for illustrative purposes.

Download video file (1,008.3KB, mov)
Supplementary Materials
NIHMS460715-supplement-Supplementary_Materials.docx (54KB, docx)

RESOURCES