Quantifying the Mechanism of Phosphate Monoester Hydrolysis in Aqueous Solution by Evaluating the Relevant ab initio QM/MM Free Energy Surfaces

Abstract

Understanding the nature of the free energy surfaces for phosphate hydrolysis is a prerequisite for understanding the corresponding key chemical reactions in biology. Here the challenge has been to move to careful ab initio QM/MM (QM(ai)/MM) free energy calculations, where obtaining converging results is very demanding and computationally expensive. This work describes such calculations, focusing on the free energy surface for the hydrolysis of phosphate monoesters, paying a special attention to the comparison between the one water (1W) and two water (2W) paths for the proton transfer (PT) step. This issue has been explored before by energy minimization with implicit solvent models and by non-systematic QM/MM energy minimization, as well as by non-systematic free energy mapping. However, no study has provided the needed reliable 2D (3D) surfaces which are necessary for reaching concrete conclusions. Our study generated in a systematic way the 2D (3D) free energy maps for several relevant systems, comparing the results of QM(ai)/MM and QM(ai)/implicit solvent surfaces, and provides an advanced description of the relevant energetics. It is found that the 1W path for the hydrolysis of methyl diphosphate (MDP) trianion is 6–9 kcal/mol higher than the 2W path. This difference becomes slightly larger in the presence of Mg²⁺ ion, since this ion reduces the pKa of the conjugated acid form of the phosphate oxygen that accepts the proton. Interestingly, the BLYP approach (which has been used extensively in some studies) gives much smaller difference between the 1W and 2W activation barriers. At any rate, it is worth to point out that the 2W transition state for the PT is not much higher that the common plateau that serves as the starting point of both the 1W and 2W PT paths. Thus, the calculated catalytic effects of proteins based on the 2W PT mechanistic models are not expected to be different from the catalytic effects predicted using the 1W PT mechanistic models calibrated on the observed barriers in solution (as was done in all of our previous EVB studies).

1 Introduction

Phosphate hydrolysis reactions are arguably the most important class of chemical reactions in biology,^1–7 and it is, thus, important to elucidate the mechanism of such reactions in solution and in proteins. At this stage, it is becoming increasingly clear that in parallel to experimental studies, theoretical approaches are crucial for resolving the underlying reaction mechanisms. Furthermore, it is gradually realized^8–11 in the theoretical community that QM/MM studies might be the only practical way of resolving the fundamental mechanistic controversies about chemical processes in condensed phases, including the ones associated with phosphate hydrolysis. The key questions in elucidating the nature of the hydrolysis of phosphate monoesters and related systems, can be formulated by considering the structural models presented in Figure 1. R₁ in the figure represents the bond between the phosphate and the leaving group, R₂ describes the bond that is being formed with the attacking nucleophile and the PT reaction coordinate is designated by X. Here the main debate has involved two issues: (a) It is not clear whether the hydrolysis follows an associative or a dissociative path, which are fully defined in terms of R₁ and R₂ (see Figure 2). Unfortunately, some recent computational studies^12,13 failed to consider the clear distinction between these two mechanisms. (b) It is also unclear whether the proton transfer (PT) from the attacking nucleophilic water molecule to the terminal phosphate oxygen occurs in a direct intramolecular manner (the 1W mechanism) or with the assistance of several additional water molecules (the 2W mechanism). Thus, it is not sufficient to explore the PT mechanism involving several water molecules while ignoring the alternative direct transfer pathway, which involves only one water molecule.

Figure 1.

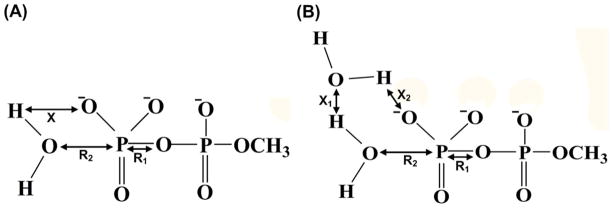
Defining the coordinates used in the present study of the hydrolysis of monomethyl pytophosphate trianion and related systems. R₁, R₂, and X define, respectively, the three reaction coordinates, which explicitly will be varied during the course of the reaction. (A) The case where the proton is transferred directly from the attacking nucleophilic water molecule to the substrate phosphate oxygen atom (direct PT (the1W mechanism)). (B) The case where the proton is transferred occurs through the assistance of an additional water molecule (water assisted PT (the 2W mechanism)).

Figure 2.

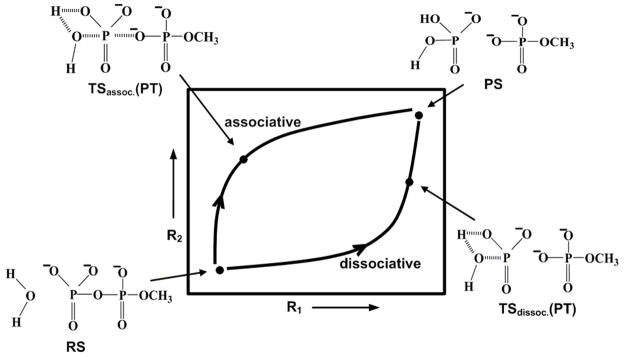
A schematic description of the potential surface for the hydrolysis of monomethyl pytophosphate trianion. The figure also provides a clear definitions of associative and dissociative mechanistic pathways associated with the corresponding hydrolysis reaction.

Traditionally, studies of the phosphate monoesters hydrolysis have been focused on the competition between the associative and dissociative mechanisms,^14,15 but recently the interest has shifted towards exploration of the possible proton transfer pathways from the nucleophilic water molecule to the phosphate oxygen atom (see the discussion and references in¹⁶). To the best of our knowledge, these issues have not been resolved experimentally and thus a consistent computational modeling is crucial for reaching firm resolution. Arguably, the first serious and systematic attempt to resolve these issues computationally (using various solvation models) has been reported by Florian and Warshel.¹⁵ Subsequent extensive and systematic computational studies of the relevant surfaces^14–16 found similar barriers for the associative and concerted paths, while considering a direct proton transfer from the attacking water molecule.

The possibility that phosphate hydrolysis involves a PT with participation of more than one water molecule has emerged from the study of Hu and Brinck.¹⁷ However, these workers neglected the entropic contribution that could in principle change the relevant conclusions. Subsequent studies found a 2W PT mechanism in phosphate monoester hydrolysis^12,13,18, but this was done without exploring the alternative 1W path, that was systematically explored in our earlier systematic studies.^14–16 Furthermore, these studies have incorrectly assigned the associative/concerted path obtained in their calculations as a dissociative mechanism. Moreover, as will be shown in the present work it is very hard to reach convincing conclusions without calculating 2D (3D) free energy surfaces, which were not obtained by those who promoted the 2W mechanism. Our recent attempt¹⁹ to address this challenging issue involved a 2D mapping, using implicit solvent models with a constrained manual TS search (moving in the direction of the gas phase RC and then performing relaxation in the given solvent model). The calculations involved the use of constraints (in particularly in the case of the path which was explored with two explicit quantum water molecules, rather than with one) in an attempt to have the same system for the 1W and 2W studies (we now conclude that this requirement is not essential). This minimization-based study¹⁹ found that the 1W PT barrier is 3–4 kcal/mol higher than the 2W PT barrier, but taking into account the deficiencies of the minimization approach mentioned above, it was rather clear that the corresponding result could not be considered as conclusive finding. In fact, the difficulties in using energy minimizations for several explicit water molecules were already discussed in Ref.²⁰ Thus, our conclusion has been that the problem is far too complex and important to be resolved by using implicit solvation models and energy minimization approaches, considering both possible difficulties of the TS search and the need for reliable free energy estimates. It was also concluded that a quantitative resolution must involve QM(ai)/MM free energy calculations with sufficiently extensive and converging sampling, using molecular dynamics (MD). Here we report the result of such a systematic QM(ai)/MM free energy study.

The current work explores several models of phosphate monoester in aqueous solution and evaluates the corresponding free energy surfaces by QM/MM MD simulations using a hybrid B3LYP density functional. Additionally, we calculate the free energy surfaces with a semi-empirical PM3/MM Hamiltonian. The resulting free energy surfaces provide a systematic and relatively rigorous picture of relevant reaction pathways where it is found that the reaction follows an associative/concerted mechanism via a nucleophilic water attack and that the proton transfer is more likely to occur through the 2W path. Additionally, it is found that the PT TS in not much higher than the common basin (the plateau) for the 1W and the 2W paths, and that the height of this plateau appears to be the key quantity that determines the overall reaction rate.

2 Methods

Our computational protocol for generating 1D free energy surfaces with QM/MM potentials involved a construction of a series of mapping potentials of the form:

$$E_m^{(i)}=E_{\text{QM}/\text{MM}}+K_m^{(i)}{\left(\xi -{\xi }_0^{(i)}\right)}^2$$ (1)

where E_QM/MM is the unbiased QM/MM potential; and the second term introduces a harmonic constraint, which improves sampling of the reaction coordinate ζ near its equilibrium point (ζ₀) and where 2 K⁽ⁱ⁾ is the force constants. Obtaining a High quality 2D free energy maps require a proper sampling along both ζ₁ and ζ₂, which were obtained with a mapping potential of the form

$$E_m=E_{\text{QM}/\text{MM}}+K_1{\left({\xi }_1-{\xi }_1^0\right)}^2+K_2{\left({\xi }_2-{\xi }_2^0\right)}^2$$ (2)

In constructing 2D free energy surfaces in R₁, R₂ coordinates we typically introduce a new mapping potential by setting new values to $R_1^0$ and $R_2^0$ with a spacing 0.1 A in the range of interest for the RCs. For the largest model of the QM region with B3LYP we used ζ = R₁ − R₂. The reaction coordinate for PT was taken as the difference in distances between the proton and the proton-donor (D) and the proton-acceptor (A): ζ = d (D − H⁺) − d (A − H⁺). The values of the force constant were gradually changed to avoid high-energy gradients in cases when ζ ≫ ζ₀ until we reached satisfactory sampling efficiency at the TS. This was achieved with force constants of 100–150 kcal/mol A² for the 2D and 1D maps along the R1, R2 and R1-R2 RCs; 75–125 kcal/mol A² for the mapping of the 1W and 2W PT RC with the PM3/MM potentials and also for the mapping of the 1W PT with the B3LYP/MM and BLYP/MM potential ; 30–50 kcal/mol A² for the mapping of the 2W PT with the BLYP/MM and B3LYP/MM potentials. Prior to switching the force constants on, we run 10 ps relaxation of the solvent with a fixed solute, while updating the QM charges every 100 steps. The MD trajectories on the potentials given by Eqs. (1) and (2) were propagated for 5–15 ps independently on each other with a step size of 1 fs at 300K (since it is an embarrassingly parallel task). The trajectories were analyzed to ensure adequate sampling along the whole range of the RCs. The last 90% of trajectories were used to construct the free energy surfaces using a combination of FEP/US^21–23 and WHAM^24,25 algorithms. Special precaution was taken by cross checking the FEP/US against the WHAM approach as well as ensuring adequate sampling. The MD trajectories were propagated using the QM/MM module of the MOLARIS-XG²⁶ simulation package. For the QM/MM calculations with the PM3²⁷ potential we used a modification²⁸ of MOPAC2009²⁹ and for the QM/MM calculations with BLYP and B3LYP//6-31G* we used the QChem3.2³⁰ and QChem4.0 packages, while for the B3LYP//6-31G*/COSMO calculations we used Gaussian09.³¹

3 Results

3.1 PM3 QM/MM results

Our QM/MM studies started with the use of the semi-empirical PM3/MM²⁹ Hamiltonian. The choice of this relatively low level of theory was made for several reasons. First, PM3/MM potential is of a low computational cost and, in principle, it can be used as a Paradynamics³² reference potential for QM(ai)/MM free energy calculations. Second, due to its low computational cost it can be used in order to rapidly explore the corresponding free energy surface and to establish in a reliable yet computationally feasible the conditions for satisfactory conditions (note that the conditions for convergence are every similar for low an high level methods).

Since one of the key aspects of this work is to provide a quantitative insight about the 1W and 2W PT mechanism, we started with the simplest systems relevant to the PT mechanism. That is, the metaphosphate anion, ${PO}_3^{-}$, with 1 QM water was chosen as starting model system (the QM region) for the 1W PT and the ${PO}_3^{-}$ anion with 2 QM water molecules was taken as a model system for the 2W PT (note that these systems essentially corresponds to taking the leaving group to infinity). The QM regions at a configuration near the TS are shown in Figure 3. The calculated free energy surface for the 1W PT mechanism along the R₁, ζ coordinates is given in Figure 4A, whereas Figure 4B compares the 1D 1W PT FES along the ζ coordinate to the corresponding surface for the 2W PT mechanism. The estimated free energy barriers are 19.4 kcal/mol for the 1W PT mechanism and 15.3 kcal/mol for the 2W PT mechanism.

Figure 3.

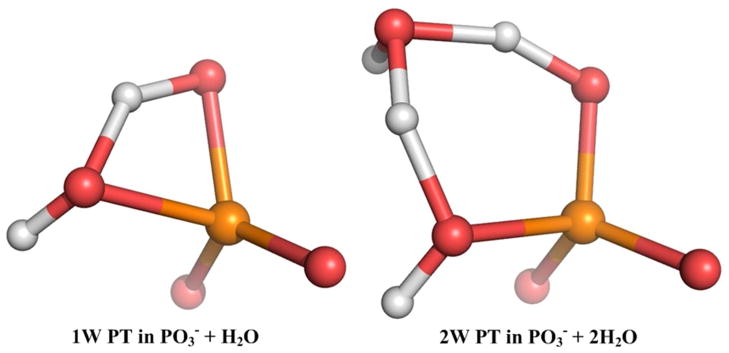
The simplest models used to study the proton transfer step of the phosphate monoester hydrolysis (PO₃⁻ + H₂O (or 2H₂O)). (LEFT) the near transition state configuration for the mechanisms involving one water molecule. (RIGHT) and two water molecules.

Figure 4.

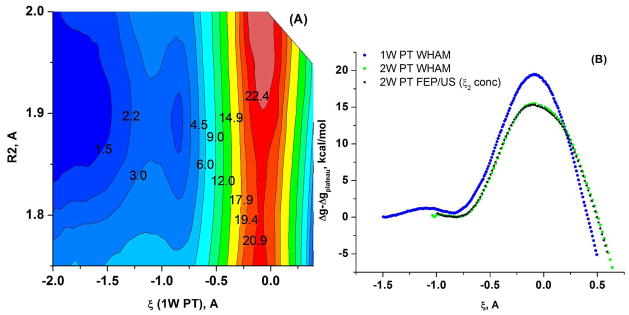
The PM3/MM free energy surfaces calculated for the 1W and 2W proton transfer mechanisms for the (PO₃⁻ + H₂O (or 2H₂O)) system. (A) The 2D free energy surface in the ζ, R₂ space, where ζ is the 1W PT coordinate, defined as the difference between the proton-donor and proton-acceptor distances. (B) A comparison of the 1D free energy surfaces along the ζ RC for the 1W PT, obtained using WHAM (black dots) and FEP/US (red dots) and for the 2W PT, obtained with WHAM (black triangles) and with FEP/US (green dots). Note that here the proton acceptor is the second water for 2W PT and the oxygen of the hydrated metaphosphate for the 1W PT.

Next, we took the methyl hydrodiphosphate (MHDP) with 2 QM water molecules as our model system (see Figure 5). In this case we reduced the solute charge from (−3) to (−2) by protonating the oxygen of the alpha-P, in order to avoid instabilities associated with a high solute charge solute³³. The 2D free energy surface was constructed in the R₁, R₂ space (Figure 6A), where one can observe a stable intermediate, ${PO}_3^{-}·H_{2}O$with R₂~1.9 A (the corresponding configurations are shown in Figure 3). Next, we calculated the free energy surfaces for the 1W PT and the 2W PT (see Figure 6B) and estimated the free energy barriers for both the 1W PT mechanism (16.2 kcal/mol) and for the 2W PT mechanism (15.9 kcal/mol). Thus by combining the free energy surfaces given in Figure 6 one can estimate the free energy changes relative to the RS of MHDP (see Table 1).

Figure 5.

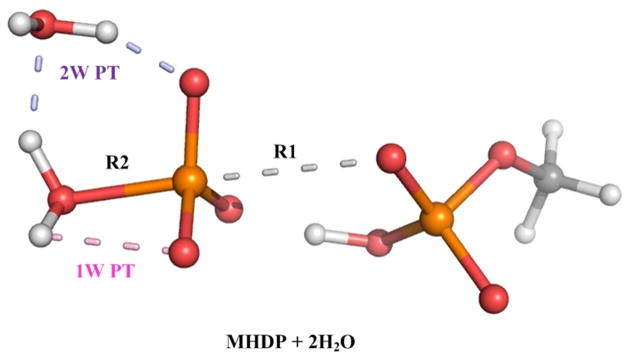
A description of the QM region used to study the hydrolysis of MHDP. Here the P-O bond (grey dashes) is broken and the two studied mechanisms for the final proton transfer step are shown as pink dashes (1W PT) and as blue dashes (2W PT).

Figure 6.

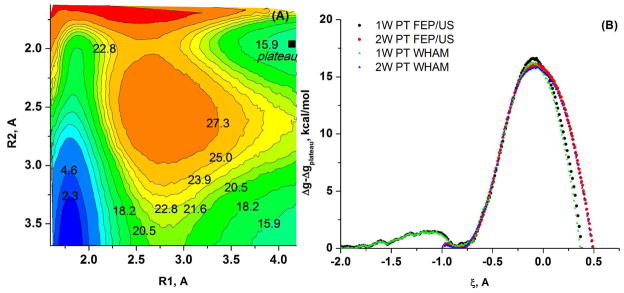
The PM3/MM free energy surface calculated for MHDP + 2 QM water molecules (the model of the QM region given in Figure 5) (A) in the R₁, R₂ space for the cleavage of the P-O bond (B) for the 1W and the 2W PT mechanisms.

Table 1.

Summary of the calculated PM3/MM activation free energies^a.

System	Method	ζ or R2, R1	ΔG‡	Description	Figure
PO3(−) with 1 QM H2O 22 A SCAAS	2D-FES in ζ, R2 space for 1W PT	ζ = −0.09, ~1.8	19.4(+15.5)b	TS 1W PT	Figure 4(A)
PO3(−) with 2 QM H2O 22 A SCAAS	2D-FES in ζ1, ζ2 space for 2W PT	ζ = −0.11, ~1.8	15.3(+15.5)b	TS 2W PT	Figure 4(B)
MHDP with 2 QM H2O 22 A SCAAS	2D-FES in R1, R2 space for P-O break	2.75, 1.9	25.0	TS1	Figure 6(A)
		1.9, 4.0	15.5	INT
MHDP with 1 QM H2O 22 A SCAAS	2D-FES in ζ, R2 space for 1W PT	ζ = −0.08, ~1.9	16.2(+15.5)	TS 1W PT	Figure 6(B)
MHDP with 2 QM H2O 22 A SCAAS	2D-FES in ζ1, ζ2 space for 2W PT	ζ = −0.06, ~1.9	15.9(+15.5)	TS 2W PT
MDP with Na+ and 16 QM H2O 18 A SCAAS	2D-FES in R1, R2 space for P-O break	1.9, 2.7	31.5	TS1	SI
		1.9, 3.6	23.5	INT
MDP with Mg2+ and 16 QM H2O PM3/MM 18 A SCAAS	2D-FES in R1, R2 space for P-O break	1.9, 2.7	23.0	TS1	Figure 8
		1.9, 3.6	13.5	INT
MTP with Mg2+ and 16 QM H2O PM3/MM 18 A SCAAS	2D-FES in R1, R2 space for P-O break	2.00, 1.85	11.6	Int1	SI
		1.92, 2.65	26.0	TS1
		1.9, 3.6	18.6	INT

^aEnergies in kcal/mol. SCAAS and FES stand, respectively, for the surface constraint all atom model⁵⁷ and free energy surface (Potential of Mean Force). The reported activation free energies (relative to the RS) do not include the NQM corrections reported in Table 3.

^bUsing the estimate of 15.5 for the height of INT found for MHDP with 2 H₂O (assuming that when R₁ reaches infinity the energy is similar). The value in parentheses designates the free energy difference between the RS for the PT step and the RS for P-O bond breaking step.

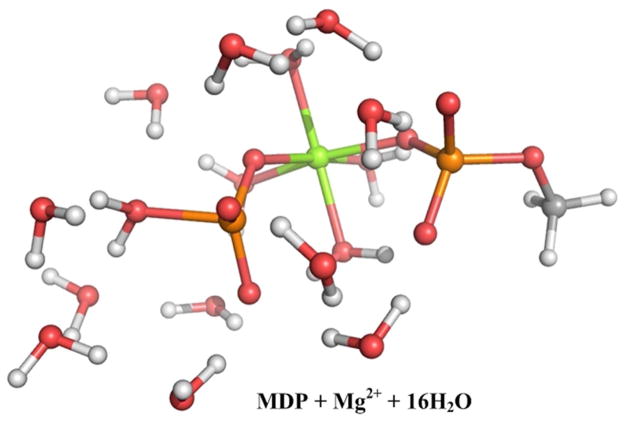
Finally, we moved to a model with a larger QM region, which included Mg²⁺ and 16 QM water (see Figure 7) and the corresponding results are summarized in Table 1. With this model we observed (see Figure 8) a reduced activation barrier along the associative path, as well as a slightly less stable INT. We note however, that Mg²⁺ with the PM3/MM potential does not maintain the octahedral coordination and seems to favor the tetrahedral coordination with 4 ligands (in contrast to the DFT/M model described below).

Figure 7.

A description of a larger model for the QM region (MDP with Mg²⁺ and 16 QM water molecule) used to study the hydrolysis reaction. Here the P-O bond is already broken and the system is at the basin prior to the final proton transfer.

Figure 8.

The PM3/MM free energy surface for the QM model of Figure 7, calculated in the R₁, R₂ space for the cleavage of the P-O bond.

While we noticed an interesting effect of Mg²⁺ (compared to Na⁺) on the mechanism of the P-O bond dissociation (see SI), this goes beyond the scope of the present work. Here our main point is that the surfaces in the R₁, R₂ space in the presence of Mg²⁺ (e.g. Figure 8) show a well-defined associative path with a stable ${PO}_3^{-}·H_{2}O$ intermediate in the right upper corner, which forms an elevated basin for the subsequent PT step. This is in a qualitative agreement with Grigorenko and coworkers’ HF//LANL2DZdp/MM minimization results¹². However, this intermediate was found to be metastable at a higher level of theory with the BLYP¹³ DFT functional. The estimated PM3/MM activation barriers for the 1W and 2W PT path starting from the above intermediate were found to have similar heights with the PT step is being the rate limiting of the overall reaction (see Figure 6B). However, these findings may simply reflect the use of the semi-emprical approach and a study with a higher level of theory, which obviously required, is reported in the next section.

3.2 QM(ai)/MM results

Next we moved to the more challenging (and much more computationally expensive) task of calculating the QM(ai)/MM free energy surfaces. Here, the high computational cost is an additional reason to carry out studies with the simplest (smallest) possible QM region model.

In this study we followed our previous work¹⁹ and use a hybrid B3LYP functional with 6-31G* basis set. Additionally we also examined here the performance of the BLYP functional (with the 6-31G and 6-31G* basis sets) in calculating the activation free energy for the 1W PT and the 2W PT, since this functional is widely used in Car-Parinello MD studies of similar systems^13,34. Furthermore, in order to compare the minimization results with an implicit solvent (reported in SI) to the much more rigorous free energy studies with the same model, we also used B3LYP//6-31G*/(COSMO) potential with MD propagated in the presence of an inert solvent (water molecules with 0 charges) that provided efficient solute thermalization.

Our MD simulation were based on the adiabatic approximation, were we evaluated the electronic density by SCF at each time step. This approach has been used for a long time since its invention by Warshel and Levitt³⁵. It is arguably more rigorous than using auxiliary MD variables for effectively achieving the same purpose. Our approach also describes the long-ranged electrostatics consistently (with the QM/MM treatment), while still being able to perform adequate sampling and at chosen levels of theory.

As in the case of the PM3/MM study, we first calculated free energy surfaces using the simplest models of the QM region given in Figure 3. This was done for the 1W PT with ${PO}_3^{-}$ plus 1 QM water and for the 2W PT with ${PO}_3^{-}$ plus 2 QM water molecules (where the residual methylphosphate is assumed to be at infinity). The calculated free energy surfaces with the BLYP//6-31G*/MM potential are depicted in Figure 9 where the 1W PT activation barrier is 6.5 kcal/mol (5.8 with 6-31G*) and the 2W PT barrier is 1.4 kcal/mol.

Figure 9.

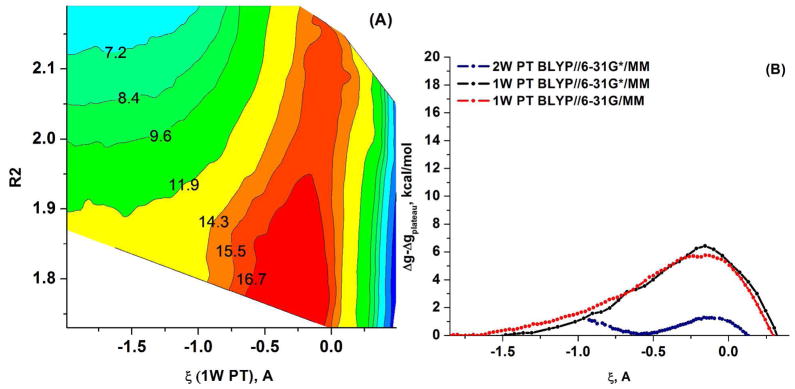
(A) The BLYP/MM free energy surfaces calculated for the 1W and 2W proton transfer mechanisms for the (PO₃⁻ + H₂O (or 2H₂O)) system. (A) The 2D free energy surface in ζ, R₂ space, where ζ is the 1W PT coordinate defined as the difference between the proton-donor and proton-acceptor distances. (B) A comparison of the 1D free energy surfaces obtained using FEP/US along the ζ RC for the 1W PT path with the 6-31G* basis set (black dots) and the 6-31G basis set (red dots) and for the 2W PT path, obtained with 6-31G* basis set (blue dots). Note that here the proton acceptor is the second water for 2W PT and the oxygen of metaphosphate for 1W PT.

Next we evaluated the free energy surfaces with the B3LYP//6-31G*/MM potential, and the corresponding results are given in Figure 10. Now we have a 14.0 kcal/mol activation free energy for the 1W PT and 1.4 kcal/mol for the 2W PT. Interestingly, with the above BLYP//6-31G*/MM potential, the difference between the barriers for the 1W and 2W paths is 5.1 kcal/mol, while with the B3LYP//6-31G*/MM potential the difference is 12.6 kcal/mol.

Figure 10.

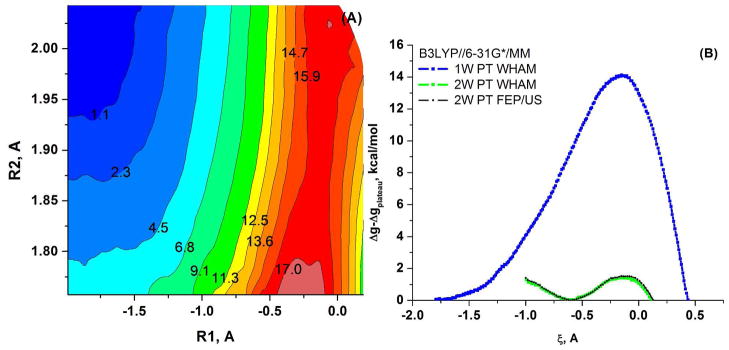
(A) The B3LYP//6-31G*/MM free energy surfaces calculated for the 1W and 2W proton transfer mechanisms for the (PO₃⁻ + H₂O (or 2H₂O)) system. (A) The 2D free energy surface in the ζ, R₂ space, where ζ is the 1W PT coordinate defined as the difference between the proton-donor and proton-acceptor distances. (B) A comparison of the 1D free energy surfaces obtained along the ζ RC for the 1W PT path, obtained by WHAM (blue dots) and for the 2W PT path, obtained by WHAM (green dots) and using FEP/US (black dots). Note that here the proton acceptor is the second water for 2W PT and the oxygen of metaphosphate for 1W PT.

We note that the 2D free energy map of the 1W PT mechanism of the PO₃⁻ + H₂O system (Figure 10A), shows a plateau at R2~1.9–2.0 A, where the PT process begins. Since this plateau is not a highly stable intermediate, as is the case of the PM3/MM simulations, we had to use constraints in some cases. That is, in the 1W PT simulations we had to use a harmonic constraint of 100 at R₂=1.85, 1.95 and 2.05 (the effect of which was, of course was removed latter). On the other hand, in 2W PT simulations we used no constraints on R₂, nevertheless R₂ in the 2W PT RS was fluctuating in the range 1.9–2.0 A.

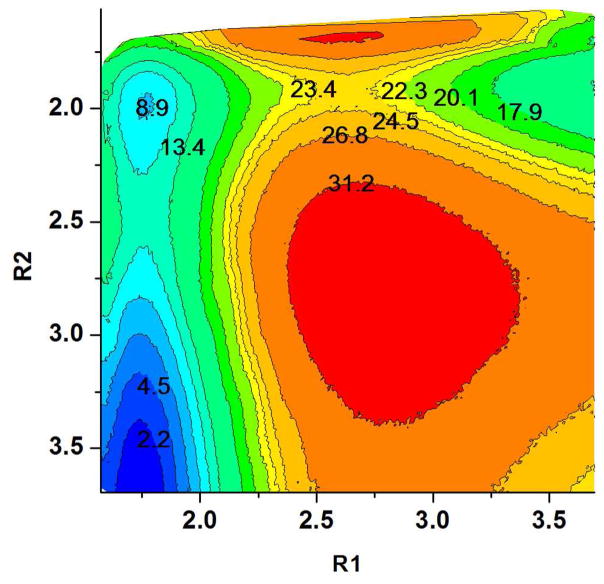
Next, we also considered the MHDP + 2 QM H₂O model for the QM region given in Figure 5. At first the free energy surface in the R₁, R₂ space was calculated for the first step in the hydrolysis (which involves the breaking P-O bond) with the B3LYP//6-31G* potential, using both explicit solvent (MM water) model and an implicit COSMO solvent model. The corresponding surfaces are given in Figure 11. The results obtained by the two solvation models are in an excellent quantitative agreement, but quite different from the PM3/MM surface of Figure 6. Here it is not entirely clear whether the explicit solvent gives a better result for the large charge separation at large R₁, since it is quite challenging to obtain perfect profile for charge recombination (see Ref. ³⁶). Furthermore the very large charge separation motion is likely to encounter some steric resistance when occurs in enzyme active site (see ref. ³⁷) which is likely to discriminate the dissociative mechanism. Nevertheless, the dissociative mechanism in Figure 11 seems to be more favorable over the associative, as is the case with the PM3/MM potential in the absence of Mg²⁺ (see Figure 6). Since at the PM3/MM level the addition of Mg²⁺ to the QM region resulted in stabilization of the associative TS (Figure 8), we also constructed the free energy surface for the large model of the QM region given in Figure 7 to examine the possible effect of Mg²⁺ with a B3LYP/MM surface and the corresponding surface is given in Figure 12. Here the B3LYP//6-31G*/MM MD trajectories were propagated by adding harmonic constraints along the R₁-R₂. RC and the corresponding PMF is given in Figure 12A. Next we estimated the 2D free energy surface in the R₁, R₂ space with the same data (see Figure 12B). This surface (as well as the sampling distribution on the R₁, R₂ surface) indicates that the Mg²⁺ ion shifts the reaction path more towards the associative pathway compared to the MHDP surface given in Figure 11. As before we took the plateau region was taken as the starting point for exploring the subsequent PT step. It should be noted here that the effect of Mg²⁺ was observed only in shifting the P-O dissociation pathway more towards the associative/concerted pathway, it has not lowered the relative height of the P-O dissociation barrier which is similar for MHDP (Figure 11) and MDP with Mg²⁺ (Figure 12).

Figure 11.

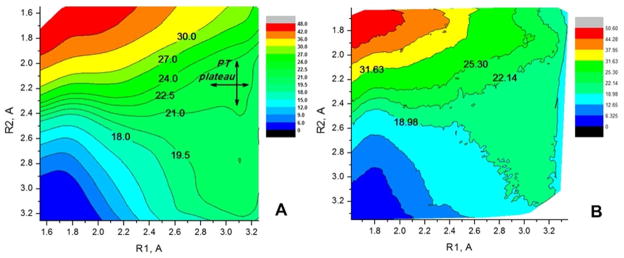
The free energy surfaces in the R₁, R₂ space for MHDP plus 2 QM H₂O (the system with the QM region given in Figure 5), for the first step of the ester hydrolysis (the cleavage of the P-O bond) obtained by (A) the PMF/COSMO model ; (B) the B3LYP//6-31G*/MM model.

Figure 12.

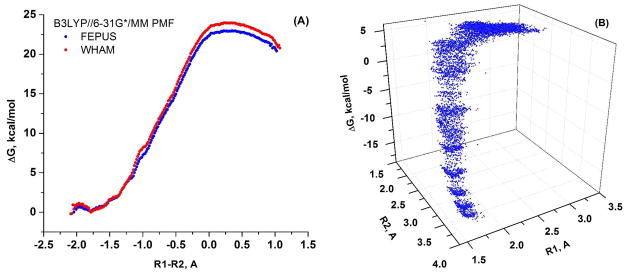
The B3LYP//6-31G*/MM free energy surface for MDP plus Mg²⁺ plus 16 QM H₂O shown in Figure 7, obtained with a 1D mapping potential, which contained an harmonic constraints on R₁-R₂ RC: (A) The 1D free energy surface calculated along the R₁-R₂ RC with FEP/US(blue) and with WHAM(red) and (B) The free energy surface calculated in the R₁, R₂ space by the FEP/US approach.

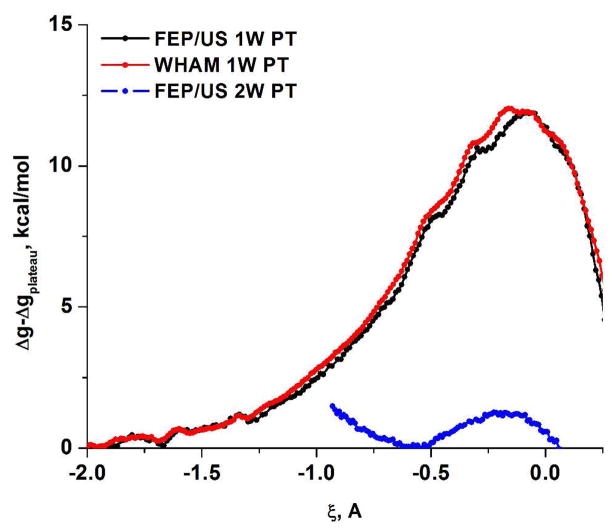
In the next step, we evaluated the PT free energy surfaces for the QM region model of Figure 5 (MHDP with 2 QM water molecules). The B3LYP//6-31G*/COSMO free energy barrier for the 1W PT is ~15 kcal/mol for (see Figure 13A) and for the 2W PT it is estimated to be ~3 kcal/mol (see Figure 15). With the explicit solvent model the B3LYP//6-31G*/MM 1W PT barrier is found to be ~12 kcal/mol (see Figure 13B) and with the 2W PT the barrier is about 1.5 kcal/mol (see Figure 14).

Figure 13.

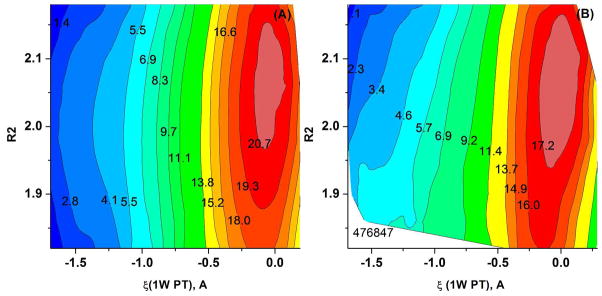
The Free energy surfaces for the 1W PT path calculated for the MHDP + 2 QM H₂O QM region of Figure 5 using (A) the PMF/B3LYP//6-31G*/COSMO and (B) B3LYP//6-31G*/MM potentials.

Figure 15.

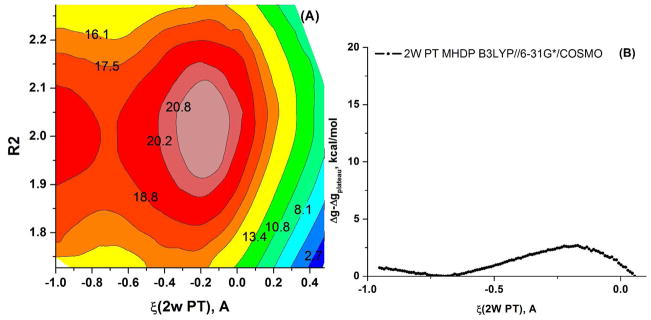
The Free energy surface for the 2W PT path calculated for the MHDP + 2 QM H₂O the QM region of Figure 5 using (A) 2D mapping with the PMF/B3LYP//6-31G*/COSMO model. (B) 1D mapping with the PMF/B3LYP//6-31G*/COSMO model.

Figure 14.

Free energy profiles calculated on B3LYP//6-31G*//MM potential for: the 1W PT mechanism using MHDP plus 1 QM water as a model for the QM region (RED was obtained using WHAM; BLACK curve using FEP/US) and for the 2W PT mechanism using MHDP plus 2 QM water (BLUE curve calculated using WHAM).

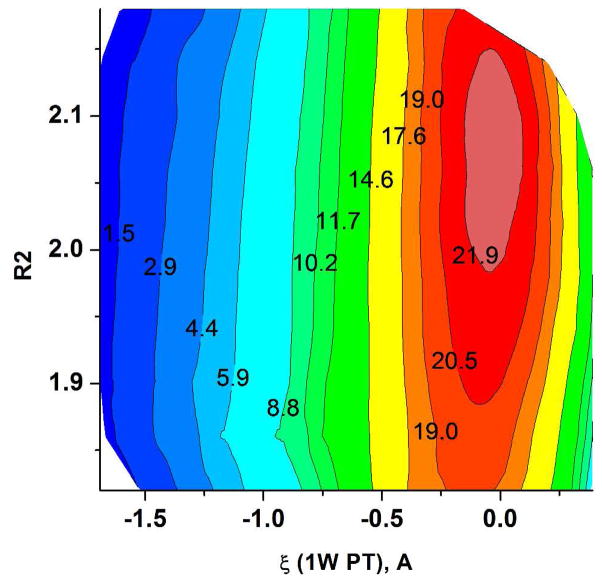
Finally, we calculated the 1W PT free energy surface for the system containing Mg²⁺ (shown in Figure 16) at the B3LYP//6-31G*/MM. In this case, we obtained a higher barrier of 18.5 kcal/mol free energy surface (see Figure 17).

Figure 16.

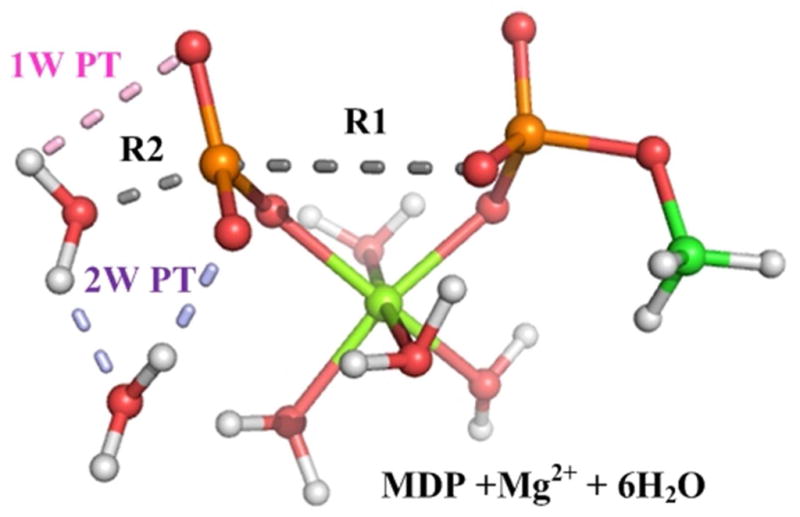
A snapshot of one the studied models for the QM region (MDP with Mg2+ and 6 QM water molecules) used to study the PT step in hydrolysis of phosphate monoester. Here the P-O bond is already broken and the system is prior to the final proton transfer.

Figure 17.

The Free energy surfaces for the 1W PT path calculated for the model of the QM region given in Figure 16, using the B3LYP//6-31G*/MM potentials.

At this point we would like to comment about the combination of the R₁/R₂ and R₂/PT surfaces in evaluating of the rate determining activation barrier. The free energy on the R₁/R₂ surface is evaluated while integrating over all other coordinates including the PT coordinate. Now by choosing a starting point for the PT calculations on the R₁/R₂ surface, we practically fix R₁ and move in R₂/ζ space until the PT is completed. Thus in order to obtain the free energy of the TS in the R₁/R₂/ζ space we have to combine properly the free energy of the PT TS obtained by a mapping along R₂/ζ coordinates to the free energy of the elevated plateau in the R₁/R₂ map (in our case at R₂ =2Å R₁ =3.2Å). Thus we should obtain the normalized probability of being at ζ. This is done as follows. We start with the free energy in the R₁/R₂ space which is evaluated formally by (see e.g. King and Warshel²³ for a 1-D treatment):

$$exp(-\beta \mathrm{\Delta }g{(R_1,R_2)}_a)=\frac{\int d\mathbf{x}\delta \left(R_1^{\prime }(\mathbf{x})-R_1\right)\delta \left(R_2^{\prime }(\mathbf{x})-R_2\right)exp\left(-\beta U(\mathbf{x})\right)}{\int d\mathbf{x}exp\left(-\beta U(\mathbf{x})\right)}$$ (3)

Where “ a “ designates the R₁/R₂ surface and x includes all the coordinates, In this way we obtain the plateau free energy, which serves as the reference RS for the PT mapping, using:

$${\mathrm{\Delta }g(\xi )|}_{PTRS}={\mathrm{\Delta }g{(R_1,R_2)}_a|}_{\mathit{plateau}}$$ (4)

Next, we evaluate the PMF for moving from the plateau to the PT TS using:

$$exp(-\beta \mathrm{\Delta }g{(\xi )}_b)=\frac{\int d\mathbf{x}\delta ({\xi }^{\prime }(\mathbf{x})-\xi )exp(-\beta U(\mathbf{x}))}{\int d\mathbf{x}exp(-\beta U(\mathbf{x}))}$$ (5)

However, having the surface “b” in the ζ/R₂ space with a fixed R₁ allows one to write:

$$exp(-\beta \mathrm{\Delta }g{(\xi )}_b)=\frac{\int \delta ({\xi }^{\prime }-\xi )exp(-\beta \mathrm{\Delta }g{(R_1,R_2,\xi )}_b{dR}_{2}d{\xi }^{\prime }}{\int exp(-\beta \mathrm{\Delta }g{(R_1,R_2,\xi )}_b{dR}_{2}d{\xi }^{\prime }}$$ (6)

Now combining Eqs. (4) and (6) we obtain:

$$\mathrm{\Delta }g(R_1,R_2,\xi )=\mathrm{\Delta }g(\xi )=\mathrm{\Delta }g{(R_1,R_2)}_a{|}_{\mathit{plateau}}+\mathrm{\Delta }g{(\xi )}_b$$ (7)

At any rate, the free energies calculated by the above approach in this section (relative to the RS of the net reaction) are summarized in Table 2.

Table 2.

Summary of the calculated BLYP//6-31G*/MM, B3LYP//6-31G*/MM and B3LYP//6-31G*(COSMO) activation free energies ^a

System	Method	ζ or R2, R1	ΔG‡	Description	Figure
PO3(−) with 1 QM H2O 22 A SCAAS	Δg(ζ, R2) 1W PT; BLYP//6-31G*/MM	ζ = −0.16, ~1.8	6.5(+21.0)b	TS 1W PT	Figure 9 (A)
PO3(−) with 2 QM H2O 22 A SCAAS	2D-FES in ζ 1, ζ 2 space; 2W PT; BLYP//6-31G*/MM	ζ = −0.10, ~1.8	1.4(+21.0)b	TS 2W PT	Figure 9(B)
PO3(−) with 1 QM H2O 22 A SCAAS nonpolar solvent	2D-FES in ζ, R2 space; 1W PT, B3LYP//6-31G*/COSMO	ζ = −0.14	14(+21)c	TS 1W PT	Figure 10A)
PO3(−) with 2 QM H2O 22 A SCAAS nonpolar solvent	2D-FES in ζ 1, ζ 2 space for 2W PT, B3LYP//6-31G*/COSMO	ζ = −0.10	1.4(+21)c	TS 2W PT	Figure 10(B)
MHDP with 2 QM H2O (20 Q atoms) COSMO solvent 22 A SCAAS nonpolar solvent	2D-FES in R1, R2 space for P-O break, B3LYP//6-31G*/COSMO	2.0, 3.2	21	plateau	Figure 11(A)
	2D-FES in ζ, R2 space for 1W PT, B3LYP//6-31G*/COSMO	1.88, −0.15	15(+21)	TS 1W PT	Figure 13(A)
	2D-FES in ζ1, ζ2 space for 2W PT, B3LYP//6-31G*/COSMO		3(+21)		Figure 15
MHDP with 2 QM H2O (20 Q atoms) 22 A SCAAS	2D-FES in R1, R2 space for P-O break, B3LYP//6-31G*/MM	2.0, 3.2	21	plateau	Figure 11(B)
	2D-FES in ζ, R2 space for 1W PT, B3LYP//6-31G*/MM	1.88, −0.15	12.3(+21)	TS 1W PT	Figure 13(B)
	2D-FES in ζ1, ζ2 space for 2W PT, B3LYP//6-31G*/MM	1.88, −0.20	1.4(+21)	TS 2W PT	Figure 14(B)
MDP with Mg2+ and 6 QM H2O 32 Q atoms 18 A SCAAS	2D-FES in ζ, R2 space for 1W PT, B3LYP//6-31G*/MM	1.88, −0.15	18(+22.5)	TS 1W PT	Figure 17
MDP with Mg2+ and 16 QM H2O 62 Q atoms 18 A SCAAS	2D-FES in R1-R2 space for P-O break, B3LYP//6-31G*/MM	dd=0.25	22.5	plateau	Figure 12

^aEnergies in kcal/mol. SCAAS and FES designate, respectively, the surface constraint all atom model⁵⁷ and free energy surface (Potential of Mean Force). The reported activation free energies (relative to the RS) do not include the NQM corrections that will be added in Table 3.

^bUsing the estimate for the height of the INT found for MHDP with 2 H₂O (assuming that R₁ reaches infinity)

^cUsing the estimate of the height of the plateau found for MDP with 16 H₂O (assuming that R₁≫1)

3.3 Implicit solvent calculations

Recently we reported a study of the monomethyl pyrophosphate trianion hydrolysis, using implicit solvent models, where we compared the 1W and 2W PT pathways by means of constrained minimization. The difficulties were compounded by attempting to find the 1W TS in the presence of the second water molecule. Here made an additional attempt to obtain the minimization results with the implicit solvent model using the QM/COSMO MD and QM/MM MD simulations as a guide. The corresponding results are given in the SI. These results are used mainly to show that the implicit solvent minimization studies can be useful once the relevant solvation TS is identified.

3.4 Nuclear Quantum mechanical and other corrections

Since the 1W PT barrier is significantly higher and steeper that the 2W PT barrier, it is likely that the 1W barrier will have a significantly larger nuclear quantum mechanical (NQM) correction. As we are dealing with a reaction in condensed phase, our method of choice is the quantized classical path (QCP)^38–40 method. This method, that was introduced by us quite early^38,40, allow one to obtain efficiently the results of path integral centroid^41,42 simulations, by developing a free particle quantum perturbation from the classical trajectory of the reacting system. That is the QCP approach expresses the free energy surface along the reaction coordinate as:

$$\mathrm{\Delta }g(\xi )=\mathrm{\Delta }{G}_m-\mathit{kT}ln{\langle \delta (x-\xi ){\langle exp\left(-\beta \left(\overline{E}-E_m(x)\right)\right)\rangle }_{E_{fp}}\rangle }_{E_m}$$ (8)

where ΔG_m is the free energy associated with the mapping potential E_m (e.g. the potential of Eq. (1) or in the case of EVB modeling the EVB mapping potential). Ē is the quantum potential of the quasi particles, given by:

$$\overline{E}=(1/P)\left[\sum _{n=1}^P\frac{m{\mathrm{\Omega }}^2}{2}+E\right]$$ (9)

where P is the number of quasiparticles and Ω = 2nπ/β h the notation < >_V designates an average obtained on the indicted potential. The mapping potential in Eq. (8) is used to propagate a classical trajectory that properly samples the potential surface. The generated coordinate of the classical trajectory, x, serves as the centroid, and < >_fp designates the average obtained by propagating the quantum quasiparticles by means of Monte Carlo or Langevin dynamics simulation on a quantum free particle potential (constrained to have its centroid at x).

Although the QCP approach has been sometimes overlooked by subsequent works⁴³ (mentioning just the much less efficient approach of running trajectory for all the quasiparticles), it was proved to be extremely effective for exploring very challenging problems such as the temperature dependence on isotope effect in enzymes.^44,45. In fact, other workers have recently adopted it.^46–49 Some authors⁴⁹ have implied that the QCP approach was proposed elsewhere⁵⁰ referring to use of the double averages in ref.⁵⁰ and misleadingly relating it to the QCP idea. Obviously double averages and double integrals as mathematical tools have been used in many fields for a very long time. However, the work of ref.⁵⁰ has nothing to do with centroid-based calculations nor it attempts to estimate the NQM correction or address the related problems. In particular, the work of Ref.⁵⁰ is not related to the QCP idea of using classical trajectory as the reference centroid for NQM calculations. This clarification is important since the QCP has been the most effective way of obtaining converging results for NQM of adiabatic reactions in condensed phase, following the earlier dispersed polaron method^35,51 that has been the method of choice for obtaining the NQM effect for diabatic reactions. At any rate, in order to obtain the NQM correction we fitted EVB potential to the QM(ai)/MM surface and performed standard QCP calculations as implemented in MOLARIS-XG.^26,52 The calculations were done in a general way fitting an EVB potential to the DFT/COSMO profile of the 1W (Figure 13A) and 2W PT (Figure 15) in the reaction of MHDP and evaluating the NQM correction for the fitted potential. We then interpolated the results to other target potentials E_TGT using:

$$\mathrm{\Delta }\mathrm{\Delta }{g}_i^{\mathit{NQM}}(E_{\mathit{TGT}})=\mathrm{\Delta }\mathrm{\Delta }{g}_{1W}^{\mathit{NQM}}(E_{\mathit{EVB}})--\left(\mathrm{\Delta }{g}_i^{\ne }(E_{\mathit{TGT}})-\mathrm{\Delta }{g}_{1W}^{\ne }(E_{\mathit{EVB}})\right)\frac{\mathrm{\Delta }\mathrm{\Delta }{g}_{1W}(E_{\mathit{EVB}})-\mathrm{\Delta }\mathrm{\Delta }{g}_{2W}(E_{\mathit{EVB}})}{\mathrm{\Delta }{g}_{1W}^{\ne }(E_{\mathit{EVB}})-\mathrm{\Delta }{g}_{2W}^{\ne }(E_{\mathit{EVB}})}$$ (10)

The NQM calculations for the EVB potential fitted to the 1W and 2W barriers displayed in Figure 18. Of course we could have repeated the NQM calculations while fitting the EVB to different target potentials³², but we used simple interpolations with eq. (10) instead.

Figure 18.

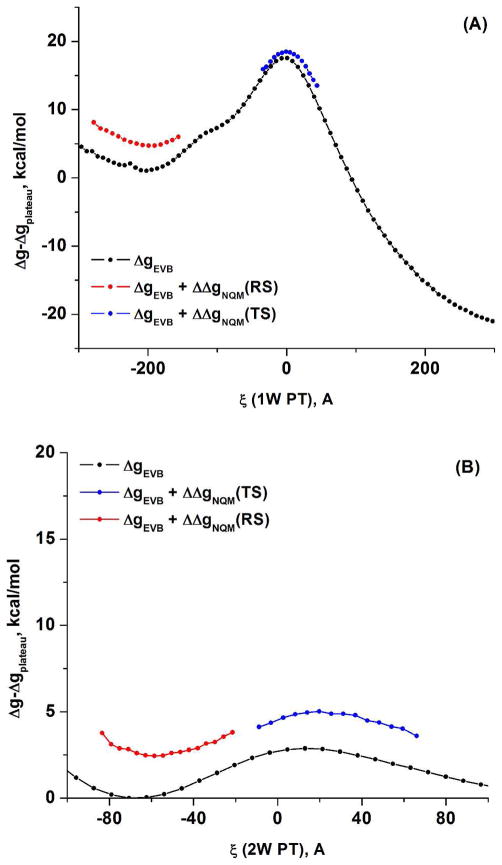
The nuclear quantum mechanical correction evaluated using the QCP approach of eq. (8) with the calibrated EVB potential for (A) the 1W PT and (B) the 2W PT for the QM region model shown in Figure 5.

We also note that the NQM–corrected free energy surfaces can be obtained with QM(ai)/MM potentials by replacing E in eq. (9) with the adiabatic QM/MM surface. This can be drastically accelerated by using the first order expansion of E at each QM call, but the results are not expected to be significantly different from those obtained when E is taken as the EVB potential. Another important consideration is the effect of moving to a more rigorous ab initio Hamiltonian, where the optimal approach would be to use the PD approach, using the lower level surface as a reference for the free energy of the higher-level surface. Here however we only performed single point estimates of the corresponding effects and reported them in Table 3.

Table 3.

Summary of the results obtained with our different studies^a

System	model	path	ΔgPT‡ + ΔgREF + ΔΔ gNQMb	Δg‡	Δg1W‡ − Δg2W‡
PO3(−) with 1 QM H2O	PM3/MM	1W PT	19.4+15.5−3.6	31.3	3.3
PO3(−) with 2 QM H2O	PM3/MM	2W PT	15.3+15.5−2.8	28.0
PO3(−) with 1 QM H2O	BLYP//6-31G*/MM	1W PT	6.5+21.0−1.0	26.5	4.1
PO3(−) with 2 QM H2O	BLYP//6-31G*/MM	2W PT	1.4+21.0+0.0	22.4
PO3(−) with 1 QM H2O	B3LYP//6-31G*/MM	1W PT	14+21−2.5	32.5	10.1
PO3(−) with 2 QM H2O	B3LYP//6-31G*/MM	2W PT	1.4+21+0.0	22.4
MHDP with 2 QM H2O	PM3/MM	2W PT	16.2+15.5−2.9	28.8	0.2
	PM3/MM	1W PT	15.9+15.5−2.9	28.5
MHDP with 2 QM H2O	B3LYP//6-31G*/COSMO	1W PT	15+21−2.7	33.3	9.6
	B3LYP//6-31G*/COSMO	2W PT	3+21−0.3	23.7
	B3LYP//6-31G*/MM	1W PT	12.3+21−2.2	31.1	8.7
	B3LYP//6-31G*/MM	2W PT	1.4+21+0.0	22.4
MDP interpolatedc	B3LYP//6-31G*/MM	2W PT→1W PT			~ 8.0
MDP with Mg2+ and 6 QM H2O	B3LYP//6-31G*/MM	1W PT	18+22.5−3.3	37.2

^aEnergies in kcal/mol.

^bThe NQM corrections were estimated using the EVB approximation of the B3LYP/MM surface of MHDP and the QCP approach (see the main text). We obtained −2.7 kcal/mol for the 1W PT and −0.3 kcal/mol for the 2W PT. The EVB barriers were 15 and 3 for 1W and 2W respectively (better agreement with the BLYP results could be easily obtained but were not needed in view of the interpolation used here). For the other systems we estimated the corrections by interpolating the calculated NQM by the relative height of the classical barrier. That is, we used $\mathrm{\Delta }\mathrm{\Delta }{g}_{\mathit{NQM}}=-2.7-(\mathrm{\Delta }{g}^{\ne }-15)\left(\frac{2.7-0.3}{15-3}\right)$, using the results of MHDP as the basis for the linear interpolation.

^cHere the 2 kcal/mol corrections reflect the estimate the effect of moving from MHDP to MDP since in this case the negative charge of the leaving group increases the pKa of the protonated form of the oxygen that accepts the proton.

3.5 Emerging Picture

Considering the extensive studies reported above it is important to provide a simple summary of our finding. Such a summary is compiled in Table 3. As can be seen from the table the difference between the QM(ai)/MM classical PMF for the 1W and 2W paths in the reaction of MHDP is about 10 kcal/mol. This difference is expected to be further reduced by about 2 kcal/mol while moving from MHDP to MDP, since in this case the negative charge of the leaving group increases the pKa of the protonated form of the oxygen that accepts the proton.

The NQM correction further reduces the difference between the 1W and 2W barriers by about 2.4 kcal/mol. Thus we estimate that the 1W activation free energy barrier is about 7–9 kcal/mol higher than the 2W barrier. In the presence of Mg²⁺ the difference increases by about 2–3 kcal/mol.

In order to establish the agreement of the total calculated barrier with the experimentally observed estimate we have to move to a higher QM level. This can be done by running the PD calculations²⁸ to estimate the free energy perturbation of moving from B3LYP//6-31G* to a higher level of theory, e.g. MP2/6-311++G**. Here however we simply consider the corresponding correction obtained in our previous work.¹⁹ The corresponding average correction was found to be about 3 kcal/mol and adding this value to the QM(ai)/MM barrier of MHDP about 23 kcal/mol gives a barrier of 26 kcal/mol. The non-equilibrium solvation effect is expected to increase the barrier by about 2–3 kcal/mol,⁵³ which makes the overall barrier associated with the hydrolysis of MHDP close to 29 kcal/mol. This is comparable (perhaps fortuitously) to the experimentally observed barrier of about 31.2 kcal/mol for the hydrolysis of PP_i^3−.54 Note that we assume here that this is a reasonable approximation for MDP and it is also taken as a reasonable approximation for monomethyl pyrophosphate trianion.

4 Concluding Discussion

The relative free energy of the 1W and 2W paths in the hydrolysis of phosphate monoesters has not been explored in a systematic in a reliable way before. Most reported studies have not compared the corresponding QM(ai)/MM free energy surfaces and clearly have not provided the necessary free energy surfaces for both the P-O bond dissociation and the PT steps. This work presents what is arguably the most careful theoretical study of the hydrolysis of phosphate monoesters in solution, exploring the relevant free energy surfaces by several approaches including: QM(DFT)/implicit solvent MD, PM3/MM MD, QM(DFT)/MM MD and also estimates the NQM correction as well as the higher level of theory corrections. This allows us to move from our previous manual mapping and incomplete minimization of the QM(ai)/implicit solvent to a much more solid evaluation of the relevant surfaces and activation free energies. It is found that in solution the 2W mechanism is more likely than the 1W mechanism, and thus should be consider as the reference reaction for the corresponding reaction in enzymes.

Exploring several models with increasing degree of complexity indicates, in agreement with our previous study¹⁹, that the 1W becomes less probable in the presence of factors that reduces the pKa of the acceptor oxygen. Thus the presence of Mg⁺² (which was not studied in our previous work) seems to increase the difference between the 1W and 2W barriers making it larger than in the case of MDP.

The present study indicates that semi-empirical approaches may give quit different results than those obtained by ab initio calculations, including the finding that with the PM3 Hamiltonian we obtain similar barrier for the 1W and 2W paths. It is also found that while the tunneling corrections reduce the 1W barrier, the effect is around 2 kcal/mol but cannot change the finding that the 2W barrier is significantly lower. It is also found that the popular BLYP functional gives much smaller differences between the 1W and 2W barriers than the difference obtained with the hybrid B3LYP DFT functional (see Section 3.2). Thus at least on the BLYP level¹³ it has not been justified not to explore the 1W path.

In the present work we chose to perform expensive and full PMF calculations instead of focusing on the TS and RD regions using the PD approach. This was justified in view of the importance of resolving the difference between the 1W and 2W landscapes, rather than demonstrating the efficiency of a particular method. However, in view of the discussed similarities between the B3LYP/COSMO and B3LYP/MM surfaces, we concluded that performing PD calculations with EVB calibrated on the COSMO TS should provide a reliable and efficient way of obtaining the relevant activation free energies. Using the PD approach should be even more important for studies in enzyme active site where direct PMF would require enormous computer time to get free energy convergence.

In considering the role of the second water in the 2W path we note that it serves merely as a proton shuttle in the TS and that overall we have a concerted PT coupled to the concerted path in the R₁/R₂ space. Thus, the second water should not be considered as a base but just as a facilitator of the PT to the phosphate oxygen near the PT TS.

Interestingly the intermediate on the reaction path found by previous studies¹³ was not found on the B3LYP 2D free energy surface for MHDP in Figure 11. On the other hand, in the presence of Mg2⁺ we did observe a flat TS region on the B3LYP surface for MDP (see Figure 12). In any case, the plateau before the PT barrier is of interest since its height appears to be the major contribution to the overall activation barrier. This means that the catalytic effect obtained on this plateau is similar to those found before by EVB studies^55,56. That is the EVB TS in our previous works was based on the ab initio charge distribution obtained before a complete 1W PT and is not much difference than the distribution at the plateau. More importantly we obtained very similar catalytic effects using the charge distributions for the associate and dissociative paths. It seems to us that as far as the catalysis is concerned, the 2W PT step has little importance to the overall catalysis, since it is only about 1–3 kcal/mol above the plateau level. In contrast, the P-O bond dissociation step is of major importance since reduction of the activation free energy barrier at this step is basis for enzymatic catalysis. This issue will be explored in subsequent works using the PD approach.

Abbreviations

MHDP

MeO-HPO₃-PO₃⁽²⁻⁾, methyl monohydrogen diphosphate

MDP

MeO-PO₃-PO₃⁽³⁻⁾, methyl diphosphate

MTP

MeO-(PO₃)₂-PO₃⁽⁴⁻⁾, methyl triphosphate