Guided Exploration of Genomic Risk for Gray Matter Abnormalities in Schizophrenia Using Parallel Independent Component Analysis with Reference

Abstract

One application of imaging genomics is to explore genetic variants associated with brain structure and function, presenting a new means of mapping genetic influences on mental disorders. While there is growing interest in performing genome-wide searches for determinants, it remains challenging to identify genetic factors of small effect size, especially in limited sample sizes. In an attempt to address this issue, we propose to take advantage of a priori knowledge, specifically to extend parallel independent component analysis (pICA) to incorporate a reference (pICA-R), aiming to better reveal relationships between hidden factors of a particular attribute. The new approach was first evaluated on simulated data for its performance under different configurations of effect size and dimensionality. Then pICA-R was applied to a 300-participant (140 schizophrenia (SZ) patients versus 160 healthy controls) dataset consisting of structural magnetic resonance imaging (sMRI) and single nucleotide polymorphism (SNP) data. Guided by a reference SNP set derived from ANK3, a gene implicated by the Psychiatric Genomic Consortium SZ study, pICA-R identified one pair of SNP and sMRI components with a significant loading correlation of 0.27 (p = 1.64×10⁻⁶). The sMRI component showed a significant group difference in loading parameters between patients and controls (p = 1.33×10⁻¹⁵), indicating SZ-related reduction in gray matter concentration in prefrontal and temporal regions. The linked SNP component also showed a group difference (p = 0.04) and was predominantly contributed to by 1,030 SNPs. The effect of these top contributing SNPs was verified using association test results of the Psychiatric Genomic Consortium SZ study, where the 1,030 SNPs exhibited significant SZ enrichment compared to the whole genome. In addition, pathway analyses indicated the genetic component majorly relating to neurotransmitter and nervous system signaling pathways. Given the simulation and experiment results, pICA-R may prove a promising multivariate approach for use in imaging genomics to discover reliable genetic risk factors under a scenario of relatively high dimensionality and small effect size.

Introduction

Imaging genomics is an emerging field dedicated to the study of genetic variants associated with brain structure and function. Structural or functional imaging markers are believed to be closer to the underlying biological mechanisms affected by genetic variants than behavioral or symptom-based measures (Rasch et al., 2010; Turner et al., 2006). A recent meta-analysis lent support for this notion, where schizophrenia (SZ) risk variants were found to show larger effects at the level of brain structure and function than behavior (Rose and Donohoe, 2012). Consequently, interest in studying imaging measures has increased. In the case of structural imaging, measurements can be obtained via different approaches, ranging from single region-of-interest (ROI) methods, to image-wide approaches such as voxel based morphometry (VBM) (Ashburner and Friston, 2005) and surface-based measures such as FreeSurfer (Fischl and Dale, 2000).

High-throughput genotyping employing genome-wide techniques has made it feasible to sample the entire genome of a substantial number of individuals (Oliphant et al., 2002; Shen et al., 2005). More targeted candidate gene strategies examining a limited number of points of genetic variations have been successfully applied to the study of illnesses such as Fragile X syndrome (Lightbody and Reiss, 2009). Yet, the candidate gene approach is less applicable when the genetic basis of a disease is complex and less understood. For instance, little success has been achieved in replicating evidence for causal genes in schizophrenia (SZ) (Duan et al., 2010) using traditional candidate gene approaches. In contrast, recent works (Derks et al., 2012; Purcell et al., 2009) lent support for a polygenic model in many cases (Gottesman and Shields, 1967) of SZ, where an aggregate of common genetic variants were shown to collectively account for a substantial proportion of variation in risk, despite concomitant evidence for rare mutations of large effect size (Xu et al., 2009). Given such evidence, an unbiased search of the entire genome may more effectively describe the genetic architecture underlying complex disorders in which a significant proportion of risk for the disorder is likely due to many genetic variants, each carrying a small proportion of disease risk and failing to reach genome-wide significance individually.

While there is growing interest in image-wide and genome-wide approaches which allow unbiased searches over a large range of variants, novel mathematical and computational methods are desired to optimally combine these two strategies. One of the most challenging problems is the correction for the huge number of statistical tests used in univariate models. The correction makes it highly difficult to identify a factor of small effect size with a practical sample size. In addition, univariate approaches are not well-suited to identify weak effects across multiple variables. For this reason, multivariate approaches show specific advantage for simultaneously assessing many variables for an aggregate effect. To better identify aggregate effects across many variables, a number of models have been derived, including principal component regression (PCReg) (Wang and Abbott, 2008), sparse reduced-rank regression (sRRR) (Vounou et al., 2010) and parallel independent component analysis (pICA) (Liu et al., 2009).

PCReg, sRRR, and pICA are designed to deal with datasets of high dimensionality and yield interpretable results. However these approaches are not able to take prior information into account. Such information can be useful to enable a guided yet flexible approach and can improve the robustness of the results compared to a fully blind approach. For instance, some genes known to participate in a biological pathway critical to a disease may help identify a set of genes contributing in a coordinated way to a larger network. The incorporation of prior information may be especially helpful in analyzing genomic data, where a component usually accounts for a small amount of variance in the data and is more difficult to identify (Liu et al., 2012). Thus, we propose parallel independent component analysis with reference (pICA-R), which extends pICA to incorporate prior information to provide a reference to guide analyses. While pICA is designed based on regular (blind) ICA to enhance correlation between two modalities, pICA-R further takes advantage of a priori knowledge to guide the analysis and pinpoint a particular component of interest embedded in a large complex dataset. In this work, we compare pICA-R with other multivariate models through simulated data and evaluate the models under several scenarios. In addition, we apply pICA-R to a real dataset consisting of whole-brain gray matter concentration images and genome-wide single nucleotide polymorphisms (SNPs) to test whether pICA-R is able to yield reliable and interpretable components given a sample size of 300.

Material and Methods

pICA-R

pICA-R is formulated by incorporating a reference constraint into pICA to guide the component extraction towards a priori knowledge. Typical pICA builds on regular infomax (Amari et al., 1996; Bell and Sejnowski, 1995) to extract independent components in parallel for each modality, followed by a conditional enhancement of the inter-modality correlations (Liu et al., 2009). In comparison, pICA-R imposes an additional constraint upon the infomax framework to minimize the distance between a certain component and the reference. The mathematical model is shown below, and Fig. 1 illustrates the flow of the approach.

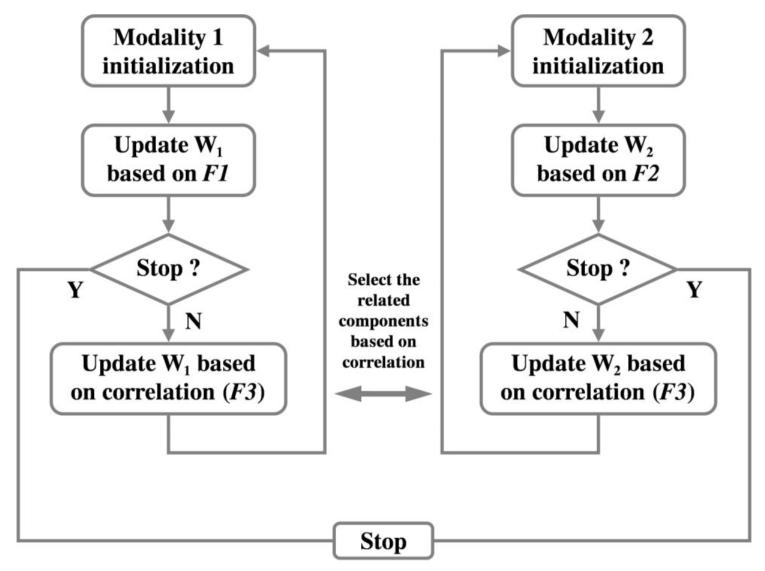
Figure 1.

Flow chart of pICA-R. W₁ and W₂ denote the unmixing matrices of the two modalities, respectively. F1, F2 and F3 represent the objective functions based on which unmixing matrices are updated.

$${\mathrm{X}}_{\mathrm{m}}={\mathrm{A}}_{\mathrm{m}}{\mathrm{S}}_{\mathrm{m}}\to {\mathrm{S}}_{\mathrm{m}}={\mathrm{W}}_{\mathrm{m}}{\mathrm{X}}_{\mathrm{m}},{\mathrm{A}}_{\mathrm{m}}={\mathrm{W}}_{\mathrm{m}}^{-1},\mathrm{m}=1,2$$ (1)

$$\begin{array}{cc}\hfill {\mathrm{Y}}_{\mathrm{m}}=\frac{1}{1+{\mathrm{e}}^{-{\mathrm{U}}_{\mathrm{m}}}},{\mathrm{U}}_{\mathrm{m}}& ={\mathrm{W}}_{\mathrm{m}}{\mathrm{X}}_{\mathrm{m}}+{\mathrm{W}}_{\mathrm{m}0}\hfill \\ \hfill \mathrm{F}1=\max \left\{\mathrm{H}\right({\mathrm{Y}}_1\left)\right\}=& \max \{-\mathrm{E}[\ln f_{y_1}\left({\mathrm{Y}}_1\right)\left]\right\}\hfill \\ \hfill \mathrm{F}2=\max \left\{\lambda \mathrm{H}\right({\mathrm{Y}}_2)+(1-\lambda \left)\right[-{\mathrm{dist}}^2(\tilde{\mathrm{r}},\mid {\tilde{\mathrm{S}}}_{2\mathrm{k}}\mid )\left]\right\}& =\max \left\{\lambda \right(-\mathrm{E}\left[\ln f_{y_2}\right({\mathrm{Y}}_2\left)\right])+(1-\lambda \left)\right(-{\mid \mid \mid {\mathrm{W}}_{2\mathrm{k}}{\tilde{\mathrm{X}}}_2\mid -\tilde{\mathrm{r}}\mid \mid }_2^2\left)\right\}\hfill \end{array}$$ (2)

$$\mathrm{F}3=\max \left\{{\Sigma }_{\mathrm{i},\mathrm{j}}{\mathrm{Corr}}^2\right({\mathrm{A}}_{1\mathrm{i}},{\mathrm{A}}_{2\mathrm{j}}\left)\right\}=\max \left\{{\Sigma }_{\mathrm{i},\mathrm{j}}\frac{{\mathrm{Cov}}^2({\mathrm{A}}_{1\mathrm{i}},{\mathrm{A}}_{2\mathrm{j}})}{\mathrm{Var}\left({\mathrm{A}}_{1\mathrm{i}}\right)\mathrm{Var}\left({\mathrm{A}}_{2\mathrm{j}}\right)}\right\}$$ (3)

Given a dataset X with dimension of sample (i.e., subjects) × feature (i.e., voxels [m=1], SNPs [m=2]), Eq. (1) illustrates the mathematical model of data decomposition, where the observed dataset X is decomposed into a linear combination of the underlying independent components, or sources. S is the component matrix, A is the loading or mixing matrix (estimated as the pseudo inverse of W), W is the unmixing matrix, and the subscript m runs from 1 to 2, denoting the data modality. Specifically, pICA-R iteratively solves the unmixing matrices W₁ and W₂ simultaneously for the two modalities, gradually maximizing the objective functions F1, F2 and F3 in the manner described in Fig. 1. In particular, F1 is the objective function of the regular infomax (Bell and Sejnowski, 1995) for modality 1, where independence among components is achieved by maximizing the entropy (H), as shown in Eq. (2). f_y(Y) is the probability density function of Y and W₀ is the bias vector. In contrast, F2 is the objective function for modality 2, where an additional closeness metric is imposed to extract maximally independent components, one of which also closely resembles the reference r. The inter-modality correlation function F3 shown in Eq. (3) is designed to maximize the correlations computed over the columns of the loading matrices A₁ and A₂, capturing connections between pairs of inter-modality components.

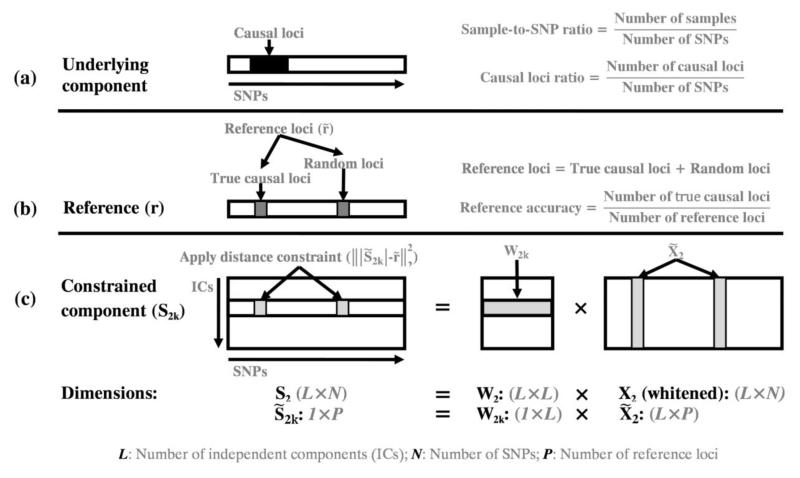
pICA-R incorporates an additional constraint to the unmixing matrix of modality 2 (W₂), detaching itself from regular blind pICA. The objective function F2 is shown in Eq. (2) and Fig. 2 illustrates how the constraint is applied. In this application modality 2 is the genomic data. The reference r is a binary vector with the same number of loci as the genomic data, where the selected reference loci are set to “1” and the rest are “0”s. This binary reference effectively serves as a mask such that the closeness between the component and reference is measured on the reference loci only. This design considers that for a given reference a number of loci are presumably of interest and set to 1, while the status of the remaining loci is to-be-determined instead of not interesting. Therefore, we choose to optimize the closeness specifically for the selected reference loci while allowing the remaining loci to show their own importance driven by data. This is equivalent to minimizing ${\mid \mid \mid {\tilde{\mathbf{S}}}_{2k}\mid -\tilde{\mathbf{r}}\mid \mid }_2^2$ in F2, where $\tilde{\mathbf{r}}$ denotes a subvector of r, ${\tilde{\mathbf{S}}}_{2k}$ denotes a subvector of S_2k (the k^th row of S₂), W_2k denotes the k^th row of W₂ and ${\tilde{\mathbf{X}}}_2$ denotes a submatrix of X₂, as illustrated in Fig. 2. ||·||₂ represents the L₂-norm Euclidian distance, and λ is a weighting parameter. It should be noted that we apply the constraint only to one modality in this work, which provides a simple proof-of-concept and also fits the proposed application in imaging genomics. The constraint can be extended to both modalities if necessary.

Figure 2.

Illustration of the applied distance constraint: (a) the underlying component with highlighted causal loci (black region); (b) the generated reference, where r is the reference vector with selected reference loci set to 1 (gray region) and other loci set to 0. $\tilde{\mathbf{r}}$ denotes a subvector consisting of all the reference loci; (c) the closeness is optimized specifically for the selected reference loci of one component. W₂ is the unmixing matrix of modality 2, X₂ is the data matrix and S₂ is the component matrix. ${\tilde{\mathbf{S}}}_{2k}$ denotes a subvector of S_2k (the k^th row of S₂), W_2k denotes the k^th row of W₂ and ${\tilde{\mathbf{X}}}_2$ denotes a submatrix of X₂.

To solve this linearly weighted multi-objective optimization problem for modality 2 (Klamroth and Tind, 2007), we have adopted several strategies to avoid local optimization and overfitting. First, the constrained component (i.e., S_2k in F2) is selected dynamically based on the data. Specifically, in each iteration, we examine the distances between the reference and all the components, and then select only the closest component to be constrained. Second, to avoid over-emphasizing the distance metric, we adaptively adjust the constraint weight λ. Starting with a heuristic weight, we monitor the overall independence (log|det(W₂)|) and the distance measure after each iteration, then adjust λ accordingly to ensure the balance between the two objectives in the objective function.

The three objective functions (F1, F2 and F3) are optimized using gradient maximization. Specifically, for F1 and F2, W₁ and W₂ are updated by the natural gradient learning rule (Amari, 1998), and for F3, A₁ and A₂ are updated by the steepest descent learning rule (Liu et al., 2009), as shown in Eq. (4). α₁, α₂, α_c1 and α_c2 denote the leaning rates.

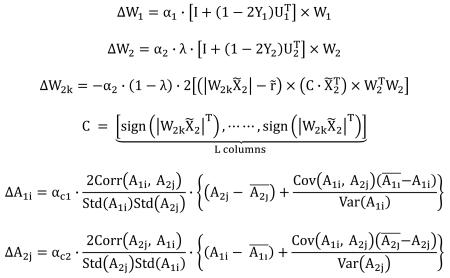Simulation

The proposed pICA-R approach was evaluated using simulated functional MRI (fMRI) and SNP data for its capability to extract factors of interest, particularly in the genetic modality. The fMRI data consisted of 200 samples (i.e., subjects) and 10K voxels. Eight non-overlapping brain networks were simulated using the SimTB toolbox ((Erhardt et al., 2011), http://mialab.mrn.org/software). The SNP data were simulated to investigate the performances of pICA-R when components accounted for different amounts of variance in the data, which was achieved through adjusting sample-to-SNP ratios, causal loci ratios, and effect sizes of causal loci. The sample-to-SNP ratio compared the sample size (or number of subjects) with the total number of SNP loci (or SNP dimensionality); the causal loci ratio compared the number of causal loci with the SNP dimensionality; the effect size of causal loci was measured by percentage of variance explained in disease status. Specifically, the SNP data consisted of 200 simulated samples (subjects), each with equal SNP dimensionality, which ranged from 10K to 500K. Eight non-overlapping SNP components were simulated using PLINK (Purcell et al., 2007), each involving 150 causal loci associated with a randomly generated case-control pattern. The resulting sample-to-SNP ratio ranged from 0.02 (200/10K) to 4.00×10⁻⁴ (200/500K), and the causal loci ratio ranged from 0.015 (150/10K) to 3.00×10⁻⁴ (150/500K). The effect size of individual causal loci ranged from 0.003 to 0.21. None of the SNP components shared common causal loci. No high linkage disequilibrium (LD) was observed among causal loci (maximum correlation < 0.39). We further designed a mixing matrix for the fMRI data where randomly selected columns were correlated to particular case-control patterns of the SNP components. The simulated brain networks were then combined into one fMRI observation matrix through this mixing matrix. Random Gaussian noise was superimposed afterwards. We did not adjust the number of components in the simulations as the ability to recover the independent hidden factors is not significantly affected by how many components are embedded, provided that the number of components can be correctly approximated. We used second-level (subject × feature) fMRI data in this simulation, however we would expect comparable performances when pICA-R is applied to structural grey matter images, given that both are feature-based maps and structure-function associations have been observed at the feature level in an ICA framework (Calhoun et al., 2006; Segall et al., 2012).

We then applied pICA-R to the simulated datasets and compared its performance with those of ICA (regular infomax), ICA with reference (ICA-R) (Lin et al., 2010) and pICA. Default settings were used for infomax, ICA-R and pICA. Since infomax, pICA and pICA-R require selection of the component number, we set this to 8, the true component number for the simulated data, for the fMRI modality in all tests. For the SNP modality, due to different data properties, the true component number may not yield reliable results (Chen et al., 2012). Therefore, in the tests with infomax and pICA, we examined component numbers ranging from 5 to 50 (in steps of 5), and selected the one yielding optimal results. The number of components was selected to be 50 in all pICA-R tests, given our observation that the proposed pICA-R tends to be robust to over-estimation.

The performance was evaluated based on accuracies of the genetic components and loadings, as well as the inter-modality connections. The SNP component accuracy was assessed by a sensitivity measure, the ratio of correctly identified causal loci (among the top 150 loci) to the built-in true causal loci. The genetic loading accuracy was reported as the absolute value of the correlation between the simulated case-control pattern and the extracted loadings. We also calculated the correlations between loadings of the two components (SNP and fMRI) that most resembled the ground truth of the two modalities, respectively, to assess the accuracy of the inter-modality connections.

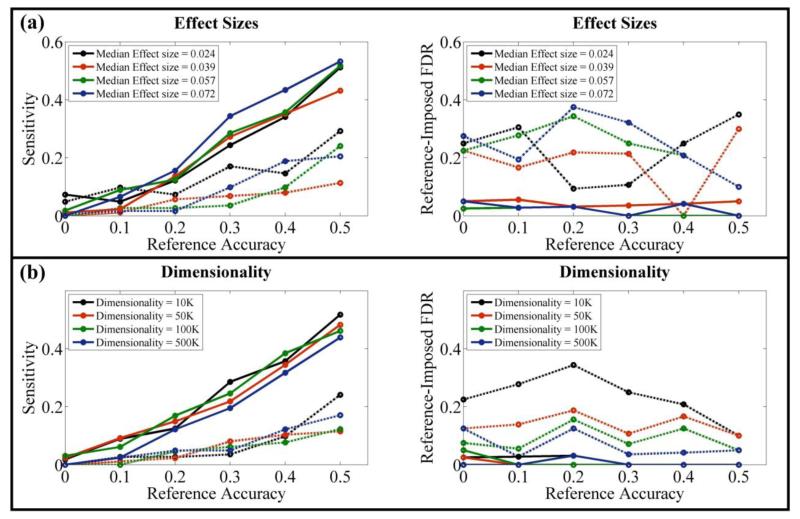
Particularly, for the two semi-blind methods (pICA-R and ICA-R), we investigated how their performances would be affected by the reference accuracies (ratio of true causal loci in the reference, as illustrated in Fig. 2). Previous work indicated that a 20-loci reference of accuracy 1 was required for ICA-R to reliably extract factors of interest when the sample-to-SNP ratio was 0.02 (Liu et al., 2012). Guided by this, we first tested a reference of accuracy 1, spanning 20 randomly selected true causal loci. We then tested a 40-loci reference of accuracy 0.5, primarily to investigate how the performances would be affected by adding random loci. Then accuracies were adjusted from 0.1 to 0.5 for the 40-loci references to investigate the influence. The performance was evaluated in terms of sensitivity (as described above) and reference-imposed false discovery rate (FDR), which was to assess the overfitting by evaluating how many referential random loci were falsely elevated as causal.

Real data experiment

Structural MRI (sMRI) and SNP data were obtained from The Mind Clinical Imaging Consortium (MCIC), a collaborative effort of four research teams from University of New Mexico-Mind Research Network, Massachusetts General Hospital, University of Minnesota and University of Iowa) and from a local COBRE (Center of Biomedical Research Excellence) study. The institutional review board at each site approved the study and all participants provided written informed consents. All healthy participants were screened to ensure that they were free of any medical, neurological or psychiatric illnesses, including any history of substance abuse. The inclusion criteria for patients were based on a diagnosis of schizophrenia, schizophreniform or schizoaffective disorder confirmed by the Structured Clinical Interview for DSM-IV-TR disorders (SCID, (First et al., 1997)) or the Comprehensive Assessment of Symptoms and History (CASH, (Andreasen et al., 1992)). After preprocessing, we obtained a total of 300 participants (160 healthy controls and 140 SZ patients) for which both sMRI and SNP data were collected. Table 1 provides the demographic information.

Table 1.

Demographic information of participants

Demographics		SZ (140)	HC (160)	P-value
Sex	Male	106	104	0.04
	Female	34	56
Age	Mean ± SD	36 ± 12	33 ± 11	0.03
	Range	18 - 63	18 - 63
Race/Ethnicity	Caucasian	109	140	0.19
	African American	20	8
	Asian	5	5
	Native Hawaiian	1	0
	American Indian	1	2
	Unreported	4	5
Collection site	Harvard	28	24	0.85
	Iowa	32	59
	Minnesota	30	19
	New Mexico	50	58

The T₁-weighted sMRI data (for details about data collection, see SI Materials and Methods) were preprocessed in Statistical Parametric Mapping 5 (SPM5, http://www.fil.ion.ucl.ac.uk/spm) using voxel based morphometry (VBM) (Ashburner and Friston, 2005), a unified model where image registration, bias correction and tissue classification are integrated. Brains were segmented into gray matter, white matter and cerebrospinal fluid based on unmodulated normalized parameters. The resulting gray matter images consisted of voxelwise gray matter concentrations. Images were re-sliced to 2 × 2 × 2 mm, resulting in 91 × 109 × 91 voxels. The gray matter images were then smoothed with 10mm full width at half-maximum Gaussian kernel. In the subsequent quality check, we further excluded two participants whose images were four standard deviations away from the average gray matter image. A mask was then generated to include only the voxels inside the brain as well as exhibiting an average gray matter concentration greater than 0.1, resulting in a total of 253,632 voxels. Finally, a voxel-wise regression analysis was performed at each voxel to eliminate the effects from age, sex and collection site. The gray matter images corrected for the above variables were then analyzed in conjunction with the SNP data.

DNA was extracted from blood samples of MCIC participants and saliva samples of COBRE participants, respectively. Genotyping for all participants was performed at the Mind Research Network using the Illumina Infinium HumanOmni1-Quad assay spanning 1,140,419 SNP loci. BeadStudio was used to make the final genotype calls. No significant difference was observed in genotyping call rates between blood and saliva samples. Next, the PLINK software package ((Purcell et al., 2007), http://pngu.mgh.harvard.edu/~purcell/plink) was used to perform a series of standard quality control procedures (Anderson et al., 2010), including missingness, relatedness, heterozygosity, Hardy-Weinberg equilibrium and minor allele frequency (MAF), resulting in the final dataset spanning 728,683 SNP loci. Population stratification was then assessed through principal component analysis (PCA) (Price et al., 2006); for additional details, see SI Materials and Methods.

We leveraged the results from an independent genome-wide SZ study to obtain genetic references. First, we selected a potential susceptibility gene ANK3 with intragenic SNPs exhibiting top genome-wide associations in the Psychiatric Genomics Consortium (PGC) SZ study ((Ripke et al., 2011), Table S10), which is currently the SZ study with the largest sample size. This gene is involved in neuronal activities (Lambert et al., 1997; Zhou et al., 1998) and therefore poses a promising candidate to be a reference in this imaging genetics study. We then identified the corresponding SNPs in ANK3 and grouped neighboring SNPs with moderate LD (|r| > 0.5) into a cluster, which could serve as a reference set. The LD threshold was determined by a visual inspection of our data, while also considering that SNPs with r² > 0.2 are not considered independent (Ripke et al., 2011). For this proof-of-principle and method development study, our primary strategy for reference selection was that, in pICA-R, the reference loci are expected to contribute simultaneously to one single component, which is the case most likely to happen for SNPs in LD. Therefore, we chose to use LD clusters as references to elicit more SNPs contributing in a coordinated manner. Finally we tested three reference sets from ANK3, each spanning more than 40 SNPs, which were to yield at least 20 true loci with an accuracy of 0.5, a reasonable size as observed in simulations. It should be noted that we only examined a limited number of references in this work, as the major purpose was to demonstrate an application of the proposed approach instead of performing a complete SZ study. While there are also other genes that are of great importance, they will be left for future investigations.

For the purpose of validating our finding, the SNP component identified by pICA-R was examined for its SZ enrichment based on the independent results of the PGC SZ study (Ripke et al., 2011). We first selected out SNPs significantly contributing to the identified component. Next, we compared the ratios of SZ-related SNPs in the selected top contributing SNPs and in the whole genome. For each SNP, the SZ-relevance was determined based on the significance of association reported in the PGC SZ study, such that a SNP exhibiting SZ association with a p-value less than P_th was considered as SZ-related. To examine the enrichment across different significance levels, we tested a P_th range from the standard level of 0.05 to a more significant level of 0.001. Then based on this criterion of SZ-relevance, we performed Fisher’s exact test to evaluate the significance of SZ enrichment in our finding compared to the whole genome.

In addition, we applied ICA, pICA and ICA-R to the sMRI-SNP dataset for a comparison. In case of ICA, we applied two separate regular ICAs to the sMRI and SNP data respectively. Then pairwise correlations were calculated based on the loadings. In case of pICA, the dataset were directly analyzed for inter-modality associations. In case of ICA-R, we applied regular ICA to the sMRI data while ICA-R was used to extract the SNP component given the same reference. As in pICA-R, the number of components was selected to be 10 for the sMRI data and 27 for the SNP data, if a component number estimation applied.

Results

Simulations

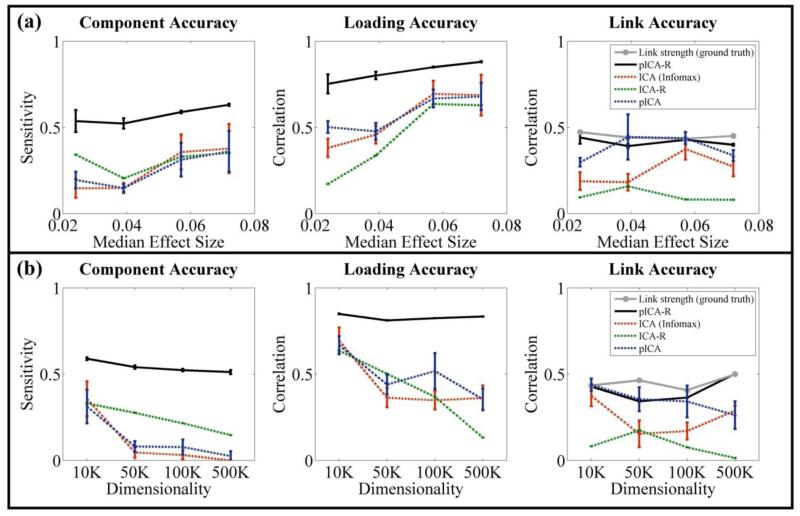
As expected, fMRI components were accurately identified (component and loading accuracies higher than 0.9) in all tests, given that each component carried a considerable amount of variance in the data. Regarding the SNP modality, with a 20-loci reference of accuracy 1, pICA-R exhibited consistently better performance than the other algorithms in identifying SNP components with different levels of sample-to-SNP ratio, causal loci ratio and effect size. Fig. 3a and 3b summarize the simulation results, where the error bar reflects mean ± SD based on 100 runs. It can be seen that accuracies of SNP components, associated loadings and connections between SNP and fMRI measured by sensitivity or correlation were all improved compared with infomax, ICA-R and pICA. Also it is noted that pICA-R was able to identify the component with a sensitivity above 0.5 given a median effect size as low as 0.024 while the sample-to-SNP ratio was controlled at 0.02 and the causal loci ratio at 0.015. While the median effect size was controlled around 0.05, pICA-R in general exhibited robust performances within the tested ranges of sample-to-SNP ratio and causal loci ratio. We also conducted a simulation at the low sample-to-SNP ratio (200/500K) with an increased causal loci ratio (1000/500K), a scenario similar to SZ application, and found that pICA-R exhibited a comparable sensitivity (0.53) using a 20-loci reference of accuracy 1 (not shown). Therefore, we assume that a reference spanning at least 20 true causal loci is suitable for the real data application provided that the causal loci ratio is above 3.00×10⁻⁴.

Figure 3.

Performance comparisons among pICA-R, ICA (infomax), ICA-R and pICA: (a) on simulated datasets with different effect sizes when the sample-to-SNP ratio was controlled at 0.02 and causal loci ratio at 0.015; (b) on simulated datasets with SNP dimensionality ranging from 10K to 500K, resulting in sample-to-SNP ratios ranging from 0.02 to 4.00×10⁻⁴ and causal loci ratios from 0.015 to 3.00×10⁻⁴, the median effect sizes were 0.057, 0.055, 0.050 and 0.050 respectively. For pICA-R and ICA-R, results were obtained with a 20-loci reference of accuracy 1. The error bars reflect mean ± SD based on 100 runs.

The reference accuracy is crucial for identifying the correct component, as illustrated in Fig. 4. As expected, pICA-R showed increased sensitivities with references of higher accuracies. It is also noted that a 40-loci reference of accuracy 0.5 yielded a sensitivity around 0.5, comparable to that obtained with a 20-loci reference of accuracy 1. Most importantly, the results indicated that when the sample-to-SNP ratio was lower than 0.004 (200/50K) and the causal loci ratio lower than 0.003 (150/50K), pICA-R started to benefit in sensitivity compared to ICA and pICA with a reference accuracy as low as 0.2. In contrast to sensitivity, the performance in reference-imposed FDR was less affected by the reference accuracy and remained below 0.05. Overall, pICA-R exhibited improvements in both sensitivity and reference-imposed FDR compared to ICA-R.

Figure 4.

Performance comparisons between pICA-R and ICA-R, with 40-loci references of different accuracies: (a) on simulated datasets with different effect sizes when the sample-to-SNP ratio was controlled at 0.02 and causal loci ratio at 0.015; (b) on simulated datasets with SNP dimensionality ranging from 10K to 500K, resulting in sample-to-SNP ratios ranging from 0.02 to 4.00×10⁻⁴ and causal loci ratios from 0.015 to 3.00×10⁻⁴, the median effect sizes were 0.057, 0.055, 0.050 and 0.050 respectively. The solid and dotted lines reflect results of pICA-R and ICA-R, respectively.

Real data experiment

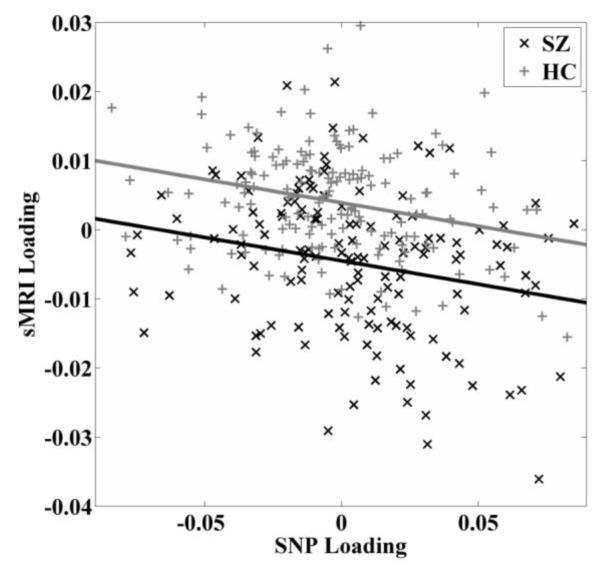
On the real sMRI and SNP dataset, the number of components was estimated to be 10 on uncorrelated voxels of the sMRI data using minimum description length (MDL) (Rissanen, 1978). For the SNP data, 27 components were extracted based on the metric of consistency (Chen et al., 2012). We tested the three reference sets generated from ANK3 (Ripke et al., 2011), and one reference set spanning 82 SNPs helped elicit significant inter-modality connection. These 82 SNPs exhibited moderate LD with an average correlation of 0.57 and were separated by an average of 1,276 base pairs. Guided by this reference, pICA-R identified one component pair exhibiting the highest correlation of −0.27 and a p-value of 1.64×10⁻⁶ (passing Bonferroni correction of 0.05/10/27). After regressing out variables (specifically age, sex, race/ethnicity, collection site and SZ diagnosis for the SNP component; race/ethnicity and SZ diagnosis for the sMRI component), the sMRI-SNP association remained significant, exhibiting a partial correlation of −0.24 (p = 2.81×10⁻⁵), as shown in Fig. 5.

Figure 5.

Scatter plots of loading coefficients associated with the identified sMRI and SNP components in patient and control group respectively. Controlling variables (age, sex, race/ethnicity, collection site) are corrected.

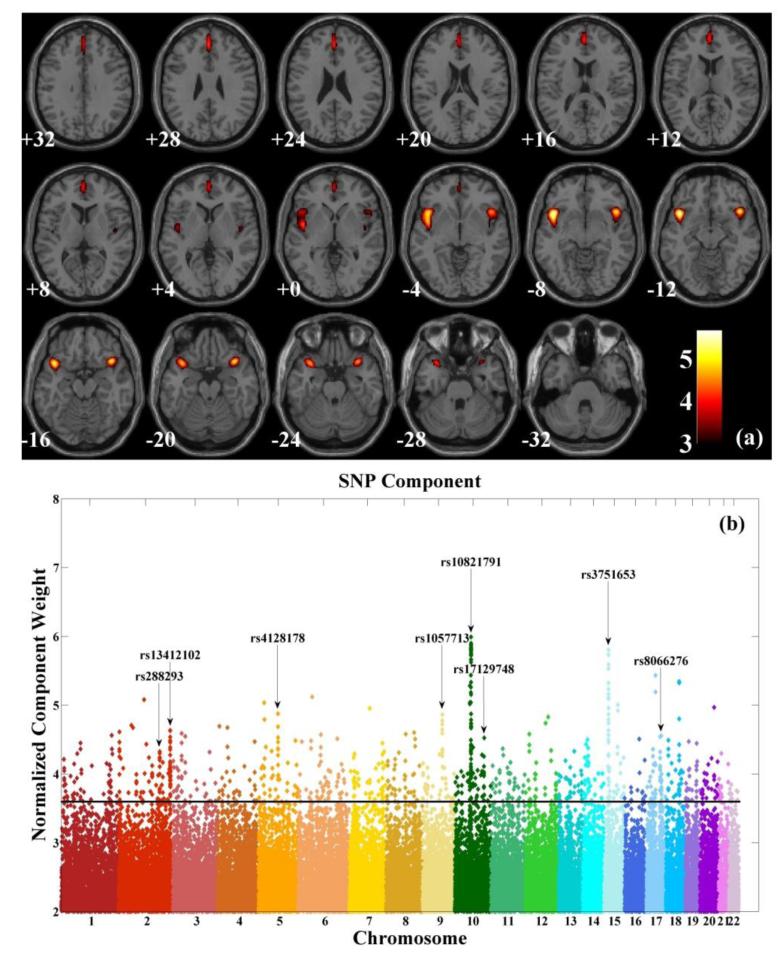
The loadings of the linked sMRI component significantly differed between SZ patients and healthy controls (two tailed t-test, p = 1.33×10⁻¹⁵). Note that effects from age, sex and collection site were already regressed out from the data and we did not observe any significant regression (two tailed t-test, p = 0.11) effect from the race/ethnicity on the sMRI component while controlling for diagnosis. We further examined whether medication affected the identified brain network in patients and found no significant regression effect (two-tailed t-test, p = 0.62) from the reported chlorpromazine equivalent dosage (Gardner et al., 2010) on the sMRI loadings while controlling for race/ethnicity. Fig. 6a shows the spatial map of the sMRI component thresholded at |Z| > 3. The identified brain network included medial and inferior frontal gyri, superior temporal gyrus, insula and anterior cingulate, as listed in Table 2.

Figure 6.

Maps of identified components: (a) spatial map of brain network for the identified sMRI component (thresholded at |Z| > 3); (b) Manhattan plot for the identified SNP component (threshold at |Z| > 3.60 for top contributing SNPs).

Table 2.

Talairach labels of identified brain regions.

Brain region	Brodmann area	L/R volume (cm3)	L/R random effects, max Z (x,y,z)
Medial Frontal Gyrus	9, 10, 6, 8	3.2/1.4	4.21(0,42,22)/3.98(2,49,10)
Inferior Frontal Gyrus	47, 13	2.6/2.8	5.09(−40,17,−14)/5.67(44,13,−9)
Superior Temporal Gyrus	38, 22, 13	2.3/3.8	4.94(−44,17,−13)/5.54(44,13,−11)
Insula	13, 22, 47	0.4/1.8	3.74(−44,9,−6)/5.28(44,9,−7)
Anterior Cingulate	32, 10	0.7/0.3	4.01(0,49,7)/3.86(2,47,9)

The loadings associated with the linked SNP component exhibited a significant group difference between patients and controls (two tailed t-test, p = 0.04). The SNP component followed a super-Gaussian distribution and Fig. S2 shows a logistic fit to the histogram. Based on the normalized component weights, we selected out 1,030 top contributing SNPs (top 1,030 based on the absolute values of the normalized component weights, corresponding to |Z| > 3.60, p = 0.003 based on the logistic fit, see Fig. S3) as our finding. Fig. 6b shows a Manhattan plot of weights of loci for the identified SNP component, where clusters spanning more than 10 top contributing SNPs are marked. Table S1 provides a summary of the identified 1,030 SNPs, including SNP position, corresponding gene, normalized component weight, and MAFs in patient and control groups. Fifty-four out of the top 1,030 contributing SNPs were from the reference set and are marked in Table S1. A complete list of the 82 reference SNPs is also provided in Table S2. After these 54 reference SNPs were excluded, 656 out of the remaining 976 SNPs had been investigated in the PGC study for associations with SZ. We then conducted Fisher’s exact test on SZ enrichment between these 656 matched SNPs and the whole genome of PGC data (spanning a total of 1,252,901 SNPs). As shown in Fig. 7, significant SZ enrichment was consistently observed within the entire range of tested P_th’s.

Figure 7.

Fisher’s exact test on SZ enrichment between the identified SNPs and the whole genome based on PGC results. P_th denotes the threshold p-value of SZ-relevance, ranging from 0.001 to 0.05.

We further investigated biological functions in which these top contributing SNPs are involved. While 522 out of 1,030 SNPs were mapped to 228 unique genes, Ingenuity Pathway Analysis (IPA: Ingenuity® Systems, http://www.ingenuity.com) indicated a significant enrichment of the domain of central nervous system development (p = 2.88×10⁻⁴) in our finding, where 7 genes were involved, as highlighted in Table 3a. The identified genes were also significantly overrepresented in glutamate receptor signaling (p = 2.75×10⁻²) and DARPP32 regulated pathway (p = 4.07×10⁻²), as well as synaptic long term depression (LTD, p = 1.58×10⁻²) and potentiation (LTP, p = 3.24×10⁻²), as highlighted in Table 3b. In addition, the DAVID (Database for Annotation, Visualization and Integrated Discovery) bioinformatics resource (Huang et al., 2009a, b) identified significant clusters functionally related to cell adhesion (p = 1.14×10⁻⁵), synaptic transmission (p = 2.86×10⁻⁴) and neuron projection morphogenesis (p = 1.75×10⁻³) respectively, as highlighted in Table 3c.

Table 3.

Biological Pathway analysis and functional annotation clustering.

1a. IPA biological function	Genes	P-value/P-value (B-H)
Coronary disease	ACE, ASIC2, CACNA1C, CERS6, CHRNA5, CSMD1, CSMD2, ITGB2, MECOM, MGAM, PPARA, PTPRM, SAMD12	2.24E-05/1.68E-02
Vascular disease	ACE, ASIC2, CACNA1A, CACNA1C, CERS6, CHRNA5, COL4A1, COL4A2 (includes EG:12827), CSMD1, CSMD2, ITGB2, MECOM, MGAM, PPARA, PTPRM, SAMD12, TEK	8.53E-05/2.25E-02
Aggregation of tumor cell lines	CMIP, DAPK3, IGF1R, ITGB2, PRKD1	9.70E-05/2.25E-02
Coronary artery disease	ASIC2, CACNA1C, CERS6, CSMD1, CSMD2, ITGB2, MECOM, MGAM, PPARA, PTPRM, SAMD12	1.20E-04/2.25E-02
Development of central nervous system	ADAM22, ASIC2, CNTNAP2, DSCAML1, MYO16, PARK2, ZBTB16	2.88E-04/4.31E-02
Atherosclerosis	ACE, ASIC2, CACNA1C, CERS6, CSMD1, CSMD2, ITGB2, MECOM, MGAM, PPARA, PTPRM, SAMD12	4.26E-04/5.33E-02
1b. IPA Canonical Pathway	Genes	P-value/P-value (B-H)
AMPK Signaling	PFKFB3, AK5, ACACB, PPP2R2C, PFKP, CHRNA5	4.17E-03/7.93E-01
Aldosterone Signaling in Epithelial Cells	DNAJC17, ASIC2, DNAJC18, PLCB1, DNAJC10, PRKD1	9.77E-03/8.08E-01
Synaptic Long Term Depression	IGF1R, PLCB1, PPP2R2C, GRM4, PRKD1	1.58E-02/8.08E-01
Maturity Onset Diabetes of Young (MODY) Signaling	CACNA1C, CACNA1A	2.04E-02/8.08E-01
Glutamate Receptor Signaling	SLC1A1, GRM4, GNG2	2.75E-02/8.08E-01
Synaptic Long Term Potentiation	CACNA1C, PLCB1, GRM4, PRKD1	3.24E-02/8.08E-01
Dopamine-DARPP32 Feedback in cAMP Signaling	CACNA1C, PLCB1, PPP2R2C, PRKD1, CACNA1A	4.07E-02/8.08E-01
Agrin Interactions at Neuromuscular Junction	ITGB2, NRG3, ARHGEF7	4.37E-02/8.08E-01
G Protein Signaling Mediated by Tubby	PLCB1, GNG2	5.01E-02/8.08E-01
RhoGDI Signaling	CDH12, ARHGEF7, CDH10, GNG2, ARHGAP8/PRR5-ARHGAP8	5.13E-02/8.08E-01
1c. DAVID functional annotation cluster	Genes	P-value/P-value (B-H)
Cell adhesion	PTPRM, CLSTN2, MAGI1, TNC, PCDH9, FBLIM1, DSCAML1, ITGB2, PTPRT, COL5A1, BTBD9, CDH12, SEMA5A, PKP2, TEK, PECAM1, CNTNAP2, RELN, CNTN4, IZUMO1, ADAM22, CDH10	1.14E-05/1.14E-02
Synaptic transmission	GRM4, ACCN1, DLGAP1, GABRR1, CHRNA5, PARK2, VIPR1, CACNA1C, KCNIP1, RIMS1, SLC1A1, CACNA1A	2.86E-04/9.18E-02
Neuron projection morphogenesis	SEMA5A, IGF1R, PTPRM, ANK3, DSCAML1, CNTN4, RELN, GAS7, CACNA1A	1.75E-03/1.78E-01

Note: P-value(B-H) represents the Benjamini-Hochberg corrected p-value of enrichment.

In addition, we applied ICA, pICA and ICA-R to the sMRI-SNP dataset for a comparison. In case of ICA, we applied two separate regular ICAs to the sMRI and SNP data respectively. Then pairwise correlations were calculated based on the loadings. In case of pICA, the dataset were directly analyzed for inter-modality associations. In case of ICA-R, we applied regular ICA to the sMRI data while ICA-R was used to extract the SNP component given the same reference. As in pICA-R, the number of components was selected to be 10 for the sMRI data and 27 for the SNP data, if a component number estimation applied.

Discussion

In this work, we present a semi-blind multivariate approach, pICA-R, to jointly analyze MRI and genetic data and identify relationships between hidden factors. pICA-R is designed to analyze multiple variants for an aggregate effect. The model employs prior information to guide the analysis while allowing the remaining variants to show their own importance driven by the data, enabling a guided yet flexible approach to improve the robustness of the results compared to a fully blind approach. In this way, a limited number of variants which comprise a small portion of a polygenic component, can help elicit other variants previously not expected of playing a role, thus improving the understanding of the underlying biology. Leveraging prior information also allows the model to pinpoint a particular component of interest embedded in a complex high-dimensional dataset and provides a better chance to dissect complex traits. Overall, pICA-R holds the promise to accelerate the pace of discoveries of trait-associated polygenic components through integrating diverse data types and incorporating knowledge learned from previous studies (Stranger et al., 2011).

The simulation results demonstrate that the approach helps capture factors of interest more accurately. As illustrated in Fig. 2a and 2b, pICA-R show consistently better results for component accuracy, component loadings and inter-modality link compared to regular ICA, ICA-R and pICA, and the improvement becomes more pronounced with lower sample-to-SNP ratio and causal loci ratio, or smaller effect size. It can be seen that the proposed approach yields a sensitivity above 0.5 at a low sample-to-SNP ratio of 4.00×10⁻⁴ (200/500K) and a causal loci ratio of 3.00×10⁻⁴ (150/500K), while the median effect size is around 0.05. This observation encourages the application of pICA-R to genomic data with comparable sample-to-SNP and causal loci ratios, where a million or so loci may be involved given an increased yet affordable sample size and hundreds of causal loci. On the other hand, it needs to be emphasized that reference accuracy plays an important role in the performance of pICA-R. As clearly shown in Fig. 4, when random loci are incorrectly selected as references, pICA-R exhibits reduced sensitivity. However, at relatively low sample-to-SNP ratios (below 200/50K), even with accuracies as low as 0.2, pICA-R still benefits in sensitivities compared to blind ICA and pICA, indicating a big tolerance of false inputs. Meanwhile, the reference-imposed FDR remains below 0.05, and decreases to 0 with accuracies greater than 0.3. This effective control on reference-imposed FDR is believed to result from a well maintained balance between independence and closeness metric such that the latter never dominates to excessively elevate the referential random loci. Based on the simulation results, a general conclusion can be drawn that a relatively accurate reference is recommended for pICA-R. Compared to a large number of reference loci with low confidence, a small set of reliable reference loci would lead to a better performance. Retrospectively, through investigating the sensitivity and reference-imposed FDR as functions of reference accuracy, we can empirically infer the quality of a reference. The simulation shows that, if more than 10% of the reference SNPs show up in the most significant (i.e., top component weights) findings, the reference accuracy is most likely higher than 0.2 and, the reference benefits the performance. In contrast, a low ratio of reference loci in the most significant findings usually indicates the distance metric being de-emphasized due to low reference accuracy.

In pICA-R, reference SNPs are predicted to contribute simultaneously to only a single component. Therefore, it may be inappropriate to directly combine multiple presumed susceptibility loci identified in univariate analyses, which may then result in a reference containing true SNP hits from multiple components. In this case, the reference is essentially of low accuracy as pICA-R is currently designed to optimize the distance between the reference and one constrained component and the true hits from other components cannot be recognized. Given a low-accuracy reference, minimizing distance will contradict with maximizing independence, which can be captured by the online monitoring of the overall independence. pICA-R will then adaptively adjust the constraint weight to de-emphasize the distance metric to assure the integrity of independent components (as reflected in simulations, Fig. 4). When the distance metric is significantly de-emphasized, pICA-R effectively converges with results from blind pICA. Particularly in this work, we adopted the most straightforward strategy to generate a reference set based on LD clusters of one single gene. Genome-wide association study (GWAS) is based on the premise that a causal variant is located on a haplotype, and thus a marker allele in LD with the causal variant should show (by proxy) an association with the trait of interest (Stranger et al., 2011). Therefore, SNPs in one LD cluster are more likely to contribute simultaneously to one single component and serve as good candidates for reference. We understand that this primary strategy has limitations, and plan to extend pICA-R to accommodate multiple reference sets where the interrelationships are unknown.

While it is true that reference accuracy plays an important role in pICA-R performance, this should not compromise the applicability of the model. First, we implement a binary reference, thus users only need to determine whether the loci are relevant or not to the trait of interest instead of specifying the accurate effect sizes. Second, the model is highly robust to inaccurate reference SNPs. As demonstrated in simulations, pICA-R outperforms blind methods with the accuracy as low as 0.2 when the sample-to-SNP ratio is lower than 4.00×10⁻³ (Fig. 3 and Fig. 4). Last but not least, while the choice of reference SNPs is informed by evidence, this is not necessarily limited to association studies. Independent molecular, cellular or system biological knowledge can also guide the selection. Even when informed by association studies, an enormous sample is not a necessity. Replication across studies can help increase confidence in the selection. For example, an association is more likely to be true and poses a good candidate for the reference if consistently observed in several independent studies of small sample sizes. Overall, we believe that the large amount of available data and information learned from previous studies are sufficient to generate testable references for a particular research interest, which can be leveraged by our pICA-R method to increase, broaden or deepen our knowledge at large.

When applied to experimental sMRI and SNP data (sample-to-SNP ratio around 4.12×10⁻⁴), pICA-R identified one sMRI-SNP component pair exhibiting a significant association (r = 0.24, p = 2.81×10⁻⁵) while controlling for age, sex, race/ethnicity, collection site and SZ diagnosis, indicating that the association was not mainly attributable to these factors. The loadings associated with the SNP component differentiated patients from healthy controls (p = 0.04), while the sMRI loadings showed a more significant group difference (p = 1.33×10⁻¹⁵). Overall, the results suggest that the identified genetic factor might underlie a proportion of variation in gray matter concentration that further contributes to SZ phenotypic symptoms (Harrison, 1999).

sMRI component

The loadings associated with the sMRI component were significantly lower in patients, indicating an overall SZ-related loss of gray matter, which has been indicated in a number of studies (Glahn et al., 2008; Gur et al., 2007; Narr et al., 2005; van Haren et al., 2007). The identified brain network consisted of dorsolateral (Brodmann Areas (BA) 9) and ventrolateral (BA6 and 47) prefrontal cortices (DLPFC and VLPFC), as well as anterior cingulate (BA32) and insular cortex (BA13). This network overlaps considerably with an SMRI component identified before in these data, and found to be heritable in a sibling-pair analysis (Turner et al., 2012). DLPFC is connected to a variety of brain areas and plays an important role in working memory (WM), executive function and other higher-order cognitive processes. Recent work also lends support for DLPFC contributing to the encoding of relational memory, which may further promote long-term memory (LTM) formation, through its role in WM organization (Blumenfeld et al., 2011; Murray and Ranganath, 2007). VLPFC, compared with DLPFC, is generally considered as involved in LTM formation, where the left frontal region is more associated with verbal memory while the non-verbal memory activates more of the right frontal region (Buckner et al., 1999). The anterior cingulate (BA32) consists of affective and cognitive subdivisions, the former more associated with emotional processes and the latter more activated by tasks requiring cognitive and attentional control (Davidson et al., 2002; Pizzagalli, 2011). The above highlighted regions have been consistently reported to be altered in SZ patients, including reductions in gray matter and cortical thickness (Cannon et al., 2002; Glahn et al., 2008; Kuperberg et al., 2003; Shenton et al., 2001; Xu et al., 2008), as well as exhibiting abnormal task-related functional activation (Glahn et al., 2005; Manoach, 2002; Minzenberg et al., 2009). Overall, our findings are in line with a considerable evidence of gray matter abnormalities in prefrontal and temporal regions as one of the characteristic deficits in SZ.

SNP reference

Although the SNP highlighted in the PGC study (rs10994359 from ANK3) is not covered in our data, the nearest SNP (rs10761503, 307bp upstream, in LD with rs10994359 with a D-prime of 1 according to the HapMap CEU LD data) is in moderate LD with the reference set (exhibiting a mean correlation of 0.43). In addition, we mapped the selected reference SNPs to the PGC data. 18 out of the 82 reference SNPs were investigated in the PGC study, and 12 were implicated for SZ relevance (p < 0.05), leading to a true causal loci ratio of 0.67 (12/18). Given that the 18 PGC-mapped SNPs were uniformly distributed along the 82 reference SNPs, this ratio of 0.67 provided a reference for estimating the number of true casual loci in our reference set, which should be about 55 (0.67*82). In fact, our results did echo this true causal loci ratio, where 54 out of the 82 reference SNPs were identified as top-contributing. The 54 identified SNPs included 9 PGC-implicated causal loci, and the remaining 45 SNPs demonstrated very high LD with the PGC findings. According to the HapMap CEU LD data, 16 SNPs are in complete LD with the 12 PGC-implicated SNPs (D-prime = 1), and another 4 demonstrate a D-prime of 0.871, 0.875, 0.939 and 0.883, respectively. For other 25 SNPs not covered in the HapMap CEU LD data, we evaluated in our data their relations with the 12 PGC-implicated SNPs and found high correlations (r > 0.96) except for one locus. These observations suggest that LD can provide good guidance in reference selection. When limited true causal loci are known, searching clusters of SNPs exhibiting LD with them may be the most effective approach to generate a testable reference in this pICA-R model.

SNP component

The SNP component was significantly associated with the sMRI component. On average, SZ patients carried higher loadings on the SNP component while exhibiting lower gray matter concentration in the identified regions of the sMRI component. The SNP component was predominantly contributed to by 1,030 SNPs exhibiting top component weights. Cross-evaluation based on PGC results confirmed that the top contributing SNPs were significantly overrepresented in terms of SZ-relevance, which validated our finding. It is noted that when the threshold of SZ-relevance (P_th) increased, the enrichment diminished, which is reasonable. The top contributing SNPs comprised a number of clusters distributed across the whole genome, which is not surprising given our model, where SNPs in LDs would exhibit comparable effects. Clusters spanning more than 10 top contributing SNPs are highlighted in Fig. 5 and marked by the corresponding cytogenetic bands, some of which have been implicated in previous studies, such as 5q15 for bipolar disorder (Scott et al., 2009), 15q15.1 for attention deficit/hyperactivity disorder (Bakker et al., 2003), as well as 17q23.3 for autism (Girirajan et al., 2011) and schizophrenia (Wahlbeck et al., 2000).

Among the 1,030 top contributing SNPs, 522 reside in a total of 228 unique genes. The remaining 508 intergenic SNPs lie within sequences not presently annotated but they could have a regulatory function on large non-coding RNAs and other regulatory non-coding RNAs.

Pathway analyses of the 228 known genes revealed that they participate in a number of neurotransmitter and nervous signaling pathways, including glutamate receptor signaling and DARPP32 regulated pathway, as well as synaptic LTP and LTD. It was noted that some pathways and clusters were no longer significant after the Benjamini–Hochberg correction; however this does not necessarily indicate a false positive finding. First, the correction was performed for all candidate pathways, which may not be independent from each other, indicating a possibility of over-correction. Second, the identified canonical pathways and functional annotation clusters remained highly stable when we adjusted the number of top contributing SNPs from 1,000 to 5,000. In particular, the enrichment became significant even after the correction at some point (Table S3 and Table S4). Finally, as emphasized by IPA, the enrichment score simply provides guidance for interpretation, and it is more important to further explore the functions of involved genes to interpret the finding. In this study, the pathway analyses results are provided to help unravel the genetic architecture. The involved genes are discussed in more details to understand the biological connections between the identified component and the disorder.

Glutamate receptor signaling (SLC1A1, GRM4, GNG2)

Glutamate receptor signaling plays a crucial role in neurocognitive processes and aberrant glutamate neurotransmission may be associated with positive and negative symptoms as well as cognitive deficits in SZ (Coyle, 2006; Egan et al., 2004; Krystal et al., 2010). Recent work also provides evidence for an association between perturbed glutamate function and gray matter volume variation in prodromal SZ (Stone et al., 2009). In particular, one SNP in GNG2 (encoding guanine nucleotide-binding protein, gamma-2) has been identified, with its minor allele relating to an increased gray matter volume in medial prefrontal cortex (Chavarria-Siles et al., 2012). Also, some glutamate transporters including SLC1A1 (encoding excitatory amino-acid transporter 3) are believed to have pivotal functions in mediating neurotoxicity, which raises the possibility of underlying structural changes in SZ (Deutsch et al., 2001; Olney and Farber, 1995). In our finding, three SNPs contributed to the glutamate pathway, including rs2150195_A (SLC1A1, ‘A’ denotes the minor allele), rs1873249_G (GRM4) and rs10150721_G (GNG2). The first SNP contributed with a positive weight, indicating an increased MAF being associated with lower gray matter concentration; and the latter two SNPs presented negative weights, implying gray matter loss being associated with decreased MAFs.

Dopamine-DARPP32 signaling (CACNA1A, CACNA1C, PLCB1, PPP2R2C, PRKD1)

These proteins modulate dopamine and DARPP32 regulated gene expression and function, which likely influences synaptic plasticity such as LTP and LTD (Jay, 2003; Svenningsson et al., 2004) as well as being associated with SZ risk (Albert et al., 2002; Howes and Kapur, 2009). In our finding, five genes are involved in this pathway, including CACNA1A (rs4926278_C and rs4926279_C), CACNA1C (rs2238070_T), PLCB1 (rs2745764_T), PPP2R2C (rs7688267_G) and PRKD1 (rs12883327_T). CACNA1C is likely a major risk gene for bipolar disorder (Ferreira et al., 2008). Meanwhile, it is of particulate interest that CACNA1A and CACNA1C (calcium channels, voltage-dependent) also participate in calcium signaling, which plays an important role in neuronal processes (Lidow, 2003; Mattson, 1992) and may also contribute to the reduction in neuronal number given its suggested role in cell death (Sastry and Rao, 2000; Toescu, 1998).

Synaptic LTP and LTD (IGF1R, PLCB1, PPP2R2C, GRM4, PRKD1, CACNA1C)

synaptic LTP and LTD are two forms of synaptic plasticity resulting in altered synaptic strength, which underlie learning and memory (Collingridge et al., 2010; Cooke and Bliss, 2006; Linden and Connor, 1995). While learning and memory impairments are well documented in SZ (Aleman et al., 1999; Paulsen et al., 1995), direct evidence has also been provided for disrupted LTP/LTD in SZ (Frantseva et al., 2008; Weng et al., 2011). In our finding, three genes are involved in both LTD and LTP processes, including PLCB1, GRM4 and PRKD1. GRM4 (encoding metabotropic glutamate receptor 4) is also implicated in glutamate signaling, while PLCB1 (1-phosphatidylinositol 4, 5-bisphosphate phosphodiesterase beta-1), PRKD1 (Serine/threonine-protein kinase D1) and PPP2R2C (Serine/threonine-protein phosphatase 2A 55 kDa regulatory subunit B gamma isoform) are also implicated in DARPP32 regulated pathway, indicating a possible convergence in pathology. On the other hand, IGF1R (Insulin-like growth factor 1 receptor, rs8038015_C and rs6598542_G) is involved only in LTD, where both of two SNPs contributed with positive weights.

Besides those genes implicated in the aforementioned neurotransmitter and nervous signaling pathways, it is noteworthy that a number of the remaining detected genes have been implicated in other neuronal processes. For instance, CNTNAP2 (encoding contactin-associated protein-like 2) and RELN (encoding reelin), as reported by DAVID, are among the functional cluster of cell adhesion, which plays an important role in brain development (Edelman, 1983; Rutishauser and Jessell, 1988). CNTNAP2 is shown to mediate intercellular interactions during latter phases of neuroblast migration and laminar organization (Strauss et al., 2006). This gene exhibits a high expression in anterior temporal and prefrontal regions in humans, yet low or absent expression in rodents (Abrahams et al., 2007), suggesting a possible role in higher cognitive functions such as language (Vernes et al., 2008). RELN is suggested to regulate neurogenesis and migration, as well as enhance synaptic LTP (Hoe et al., 2009; Pujadas et al., 2010; Spalice et al., 2009). In addition, RELN mutations have been associated with SZ (Guidotti and Di-Giorgi-Gerevini, 2002; Wedenoja et al., 2008).

It’s noted that IPA indicates an enrichment of coronary artery and vascular disease in the identified component, as shown in Table 3a. While comorbidity between these diseases and SZ has been documented, most of the previous works highlighted environmental factors, such as cigarette smoking and metabolic syndrome (Hennekens et al., 2005; Jeste et al., 1996). This issue may deserve further investigation.

Combining the sMRI and SNP findings, pICA-R revealed an association between one genetic component and SZ-related reduction in gray matter concentration in distributed brain regions. The identified brain regions are among those shown to exhibit gray matter deficits partly attributable to genetic factors (Cannon et al., 2002; Thompson et al., 2001). The genetic component reflects enrichment in neuronal processes. It is noteworthy that both genetic and imaging findings show a particular relevance to cognition, especially memory function. While the underlying mechanism remains to be elucidated, our finding strongly suggests that the identified genetic component may affect neurobiological conditions that play a role in the cognitive deficits of SZ.

The limitations of this study lie in the participants’ population stratification, effects from multiple data collection sites, and the possible effect of antipsychotic medications on the majority of the SZ subjects, which were addressed in different ways. Population stratification effects were minimized through PCA correction ((Price et al., 2006), see supplementary information). Regarding the sMRI-SNP association, after regressing out controlling variables (specifically age, sex, race/ethnicity, collection site and SZ diagnosis for the SNP component; race/ethnicity and SZ diagnosis for the sMRI component), the sMRI-SNP association remained significant, exhibiting a partial correlation of −0.24 (p = 2.81×10⁻⁵). In addition, in a Caucasian-only subset (109 SZ versus 141 HC), pICA-R also identified a same sMRI-SNP association (r = −0.31, p = 4.93×10⁻⁷), which remained significant after controlling for the above listed variables (partial correlation, r = −0.29, p = 2.94×10⁻⁶). Therefore, we concluded that the finding was robust to the population structure. The influence of multiple collection sites was assessed through the controlling variable of collection site. Specifically, we performed a voxel-wise regression to eliminate the site effect from the sMRI data. Regarding the SNP modality, no significant site effect was observed, which was expected given that genotyping for all participants was performed at the Mind Research Network. The subsequent partial correlation and regression analyses indicated that the identified sMRI-SNP association was not majorly due to any of these controlling variables (age, sex, race/ethnicity, collection site and SZ diagnosis). We examined medication effects in the patient group and found no significant regression effect from the reported chlorpromazine equivalent dosage on the identified gray matter concentration reduction in prefrontal and temporal regions. This observation is consistent with the previous report where progressive cortical thinning was demonstrated in the absence of antipsychotic medication in twins discordant for SZ, supporting a familial contribution to this endophenotype (Brans et al., 2008). Overall, our data suggests that, independent from exposure to antipsychotic medications, specific genetic polymorphisms contribute to reduction in grey matter concentration in a prefrontal-temporal network in this illness.

Being aware of the importance of excluding correlated SNPs prior to the enrichment analysis, we examined the 1,030 top contributing SNPs in our data and then excluded SNPs in high LD (r² > 0.85, as suggested in PLink). However, we could not examine the LD in the background as the PGC genotype data were not available. While in this case an enrichment test might be skewed by an underestimation, the results still indicated a significant SZ enrichment in the identified component for the tested range of p_th (Fig. S5). Overall, these results suggested a low possibility that the SZ enrichment observed in the indentified component is a false positive.

In summary, our study provides proof-of-concept for the application of pICA-R in imaging genomics. This semi-blind multivariate approach is designed to reveal relationships between two modalities. Our simulations indicate that pICA-R helps extract the factor of interest with improved accuracy. When applied to experimental data, pICA-R identified a significant sMRI-SNP association under the guidance of a reference derived from ANK3, a gene implicated in the PGC SZ study. The sMRI findings are in line with those reported in prior, related work, while the SNP findings are validated through the independent PGC study, and the inter-modality connection suggests that the SZ-related reduction in gray matter concentration observed in frontal and temporal regions is partly attributable to a combined effect from multiple genetic variants involved in neurotransmission and nervous signaling pathways. Given the relatively small sample size, our findings may need further replication in larger studies. However, we believe, this pilot study demonstrates the ability of pICA-R as a promising approach for extracting reliable factors accounting for small amounts of variance in high-dimensional data. The method is a general one which can be applied to other modalities and to the study of healthy human brain as well as other diseases.

Highlights.

• A novel reference guided multivariate approach to reveal relationships of features.

• Designed for imaging genomics to extract specific genetic factors from the genome.

• Simulation and real data application demonstrate its feasibility.

• Schizophrenia-related gray mater reduction related to multiple genetic variants.