Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2013 Oct 16;33(42):16483–16489. doi: 10.1523/JNEUROSCI.2094-13.2013

Integration of Direction Cues Is Invariant to the Temporal Gap between Them

Roozbeh Kiani 1,4,✉, Anne K Churchland 2,4, Michael N Shadlen 3,4
PMCID: PMC3797371  PMID: 24133253

Abstract

Many decisions involve integration of evidence conferred by discrete cues over time. However, the neural mechanism of this integration is poorly understood. Several decision-making models suggest that integration of evidence is implemented by a dynamic system whose state evolves toward a stable point representing the decision outcome. The internal dynamics of such point attractor models render them sensitive to the temporal gaps between cues because their internal forces push the state forward once it is dislodged from the initial stable point. We asked whether human subjects are as sensitive to such temporal gaps. Subjects reported the net direction of stochastic random dot motion, which was presented in one or two brief observation windows (pulses). Pulse strength and interpulse interval varied randomly from trial to trial. We found that subjects' performance was largely invariant to the interpulse intervals up to at least 1 s. The findings question the implementation of the integration process via mechanisms that rely on autonomous changes of network state. The mechanism should be capable of freezing the state of the network at a variety of firing rate levels during temporal gaps between the cues, compatible with a line of stable attractor states.

Introduction

To make decisions, we often gather discrete pieces of evidence and combine them. Psychologists have long explained this process using abstract models based on integration of evidence in favor of different options (Laming, 1968; Link and Heath, 1975; Vickers and Smith, 1985; Luce, 1986; Smith, 1988; Link, 1992; Ratcliff and Smith, 2004). These models accurately explain the statistics of choices and reaction times. Moreover, electrophysiological studies in primates performing simple perceptual decisions have uncovered a neural correlate of the integration process in the parietal, prefrontal, and superior colliculus neurons (Cook and Maunsell, 2002; Roitman and Shadlen, 2002; Gold and Shadlen, 2007; Ratcliff et al., 2007; Churchland et al., 2008; Kiani et al., 2008; Heitz and Schall, 2012). Neural responses reflect both the gradual accumulation of evidence and the termination of the process when the accumulation reaches a stereotyped level.

Several theoretical studies propose that a common mechanism can account for both the integration of evidence into a decision variable (DV) as well as the divergence of such a DV into a terminal “attractor” state representing the decision outcomes (Brown and Holmes, 2001; Usher and McClelland, 2001; Wang, 2002; Wong and Wang, 2006; Albantakis and Deco, 2011; Miller and Katz, 2013). The idea is appealing because coupling local recurrent excitation and lateral inhibition could give rise to both integration and the competition between alternatives. However, in this framework, the evolution of a DV is determined by both the input to the network (e.g., evidence) and the network interactions themselves. Hence, the DV will tend to drift away from states that ought to be determined purely by the evidence. The strong prediction is that sources of evidence will affect decisions differently if they are separated by gaps in time: The network interactions cause the decision process to be sensitive to the length of gaps. For longer gaps, either the DV is absorbed into a basin of attraction, making later information less effective, or the DV retraces back to the starting point, effectively erasing the earlier information.

We tested this prediction in human observers trained to make perceptual decisions about the direction of motion in noisy dynamic random dot displays. We provided one motion “pulse” or a pair of motion pulses separated by different temporal gaps. We report that (1) subjects are readily able to integrate information from two visual motion cues to improve their accuracy, (2) performance did not depend on the interval between the cues, and (3) the second cue had the larger leverage on decisions.

Materials and Methods

Five adult human subjects, three male and two female, participated in this experiment. All subjects, except for one of the authors (R.K.), were naive to the purpose of the experiment. Observers had normal or corrected-to-normal vision. They provided informed written consent before participation in the study. All procedures were approved by the institutional review board at the University of Washington.

Motion direction discrimination task.

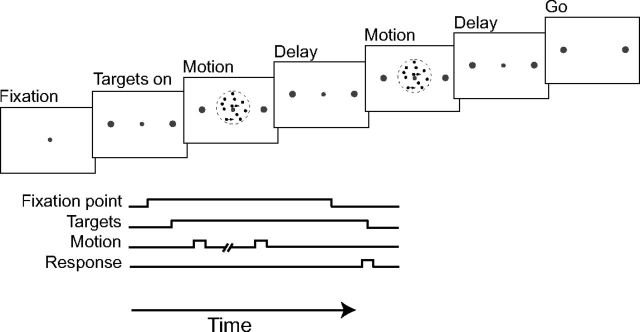
Observers were seated in an adjustable chair in a semidark room with chin and forehead supported before a CRT display monitor (17 inch, PF790, View Sonic; refresh rate, 75 Hz; screen resolution, 800 × 600; viewing distance, 57 cm). Each trial began with the appearance of a red fixation point (0.3° diameter) at the center of the display. Subjects were instructed to maintain gaze on the fixation point throughout the trial. The subject pressed a keyboard space bar to signal readiness for the trial. Immediately, two red targets (0.5° diameter) appeared on the right and left side of the screen (10° eccentricity) corresponding to the two possible motion directions (rightward and leftward), which the subject had to discriminate. After a short delay (200–500 ms, truncated exponential distribution), the dynamic random dot stimulus was presented within a 5° circular aperture at the center of screen. The dots were white 2 × 2 pixel squares (0.088° per side, luminance = 69.6 cd/m2) on black background (luminance = 0.1 cd/m2), creating an average dot density of 16.7 dots/degree2/s. The motion stimulus is described in detail previously (Shadlen and Newsome, 2001; Roitman and Shadlen, 2002). Briefly, the stimulus consisted of three independent and interleaved sets of dots presented on successive video frames. When a set was replotted, three frames (40 ms) later a fraction of dots was displaced coherently along the motion direction, while the rest of dots were relocated randomly. The fraction of coherently moving dots (hereafter termed “coherence”) specified the stimulus strength. Motion direction and coherence varied randomly from trial to trial. At the end of motion stimulus, a 400–1000 ms delay period (truncated exponential) was imposed before the Go signal, disappearance of the fixation point, was presented. The subject was required to report the net direction of motion within 1 s after the Go signal by pressing a left or right key. Distinctive auditory feedback was delivered for correct and error responses. On trials with 0% coherence, the type of feedback was chosen randomly.

Subjects were presented with one or two 120-ms-long motion pulses (Fig. 1). On single-pulse trials, motion coherence was randomly chosen from these following values: 0%, 3.2%, 6.4%, 12.8%, 25.6%, and 51.2%. On double-pulse trials, the coherence of each pulse was randomly chosen from 3.2%, 6.4%, and 12.8%, allowing nine different coherence sequences. The two pulses were separated by 0, 120, 360, or 1080 ms. For the 0 ms interpulse interval, the second pulse was a smooth continuation of the first pulse—the first frame of the second pulse related to the third to the last frame of the first pulse, and so on—to avoid breaking the motion. For nonzero interpulse intervals, the second pulse was not a continuation of the first sequence, but similar results were obtained when the two pulses were related in the same fashion as the 0 ms interpulse interval. The motion direction was always consistent for the two pulses, and subjects were informed of this fact. They were also informed that random fluctuations in the stimulus could produce contradictory direction percepts for the two pulses, but they had to choose the direction that best matched the overall stimulus. The 42 possible trial types (6 single-pulse and 9 × 4 double-pulse trial types) were randomly interleaved in blocks 300 trials long. Subjects were instructed to perform as accurately as possible. Their overall probability of being correct was shown on the screen at the end of each block and was compared with the instructed target: 80% probability of being correct, a level of accuracy extremely difficult to achieve for the brief and mainly weak stimuli used in this experiment. Each subject ran one or two blocks per day until 2400–3300 trials were collected. The results were largely consistent across subjects. For the analyses below, we have pooled the data across subjects.

Figure 1.

Figure 1.

Open in a new tab

Direction discrimination task with brief motion pulses. Subjects were asked to identify the direction of motion in a dynamic random dot display, presented in one or two 120 ms epochs. The strength of motion was randomized across trials and between the motion pulses, but the direction of motion (left or right) was the same for both pulses on double-pulse trials. The interval between pulses ranged from 0 to 1.08 s. See Materials and Methods.

Analysis of behavioral data.

We use a variety of logistic regression models to assess the impact of stimulus parameters on binary outcomes. In the following models, we use Logit[P] as shorthand for log(P1−P) and denote fitted coefficients, βi. Fitting is by maximum likelihood under a binomial error model (i.e., a GLM).

For single-pulse trials, the probability of a correct choice is given by the following:

graphic file with name zns04213-4603-m01.jpg

where C is motion coherence. A modified version of Equation 1 was used to test for a right/left bias:

graphic file with name zns04213-4603-m02.jpg

where C± is signed motion coherence—positive for rightward motion and negative for leftward motion. The null hypothesis is lack of bias (H0:β0 = 0).

To evaluate the effect of interpulse interval on performance, we fit the following:

graphic file with name zns04213-4603-m03.jpg

where C1 and C2 are motion strengths of the first and second pulses, respectively, and T is the interpulse interval. When applied to double-pulse trials with equal pulse strength (C1 = C2), the redundant regression terms (β2C2 and β5C2T) were dropped. The null hypothesis is that performance does not depend on interpulse interval (H0:β3–5 = 0).

We estimated the expected accuracy (Pe) that would be achieved in double-pulse trials under the assumption of perfect integration. We assumed that the decision is determined by the sign of the sum of two random numbers (i.e., the pieces of evidence conferred by the two pulses). The distribution of the evidence can be inferred from the accuracy of the performance on single-pulse trials:

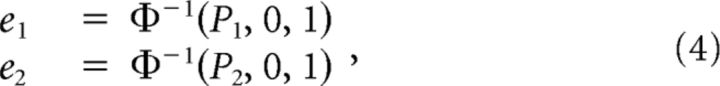graphic file with name zns04213-4603-m04.jpg

where P1 and P2 are the probabilities of correct single-pulse discriminations based on Equation 1, and e1 and e2 are the inferred evidence that underlie P1 and P2, respectively. Φ is the normal cumulative distribution function:

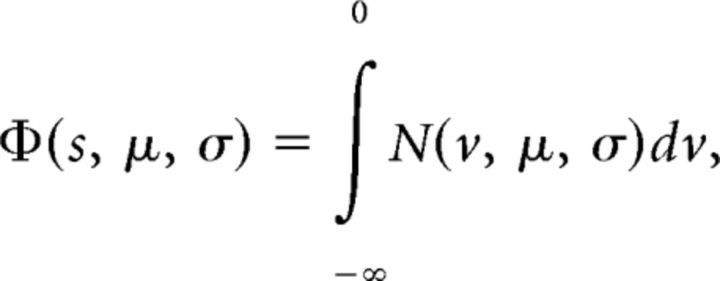graphic file with name zns04213-4603-m05.jpg

and Φ−1 is its inverse (quantile function). N(v, μ, σ) is the normal probability density function with mean (μ) and SD (σ). The expected accuracy for double-pulse trials becomes the following:

graphic file with name zns04213-4603-m06.jpg

We used the fit estimates of P1 and P2 (Eq. 1) rather than the observed proportions because the former were more precise, but similar results were obtained using the proportions. We compared the expected accuracy of the perfect integrator to the observed accuracy on double-pulse trials using logistic regression, as follows:

graphic file with name zns04213-4603-m07.jpg

where Pe is the expected probability correct (Eq. 5). Positive β indicates accuracies that are higher than expected. We also considered a perfect integrator with knowledge of motion coherence associated with the two pulses. To optimally exploit this knowledge, the evidence from each pulse must be scaled by the known coherence (Gold and Shadlen, 2001).

To assess the effect of pulse sequence on choice accuracy, we fit the following:

graphic file with name zns04213-4603-m08.jpg

where C1 and C2 are motion strengths of the first and second pulses. β2 indicates how the accuracy changes from trials in which C1 > C2 to trials with a reversed sequence of motion pulses C2 > C1. The null hypothesis is that the accuracy does not change with the sequence of motion pulses (H0:β2 = 0).

To test for an interaction between the two pulses (e.g., a stronger pulse 1 reduces the effect of pulse 2) we used the following regression:

graphic file with name zns04213-4603-m09.jpg

This regression was applied to all double-pulse trials. The null hypothesis is that the increased efficacy of the second pulse was due to increased sensitivity rather than an interaction of motion pulses (H0:β3 = 0). Note that β2 > β1 indicates greater sensitivity to the second pulse on the decision.

Motion energy analysis.

We examined the relationship between choice and the moment-by-moment fluctuation of motion information in the random dot stimuli. Due to the stochastic nature of the random dot stimulus, the strength of motion fluctuates from trial to trial, motion pulse to motion pulse, and moment to moment. The motion energy on each pulse (Adelson and Bergen, 1985) was calculated by using two pairs of quadrature spatiotemporal filters, as specified in Kiani et al. (2008). Each pair was selective for one of the two opposite directions in our experiment. The filters were convolved with the three-dimensional spatiotemporal pattern of each motion pulse. For each quadrature pair, the convolution results were squared and summed together, then integrated over space to calculate the motion energy along the filter direction as a function of time. The net motion energy displayed in Figure 4 is the difference in motion energy along the stimulus direction minus its opposite.

Figure 4.

Figure 4.

Open in a new tab

The second pulse had the larger influence on choice. Each panel shows the average motion energy profiles for the first and second pulses, sorted by choice. Only trials with equal pulse strength are included. The shaded region around the mean indicates SEM. The black horizontal bars show the stimulus presentation period. Data were pooled for all nonzero interpulse intervals. Motion coherences are indicated at the top of each panel: A, 12.8%; B, 6.4%; C, 3.2%. The units of motion energy are arbitrary, but are identical for all motion strengths. The degree of influence on choice can be ascertained by comparing the energy accompanying correct and erroneous choices (red and blue, respectively).

The following regression analysis was used to test whether the difference between motion energy profiles for correct and error responses was larger for the second pulse compared with the first pulse:

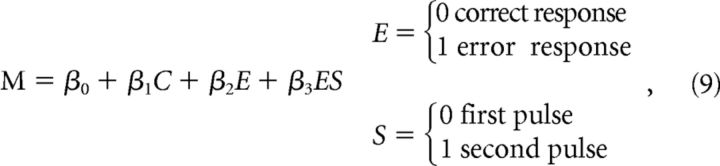graphic file with name zns04213-4603-m10.jpg

where C is the pulse coherence. E is an indicator variable for errors, and S is an indicator variable for the pulse sequence. M is the integral of the motion energy in a 200 ms window starting 50 ms after pulse onset. To avoid overlap in the windows for the first and second pulse, only double-pulse trials with nonzero interpulse interval were used in this analysis. The null hypothesis is that the differences in motion energy profiles for correct and error responses are equal for both pulses (H0:β3 = 0).

We used logistic regression to test whether the choice was more influenced by the motion energy of the second pulse than that of the first pulse. The regression for double-pulse trials with equal motion strength was as follows:

graphic file with name zns04213-4603-m11.jpg

where M1 and M2 are the motion energy of the first and second pulses, respectively. The null hypothesis is that the second pulse is not more effective (H0:β3 = 0). For trials with unequal motion strength, the regression is modified to the following:

graphic file with name zns04213-4603-m12.jpg

and the null hypothesis is β4 = 0.

Results

Five human subjects reported the perceived direction of motion in trials with one or two 120 ms motion pulses (Fig. 1). The single-pulse and double-pulse trials were randomly intermixed. The strength of each pulse, the motion direction, and the interpulse interval varied randomly across trials. In double-pulse trials, pulses always had consistent direction. Subjects were informed of this consistency and were extensively trained before data collection to achieve high levels of accuracy (see Materials and Methods).

Accuracy in double-pulse trials was independent of interpulse interval

Although the motion pulses were brief, they reliably influenced decisions about direction. As shown in Figure 2, accuracy improved with motion strength and with the number of pulses. For single-pulse trials, the accuracy ranged from 0.59 for 3.2% coherence to nearly perfect (0.997) for 51.2% coherence, and the subjects did not have any significant choice bias (Eq. 2, β0 = −0.04 ± 0.05, p = 0.39). These single-pulse trials provided a baseline for the comparison of performance in double-pulse trials.

Figure 2.

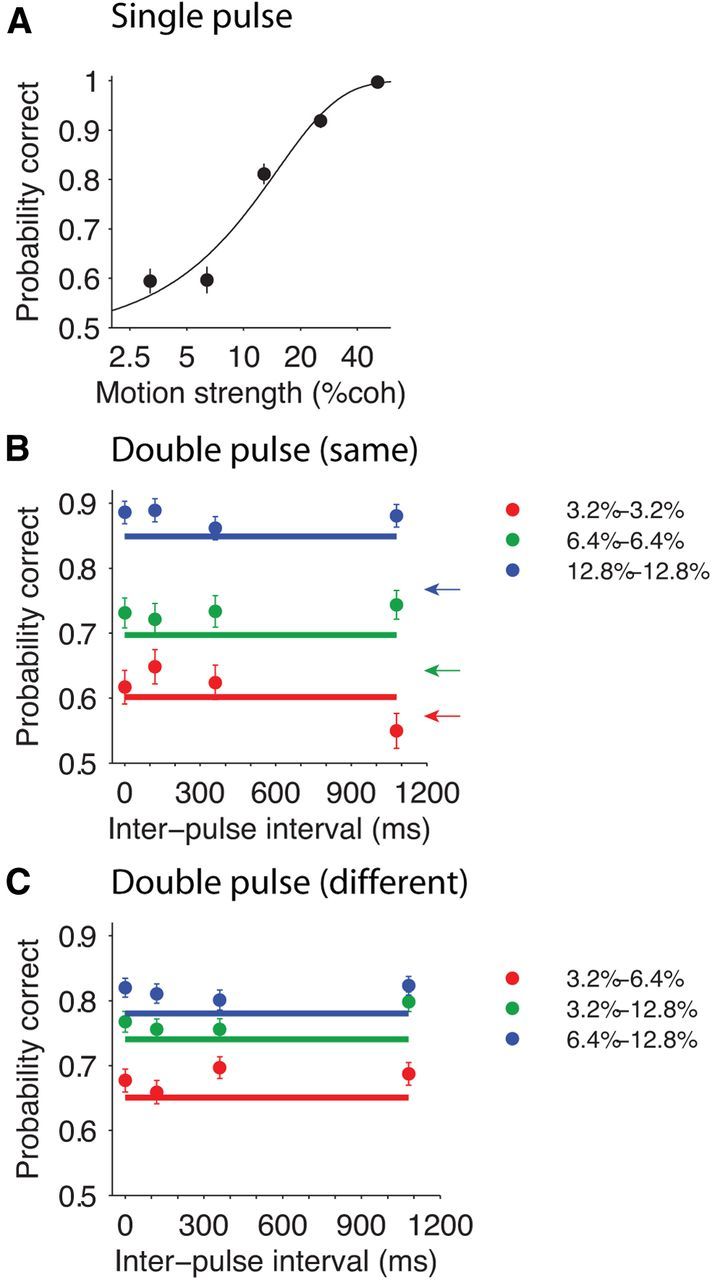
Figure 2.

Open in a new tab

Choice accuracy in double-pulse trials was independent of the interpulse interval. A, Accuracy in single-pulse trials. The curve is the fit of a logistic function (Eq. 1) to the data. B, Accuracy in double-pulse trials with same pulse strengths. Horizontal lines show the expected accuracy of a perfect integrator based on the single-pulse performance. Arrows show the value of the logistic fit for single-pulse trials of similar motion strength. C, Accuracy in double-pulse trials with different pulse strengths. Each data point represents pooled data from the pulse sequence indicated by the legend and its reverse order (e.g., 3.2–6.4% and 6.4–3.2%). Horizontal lines show the expected accuracy of a perfect integrator based on single-pulse performance. Error bars indicate SEM. coh, Coherence.

Not surprisingly, performance accuracy improved in the double-pulse trials (Fig. 2B,C). Importantly, this improvement was apparent for all interpulse intervals. In fact, the performance was largely unaffected by interpulse interval in the tested range for both double-pulse trials with equal pulse strength (Fig. 2B; Eq. 3, p ≥ 0.1; Table 1, results of individual subjects) and those with unequal pulse strength (Fig. 2C; Eq. 3, p > 0.1). The evidence from the first pulse was thus maintained without any significant decay or loss during the interpulse interval. It is striking that the two pulses separated by up to 1 s supports a level of accuracy that is indistinguishable from a pair of pulses that are separated by 100 ms or by no gap at all (i.e., a single pulse with duration of twice a single pulse).

Table 1.

Performance was largely unaffected by interpulse interval for double-pulse trials with equal pulse strength and with unequal pulse strength

Subjects Equal strength
 Unequal strength
β3 β4 β3 β4 β5
S1 −0.52 ± 0.40 (p = 0.18) 5.1 ± 6.3 (p = 0.41) 0.26 ± 0.51 (p = 0.61) −0.25 ± 4.0 (p = 0.95) −2.0 ± 4.1 (p = 0.63)
S2 −0.59 ± 0.38 (p = 0.12) 4.5 ± 5.4 (p = 0.41) −0.001 ± 0.48 (p = 0.99) 3.8 ± 3.6 (p = 0.29) −3.1 ± 3.8 (p = 0.42)
S3 −0.75 ± 0.38 (p = 0.05) 9.5 ± 5.3 (p = 0.07) 0.33 ± 0.50 (p = 0.51) 6.5 ± 3.9 (p = 0.09) −8.1 ± 3.9 (p = 0.04)
S4 0.27 ± 0.44 (p = 0.54) −3.1 ± 6.1 (p = 0.61) −0.28 ± 0.54 (p = 0.60) 0.70 ± 4.1 (p = 0.87) 4.4 ± 4.3 (p = 0.31)
S5 0.39 ± 0.41 (p = 0.35) −4.4 ± 5.6 (p = 0.43) 0.01 ± 0.51 (p = 0.99) 1.3 ± 4.0 (p = 0.75) −0.52 ± 4.0 (p = 0.90)
Open in a new tab

Each row shows the coefficients of Equation 3 (mean ± SE) and their associated p values.

Accuracy in double-pulse trials exceeded expectations based on single-pulse trials

From the probability correct for individual pulses, it is possible to predict the expected accuracy of a perfect integrator in double-pulse trials. A perfect integrator would combine the motion information from both pulses, without loss. For same-coherence pulses, the signal-to-noise ratio (SNR) of the motion evidence would increase by 2 times that of the single pulse. This follows simply because the expected sum of two independent random samples is twice the sample mean, but the SD is only 2σ. This increased SNR predicts an expected probability correct, which is indicated by the solid lines in Figure 2B. Surprisingly, the observed accuracy exceeded the predictions based on the perfect integrator analysis (Eq. 6, β = 0.13 ± 0.04, p = 3 × 10−4). We also observed high accuracies when the pulses were unequal (Fig. 2C; Eq. 6, β = 0.16 ± 0.03, p = 2.4 × 10−10). In this case, we entertained the possibility that the integrator could identify the two coherences and optimally weight their contributions, but even this unrealistic assumption led us to underestimate the observed performance (Eq. 6, β = 0.07 ± 0.03, p = 0.006).

How is this possible? The perfect integrator analysis poses a theoretical limit on the expected accuracy, but only if the subjects were using all of the motion information in single-pulse trials efficiently. If they ignored some information in the first pulse but harvested more information from the second pulse, they could outperform the expected accuracy based on single-pulse trials. In other words, the better-than-expected performance in double-pulse trials was actually explained by underperformance in single-pulse trials.

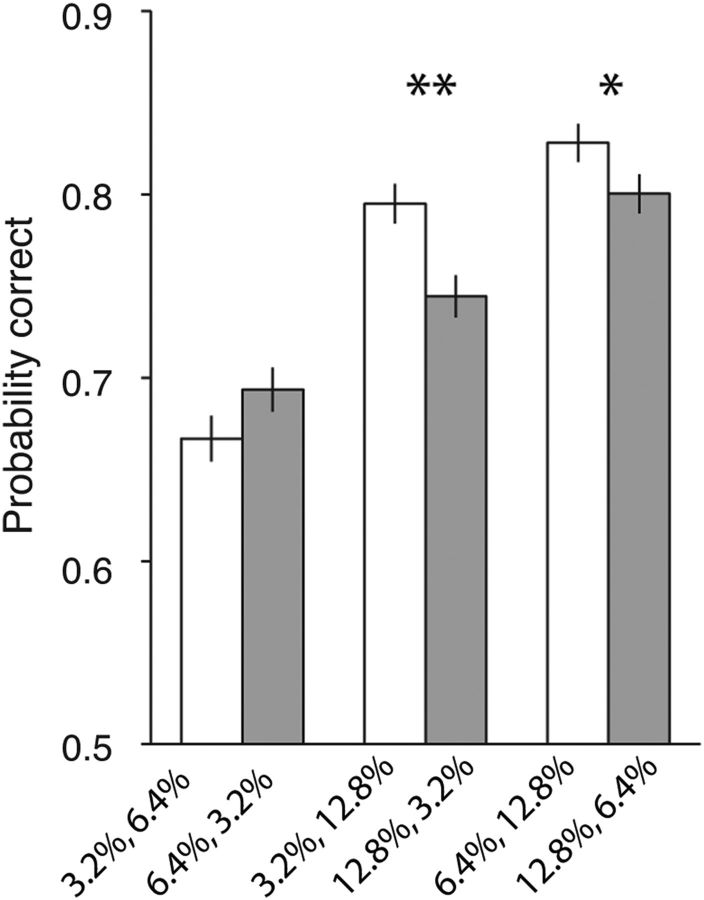
If this hypothesis is correct, the accuracy should depend on the order of pulses in the sequence. It predicts that subjects should be more accurate when a strong pulse follows a weak pulse, compared with the other way around. As shown in Figure 3, subjects were more accurate in double-pulse trials with unequal pulse strength when the stronger motion appeared second (Eq. 7, β2 = 1.16 ± 0.38, p = 0.002). Although accuracy was lower with the opposite ordering, the weaker second pulse was still leveraged more effectively than expected based on single-pulse presentations, consistent with the hypothesis that the second of the two pulses is processed more efficiently (Eq. 6: weak–strong sequence, β = 0.21 ± 0.04, p = 1.5 × 10−8; strong–weak sequence, β = 0.12 ± 0.04, p = 0.009). Moreover, this increased efficacy was independent of the strength of the first pulse (Eq. 8, β3 = 1.93 ± 14.8, p = 0.89).

Figure 3.

Figure 3.

Open in a new tab

Choice accuracy depended on the sequence of motion pulses. Probability correct for double-pulse trials with unequal pulse strength was calculated by pooling data across all intertrial intervals. Overall, the weak–strong pulse sequence resulted in higher accuracy than the strong–weak sequence. Error bars indicate SEM. *p < 0.05, **p < 0.01.

In a second test of this assertion, we exploited the variability of the random dot motion display to infer its influence on choice. The motion information in the random dot stimulus is stochastic, meaning that there is variability in the motion energy (Adelson and Bergen, 1985; Kiani et al., 2008) of pulses sharing the same coherence value. These fluctuations are known to influence the choice (Kiani et al., 2008; Resulaj et al., 2009), and they can inform us about the parts of the stimulus that bear more strongly on the decision (Ahumada, 2002; Neri, 2004; Kiani et al., 2008; Nienborg and Cumming, 2009). Figure 4 shows the average motion energy for double-pulse trials with equal pulse strength. The difference of the motion energy profiles for correct and error responses is larger for the second pulse than the first pulse (Eq. 9, β3 = −12.9 ± 3.6, p = 3.4 × 10−4), suggesting a smaller influence of the first pulse on the decision. A logistic regression confirmed the influence of trial-to-trial fluctuations of motion energy on choice (Eq. 10, β2 = 27.0 ± 5.8, p = 3.7 × 10−6) and a larger influence of the motion energy of the second pulse (Eq. 10, β3 = 32.9 ± 8.6, p = 1.4 × 10−4). Similar results were obtained for double-pulse trials with unequal pulse strength (Eq. 11, β4 = 22.7 ± 6.0, p = 1.4 × 10−4). The motion energy analysis thus provides independent confirmation of the asymmetric influences of the two pulses.

Discussion

Decisions are often based on fragments of evidence that arrive at different times. To render a decision, the brain must be capable of combining the fragments and maintaining a neural representation of the combined evidence in the intervals separating their arrival. Our experiment investigates this process in a simplified setting. Subjects were shown two short pulses of motion stimuli, which provided evidence for a common direction but often separated by a gap of time. Our main finding is that subjects combine evidence across these gaps of time without loss, regardless of the length of the gap interval. Compared with their performance with single pulses, subjects attained the same degree of improvement from a second pulse whether it followed immediately or up to 1 s after the first pulse. This implies that the state of the evidence from the first pulse was stable through the gap. It does not leak or drift away from the state attained at acquisition, and it can be combined with the next piece of evidence.

Of course, many mathematical models of decision making assume precisely this property of perfect integration (Wald and Wolfowitz, 1947; Laming, 1968; Ratcliff and Smith, 2004; Shadlen et al., 2006; Beck et al., 2008; Purcell et al., 2010; Smith and McKenzie, 2011; Brunton et al., 2013), but they do not specify how circuits composed of neurons can achieve it. Several models, spanning a range of biophysical realism, appear capable of supporting integration in the time span of many tenths of seconds to seconds, despite time constants of the neural elements an order of magnitude faster (Hille, 2001; Wang, 2002). A common strategy is to balance the natural decay modes of the circuit with recurrent excitation such that the network can hold a stable firing rate. Such a network can operate as an integrator of external input (Seung et al., 2000; Koulakov et al., 2002; Wang, 2002; Goldman et al., 2003; Furman and Wang, 2008; Cain et al., 2013).

One class of models exploits inhibition to achieve a competition among alternatives, thereby coupling in a common dynamical framework (1) the integration of momentary evidence and (2) the establishment of a commitment to a decision (Wang, 2002; but see Lo and Wang, 2006). Thus, they are often characterized by stable point attractors—decisional states—and network dynamics that push the state of the network toward these point attractors. Such models successfully account for several aspects of the decision-making process when the stream of evidence is continuous (Wang, 2002; Wong and Wang, 2006). However, they also predict that a temporal gap in the stream of evidence, as in this experiment, will lead to significant deviation from an ideal accumulation process. This is because the state of the network evolves in accordance with its inherent dynamics, even in the absence of evidence. If the gap between the pieces of evidence is long enough, either a stable decision point will be attained, based solely on the first pulse, or the network will regress to its starting point, thereby losing the initial evidence. The present findings pose a serious challenge for such mechanisms or any other mechanism that would allow for drift in the decision variable toward one of the choice alternatives in the absence of evidence.

There are potential remedies that would allow point attractor models to act more like ideal integrators, for example, by adding a mechanism that freezes the state of the network in the absence of evidence, or by making the basin of attraction very shallow to retard autonomous progress toward the attractor state. Another possibility is to push the network into a parameter regime in which strong momentary evidence makes the network “jump” from the initial stable state to a decision state, while weak momentary evidence quickly decays and returns the network to its initial state (Miller and Katz, 2010, 2013). If the decay is fast enough, the performance of the network can become more or less invariant to the interval between the momentary evidence. However, in this parameter regime, integration is effectively replaced by a sequence of mini-decisions based on momentary evidence. Thus, just like its conceptual predecessor—the high-threshold model (Laming, 2013)—this parameter regime loses information.

A more enticing remedy is to circumvent the major limitation of point attractor decision networks by replacing the choice attractor states with a multi-stable attractor network (Seung et al., 2000; Koulakov et al., 2002; Furman and Wang, 2008) in which the stable states correspond to the values that the decision variable could obtain. In the extreme, the number of stable states can be so high that the network can represent a continuous variable, or what is termed a “line attractor” (Seung et al., 2000). In recurrent network models (Usher and McClelland, 2001; Wang, 2002; Albantakis and Deco, 2011), this can be achieved by removing nonlinearities and balancing the leak, recurrent excitation, and inhibition among the integrators (Usher and McClelland, 2001; Bogacz et al., 2006), although the balance must be exact.

Indeed, a known limitation of line attractor models arises from their sensitivity to disturbance. Even the slightest noise can cause the state of the network to meander along the stable states and lose the stored decision variable (Pouget and Latham, 2002). It has been suggested that this problem can be mitigated if the network is composed of hysteretic units (Koulakov et al., 2002; Goldman et al., 2003; Cain et al., 2013). Such robust models offer a theoretical framework for biologically plausible networks that can represent and integrate parametric values (Wang, 2002; Machens et al., 2005).

In addition to the lossless representation of information during the gap between pulses, we also made the peculiar observation that subjects obtained more information from a second pulse. We detected this by observing that subjects exceeded the predicted accuracy of a perfect integrator that used all the information from the first pulse. The implication is that the measured accuracy from the first pulse was suboptimal. This is supported directly by estimating the accuracy of a perfect integrator for the double-pulse trials and by the analyses in Figures 3 and 4, which clearly indicate greater leverage of the second pulse on choice.

There are several ways to justify this suboptimal behavior. It could arise because the subject curtails processing of the first pulse prematurely, as in bounded evidence accumulation (Kiani et al., 2008), but continues the accumulation process for the second pulse (Resulaj et al., 2009) when it is shown. Alternatively, the subject could boost the influence of the second pulse by paying more attention to it (Treue and Maunsell, 1999; Reynolds and Chelazzi, 2004) or through other means such as a time-dependent increase in gain (Ditterich, 2006) or urgency gating (Cisek et al., 2009; Miller and Katz, 2013). Among those, inadequate attention to the first pulse seems unlikely, since subjects were clearly aware that they would receive only one motion pulse on a sizeable proportion of trials (14%). A leaky integration process can lead to a larger influence of the second pulse too (Kiani et al., 2008; Rüter et al., 2012), but it is incompatible with the invariance to interpulse intervals, as explained above.

We speculate that in their attempt to achieve high accuracy, subjects may have tried to ascertain information from the first pulse about the trial type (i.e., one or two pulses) and difficulty. For example, the probability of a second pulse is larger if the coherence of the first pulse is low (see Materials and Methods), and the coherences of the first and second pulse, were they known, would support more accurate cue combination, compatible with an optimal Bayesian strategy. Although subjects did not actually benefit from this strategy, as evidenced by the suboptimal performance in one-pulse trials, the attempt might have led to some loss of information, owing perhaps to a division of processing resources.

In addition to explaining the improvement of performance from single-pulse to double-pulse trials, the loss of information on the first pulse explains why a strong–weak sequence would lead to lower choice accuracy than a weak–strong sequence. Simply put, when the stronger pulse is presented first, curtailing its impact is more detrimental. Regardless of the exact mechanism, however, our observations suggest that the weaker influence on a decision of the first of two samples of evidence may not be a sign of forgetfulness or “integration leak” but the accumulation of discounted early information by an otherwise perfect integration mechanism—one that is capable of maintaining the fidelity of accumulated evidence for at least 1 s while awaiting another influential fragment, morsel, or bit.

Footnotes

This research is supported by Howard Hughes Medical Institute. We thank Xiao-Jing Wang, Tim Hanks, and Braden Purcell for helpful discussions.

The authors declare no competing financial interests.

References

  1. Adelson EH, Bergen JR. Spatiotemporal energy models for the perception of motion. J Opt Soc Am A. 1985;2:284–299. doi: 10.1364/JOSAA.2.000284. [DOI] [PubMed] [Google Scholar]
  2. Ahumada AJ., Jr Classification image weights and internal noise level estimation. J Vis. 2002;2(1):8, 121–131. doi: 10.1167/2.1.8. [DOI] [PubMed] [Google Scholar]
  3. Albantakis L, Deco G. Changes of mind in an attractor network of decisionmaking. PLoS Comput Biol. 2011;7:e1002086. doi: 10.1371/journal.pcbi.1002086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Beck JM, Ma WJ, Kiani R, Hanks T, Churchland AK, Roitman J, Shadlen M, Latham PE, Pouget A. Probabilistic population codes for Bayesian decision making. Neuron. 2008;60:1142–1152. doi: 10.1016/j.neuron.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychol Rev. 2006;113:700–765. doi: 10.1037/0033-295X.113.4.700. [DOI] [PubMed] [Google Scholar]
  6. Brown E, Holmes P. Modeling a simple choice task: stochastic dynamics of mutually inhibitory neural groups. Stochast Dyn. 2001;1:159–191. doi: 10.1142/S0219493701000102. [DOI] [Google Scholar]
  7. Brunton BW, Botvinick MM, Brody CD. Rats and humans can optimally accumulate evidence for decision-making. Science. 2013;340:95–98. doi: 10.1126/science.1233912. [DOI] [PubMed] [Google Scholar]
  8. Cain N, Barreiro AK, Shadlen M, Shea-Brown E. Neural integrators for decision making: a favorable tradeoff between robustness and sensitivity. J Neurophysiol. 2013;109:2542–2559. doi: 10.1152/jn.00976.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Churchland AK, Kiani R, Shadlen MN. Decision-making with multiple alternatives. Nat Neurosci. 2008;11:693–702. doi: 10.1038/nn.2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cisek P, Puskas GA, El-Murr S. Decisions in changing conditions: the urgencygating model. J Neurosci. 2009;29:11560–11571. doi: 10.1523/JNEUROSCI.1844-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cook EP, Maunsell JH. Dynamics of neuronal responses in macaque MT and VIP during motion detection. Nat Neurosci. 2002;5:985–994. doi: 10.1038/nn924. [DOI] [PubMed] [Google Scholar]
  12. Ditterich J. Computational approaches to visual decision making. Novartis Found Symp. 2006;270:114–126. doi: 10.1002/9780470034989.ch10. [DOI] [PubMed] [Google Scholar]
  13. Furman M, Wang XJ. Similarity effect and optimal control of multiple-choice decision making. Neuron. 2008;60:1153–1168. doi: 10.1016/j.neuron.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gold JI, Shadlen MN. Neural computations that underlie decisions about sensory stimuli. Trends Cogn Sci. 2001;5:10–16. doi: 10.1016/S1364-6613(00)01567-9. [DOI] [PubMed] [Google Scholar]
  15. Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci. 2007;30:535–574. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
  16. Goldman MS, Levine JH, Major G, Tank DW, Seung HS. Robust persistent neural activity in a model integrator with multiple hysteretic dendrites per neuron. Cereb Cortex. 2003;13:1185–1195. doi: 10.1093/cercor/bhg095. [DOI] [PubMed] [Google Scholar]
  17. Heitz RP, Schall JD. Neural mechanisms of speed-accuracy tradeoff. Neuron. 2012;76:616–628. doi: 10.1016/j.neuron.2012.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hille B. Ion channels of excitable membranes. Ed 3. Sunderland, MA: Sinauer Associates; 2001. [Google Scholar]
  19. Kiani R, Hanks TD, Shadlen MN. Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. J Neurosci. 2008;28:3017–3029. doi: 10.1523/JNEUROSCI.4761-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Koulakov AA, Raghavachari S, Kepecs A, Lisman JE. Model for a robust neural integrator. Nat Neurosci. 2002;5:775–782. doi: 10.1038/nn893. [DOI] [PubMed] [Google Scholar]
  21. Laming D. Probability summation—a critique. J Opt Soc Am A Opt Image Sci Vis. 2013;30:300–315. doi: 10.1364/JOSAA.30.000300. [DOI] [PubMed] [Google Scholar]
  22. Laming DRJ. Information theory of choice reaction time. New York: Wiley; 1968. [Google Scholar]
  23. Link SW. The wave theory of difference and similarity. Hillsdale, NJ: Erlbaum; 1992. [Google Scholar]
  24. Link SW, Heath RA. A sequential theory of psychological discrimination. Psychometrika. 1975;40:77–105. doi: 10.1007/BF02291481. [DOI] [Google Scholar]
  25. Lo CC, Wang XJ. Cortico-basal ganglia circuit mechanism for a decision threshold in reaction time tasks. Nat Neurosci. 2006;9:956–963. doi: 10.1038/nn1722. [DOI] [PubMed] [Google Scholar]
  26. Luce RD. Response times: their role in inferring elementary mental organization. Belfast: Oxford UP; 1986. [Google Scholar]
  27. Machens CK, Romo R, Brody CD. Flexible control of mutual inhibition: a neural model of two-interval discrimination. Science. 2005;307:1121–1124. doi: 10.1126/science.1104171. [DOI] [PubMed] [Google Scholar]
  28. Miller P, Katz DB. Stochastic transitions between neural states in taste processing and decision-making. J Neurosci. 2010;30:2559–2570. doi: 10.1523/JNEUROSCI.3047-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Miller P, Katz DB. Accuracy and response-time distributions for decision-making: linear perfect integrators versus nonlinear attractor-based neural circuits. J Comput Neurosci. 2013 doi: 10.1007/s10827-013-0452-x. doi: 10.1007/s10827-013-0452-x. Advance online publication. Retrieved September 8, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Neri P. Estimation of nonlinear psychophysical kernels. J Vis. 2004;4(2):2, 82–91. doi: 10.1167/4.2.2. [DOI] [PubMed] [Google Scholar]
  31. Nienborg H, Cumming BG. Decision-related activity in sensory neurons reflects more than a neuron's causal effect. Nature. 2009;459:89–92. doi: 10.1038/nature07821. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Pouget A, Latham P. Digitized neural networks: long-term stability from forgetful neurons. Nat Neurosci. 2002;5:709–710. doi: 10.1038/nn0802-709. [DOI] [PubMed] [Google Scholar]
  33. Purcell BA, Heitz RP, Cohen JY, Schall JD, Logan GD, Palmeri TJ. Neurally constrained modeling of perceptual decision making. Psychol Rev. 2010;117:1113–1143. doi: 10.1037/a0020311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychol Rev. 2004;111:333–367. doi: 10.1037/0033-295X.111.2.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ratcliff R, Hasegawa YT, Hasegawa RP, Smith PL, Segraves MA. Dual diffusion model for single-cell recording data from the superior colliculus in a brightness discrimination task. J Neurophysiol. 2007;97:1756–1774. doi: 10.1152/jn.00393.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Resulaj A, Kiani R, Wolpert DM, Shadlen MN. Changes of mind in decision making. Nature. 2009;461:263–266. doi: 10.1038/nature08275. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Reynolds JH, Chelazzi L. Attentional modulation of visual processing. Ann Rev Neurosci. 2004;27:611–647. doi: 10.1146/annurev.neuro.26.041002.131039. [DOI] [PubMed] [Google Scholar]
  38. Roitman JD, Shadlen MN. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J Neurosci. 2002;22:9475–9489. doi: 10.1523/JNEUROSCI.22-21-09475.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Rüter J, Marcille N, Sprekeler H, Gerstner W, Herzog MH. Paradoxical evidence integration in rapid decision processes. PLoS Comput Biol. 2012;8:e1002382. doi: 10.1371/journal.pcbi.1002382. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Seung HS, Lee DD, Reis BY, Tank DW. Stability of the memory of eye position in a recurrent network of conductance-based model neurons. Neuron. 2000;26:259–271. doi: 10.1016/S0896-6273(00)81155-1. [DOI] [PubMed] [Google Scholar]
  41. Shadlen MN, Newsome WT. Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J Neurophysiol. 2001;86:1916–1936. doi: 10.1152/jn.2001.86.4.1916. [DOI] [PubMed] [Google Scholar]
  42. Shadlen MN, Hanks TD, Churchland AK, Kiani R, Yang T. The speed and accuracy of a simple perceptual decision: a mathematical primer. In: Doya K, Ishii S, Pouget A, Rao RPN, editors. Bayesian brain: probabilistic approaches to neural coding. Cambridge: MIT; 2006. pp. 209–237. [Google Scholar]
  43. Smith PL. The accumulator model of two-choice discrimination. J Math Psychol. 1988;32:135–168. doi: 10.1016/0022-2496(88)90043-0. [DOI] [Google Scholar]
  44. Smith PL, McKenzie CR. Diffusive information accumulation by minimal recurrent neural models of decision making. Neural Comput. 2011;23:2000–2031. doi: 10.1162/NECO_a_00150. [DOI] [PubMed] [Google Scholar]
  45. Treue S, Maunsell JH. Effects of attention on the processing of motion in macaque middle temporal and medial superior temporal visual cortical areas. J Neurosci. 1999;19:7591–7602. doi: 10.1523/JNEUROSCI.19-17-07591.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Usher M, McClelland JL. The time course of perceptual choice: the leaky, competing accumulator model. Psychol Rev. 2001;108:550–592. doi: 10.1037/0033-295X.108.3.550. [DOI] [PubMed] [Google Scholar]
  47. Vickers D, Smith P. Accumulator and random-walk models of psychophysical discrimination: a counter-evaluation. Perception. 1985;14:471–497. doi: 10.1068/p140471. [DOI] [PubMed] [Google Scholar]
  48. Wald A, Wolfowitz J. Optimum character of the sequential probability ratio test. Ann Math Statist. 1947;19:326–339. [Google Scholar]
  49. Wang XJ. Probabilistic decision making by slow reverberation in cortical circuits. Neuron. 2002;36:955–968. doi: 10.1016/S0896-6273(02)01092-9. [DOI] [PubMed] [Google Scholar]
  50. Wong KF, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. J Neurosci. 2006;26:1314–1328. doi: 10.1523/JNEUROSCI.3733-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES