The Neuromuscular Transform of the Lobster Cardiac System Explains the Opposing Effects of a Neuromodulator on Muscle Output

Abstract

Motor neuron activity is transformed into muscle movement through a cascade of complex molecular and biomechanical events. This nonlinear mapping of neural inputs to motor behaviors is called the neuromuscular transform (NMT). We examined the NMT in the cardiac system of the lobster Homarus americanus by stimulating a cardiac motor nerve with rhythmic bursts of action potentials and measuring muscle movements in response to different stimulation patterns. The NMT was similar across preparations, which suggested that it could be used to predict muscle movement from spontaneous neural activity in the intact heart. We assessed this possibility across semi-intact heart preparations in two separate analyses. First, we performed a linear regression analysis across 122 preparations in physiological saline to predict muscle movements from neural activity. Under these conditions, the NMT was predictive of contraction duty cycle but was unable to predict contraction amplitude, likely as a result of uncontrolled interanimal variability. Second, we assessed the ability of the NMT to predict changes in motor output induced by the neuropeptide C-type allatostatin. Wiwatpanit et al. (2012) showed that bath application of C-type allatostatin produced either increases or decreases in the amplitude of the lobster heart contractions. We show that an important component of these preparation-dependent effects can arise from quantifiable differences in the basal state of each preparation and the nonlinear form of the NMT. These results illustrate how properly characterizing the relationships between neural activity and measurable physiological outputs can provide insight into seemingly idiosyncratic effects of neuromodulators across individuals.

Introduction

The translation of neural commands into muscular output is a complex phenomenon that depends on multiple physiological factors. Presynaptically, the release of neurotransmitter at the neuromuscular junction is a history-dependent function of membrane potential and calcium dynamics (Katz and Miledi, 1968; Barrett and Stevens, 1972). Postsynaptically, receptor activation triggers Ca²⁺ influx and additional release from internal stores (Berridge et al., 2000; Endo, 2009), ultimately leading to muscle contraction. Finally, the contractile properties of the muscle fiber depend on a number of variables, including the initial length and contractile force of the fiber (Hooper and Weaver, 2000). This mapping of a neural signal into a muscular contraction is termed the neuromuscular transform (NMT). Several studies have investigated the NMT from a theoretical standpoint (Brezina and Weiss, 2000; Brezina et al., 2000a, 2000b); others have used a “decoding” algorithm to capture the NMT (Stern et al., 2007, 2009).

In this paper, we experimentally examine the NMT of the cardiac neuromuscular system in the American lobster (Homarus americanus), in which the cardiac central pattern generator (CPG) sends rhythmic, single-phase neural commands to the striated cardiac muscle. The activity of the cardiac CPG is modifiable by a large number of neuropeptides, amines, and other biogenic signaling molecules, which alter cardiac output to meet external demands under normal physiological conditions (Cooke, 2002). For example, walking on an underwater treadmill elicits an increase in heart rate (Guirguis and Wilkens, 1995).

A general problem that arises in the study of neural circuits is that similar perturbations can evoke different effects across preparations, a broad phenomenon called “state dependence” (Nadim et al., 2008). State dependence is particularly perplexing when different preparations show qualitatively opposite responses to an experimental manipulation (Djokaj et al., 2001; Spitzer et al., 2008; Grashow et al., 2009). A recent study showed that perfusion of the neuropeptide C-type allatostatin (AST-C) through intact lobster hearts produced inconsistent motor-level effects; AST-C increased contraction amplitude in some preparations but decreased amplitude in others (Wiwatpanit et al., 2012). We now show that this puzzling result can arise in a state-dependent manner from the nonlinear shape of the cardiac NMT.

Our results also speak to a growing literature on the intrinsic variability of neural systems (Marder and Goaillard, 2006; Marder and Taylor, 2011). Many studies have measured the variability of network components on an electrophysiological or molecular level. For example, the peak conductance of intrinsic ion currents (Swensen and Bean, 2005; Schulz et al., 2006), the voltage dependence of these currents (Amendola et al., 2012), and the strength of chemical synapses and modulator-invoked currents (Goaillard et al., 2009; Roffman et al., 2012) have all been shown to vary over severalfold ranges across individuals. In comparison, fewer studies have commented on variability at the level of circuit activity and motor behaviors (Horn et al., 2004; Lum et al., 2005; Williams et al., 2013). We investigate the variability of motor neuron activity and muscle movements in semi-intact lobster hearts, as well as variability in the shape of the cardiac NMT across stimulated heart preparations.

Materials and Methods

Physiological recordings.

H. americanus of either sex were purchased from local seafood markets (Harpswell) and kept in 10°C tanks of recirculating sea water. All dissections and experiments were carried out in chilled physiological saline (in mm as follows: NaCl 479.12, KCl 12.74, CaCl₂ 13.67, MgSO₄ 20.00, Na₂SO₄ 3.91, Trizma base 11.45, and maleic acid 4.82, pH 7.45; chemicals from Sigma-Aldrich). Lobsters were covered in ice for 20 min before dissection. The dorsal thoracic carapace and the heart were jointly removed from the animal. Saline was perfused through the posterior artery, which was cannulated with a polyethylene tube. A second inflow tube in the bath maintained temperature between 9° and 11°C, using an in-line peltier temperature regulator (CL-100 bipolar temperature controller and SC-20 solution heater/cooler; Warner Instruments). Two outflow tubes were positioned at the posterior end of the heart, drawing the saline across the heart at ∼2.5 ml/min. Our experimental procedures have been described in detail previously (Stevens et al., 2009; Wiwatpanit et al., 2012).

In semi-intact heart preparations, the thoracic carapace and heart were pinned ventral side up on a Sylgard (KR Anderson)-coated dish. Contraction force was recorded by tying 6-0 surgical suture silk (Teleflex) around the anterior arteries, and connecting them to a Grass FT03 force–displacement transducer (Astro-Med). The force transducer was angled at 30° above horizontal and stretched to give a baseline deflection equivalent to that produced by a 2 g weight. Thus, all measurements of muscle movements are given in units of grams. This signal was amplified with an ETH-250 Bridge/Bio amplifier (CB Sciences) and a Brownlee 410 instrumentation amplifier (Brownlee Precision), and then recorded on a computer using a Micro 1401 Plus data acquisition board and Spike2 software (Cambridge Electronic Design). Activity of one of the anterolateral cardiac motor nerves was recorded extracellularly using a suction electrode, which was inserted into the heart by making a small incision in the cardiac tissue. This cut modestly decreased contraction amplitude (<15% decrease) in some cases. This signal was amplified by an A-M systems Model 1700AC amplifier (A-M Systems) and a Brownlee 410 instrumentation amplifier. The signal was digitized and recorded in the same manner as the force recording. This procedure produced stable recordings for at least 8 h (Stevens et al., 2009). All semi-intact data were taken from previous projects in our laboratory (see Acknowledgments). Some of these data have been included in previous publications. Control data from two publications (Stevens et al., 2009; Wiwatpanit et al., 2012) were included in our analysis of 122 baseline semi-intact preparations. Data from semi-intact hearts in bath-applied AST-C were previously published (Wiwatpanit et al., 2012).

In stimulated heart preparations, the heart was prepared as described above, but with the cardiac CPG removed. Bursts of electrical stimuli were applied to one of the remaining motor nerves through a suction electrode. The electrical impulses were generated by the Micro 1401 data acquisition board, commanded by a custom-written Spike2 Sequencer file. Impulse trains contained 15 bursts of spikes at 60 Hz; the heart was left unstimulated for 60 s between trains. We averaged the final two contractions of the heart in all of our analyses, as this “steady-state” behavior typifies cardiac function in a natural setting. We sampled the heart's response to 36 different stimulation patterns, which sampled a 6 × 6 grid of stimulation duty cycle (levels = 0.0666, 0.1333, 0.2, 0.2666, 0.3333, and 0.4) and burst frequency (levels = 0.25, 0.40, 0.55, 0.70, 0.85, and 1.0 Hz). These ranges are consistent with what is typically observed experimentally (see Results; Fig. 3).

Figure 3.

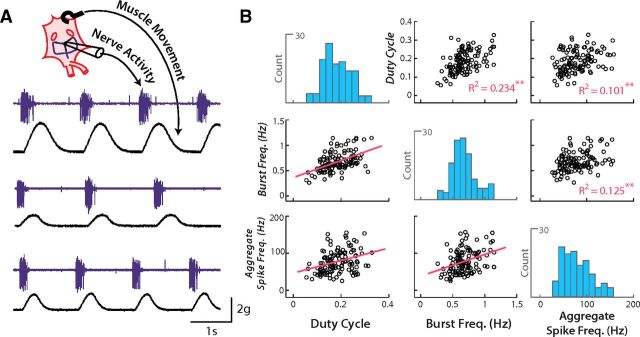
Cardiac motor neuron activity is intrinsically variable across semi-intact heart preparations. A, Three example semi-intact heart experiments showing interanimal variability across preparations. The schematic at the top of the panel illustrates the experimental setup. Purple traces show extracellular suction electrode recordings of an anterolateral cardiac motor nerve; black traces show the heart contractions as measured by a force transducer (see Materials and Methods). (compare with Fig. 1C). B, Scatterplot matrix showing measured neural activity patterns across 122 semi-intact preparations. The scatterplots represent all pairwise relationships between motor neuron duty cycle, burst frequency, and spike frequency. Below the diagonal, red lines indicate the best fit line for each pairwise relationship. Above the diagonal, the R² value for each pairwise relationship is listed. **p < 0.001. Histograms along the diagonal represent the distribution for each of these three variables.

Rounding error caused slight discrepancies between the desired duty cycle and administered duty cycle; these discrepancies were small (the absence or presence of a single spike from a burst). The 36 stimulation patterns were administered in a different random order for each preparation. Preparations that systematically decreased in contraction amplitude over the course of the experiment were discarded. In this paper, all data from stimulated muscle preparations are novel.

Data analysis and statistics.

Data from semi-intact preparations were analyzed with custom-written Spike2 scripts and with scripts provided by Dr. Dirk Bucher (available at: http://www.whitney.ufl.edu/BucherLab/Spike2_Scripts2_box.htm). The effects of AST-C were quantified by comparing time-averaged neural and muscle activity in baseline conditions (200 s just before peptide application) and during the perfusion of peptide through the heart (200 s at the peak of peptide effect, 5–8 min after the onset of AST-C application). As described by Wiwatpanit et al. (2012), the lobster heart sometimes exhibits biphasic responses to AST-C; in these cases, we analyzed 200 s around the peak of the second effect of the peptide (see Wiwatpanit et al., 2012). Data from stimulated muscle recordings were analyzed in the MATLAB computing environment (R2012b, MathWorks). The unit of replication (n) in all experiments was the number of heart preparations; multiple experiments were not performed in the same animal.

Multiple linear regression models were constructed using the LinearModel class in the MATLAB Statistics Toolbox (MathWorks). A linear regression model is a descriptive model that estimates the relationships among independent (i.e., predictor) and dependent (i.e., response) variables; it does not provide a mechanistic account of a biological system. Multiple linear regression is applied to a dataset with repeated joint observations of one dependent variable (y) and several independent variables (x₁, x₂, …, x_k). Each observation of the dependent variable (indexed by i = 1, 2, …, n) is modeled by a linear predictor function plus a noise term (ϵ_i, assumed to be independent and identically distributed random variables from a normal distribution):

The parameters of the model (β_o, …, β_k) are estimated by minimizing the sum of squared residuals. For each regression model, we used ANOVA to determine whether each term in the model had a significant predictive effect, after controlling for the effects of all other terms in the model. This is done by comparing the explanatory power of the full regression model to a reduced model that contains fewer terms by computing extra sums of squares (see Chapter 7 of Kutner et al., 2004). We report the extra sums of squares in Tables 1 and 2; these ANOVA tables were calculated using the “anova” MATLAB function within the LinearModel class with the parameter “sstype” set to three.

Table 1.

ANOVA tables for regression models predicting contraction duty cycle^a

	Stimulated heart preparations				Across semi-intact preparations
	Sum of squares	df	F	p	Sum of Squares	df	F	p
Duty cycle	0.0515	1	461.2	1E-20	0.0123	1	6.442	0.012
Burst frequency (Hz)	0.0710	1	635.3	1E-22	0.0570	1	29.943	3E-07
Interaction	0.0088	1	78.8	4E-10	0.0102	1	5.355	0.022
Error	0.0036	32			0.2227	118

^aSee Figure 4A, C.

Table 2.

ANOVA tables for regression models predicting contraction amplitude^a

	Stimulated heart preparations				Across semi-intact preparations
	Sum of squares	df	F	p	Sum of squares	df	F	p
Duty cycle	0.3201	1	157.0	1E-13	0.893	1	1.715	0.19
Burst frequency (Hz)	0.1189	1	58.3	1E-08	0.262	1	0.504	0.48
Interaction	0.0100	1	4.9	0.034	0.561	1	1.078	0.30
Duty cycle (quadratic)	0.2847	1	139.6	5E-13	0.020	1	0.039	0.84
Error	0.0632	31			60.929	117

^aSee Figure 4B, D.

Results

A direct, brute-force characterization of the cardiac NMT

In the intact crustacean heart, muscle contractions are induced by rhythmic motor nerve discharges generated by the cardiac CPG. Simultaneously, the cardiac muscle tissue influences the neural activity of the cardiac CPG through stretch mechanoreceptors and nitric oxide signaling pathways (Cooke, 2002; Mahadevan et al., 2004; Fig. 1A). We used a stimulated muscle protocol to characterize the cardiac NMT, which comprises the feed-forward component of the intact neuromuscular system (Fig. 1B,C). In this protocol, the cardiac CPG is removed, and muscle contractions are elicited by electrical pulses delivered through a suction electrode (see Materials and Methods).

Figure 1.

The crustacean cardiac system and experimental procedure for characterizing the NMT. A, Schematic diagram of the intact crustacean cardiac system. The cardiac CPG (green box) sends feed-forward neural commands to the cardiac tissue, which provides feedback to the cardiac ganglion. The cardiac ganglion consists of four premotor neurons (in blue) and five motor neurons (in red), all of which are spontaneously oscillatory. B, In stimulated heart preparations, the cardiac CPG is removed (top) and the motor nerve is electrically stimulated by a suction electrode (bottom). C, Example trace from a stimulated heart preparation. The schematic on the left illustrates a more realistic representation of the crustacean heart than the diagrams in A and B. The cardiac motor nerve is stimulated (red trace), and muscle movement (black trace) is recorded via a force transducer.

Theoretically, the NMT maps any arbitrary neural input to a muscle movement within a stimulated muscle preparation. However, the spontaneous activity of the cardiac CPG is relatively constrained; periodic bursts of action potentials are produced with various burst frequencies and duty cycles (defined as burst duration divided by cycle period). We therefore approximated the cardiac NMT by measuring muscle movement in response to 36 different electrical stimulation patterns by independently varying burst frequency and burst duty cycle over six physiologically plausible levels (two example stimulation patterns are shown in Fig. 1C).

The spike frequency within each stimulated burst was held constant at 60 Hz, which is representative of what has been measured in intracellular recordings of the cardiac motor neurons (P. Dickinson, unpublished observations; also see García-Crescioni et al., 2010). We chose to limit our analysis to burst frequency and burst duty cycle because spike frequency is difficult to accurately measure and interpret in semi-intact preparations of the cardiac system. The CG contains five motor neurons, which occasionally produce simultaneous spikes. Extracellular recordings of the cardiac motor nerve erroneously register these simultaneous spikes as a single event; intracellular recordings are the only accurate method for estimating spike frequency, but these recordings cannot be reliably achieved in semi-intact heart preparations. Thus, our characterization of the cardiac NMT is only partial: a complete description of the NMT would also consider the effects of spike frequency on motor output.

It is well documented that crustacean cardiac muscle and other neuromuscular systems exhibit history-dependent responses to electrical stimulation resulting from short-term plasticity phenomena (Hooper and Weaver, 2000). Over repeated electrical stimulations, the motor responses approach a stable, steady-state behavior (Fig. 1C). This steady-state behavior is the most physiologically relevant, as the heart is usually constitutively active. We applied 15 periodic bursts for each stimulation pattern, which was sufficiently long for the system to reach its steady state.

The responsiveness of the cardiac muscle to electrical stimulation varied appreciably across preparations (Fig. 2A, left). The strongest muscle contraction was usually elicited by a duty cycle of 0.19 applied at 0.25 Hz. At this stimulation, the amplitude of the muscle response ranged from 0.43 to 4.37 g (mean ± SD, 1.49 ± 0.96 g). A significant portion of this variability reflects uncontrollable variations in experimental procedure for the stimulated muscle preparation; for example, the quality of suction on the electrode will vary across experiments, which could influence the number/strength of activated motor nerve terminals within a preparation. However, intrinsic interanimal differences are also likely to contribute to this variability (see Discussion). For example, the overall size of the heart varies across animals and may be expected to correlate positively with the amplitude of stimulated heart contractions. Additionally, the branching and innervation patterns of the anterolateral nerves may vary across preparations, which could cause an identical pattern of motor neuron activity to activate different sets of muscle fibers across preparations.

Figure 2.

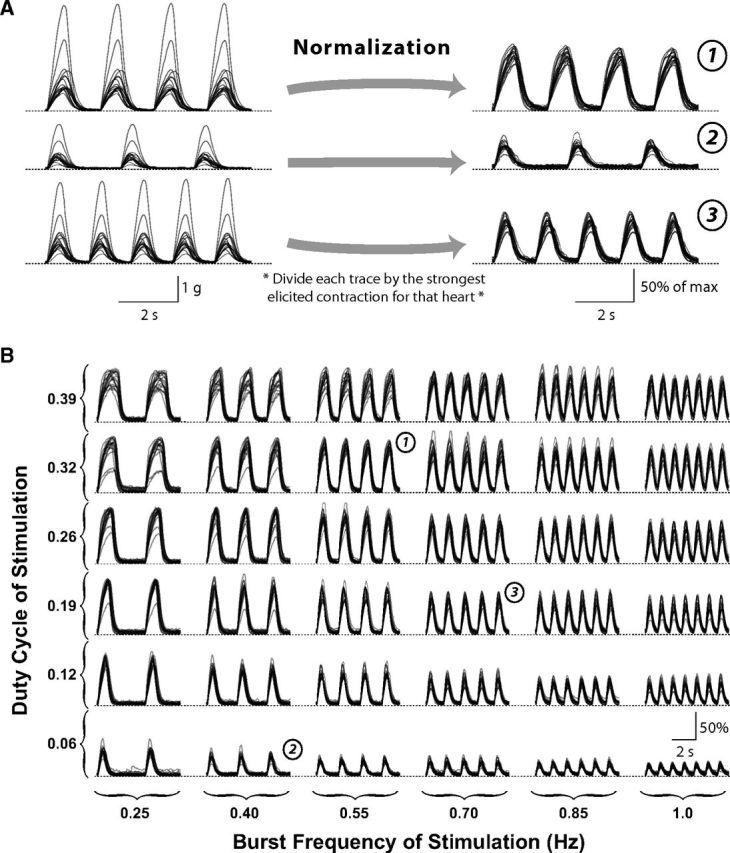
The cardiac NMT measured in 16 stimulated heart preparations. Muscle movement traces from each preparation are overlaid. A, Response of the hearts to three representative patterns of electrical stimulation (see B, matching circled numbers). Traces on the left represent raw movement recordings, which vary significantly in amplitude. Traces on the right represent normalized by dividing each trace by the peak amplitude for that heart across all stimulation patterns. B, Normalized steady-state movement recordings for each of the 36 stimulation patterns.

Despite these large differences in muscle sensitivity, the waveform of the muscle response was similar across preparations. When normalized to the maximal response across all stimulation patterns, the stimulated muscle responses were highly reproducible across preparations (Fig. 2A). Figure 2B shows the normalized, steady-state muscle force recordings for each of the 36 stimulation patterns (n = 16). Overall, the reproducibility of normalized responses suggests that the NMT, when averaged across preparations, might be effective at predicting muscle movements from spontaneous neural activity in individual hearts.

Predicting muscle movements from naturally variable neural inputs

Figure 2B shows that the lobster heart produces different movements as the frequency and duty cycle of rhythmic neural input vary. It is therefore natural to ask how variable these neural inputs are in the intact organism. Furthermore, if neural activity measures do vary over fairly large ranges, then the NMT should predict how these variable neural inputs elicit different muscle behaviors. To address these questions, we examined the natural variability of cardiac CPG activity across 122 semi-intact heart preparations, in which muscle contractions and motor nerve impulses can be recorded simultaneously (see Materials and Methods; Fig. 3A).

Across these preparations, motor neuron duty cycle, burst frequency, and intraburst spike frequency varied threefold to fivefold (Fig. 3B). The duty cycle and burst frequency of the cardiac motor neurons varied approximately over the same ranges used for our stimulation protocol in Figure 2B. However, all neural activity measures, including burst frequency and duty cycle, exhibited significant positive linear correlations (t test of Pearson's linear correlation coefficient, df = 120, p < 0.01 in all cases; the coefficients of determination are listed in Fig. 3B). Thus, under baseline conditions, we observed few preparations with low burst frequencies and high duty cycles (Fig. 2B, upper left corner), and few preparations with high burst frequencies and low duty cycles (Fig. 2B, lower right corner).

We then assessed the ability of the cardiac NMT to predict muscle movements from motor neuron duty cycle and burst frequency across semi-intact preparations by fitting multiple linear regression models. We fit models to predict two features of muscle movements: contraction amplitude and contraction duty cycle (defined as the duration of a contraction above half-amplitude multiplied by the contraction frequency). The contraction frequency was not studied because the crustacean heart is entirely neurogenic; thus, contraction frequency was always equal to motor neuron burst frequency. All models used the frequency and duty cycle of motor neuron activity as independent/predictor variables. Including spike frequency as an additional independent variable did not improve the predictive power for any of the models (data not shown).

Figures 4A and 4B, respectively, show the mean contraction duty cycle and amplitude of the stimulated hearts (Fig. 2) at each level of stimulation duty cycle and burst frequency. The results of our linear regression analysis, which quantify the predictive power of these data, are summarized in Tables 1 and 2. Contraction duty cycle was positively affected by motor neuron duty cycle, positively affected by motor neuron burst frequency, and negatively affected by their first-order interaction (Fig. 4A, top; p < 0.05 for all effects; see Table 1). Conceptually, the negative interaction term means that the slope of the lines in Figure 4A significantly decrease as stimulation frequency increases; the least-squares estimate of slope at the lowest frequency was 0.76 (Fig. 4A, black line), whereas the estimated slope at the highest frequency was 0.40 (Fig. 4A, yellow line). The NMT predicts that these same statistical effects on contraction duty cycle would be present across semi-intact preparations.

Figure 4.

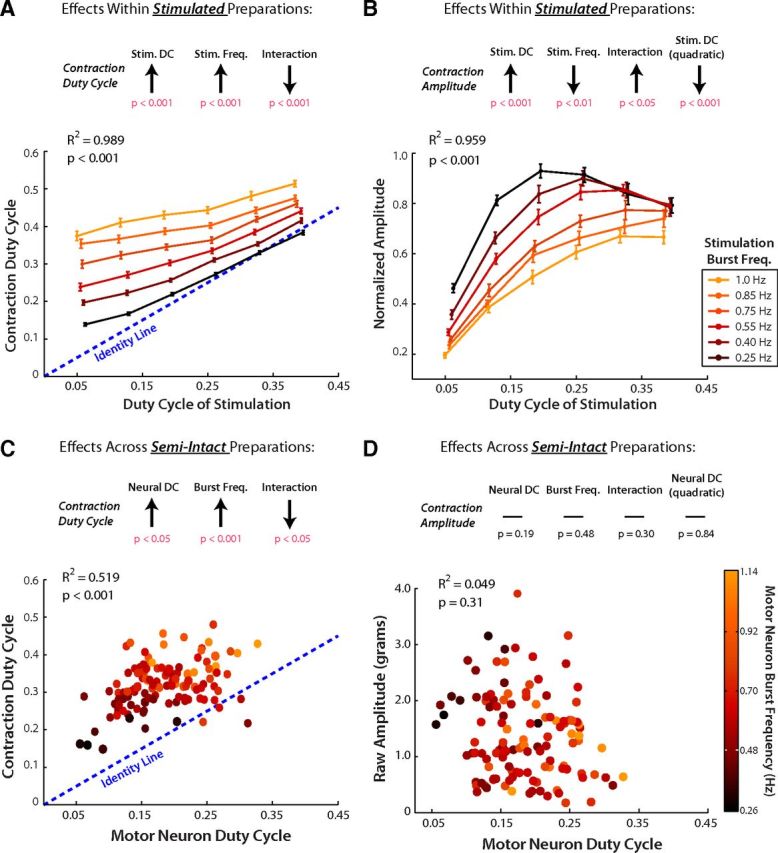
Predicting contraction duty cycle and amplitude from neural inputs within stimulated preparations and across semi-intact hearts. A, C, Linear models were fit to the form y = b₀ + b₁x₁ + b₂x₂ + b₃x₁x₂; where y = muscle contraction duty cycle, x₁ = stimulation/neural duty cycle, and x₂ = stimulation/neural burst frequency. B, D, Linear models were fit to the form z = b₀ + b₁x₁ + b₂x₂ + b₃x₁x₂ + b₄x₁²; where z = muscle contraction amplitude. All estimates for regression parameters (b₁, b₂, etc.) were obtained using ordinary least-squares. Arrows at the top of each panel schematically indicate the sign and significance of each regression parameter using ANOVA; full ANOVA results are given in Tables 1 and 2. Plots at the bottom of each panel indicate the dependent variable on the vertical axis, neural/stimulation duty cycle on the horizontal axis, and neural/stimulation burst frequency on a color scale (see legends to the right of B, D). A, B, Effects of stimulation duty cycle and burst frequency on muscle contraction duty cycle (A) and contraction amplitude (B) within stimulated heart preparations. Error bars indicate mean ± SE (n = 16 preparations). C, D, Effects of spontaneous motor neuron duty cycle and burst frequency on muscle contraction duty cycle (C) and contraction amplitude (D) across semi-intact heart preparations (n = 122).

We repeated this analysis for contraction amplitude. Within stimulated preparations, contraction amplitude was negatively related to burst frequency, and nonlinearly related to stimulation duty cycle (Fig. 4B). We performed a linear regression analysis with a quadratic term for stimulation duty cycle and a first-order interaction term for burst frequency and stimulation duty cycle (Table 2). The estimates for each of these regression terms were statistically significant (Fig. 4B, top; Table 2).

We then fit linear regression models to our semi-intact heart data and compared these fits with the models fit to data from stimulated preparations. Figures 4C and 4D, respectively, show how contraction duty cycle and amplitude empirically covaried with motor neuron duty cycle and burst frequency across all semi-intact preparations. Qualitatively, one can see that the NMT prediction for contraction duty cycle resembled the observed trends across semi-intact preparations (compare Fig. 4A with Fig. 4C), whereas the NMT prediction for contraction amplitude was not successful (compare Fig. 4B with Fig. 4D). We again used linear regression to examine these observations quantitatively.

For contraction duty cycle, the best-fit regression parameters across semi-intact data were not significantly different from those fit to the NMT (Table 3, 95% confidence intervals). The overall regression model for contraction duty cycle across semi-intact preparations was significant (F test vs constant model, F = 42.1, error df = 118, p < 0.001) and was predicted by spontaneous neural output with moderate accuracy (R² = 0.519).

Table 3.

95% confidence intervals of regression model coefficients for predicting contraction duty cycle^a

	Stimulated heart preparations			Across semi-intact preparations
	Lower bound	Estimate	Upper bound	Lower bound	Estimate	Upper bound
Duty cycle	0.792	0.875	0.959	0.122	0.557	0.992
Burst frequency (Hz)	0.350	0.381	0.412	0.229	0.360	0.490
Interaction	−0.659	−0.536	−0.413	−1.354	−0.729	−0.105

^aThe regression model fit to data from stimulated heart preparations is not significantly different from the model fit to data across semi-intact heart preparations.

Interestingly, neural duty cycle and burst frequency did not significantly predict contraction amplitude across semi-intact preparations. The linear regression model did not predict contraction amplitude significantly better than chance (Fig. 4D; R² = 0.049; F test vs constant model, F = 1.52, error df = 117, p = 0.20). Naively, one might expect that neural activity, especially in a simple invertebrate system, would correlate with all features of muscle output. Our data contradict this expectation and suggest that other factors, in addition to neural activity, substantially influence contraction amplitude across semi-intact heart preparations (see Discussion).

The cardiac NMT provides insight into the inconsistent effects of the neuropeptide AST-C

Predicting the amplitude of heart contractions across semi-intact preparations is a difficult task because many important factors (e.g., the size of heart) undoubtedly vary across individuals. To diminish the effects of these confounding variables, we assessed the ability of the NMT to predict changes in contraction amplitude within semi-intact preparations. Specifically, we took advantage of the neuropeptide AST-C, which selectively modulates the neural commands of the cardiac CPG without affecting the neuromuscular junction or contractility of cardiac muscle fibers (Wiwatpanit et al., 2012; A. Calkins and P. Dickinson, unpublished observations). The NMT predicts how the modulator-induced changes in neural activity should affect motor output. To assess this prediction, we reanalyzed previously published data on the effects of AST-C on semi-intact preparations of the lobster heart (Wiwatpanit et al., 2012).

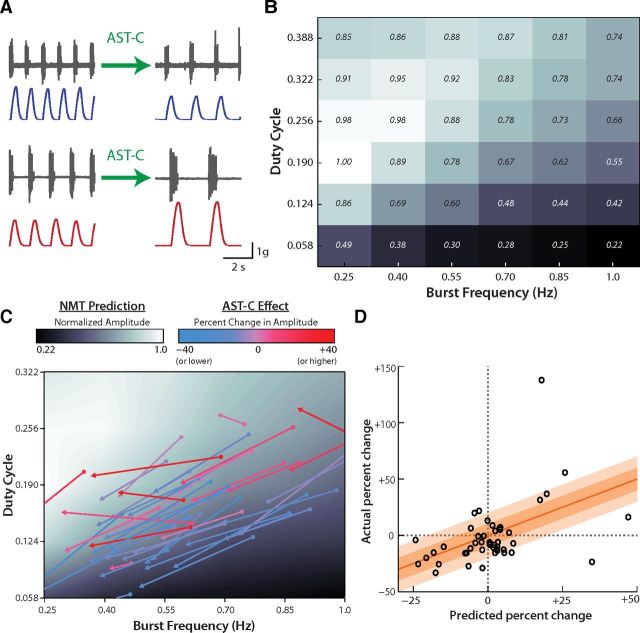
As previously reported, bath application of AST-C to semi-intact heart preparations always elicited a decrease in heart rate but had inconsistent effects on contraction amplitude. AST-C increased amplitude in some preparations but decreased amplitude in others (Fig. 5A; Wiwatpanit et al., 2012). We asked whether these differential effects on amplitude could be explained by the NMT. Figure 5B shows the NMT prediction of contraction amplitude for various neural inputs. This prediction is a two-dimensional surface that maps burst frequency and duty cycle to contraction amplitude (normalized on a scale of 0 to 1, as in Fig. 2A; numbers represent mean normalized amplitude). Because we characterized the NMT over a discrete 6 × 6 grid (Fig. 2B), we approximated this surface by linearly interpolating between these sampled locations (Fig. 5C, background black/white scale). This approach differs from the regression analysis presented in Figure 4; by linearly interpolating between our sampled points, we created a lookup table to directly estimate the amplitude of muscle contractions for any pattern of motor neuron activity within the ranges we sampled experimentally.

Figure 5.

The cardiac NMT explains the differential effects of AST-C on contraction amplitude. A, In semi-intact heart preparations, bath application of the neuropeptide AST-C consistently decreases heart rate but either decreases (top) or increases (bottom) contraction amplitude. The experimental recordings show the extracellular motor nerve activity (gray traces) above the muscle contractions (blue trace and red trace). B, The NMT prediction for relative contraction amplitude (normalized to the largest response within preparations) across different levels of motor neuron burst frequency and duty cycle. Dark tiles represent low-amplitude contractions; light tiles represent large-amplitude contractions (the precise numeric value is given in the center of each tile). C, The effects of AST-C in 48 semi-intact preparations. The black/white background illustrates the cardiac NMT prediction for amplitude (similar to B, except we linearly interpolated to estimate the NMT prediction between the sampled 6 × 6 grid of points). Each arrow indicates the change in neural activity induced by AST-C (tail = control; tip = after AST-C application). Each arrow is colored by the effect of AST-C on contraction amplitude (see color bar above plot). D, The expected versus observed percentage changes in contraction amplitude induced by the application of AST-C. If the NMT model were perfect, all data points would fall on the identity line (y = x, orange-red line). The dark and light orange bands around the identity line indicate the ±10% and 20% change, respectively, in amplitude from the identity line.

The application of AST-C changes the burst frequency and duty cycle of the cardiac motor neurons, which can be conceptualized as a movement along the two-dimensional NMT surface. Figure 5C represents these movements for 48 semi-intact heart preparations as vectors. Each vector is colored according to the motor-level effects of AST-C in that preparation: preparations in which AST-C elicited an increase in contraction amplitude (shades of red), those in which AST-C elicited a decrease in amplitude (shades of blue), and those in which AST-C did not substantially affect amplitude (shades of pink and purple).

Figure 5C illustrates several important messages. First, the initial (premodulation) and final (postmodulation) states cover much of the input space of the cardiac NMT. As in Figure 3B, the burst frequency and duty cycle of motor neuron firing are positively correlated, leaving the upper left and lower right corners of the plot empty. Second, the effects of AST-C on motor neuron firing are variable. The vectors are of different lengths (minimum length = 0.0472; maximum length = 0.4206) and directions (largest angle between any two vectors = 36.9°). We have observed similar levels of variability in the effects of other neuropeptides on the cardiac CPG (data not shown). Third, the coloring of the vectors shows visible trends that relate to the differential effects of AST-C on contraction amplitude. At high burst frequencies, the red vectors tend to start at higher duty cycles than the blue vectors. At lower frequencies, the red vectors tend to move more horizontally, toward the white “peak” of the NMT surface, relative to the blue vectors. Fourth, although these trends are visible, they are noisy. The red and blue vectors do not completely separate into two nicely defined groups but rather arise from a more or less continuous distribution.

How well does the NMT predict the effects of AST-C on contraction amplitude across these experiments? We calculated the expected percentage change in amplitude based on the interpolated NMT surface (Fig. 5C, black/white background) and compared this prediction with the observed change in amplitude elicited by AST-C (Fig. 5D). For a handful of experiments, the neural duty cycle or burst frequency went slightly outside the range of tested stimulation patterns (Fig. 5C, vectors moving off the map). In these cases, we used the nearest prediction of the NMT as an approximation, which produced reasonably accurate predictions in all cases.

Figure 5D plots the predicted change in amplitude given by the NMT surface, against the observed effects of AST-C on contraction amplitude. If the NMT were perfectly predictive, all data points would fall on the identity line (Fig. 5D, red-orange line). Overall, the explanatory power of the NMT was statistically significant: the identity line falls within the 95% confidence limits of the best-fit line (slope = 0.87 ± 0.53; intercept = −3.48 ± 7.11). By conventional goodness-of-fit measures, the NMT prediction was limited (R² = 0.18). These statistics are somewhat skewed by the non-normal distribution of these data and the presence of several outliers. The model is more fairly judged on a qualitative level, on which there are three promising observations. First, the vast majority of points fall within 20% of the NMT prediction (Fig. 5D, light orange band), and many fall within 10% of this prediction (Fig. 5D, dark orange band). Second, the data points fall above and below the NMT prediction in an unpatterned manner, suggesting that the NMT did not consistently underestimate or overestimate the effects of AST-C. Third, and most importantly, the NMT predicts that AST-C should produce both increases and decreases in contraction amplitude across the dataset and thus provides a simple explanation for the phenomenon illustrated in Figure 5A. Together, these observations show that the preparations used in this study vary substantially in their basal physiological state, yet this variability and the response to neuromodulator are consistent with the expectations of the pooled NMT shown in Figure 2B.

The nonlinear form of the cardiac NMT predicts state-dependent effects

Given that the cardiac NMT held significant predictive power for the effects of AST-C on contraction amplitude, it is natural to comment on the general features of the cardiac NMT with the hope of providing insight into other neural perturbations. Figure 6 illustrates two important features of the cardiac NMT that influence the motor-level effects of neural perturbations. In Figure 6A, two hypothetical preparations have different baseline neural activity patterns but receive the same neural perturbation (in terms of magnitude and direction). This results in differential effects on contraction amplitude resulting from the nonlinear shape of the cardiac NMT. This is an example of state dependence (Nadim et al., 2008). Thus, even if the effects of a neuromodulator were perfectly consistent across preparations, we would expect it to have variable effects on contraction amplitude because of baseline variability in semi-intact heart preparations. Figure 6B illustrates how the direction of neural perturbations influences the predicted change in contraction amplitude. Relatively small neural perturbations (short blue and red arrows) can produce much larger effects on contraction amplitude than quite substantial perturbations (Fig. 6B, long purple arrow).

Figure 6.

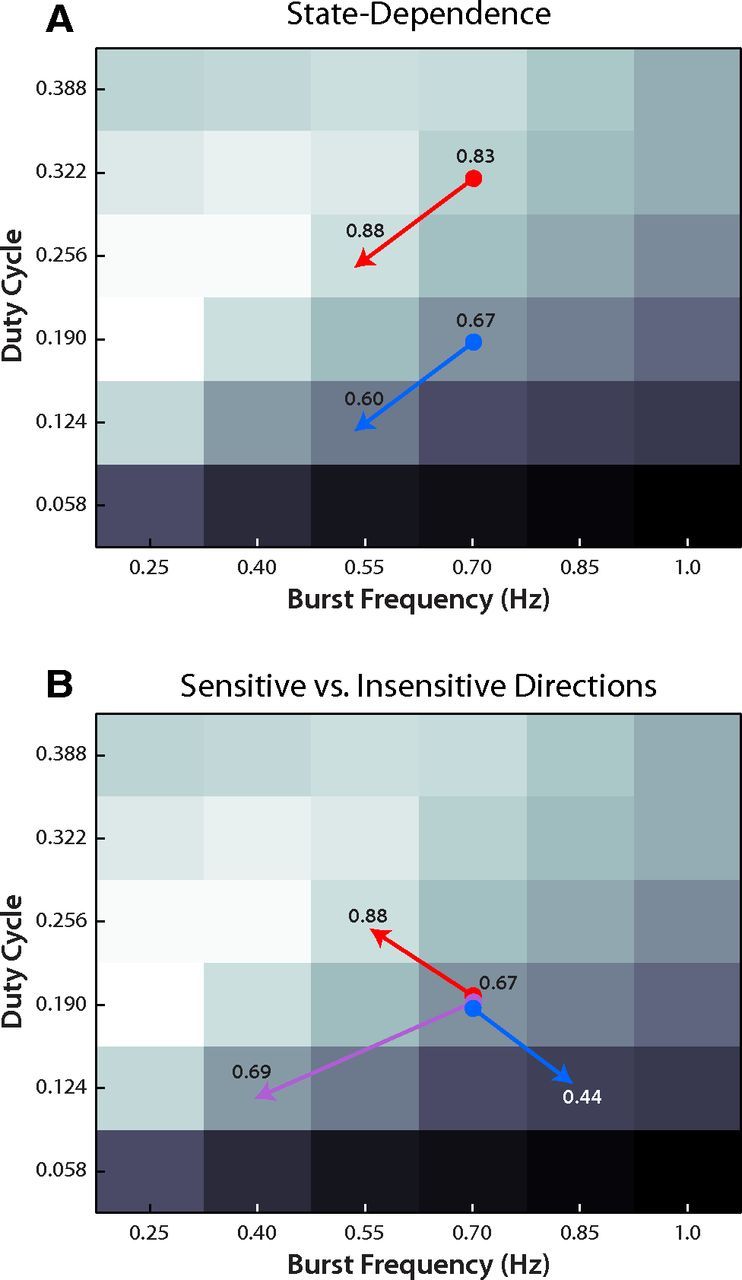
The predicted changes in contraction amplitude resulting from hypothetical manipulations of neural activity. Black-and-white background represents the cardiac NMT prediction for contraction amplitude at various levels of neural stimulation (data are depicted as in Fig. 5B; white represents high-amplitude contractions; black represents low-amplitude contractions). A, B, Red arrows indicate manipulations that increase contraction amplitude; blue arrows indicate manipulations that decrease contraction amplitude. B, Purple arrow indicates a manipulation that approximately preserves contraction amplitude. Decimal numbers indicate normalized amplitude measurements for the initial and final neural activity patterns (same as Fig. 5B).

Discussion

A major goal in neuroscience is to understand the mechanisms by which neural activity influences measurable physiological variables, such as the membrane potential of a postsynaptic cell, the release of hormones into the bloodstream, the aggregate activity of a brain region, or the length of a muscle. The input–output relationships between neural activity and these downstream variables are often multidimensional and nonlinear. Our analysis illustrates how natural interanimal variability in neural systems can interact with these underlying nonlinearities to produce qualitatively opposite experimental results across preparations.

Understanding anomalous or inconsistent responses across a population of genetically variable animals, or even genetically identical ones, is an important but difficult task that spans multiple fields in biology (Korobkova et al., 2004; Marder and Taylor, 2011) and medicine (Wilkinson, 2005; Bosmans et al., 2006). Several examples of this variability can be found in simple invertebrate neural circuits: serotonin elicits either increases or decreases in the cycle frequency of the pyloric CPG motor rhythm (Spitzer et al., 2008), octopamine causes either increases or decreases in neuromuscular transmission onto the closer muscle in crabs (Djokaj et al., 2001), and serotonin can either potentiate or diminish the synaptic response of the lateral giant neuron in crayfish depending on the individual's social status (Yeh et al., 1997).

One possibility is that these differential effects are an evolutionary adaptation, which allows individuals to tune their responses to external events based on circumstantial factors (Yeh et al., 1997). Alternatively, these differences may incidentally arise from natural interanimal variability in network parameters (Goldman et al., 2001; Grashow et al., 2009). This second possibility may not immediately occur to biologists who are trained to find evolutionary meaning behind experimental results. However, under the right conditions, a nonlinear biological system can be expected to respond differentially across preparations, even when the experimental perturbation is identical (Drion et al., 2011; Ransdell et al., 2013).

Variability in the crustacean cardiac system across preparations

In the lobster (H. americanus) cardiac system, motor neuron activity is transduced into muscle contractions by a nonlinear NMT. We characterized the cardiac NMT and assessed its ability to predict features of muscle movement from motor neuron activity in semi-intact hearts. Across semi-intact preparations, the NMT was moderately successful at predicting contraction duty cycle from spontaneous motor neuron activity but was unable to predict contraction amplitude in a statistically significant manner (Fig. 4). This result emphasizes that the properties and dynamics of neuromuscular systems are unique to each animal, which confounds our ability to make precise predictions across preparations in the absence of detailed and comprehensive individual measurements. The cardiac NMT performed more reliably when individual differences were mitigated by manipulating neural activity within preparations with AST-C (Fig. 5).

The predictive power of the cardiac NMT is also limited by a few experimental constraints of our study. Although there are five motor neurons in the cardiac ganglion, we could only measure their aggregate activity in semi-intact preparations via extracellular recordings of the cardiac motor nerve. Our estimations of intraburst spike frequency were particularly limited because simultaneous spikes from the five motor neurons are registered as a single event. This limitation also prevented us from exploring the potential effects of spike timing on motor output (Zhurov and Brezina, 2006; Brezina, 2007). As in any experiment, there are also likely uncontrollable differences in dissection procedure and overall lobster health across preparations. These discrepancies are expected to decrease the predictive power of the NMT but should not introduce systematic biases or errors into our analysis.

In addition to these experimental sources of variability, there are likely intrinsic sources of biological variability across semi-intact heart preparations. First, different animals likely require different levels of cardiac output to thrive (e.g., because of body size differences); therefore, neuronal and muscular parameters may be tuned differentially across individuals. Second, even if two different lobsters have similar demands of the cardiac system, the heart might satisfy these needs differentially. For example, an animal with a high heart rate and low stroke volume can have the same cardiac output as an animal with a lower heart rate and a higher stroke volume. Similarly, contractions with different amplitudes and duty cycles might produce similar stroke volumes. Finally, cardiac output may not need to be tightly maintained for most individuals to survive.

Explaining the differential effects of AST-C on contraction amplitude in semi-intact hearts

Although interanimal variability limited the predictive power of the NMT across semi-intact preparations, the NMT provided greater insight on manipulations within preparations. We reanalyzed previously published data, which showed that the neuropeptide AST-C had differential effects on the amplitude of semi-intact heart contractions (Wiwatpanit et al., 2012). Wiwatpanit et al. (2012) provided an intuitive explanation of this result based on the variable effects of AST-C on the frequency and burst duration of cardiac motor neuron activity. Specifically, they argued that AST-C caused an increase in burst duration (which would tend to increase contraction amplitude) and a decrease in burst frequency (which would tend to decrease contraction amplitude); the balance between these opposing effects would determine the motor-level effects of the neuropeptide.

The present analysis builds upon this preliminary explanation in two important respects. First, our experimental characterization of the cardiac NMT allows us to concretely predict the motor-level effects of changing neural input. It is important to consider a precise characterization of the NMT because its nonlinear nature leads to predictions that cannot be intuitively deduced. For example, the nonlinear shape of the cardiac NMT predicts that the effects of AST-C should be state-dependent (Fig. 6A), in addition to being sensitive to the “direction” of the modulatory perturbation.

Second, we use the NMT to construct a model that predicts the effects of AST-C on each preparation. This allows us to globally evaluate the entire dataset rather than artificially grouping the data and comparing means. From this perspective, the differential effects of AST-C on contraction amplitude appear to arise, more or less continuously, from the baseline variability in neural activity and the variable effects of AST-C on neural activity.

This model-based approach improves our ability to identify preparations that are truly anomalous. For example, consider the two data points that are farthest to the right in Figure 5D. In an absolute sense, these preparations exhibited somewhat typical responses to AST-C (the actual percent change is similar to the rest of the data points). However, these two points fall well below the expected change in contraction amplitude, as predicted by the NMT. Therefore, without the NMT as a model, it would be difficult to identify these points as anomalous.

Do the differential effects of AST-C serve a biological function?

In semi-intact hearts, the frequency and duty cycle of the cardiac motor neurons are substantially variable across preparations. This variability is consistent with, but perhaps somewhat greater than, variability in other CPG systems. For example, the cycle frequency of the pyloric rhythm in the crustacean stomatogastric ganglion varies severalfold across individuals, but motor neurons fire with stereotyped duty cycles (Bucher et al., 2005; Goaillard et al., 2009). The application of a neuromodulator adds an additional level of variability because each preparation will exhibit a unique response based on variable receptor expression levels (Spitzer et al., 2008), and state-dependent interactions between modulator-invoked currents and intrinsic ionic currents (Goldman et al., 2001). For the neuropeptide AST-C, we have shown that these sources of variability, combined with the nonlinear shape of the cardiac NMT, give rise to qualitatively opposite motor-level effects. This result is a concrete example of how nonintuitive effects can arise from intrinsic biological variability.

An open question of interest is whether the opposing effects of AST-C on contraction amplitude directly serve an adaptive purpose. For example, the differential effects of serotonin on the lateral giant neuron in crayfish are tied to social status, which has been hypothesized to help subordinate crayfish effectively escape from dominant attackers (Yeh et al., 1997). It is possible that the inconsistent effects of AST-C on contraction amplitude also serve some unknown adaptive function. For instance, the modulatory effects of AST-C might change over the course of the lobster molt cycle, which is known to influence cardiac output (DeFur et al., 1985). Alternatively, the qualitatively opposing effects of AST-C could arise incidentally from random variability across a population of genetically distinct individuals. In either case, our study highlights the importance of two biological principles that are inescapable when trying to understand neuromodulation. First, biological systems are highly nonlinear, self-regulating entities that are often difficult to understand in reductionist terms. Second, and possibly as a consequence of the first, the components and properties of biological systems exhibit variability that underlies emergent physiological differences.