Abstract
Hybridization of dominant vibrational modes with meta-surface resonance allows detection of both structural changes and surface orientations of bound helical peptides. Depending on the resonance frequency of meta-molecules, a red- or blue- shift in peptide Amide-I frequency is observed. The underlying coupling mechanism is described by using a temporal coupled mode theory that is in very good agreement with the experimental results. This hybridization phenomenon constitutes the basis of many nanophotonic systems such as tunable coupled mode bio-sensors and dynamic peptide systems driven by infrared signals.
Orientation difference of helical peptides tethered to functionalized metamaterial surface at one or two points can be detected by using the information extracted from the hybridization of the vibrational modes of peptides and Fano resonance of the metamaterial substrate in Fourier transform infrared spectroscopy (FTIR). Infrared (IR) absorption is sensitive to conformation and configuration of the molecular bonds1, which could reflect the orientation information of the surface tethered analytes. Tethering peptides with controllable orientation is a key step for incorporating biological function of proteins onto inorganic surfaces and has applications such as biosensing, proteomics, electrochemistry and molecular electronics2,3,4. One advantage of surface functionalization with small peptides is the control over the orientation of the surface associated protein which is not the case for other interactions such as ligand receptor binding of biotin/avidin5,6,7,8. Moreover, the small peptides do not significantly affect the chemical properties of the surface which is also not the case for ligand-receptor interactions5,6,7,9. Binding and structural signature of peptides can be obtained with IR spectroscopy. It provides a non-invasive approach and is not restricted to an isotopic probe as in nuclear magnetic resonance (NMR) or to a perturbative probe as in fluorescence spectroscopy techniques10.
It has recently been demonstrated that incorporation of surface plasmon11 and metamaterial12 resonances enriched the Raman13,14,15,16,17,18,19 and infrared spectroscopies15,16,17,19,20,21,22,23,24,25,26,27 by mainly increasing the signal to noise ratio (SNR). A surface coated with resonant metallic nano-shells provided simultaneous enhancement for both surface enhanced Raman spectroscopy (SERS) and surface enhanced infrared absorption (SEIRA)15,16,28. A resonant near field enhancement can be achieved by coupling to the vibrational modes of molecules by using gold nanowires29, split ring resonators30,31 and other metamaterial inspired designs17,19,21,22,24,25,26,32. Resonance frequency of such structures depends on the unit cell geometry and content, and can be tuned to the vibrational mode of interest33,34. In order to achieve an ultrasensitive response with sharp spectral features, specifically arranged multiple nano-antennas were utilized within a unit cell and a Fano-type interaction, which yields a constructive or destructive interference at the far field, was observed32,35.
By using a Fano-resonant metamaterial substrate during the study of self-assembled organic monolayers signal enhancement at the Amide I/II vibrational modes can be achieved and the refractive index-shift at the Fano resonance can be used to estimate monolayer thicknesses. In the present paper, we study two peptide systems and observe hybridization between Fano resonances and Amide I/II vibrational modes when the Fano resonance is tuned to both higher and lower frequencies than the vibrational lines which yield both red- and blue- shifts of vibrational modes. We also observed that the magnitude of shift could be useful for qualitative detection of peptide orientation and structure on the top and side surfaces. Moreover, increased SNR enabled us to compare the magnitude of Amide-I and Amide-II absorption bands whose ratio provides another means to identify peptide orientation. In addition to these results, we also provide other outcomes of this specific SIERA technique: detecting relative increments in the mass content of the peptide layer, higher sensitivity at the Fano resonance, and increased signal from vibrational lines for better tuned Fano resonance.
Results
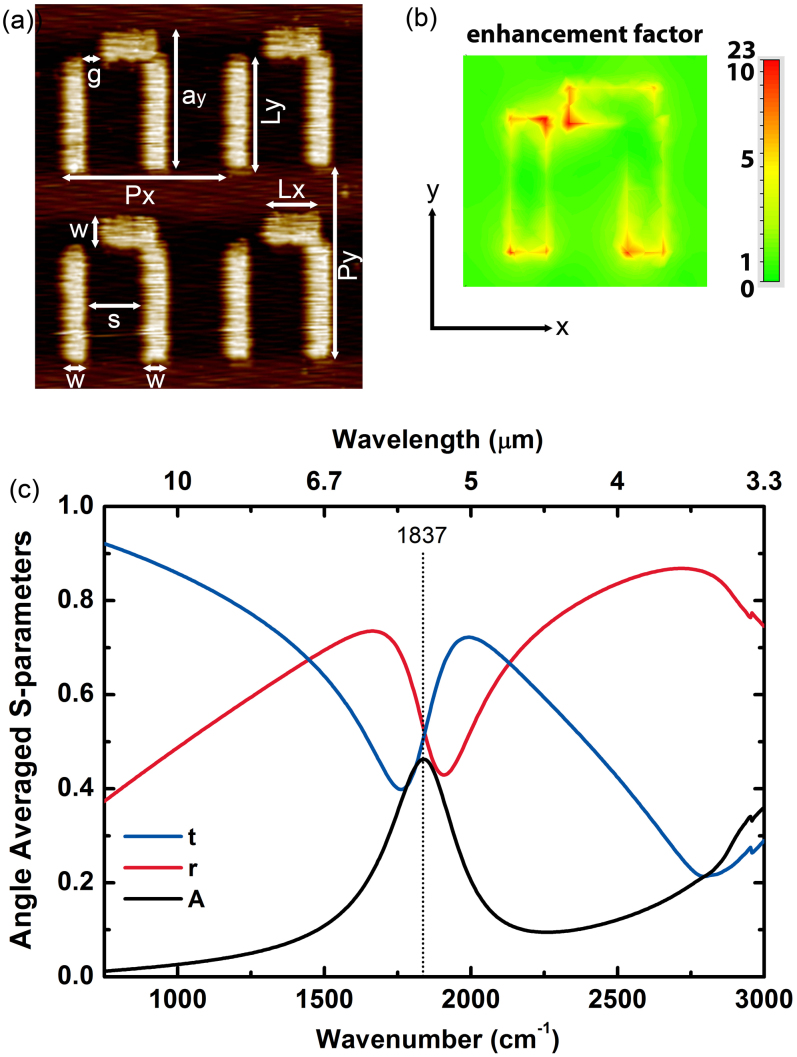
Atomic force microscopy (AFM) micro-graph of metamaterial unit cells composed of gold (Au) nano-antennas on quartz substrate is shown in Fig. 1(a). The unit cell is composed of a thin, long nano-strip and an L-shaped nano-strip placed nearby. We fabricated 13 such resonator arrays with scaled parameters on two wafers by using the standard e-beam lithography followed by thin film deposition. A thin chromium (Cr) layer was deposited before the gold in order to provide adhesion to quartz substrate.
Figure 1.
(a) AFM micro-graph for four nearby unit cells of a representative metamaterial surface. The unit cell parameters are as follows: The periods in the x- and y-directions are Px = 2.04 μm and Py = 1.96 μm, the width of the strips is w = 0.30 μm, the length of the strips in the x-direction is Lx = 0.74 μm and in the y-direction it is Ly = 1.16 μm, the side length of the resonator at the y-direction is ay = 1.42 μm, the separation between the two strips is s = 0.72 μm, the split width at the coupling region is g = 0.2 μm. These parameters were measured with approximately ±10 nm uncertainty. The thickness of the gold (Au) thin film is h ~ 70 nm, and the chromium (Cr) adhesion layer between the gold layer and quartz substrate is approximately 5 nm thick. (b) The electric field map of the enhancement factor at the Fano resonance frequency. (c) Simulated transmission, reflection and absorption coefficient of the metamaterial surface. In the simulations angle of incidence was averaged over the azimuthal and polar coordinates.
The geometry of the resonators obtained from AFM measurements was transferred to simulation domain and full wave finite element method (FEM) and finite integration (FI) method electromagnetic simulations were performed in order to investigate the spectral and near field characterization of metamaterial surfaces. Fano resonance of the metamaterial structure can be excited for an incident electromagnetic wave with the electric field polarized in the y-direction. The localized near field enhancement factor could be very large at the Fano resonance. Results of the finite element method simulations for a metamaterial unit cell periodically arranged in the x- and y- directions is shown in Fig. 1(b) and 1(c). The dominant coupling effect is due to the enhanced electric field near the meta-surface. The maximum component of this electric field is perpendicular to the metal surface. There is a tilt angle due to the difference in adsorption characteristics as described in Ref. 38. Therefore, for the front face, molecular orientation is in the z-direction, and for the side faces it is either in the x-direction or in the y-direction. The surface area of the antenna's top face is almost two times the total surface area of the side faces. The calculated enhancement factor at 5 nm above the gold surface is about e.f. = 22. We estimate from numerical simulations that the near field enhancement at the side faces is not less than that of the top face. Therefore the effects of the side faces and the top face on the detection signal are on the same order (See Supplementary Section A online for details). Spectral transmission, reflection and absorption coefficients are plotted in Fig. 1(c) with 15° to 35° angle of incidence averaging for the azimuthal and polar angles. Peak of the absorption coefficient corresponds to the Fano resonance frequency which is 1837 cm−1.
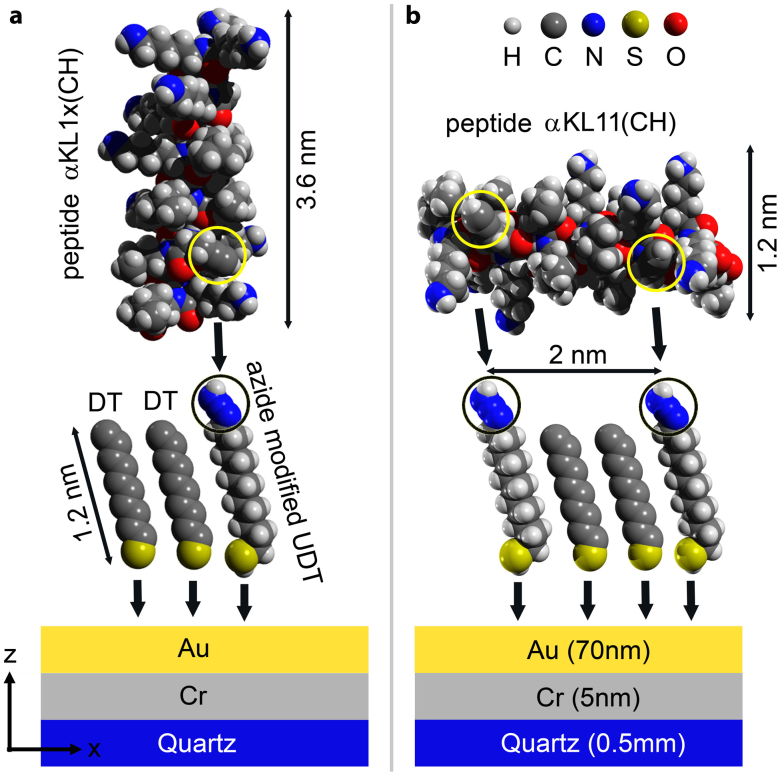
Before functionalizing gold nano-antennas, the substrates were cleaned with “piranha solution” which removes any organic contaminants from the surface36,37. A self-assembled monolayer (SAM) of 11-bromo-1-undecanethiol (BrUDT) and decanethiol (DT) was created. These thiols form strong gold-sulfur bond to the surface as illustrated in Fig. 2(a) and Fig. 2(b). The two α-helical peptides under study with one and two alkyne groups are LKKLXKKLLKKLLKKGLKKL (αKL1x(CH)) and LKKLXKKLLKKLLKKXLKKL (αKL11(CH)). The αKL1x(CH) reacts with the surface at single point and have a tendency to orient the helix primary axis perpendicular to the surface. We refer to this case as vertical peptide. On the other hand, the αKL11(CH) reacts with the azide-terminated surface through a Huisgen cycloaddition and forms helices parallel to the surface38 that are referred to as horizontal peptides.
Figure 2. Schematics of functionalization (not to scale).
(a) primary structure of αKL1x(CH) peptide (containing an alkyne group), decanethiol (DT), and azide modified undecanethiol (UDT). Azide and alkyne groups are circled. The alkyne groups make a single bond with the azides. (b) Primary structure of αKL11(CH) peptide and its two alkyne groups, which make two bonds with azides are illustrated.
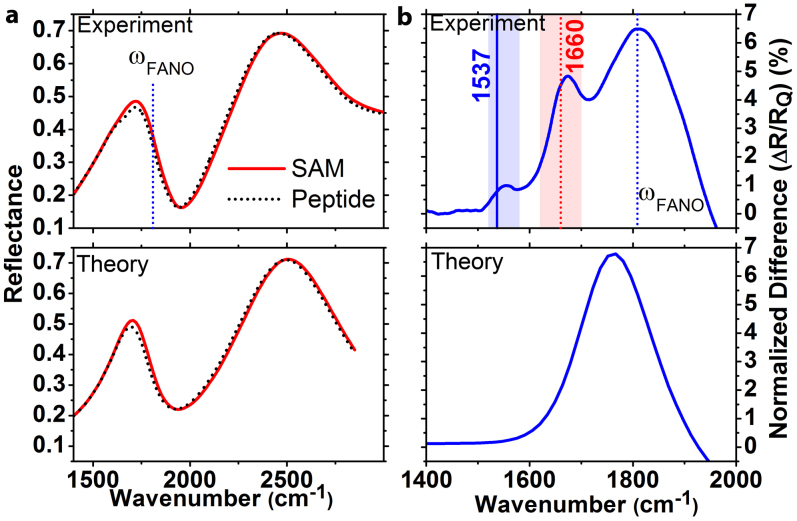
The spectral characteristics of metamaterial surfaces before and after functionalization are investigated by using a conventional Fourier transform infrared (FTIR) spectrometer equipped with a microscope. In Fig. 3(a) typical reflectance (R) spectra after the SAM and peptide deposition steps are shown. The electric field polarization was parallel to the nano-strips. We see reflectance maxima at around the two lowest order modes (quadrupole and dipole) of the metamaterial surface. The coupling of the broadband dipole and narrowband quadrupole modes generates a Fano resonance with ultra-sharp spectral features. The resonance frequencies of metamaterial surface strongly depend on the surrounding medium and shifts to lower frequencies in the presence of an ultra-thin bio-coating with refractive index larger than 1. We observed these tiny spectral shifts consistently for 42 experimental sets and showed spectra of a typical set in Fig. 3 (a). The sensitivity of a metamaterial surface to index change is maximal at the Fano resonance frequency. This behavior could be clearly seen at the normalized reflectance difference spectra: ΔR/RQ, where ΔR = RSAM − RPROTEIN, and RQ is the reflectance peak at around the quadrupole resonance. In Fig. 3(b), the maximum of the normalized difference spectra corresponds to the Fano resonance frequency. Also, we can resolve the Amide-I (1620–1700 cm−1) and Amide-II (1520–1580 cm−1) vibrational modes of the peptides in the same figure, which are not visible in the absence of field enhancements provided by the metamaterial substrates.
Figure 3.
(a) Reflectance spectra for a typical metamaterial substrate after SAM and peptide functionalization steps. (b) Corresponding normalized difference spectrum of the two reflectance spectra. Spectral positions of theoretical Amide-I/II absorption peaks are indicated with vertical lines. Experimental results and analytical model results are shown at the top and bottom parts of the figure, respectively.
The index induced shift can be approximately quantified by developing a coupled mode theory for the asymmetric metamaterial unit cell39. The complex quadrupole and dipole mode amplitudes can be denoted by: a1 and a2. These modes interact with free space via incoming waves with amplitudes denoted by 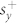 and
and 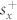 for the respective polarizations. The resonance frequencies and loss rates are denoted by ω1, ω2 and γ1, γ2 respectively. In this case, the dynamic equation for the mode amplitudes is as follows:
for the respective polarizations. The resonance frequencies and loss rates are denoted by ω1, ω2 and γ1, γ2 respectively. In this case, the dynamic equation for the mode amplitudes is as follows:
Here κ12 are the coupling coefficients for the metamaterial antennas within the unit cell and μ describes the coupling to the external fields. The reflection coefficient can be obtained by using the dynamic equations, energy conservation and time reversal conditions and can be approximated by a double Lorentzian function as follows40:
Here a1 and a2 denote the renormalized coupling coefficients. The quality factor for the quadrupole and dipole resonances is estimated as 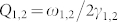 . The presence of a biological layer can be approximated as a homogeneous uniform coating, that enters the equations as a perturbation. Thereby, index-induced shift can be formulated with the first order perturbation theory as:
. The presence of a biological layer can be approximated as a homogeneous uniform coating, that enters the equations as a perturbation. Thereby, index-induced shift can be formulated with the first order perturbation theory as:
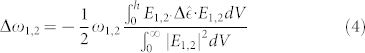 |
where E is the electric field near the surface and 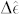 is the permittivity tensor of the medium. In the presence of the SAM of peptide, the reflection coefficient is calculated by substituting the new resonance frequencies for the dipole and quadrupole modes to the Eq. 3 as
is the permittivity tensor of the medium. In the presence of the SAM of peptide, the reflection coefficient is calculated by substituting the new resonance frequencies for the dipole and quadrupole modes to the Eq. 3 as 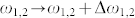 . The reflectance spectra before and after the peptide deposition are shown in Fig. 3. The peak of the normalized difference spectra is at the Fano resonance frequency and its magnitude is proportional to the multiplication of index shift and spectral slope. In Fig. 3(b), experimental data show one broad peak originated from the index-induced shift and two additional local peaks that correspond to the absorption of the peptide vibrational modes that are not taken into account in this theory. The main peak in the theoretical difference spectrum seems red shifted slightly from the Fano resonance and this situation is in disagreement with the experimental data. The reason behind this disagreement is that, in the theoretical model the Amide modes are not considered. As a result, even though this simple theoretical model can explain the magnitude of Fano resonance shift, it cannot exactly explain the position of the Fano resonance and we see a slight disagreement between the experiment and theory in Fig. 3(b).
. The reflectance spectra before and after the peptide deposition are shown in Fig. 3. The peak of the normalized difference spectra is at the Fano resonance frequency and its magnitude is proportional to the multiplication of index shift and spectral slope. In Fig. 3(b), experimental data show one broad peak originated from the index-induced shift and two additional local peaks that correspond to the absorption of the peptide vibrational modes that are not taken into account in this theory. The main peak in the theoretical difference spectrum seems red shifted slightly from the Fano resonance and this situation is in disagreement with the experimental data. The reason behind this disagreement is that, in the theoretical model the Amide modes are not considered. As a result, even though this simple theoretical model can explain the magnitude of Fano resonance shift, it cannot exactly explain the position of the Fano resonance and we see a slight disagreement between the experiment and theory in Fig. 3(b).
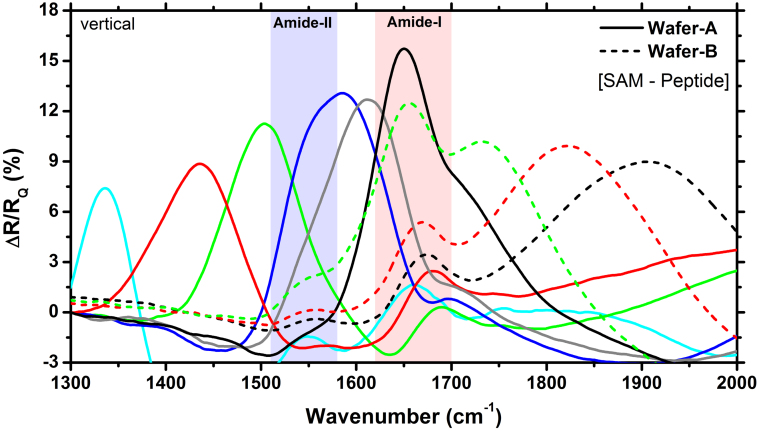
Metamaterial Fano resonance can be tuned to the frequency of peptide vibrational modes by scaling the geometry in the x-y plane. In Fig. 4, we demonstrate metamaterial substrates whose Fano resonance frequency spans the Amide-I and Amide-II vibrational modes of peptides. As the Fano resonance frequency is tuned to the vibrational modes the near field enhancement gets larger and thereby more energy is converted to the molecular vibrations yielding larger absorption values. This absorption is reflected as an increase at the normalized difference spectra which reaches a maximum value at around the Amide-I frequency. We also observe consistent increase of the signal magnitude as the Fano resonance approaches the Amide-I/II lines as shown in Fig. 4 (Wafer-B).
Figure 4. Normalized experimental difference spectra for different metamaterials fabricated on two different wafers.
The metamaterial substrates were functionalized with αKL1x(CH) peptides (vertical to the surface). Vibrational bands of the Amide-I/II are indicated with vertical bars. The difference peak is maximal when the Fano resonance is tuned to the vibrational modes.
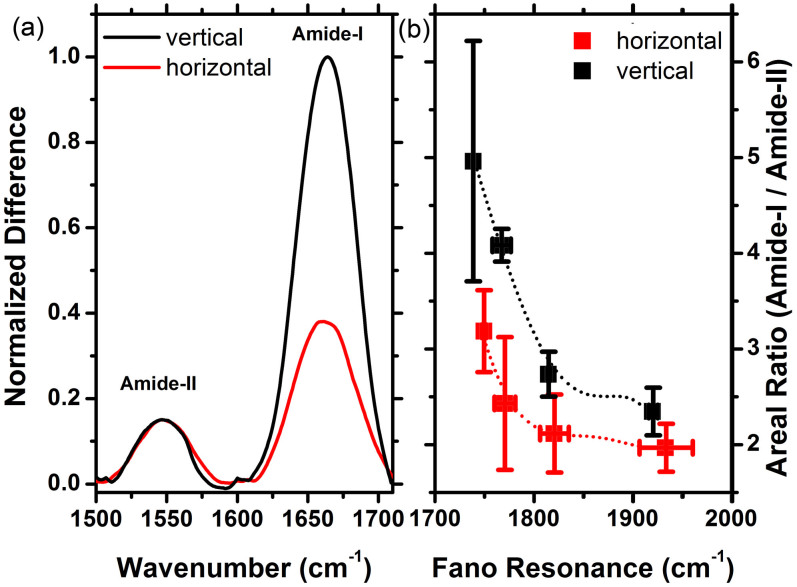
Information on the surface orientation of different peptide systems can be obtained by comparing the areal ratios of different absorption peaks. In Fig. 5, we compare the baseline corrected Amide-I and Amide-II ratios for the two surface functionalizations. Normalized experimental difference spectra including the Fano peak is assumed to be the baseline. In order to correct the curvature and slope, a function that closely parallels the normalized experimental difference spectra is used. This baseline is then subtracted from the spectrum which removes the baseline problem without altering the spectral data of interest. Interaction of the vibrational modes with the enhanced near field is determined by the C = O (Amide-I) and dominant C-N (Amide-II) directional tensors. By using the primary structure of the peptides, we extracted and diagonalized the directional cosine tensors for Amide-I and Amide-II modes as <cos2θI>mm = (0.07, 0.07, 0.86) (highly anisotropic) and <cos2θII>mm = (0.32, 0.29, 0.39) (almost isotropic), where m = i, j, k represents a coordinate system for which peptide helical axis is parallel to the k direction. Depending on the type and surface bonding of the peptide, the coordinate system i, j, k makes an angle with the laboratory coordinate system x, y, z. For the vertical peptide, the angle between these coordinate systems is smaller than the horizontal peptide case. Therefore, Amide-I interacts with the near field anisotropically, whereas Amide-II interacts isotropically. When the peptides are arranged perpendicular to the surface, Amide-I mode is expected to interact strongly with the E-field, which is perpendicular to the metal surface. On the other hand, when the peptides are arranged horizontally a smaller interaction between E-field and Amide-I is expected. Moreover, the interaction with the almost isotropic Amide-II is expected to be the same for the two configurations. Therefore, the baseline corrected absorption peaks were normalized to the Amide-II maximum. The normalized spectra for a typical meta-surface are shown in Fig. 5(a) (See Supplementary Section C online). From this figure we see that, the magnitude of the Amide-I peaks for the vertical and horizontal orientations are considerably distinct. We calculated the areal ratio of the Amide-I to Amide-II for the 16 experiments and plotted the average values with error bars in Fig. 5(b). Multiple sets of cleaning protocols applied on the same substrate reduce its quality that results in larger error bars. The large error bar in Fig. 5(b) corresponds to the last experiment set of the Wafer-B. The results suggest that the orientation difference can be clearly identified from the Amide ratios. As the Fano resonance approaches the Amide-I frequency, the near field enhancement increases which results in a larger areal ratio.
Figure 5.
(a) A representative difference spectra (normalized and baseline corrected) for the two functionalized surfaces with vertical and horizontal peptide orientations. (See Supplementary Section B online for surface adsorption density analysis.) (b) Areal ratio of Amide-I to Amide-II modes obtained from averaged experimental data sets for the studied orientation configurations together with the error bars.
Discussion
We provide the dynamics of the interaction of the metasurface with the individual vibrational modes theoretically by developing a temporal coupled mode theory (TCMT). As the SNR for Amide-I mode is typically higher than the SNR of Amide-II, we limit our analysis to Amide-I for the present part of the study. A two mode TCMT that includes the dominant Amide-I and metamaterial Fano resonances has the following governing equations:
Here af and aAI denote the mode amplitudes for the Fano and Amide-I modes, ωf and ωAI denote the natural (uncoupled) frequencies, γf and γAI are the corresponding loss rates, and κfAI and κAIf are the corresponding coupling coefficients for Amide-I and metamaterial Fano resonances respectively.
The hybridization of peptide and metamaterial resonances was observed experimentally in the present study. It yields a different type of Fano resonance and provides a novel detection mechanism. Interaction of a meta-molecule Fano resonance and narrowband peptide Amide-I/II vibrational lines creates a coupled system. In this new system, Amide and metamaterial resonance frequencies are eigenvalues of the Eqs. 5–6 and they are slightly shifted as follows:
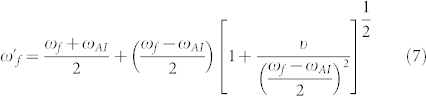 |
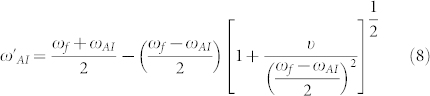 |
Here 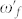 and
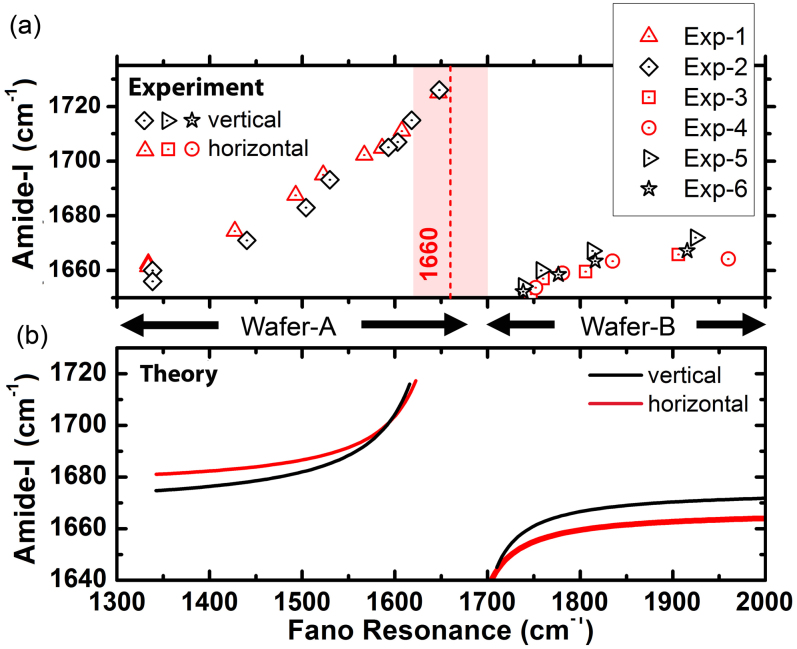
and 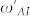 represent the Fano and Amide-I frequencies of the coupled system, and υ describes the coupling of the metamaterial and peptide modes. We expect a blue-shift for the Amide-I frequency as the metamaterial resonance approaches from low frequencies and a red-shift of Amide-I frequency as the metamaterial resonance approaches from high frequencies. Amide-I spectral peak versus metamaterial Fano resonance of the coupled system are plotted in Fig. 6(a). When the meta-molecule Fano resonance is matched to Amide-I mode, a 90° phase difference for the two modes is expected, which appears as a discontinuity in the spectra. If an actual surface resonant at Amide-I frequency could be fabricated, then coupling related maximum shifts proportional to the square root of coupling coefficient are expected to be observed which can be derived from the Eqs. 7–8 of the theoretical analysis. Similarly, a discontinuity at around the Amide-II frequency is seen when the meta-molecule resonance spans through the Amide-II band (not shown). The points in Fig. 6(a) are deconvolved peak frequencies, which are determined by using second derivative spectra of 33 experiment sets (See Supplementary Section C online). Each data point in Fig. 6(a) represents an experiment set. There are 6 experiment sets representing the total number of functionalizations. Here the expected red- and blue- shifts agree well with the dominant coupling behavior of meta-molecule Amide modes.
represent the Fano and Amide-I frequencies of the coupled system, and υ describes the coupling of the metamaterial and peptide modes. We expect a blue-shift for the Amide-I frequency as the metamaterial resonance approaches from low frequencies and a red-shift of Amide-I frequency as the metamaterial resonance approaches from high frequencies. Amide-I spectral peak versus metamaterial Fano resonance of the coupled system are plotted in Fig. 6(a). When the meta-molecule Fano resonance is matched to Amide-I mode, a 90° phase difference for the two modes is expected, which appears as a discontinuity in the spectra. If an actual surface resonant at Amide-I frequency could be fabricated, then coupling related maximum shifts proportional to the square root of coupling coefficient are expected to be observed which can be derived from the Eqs. 7–8 of the theoretical analysis. Similarly, a discontinuity at around the Amide-II frequency is seen when the meta-molecule resonance spans through the Amide-II band (not shown). The points in Fig. 6(a) are deconvolved peak frequencies, which are determined by using second derivative spectra of 33 experiment sets (See Supplementary Section C online). Each data point in Fig. 6(a) represents an experiment set. There are 6 experiment sets representing the total number of functionalizations. Here the expected red- and blue- shifts agree well with the dominant coupling behavior of meta-molecule Amide modes.
Figure 6.
(a) Experimental data showing the dependence of Amide-I/II peaks on the meta-molecule Fano resonance frequency. The experimental data is gathered from two different wafers and a typical line for Amide-I natural vibrational band at 1660 cm−1 is indicated. (b) The theoretical fits of the experimental data (γf ≈ 31 cm−1, 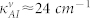 ,
, 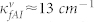 , and γf ≈ 31 cm−1,
, and γf ≈ 31 cm−1, 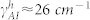 ,
, 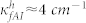 ) for Wafer-A and Wafer-B. The overall coupling coefficients for the Wafer-A (low frequency region) and Wafer-B (high frequency region) cases were different mainly due to the fabrication details.
) for Wafer-A and Wafer-B. The overall coupling coefficients for the Wafer-A (low frequency region) and Wafer-B (high frequency region) cases were different mainly due to the fabrication details.
Half of the data in Fig. 6, which is shown in black color, corresponds to the surface functionalization with αKL1x(CH) peptide. In this case, the helices have a tendency to be oriented perpendicular to the surface. The other half of the data, which is shown in red color, corresponds to αKL11(CH) peptide and the helices have a tendency to orient themselves parallel the surface. The overall coupling coefficient ( ) given in Eqs. (7)–(8) can be written as follows:
) given in Eqs. (7)–(8) can be written as follows:
We fit the Eqs. 7–8 to the experimental data by using the overall coupling coefficients and natural Amide-I frequency (ωAI) as flexible parameters. The data points from Wafer-A and Wafer-B are fit separately. In Fig. 6(b), we see that the overall coupling coefficient for the vertical and horizontal cases remains almost the same, however, Amide-I natural frequencies of the vertical and horizontal peptides are slightly different. In the case of Wafer-B samples, for the horizontal peptide we extracted 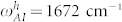 cm−1 with a confidence interval of [1668 1677] and for the vertical peptide we got
cm−1 with a confidence interval of [1668 1677] and for the vertical peptide we got 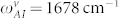 cm−1 with a confidence interval of [1672 1685] by using algorithms of commercial nonlinear curve fitting software. This provides a direct evidence for detecting the differences in surface binding of the peptides and related secondary structure change. The changes in the bond lengths and angles are expected to be larger for the vertical case, which explains the slightly higher Amide-I frequency with respect to its unbound case.
cm−1 with a confidence interval of [1672 1685] by using algorithms of commercial nonlinear curve fitting software. This provides a direct evidence for detecting the differences in surface binding of the peptides and related secondary structure change. The changes in the bond lengths and angles are expected to be larger for the vertical case, which explains the slightly higher Amide-I frequency with respect to its unbound case.
We estimate the loss coefficient of Amide-I modes (γAI) from the baseline corrected spectra. The loss coefficient for the metamaterial Fano mode (γf) was estimated semi-analytically by considering multiple factors: a theoretical fit to the experimental reflectance spectra, and corresponding absorption spectra derived from numerical simulations. For the representative sample, we extract the loss coefficients as γf ≈ 31 cm−1 and 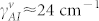 for the vertical peptide, and
for the vertical peptide, and 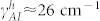 for the horizontal peptide. Theoretical coupling coefficient (κfAI) is proportional to the index shift (Δω) given in Eq. 4 and the ratio of the coupling coefficients (κfAI) for the vertical and horizontal peptides can be simplified as:
for the horizontal peptide. Theoretical coupling coefficient (κfAI) is proportional to the index shift (Δω) given in Eq. 4 and the ratio of the coupling coefficients (κfAI) for the vertical and horizontal peptides can be simplified as:
 |
Here av is the angle for the vertical case between the prolate ellipsoid principal axis and the surface plane, and ah is the corresponding angle for the horizontal case. From independent GRAS-IR measurements these average angles were estimated as follows38: ah = 30° and av = 75°. These values are used to calculate the theoretical ratio rκ = 3.3. We also calculate the ratio of the coupling coefficients by comparing the index shifts at the Fano resonance for the vertical and horizontal cases from experiments as shown in Fig. 3 and Fig. 4 as rκ = 3.0. We have seen a very good agreement between these theoretical and experimental results for the ratios of the coupling coefficients.
Estimation of the overall coupling coefficients of the peptide and metasurface can be done with two different methods. In the first method, the coefficient  is obtained by using a single pixel reflection measurement. Then, we obtain the transmission spectra semi-analytically and thereby the absorption spectra for the bare and functionalized metasurfaces. On the other hand, the second method utilizes reflection measurement data of multiple pixels. By fitting the theoretical Eq. 7–8 to the experimental data the overall coupling coefficient (υ) can be extracted as shown in Fig. 6. The overall coupling coefficients obtained from the second method agree very well with the analysis parameters extracted from the first method. (See Supplementary Section D online for details).
is obtained by using a single pixel reflection measurement. Then, we obtain the transmission spectra semi-analytically and thereby the absorption spectra for the bare and functionalized metasurfaces. On the other hand, the second method utilizes reflection measurement data of multiple pixels. By fitting the theoretical Eq. 7–8 to the experimental data the overall coupling coefficient (υ) can be extracted as shown in Fig. 6. The overall coupling coefficients obtained from the second method agree very well with the analysis parameters extracted from the first method. (See Supplementary Section D online for details).
To sum up, hybridization of resonant spectroscopy substrates with vibrational modes of mobilized organic molecules provides a detection mechanism beyond the well-known index-induced shift of the surface enhanced spectroscopy. We studied resonant coupling of meta-molecule arrays to the dominant Amide vibrational modes of helical peptides. The peptides tethered to the surface in a controllable manner results in vertically or horizontally oriented self-assembled monolayers. Depending on the resonance frequency of the meta-molecule arrays, both red- and blue-shifts of Amide vibrational modes were measured. The results are signature of a new type of Fano resonance between meta-molecules and peptides. The coupled mode theory analysis supports this optical, label-free, non-perturbative technique and provides information on tiny changes of the structure and orientation of bound peptides. Presented fundamental innovation forms the basis of many future nanophotonic systems and has applications in biosensing, proteomics, and electrochemistry. As an example, we foresee dynamic peptide systems tethered to tunable meta-surfaces, triggered by mid-infrared signals providing vibrational modulation.
Methods
Design simulations
The metasurface unit cell was designed via numerical simulations by using finite element method (FEM) and finite integration (FI) solvers. For the characterization simulations, we used a linearly polarized plane wave propagating at the −z-direction towards the antennas, the E-field is at the y-direction parallel to the antenna and the H-field is at the x-direction perpendicular to the antennas. The permittivity of the gold metasurface was modeled with Drude dispersion using the formula:  , where ωp was the plasma frequency and vc was the collision frequency. We used ωp = 13250 × 1012 rad/s and vc = 130 THz for gold.
, where ωp was the plasma frequency and vc was the collision frequency. We used ωp = 13250 × 1012 rad/s and vc = 130 THz for gold.
Fabrication
The designed metasurfaces are fabricated by using the e-beam lithography. We first clean the sample with acetone and isopropanol. Then coat it with bilayer of PMMA and pattern it with the e-beam. E-beam dosage was 300 nC/cm2 and the beam current was 10 pA. After pattern writing, we have developed it in 1:3 MIBK:IPA developer for 40 s. We fabricated substrates that include multiple resonator arrays with an area at most 250 μm2. The atomic force microscopy (AFM) characterization was performed using an Agilent 5500 AFM in tapping mode.
Chemistry
Because the resonator arrays are gold, the oxidation of the metal surfaces was not a concern under ambient conditions. This is a great advantage of using gold. Before functionalization, we cleaned the resonator arrays with the “piranha solution” (1:3 sulfuric acid: 30% hydrogen peroxide) which removes any organic contaminants from the surface. We have also tried other cleaning protocols like Air plasma, O2 plasma and RCA-1, and decided that cleaning with the piranha solution works as the best. As the first step of the functionalization, a self-assembled monolayer (SAM) of 11-bromo-1-undecanethiol (BrUDT) and decanethiol (DT) was created with 25% and 75% relative concentrations. After rinsing, Br-terminated SAMs were immersed into saturated sodium azide solution and an azide terminated SAM was obtained.
Measurements
For the spectral characterization of metamaterial surfaces, we used Thermo Scientific Nicolet 6700 Spectrometer with KBr beam splitter. It is equipped with a Continuum Microscope with liquid N2 cooled mercury cadmium telluride (MCT) detector and Parker Balston purge gas generator. The IR beam was focused with a 15× cassegrain objective and the physical aperture was set to 100 μm2. The angle of incidence was 25° with ±10° angular divergence and 128 scans were averaged with 4 cm−1 resolution. Then the residual lines of H2O vapor and CO2 were subtracted and the spectra were smoothed with a 19 point 2nd order Savitzky-Golay function.
Author Contributions
K.B.A. conceived the idea, designed and performed spectroscopy experiments, developed analytical tools, and wrote the paper; I.F.G. developed and performed functionalization experiments; K.B.A. and I.F.G. analyzed the data. K.B.A. is the mainly contributing author of this paper.
Supplementary Material
Supplementary Information
Acknowledgments
This research was supported by the Office of Naval Research (grant N00014-10-1-0929), the Air Force Office of Scientific Research (grant FA8650-090-D-5037), the National Science Foundation (grant CMMI-0928664), and the Welch Foundation (grant F-1699). We gratefully acknowledge M. Gadush for peptide synthesis, L. Webb for reactants, R. Garcia, D. Fozdar and N. Arju for their help with fabrication of samples, G. Shvets for FTIRM, A. Alu and X. Xiang for simulation software, J. Bolinger for his help with AFM measurements, and the TUBITAK 2232 program.
References
- Dluhy R. A., Stephens S. M., Widayati S. & Williams A. D. Vibrational spectroscopy of biophysical monolayers - applications of ir and raman-spectroscopy to biomembrane model systems at interfaces. Spectroc. Acta Pt. A-Molec. Biomolec. Spectr. 51, 1413–1447 (1995). [Google Scholar]
- Brown S. Metal-recognition by repeating polypeptides. Nat. Biotechnol. 15, 269–272 (1997). [DOI] [PubMed] [Google Scholar]
- Whaley S. R., English D. S., Hu E. L., Barbara P. F. & Belcher A. M. Selection of peptides with semiconductor binding specificity for directed nanocrystal assembly. Nature 405, 665–668 (2000). [DOI] [PubMed] [Google Scholar]
- Barton S. C., Gallaway J. & Atanassov P. Enzymatic biofuel cells for Implantable and microscale devices. Chem. Rev. 104, 4867–4886 (2004). [DOI] [PubMed] [Google Scholar]
- Green N. M. Avidin. Adv. Protein Chem. 29, 85–133 (1975). [DOI] [PubMed] [Google Scholar]
- Nelson K. E. et al. Surface characterization of mixed self-assembled monolayers designed for streptavidin immobilization. Langmuir 17, 2807–2816 (2001). [Google Scholar]
- Haussling L., Ringsdorf H., Schmitt F. J. & Knoll W. Biotin-functionalized self-assembled monolayers on gold - surface-plasmon optical studies of specific recognition reactions. Langmuir 7, 1837–1840 (1991). [Google Scholar]
- Demir H. V. et al. Spatially Selective Assembly of Quantum Dot Light Emitters in an LED Using Engineered Peptides. ACS Nano 5, 2735–2741 (2011). [DOI] [PubMed] [Google Scholar]
- Seker U. O. S., Zengin G., Tamerer C., Sarikaya M. & Demir H. V. Assembly Kinetics of Nanocrystals via Peptide Hybridization. Langmuir 27, 4867–4872 (2011). [DOI] [PubMed] [Google Scholar]
- Williams A. J. & Gupta V. K. Structure and formation of self-assembled monolayers of helical poly (gamma-benzyl L-glutamate) by surface plasmon resonance and infrared spectroscopy. Thin Solid Films 423, 228–234 (2003). [Google Scholar]
- Ozbay E. Plasmonics: Merging Photonics and Electronics at Nanoscale Dimensions. Science 311, 189–193 (2006). [DOI] [PubMed] [Google Scholar]
- Soukoulis C. M. & Wegener M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nature Photon. 5, 523–530 (2011). [Google Scholar]
- Kneipp K. et al. Single molecule detection using surface-enhanced Raman scattering (SERS). Phys. Rev. Lett. 78, 1667–1670 (1997). [Google Scholar]
- Genet C. & Ebbesen T. W. Light in tiny holes. Nature 445, 39–46 (2007). [DOI] [PubMed] [Google Scholar]
- Lal S. et al. Tailoring plasmonic substrates for surface enhanced spectroscopies. Chem. Soc. Rev. 37, 898–911 (2008). [DOI] [PubMed] [Google Scholar]
- Mayer K. M. et al. A label-free immunoassay based upon localized surface plasmon resonance of gold nanorods. ACS Nano 2, 687–692 (2008). [DOI] [PubMed] [Google Scholar]
- Love S. A., Marquis B. J. & Haynes C. L. Recent Advances in Nanomaterial Plasmonics: Fundamental Studies and Applications. Appl. Spectrosc. 62, 346A–362A (2008). [DOI] [PubMed] [Google Scholar]
- Mulvihill M. J., Ling X. Y., Henzie J. & Yang P. D. Anisotropic Etching of Silver Nanoparticles for Plasmonic Structures Capable of Single-Particle SERS. J. Am. Chem. Soc. 132, 268–274 (2010). [DOI] [PubMed] [Google Scholar]
- Nagao T. et al. Plasmons in nanoscale and atomic-scale systems. Sci. Technol. Adv. Mater. 11, (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartstein A., Kirtley J. R. & Tsang J. C. Enhancement of the Infrared Absorption from Molecular Monolayers with Thin Metal Overlayers. Phys. Rev. Lett. 45, 201–204 (1980). [Google Scholar]
- Adato R. et al. Ultra-sensitive vibrational spectroscopy of protein monolayers with plasmonic nanoantenna arrays. Proc. Natl. Acad. Sci. U. S. A. 106, 19227–19232 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bukasov R. & Shumaker-Parry J. S. Silver Nanocrescents with Infrared Plasmonic Properties As Tunable Substrates for Surface Enhanced Infrared Absorption Spectroscopy. Anal. Chem. 81, 4531–4535 (2009). [DOI] [PubMed] [Google Scholar]
- Dhawan A., Norton S. J., Gerhold M. D. & Vo-Dinh T. Comparison of FDTD numerical computations and analytical multipole expansion method for plasmonics-active nanosphere dimers. Opt. Express 17, 9688–9703 (2009). [DOI] [PubMed] [Google Scholar]
- Guo Z. R. et al. Achieving high-purity colloidal gold nanoprisms and their application as biosensing platforms. J. Colloid Interface Sci. 348, 29–36 (2010). [DOI] [PubMed] [Google Scholar]
- Heer J., Corwin L., Cilwa K., Malone M. A. & Coe J. V. Infrared Sensitivity of Plasmonic Metal Films with Hole Arrays to Microspheres In and Out of the Holes. J. Phys. Chem. C 114, 520–525 (2010). [Google Scholar]
- Enders D., Nagao T., Pucci A., Nakayama T. & Aono M. Surface-enhanced ATR-IR spectroscopy with interface-grown plasmonic gold-island films near the percolation threshold. Phys. Chem. Chem. Phys. 13, 4935–4941 (2011). [DOI] [PubMed] [Google Scholar]
- Weber D. et al. Longitudinal and transverse coupling in infrared gold nanoantenna arrays: long range versus short range interaction regimes. Opt. Express 19, 15047–15061 (2011). [DOI] [PubMed] [Google Scholar]
- Wang H., Kundu J. & Halas N. J. Plasmonic nanoshell arrays combine surface-enhanced vibrational spectroscopies on a single substrate. Angew. Chem. Int. Ed. 46, 9040–9044 (2007). [DOI] [PubMed] [Google Scholar]
- Neubrech F. et al. Resonant Plasmonic and Vibrational Coupling in a Tailored Nanoantenna for Infrared Detection. Phys. Rev. Lett. 101, (2008). [DOI] [PubMed] [Google Scholar]
- Cubukcu E., Zhang S., Park Y.-S., Bartal G. & Zhang X. Split ring resonator sensors for infrared detection of single molecular monolayers. Appl. Phys. Lett. 95, (2009). [Google Scholar]
- Pryce I. M., Kelaita Y. A., Aydin K. & Atwater H. A. Compliant Metamaterials for Resonantly Enhanced Infrared Absorption Spectroscopy and Refractive Index Sensing. ACS Nano 5, 8167–8174 (2011). [DOI] [PubMed] [Google Scholar]
- Hao F., Nordlander P., Sonnefraud Y., Van Dorpe P. & Maier S. A. Tunability of Subradiant Dipolar and Fano-Type Plasmon Resonances in Metallic Ring/Disk Cavities: Implications for Nanoscale Optical Sensing. ACS Nano 3, 643–652 (2009). [DOI] [PubMed] [Google Scholar]
- Alici K. B., Bilotti F., Vegni L. & Ozbay E. Optimization and tunability of deep subwavelength resonators for metamaterial applications: complete enhanced transmission through a subwavelength aperture. Opt. Express 17, 5933–5943 (2009). [DOI] [PubMed] [Google Scholar]
- Alici K. B., Serebryannikov A. E. & Ozbay E. Radiation properties and coupling analysis of a metamaterial based, dual polarization, dual band, multiple split ring resonator antenna. J. Electromagn. Waves Appl. 24, 1183–1193 (2010). [Google Scholar]
- Luk'yanchuk B. et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 9, 707–715 (2010). [DOI] [PubMed] [Google Scholar]
- Evans S. D., Sharma R. & Ulman A. Contact-angle stability - reorganization of monolayer surfaces. Langmuir 7, 156–161 (1991). [Google Scholar]
- Fischer L. M. et al. Gold cleaning methods for electrochemical detection applications. Microelectron. Eng. 86, 1282–1285 (2008). [Google Scholar]
- Gallardo I. F. & Webb L. J. Tethering Hydrophobic Peptides to Functionalized Self-Assembled Mono layers on Gold through Two Chemical Linkers Using the Huisgen Cycloaddition. Langmuir 26, 18959–18966 (2010). [DOI] [PubMed] [Google Scholar]
- Haus H. A. & Huang W. P. Coupled-mode theory. Proc. IEEE 79, 1505–1518 (1991). [Google Scholar]
- Wu C. H. et al. Fano-resonant asymmetric metamaterials for ultrasensitive spectroscopy and identification of molecular monolayers. Nat. Mater. 11, 69–75 (2012). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information