Probing the Flexibility of Tropomyosin and Its Binding to Filamentous Actin Using Molecular Dynamics Simulations

Abstract

Tropomyosin (Tm) is a coiled-coil protein that binds to filamentous actin (F-actin) and regulates its interactions with actin-binding proteins like myosin by moving between three positions on F-actin (the blocked, closed, and open positions). To elucidate the molecular details of Tm flexibility in relation to its binding to F-actin, we conducted extensive molecular dynamics simulations for both Tm alone and Tm-F-actin complex in the presence of explicit solvent (total simulation time >400 ns). Based on the simulations, we systematically analyzed the local flexibility of the Tm coiled coil using multiple parameters. We found a good correlation between the regions with high local flexibility and a number of destabilizing regions in Tm, including six clusters of core alanines. Despite the stabilization by F-actin binding, the distribution of local flexibility in Tm is largely unchanged in the absence and presence of F-actin. Our simulations showed variable fluctuations of individual Tm periods from the closed position toward the open position. In addition, we performed Tm-F-actin binding calculations based on the simulation trajectories, which support the importance of Tm flexibility to Tm-F-actin binding. We identified key residues of Tm involved in its dynamic interactions with F-actin, many of which have been found in recent mutational studies to be functionally important, and the rest of which will make promising targets for future mutational experiments.

Introduction

Tropomyosin (Tm) is a prototype α-helical coiled coil comprised of a sequence of heptad amino acid repeats (abcdefg)_n, which is stabilized by hydrophobic core residues at the a and d positions. However, the canonical hydrophobic core residues of Tm are subject to irregular interruptions by destabilizing residues (1), including six clusters of core alanines (so-called Ala clusters (1–3)), and other acidic residues (D137 and E218) and polar residues (such as Q263 and Y267) (4). The functional role of these destabilizing residues has been under active investigation (5). Tm regulates the cooperative binding of myosin with filamentous actin (F-actin) in muscle, and the interactions of various actin-binding proteins with F-actin in nonmuscle cells (6). To fulfill its regulatory function, Tm must adopt a superhelical conformation to wrap around and bind to the F-actin helix. How Tm attains shape matching with F-actin remains controversial. In one view, Tm is preshaped semirigidly to match F-actin’s helical shape (7). In an alternative view, Tm may flexibly sample many conformations, some of which match F-actin’s helical shape. A key source of flexibility is Tm’s noncanonical destabilizing regions, including six Ala clusters (1–3), where, it has been proposed (2,8), local axial staggering between two Tm chains induces local bending of Tm backbones. In addition, side-chain flexibility may result from poor packing in the destabilizing regions of Tm (9). In support of high flexibility in Tm, deviations from the canonical coiled-coil structure, such as local axial staggering and local bending, have been observed in several x-ray structures of Tm fragments (2,4,8,10–12). However, the low-resolution electron microscopy (EM) studies of thin filaments seem to favor the picture of a curved and semirigid Tm that adopts three average azimuthal positions (i.e., blocked, closed, and open positions) on the surface of F-actin (13–18).

Molecular dynamics (MD) is the method of choice for simulating protein dynamics in the presence of water and ions in atomic detail (19). MD simulation can, in principle, resolve the controversy over the role of Tm flexibility in Tm-F-actin binding, thanks to its ability to simulate Tm dynamics and Tm-F-actin interactions under physiological conditions. MD may also allow detailed simulations of effects of mutations on Tm flexibility and binding to F-actin (such as mutations D137L (20), D175N, and E180G (21)). Compared with x-ray crystallography and EM, MD simulation is free from the influence of crystal packing and protein modifications in x-ray crystallography, and limited resolution (>20 Å) and loss of structural variations by helical averaging in EM reconstructions. However, for a large biomolecular system like the Tm-F-actin complex with explicit solvent, it remains unfeasible to perform MD simulations for more than tens of nanoseconds. Recently, an extended bias-potential MD method named accelerated MD (aMD) (22) has been developed that can reach timescales >1000 times greater than those accessible using standard MD (23). We have previously used aMD to observe an allosteric transition of the microsecond timescale in hemoglobin (24).

Previous MD studies by Lehman and co-workers (25–28) suggested that the average Tm conformation is preshaped for binding F-actin and that Tm flexibility is highly delocalized. In particular, they found no significant correlation between Ala clusters and regions with high flexibility (26). Although an all-atom model for the Tm-F-actin complex was constructed and key Tm-F-actin interactions were predicted based on that model (28), no extensive MD simulations of the dynamic interactions between Tm and F-actin have been conducted, leaving key questions unanswered. How does F-actin binding affect the Tm flexibility? How correlated are the Tm fluctuations over the surface of F-actin involving seven quasiequivalent regions (i.e., periods P1–P7)? How does Tm flexibility affect its binding to F-actin? How do seven Tm periods participate in F-actin binding with different contributions (5,29)?

To address the above open questions and elucidate the structural basis of Tm flexibility in relation to Tm-F-actin binding, we conducted extensive MD/aMD simulations for both Tm alone and Tm-F-actin complex in the presence of explicit solvent and ions. Our simulations are more extensive (total simulation time = 440 ns) than previously published MD studies of Tm dynamics (25–28). Based on the MD/aMD simulations, we analyzed the local flexibility of the Tm coiled coil using six parameters (see Methods). Contrary to previous MD studies (25–28), we found a clear correlation between the regions with high local flexibility and a number of destabilizing regions of Tm, including six Ala clusters. Despite the stabilization by F-actin binding, the distribution of local flexibility in Tm is similar in the absence and presence of F-actin. Our MD/aMD simulations also showed variable fluctuations of individual Tm periods from the closed position toward the open position. In addition, we performed Tm-F-actin binding calculations based on the MD/aMD simulations, which approximately quantify the contributions of electrostatic and nonpolar forces to Tm-F-actin binding with residue-level details. Thanks to enhanced conformational sampling by aMD, we found stronger Tm-F-actin binding based on the aMD simulations than on the MD simulations, which supports the importance of Tm flexibility for Tm-F-actin binding. Finally, we identified key residues of Tm involved in its dynamic interactions with F-actin, many of which were found by recent mutational studies to be functionally important, and the rest of which will make promising targets for future mutational experiments.

Methods

System preparation and MD simulation

A model of full-length Tm in complex with a 15-actin filament was constructed by Li et al. (28) based on EM data. Starting from this initial model, we prepared two systems—one for Tm alone (system 1) and the other for Tm bound with F-actin (system 2). We also prepared another system (system 3) for Tm alone based on a 7-Å x-ray structure of full-length Tm (PDB ID: 1c1g). The hydrogen atoms are added with the visual molecular dynamics (VMD) program (30). All systems are immersed in a rectangular box of water molecules extending up to 8–10 Å from the proteins in each direction using VMD. To ensure a physiological ionic concentration of 0.15 M and zero net charge, Na⁺ and Cl⁻ ions are added to the systems by VMD. After adding solvent and ions, systems 1, 2, and 3 have 517,452, 658,781, and 502,573 atoms, respectively.

The systems are refined with two rounds of energy minimization using the steepest-descent method: first, a 5000-step energy minimization with harmonic constraints (force constant = 10 kcal/mol/Ų) applied to all protein-backbone heavy atoms (N, Cα, and C), then a 5000-step energy minimization with harmonic constraints (force constant = 0.01 kcal/mol/Ų) applied to Cα atoms only. The systems are then heated to 300 K over 300 ps by MD with harmonic constraints (force constant = 0.01 kcal/mol/Ų) applied to Cα atoms only. Then the systems are equilibrated for 500 ps with MD performed in the NVT ensemble with the same constraints applied in heating. Then the systems are subject to a 20-ns production run with MD performed in the NPT ensemble with harmonic constraints (force constant = 0.01 kcal/mol/Ų) applied to the Cα atoms of F-actin only. The Nosé–Hoover method (31) is used with temperature T = 300 K and pressure P = 1 atm. The periodic boundary conditions are applied to the systems. A 10-Å switching distance and a 12-Å cutoff distance are used for nonbonded interactions. The particle mesh Ewald (PME) method (32) is used to calculate long-range electrostatic interactions. The SHAKE algorithm (33) is used to constrain the bond lengths of hydrogen-containing bonds, which allows a time step of 2 fs for MD simulations. The atomic coordinates of the systems are saved every 2 ps during MD simulations for later analysis. The energy minimization and MD simulation are carried out with the NAMD program version 2.9b2 (34) using the CHARMM27 force field (35) and the TIP3P water model (36). Four MD trajectories were generated for each of systems 1 and 3. Ten MD trajectories were generated for system 2 to enhance the sampling for a larger system.

Accelerated MD simulation

To enhance MD simulations of Tm flexibility, we used aMD (22) to simulate Tm dynamics in the presence of F-actin. aMD accelerates slow conformational dynamics of proteins by adding a boost potential, $\Delta V={\left(E-V\right)}^2/[\alpha +\left(E-V\right)]$, to the dihedral potential, V, of the system (22). During an aMD simulation, the boost potential is turned on if the dihedral potential energy, V, falls below a threshold energy, E. Another parameter for the boost potential is the acceleration factor, α, which determines the depth of the dihedral potential basin below E. Following recommendations from previous aMD studies (for example, see Pierce et al. (23)), we chose the aMD parameters as follows: E is set equal to the average dihedral potential energy (31,781.6 kcal/mol), obtained from a classical MD simulation plus 4 kcal/mol times the number of solute residues (6193), and α is then set to 1/5 of this value. The above procedure has yielded E = 56,553.6 kcal/mol and α = 4954.4 kcal/mol. The NAMD implementation of aMD is used (37). Four 20-ns aMD trajectories were generated for system 2.

Local flexibility analysis of the Tm coiled-coil

In Tm, two α-helical chains (named A and B) form a coiled coil that displays a seven-amino-acid long heptad periodicity (with seven positions a-b-c-d-e-f-g). In the hydrophobic core of Tm, a d residue of chain A is packed between two a residues of chain B (named a′ and a″) in a knob-into-hole manner (see Fig. 1, inset). To characterize the backbone flexibility of each d residue in local packing, we use three distances between the Cα atomic positions of d, a′, and a″ residues (denoted as d_a′d, d_a″d, and d _a′a″; see Fig. 1, inset) to calculate the three parameters discussed below.

Figure 1.

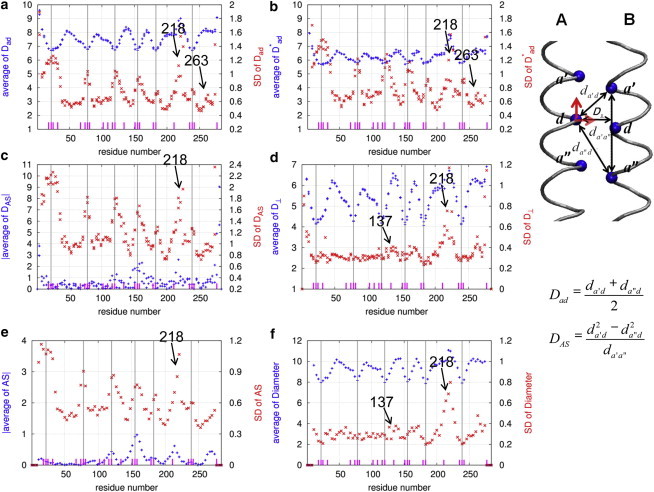
Results of local flexibility analysis of Tm in the absence of F-actin (system 1) using six parameters: $D_{ad}$ (a), $D_{ad}^{\ast }$ (b), $D_{AS}$ (c), $D_{\perp }$ (d), AS (e), and diameter (f). For definitions of these parameters, see Methods. The average and SD of the above parameters as a function of the a and d residue positions of Tm are shown as symbols and , respectively. The long vertical lines mark the center positions of six Ala clusters (A22, A78, A120, A155, A183, and A239). The positions of individual core Ala residues are marked by short dashes. The calculations are based on the last 10 ns of four 20-ns MD trajectories of system 1. (Inset) The hydrophobic interface between chains A and B of the Tm coiled coil is shown. Three core residues in each chain (at the a′, d, and a″ positions) are shown as spheres, and the distances between these residues ($d_{a\text{'}d}$, $d_{a"d}$, and $d_{a\text{'}a"}$) and the perpendicular distance, $D_{\perp }$, between the d residue and line $a\text{'}$-$a"$ are shown by double-headed arrows. The two orthogonal motions (i.e., axial and lateral motion) of the d residue in chain A relative to chain B are highlighted by two bold arrows. To see this figure in color, go online.

$D_{ad}=\left(\right(d_{a\text{'}d}+d_{a"d}\left)\right)/2$ measures how closely the d residue of chain A is packed between the a′ and a″ residues of chain B.

$D_{\text{AS}}=\left(\right(d_{a\text{'}d}^2-d_{a"d}^2\left)\right)/d_{a\text{'}a"}$ measures the axial displacement of the d residue of chain A along the a′-a″ direction, where a large $\left|D_{\text{AS}}\right|$ indicates a large axial staggering (AS) of this d residue relative to chain B (see Brown et al. (2)), and a positive/negative $D_{\text{AS}}$ corresponds to an axial displacement toward the C/N-terminus of Tm.

$D_{\perp }$ measures the perpendicular distance between the d residue of chain A and the line a′-a″ (see Fig. 1, inset), which is related to the local diameter of the Tm coiled coil (see Brown (38)).

To probe the side-chain flexibility of the d residue of chain A packed between the a′ and a″ residues of chain B, we calculate $D_{ad}^{\ast }=\left(\right(d_{a\text{'}d}^{\ast }+d_{a"d}^{\ast }\left)\right)/2$ using the distances between the side-chain centroid positions of d, a′, and a″ residues (denoted as $d_{a\text{'}d}^{\ast }$ and $d_{a"d}^{\ast }$).

In a similar way, the above parameters are defined for each a residue of chain A packed between two adjacent d residues of chain B using the distances between the three residues.

To assess local bending of Tm based on 500 snapshots of the last 10 ns of an MD/aMD trajectory, we define the bending angle, θ_b, at a given residue position n as the angle between the two vectors ${\overrightarrow{r}}_{mn+7}-{\overrightarrow{r}}_{mn}\text{and}{\overrightarrow{r}}_{mn}-{\overrightarrow{r}}_{mn-7}$, where ${\overrightarrow{r}}_{mn}$, ${\overrightarrow{r}}_{mn-7}$, and ${\overrightarrow{r}}_{mn+7}$ are the Cα atomic positions of residues n, n − 7, and n + 7 in snapshot m. Then we average θ_b over 500 snapshots.

Tm-actin binding calculation

As in our previous papers (39,40), we calculate the Tm-actin binding free energy ΔG (not including the entropy contribution) for each of the 5 actin subunits interacting with periods P2–P6 of Tm (periods P1 and P7 are excluded because they are in the overlap regions, which are not properly modeled here). We extract 100 snapshots of the last 10 ns of each MD/aMD trajectory for system 2 (after stripping all waters and ions), then calculate ΔG for each snapshot and average ΔG over 100 snapshots. Following a continuum solvent model (see Eriksson and Roux (41)), ΔG is expressed as ΔG = ΔG_np + ΔG_elec. Here the nonpolar contribution ΔG_np = αE_vdW is empirically written as a fraction (α < 1) of the van der Waals (vdW) interaction energy, E_vdW, between Tm and actin, and the electrostatic contribution ΔG_elec = βΔE_elec is empirically written as a fraction (β < 1) of the change in electrostatic energy, ΔE_elec, from unbound Tm and actin to Tm-actin complex. E_elec is calculated using the Poisson-Boltzmann (PB) method (42,43). α = 0.158 and β = 0.153 were obtained from the fitting of kinesin-microtubule binding data (39). For the PB calculation (42,43), a dielectric constant of ε_i = 4 is used for the protein interior (44–47). A dielectric constant of ε_e = 80 is used for the exterior aqueous environment. A probe radius of 1.4 Å is used to define the molecular surface corresponding to the dielectric boundary. The salt concentration is set to 0.12 M, which approximately corresponds to a typical buffer condition of 100 mM KCl. All the PB calculations are performed using the PBEQ module (43,48,49) of CHARMM program (50). The atomic Born radii used here were previously calibrated in Nina et al. (49). Next, we used CHARMM to partition ΔG, E_vdW, and ΔE_elec into contributions from individual Tm residues (denoted as ΔG_n, E_vdW,n, and ΔE_elec,n for residue n). We select a subset of Tm residues with |ΔG_n| greater than three times its average over all residues, which are predicted to be important to actin-Tm binding.

Results

MD and aMD simulations of Tm dynamics

To fully explore the dynamics of Tm, we constructed three systems with explicit solvent and ions (systems 1 and 3 for Tm alone using different initial models, and system 2 for Tm bound with F-actin; see Methods) and then completed extensive MD and aMD simulations of Tm dynamics, resulting in the following 22 trajectories (total simulation time = 440 ns): eight 20-ns MD trajectories of Tm alone (systems 1 and 3), ten 20-ns MD trajectories of Tm bound with F-actin (system 2), and four 20-ns aMD trajectories of Tm bound with F-actin (system 2). To our knowledge, this is the most extensive MD study of Tm dynamics performed to date. We used the principal component analysis to visualize and compare the regions of conformational space sampled by these trajectories (see Supporting Material).

We analyzed the root mean-squared deviation (RMSD) relative to the initial model of Tm for each MD/aMD trajectory. Despite large fluctuations, most simulations reached a stable state within <10 ns (see Fig. S1): the four MD trajectories for system 1 stabilize at RMSD 5–9 Å (see Fig. S1 a), two out of four MD trajectories for system 3 stabilize at RMSD 4–6 Å (see Fig. S1 b), ten MD trajectories for system 2 stabilize at RMSD 2–5 Å (see Fig. S1 c), and four aMD trajectories for system 2 stabilize at RMSD 3–6 Å (see Fig. S1 d). Based on the RMSD analysis, we selected and combined the stable conformations visited by the last 10 ns of all 20-ns MD/aMD trajectories to generate an extensively sampled structural ensemble for semiquantitative analysis of Tm flexibility and Tm-F-actin binding (see below). In particular, we analyzed the local flexibility of Tm in relation to its destabilizing regions (including six Ala clusters) and critically examined previous proposals on Tm flexibility based on x-ray structural data (2,4,8,12,38,51). To make sure the analysis results are insensitive to the truncation of trajectories, we repeated the analysis for the last 5 ns of MD trajectories (see Fig. S3). We also verified that the analysis results are not affected by the differences in initial model between systems 1 and 3 (see Fig. S4).

Global flexibility analysis

To explore the global flexibility of Tm, we calculated the global root mean-squared fluctuation (RMSF) at every residue position of Tm based on the last 10 ns of each MD/aMD trajectory (see Supporting Methods). Then we computed the average of the global RMSF over all Tm residues (denoted as $\langle \text{RMSF}\rangle$) to assess the overall flexibility of Tm. In the absence of F-actin, Tm is highly flexible in system 1 ($\langle \text{RMSF}\rangle$ = 2.47 ± 0.17 Å), and somewhat more flexible in system 3 ($\langle \text{RMSF}\rangle$ = 2.92 ± 0.06 Å) (see Table S1). When bound with F-actin, Tm is less flexible with $\langle \text{RMSF}\rangle$ = 1.57 ± 0.09 Å during MD simulations and 1.79 ± 0.06 Å during aMD simulations (see Table S1). The higher flexibility of Tm during aMD simulations can be attributed to enhanced conformational sampling by aMD (23). We also calculated the local RMSF for individual Tm periods to demonstrate that the local flexibility of Tm is adequately sampled, which allows a statistically meaningful analysis of the local flexibility of Tm (see Supporting Material for details).

Local flexibility analysis of the Tm coiled coil

Tm has six Ala clusters that replace canonical leucine or other large nonpolar residues at the hydrophobic interface between the two chains of the Tm coiled coil (1–3). It was proposed that the Ala clusters induce local axial staggering between two Tm chains, which causes nearby regions of Tm to bend (2,8). However, a recent analysis of Tm x-ray structures and MD trajectories did not find significant correlation between the Ala clusters and the regions with large axial displacement or local curvature (26). To shed light on this controversy, we analyzed the local flexibility of Tm based on extensive MD and aMD simulations of Tm dynamics.

To explore various aspects of local flexibility in Tm (including backbone and side-chain flexibility within and between two Tm chains), we calculated the following four parameters at every a/d position of Tm (see Methods): $D_{ad}$, measuring the closeness of Cα packing at the hydrophobic interface of the Tm coiled coil; $D_{ad}^{\ast }$, measuring the closeness of side-chain packing at the hydrophobic interface of the Tm coiled coil; $D_{AS}$, measuring the axial staggering between two Tm chains; and $D_{\perp }$, measuring the lateral separation between two Tm chains. Using these parameters, we can dissect local motions between two Tm chains in terms of two orthogonal motions (see Fig. 1, inset)—an axial motion parallel to the coiled-coil axis (affecting $D_{ad}$ and $D_{\text{AS}}$) and a lateral motion perpendicular to the coiled-coil axis (affecting $D_{ad}$ and $D_{\perp }$). We calculated both the average and the standard deviation (SD) of the above parameters based on the last 10 ns of MD/aMD trajectories in the absence or presence of F-actin.

Tm flexibility in the absence of F-actin

In the absence of F-actin, the average of $D_{ad}$ exhibits six valleys (i.e., local minima) corresponding to six Ala clusters (A18-A22-A25-K29-A32-S36, A74-A78-A81, A116-A120-S123, A151-A155-A158, A179-A183-S186, and A235-A239-A242; see Minakata et al. (4)) centered at six core Ala residues (A22, A78, A120, A155, A183, and A239) (see Fig. 1 a). This is consistent with the close packing of the coiled coil near the Ala clusters due to the small size of Ala residues. To further validate these structural features, we calculated $D_{ad}$ for several high-resolution x-ray structures of Tm fragments (PDB IDs: 1ic2, 2efr, 2efs, 2b9c, and 2d3e). We found similar valleys in $D_{ad}$ near the six Ala clusters in these structures, although some of them are slightly shifted due to truncation and modification of Tm (see two valleys near A78 and A120 in Fig. 2 a). Notably, unlike the MD trajectories and the x-ray structures, the initial model for our MD simulations as built in Li et al. (28) does not exhibit these valleys in $D_{ad}$ (see Fig. 2 a). Therefore, our MD simulation is able to recover the observed structural features of Tm not present in the initial model. We also analyzed Tm flexibility based on the MD trajectories starting from a different initial model of Tm (system 3; see Methods), and found a similar distribution of flexibility in Tm (see Fig. S4). Taken together, these findings have validated the ability of our MD simulation and flexibility analysis to uncover new structural and dynamic features of Tm independent of the quality of the initial model.

Figure 2.

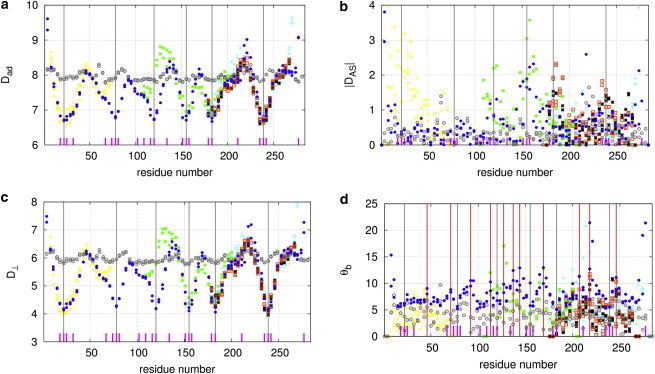
Results of local flexibility analysis of Tm in the absence of F-actin in comparison with x-ray structures of Tm fragments using four parameters: $D_{ad}$ (a), $D_{AS}$ (b), $D_{\perp }$ (c), and θ_b (d). The gray vertical lines mark the center positions of six Ala clusters (A22, A78, A120, A155, A183, and A239). The positions of individual core Ala residues are marked by short dashes. The red vertical lines in d mark peaks of average θ_b. The data points are represented as follows: MD simulations of system 1 , PDB structures 2d3e, 1ic2, 2efr, 2efs, and 2b9c, and the initial model from Li et al. (28) .To see this figure in color, go online.

As an indicator of backbone flexibility in the hydrophobic interface of the Tm coiled coil, the SD of $D_{ad}$ exhibits seven pronounced peaks, six of which align very well with the six valleys in the average of $D_{ad}$ (see Fig. 1 a) where the six Ala clusters are located. In addition, a seventh peak is near another destabilizing core residue, E218 (see Fig. 1 a). This finding is, to our knowledge, the first dynamics evidence that supports the colocalization of six Ala clusters with regions of high local flexibility in Tm, although such a correlation was proposed based on the comparison of x-ray structures of Tm fragments solved under different crystallization conditions (2,8).

As indicators for side-chain packing and flexibility in the hydrophobic interface of the Tm coiled coil, the average and SD of $D_{ad}^{\ast }$ exhibit features similar to those seen for $D_{ad}$ (see Fig. 1 b). The valleys in the average of $D_{ad}^{\ast }$ are less pronounced than those in $D_{ad}$, whereas the peaks in the SD of $D_{ad}^{\ast }$ are more pronounced than in $D_{ad}$ (see Fig. 1, a and b). Therefore, to adequately describe local flexibility in the hydrophobic interface of the Tm coiled coil, it is necessary to take into account side-chain fluctuations in addition to backbone fluctuations (5). Both contribute to the high flexibility near the Ala clusters.

The local flexibility in the hydrophobic interface of the Tm coiled coil may involve two orthogonal motions between the two Tm chains, an axial motion parallel to the coiled-coil axis and a lateral motion perpendicular to the coiled-coil axis (see Fig. 1, inset). To test the proposal that the axial motion is the main contributor to the local flexibility of Ala clusters (2), we analyzed the average and SD of $D_{\text{AS}}$ (see Methods). Interestingly, the SD of $D_{\text{AS}}$ displays seven peaks (see Fig. 1 c), which match well with the seven peaks in the SD of $D_{ad}$, including six peaks near the six Ala clusters (see Fig. 1 a). Only some of these peaks are found in the average of $D_{\text{AS}}$ (see Fig. 1 c), suggesting that the axial staggering in Tm is highly dynamic and thus cannot be fully captured by averaging over MD trajectories. To further validate the above finding, we also calculated $D_{\text{AS}}$ for several high-resolution x-ray structures of Tm fragments and found similar peaks near the Ala clusters (see Fig. 2 b), some of which were also found by a previous structural analysis (4). Taken together, both MD simulations and x-ray structures of Tm support the proposal that the six Ala clusters are hotspots for local axial motion between two Tm chains (2), which may lead to elevated local flexibility, as observed in the SD of $D_{ad}$ (see Fig. 1 a).

To assess whether the lateral motion between two Tm chains also contributes to the local flexibility of Tm, we analyzed the average and SD of $D_{\perp }$ (see Methods). Although the average of $D_{\perp }$ exhibits six valleys at the six Ala clusters, the SD of $D_{\perp }$ shows no peaks at the Ala clusters but a prominent peak at E218 (see Fig. 1 d). Thus, the lateral motion between two Tm chains is not involved in the high local flexibility near the Ala clusters.

To further check the robustness of our finding based on the analysis of $D_{\text{AS}}$ and $D_{\perp }$, we analyzed two alternative parameters for measuring the AS and coiled-coil diameter using the CCbends program (38). Indeed, the distributions of AS and diameter are very similar to those of $D_{\text{AS}}$ and $D_{\perp }$, respectively (see Fig. 1, e and f), which confirms our finding that the six Ala clusters, corresponding to six peaks in $D_{\text{AS}}$ and AS, are hotspots for the axial motion but not the lateral motion between two Tm chains.

In addition to the six Ala clusters, a region near E218 is also found to be very flexible, with large axial and lateral fluctuations between the two Tm chains (see Fig. 1). The region near E218 is known to be structurally unstable, with a noncanonical core residue, E218, at the hydrophobic interface of the Tm coiled coil (4). Intriguingly, another well-known noncanonical core residue, D137 (52), does not correspond to any peak in the SD of $D_{\text{AS}}$, although it is near a minor peak in the SD of $D_{\perp }$ (see Fig. 1 d). In addition, the flexibility of D137 and E218 changes differently upon the binding of F-actin (see below). Therefore, the local flexibility near D137 and E218 may differ in the structural details. It is unclear how such differences relate to the finding that the region near D137 (such as R133 and E131; see Moore et al. (20)) is highly susceptible to proteolysis, whereas the region near E218 is not. We also found moderately high flexibility near Q263, corresponding to a minor peak in the SD of $D_{ad}$ and $D_{ad}^{\ast }$ (see Fig. 1, a and b). This region was found to be unstable in both solution (53,54) and the crystal structure of a Tm fragment (12).

In sum, we found a clear correlation between the positions of destabilizing residues (including six Ala clusters and two other destabilizing regions near E218 and Q263) and the regions with high local flexibility in the hydrophobic interface of the Tm coiled coil. The high flexibility in the Ala clusters is due to large axial motion between two Tm chains.

How does the local flexibility of Ala clusters and other destabilizing regions enable Tm to conform to the contours of F-actin? Brown and co-workers proposed that the local AS between two Tm chains can induce local bending of Tm backbones in nearby regions (2,8). In support of this proposal, local bending was indeed observed in several x-ray structures of Tm fragments near the destabilizing regions (2,4,8,10–12). However, the occurrence of local bending seems to depend on crystal packing conditions, and whether such local bending is intrinsic to Tm dynamics in solution remains to be shown.

To test the above proposal, we analyzed the average local bending angle (denoted as θ_b, see Methods) at each a/d residue position of Tm based on the last 10 ns of MD trajectories. The distribution of the average θ_b features multiple peaks at residues 46, 71, 92, 113, 127, 137, 144, 169, 207, 218, and 246 (with average θ_b > 10°; see Fig. 2 d). It is encouraging that many of these local bending hotspots coincide with local bending regions found in several x-ray structures of Tm fragments (such as residues 46, 113, 127, 144, 169, 218, and 246; see Fig. 2 d). In particular, Tm is remarkably bent at E218 in both our MD simulations (see Fig. 2 d) and the x-ray structure of a Tm fragment (PDB ID: 2d3e) (12). Notably, the initial model of our MD simulations as built in Li et al. (28) does not exhibit these peaks in θ_b (see Fig. 2 d), which only arise from extensive MD simulations. Unlike those highly flexible regions identified by the analysis of $D_{ad}$ and $D_{\text{AS}}$ (see Fig. 1, a and c), the local bending hotspots do not coincide with the destabilizing regions including the six Ala clusters (see Fig. 2 d). Instead, they are mostly located adjacent to the destabilizing residues (within ≤25 residues). Thus, it is likely that the local axial motion at Ala clusters may be transmitted over some distance to induce local bending in nearby regions (2,8). This idea was supported by a recent correlation analysis of helical staggers in Tm (55).

Tm flexibility in the presence of F-actin

For the MD simulations of Tm in the presence of F-actin, the distribution of local flexibility in Tm remains largely unchanged compared with Tm alone (see Fig. S5). The averages of $D_{ad}$, $D_{ad}^{\ast }$, and $D_{\perp }$ still exhibit six valleys corresponding to six Ala clusters (see Fig. S5, a, b, and d). The SDs of $D_{ad}$, $D_{ad}^{\ast }$, and $D_{\text{AS}}$ exhibit seven pronounced peaks, six of which correspond to the six Ala clusters (see Fig. S5, a–c). Notably, F-actin binding greatly reduces the peak at E218 in the SD of $D_{ad}$, $D_{ad}^{\ast }$, and $D_{\perp }$ (see Fig. S5, a, b, and d). However, D137 remains highly flexible despite F-actin binding, with a pronounced peak at D137 in the SD of $D_{\perp }$ (see Fig. S5 d).

For the aMD simulations of Tm in the presence of F-actin, we found a similar distribution of local flexibility (e.g., peak positions in the SDs of $D_{ad}$, $D_{ad}^{\ast }$, $D_{AS}$, $D_{\perp }$), although aMD substantially enhances the height of these peaks (see Fig. S6), thanks to enhanced conformational sampling by aMD.

In sum, F-actin binding does not change the distribution of local flexibility in Tm, especially the high flexibility of six Ala clusters. Two destabilizing regions near residues D137 and E218 remain flexible, although F-actin binding greatly reduces the flexibility of E218.

Analysis of Tm fluctuations over the surface of F-actin

Thus far, we have focused on the internal flexibility of Tm in the absence and presence of F-actin. Another key aspect of Tm dynamics is its fluctuations relative to F-actin. In the three-state steric blocking model (13,56), Tm is thought to move over the F-actin surface from the blocked position in the absence of Ca²⁺ to the closed position and then the open position in the presence of Ca²⁺ and strong-binding myosin heads. In one scenario, Tm rapidly fluctuates between these positions, and its transient exposure of the myosin-binding site on F-actin would allow myosin to bind and would favor binding of Tm at the open position. To assess this postulate, we analyzed how the periods P2–P6 of Tm fluctuate relative to the closed and open positions during the MD/aMD simulations. Our MD/aMD simulations start from an initial model of Tm bound with F-actin in the absence of troponin, presumably near the closed position (28), although it is near the blocked position as modeled by another EM-based study (17). To measure the distances between Tm and the closed and open positions (denoted D_C and D_O), we calculated the minimal Cα-Cα distances between Tm and two representative residues (D25 and P307) on five actin subunits in contact with the periods P2–P6 of Tm (see Fig. 3). Residues D25 and P307 are close to Tm at the closed and open positions, respectively (see Fig. 3). We average the minimal distances from Tm to D25 and P307 (corresponding to D_C and D_O) over the last 10 ns of each MD/aMD trajectory. Then we subtract the values of D_C and D_O as calculated for the initial model (28) to obtain the changes in D_C and D_O during the MD/aMD simulations (denoted δD_C and δD_O; see Table S2): as a Tm period moves from the closed position to the open position, δD_C becomes more positive and δD_O becomes more negative.

Figure 3.

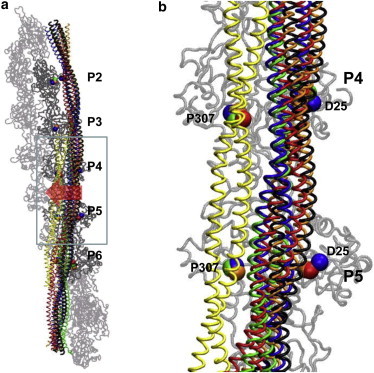
Average structures of Tm bound with F-actin in comparison with the Tm models at the closed and open positions. (a) Global view of the entire Tm bound with F-actin. (b) Enlarged view of periods P4 and P5 in Tm. The average structures of Tm from four aMD simulations are colored blue, red, green, and orange; the Tm model at the closed position (28) is colored black; and the Tm model at the open position (57) is colored yellow. Two actin residues (D25 and P307) are shown as reference points for the closed and open positions of Tm and colored the same as Tm. Five actin subunits in contact with periods P2–P6 of Tm are colored dark gray, and those not in contact with Tm are colored light gray. The block arrow in a indicates the shift of Tm from the closed position to the open position.

During the ten MD simulations of Tm bound to F-actin, the periods P2–P6 of Tm fluctuate near the closed position (−3.1 Å ≤ δD_C ≤ 5.8 Å; see Table S2), with a variable shift toward the open position (−5.8 Å ≤ δD_O ≤ 0 Å; see Table S2). Upon averaging over the ten MD trajectories, whereas P4 undergoes the largest shift away from the closed position (with an average of δD_C ∼ 1.8 Å; see Table S2), P5 shows the greatest variation in δD_C (with SD of δD_C ∼2.2 Å; see Table S2), highlighting the dynamic role of these periods in driving the movement of Tm on F-actin. During the four aMD simulations of Tm bound to F-actin, the periods P2–P6 of Tm undergo a larger shift toward the open position (−7.5 Å ≤ δD_O ≤ −0.1 Å; see Table S2 and Fig. 3). Upon averaging over the four aMD trajectories, P5 undergoes the largest shift away from the closed position (with an average for δD_C ∼3.1 Å; see Table S2). Among the four aMD trajectories, the largest shift is observed during the second aMD simulation, where the periods P2–P6 of Tm shift away from the closed position by 1–4.2 Å and toward the open position by 2.5–7.5 Å (see Table S2). Notably, some periods of Tm fluctuate more than halfway between the closed and open position (δD_O is −11 Å for Tm at the open position (57)). Therefore, within the timescales of our MD/aMD simulations, individual periods of Tm are fluctuating variably from the closed position toward the open position, in contrast with the proposal that Tm moves over the F-actin surface semirigidly based on EM studies (13–18). We also used principal component analysis to analyze the relative motions between Tm and F-actin (see the Supporting Material).

In sum, our MD/aMD simulations showed variable fluctuations of individual Tm periods from the closed position toward the open position, which may allow transient exposure of at least one myosin-binding site on F-actin for strong binding of myosin and activation of the thin filament. Therefore, the initial binding of myosin during cooperative activation of F-actin-Tm may be primarily defined by the dynamic availability of a binding site on F-actin rather than a preferred binding site on F-actin-Tm with reference to the Tm sequence. Further simulations are underway to explore the structural dynamics of Tm bound with both F-actin and myosin near the open position.

Binding calculation between Tm and actin subunits

Based on the MD/aMD simulations of Tm bound with F-actin, we performed intermolecular binding calculations between Tm and F-actin, which take into account both electrostatic and nonpolar contributions to Tm-F-actin binding with residue-level detail (see Methods). To this end, we kept 100 snapshots of the last 10 ns of each MD/aMD trajectory. For each snapshot, we calculated the binding free energy, ΔG (not including the entropy contribution; see Methods), between Tm and each of five actin subunits interacting with the periods P2–P6 of Tm (see Fig. 3), and then averaged the ΔG values over all snapshots (see Methods). We established and applied this protocol in two recent studies of the binding between kinesin motor and microtubule in three biochemical states (39,40).

The total ΔG (i.e., the sum of ΔG over all five actin subunits) varies significantly between the MD and aMD trajectories (see Table S3). Interestingly, the total ΔG seems to correlate with the overall flexibility of Tm (measured by $\langle \text{RMSF}\rangle$; see Table S1). Tm binds more strongly with F-actin and has higher $\langle \text{RMSF}\rangle$ during the aMD simulations than during the MD simulations (see Table S3). This finding supports the importance of Tm flexibility for its binding to F-actin. Among the four aMD trajectories, the second has the highest $\langle \text{RMSF}\rangle$ (see Table S1) and the largest shift toward the open position (see Table S2), but it also has the weakest binding to F-actin (see Table S3). This may be attributed to the less favorable Tm-F-actin interactions at the open position in the absence of myosin binding (28). Therefore, the Tm-myosin interactions must be included to account for the strong binding of Tm to myosin-decorated F-actin at the open position (57).

For all MD/aMD trajectories, the nonpolar contribution is consistently greater than the electrostatic contribution. Although this finding is at odds with the previous proposal that the electrostatic forces dominate Tm-F-actin binding (28,58), it does not downgrade the importance of electrostatic forces in Tm-F-actin binding. In fact, the electrostatic contribution is more important in Tm-F-actin binding (ΔE_elec/E_vdW ≥ 0.4; see Table S3) than in myosin-F-actin binding (ΔE_elec/E_vdW ≤ 0.2; see Zheng and Li (59)). Thanks to the flexibility of both Tm and F-actin, Tm moves closer to F-actin during the MD/aMD simulations, forming more extensive contact than in the initial model. As a result, we found a higher nonpolar contribution to Tm-F-actin binding than was found in previous calculations, which did not fully account for flexibility (28,58). We note that both nonpolar and charged residues at the Tm-F-actin interface are involved in the nonpolar contribution of ΔG (see Table S4). Thus, our finding does not contradict the recent finding that mutations of charged surface residues of Tm had a larger effect on Tm-F-actin binding than did mutations of nonpolar residues (60,61). In fact, as predicted by our binding calculation, the Tm residues most involved in Tm-F-actin binding are primarily charged and polar residues (see below).

Given the large variations of ΔG between different trajectories and periods of Tm (see Table S3), we cannot determine which period contributes the most to Tm-F-actin binding. Such strong variations in ΔG are not unexpected given the observed high flexibility of Tm even in the presence of F-actin. More extensive MD/aMD simulations will be needed to yield statistically meaningful differences in ΔG between different periods of Tm.

The calculated values of ΔG are not comparable to experimental binding measurements (mM/μM affinity for Tm without/with cooperativity) for the following reasons: first, the entropic cost of Tm-F-actin binding is not taken into account (due to large uncertainty in entropy calculation), which would have made |ΔG| much smaller; second, the head-to-tail interactions in the overlap regions of Tm, known to be essential for cooperative Tm-F-actin binding, are missing in our simulations (62). Despite such caveats, we should stress that the objective of our binding calculation is not to accurately reproduce the experimental ΔG, but to semiquantitatively analyze the contributions of individual Tm residues to Tm-F-actin binding and to identify those key residues involved in Tm-F-actin binding (see below).

To identify key Tm residues involved in Tm-F-actin binding, we partitioned ΔG into contributions from individual Tm residues (denoted as ΔG_n for residue n; see Methods and Table S4). To fully sample the dynamic interactions between Tm and F-actin, these per-residue contributions are averaged over the last 10 ns of ten MD trajectories. By ranking the per-residue contributions, the following actin-binding residues of Tm were found (see Table S4 and Fig. S9): K37, V44, Q47, K48, K51, E54, D55, D58, K59, and E62 of P2; A86, N89, R90, Q93, L94, E97, D100, R101, and E104 of P3; R125, K128, V129, E131, S132, Q135, K136, E138, and E142 of P4; R160, R167, V170, I171, E173, S174, E177, R178, and E181 of P5; and K198, N202, K205, E208, A209, E212, K213, Q216, D219, and E223 of P6. Among these residues, the highest-contributing residues (with ΔG_n < −0.2; see Table S4) are dominated by basic residues like K48, K51, R90, R125, K128, R160, R167, and K205, along with other polar residues like Q93, Q135, and Q216, and only one acidic residue, E212, and one nonpolar residue, V170. Most of these residues are located in the first halves of periods P2–P6, in agreement with a recent mutational study (60). Most of the above residues are at b, c, or f positions of the coiled-coil surface, although some are at e or g positions (Q47, E54, N89, E131, E138, E173, and E208), which may also be involved in the stabilization of the Tm coiled coil.

Among the above residues, 21 (underlined residues) were validated by recent mutational studies of evolutionarily conserved residues at the Tm-F-actin interface (60,61), and the rest will serve as targets for future mutational studies. Many of the above actin-binding residues were also predicted by a previous modeling study of the Tm-F-actin complex (28). In addition to what was predicted in Li et al. (28), we predicted many additional actin-binding residues in periods P2–P6 of Tm (including K51, D55, K59, A86, N89, Q93, L94, V129, E131, Q135, K136, E138, R160, I171, E173, S174, E177, R178, K198, N202, E212, K213, Q216, and E223), thanks to extensive MD simulations of dynamic interactions between Tm and F-actin. Our finding of more actin-binding residues does not imply stronger binding between Tm and F-actin, because most of the above residues form transient and weak interactions with F-actin during the MD simulations as Tm fluctuates over the surface of F-actin. These dynamic interactions cannot be fully captured by a static snapshot of the Tm-F-actin interface and are consistent with the view that the functional blocked, closed, and open positions of Tm on F-actin are averages of dynamic structures. We note that our predictions are limited to those Tm residues directly involved in the interactions with F-actin, and our method cannot predict Tm residues that are indirectly involved in F-actin binding via changes in dynamics or stability.

We also performed ΔG partition based on the four aMD trajectories (see Table S4). We found more actin-binding residues of Tm based on the aMD simulations in addition to those found based on the MD simulations, including K49, A83, K118, I146, and L185 (see Table S4). This finding further supports the importance of extensive MD/aMD simulations to the study of Tm-F-actin interactions.

Conclusion

By performing total 440-ns MD/aMD simulations of explicitly solvated Tm in the absence or presence of F-actin, we successfully captured key dynamic features of Tm observed by x-ray crystallography studies but not by previous, less extensive and/or implicit-solvent-based MD simulations (25–28,63) and normal mode analysis (63). Our finding of good correlation between key destabilizing regions of Tm (including six Ala clusters) and regions with high local flexibility has given strong support to the proposal that these regions are involved in the Tm flexibility that is critical for Tm function. Thanks to the enhanced conformational sampling by aMD, we observed variable fluctuations of Tm from the closed position toward the open position on the F-actin surface and uncovered new potential interactions between Tm and F-actin that will make good targets for future mutational studies.

This study validates the MD-based approach to the investigation of Tm flexibility and the dynamic interactions between Tm and F-actin. In the future, we will use this approach to investigate how specific Tm mutations perturb Tm dynamics and its interactions with F-actin, and to perform mutational and binding experiments to test the computational predictions.