A Bacterial Swimmer with Two Alternating Speeds of Propagation

Abstract

We recorded large data sets of swimming trajectories of the soil bacterium Pseudomonas putida. Like other prokaryotic swimmers, P. putida exhibits a motion pattern dominated by persistent runs that are interrupted by turning events. An in-depth analysis of their swimming trajectories revealed that the majority of the turning events is characterized by an angle of ϕ₁ = 180° (reversals). To a lesser extent, turning angles of ϕ₂ = 0° are also found. Remarkably, we observed that, upon a reversal, the swimming speed changes by a factor of two on average—a prominent feature of the motion pattern that, to our knowledge, has not been reported before. A theoretical model, based on the experimental values for the average run time and the rotational diffusion, recovers the mean-square displacement of P. putida if the two distinct swimming speeds are taken into account. Compared to a swimmer that moves with a constant intermediate speed, the mean-square displacement is strongly enhanced. We furthermore observed a negative dip in the directional autocorrelation at intermediate times, a feature that is only recovered in an extended model, where the nonexponential shape of the run-time distribution is taken into account.

Introduction

Among the fundamental modes of motility in biological systems, bacterial swimming is one of the most prominent examples (1). It is central to a wide range of biological functions, including processes as diverse as intestinal functions, the spreading of infections, or the early stages of biofilm formation (2). Swimming bacteria propel themselves with the help of flagella. A flagellum is composed of a helical filament that is connected via a hook to a rotary motor. The motor is embedded in the cell wall and drives the rotation of the filament (3). The swimming pattern and motion parameters depend on the number and distribution of the flagella across the cell body. In particular, we distinguish the polar arrangement of a single flagellum at one end of the cell (monotrichously flagellated) from a tuft of several flagella at one end of the cell (lophotrichous arrangement), and a uniform distribution of several flagella across the cell body (peritrichous arrangement) (4).

The most thoroughly studied prototypical example of a bacterial swimmer is the enteric bacterium Escherichia coli (5). The rod-shaped cells of ∼2 μm in length are uniformly covered with flagella that may extend several body lengths out into the surrounding. Rotation of the helical filaments drives the swimming motility of these cells (6,7). During counterclockwise rotation of the flagellar motors, the helical filaments form a coherent bundle that pushes the cell forward (8). If one or more motors change to clockwise rotation, the bundle flies apart and the persistent mode of swimming ends in a tumbling event (9). During tumbling, the cell body rapidly reorients. Once the motors resume counterclockwise rotation, the bundle is reassembled and a new swimming direction is randomly selected from the tumbling process with a preferred turning angle of ∼70°. This results in the typical run-and-tumble swimming pattern, where periods of persistent displacement and reorientation events alternate. In response to external chemical cues, E. coli cells are able to adapt their tumbling frequency to bias their direction of motion toward or away from a chemical source, a phenomenon known as chemotaxis (10).

In contrast, species that are decorated with a single polar flagellum are, in many cases, restricted to a much simpler run-and-reverse pattern of motion. Depending on the helicity of the filament and the sense of rotation of their flagellar motor, they either move in a pushing mode, where the flagellum is oriented backward and drives the cell body from behind, or in a pulling mode, where the flagellum is oriented in the swimming direction and pulls the cell body forward. By changing the rotary direction of their motor, monotrichously flagellated bacteria can switch from pushing to pulling mode and vice versa, thereby reversing their swimming direction by 180°. In this case, a reorientation to other swimming directions can be achieved only by deviations from the turning angle of a perfect reversal (180°) and by rotational diffusion during the straight runs. Numerous examples of run-and-reverse swimming can be found among the marine bacteria (11). For example, Pseudoalteromonas haloplanktis and Shewanella putrefaciens rely on this swimming pattern to achieve chemotactic tracking of individual moving algae (12,13).

Recent work has demonstrated that bacteria with a single polar flagellum can also exhibit more-complex swimming patterns. For example, the marine bacterium Vibrio alginolyticus may execute an additional flicking motion with its flagellum that results in a reorientation of its swimming direction by ∼90° (14). Instead of a simple run-and-reverse pattern, V. alginolyticus follows a cyclic three-step swimming protocol (run-reverse-flick): a forward run is followed by a reversal of the swimming direction. When switching back to forward motion, the flagellum flicks to select a new swimming direction. In the presence of chemoattractants, the run times of the swimming pattern are adapted so that V. alginolyticus can rapidly respond and localize chemoattractant sources in its vicinity (14,15).

In this work, we investigate the swimming pattern of the soil bacterium Pseudomonas putida. Like E. coli, P. putida carries several flagella. However, they are not evenly distributed over the cell body. Harwood et al. (16) reported that P. putida carries a tuft of up to seven flagella polarly arranged at one end of the cell body. They furthermore reported that the swimming pattern does not show the characteristic tumbling events known from E. coli, but is rather dominated by abrupt directional changes, including reversals of the swimming direction. Later, the turning angle and run-time distributions were also measured (17,18).

In this article, we confirm the bimodal turning angle distribution that has been reported by others, though with different weighting of the two preferred angles. Furthermore, we observe, to our knowledge for the first time, that the swimming speed of individual P. putida cells changes, on average, by a factor of two upon a reversal in their swimming direction. We present a simple theoretical model that incorporates the two distinct swimming speeds and correctly captures the mean-square displacement (MSD) of a population of P. putida cells. The model furthermore highlights that the two swimming speeds result in an increased MSD as compared to a population of cells that move with a constant intermediate speed. Finally, an analysis of the directional autocorrelation reveals a pronounced negative dip at times at ∼2 s. Only with an extended theoretical model that incorporates the nonexponential character of the run-time distribution can we explain this prominent feature in the directional autocorrelation function.

Materials and Methods

Bacterial cell culture

P. putida KT 2240 cells from –80°C frozen stock were grown to stationary density in an overnight shaking culture of Lysogeny broth medium (LB-Medium Lennox, 10 g/L Tryptone, 5 g/L NaCl, Yeast Extract 5 g/L, adjusted to pH = 7.0; AppliChem, Darmstadt, Germany). Approximately 50 μL of the dense cell suspension were dispersed on a solid agar dish (LB-Medium, 1.5% Agar-Agar; AppliChem). The dish was incubated for 24 h at 30°C. With a sterile inoculation loop, a single colony from the confluent cell layer was picked and streaked onto a new LB-dish, which was then again incubated for another 24 h.

Before an experiment, a 50-mL flask with N-Medium (5 g/L Peptone, 3 g/L meat extract, adjusted to pH = 7.0) was inoculated with a single loop pick from the stationary LB-dish and the suspension was grown overnight on a shaker at 30°C rotating with 300 rpm. Cells from the stationary shaking culture were diluted with N-Medium to an optical density of 0.01 (OD600 BioPhotometer; Eppendorf, Hamburg, Germany), corresponding to a number density of 10⁷ cells per mL.

Setup and imaging

To perform time-lapse recordings of swimming bacteria, the diluted cell suspension was filled into a transparent microchannel, measuring 1 mm in width, 17 mm in length, and 400 μm in height (μ-Slide VI 0.4; Ibidi, Martinsried, Germany). After 5 min, an initial population of isolated cells had attached to the glass bottom of the channel, and the channel was sealed at the sides with a Male Luer Lock Connector (natural polypropylene; Ibidi, Martinsried, Germany). The microchannel thus provides a hydrodynamically stable platform to monitor bacterial swimming motility free of the influence of convection and evaporation. During the next 6 h, the cells on the surface formed the cores of growing colonies. Cells were dividing with an approximate doubling time of 1 h. At the same time, the number of cells coexisting in the swimming phase also increased continuously. Approximately 7 h after filling, the swimming cells were populating the entire volume of the channel.

The cells had an average size of 4.65 ± 0.23 μm × 1.93 ± 0.04 μm. We determined the cell size based on 500 segmented images of a typical recording, each image showing an average number of ∼60 cells. From the contour of each cell in every image, we determined the length of the major and minor axes of an ellipse having the same moments of inertia as the cell with a built-in MATLAB program function (The MathWorks, Natick, MA). Averaging over all cells in all images, we found the values given above for the major and minor axes, respectively. We worked with cell densities of ∼100 cells per mm² in the field of view far away from the surface. On average, the distance between neighboring cells is thus ∼100 μm, i.e., two orders of magnitude larger than the cell size. In addition, we manually excluded from our analysis the rare cases, where cells seemed to interact with neighboring cells. Therefore, we can assume that hydrodynamic interactions between the cells do not play any role in our data and, consequently, no collective patterns of any kind emerge. The channel was mounted on the stage of an inverted IX-71 microscope (Olympus, Hamburg, Germany), equipped with an EoSens MC 1362/63 high-speed B/W camera (Mikrotron, München, Germany).

We recorded a sequence of phase-contrast images with a 20× UPLFLN-PH objective (Olympus, Hamburg, Germany) for 1 min at a rate of 25 frames/s in the center of the microchannel, >150 μm away from both the top and bottom interfaces. Eight-bit images with a resolution of 1280 × 1024 pixels were stored for further processing.

Segmentation and cell tracking

We used a custom-made MATLAB program (Ver. 8.0.0.783, R2012b; The MathWorks, Ismaning, Germany) to binarize the images and extract information about the cell positions in the microchannel.

First, a bandpass filter was applied to correct for high-frequency noise from the CMOS-sensor of the camera and for spatial modulations at frequencies lower than the average cell size that may arise due to uneven illumination. The filtered images were then converted into binary images using isodata thresholding (19). From the binary image sequence, a background image was constructed by calculating the average intensity over time for each image pixel. The resulting background image was subtracted from each image in the sequence to exclude nonmoving cells.

After applying a second isodata thresholding and a 3 × 3 binary median filter, the binarized images accurately captured the contour of all swimming cells in the field of view. The positions of all cells in each frame were determined by calculating the centroid (center of mass) of the corresponding connected region in the binary image. We then used a MATLAB version of the cell-tracking algorithm by Crocker and Grier (20) to link the centroid positions to form trajectories in time and space.

Our imaging method yields a quasi two-dimensional projection of the swimming pattern. However, the tracking depth of our setup is only d = ±7 μm. Furthermore, trajectories slower than 10 μm/s and shorter than 2 s were excluded from the analysis. This ensures that we restrict our analysis mostly to trajectories that lie in a narrow zone around the focal plane. If a cell swims along a straight trajectory for >2 s with the mean speed of our cell population and at a maximum grazing angle with the focal plane, the speed will be underestimated by at most 3%. Note, however, that the error may become larger in cases where there are additional turning events in the trajectory. Similarly, the measured values of the turning angles may also be affected by the finite tracking depth of our system. In particular, turning angles of ϕ < 90° will be underestimated whereas angles of ϕ > 90° will be overestimated if the runs before and after the turning event do not lie in a plane parallel to the focal plane of our imaging system. However, the qualitative shape of the turning angle distribution reported below is not influenced by these effects.

Analysis of the cell trajectories

We analyzed a data set of 814 trajectories in total. After visual inspection of the entire data set, 269 trajectories were discarded (floating dead cells, cells in the course of division, etc.). For further analysis, we smoothed the remaining 545 trajectories by running averages over three points. Turning events were identified by rapid changes in the cells’ speed and/or angular velocity, as presented in Fig. 1, A and B. In addition to using the algorithm presented below, we manually checked and identified the turn events in each trajectory.

Figure 1.

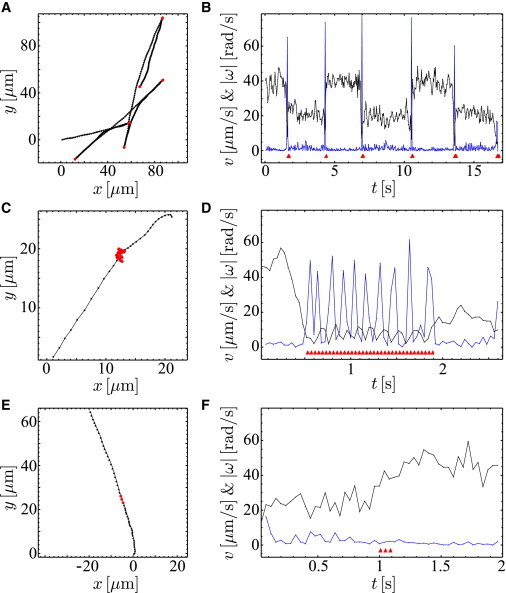
Swimming trajectories of P. putida with typical turning events. (A) Trajectory with several successive reversals (ϕ₁ = 180°, positions of the reversals marked in red). (C) Trajectory with a typical pausing event (ϕ₂ = 0°, position marked in red). (E) Trajectory with a typical speed change event (ϕ₂ = 0°, position marked in red). (B, D, and F) Speed (v, black) and absolute value of the angular velocity (|ω|, blue) over time for the trajectories (A, C, and E), respectively. (Red triangles) Time points of the corresponding events. To see this figure in color, go online.

Given the trajectory of a cell, r(t) = [x(t), y(t)], we defined its velocity by

$$\mathbf{v}\left(t\right)=\frac{\mathbf{r}\left(t\right)-\mathbf{r}\left(t-\Delta t\right)}{\Delta t},$$

where Δt = 0.04 s is the time resolution. After rewriting the velocity in polar coordinates as

$$\mathbf{v}\left(t\right)=v\left(t\right)\left[\text{cos}\phi \left(t\right),\text{sin}\phi \left(t\right)\right]$$

with speed v(t) = |v(t)|, we obtained the angular velocity as

$$\omega \left(t\right)=\frac{\phi \left(t\right)-\phi \left(t-\Delta t\right)}{\Delta t}.$$

Our algorithm to detect turns is a modified version of the algorithm presented in Masson et al. (21).

First, we tracked the speed v(t) of each trajectory and identified all local minima, which were located at times t_min. The two neighboring speed maxima around t_min at t_1,2 were used to determine the depth of the minimum

$$\Delta v=\text{max}\left[v\left(t_1\right)-v\left(t_{\text{min}}\right),v\left(t_2\right)-v\left(t_{\text{min}}\right)\right].$$

If Δv/v(t_min) > 3.5, the cell was said to be in the turning state for those times t around t_min, where v(t) ≤ v(t_min) + 0.2 Δv.

Second, our alternative criterion to identify turns was based on dramatic changes in the absolute value of the angular velocity |ω(t)|. We determined the times t_max, where |ω(t)| displayed local maxima and denoted the positions of the neighboring minima as t_1,2. We identified a turning state if the angular change |Δφ| during the time interval t₂–t₁ was significantly larger than expected, according to rotational diffusion of the velocity direction. More precisely, if

$$\left|\Delta \phi \right|>\gamma \sqrt{D_r\left(t_2-t_1\right)}$$

with γ = 7.3 and D_r = 0.1 rad² s⁻¹, we defined tumbling on the subinterval around t_max, where

$$\left|\left|\omega \left(t_{\text{max}}\right)\right|-\left|\omega \left(t\right)\right|\right|\le 0.9\Delta \omega$$

with

$$\Delta \omega =\text{max}\left[\left|\omega \left(t_{\text{max}}\right)\right|-\left|\omega \left(t_1\right)\right|,\left|\omega \left(t_{\text{max}}\right)\right|-\left|\omega \left(t_2\right)\right|\right].$$

Results

In this section, we first focus on our experimental results. We present a large data set of experimentally recorded swimming trajectories that we analyzed with respect to speed and changes in the direction of propagation of the bacteria. We then present a theoretical description that captures the main features of the swimming pattern of P. putida.

P. putida displays two distinct classes of turning events

P. putida exhibits a typical bacterial swimming pattern that consists of a sequence of straight runs interrupted by turning events. A closer look reveals that for most turns, the angle of propagation changes by ∼ϕ₁ = 180°, i.e., the cell reverses its direction of motion. The reversals are rapid events that take 0.13 ± 0.004 s on average. An example of a trajectory that displays several reversals can be seen in Fig. 1 A. In Fig. 1 B, the corresponding swimming speed and absolute value of the angular velocity are shown as a function of time. The sharp localized peaks in the angular velocity together with the rapid jumps in the swimming speed confirm that reversals are short and sudden events that interrupt the constant swimming motion of the persistent runs.

To a lesser extent, a second class of turning events can also be observed. In those cases, the direction of propagation before and after the event remains similar, resulting in a turning angle of ∼ϕ₂ = 0°. In contrast to the reversals, the phenomenology of the ϕ₂-events is more diverse. In particular, two types of ϕ₂-events can be distinguished.

• 1.We observe pausing events that interrupt the persistent swimming for a certain time. During this time, the body of the bacterium performs a jiggling motion before resuming the next run. In Fig. 1 C, an example of a trajectory with a pausing event can be seen. When following the swimming speed and angular velocity over time, we notice that the speed remains close to zero during the pausing, whereas the angular velocity shows a sequence of large repeated spikes that reflect the jiggling motion of the cell body (see Fig. 1 D).
• 2.We notice rapid speed changes in some of our trajectories. A representative case can be seen in Fig. 1 E. Here, the angular velocity remains low throughout the time series, while the swimming speed undergoes a clear change (see Fig. 1 F).

Movie S1, Movie S2, Movie S3, Movie S4, Movie S5, and Movie S6 showing examples of the different turning scenarios, among them the three example trajectories displayed in Fig. 1 can be found in the Supporting Material.

The turning angle distribution reflects the presence of two classes of turning events in the swimming trajectories of P. putida. As can be seen in Fig. 2, the distribution has a bimodal shape with a preferred turning angle at ϕ₁ = 180°. A second smaller peak is found at ϕ₂ = 0°. Even though the peak positions and heights differ, the bimodal turning angle distribution is in agreement with earlier results (17,18).

Figure 2.

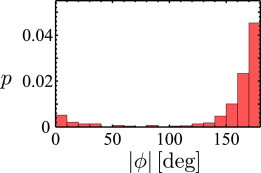
Turning angle distribution of a population of swimming P. putida cells. Maxima at ϕ₁ = 180° and ϕ₂ = 0° indicate the two classes of turning events. To see this figure in color, go online.

Upon a reversal of the swimming direction, the speed changes by a factor of two

A closer analysis of the trajectories reveals that in many cases, the swimming speeds before and after a reversal event are different. In particular, the time series shown in Fig. 1 B suggests that upon a reversal, the speed changes by a factor of two. We have systematically analyzed all reversal events and evaluated the difference between the swimming speed before the reversal, v_k, and after the reversal, v_k+1, normalized by the sum of both speeds, Q = (v_k+1 − v_k)/(v_k+1 + v_k). If v_k+1 and v_k differ by a factor of two, Q takes the value of ±1/3. In Fig. 3, we show distributions of Q for reversals (A) and ϕ₂-events (B) separately. In Fig. 3 A, the two maxima at Q = ±1/3 clearly indicate that in the case of a reversal event (ϕ₁ = 180°), the swimming speed indeed changes by a factor of two. The speed distribution of trajectories with reversal events is shown in Fig. 4 A. Here, the presence of two distinct swimming speeds is less obvious, indicating that the speed values are different from one cell to another. Nevertheless, a close match of the speed distribution can be obtained by the fitted sum of two Gaussians. The center values and widths of the two Gaussians yield estimates of the two swimming speeds (μ_i) and their standard deviations (σ_i) averaged over all reversal events,

$${\mu }_1=19\text{.}4\mu \text{m}{\text{s}}^{-1}{,\sigma }_1=8\text{.}7\mu \text{m}{\text{s}}^{-1},\text{and}$$

$${\mu }_2=38.3\mu \text{m}{\text{s}}^{-1},{\text{σ}}_2=9\text{.}5\mu \text{m}{\text{s}}^{-1}\left(\frac{{\mu }_2}{{\mu }_1}=1\text{.}97\right)\text{.}$$

For the ϕ₂-events, on the other hand, a different behavior is observed (see Fig. 3 B). Even though the Q values show a broad distribution also in this case, the maximal probability is centered at ∼Q = 0, i.e., there is no systematic difference in the swimming speeds before and after the ϕ₂-events.

Figure 3.

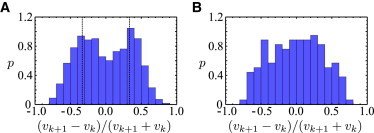
Difference between the swimming speeds before and after a turning event, normalized by the sum of the two swimming speeds (denoted by Q in the main text). (A) Distribution of this quantity for reversal events (ϕ₁ = 180°). (Dashed vertical lines) Positions of Q = ±1/3. The maxima at ±1/3 indicate that the swimming speeds before and after a reversal differ by a factor of two. (B) Distribution for turning events with ϕ₂ = 0°. On average, no systematic difference between the swimming speeds before and after the turning event can be observed. To see this figure in color, go online.

Figure 4.

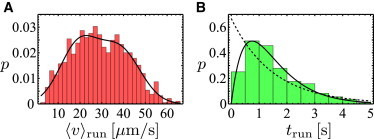
Analysis of trajectories with reversal events only (ϕ₁ = 180°). (A) Distribution of swimming speeds (average value for each run, red bars) fitted by a sum of two Gaussian distributions (solid line). The mean run speeds (μ_i) and standard deviations (σ_i) of the two fits are μ₁ = 19.4 μm s⁻¹, σ₁ = 8.7 μm s⁻¹; and μ₂ = 38.3 μm s⁻¹, σ₂ = 9.5 μm s⁻¹ (μ₂/μ₁ = 1.97), respectively. (B) Distribution of run times (green bars) with a mean run time of τ = 1.50 ± 0.07 s. Only runs between two reversal events are included. The exponential fit (dashed line) and the fit of a γ-distribution (solid line) are uniquely defined by the mean run time τ and contain no further fit parameter. To see this figure in color, go online.

Run times and swimming speeds are not correlated

Are the two alternating swimming speeds related to distinct run times?

In Fig. 4 B, the run-time distribution for trajectories with reversal events is shown (note that this is the majority of trajectories, ∼66%). The run-time distribution shows a maximum at ∼1 s and yields an average run time of 1.50 ± 0.07 s. The reversal events, for comparison, are much faster than the runs and take only 0.13 ± 0.004 s on average.

Let us now consider correlations between the swimming speeds and run times. In Fig. 5 A, a scatter plot is shown, where each point marks the run time that corresponds to a run with a given average speed. No correlation between the speed and the run time is observed, i.e., for each value of the swimming speed, we find the same distribution of run times. We have furthermore determined the run-time distributions separately for slow and fast runs. In both cases, similar distributions are found (data shown in the Supporting Material). We have also considered correlations between the durations of successive runs that are interrupted by a reversal event. The corresponding scatter plot is displayed in Fig. 5 B. Its shape can be explained by an overlay of two independent distributions of the type shown in Fig. 4 B. Thus, also in this case, no correlations are found.

Figure 5.

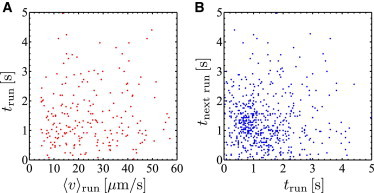
Run time and speed correlations for trajectories with reversal events only (ϕ₁ = 180°). (A) Scatter plot of the run time as a function of average swimming speed. (Dots) Runs between two reversal events. No correlation between the duration of a run and its average speed is observed. (B) Scatter plot of the run time as a function of the duration of the previous run. No correlations between the run times of successive runs are found. To see this figure in color, go online.

A simple random-walk model captures the mean-square displacement of P. putida

Based on the analysis of the swimming trajectories presented above, we first propose a simple random-walk model to capture the macroscopic spreading of a population of swimming P. putida cells. Here, it was our goal to obtain as much analytical insight as possible by including only the most prominent characteristics of the swimming pattern into the model. Because the swimming pattern is dominated by the reversal events, we concentrate our theoretical description on the subset of trajectories that contain reversal events only (ϕ₁ = 180°, 66% of the total number of trajectories). The following features are included in our model:

• 1.We approximate the run times as exponentially distributed with a mean run time τ, implying that runs are interrupted at a turning rate λ = τ⁻¹. According to the distribution of run times in Fig. 4 B, we set τ = 1.50 s. Because τ exceeds the duration of reversal events by one order of magnitude, our model neglects the duration of the reversals.
• 2.Similar to earlier work on the run-and-tumble motion of E. coli (22), we express the directional persistence between successive runs by the persistence parameter α = 〈cos ϕ〉, defined as the mean cosine of the turning angle ϕ. An ideal reversal would correspond to α = −1; for our data set, we obtain α = −0.95, which reflects the width of the peak at ϕ₁ = 180° in the turning angle distribution of Fig. 2.
• 3.Each turning event comes along with a change in the bacterium’s speed v(t). We assume that the speed alternates between two constant values v₁ and v₂ (recall Fig. 1 B for illustration). The values of v₁ and v₂ are estimated by the mean values μ_1,2 from the Gaussian fits presented in Fig. 4 A.
• 4.We include fluctuations in our model such that the persistent runs are not perfectly straight, due to rotational diffusion of the velocity direction. The origin of rotational diffusion is a combination of intrinsic fluctuations within the signaling network and the propulsion machinery of the cells on the one hand, and thermal noise in the fluid on the other hand. We denote the cell’s velocity direction by the unit vector e(t). During a run, its dynamics is governed by 〈e(t)⋅e(0)〉 = exp(−2D_rt), where D_r is the rotational diffusion constant (23,24). Using the directional autocorrelation function of the runs (see the Supporting Material), we obtain D_r = 0.023 rad² s⁻¹. This value is consistent with D_r = 0.062 rad² s⁻¹ for E. coli (25). The corresponding timescale, 1/(2D_r) = 21.7 s, during which directional correlations decay, clearly exceeds the duration of the runs.

Based on the properties described above, we can phrase a model that can be solved analytically (see the Supporting Material for details of the derivation).

We first determine the velocity autocorrelation function,

$$\langle \mathbf{v}\left(t\right)\cdot \mathbf{v}\left(0\right)\rangle =e^{-\left(\lambda +2D_r\right)t}\left(\frac{v_1^2+v_2^2}{2}\text{cosh}\left(\lambda \alpha t\right)+v_1{v}_2\text{sinh}\left(\lambda \alpha t\right)\right).$$ (1)

In particular, for α = 1 and D_r = 0, Eq. 1 yields the speed autocorrelation function 〈v(t)v(0)〉, which decreases monotonically from

$$\frac{v_1^2+v_2^2}{2}\text{for}t=0\text{to}{\left[\frac{\left(v_1+v_2\right)}{2}\right]}^2$$

for large times. Setting the speeds to unity, Eq. 1 corresponds to the directional autocorrelation function

$$\langle \mathbf{e}\left(t\right)\cdot \mathbf{e}\left(0\right)\rangle =\text{exp}\left(-\left[\lambda \left(1-\alpha \right)+2D_r\right]t\right),$$

in agreement with Lovely and Dahlquist (22). In the Supporting Material, we present the derivation of Eq. 1 and demonstrate how it is related to the MSD 〈[r(t) – r(0)]²〉 of the random walker. In Fig. 6, the experimental result for the MSD is shown (red dots) together with the analytical result (dashed blue line). At short times, the MSD displays a ballistic regime, whereas for larger times we approach the diffusive limit. Our simple model thus captures the MSD reasonably well, also with very good agreement at short times.

Figure 6.

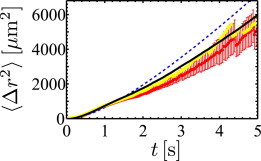
Mean-square displacement. The experimental data (red) is shown together with the results of a simple analytical model (dashed blue line), an improved model (black), and a full numerical simulation (yellow). To see this figure in color, go online.

The diffusive regime of the random walk is characterized by the diffusion coefficient

$$D={\text{lim}}_{t\to \infty }\frac{\langle {\left[\mathbf{r}\left(t\right)-\mathbf{r}\left(0\right)\right]}^2\rangle }{6t}$$

(in three dimensions). For D, we obtain

$$D=\frac{2D_r\left(v_1^2+v_2^2\right)+\lambda \left(v_1^2+v_2^2+2\alpha v_1{v}_2\right)}{6\left[2D_r+\lambda \left(1-\alpha \right)\right]\left[2D_r+\lambda \left(1+\alpha \right)\right]}.$$ (2)

For equal swimming speeds v, Eq. 2 reduces to the well-known result (22)

$$D=\frac{v^2}{3\left[2D_r+\lambda \left(1-\alpha \right)\right]}.$$

To illustrate the significance of the two alternating speeds v₁, v₂, we compare the diffusion coefficient from Eq. 2 to a random walker moving constantly at the mean speed $\overline{v}$ = (v₁ + v₂)/2 with diffusion constant $D_{\overline{v}}$. Using Eq. 2, we can demonstrate that D ≥ $D_{\overline{v}}$. This shows that the alternating speeds enhance the diffusion coefficient. Thus, bacteria undergoing run-and-reverse motion, with alternating velocities, spread faster then bacteria showing run-and-reverse behavior with a constant intermediate velocity. For the presented parameters of P. putida, we obtain D = 580 μm² s⁻¹ ≈ 2.8 × $D_{\overline{v}}$. Note that the experimental trajectories are too short in time to reliably estimate the diffusion coefficient D from the data. Instead, we can compare the prediction of the analytical model to an estimate of D based on the refined model presented below.

A nonexponential run-time distribution leads to negative values in the directional autocorrelation

To test the model description proposed above, we have analyzed directional autocorrelations in our data and compared the experimental results to the modeling prediction (see the Supporting Material for details). In Fig. 7, the autocorrelation functions of the direction (A), the speed (B), and the velocity of propagation (C) are shown. When comparing the experimental results (red data points) to the prediction of our simple random-walk model (blue dashed line), it becomes clear that the model does not recover one of the most prominent features of the experimental curves. The directional autocorrelation of the experimental trajectories becomes negative for intermediate times at ∼2 s. This observation cannot be explained based on our simple random-walk model.

Figure 7.

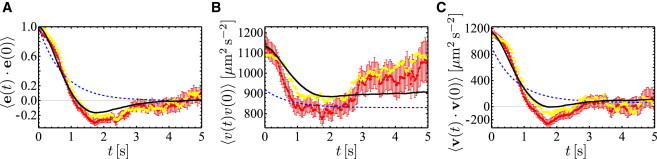
Autocorrelation functions of direction (A), speed (B), and velocity of propagation (C). In each panel, the experimental data (red) is shown together with the results of a simple analytical model (dashed blue line), an improved model (black), and a full numerical simulation (yellow). To see this figure in color, go online.

We therefore propose an extended version of our model that takes into account the nonexponential shape of the run-time distribution displayed in Fig. 4 B. We observe that the distribution p of run times t can be well described by a γ-distribution with a shape parameter of 2,

$$p\left(t\right)=\frac{t}{{\left(\tau /2\right)}^2}\text{exp}\left(-\frac{t}{\tau /2}\right),$$ (3)

where τ denotes the mean run time. It increases linearly for small times and features both the pronounced maximum and the exponential tail for large times. In our more detailed model, the distribution of the mean run speeds of cells is also taken into account. Based on the result of our fitting in Fig. 4 A, we now treat the speeds v_1,2 as Gaussian variables with means μ_1,2 and variances σ_1,2. For each new run event, the speed is drawn according to the corresponding Gaussian.

In this more realistic model, taking into account the peaked run-time distribution, we recover negative directional autocorrelations. However, they are not as pronounced as in the experimental data. Several additional aspects need to be taken into account to reduce this discrepancy (see the Supporting Material for a further discussion of these points).

The tracked trajectories usually start with a run, which in general began before the recording. In contrast to exponentially distributed run times, where the probability to tumble within a small time interval is time-independent, we now have to consider that the distribution of the first run times is different. In the Supporting Material, we calculate the corresponding renewal distribution of the first run time for the γ-distribution (Eq. 3) and show that the mean is given by 0.75τ. This result is consistent with the experimental data for which the average first run time is 1.28 s ≈ 0.85τ. Further inspection of the mean run speeds shows that for 62% of our trajectories, a cell starts with the larger speed v₂; it turns out that this fact needs to be implemented to satisfactorily explain the speed autocorrelation function. Finally, it is important to realize that our trajectories are relatively short in time with an average duration of 3.4 s. Hence, the majority of trajectories contains only a single reversal event. This also has an effect on the directional autocorrelation function.

We performed numerical simulations of our extended model, taking the above aspects into account. The results of these simulations show a remarkably better agreement with the experimental data than the simple model. For the MSD in Fig. 6 the result of the extended model is displayed in black and gives a clear improvement with respect to the simple model (dashed blue line). Long-time simulations up to 10⁴ s yield a diffusion coefficient of ∼D = 470 μm² s⁻¹ (compared to the value of D = 580 μm² s⁻¹ for the simple model). In addition, the autocorrelation functions in Fig. 7 are captured much closer by the extended model. In particular, it reproduces the negative dip of the directional autocorrelations, as well as the steep decrease in the speed autocorrelations after ∼1 s.

We also present numerical simulations in Figs. 6 and 7 (yellow curves), which are obtained by taking the exact sequences of run times and mean run speeds of each experimental trajectory. Note that details of speed fluctuations are not required; turning angles and the influence of rotational diffusion are only modeled according to our approach described above. We find that the MSD and all correlation functions are very well reproduced. This is a further justification that the random-walk approach is appropriate to describe the motility pattern of P. putida. In particular, the shape of the directional autocorrelation function including the negative dip is also very well reproduced. As the simulation neglects speed fluctuations during the runs, we observe that the initial value of the speed correlation function is slightly below the experimental value.

Discussion

We have investigated the swimming behavior of the soil bacterium P. putida. We observed a typical bacterial swimming pattern consisting of a sequence of straight runs that are interrupted by turning events. A closer analysis of the turning angles revealed a bimodal distribution with a preferred turning angle at ϕ₁ = 180° and a second smaller maximum at ϕ₂ = 0°. Thus, after having completed a run, a swimming P. putida cell will either reverse its direction or, less likely, continue to swim in the same direction. The bimodal character of the turning angle distribution of P. putida has already been reported earlier (17,18). Contrary to their result, we find the large angle to be the more likely one. In addition, the positions of the two peaks in the histogram differ. Note, however, that Davis et al. (18) have already shown that the peak positions and heights may vary between different populations and sensitively depend, for example, on the cell density of the culture. Given the differences in experimental conditions, we may thus conclude that our results are in qualitative agreement with earlier reports in the sense that P. putida displays a bimodal turning angle distribution with a peak at low and one at high values of the turning angle.

Run-and-reverse patterns have been reported for numerous monotrichously flagellated species such as Pseudoalteromonas haloplanktis or Shewanella putrefaciens (12,13). It is considered the typical swimming behavior of marine bacteria (11). In the case of monotrichously flagellated swimmers, the reversal is induced by a change in the rotational direction of the motor that propels the flagellum. Upon such a reversal, the mode of propagation of the bacterium changes from pushing to pulling.

For lophotrichously flagellated bacteria like P. putida, the flagellar dynamics during a reversal event have never been imaged directly. It has been conjectured that reversals in the swimming trajectories of P. putida may be caused by synchronous reversals of the flagellar motors (16). In this case, the entire flagellar bundle would switch from a pushing to a pulling mode, analogous to the single flagellum of monotrichously flagellated species. On the one hand, there are strong indications that a pulling flagellar bundle may be unstable and will experience jamming (8,26); on the other hand, to continuously remain in the pushing mode, the cell body would have to turn by 180° during a reversal. But even when imaging with a twofold increased frame rate (50 frames/s), we never observed the turning of a cell body upon a reversal. Moreover, a simple estimate shows that the force required to turn the cell body in a time below the resolution of our 50-Hz imaging exceeds the normal propulsive force of a bacterium by a factor of eight.

We performed additional recordings of cells swimming close to a solid/liquid interface to get further insight into the swimming mechanism (data shown in the Supporting Material). We observed that the cell density increased in the vicinity of the interface as compared to the bulk fluid. Furthermore, in agreement with earlier results from E. coli, the curvature of cell trajectories was increased at the solid/liquid interface (27). Cells preferentially turned to the right (negative angular velocity).

How can we reconcile these observations?

A possible scenario to stay in the pushing mode upon a reversal without turning the cell body would be that P. putida flips the direction of the flagellar filaments, so that they point backward even though the side of the cell where the motors are located is pointing to the front. Note that a similar flagellar mechanism has been proposed earlier for the reversal of bacterial locomotion at an obstacle (28).

This scenario is in agreement with the negative angular velocity observed for near-boundary swimming because a twist to the right would be expected both before and after the reversal. From the increased cell density near a boundary, on the other hand, no conclusions on the flagellar arrangement can be drawn. Although hydrodynamic interactions predict an increased near-wall density for cells moving in a pushing mode (29,30), the influence of such interactions on cell-surface scattering was shown to be negligible (31). The accumulation of cells near the interface could be instead attributed to collision effects, independent of the propulsion mode (32,33). To unambiguously clarify the flagellar dynamics during a reversal event, direct imaging of the flagella is required. Unfortunately, so far our fluorescence staining experiments have not been successful because the bacteria were rapidly damaged by the high phototoxicity of the fluorescence excitation light. The flagellar dynamics of P. putida during a reversal event thus remains an open question.

In addition to reversals with an angle of ϕ₁ = 180°, a second type of turning event was observed with an angular change of ϕ₂ = 0° between the successive runs.

What is the purpose of this swimming pattern?

The photosynthetic bacterium Rhodobacter sphaeroides is equipped with a single flagellum that can only rotate in one direction. Its trajectories consist of straight runs that are interrupted by pausing events with a duration of up to several seconds. In this case, apart from rotational diffusion during the runs, the cells have only limited possibilities to reorient and randomize their direction of movement. On the one hand, Brownian motion acting on the cell body during the intermittent pausings induces changes in the direction of motion (34); on the other hand, polymorphic transitions that are initiated when the motor resumes rotation may reorient the cell body (35). Here, we conjecture that the ϕ₂ events may serve a similar purpose. They provide an additional degree of freedom that P. putida may utilize to modulate its swimming behavior to affect, for example, the overall diffusion coefficient of its motion. In a recent analysis based on a tethering assay, the existence of pausings in the rotation of the flagellar motor of P. putida has been clearly confirmed (36).

Note also that additional turning strategies have been developed to enhance the efficiency of reorientation. For monotrichously flagellated species that can reverse the rotation of their flagellar motor, the spread in the angle of the reversal events is, in addition to a small degree of directional diffusion during the runs, the only feature by which many of them can enhance changes in their orientation that are required, e.g., for chemotactic responses. Recently, an additional type of turning event has been identified in the swimming pattern of Vibrio alginolyticus, a bacterium that also uses a single polar flagellum to drive its motion (14). After a reversal, the flagellum of V. alginolyticus performs a flick that randomly reorients its swimming direction. This allows V. alginolyticus to efficiently adapt its motion in response to chemotactic stimuli.

As a prominent feature of the swimming pattern of P. putida, we observed that, upon a reversal, the swimming speed changed, on average, by a factor of two. A difference in swimming speed between forward and backward motion has also been reported for V. alginolyticus (37) but was later attributed to near-wall effects (38). In our case, recordings are taken far away from the boundaries of the chamber, so that wall effects can be excluded. However, whereas the motion of V. alginolyticus is driven by a single polar flagellum, P. putida is decorated with a tuft of several flagella at one end of the cell. If indeed a reversal marks a flipping of the orientation of the flagellar filaments, different propulsion efficiencies and drag coefficients may be the reason for the different speeds observed. What sets the value of the factor between the two swimming speeds and how it depends on the environmental conditions remains to be explored in future studies. Note that we did not observe correlations between the run time and the mean run speed. This is consistent with recent results by others showing that the rotary motor of P. putida cells spends similar fractions of time in the modes of clockwise and counterclockwise rotation (36).

We have proposed a theoretical description that includes the alternating swimming speeds. To our knowledge, it is the first time that alternating speeds are incorporated into a model of this kind. Our approach clearly shows the minimal requirements to account for the different features observed in our data. In its simplest, analytically accessible version, including exponentially distributed run times, the persistence parameter α, rotational diffusion, and the two alternating swimming speeds, our model yields an accurate approximation of the MSD, i.e., the macroscopic spreading of a population of P. putida cells. The directional autocorrelation function, however, can be only recovered in an extended version of the model. In particular, the nonexponential shape of the run-time distribution has to be included into the model to capture the experimentally observed negative minimum in the directional autocorrelation. Moreover, our model highlights that the two alternating speeds result in an increased diffusion constant as compared to a bacterium that swims with a constant intermediate speed. Thus, this feature allows the bacterium to explore its environment more efficiently, without an increased energetic cost.