Measuring Actin Flow in 3D Cell Protrusions

Abstract

Actin dynamics is important in determining cell shape, tension, and migration. Methods such as fluorescent speckle microscopy and spatial temporal image correlation spectroscopy have been used to capture high-resolution actin turnover dynamics within cells in two dimensions. However, these methods are not directly applicable in 3D due to lower resolution and poor contrast. Here, we propose to capture actin flow in 3D with high spatial-temporal resolution by combining nanoscale precise imaging by rapid beam oscillation and fluctuation spectroscopy techniques. To measure the actin flow along cell protrusions in cell expressing actin-eGFP cultured in a type I collagen matrix, the laser was orbited around the protrusion and its trajectory was modulated in a clover-shaped pattern perpendicularly to the protrusion. Orbits were also alternated at two positions closely spaced along the protrusion axis. The pair cross-correlation function was applied to the fluorescence fluctuation from these two positions to capture the flow of actin. Measurements done on nonmoving cellular protrusion tips showed no pair-correlation at two orbital positions indicating a lack of flow of F-actin bundles. However, in some protrusions, the pair-correlation approach revealed directional flow of F-actin bundles near the protrusion surface with flow rates in the range of ∼1 μm/min, comparable to results in two dimensions using fluorescent speckle microscopy. Furthermore, we found that the actin flow rate is related to the distance to the protrusion tip. We also observed collagen deformation by concomitantly detecting collagen fibers with reflectance detection during these actin motions. The implementation of the nanoscale precise imaging by rapid beam oscillation method with a cloverleaf-shaped trajectory in conjunction with the pair cross-correlation function method provides a quantitative way of capturing dynamic flows and organization of proteins during cell migration in 3D in conditions of poor contrast.

Introduction

Cells are intricately connected to the external environment through the cytoskeleton. A multitude of parameters are involved in the regulation of the actin cytoskeleton dynamics to achieve spatially organized structures. These actin structures not only connect the cell physically to the external environment, but they also generate forces that drive various motile activities of cells including cell migration (1). When cells are cultured on a two-dimensional (2D) stiff surface, branched actin networks often form in the lamellipodia and are described as broad, thin protrusions extending at the front of a cell (2). The F-actin retrograde flow, which is driven by F-actin polymerization in the lamellipodia and myosin II activity in the lamella and cell center (3), has been shown to correlate with traction force that facilitates cell migration in 2D (4). The mechanical behavior of the F-actin cytoskeleton network in living cells and the molecular scale mechanisms underlying such dynamic patterns are burgeoning research topics.

The quest for understanding actin flow dynamics has been pursued in different cellular organizations, including neuronal growth cone (5), filopodium tips (6), and dendritic spines (7). In addition to the diligent use of photoactivatable fluorophores to trace actin (6,8), a major technique to study actin flow dynamics in 2D is by total internal reflection fluorescence microscopy (TIRFM) combined with sophisticated image analysis methods such as fluorescent speckle microscopy (FSM) (9) and spatial temporal image correlation spectroscopy (STICS) (10,11). When imaging fluorescently labeled actin, TIRFM allows selective excitation within 100 nm above the culture dish surface, which avoids unwanted background fluorescence from the large contribution of G-actin and therefore increasing the contrast. By incorporating a low concentration of fluorescently labeled actin monomers into the F-actin network, FSM can trace the resulting random pattern of intensity maxima and minima by spatially correlating the positions of the labeled proteins over time. Although for FSM, while it is possible to use three-dimensional (3D) imaging methods such as spinning disk imaging, better contrast is obtained when FSM is used with TIRFM. Alternatively, STICS (11) can also be used to track molecular flows. STICS is based on image cross-correlation of fluorescence fluctuations among successive time series images. The temporal information comes from the comparison between frames at two different times, therefore the maximum time resolution that can be measured is limited by the frame rate (typically, milliseconds to seconds). STICS is limited also in the spatial scales to which it can be applied. Unlike FSM, however, it can detect directed movements even in the presence of high background, as long as intensity fluctuations can be discerned.

The knowledge of actin dynamics acquired from observations made in two dimensions is important to determine the basic mechanisms of actin dynamics ultimately responsible for cytoskeleton reorganization needed for cell movement. Nevertheless, recent studies showed that the dimensionality and mechanical aspect of the microenvironment play a crucial role in determining cell shape, motility, and division (12). When cells are cultured in a more physiologically relevant 3D matrix, the external force distribution is no longer homogeneous from the ventral side of the cell as in a 2D situation. Rather, cells are surrounded by soft and possibly spatially discrete matrix. The differences of external force amplitude and distribution result in distinct actin cytoskeleton organization in 3D, and may result in different F-actin dynamics (12).

Current methods used to image cells in 3D matrices do not provide information regarding spatial-temporal dynamics of proteins. For example, in conventional z-stack 3D imaging, either the voxel resolution or the time will have to be compromised, which prevents direct application of speckle analysis or STICS in 3D. The requirement of low background and a low level of fluorescence intensity (few molecules are labeled) also make difficult the implementation of FSM to 3D actin studies.

Here, we propose a method for measuring molecular flow in 3D with high spatial-temporal resolution based on the nanoscale precise imaging by rapid beam oscillation (nSPIRO) method (13) and pair cross-correlation function (pCF). In references (14–18) the basis for the orbital tracking and the pair correlation approach are described. Originally nSPIRO was developed as a tool for resolving isolated fluorescent nanostructures in 3D (13). Briefly, in the nSPIRO method, the excitation laser beam orbits around the center of mass of the fluorescent object. If the particle moves, the intensity along the orbital trace will change in the direction of movement. The orbital tracking feedback mechanism (19) will recenter the orbit position back to the center of mass of the fluorescent particle. In the nSPIRO method, the distance of the surface of the object to the laser orbit is measured by modulating the orbit radius (13). Once the distance from the orbit is known with a precision of ∼10 nm (13), the shape of the object can be reconstructed. For this work, we adapted nSPIRO for tracking the position and the shape of cell protrusions using a clover pattern, which also provides information on the protrusion interior. In addition, by orbiting the excitation beam at two alternate positions along the cell protrusion, we are able to detect motion from one position to the other using the pair-correlation approach. Because intensities along each orbit are sampled at a given pixel dwell time (in the μs timescale), we could also detect molecular diffusion in the protrusions.

A crucial aspect of our approach is that we detect the motion of molecules and actin bundles using the correlation approach. Indeed, the fluorescence intensity at the protrusions due to actin-eGFP is relatively uniform so that there is not enough contrast to discern features. However, the spatial and temporal correlation analysis increases the contrast by separating structures on the basis of their temporal fluctuation behavior. In this work we show that this combined approach (nSPIRO and pCF) is able to capture actin flow as well as F-actin dynamics in the 3D context, and the location of F-actin bundle can be determined with high precision based on the correlation analysis. By recording simultaneously the collagen signal using confocal reflection microscopy, we also found that collagen fibers moved in concert with the actin-bundle flow.

Materials and methods

Cell culture preparation

The MDA-MB-231 cell line (American Type Culture Collection, HTB-26) was cultured in Dulbecco’s modified Eagle’s medium (DMEM) with high glucose (Sigma, St. Louis, MO) supplemented with 10% (v/v) fetal bovine serum (FBS) at 37 C in a 5% CO₂ humid incubator.

MDA-MB-231 cells were prepared to stably express actin-eGFP. First, the actin-eGFP fusion plasmid was inserted into the pQCXIP retroviral expression vector. Second, the retrovirus was prepared using the packaging cell line GP2-293. MDA-MB-231 cells were then infected with retrovirus for 24 h and selected with puromycin at 1 μg/ml for a few days to obtain the stable line. For transient transfection of Lifeact-eGFP (Ibidi, Verona, WI), MDA-MB-231 cells were transfected using Lipofectamine 2000 (Invitrogen, Carlsbad, CA), according to the manufacturer’s protocol.

Rat tail type I collagen with a stock concentration of 3.75 mg/ml was purchased from BD Biosciences (Franklin Lakes, NJ). Collagen was diluted with 10X phosphate buffered saline (PBS) and water to achieve a final concentration of 1X PBS and 2 mg/ml collagen. NaOH was added to neutralize collagen solution before mixing with cells to a pH = 7.4. Cells in serum-free DMEM were mixed with collagen solution. 250 μl cell-collagen mixture with 5 × 10⁴ cells/ml was added to 8-well Lab-Tek chambered coverglass with a surface area of 0.7 cm² per well (Thermo Scientific, Rochester, NY).

Collagen was polymerized at 20°C for 1 h and then at 37°C for 20 min. Full medium was applied after polymerization. Matrices with the added cells were kept at 37°C in a 5% CO₂ incubator. Images were taken under room temperature after 2 to 4 days of collagen polymerization.

Pharmacological treatment

MDA-MB-231 cells were cultured in type I collagen matrix for 2 days before pharmacological treatment. To stabilize F-actin, jasplakinolide (Molecular Probes) was used at 1 μM final concentration. The measurement was performed after 5 min incubation. The actin monomer sequestering drug latrunculin B (Molecular Probes) was also used at 1 μM final concentration, and the measurement was performed after 30 min of treatment. For myosin II inhibition, 50 μM (−)-blebbistatin (Sigma-Aldrich) was added. Measurements were done after incubation at 37°C for 10 min.

2-photon raster imaging

Second harmonic generation (SHG) of collagen fibers together with eGFP emission were collected by the LSM 710 (Carl Zeiss, Maple Grove, MN) equipped with a 40× 0.75 N.A. water immersion objective. The Mai-Tai laser (Newport, Irvine, CA) was set to an excitation wavelength of 900 nm. The collagen SHG emission signal was collected between 442 and 463 nm, and eGFP emission was collected in the range of 523–646 nm.

nSPIRO

The hardware and software for the tracking routine were implemented on an Olympus FV1000 confocal microscope (Olympus, Japan). The galvano scanner and z-Nano-drive stage (MCL, Madison, WI) were driven by the IOtech card (Measurement Computing, Norton, MA) to control the laser beam position. Cells were imaged and cell protrusions were tracked using a 40× 0.8 N.A. water immersion objective with a working distance of 3 mm. The LASOS Ar-Ion laser was set to an excitation wavelength at 488 nm (0.1% power) to excite eGFP. The signal was split using a 505 nm band pass dichroic to detect two channels: for eGFP emission and collagen reflection. The eGFP emission was collected between 505 and 605 nm. Reflection from collagen was detected using 465–495 nm filter. Data were acquired and processed by the SimFCS software (www.lfd.uci.edu, UCI, Irvine).

The laser orbital pattern was stored in the memory of the IOtech card, and the center offset of the orbital plane was updated according to the tracking mechanism described previously (13). The fluorescence intensity at 128 points along the orbit was collected, with pixel dwell time of 64 μs (8.2 ms/orbit). The pixel coordinate of the orbit is determined by the following equation

$$\text{x}=\left(\text{r}+\text{r}\times \text{sin}\left(4\theta \right)\right)\times \text{cos}\left(\theta \right)\text{,}$$ (1)

$$\text{z}=\left(\text{r}+\text{r}\times \text{sin}\left(4\theta \right)\right)\times \text{sin}\left(\theta \right)\text{,}$$ (2)

where r is the acquisition radius, and θ spans from 0 to 360°. Because the radius alternates four times during an orbital period, this results in a four-leaf clover shape (Fig. 1 A). This pattern penetrates the cell protrusion, providing information about the position of the cell protrusion surface as well as the protrusion core. The orbit radius was set at different values between 0.5 and 1.5 μm, depending on the diameter of the cell protrusion. The distance from the center of the orbit to the farthest pixel is two times the radius (Eqs. 1 and 2). For the data acquired with a clover shape orbital scanning across a cylinder as shown in Fig. 1 A, we represented the intensities along the orbits as a pseudoimage with the x-direction representing pixels along the orbit and y direction representing time. The expected pseudoimage will have four repeated patterns as illustrated in Fig. 1 B. The position of both cylinder core (blue) and periphery (green) can be discerned by the relative position to the background (black). If there is a bright object inside the cylinder but not at the cylinder center as indicated by the red spot in Fig. 1 E, it will give a characteristic signature in the pseudoimage, namely, at one (or more) column the intensity will be higher. The mapping of the columns on the actual protrusion gives the position and size of the region of the bright object (Fig. 1 F).

Figure 1.

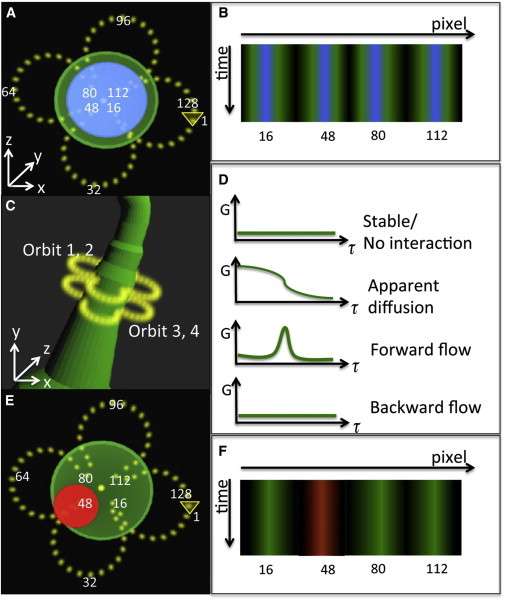
Experimental design. (A) A four-leaf clover-shaped laser orbit (yellow) across a cell protrusion. 128 pixels are collected along the orbit, starting at the arrow. (B) The data are shown as a 2D pseudoimage where x axis represents the pixel number along the orbit and the y axis is time. Using this method, structures within the protrusion (blue) and at the periphery (green) can be detected. The cell boundary is defined by the interface of black (the background) and green. (C) Four orbits are collected sequentially with no time delay between them. Orbit 1, 2 and orbit 3, 4 are done at the same position, respectively. The distance between orbit 1, 2 and orbit 3, 4 is fixed. The orbit center is adjusted by nSPIRO feedback to be at the center of the protrusion. The four-orbit pattern is continuously repeated for several minutes of acquisition. (D) The molecule dynamics between pixels can be discerned using correlation functions. Not only the diffusion can be detected by correlating points along one orbit, but also the directional flow can be measured by correlating points at two adjacent orbits. The peak of the correlation function indicates the time a fluorescent structure takes to travel from one point to another. (E) If the cell protrusion contains an object indicated in red, for example an F-actin bundle, the pseudoimage will show the object at a specific location along the orbit as shown in (F). To see this figure in color, go online.

pCF analysis

The intensity fluctuations collected along the orbit at two different planes as described previously was used to obtain information about the flow of molecules between these two positions. For this purpose, the pCF in Eq. 3 was implemented. In this function, F_a and F_b indicate the intensity in the upper and lower orbits, respectively. x is the pixel position, and $\tau$ is the correlation time

$$G_{ab}\left(x,\tau \right)=\frac{<F_a\left(x,t\right)F_b\left(x,t+\tau \right)>}{<F_a\left(x,t\right)><F_b\left(x,t\right)>}-1.$$ (3)

Data were acquired and analyzed using the SimFCS program developed at the Laboratory for Fluorescence Dynamics (available at http://www.lfd.uci.edu).

Experimental design

The nSPIRO orbital tracking method has been applied to study protein dynamics and distribution on cell surfaces (13). By modifying the laser path as a four-leaf clover shape as defined in Eqs. 1 and 2 (Fig. 1 A), the spatial information of both protrusion core and periphery can be obtained. We note that the symmetry with respect to the center of an orbit of the clover shape and of a circular orbit is the same so that the tracking algorithm (19), which is based on the symmetry of the intensity along the orbit, can be used without modifications for these two kinds of orbits.

As described in the Introduction, to measure flow along the cell protrusion, we introduced another variation of the nSPIRO technique, which involves measuring the fluorescence intensity at two positions at a given distance along the cell protrusion. Fig. 1 shows the conceptual experimental design. To quantify flow, we spatially and temporally correlate the fluorescence intensity fluctuations between pixels along the orbit at the upper position and pixels at the lower position (Fig. 1 C and Eq. 3). To increase the signal/noise ratio, and to compare correlations at the same position with correlations at two different positions, laser orbits with a period of 8.2 ms were repeated twice at the same position before moving to the second position 0.5 μm apart along the protrusion without a time delay between orbits. As a result, four orbits were done in each cycle of 32.8 ms. In Fig. 1 C, orbits are denoted as orbit 1, 2, 3, and 4, sequentially.

The spatiotemporal dynamics at the cylinder surface and interior can be extracted with the pCF analysis of the intensity traces. Different correlation patterns allow us to detect apparent diffusion as well as directional flow (Fig. 1 D). For example, by correlating the orbits from the same position (orbit 1 and orbit 2 from Fig. 1 C), the location of stable structures (slow apparent diffusion) can be determined by long, persistent correlations. By correlating the orbits from different positions (orbit 1 and orbit 3 from Fig. 1 C), the direction and speed of the flow of these relatively stable structures can be determined by the appearance of a peak at later time in the pCF.

Determination of the cell protrusion size

Based on the four-leaf clover pattern and the size of the point spread function (PSF), the cylinder shape can be determined by the intensity modulation along the orbit. We simulated a stationary cylinder with given surface density of fluorophores, and acquired the intensity following a modulated orbital pattern corresponding to the experimental cloverleaf pattern with added noise. Fig. 2, A and B, show the simulation results obtained using similar conditions of the real data acquisition (PSF size: 300 nm in the xy direction and 900 nm in the z direction; orbit radius: 0.55 μm and noise level between 0% and 20%). Fig. 2 A shows the power spectrum of the intensity profile after Fourier transformation. The amplitude of the fourth harmonic is prominent as expected given the fourfold symmetry of the clover pattern. The relationship between the amplitude of the modulation at the fourth harmonic and the radius of the simulated cylinder is shown in Fig. 2 B, which is shown to be largely independent upon the added noise. Thus, by measuring the average modulation amplitude of the intensity along the orbit, we can estimate the size of the cylinder. As shown by the simulations, for smaller cylinder radii (in the range of 0.3–0.4 μm) the error in determining the size is larger than for larger cylinder radii. Under our experimental conditions, the radius of the cylinder can be estimated with an error of ∼1% (i.e., ± 0.01 μm for a radius of 1 μm) providing nanometer resolution of the position of the cylinder surface with respect to the orbit.

Figure 2.

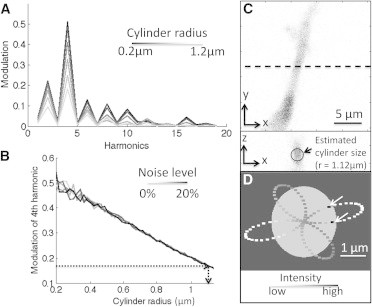
Fourth harmonic modulation of orbit intensity profile correlates with cylinder radius. (A) For a given radius of the four-clover patterned orbit (0.55 μm), a larger fluorescent cylinder radius results in smaller modulation amplitude. The modulation change is most significant at the fourth harmonic. (B) The relationship between the modulation amplitude at the fourth harmonic and the cylinder radius is largely independent on the noise (in the range 0–20%), especially at larger cylinder radius. The horizontal dotted line shows that the measured modulation of 0.17 corresponds to a cylinder radius of 1.12 μm. (C) Raster scan of a cell protrusion (top) and its cross-section scan through the dashed line (bottom). By performing an orbital scan using the clover pattern at a position along the cell protrusion we can obtain the amplitude of the fourth harmonic modulation and estimate the diameter of the cell protrusion at that location, as indicated by the circle at the bottom panel. (D) Determination of the position of coherent motion by the pair-correlation method in a protrusion that shows motion. The protrusion for this part D of the figure was larger (1.25 ± 0.01 μm) than the protrusion shown in D. The gray scale along the clover shape trajectory is based on the intensity profile, and the black dots (indicated by arrows) are the positions of detected actin flow by the pCF method.

Fig. 2 C shows the raster scan in the x-y plane of a cell protrusion (top) and the x-z scan (bottom) obtained at the height corresponding to the dotted line in the top panel. The x-z scan shows that the cell protrusion radius is ∼1 μm. A more precise value can be obtained by orbiting at this cross section with the four-leaf clover pattern and measuring the modulation of the fourth harmonic, which for this protrusion was 0.17± 0.01. Using the graph in Fig. 2 B, we can then estimate the cylinder size to be ∼1.12 ± 0.01 μm.

The F-actin bundle cannot be directly measured in the intensity profile because the cylinder is filled with actin monomers and the contrast is poor. To illustrate how we determine the position of actin bundles we use the pCF approach, which detects the actin bundles if they are moving. In the protrusion shown in Fig. 2 C we were unable to detect any motion of actin bundles; therefore, we show the reconstruction of another protrusion in Fig. 2 D, which was scanned with a larger orbit than that in Fig. 2 C. For this example, we repeated the simulations for the effective value of the orbit radius. Using the same procedure described for the determination of the radius of the protrusion in Fig. 2 C, we found that the protrusion of the cell shown in Fig. 2 D had a radius of 1.25 ± 0.01 μm. The gray circle in Fig. 2 D represents the protrusion size and the black dots (indicated by white arrows) are the positions at which we detected actin flow using the pair-correlation method.

Detection limits and technical considerations

There are certain limitations in the time and spatial resolution that can be obtained with the current setup. The time resolution is limited by 1), the laser orbit speed, 2), the distance of two orbit planes, and 3), the photobleaching rate. The orbit speed is determined by the speed of the piezo and z-Nano-drive stage. In our setup the minimum orbit period is ∼8 ms when the orbit has a component in the z-direction, otherwise for orbits in the x-y direction the minimum orbit period is 0.5 ms. The smallest distance of two orbit planes that allows efficient flow detection of very slow flows is limited by the size of PSF. In our study, we used a distance of 500 nm between two orbit planes to avoid large overlapping of the observation volume. Because we can detect movements on the order of 1/10 of this distance, the minimum flow rate that we can detect is in principle ∼50 nm/10 min acquisition time. Of course, in this case overall sample movement must be subtracted using fiducial markers. Although longer acquisitions can be done, sample bleaching and actin turnover during the measurement might hinder the detection of slower flow.

For faster dynamic measurement, considering the orbit period of 8.2 ms and 4 orbits per cycle, the diffusion detection limit using autocorrelation of points at the same orbit location is ∼0.1 μm²/s. However, by calculating intensity correlation among pixels along the scanning orbit, it is possible to obtain information about much faster diffusing molecules (∼100 μm²/s) (20).

For spatial resolutions there are two major considerations. For the determination of the surface position with respect to the orbit, the ultimate precision is determined by the number of photons collected per measurement time (per orbit). Our simulations show that if we can determine the modulation with a 1% error then the estimation of the distance of the surface from the orbit can be obtained with an error of ∼0.01 μm (Fig. 2 C). In the direction along the cylinder surface, the resolution is determined by the size of the PSF, which is ∼0.3 μm in our setup.

Results

Stable protrusions show internal stable structures but no internal flow is detected

First, we selected a relatively stable cell protrusion to perform the nSPIRO orbital tracking. Fig. 3 A shows the raster scan image of a typical MDA-MB-231 cell labeled with actin-eGFP (green) in a type I collagen matrix (red, reflection from collagen). Neither filament-like structures nor clear concentration inhomogeneity can be seen in the cell protrusions from raster scan images, which may be due to the high percentage of background actin monomers in the cytoplasm. There is also no distinct feature from intensity pseudoimages acquired by orbital scans (Fig. 4, A and C). However, by calculating the correlation of two orbits at the same position (orbit 1 and orbit 2, Fig. 4 A), correlations at a very long time (seconds) can be identified close to the cell periphery (Fig. 4 B), indicating the existence of a relatively stable actin structure. The correlation between orbits at different positions (orbit 1 and orbit 3, Fig. 4 C), on the other hand, was very weak (Fig. 4 D), indicating either fast diffusion or the absence of actin-eGFP flow across those two orbital planes.

Figure 3.

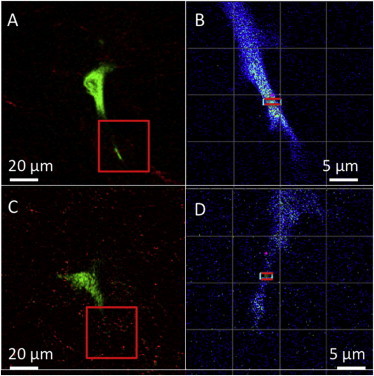
Raster scan images of stable cell protrusion and protrusion tip of MDA-MB-231 cells in 3D type I collagen matrix. (A) Reflection signal from collagen (red) and actin-eGFP signal (green) were collected simultaneously. The red box indicates the protrusion chosen for the orbital scanning. (B) Orbital scan was performed on the cell protrusion at the red bar locations. The orbit radius was 1.46 μm and the distance between orbits was 0.5 μm. (C) MDA-MB-231 cell with active cell protrusion tip. (D) A smaller radius (1 μm) was used for orbital tracking whereas the distance between the orbits remained at 0.5 μm. To see this figure in color, go online.

Figure 4.

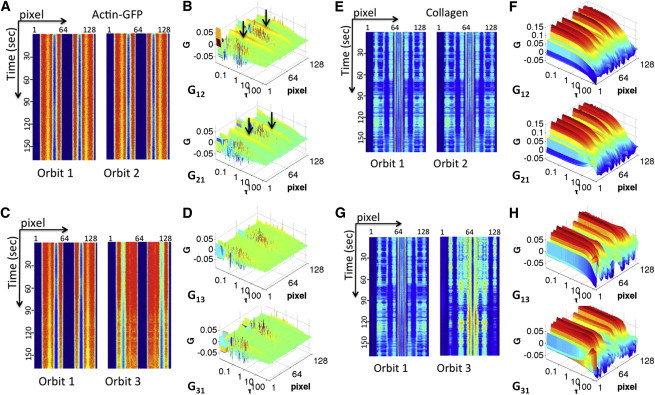
Pair-correlation analysis of a stable protrusion. (A) The intensity pseudoimages of actin-eGFP at a stable protrusion at orbit 1 and orbit 2 (same position). (B) Pair-correlation of orbit 1 to orbit 2 (G₁₂) and orbit 2 to orbit 1 (G₂₁). Both show long correlation at specific positions, indicated by arrows. (C) The intensity pseudoimages of actin-eGFP at a stable protrusion at orbit 1 and orbit 3 (0.5 μm apart). (D) Pair-correlation of orbit 1 to orbit 3 (G₁₃) and orbit 3 to orbit 1 (G₃₁). No significant correlation can be seen from either direction. (E) The intensity pseudoimages of collagen reflection signal at orbit 1 and orbit 2 (same position). (F) Pair-correlation of orbit 1 to orbit 2 (G₁₂) and orbit 2 to orbit 1 (G₂₁). Both show long correlation at specific positions that are distinct from the actin-eGFP channel. (G and H) The intensity pseudoimages of collagen reflection signal at orbit 1 and orbit 3 (0.5 μm apart), and their corresponding correlation results. The long consistent correlation pattern suggests the stable microenvironment. To see this figure in color, go online.

The reflection signal from collagen was also analyzed. As expected from a relatively stable structure, the collagen signal pair-correlation of either orbits from the same position or at different positions exhibit strong correlation at long time lags (Fig. 4, E–H), indicating a stable microenvironment near the cell protrusion. Notice the intensity difference of the actin-eGFP channel and reflection channel. The location where the reflection channel shows highest intensity corresponds to the low intensity region of the actin-eGFP channel. This suggests that the reflection signal from collagen is much stronger than reflections due to the cell body.

In 3D, the protrusion tip shows evidence of actin flow

We hypothesize that the protrusion tip in 3D may be the equivalent of cell front border in 2D in terms of relative cellular position and may exhibit higher actin flow speed. Fig. 3, C and D, shows the region chosen (close to the protrusion tip) for this measurement. Although there is no distinguishable actin structure from either raster scan or orbital scan (Fig. 5, A and C), by applying the correlation analysis, actin stable structures as well as dynamics can be readily seen (Fig. 5, B and D). The pair-correlation of orbits at the same position, again, showed the existence of stable structures (Fig. 5 B). For pair-correlation of orbits at different positions, a delayed correlation peak was observed when correlating orbit 1 to orbit 3, whereas correlation of orbit 3 to orbit 1 showed no correlation (Fig. 5 D). This result is consistent with the prediction of directional flow. Furthermore, the position of actin flow coincides with the position of stable structure (Fig. 5, B and D), which indicates that the stable structure, most likely an F-actin bundle, contributes to the flow. Interestingly, the collagen reflection signal also shows the evidence of flow (Fig. 5 H). This outcome implies that the movement of the cell protrusion tip due to actin-bundle flow also shifts the nearby collagen fibers. Because the time between each orbit and the distance between orbits are known, the flow rate of actin-eGFP can be calculated. Fig. 5 D shows that the peak of correlation occurs at around 20 s. Based on the distance between orbits (0.5 μm), the average actin flow rate was ∼1.5 μm/min. This result is in the range of actin flow rate observed in the 2D system using FSM (21). We also noticed that at the same position, the actin flow rate might change over time.

Figure 5.

Pair-correlation analysis of an active protrusion tip. (A) The intensity pseudoimage of actin-eGFP at the protrusion tip at orbit 1 and orbit 2 (same position). (B) Pair-correlation of orbit 1 to orbit 2 (G₁₂) and orbit 2 to orbit 1 (G₂₁). Similar to the analysis from a stable protrusion, both correlation functions show long correlation at specific positions, indicated by arrows. (C and D) However, when correlating the intensity of actin-eGFP at the protrusion tip at orbit 1 and orbit 3 (0.5 μm apart), the flow (and its direction) was captured, as can be seen from the prominent peak in G₁₃ (pointed by arrows). At the same location, G₃₁ shows no significant correlation in the opposite direction. (E–H) For the collagen channel, the correlation at orbits at the same position shows long, consistent correlation, whereas the correlation of orbits 0.5 μm apart shows the pattern of flow similar to actin-eGFP nearby (panel H), suggesting the actin flow also changes the collagen position around the protrusion. To see this figure in color, go online.

Using the approach illustrated in Figs. 4 and 5 we performed multiple measurements on the same cell protrusion at different positions as shown in Fig. 6 A. The flow speed decreases when the measurement was done further away from the cell protrusion tip. Fig. 6 B summarizes the actin flow speed versus the distance to the protrusion tip of 37 independent measurements, which lies between 0 and 1.5 μm/min. We further investigated whether the actin flow in cell protrusion is related to myosin II activity. The myosin II inhibitor blebbistatin was added to MDA-MB-231 cells for 10 min. With blebbistatin treatment, of all measurements within 10 μm of protrusion tip, 3 out of 12 measurements showed flow faster than 0.5 μm/min. In contrast, without blebbistatin treatment, we were able to detect actin flow in 25 out of 37 measurements (binomial test P value < 0.01).

Figure 6.

F-actin flow rate versus distance to the cell protrusion tip. (A) Two examples of actin flow profile along cell protrusions in 3D. In these two examples, the flow rate is slower close to the cell body. (B) Distance to protrusion tip versus actin flow rate for 37 independent measurements. The dashed line represents the detection limit. (C) With blebbistatin treatment, the percentage of measured actin flow with flow rate higher than 0.5 μm drops significantly compared to nontreated cells (P value < 0.01).

F-actin is close to the cell periphery

The spatial information from correlation analysis of pseudoimages was extracted. Interestingly, from Fig. 4 B and Fig. 5 B, the stable structures appeared to be close to the cell border, whereas the protrusion core has only weak correlation, most likely due to fast diffusing species (G-actin or actin oligomers). In addition, actin flow was also detected near the cell border. Taken together, the most plausible hypothesis is that in cell protrusions, F-actin is distributed close to the cell membrane, whereas G-actin occupies most of the space within the cell protrusion. The actin diffusion coefficient estimated by image correlation of pixels within an orbit is between 0.02 μm²/s and 0.8 μm²/s. This wide range may be partially due to colocalization of G-actin and actin polymers in different proportions.

As described previously in the experimental design section, we can reconstruct the protrusion cross section based on the intensity profile and the position of F-actin bundle using the pair-correlation map. As shown in Fig. 2 C, the position of F-actin is close to the protrusion border. Although it is difficult to discern the position of F-actin in 3D by a raster scan of actin-eGFP expressing cells (Fig. 7 A), we imaged MDA-MB-231 cells transfected with Lifeact-eGFP to confirm the position of F-actin in cell protrusions (Fig. 7 B). Lifeact is a short peptide that stains F-actin structures in eukaryotic cells and has been used to visualize F-actin organization in vivo (22). The affinity of Lifeact to F-actin is 8- to 30-fold higher than to G-actin (22). In line with the observation from correlation analysis, when cultured in 3D type I collagen matrix, the expression of Lifeact-eGFP in MDA-MB-231 cells shows high intensity along cell periphery, with low expression at the protrusion core.

Figure 7.

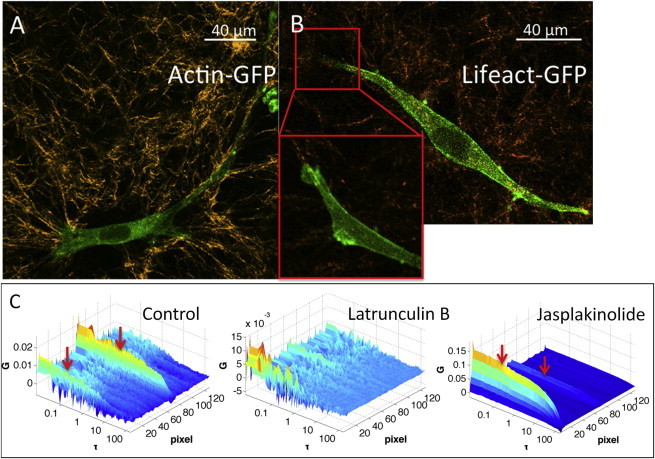
F-actin position in 3D verified by Lifeact and pharmacological treatment. (A) Actin-eGFP (green) showed relatively homogeneous distribution in a cell except low intensity at the nucleus. Collagen SHG is shown in yellow. (B) Lifeact-eGFP showed much higher intensity near the cell periphery, in line with our observation of F-actin position using the correlation approach. (C) Pair-correlation of orbit 1 to orbit 2 (G₁₂) of MDA-MB-231 without treatment (control), treated with latrunculin B, and treated with jasplakinolide. The red arrows indicate the position of long correlations corresponding to F-actin, which was abolished by the treatment with latrunculin B. Jasplakinolide, on the other hand, increased the long time correlations, indicating more stable F-actin. To see this figure in color, go online.

To verify that the long correlation time from two orbits at the same position reflects the F-actin stability, MDA-MB-231 cells were treated with either 1 μM jasplakinolide, which stabilizes F-actin (23), or 1 μM latrunculin B, which induces actin disassembling (24). As shown in Fig. 7 C, compare to the untreated cell (control), the long correlation time disappeared after latrunculin B treatment. On the contrary, with jasplakinolide treatment, F-actin stabilization is reflected by long-time stable correlation as indicated by red arrows.

Discussion

The organization of the actin cytoskeleton has a central role in transmitting force and in sensing the mechanical microenvironment of cells. In addition, the assembly and disassembly of F-actin bundles as well as the contraction of stress fibers are needed for cell locomotion. Due to the small diameter and high packing density of F-actin, it has been challenging to visualize actin dynamics, and the problem worsens in the 3D context. By combining correlation spectroscopy with the nSPIRO technique to acquire high spatial-temporal resolution images in 3D, we established a quantitative fluctuation-based assay to measure the actin flow in a cell protrusion in the 3D context.

We also explored a novel, to our knowledge, aspect of the pCF analysis. By carefully designing the acquisition pattern (four-leaf clover pattern) and choosing correlation between orbit pairs, a wide range of spatiotemporal fluctuations can be evaluated. Using the clover scan pattern, the timescale available for analysis can range from microseconds (pixel to pixel within an orbit) to several minutes (time correlation of two orbits at different locations). We showed by simulations that using the power spectrum of the intensity profile along the cloverleaf orbit pattern, specifically fourth harmonic in this study, we can localize the surface of cell protrusion with a precision in the order of 10 nm (Fig. 2 C). Because the detection of flow is based on correlation, it is possible to obtain spatial resolution of the moving filaments below the size of the PSF (17), similarly to FSM, which is after all a spatial correlation method.

We found that at cell protrusions, F-actin is present near the cell periphery and that the core of a cell protrusion is filled with relatively fast diffusive actin. Similar to this notion, it has been shown that F-actin appears close to the membrane in vitro (25). A recent study also reveals that in the 2D situation F-actin forms thin sheet-like but vertically separated cytoskeleton structure at the cell protrusion (26). This is consistent with our observation in 3D that the protrusion core is void of F-actin. Although the overall F-actin distribution may seem different in 2D and 3D due to the lack of dorsal-ventral polarization in 3D and the decreased matrix stiffness/surface attachment area that may alter the cell tension distribution, F-actin organization may still follow similar mechanisms, possibly through the regulation of actin binding proteins. For example, cofilin, which severs actin filaments, shows decreased binding affinity to F-actin under tension (27). Arp2/3 complex, which nucleates actin branched networks, has also been shown to preferentially facilitate branch formation on the convex face of the curved filament (28). These physical properties may contribute to the observation that in the 3D environment F-actin tends to organize along cell membranes where the tension is high (Fig. 6 B), whereas the sheet-like structure is more prominent in 2D, where tension distributes evenly on the ventral side of the cell.

The actin flow rate we measured in 3D (∼1.5 μm/min near the protrusion tip and below 0.5 μm/min toward cell body) is comparable to the actin flow rate reported in 2D, which ranges from 1.5 μm/min in the distal lamellipodium to 0.12 μm/min in the lamella (4). This rate is also similar to the actin flow rate in dendritic filopodia, which has an average speed of ∼1 μm/min (7). The similar kinetics suggests that the fundamental mechanisms such as actin assembly/disassembly are at the basis of the mechanism inducing the motion. We observed that myosin II inhibition slows down actin flow on cell protrusion in 3D, indicating that myosin II also plays a role in regulating actin dynamics in 3D. Whether this is through the inhibition of possible stress fiber contraction or disrupted actin network disassembly (29), however, requires further studies. We note that these results were based on a particular cell line in one type of extracellular matrix. The influence of cell type and the extracellular matrix on F-actin dynamics are the subjects for further scrutiny.

In this study, we used actin-eGFP as a marker to study actin dynamics and organization. Although actin-eGFP provides a direct measure of actin dynamics for both G-actin and F-actin, it has been shown that actin-eGFP transfected cells may exhibit altered cell spreading, cell adhesion strength, and cell deformation (30). A recent study on yeast also showed that actin with fluorescent tag hinders its interaction with formin, thus the incorporation of actin-eGFP into F-actin through formin-mediated assembly may be underrepresented (31). We noticed that in our measurement, F-actin is not homogeneously distributed around cell protrusions. Whether this is due to possible biased actin-eGFP incorporation or is related to the discrete collagen fiber distribution is unclear. To fully understand the actin dynamics and organization, thus, may require more than one probe to validate the observations. One possibility is to perform similar measurements with Lifeact-eGFP transfected cells, which display similar kinetics as nontransfected cells (32). Nevertheless, the indirect labeling by Lifeact may need extra consideration for quantitative study, and the information of G-actin will be lacking.

The lack of appropriate techniques has been the major reason of our poor understanding of cellular dynamics in 3D. Here, we propose an imaging method that allows multiple layers of information being revealed in a single data acquisition mode. Due to its flexibility and simplicity in terms of data acquisition, the method can be adapted to a wide variety of biological systems for high spatial-temporal resolution dynamic and structure detection. The major challenge lies in finding the appropriate acquisition parameters to cover the dynamic range of interest, as stated previously in Experimental design and Detection limits and technical considerations. In addition, the correlation analysis requires careful interpretation, especially with unconventional scanning patterns. The ability to collect data from multiple channels, as shown here (actin-eGFP and reflection from collagen), enables the comparison of movements of multiple structures at the same position. By analyzing actin and collagen flows together, it is possible to have a 3D fine-scale matrix remodeling measurement around the cell. By expanding the current method to multiple orbits, a high spatial-temporal resolution of actin flow map can be achieved, which will be helpful in understanding the organization of actin cytoskeleton in the 3D environment and answer questions like cell protrusion formation and cell migration mechanism in 3D.