Effects of Parkinson’s disease on optimization and structure of variance in multi-finger tasks

Abstract

We explored the role of the basal ganglia in two components of multi-finger synergies by testing a group of patients with early-stage Parkinson’s disease and a group of healthy controls. Synergies were defined as co-varied adjustments of commands to individual fingers that reduced variance of the total force and moment of force. The framework of the uncontrolled manifold hypothesis was used to quantify such co-variation patterns, while average performance across repetitive trials (sharing patterns) was analyzed using the analytical inverse optimization (ANIO) approach. The subjects performed four-finger pressing tasks that involved the accurate production of combinations of the total force and total moment of force and also repetitive trials at two selected combinations of the total force and moment. The ANIO approach revealed significantly larger deviations of the experimental data planes from an optimal plane for the patients compared to the control subjects. The synergy indices computed for total force stabilization were significantly higher in the control subjects compared to the patients; this was not true for synergy indices computed for moment of force stabilization. The differences in the synergy indices were due to the larger amount of variance that affected total force in the patients, while the amount of variance that did not affect total force was comparable between the groups. We conclude that the basal ganglia play an important role in both components of synergies reflecting optimization of the sharing patterns and stability of performance with respect to functionally important variables.

Introduction

Parkinson’s disease (PD) is a brain disorder associated with a lack of dopamine production by the substantia nigra of the basal ganglia. Neural circuits involving the basal ganglia have been strongly implicated in motor coordination, primarily based on the profound deficits of motor function in patients with basal ganglia disorders (reviewed in Fahn and Jankovic 2007). The scheme based on distributed processing modules in the brain suggested by Houk (2005) considers the cortico-basal-thamalo-cortical circuit as one of the two main neural pathways involved in the coordination of natural movements (we do not address the other pathway involving trans-cerebellar loops in this paper).

At any level of description, the system for production of natural movements is redundant (Bernstein 1967). This means that its elements produce more variables (elemental variables) compared to the number of constraints associated with everyday tasks. Two approaches have been used to address the issue of motor redundancy. One of them is based on ideas of optimization: The central nervous system is assumed to facilitate patterns of elemental variables that minimize a particular cost function (reviewed in Prilutsky and Zatsiorsky 2002). The other approach is based on the principle of motor abundance (Gelfand and Latash 1998: Latash 2012), which assumes that families of solutions are facilitated that equally are capable of solving the task, and elemental variables are organized to produce co-varied adjustments that stabilize (reduce variance of) important performance variables. Such organizations have been addressed as synergies (Latash et al. 2007; Latash 2008). Although traditionally the two approaches have been considered separately, several groups have tried to combine the idea of abundance with ideas of optimal control (Todorov and Jordan 2002; Diedrichsen et al. 2010; Park et al. 2010).

Over the past years, we have used two methods to quantify changes in multi-finger coordination. One of the methods is associated with the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2007). This hypothesis assumes that the neural controller organizes a sub-space (which is the UCM) within the space of elemental variables corresponding to a desired value of an important performance variable and then limits variance (V_ORT) orthogonal to the UCM; relatively large amounts of variance (V_UCM > V_ORT) are allowed within the UCM. The relative difference between V_UCM and V_ORT may be used as a quantitative index of a synergy stabilizing the performance variable. The other method is called analytical inverse optimization (ANIO, Terekhov et al. 2010). It uses a particular computational method to discover a cost function based on experimental observations in a subject who produces naturally a broad range of task-related variables. Further, the cost function is used to compute solutions for the same set of tasks. The two solution sets, experimental and computed, are compared, and a metric of their closeness (D-angle) may be used to estimate how consistently the subject follows his or her own optimization principle (for more detail see Terekhov and Zatsiorsky 2010; Park et al. 2011).

Several studies have reported changes in motor coordination in PD (Bertram et al. 2005; Fradet et al. 2009; Brown and Almeida 2011; Park et al. 2012). In particular, a recent study of early-stage patients with PD indicated a significant drop in the index of multi-finger synergy stabilizing total force produced by the four fingers of the hand pressing in parallel (Park et al. 2012). These results were obtained while the patients were on their antiparkinsonian medications optimized by their movement disorder specialist, and their overall performance showed only minor differences from that of age-matched healthy controls. These findings stood in stark contrast to earlier results reported for multi-joint reaching movements performed by cortical stroke survivors (Reisman and Scholz 2003). In the latter study, the patients showed rather dramatic changes in the overall performance but the synergy index (the relative amounts of V_UCM and V_ORT in the total joint configuration variance) was similar between the ipsilesional (relatively spared) and contralesional (strongly affected) limbs. Taken together, these studies suggest that cortical structures may be crucial for defining overall patterns of performance, while synergies stabilizing those patterns depend more on proper functioning of subcortical structures. Consistent with this hypothesis, we found that patients with multisystem atrophy-cerebellar type, another movement disorder with primary subcortical (cerebellar) dysfunction, also display a significant drop in the index of multi-finger synergy (Park et al. 2013).

In this study, we applied the UCM-based analysis of synergies and ANIO to multi-finger force and moment-of-force production tasks in persons with PD. Based on our prior study (Park et al. 2012), our first hypothesis was that the patients with PD would show significantly smaller indices of multi-finger synergies computed with respect to both total force and total moment of force production. An earlier study showed large differences in synergies stabilizing the moment of force in older healthy persons and modest differences in force-stabilizing synergies (Olafsdottir et al. 2007). Thus, our second hypothesis was that PD would be associated with particularly profound changes in moment-stabilizing synergies. In the past, ANIO has shown significant changes in the measure of consistency in following an optimization principle with relatively mild changes in the state of the system for movement production with healthy aging (Park et al. 2011a) and fatigue (Park et al. 2011b). Thus, our third hypothesis was that patients with PD would show poor consistency in following an optimization principle discovered with ANIO.

Methods

Subjects

Eight patients with idiopathic Parkinson’s disease (PD; age: 64.25 ± 8.08 yr; 5 males) at Hoehn-Yahr (HY) stage I or II and eight age-matched control subjects (CS; age: 60.25 ± 10.18 yr; 3 males) participated in this study. The patients were selected randomly from a larger pool of participants of an ongoing clinical and neuroimaging study in which all PD subjects were diagnosed by movement disorders specialists. All participants had a history of a significant response to dopaminergic replacement treatment. PD subjects were tested while on antiparkinsonian medications optimized by their movement disorders specialist. None of subjects in the CS group had a history of neuropathies or traumas to their upper extremities. The study protocol followed the Helsinki principles, and was reviewed and approved by the Pennsylvania State University-Hershey Medical Center Institutional Review Board. Written informed consent was obtained from all subjects.

Equipment

Four piezoelectric force sensors (Model 208A03, PCB Piezotronics Inc., Depew, NY, USA) were used to measure vertical forces (normal to the surface of the sensors) by individual fingers. The sensors were placed into a customized flat panel (140 × 90 × 5 mm), and the top of each sensor was covered with sandpaper (300-grit) in order to increase the friction. The position of each sensor in the forward-backward direction was adjusted according to the hand anatomy of individual subject. The distance between adjacent sensors was 3.0 cm in the medio-lateral direction. The four force signals were digitized at 200 Hz with a 16-bit resolution (PCI-6225, National Instrument, Austin, TX) with a customized LabVIEW program (LabVIEW 8.5, National Instrument, Austin, TX). Matlab (Matlab 7.4.0, Mathworks, Inc) programs were written for data processing and analysis.

Experimental procedures

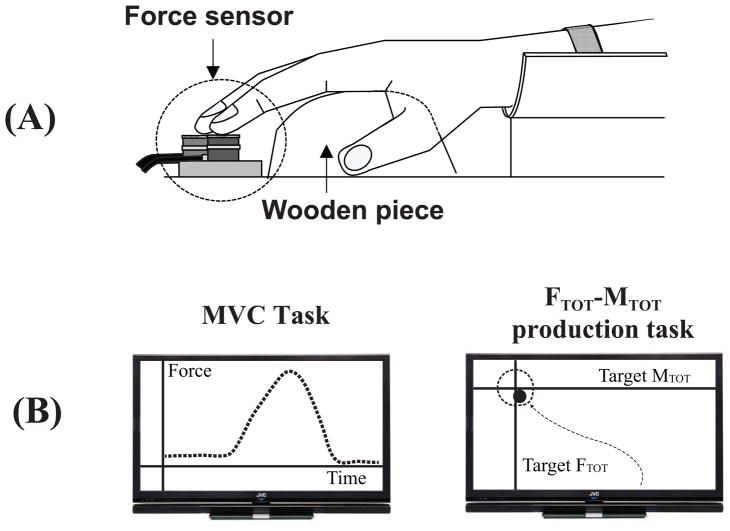
Before the experiments, subjects had a 10–20 min orientation session. During the session, the subjects performed enough practice trials to become familiar with the experimental setup and to ensure that they were able to perform the tasks. The subjects were tested while sitting in a chair; the forearm and wrist were held stationary with a wrist-forearm brace and Velcro straps on the table. The subjects placed the fingertips on the centers of corresponding sensors and were instructed to keep the fingertips on the sensors at all times (Fig. 1A). A wooden piece was placed under the palm to ensure the consistent configuration of the hand and fingers during the finger force measurement. The 19-inch computer screen was positioned 0.5 m in front of the subject; it was used to set tasks and provide real-time feedback. The experiment consisted of maximal voluntary contraction (MVC) tasks and accurate total force (F_TOT) and moment (M_TOT) production tasks.

Figure 1.

A: The experimental setup. A wooden piece was placed underneath the subject’s right palm in order to avoid changes in the configuration of the hand and fingers. B: The feedback computer screens during the MVC task (left) and accurate total force (F_TOT) and total moment of force (M_TOT) production tasks (right). During each trial for the accurate F_TOT-M_TOT production tasks, the screen showed a target and a cursor with coordinates corresponding to the current F_TOT along the vertical axis and M_TOT along the horizontal axis.

The maximal voluntary contraction (MVC) forces of all four finger together (MVC_IMRL) and the index finger alone (MVC_I) were measured in order to scale the task space in the {F_TOT, M_TOT} production tasks according to the individual subject’s finger force strength. For each MVC task, each subject performed three consecutive attempts (with 1-min rest intervals), and the highest values of MVC_IMRL and MVC_I over three attempts were selected. During these trials, feedback on the total force of the instructed finger(s) was provided, and the subject was encouraged to press as strongly as possible at any time within the 10-s time window.

For the accurate force-moment production tasks, the subjects were instructed to produce various combinations of {F_TOT, M_TOT} as accurately as possible. The levels of F_TOT included 5% to 45% of MVC_IMRL at 5% intervals (nine levels). Since the panel with the force sensors was fixed to the table, there was no actual rotation of the hand and the panel. M_TOT was computed with respect to the center-point between the middle (M) and ring (R) finger sensors assuming lever arms d_I = −4.5 cm, d_M = −1.5 cm, d_R = 1.5 cm, d_L = 4.5 cm (I – index, M-middle, R – ring, L - little). Note that we used M_TOT for a linear function of normal finger forces that only approximated the actual moment of force; in particular, we did not consider possible changes in the coordinates of finger force application and the contribution of shear forces. In other words, both F_TOT and M_TOT were computed from normal finger forces. As a result, the subjects were given two constraints on normal force components only. Their sum had to be a number (F_TOT) and their linear combination multiplied by some coefficients (nominal moment arms) had to be another number (M_TOT). The presence of two constraints is a necessary requirement for application of the ANIO method (Terekhov et al. 2010). The actual physical (mechanical) nature of constraints is irrelevant as long as they are kept constant over a range of values. We address the two constraints as “total force” and “total moment of force” only to link them to intuitively understandable mechanical variables.

There were 16 levels of M_TOT, from 4.0SU to 4.0PR at 0.5PR intervals; PR – pronation, SU – supination. 1PR was defined as the product of 7% of MVC_I by the lever arm of the index finger (d_I = −4.5 cm) (Park et al. 2010, 2011). Table 1 shows the 81 {F_TOT, M_TOT} combinations. The task space formed a triangle. This was done to avoid low F_TOT and high M_TOT combinations to avoid large performance errors. On the feedback screen (Fig. 1B), the vertical and horizontal axes represented F_TOT and M_TOT, respectively; each target {F_TOT, M_TOT} combination was shown as a dot. The subjects were asked to reach the target within 6 s and maintain the finger force values for at least 1–2 s. The cursor showed the computed F_TOT and M_TOT produced by the subjects.

Table 1.

The combinations of target total force (F_TOT) and moment of force (M_TOT)

FTOT (%MVC)	MTOT
					SU							PR
45	−4.0	−3.5	−3.0	−2.5	−2.0	−1.5	−1.0	−0.5	0.0	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0
40		−3.5	−3.0	−2.5	−2.0	−1.5	−1.0	−0.5	0.0	0.5	1.0	1.5	2.0	2.5	3.0	3.5
35			−3.0	−2.5	−2.0	−1.5	−1.0	−0.5	0.0	0.5	1.0	1.5	2.0	2.5	3.0
30				−2.5	−2.0	−1.5	−1.0	−0.5	0.0	0.5	1.0	1.5	2.0	2.5
25					−2.0	−1.5	−1.0	−0.5	0.0	0.5	1.0	1.5	2.0
20						−1.5	−1.0	−0.5	0.0	0.5	1.0	1.5
15							−1.0	−0.5	0.0	0.5	1.0
10								−0.5	0.0	0.5
5									0.0

The levels of target F_TOT and M_TOT were given as the percent of four fingers MVC (maximal voluntary contraction) and multiples of 1PR, respectively. 1PR was defined as the product of 7% index finger MVC by the lever arm of the index finger (4.5 cm). The {F_TOT; M_TOT} combinations shown in bold were performed 20 times each for the analysis of multi-finger synergies.

The subjects performed one trial for each {F_TOT; M_TOT} combination in a random order for a total of 81 trials. Using ANIO analysis requires that individual trials cover a broad range of constraint values. In our case, this meant covering a broad range of {F_TOT; M_TOT} combinations. It is assumed that a single cost function is applicable over this broad range. Using multiple trials is certainly preferred because it allows defining performance for each {F_TOT; M_TOT} combination more accurately. However, this would also prolong the time of the experimental session and could potentially lead to fatigue in the patients. Since covering a broad range of force-moment values is paramount for ANIO, we asked the subjects to perform each task only once for each {F_TOT; M_TOT} combination. We would also like to emphasize that the tasks were very simple, without time pressure, and the subjects felt comfortable performing them after a few (5–6) practice trials. So, we did not expect effects of practice to play a major role. Finger forces from these trials were used to compute a cost function with the ANIO approach. Two sets of {F_TOT; M_TOT} combinations, {30% of MVC_IMRL, 2PR} and {30% of MVC_IMRL, 2SU}, were performed 20 times each by each subject. These sets of trials were used to perform analysis of synergies within the UCM hypothesis framework. After each block of 5 trials, a 20-s break was given. The entire experiment for each subject lasted approximately 1 h.

Data Analysis

Initial data processing

The 4^th-order, 5-Hz Butterworth low-pass digital filter was applied to the original force data. The filtered finger force data from each trial were averaged over 1.5 s in the middle of the time period where steady-state values of individual finger forces were observed. The steady-state time period was identified by visual data inspection. For some of further analyses, the task space was divided into six areas, and average values of outcome variables were computed within each area. The six areas were identified for three levels of total force (Low: 10–20%; Mid: 25–35%; High: 40–45% of MVC) and two levels of total moment (PR and SU).

Task constraints

There were two constraints for each trial:

$$F_{\mathit{TOT}}=F_I+F_M+F_R+F_L=\alpha ·{\mathit{MVC}}_{\mathit{IMRL}},$$ (1)

where α indicates a given percentage of MVC (α = 5 to 45% at 5% interval).

$$M_{\mathit{TOT}}=d_I·F_I+d_M·F_M+d_R·F_R+d_L·F_L=\beta ·0.07·d_I·{\mathit{MVC}}_I=\beta ·1\text{PR}$$ (2)

where d stands for the lever arm; β = −4 to 4 at 0.5 intervals.

The ANIO approach

The ANIO requires knowledge of the surface on which the experimental results are mainly located (explained in Terekhov et al. 2010). During the first step, we performed principal component analysis (PCA) on the finger force data. The purpose of the PCA analysis was to check whether finger force data were indeed confined to a plane. PCA was performed on 81 observations for each subject, which covered over all {F_TOT, M_TOT} combinations. The Kaiser Criterion (Kaiser, 1960) was employed to extract the significant principal components (PCs), and the percent variance explained by the first two PCs was computed.

We assume non-sticking contact between the finger tips and force sensors throughout the experiment (i.e., soft-finger contact). Therefore, forces could only be positive. The task involved two constraints (F_TOT and M_TOT values) and four elemental variables (finger forces). Thus, the solutions of this undetermined system were expected to be confined to a two-dimensional hypersurface in the four-dimensional finger force space.

We followed the necessary steps in ANIO as described in detail in Terekhov et al. (2010). In particular, we checked whether the experimental data lied on a hyperplane (and not for instance on a curved hypersurface) and then defined the observed hyperplane mathematically as:

$$A·F^T=b$$ (3)

where A is a 2× 4 matrix composed of the transposed vectors of the two lesser principal components obtained from the PCA from the finger force data. Note that the data points showed deviations from the hyperplane due to the variability of performance. Also, the plane computed from Eq. 3 was affected by experimental errors.

We found that the desired objective function could be expressed as:

$$J=\frac{1}{2}\sum _i{k}_i{(F_i)}^2+\sum _i(w_i)F_i$$ (4)

where i = {I, M, R, and L}.

The values of the coefficients of the second-order terms k_i were determined by minimizing the dihedral angle between the two planes: the plane of optimal solutions and the plane of experimental observations. The values of the coefficients of the first-order terms w_i were found to correspond to a minimal vector length (w = (w_I, w_M, w_R, w_L)^T) bringing the theoretical and the experimental plane as close to each other as possible. All the coefficients were normalized by the square root of the sum of the second-order coefficients squared (i.e., by ( $\sqrt{(k_I^2+k_M^2+k_R^2+k_L^2)}$) for across-subjects comparisons.

If the coefficients of the second-order terms are positive, the function complies with the assumption of the objective function minimization. Further, the computed cost function was used to generate optimal finger forces for the same sets of {F_TOT, M_TOT} combinations as those used in the experiment. The computed data formed a plane in the four-dimensional finger force space. The angle between this plane of optimal solutions and the plane determined by the experimental observations (the dihedral angle, D-angle) was computed. This angle can be viewed as a metric of goodness of fit. It can also be interpreted as an index of consistency in following a single objective function: If the subjects were always following a single objective function over all {F_TOT; M_TOT} combinations, the angle would be very small; if the subjects used different objective functions over different areas of the {F_TOT; M_TOT} workspace, the angle would be expected to increase because the analysis would substitute many different functions with a single one.

Synergy analysis

The finger force data were analyzed within the framework of the UCM hypothesis (Scholz and Schöner 1999) using the sets of 20 trials at the same {F_TOT; M_TOT} combinations. Briefly, two variance components were computed across the 20 trials. One of the components (V_UCM) did not change the averaged across trials magnitude of the selected performance variable, while the other component (V_ORT) did (for details see Latash et al. 2001; Park et al. 2010). V_UCM and V_ORT were computed with respect to F_TOT, M_TOT, and {F_TOT, M_TOT} simultaneously as the performance variables. Note that in the analyses with respect to F_TOT and M_TOT, the dimensionality of the UCM is 3, while the dimensionality of the orthogonal space is 1. In the analyses with respect to {F_TOT, M_TOT}, the dimensionality of both the UCM and the orthogonal space is 2.

For each condition and at each point in time, variance components were computed using demeaned force data as detailed below: Changes (from the mean) in the force are given by the vector $df={\left[\begin{array}{cccc}{df}_I& {df}_M& {df}_R& {df}_L\end{array}\right]}^T$, where T is a sign of transpose. Changes in the value of the total force can be written as a function of df as follows:

$${dF}_{\mathit{TOT}}=J_F·df$$ (5A)

$${dM}_{\mathit{TOT}}=J_M·df$$ (5B)

Where $J_F=\left[\begin{array}{cccc}1& 1& 1& 1\end{array}\right]$ and $J_M=\left[\begin{array}{cccc}{d}_I& d_M& d_R& d_L\end{array}\right]$ are the Jacobians that link infinitesimal changes in finger forces with changes in F_TOT and M_TOT. Similarly, for the {F_TOT, M_TOT} related analysis, $J_{FM}=\left[\begin{array}{cccc}1& 1& 1& 1\\ d_I& d_M& d_R& d_L\end{array}\right]$. An orthogonal set of eigenvectors in force space, e_i defines the sub-space where finger force variations do not alter the total force/moment, i.e.

$$0=J_F·e_i;(\text{similarly},0=J_M·e_i;0=J_{FM}·e_i)$$ (6)

These eigenvectors spanned the null-space of the corresponding Jacobians. Then, the mean-free forces df were projected onto these directions and summed:

$$f_{\left|\right|}=\sum _{i=1}^{n-p}\left(e_i^T·\mathrm{d}f\right)e_i$$ (7)

where n = 4 is the number of degrees of freedom of the f vector, and p is the number of degrees of freedom of the performance variable (p = 1 for the F_TOT and M_TOT related analyses, and p = 2 for the{F_TOT, M_TOT} related analysis). The component orthogonal to the null space is given by:

$$f_{\perp }=\mathbf{d}f-f_{\left|\right|}$$ (8)

The amount of variance per DOF within the UCM is then given by:

$$V_{\mathit{UCM}}=\frac{\sum {\mid f_{\left|\right|}\mid }^2}{(n-p)N_{\mathit{trials}}}$$ (9)

This is the variance that does not affect the selected performance variable (F_TOT, M_TOT, or {F_TOT, M_TOT}). Similarly, the amount of variance per DOF orthogonal to the UCM is given by:

$$V_{\mathit{ORT}}=\frac{\sum {\mid f_{\perp }\mid }^2}{{pN}_{\mathit{trials}}}$$ (10)

This is the variance that affects that performance variable. Note that V_UCM and V_ORT are normalized per DOF in the corresponding spaces.

Further, an index reflecting the relative amounts of V_UCM and V_ORT was computed as:

$$\mathrm{\Delta }V=\frac{V_{\mathit{UCM}}-V_{\mathit{ORT}}}{V_{\mathit{TOT}}},$$ (11)

where V_TOT stands for the total finger force variance, and each variance index is computed per DOF in the corresponding spaces. The index was computed with respect to F_TOT (ΔV_F), M_TOT (ΔV_M), and {F_TOT, M_TOT} (ΔV_FM). Prior to statistical analysis (see later), this index was transformed using a Fisher z-transformation (ΔV_z) adapted to the boundaries of ΔV.

Statistics

The data are presented as means and standard errors. Mixed-design ANOVAs with repeated measure were used. For the sets of 81 combinations of {F_TOT, M_TOT}, we explored how the main outcome variables are affected by Group (2 levels: PD and CS) and by other factors such as Finger (4 levels: I, M, R, and L), Force (3 levels: Low, Mid, and High), and Moment (2 levels: PR and SU). The main outcome variables include the amount of variance explained by the first two PCs, the finger force loadings in the first two PCs, and the coefficients (k_i and w_i) in the cost function (J). For the sets of 20 repetitive trials for two {F_TOT, M_TOT} combinations, the following factors were used: Group, Moment, Finger, and Analysis (3 levels: F_TOT, M_TOT, {F_TOT, M_TOT}).

Significant effects were further explored with Mann-Whitney and Wilcoxon’s signed-rank tests with Bonferroni p-value adjustments for multiple comparisons. Prior to statistic comparisons, variables with computational boundaries were transformed using Fisher’s z-transformation adjusted to the boundaries of each variable. In addition, Mauchly’s sphericity test was used to confirm the assumptions of sphericity, and the Greenhouse-Geisser criterion was used to reduce the number of degrees-of-freedom if the sphericity assumption was violated. The level of significance was set at p < 0.05.

Results

Principal component analysis

The principal component analysis (PCA) was the first step in the application of the ANIO method. PCA was performed on the sets of 81 finger force combinations (see Methods) in each subject, which covered a broad range in the {F_TOT, M_TOT} task space. The percentage of the total variance explained by the first two PCs was significantly larger for the CS group (CS: mean 85.1%; range 92.1%–72.0%) as compared to the PD group (PD: mean 78.0%; range 84.6%–61.1%), which was confirmed by the Mann-Whitney tests (p < 0.05).

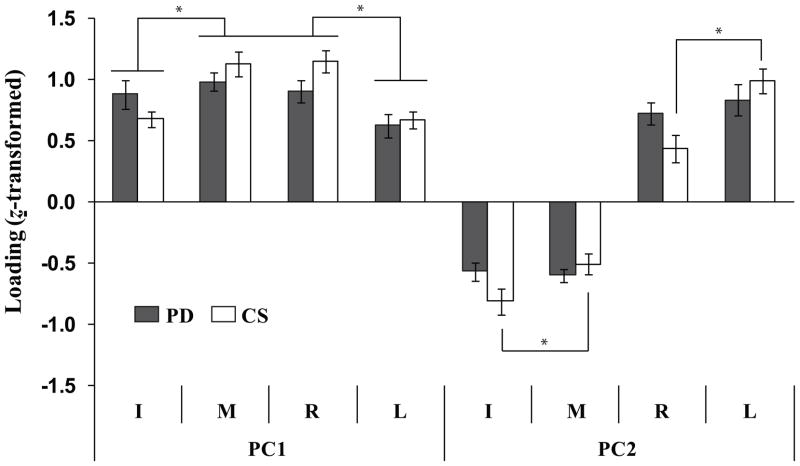
The loadings of all four finger forces in PC1 were positive, while the loadings for the M and R finger forces were larger than those for the I and L fingers for both groups (Fig. 2). In PC2, both groups showed negative loadings for the I and M finger forces and positive loadings for the R and L finger forces. For the CS group only, the absolute magnitudes of loadings of the lateral finger forces (I and L finger forces) were larger than those of the central finger forces (M and R finger forces). These findings were supported by two-way repeated measure ANOVAs on z-transformed absolute magnitudes of the PC loadings with factors Finger (4 levels: I, M, R, and L) and Group (2 levels: PD and CS). The main effect of Finger was significant on both PC1 and PC2 loadings (F_[3,42] = 10.84, p < 0.001 for PC1; F_[3,42] = 7.59, p < 0.01 for PC2). The Group × Finger interaction was significant on PC2 loadings (F_[3,42] = 4.04, p < 0.05), which reflected the fact that the absolute values of the loadings for the I and L finger forces were higher than the loadings for the M and R finger forces for the CS group only (p < 0.05). In addition, post-hoc comparisons confirmed that I, L < M, R in the PC 1 finger force loadings (p < 0.05).

Figure 2.

The loading factors of PC1 and PC2 for the PD (gray bars) and CS (white bars) groups. The average z-transformed PC loadings of individual finger forces across subjects in each group are presented with standard error bars. I, M, R, and L stand for the index, middle, ring and little finger, respectively. The asterisks show statistically significant differences at p < 0.05.

Results of the ANIO analysis

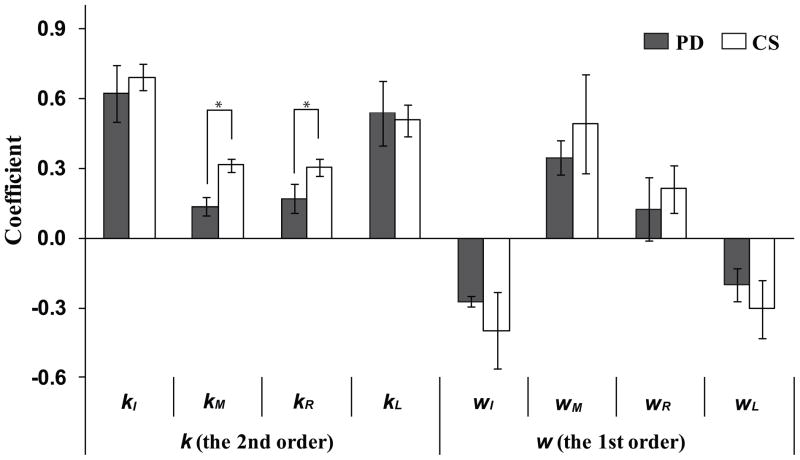
Based on the outcome of PCA, we assumed that the cost-function was quadratic with linear terms: $J=\frac{1}{2}{\displaystyle \sum _i}{k}_i·F_i^2+{\displaystyle \sum _i}{w}_i·F_i$ (see Methods and Terekhov et al. 2010). The coefficients at the quadratic (k_i) and linear terms (w_i) were computed to provide the best fit for the experimental data for each subject separately. The k_i coefficients were positive for all subjects. This observation confirms the applicability of the ANIO approach (Terekhov et al. 2010; Terekhov and Zatsiorsky 2011).

Overall, the second-order coefficients (k_i) for the central finger forces (k_M and k_R) within the CS group were larger than those in the PD group (p < 0.05, Mann-Whitney tests), while k_I and k_L were larger than k_M and k_L (p < 0.05, Wilcoxon’s signed-ranks tests) for both groups (Fig. 3). There was no significant difference in the first-order coefficients between the CS and PD groups (Fig. 3). The coefficients at the linear term (w) for the lateral finger (w_I and w_L) forces were negative, while the linear coefficients of the central finger forces (w_M and w_R) were positive in both groups.

Figure 3.

The coefficients at the second-order (k) and first-order (w) terms of individual finger forces within the cost function (J) computed using the ANIO method for the PD (gray bars) and CS (white bars) groups. Values are averages and standard error across subjects. I, M, R, and L stand for the index, middle, ring and little finger, respectively. The asterisks show statistically significant differences between the PD and CS groups at p < 0.05.

The cost function J was further used to compute finger forces for the same range of tasks as those used in the experiment for each subject separately. The computed data formed a plane (the plane of optimal solutions) in the four-dimensional finger force space. The average angle between the plane of optimal solution and the plane of experimental observations (D-angle) in the CS group (4.43 ± 1.85°) was smaller than that in the PD group (10.72 ± 3.00°) (p < 0.05, Mann-Whitney test).

Analysis of variance structure

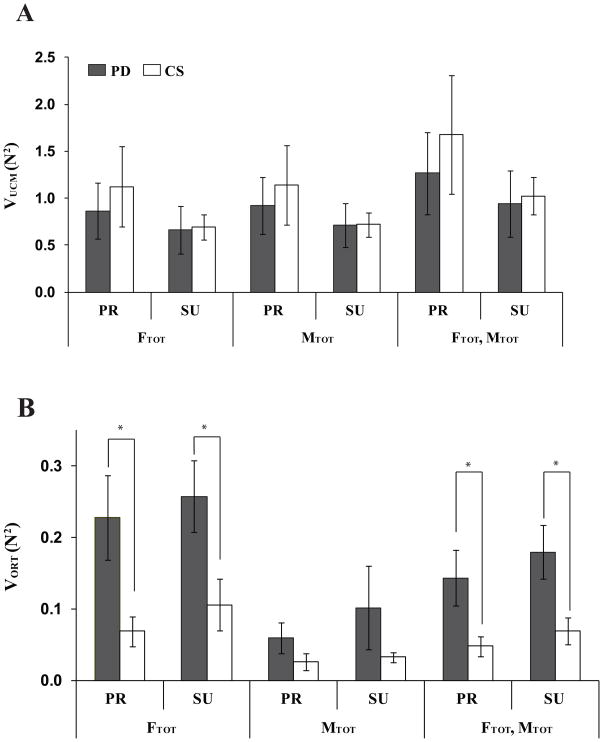
The framework of the UCM hypothesis was used to compute two components of finger force variance (V_UCM and V_ORT) with respect to stabilizing F_TOT, M_TOT, and their combinations, {F_TOT, M_TOT}, separately. Across all analyses and subjects, V_UCM > V_ORT (Fig. 4). This implies that most variance in the finger force space was compatible with average across trials values of the performance variables (F_TOT, M_TOT, or {F_TOT, M_TOT}) for both groups. In other words, there were multi-finger synergies stabilizing the performance variables.

Figure 4.

Two components of variance, A: V_UCM and B: V_ORT in the finger force space computed with respect to F_TOT, M_TOT, and {F_TOT; M_TOT} stabilizations for the PD (gray bars) and CS (white bars) groups. Variances were quantified per degree-of-freedom of the corresponding subspaces. The average values across subjects are presented with standard error bars. PR and SU stand for pronation and supination, respectively. The asterisks show statistically significant differences between the PD and CS groups at p < 0.05.

We performed analyses of the two variance components (V_UCM and V_ORT) and the synergy index (ΔV) to explore the effects of PD on stabilization of total force, total moment of force, and their combination. There was no significant difference in V_UCM magnitudes between the PD and CS groups, although, across all analyses, the average amount of V_UCM for CS was slightly larger than for PD (by about 14%, Fig. 4A). In contrast, V_ORT for the PD group was significantly larger than that for the CS group (by about 160%, Fig. 4B). The group difference in V_ORT was significant for the F_TOT and {F_TOT, M_TOT} analyses; it was smaller (under the significance level) for the M_TOT analysis. Taken together, these results mean that the relative amount of variance that affected performance variables was larger in the PD group.

There were also differences common for the two groups in the variance indices across the two conditions (different directions of the moment of force) and three analyses (with respect to F_TOT, M_TOT, and {F_TOT, M_TOT}). In particular, for both groups, V_UCM for {F_TOT, M_TOT} was larger than V_UCM computed for F_TOT and M_TOT separately. In addition, V_ORT during the SU tasks was larger than during the PR tasks. ANOVAs with factors Group (2 levels: PD and CS), Moment (2 levels: PR and SU), and Analysis (3 levels: F_TOT, M_TOT, and {F_TOT, M_TOT}) were performed separately on V_UCM and V_ORT. There was a main effect of Analysis for both V_UCM and V_ORT (F_[1.02,14.22] = 18.09, p < 0.001 for V_UCM; F_[1,14] = 16.71, p < 0.001 for V_ORT). The main effects of Group and Moment were significant only for V_ORT (Group: PD > CS, F_[1,14] = 6.49, p < 0.05; Moment: PR < SU, F_[1,14] = 6.68, p < 0.05). There was a significant two-way Group × Analysis interaction for V_ORT (F_[2,28] = 3.76, p < 0.05), which reflected the fact that the effect of Group on V_ORT (PD > CS) was significant only for the F_TOT and {F_TOT, M_TOT} analyses.

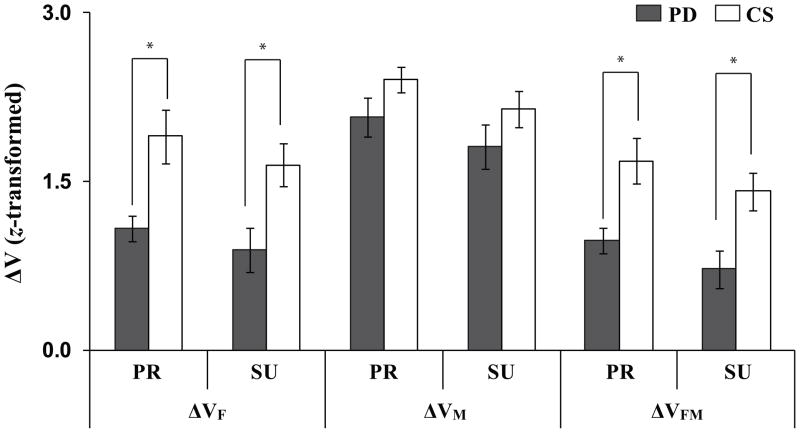
The different effects of PD on V_UCM and V_ORT were reflected in the group differences in the synergy index (ΔV). This index for the PD group was smaller than for the CS group, especially for the analyses of F_TOT (ΔV_F) and {F_TOT, M_TOT} (ΔV_FM); there was no significant difference between the groups in ΔV_M. In addition, ΔV differed between the three analyses (ΔV_M > ΔV_F > ΔV_FM) and between the two moment directions (PR tasks > SU tasks). These results are illustrated in Figure 5. A three-way repeated measures ANOVA with the factors Group (2 levels), Moment (2 levels), and Analysis (3 levels) was performed on z-transformed ΔV values. The main effects of Analysis (F_[1.02,14.31] = 57.21, p < 0.001), Moment (F_[1,14] = 15.41, p < 0.01), and Group (F_[1,14] = 8.63, p < 0.05) were observed with a significant Analysis × Group interaction (F_[2,28] = 3.53, p < 0.05). The pairwise comparisons confirmed that ΔV_M > ΔV_F > ΔV_FM (p < 0.001). The significant Analysis × Group interaction reflected that the PD group showed smaller ΔV with respect to F_TOT and {F_TOT, M_TOT} as compared to the CS group (Mann-Whitney tests, p < 0.01), but not with respect to M_TOT (ΔV_M).

Figure 5.

Z-transformed synergy indices, ΔV, computed with respect to F_TOT (ΔV_F), M_TOT (ΔV_M), and {F_TOT, M_TOT} stabilization (ΔV_FM) for the PD (gray bars) and CS (white bars) groups. Average values across subjects are presented with standard error bars. PR and SU stand for pronation and supination, respectively. The asterisks show statistically significant differences between the PD and CS groups at p < 0.05.

Discussion

The current study produced both expected and unexpected results. Our first hypothesis that patients would show significantly smaller indices of multi-finger synergies computed with respect to total force, total moment-of-force, and both combined was confirmed. These findings are a natural extension of an earlier study using accurate force production trials in PD patients (Park et al. 2012). The second hypothesis, however, was not supported by the observed data. PD subjects showed a much bigger difference than the control group in the indices of force-stabilizing synergies, while the differences for the moment-stabilizing synergies were small and under the significance level. The third hypothesis that PD subjects would show lower consistency in following an optimization principle compared to an age matched control group was supported. These and other observations lead to a series of implications on the role of the basal ganglia in the organization of motor synergies as discussed below.

Motor synergies: Definitions and mechanisms

Recently, the notion of synergy (including muscle synergy) has been used in two meanings. The more traditional approach defines synergies as correlated changes in a subset of elemental variables (for example, muscle activations, joint trajectories, digit forces, etc.) over the time course of an action or over similar actions with different characteristics (D’Avela et al. 2003; Ivanenko et al. 2004; Ting and Macpherson 2005). Within this definition, synergies have been identified and quantified using matrix factorization techniques such as factor analysis, independent component analysis, and non-negative matrix factorization (reviewed in Tresch et al. 2006). Several recent papers questioned the utility of the notion of muscle synergies defined in this way (Tresch and Jarc 2009; De Rugy et al. 2013).

A more recent, alternative definition has been developed based on the principle of abundance (Gelfand and Latash 1998; Latash 2012). According to this approach, synergies are defined in the space of elemental variables (finger forces in our study) as neural mechanisms that organize co-varied across repetitive trials changes in the elemental variables that stabilize (reduce variance of) potentially important performance variables (F_TOT, M_TOT, and {F_TOT, M_TOT}). This definition considers synergies as neural mechanisms with a specific purpose, i.e., to ensure the stability of action in the presence of secondary tasks that may involve the same elements and unexpected changes in the conditions (“perturbations”) (Scholz et al. 2000; Zhang et al. 2008; Mattos et al. 2011). In our opinion, this definition creates a fruitful framework for analysis of the neural control of natural movements and its outcomes, and thus it is more relevant to the functional changes associated with movement disorders.

Two aspects of synergies in the second definition typically are quantified, sharing and covariation. Sharing reflects the average involvement of elemental variables across multiple repetitions of a task. These patterns have been shown to be consistent across ranges of performance variables (Li et al. 1998; Danna-dos-Santos et al. 2008). The other aspect reflects co-variation patterns in the space of elemental variables seen over individual trials at the same task. Sharing patterns commonly have been viewed as reflecting an optimization principle, and we used the method of analytical inverse optimization (ANIO) to define cost functions for individual participants (Terekhov et al. 2010). The patterns of co-variation have been quantified using methods developed within the UCM hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2002, 2007). Our results show that both methods are sensitive to quantify changes in motor coordination (reflected in the indices of the two aspects of synergies) in early-stage PD. These methods go beyond detecting changes in general movement patterns that are commonly used for clinical diagnosis of PD.

Note that having large amounts of variance compatible with a value of a performance variable (V_UCM) leads to higher synergy indices but violates an optimization principle since by definition only one point within the UCM is optimal. As a result, there is an inherent trade-off between the two aspects, optimization and strong synergies (Park et al. 2010). One of the main results of our study shows that stronger synergies do not necessarily mean lower consistency in following an optimization principle; indeed, control subjects showed higher synergy indices and lower D-angle values. The dysfunction of the basal ganglia associated with PD had detrimental effects on both the consistency in following an optimization principle and the ability to stabilize performance by structuring the variance within the space of commands to fingers.

A drop in the synergy index may be associated with an increase in V_ORT, a decrease in V_UCM, or both. PD patients consistently showed unchanged values of V_UCM and increased V_ORT across the two tasks and three analyses. This is not a trivial result. If one assumes that the general level of variability within the central nervous system is increased in PD (Contreras-Vidal and Stelmach 1996), an increase in both V_ORT and V_UCM may be expected. It may be coincidental that the expected increase in V_UCM was nearly perfectly balanced by the impaired ability to unite fingers into synergies (cf. Park et al. 2012). An alternative interpretation is that having a certain amount of V_UCM may be by itself a self-imposed constraint, and V_ORT is adjusted to the total amount of variance.

Within the definition accepted in this study, synergies have been described as products of an optimal feedback control scheme, a feed-forward scheme, a scheme with central back-coupling loops, and a hierarchical scheme based on ideas of equilibrium-point control developed recently as the control with referent body configurations (Todorov and Jordan 2002; Goodman and Latash 2006; Latash et al. 2005; Martin et al. 2009; Latash 2010). The latter approach views a sequence of few-to-many mappings organized in a synergic way with the help of back-coupling loops (as in Latash et al. 2005). Within this scheme, relatively large variations in the elemental variables are allowed as long as the task-related performance variables remain relatively unchanged. At the lowest level of this hierarchy, the mechanism of the tonic stretch reflex unites motor units into a synergy stabilizing equilibrium state of the system “muscle plus its reflex feedback loops plus external force.” The results of our study suggest that the cortico-basal-thalamo-cortical circuit likely is involved in ensuring both consistent patterns of the hypothesized few-to-many mapping (reflected in the higher D-angle values) and defining proper values of the gains in the back-coupling loops.

The role of cortical vs. subcortical (cerebellar and basal ganglia) involvement in synergies

Traditionally, the neural mechanisms of synergies have been associated with cortical motor areas and the cerebellum. The hypothesis on the involvement of the cerebellum dates back to the classical studies by Felix Babinski (Smith 1993). More recently, studies on monkeys have suggested that signals from the dentate nuclei are more closely related to control of muscle synergies rather than prime movers of the explicitly required action (Thach et al. 1992; also see Rispal-Padel et al. 1981). A few studies have provided rather direct physiological evidence for a role of the cerebellum in coordinating a variety of multi-joint actions. In one of those studies, principal component analysis of the activity patterns of a large set of neurons within the dorsal spinocerebellar tract was performed during hindlimb motion simulating walking (Bosco and Poppele 2002). The two principal components that accounted for most of the variance of the neuronal activity were related not to individual joint movements but to the whole limb length and orientation changes during the leg movement cycle, which can be considered important performance variables for locomotion stabilized by co-varied joint rotations.

Studies of cortical neuronal populations also have revealed patterns of activity related to global performance variables such as the spatial trajectory of the effector’s endpoint or the force vector applied by an end-effector rather than to activations of specific muscles (Georgopoulos et al. 1982; Schwartz 1993; Coltz et al. 1999; Cisek and Kalaska 2005). Studies of the cortical control of the human hand have resulted in a hypothesis that has direct relevance to the topic of synergies (Schieber and Santello 2004). Marc Schieber synthesized these observations and suggested an idea of a cortical piano (Schieber 2001; Schieber and Rivlis 2007). This idea implies that individual cortical neurons are similar to piano keys, while functional movements involve “playing chords.” In other words, neurons may be united functionally in groups that are used flexibly to produce desired motor effects.

Note, however, that the mentioned studies used the notion of synergy loosely and did not quantify synergies within the principle of abundance. A study by Reisman and Scholz (2003) questioned the importance of the cortex for synergies. That study showed that whereas patterns of reaching movements by stroke survivors performed by the contralesional arm were significantly impaired, the structure of joint configuration variance was not different between movements performed by the ipsilesional (less impaired) and contralesional arms. The total amount of joint configuration variance was increased during reaching movements by the contralesional arm, but the relative amount of V_UCM was unchanged. These observations are in stark contrast to our findings in the studies of patients with early-stage PD (see also Park et al. 2012). The PD patients showed relatively mild changes in the general characteristics of performance, whereas the structure of variance was changed significantly. Changes in the indices of multi-finger synergies could even be significant in the apparently unaffected hands of PD patients (HY stage I; Park et al. 2012).

The changes in both aspects of synergies, optimization and structure of variance, observed in the current study may reflect either the importance of the basal ganglia for synergies or the involvement of other brain structure such as the cerebellum in PD. The basal ganglia have been implicated in uniting the postural and locomotor synergies (Mori 1987) and in the grasp-lift synergy (Forssberg et al. 1999), but in those studies synergies were defined in the traditional way as proportional changes within a set of elemental variables. Several recent brain-imaging studies have suggested cerebellar involvement in PD (Lewis et al. 2007, 2011; Yu et al. 2007; Wu et al. 2011). In particular, weakened striatum-cerebellar connections have been documented (Wu et al. 2011) possibly related to problems with action initiation. It is feasible that some of the changes in synergy characteristics observed in our study reflect changes involving both the basal ganglia and the cerebellum. This assumption is supported by a recent study of patients with multisystem atrophy–cerebellar type (Park et al. 2013) that has shown changes in multi-finger synergies qualitatively similar to those described in the current study. Whether effects of PD on synergies are due to the primary problem with the basal ganglia or secondary involvement of the cerebellum, our observations provide strong support for the crucial role of subcortical structures in multi-finger synergies that have traditionally been viewed as an example of a high-level cortical coordination.

Clinical Implications

PD is diagnosed clinically by the presence of resting tremor, rigidity, and bradykesia. It is known that more than 50–80% of dopaminergic neurons in the substantia nigra of the basal ganglia already are lost at the time of diagnosis using these criteria. Changes in motor coordination are not mentioned explicitly among the cardinal signs of PD. This study, together with our earlier observations on multi-finger coordination in PD patients, suggests that changes in multi-finger synergies may be an early, objective, reliably detectable sign of this disorder. This hypothesis is supported by the fact that significant changes in synergy indices can be seen in the asymptomatic hands of PD patients at HY stage I (Park et al. 2012).

The observation of decreased synergy index values and increased magnitudes of the D-angle are qualitatively similar to earlier reports on the changes in the two aspects of synergies that accompany healthy aging (Park et al. 2011a) and fatigue of the index finger in young healthy persons (Park et al. 2011b). Across all comparisons, there was a drop in the synergy index and an increase in the D-angle reflecting a drop in consistency in following an optimization principle. Because the origins of the suboptimal motor performance are very different across the three comparisons, the similarity of the effects on optimization and structure of variance suggests that these effects may reflect similar adaptive changes within the central nervous system due to aging, fatigue, and neurological disorders. Since it is known that there is decreasing dopamine content in the brain that occurs with normal aging (Bäckman et al. 2006; see also Chowdhury et al. 2013), it would be very interesting to investigate the role of nigrostriatal dopaminergic changes in age-and fatigue-related synergy changes.

Using a set of single trials for the ANIO analysis may be viewed as a drawback of the study. We would like to emphasize, however, that the tasks were very simple and, after a brief familiarization process, all subjects felt comfortable performing them. So, we do not expect the lack of extensive practice to be an important factor affecting the reconstructed objective functions. Note also that a recent study explored robustness of objective functions reconstructed with ANIO in young, healthy subjects and showed no major changes in those functions over repetitive tests on three days (Niu et al. 2012).