Investigation of prescribed movement in fluid–structure interaction simulation for the human phonation process

Abstract

In a partitioned approach for computational fluid–structure interaction (FSI) the coupling between fluid and structure causes substantial computational resources. Therefore, a convenient alternative is to reduce the problem to a pure flow simulation with preset movement and applying appropriate boundary conditions. This work investigates the impact of replacing the fully-coupled interface condition with a one-way coupling. To continue to capture structural movement and its effect onto the flow field, prescribed wall movements from separate simulations and/or measurements are used.

As an appropriate test case, we apply the different coupling strategies to the human phonation process, which is a highly complex interaction of airflow through the larynx and structural vibration of the vocal folds (VF). We obtain vocal fold vibrations from a fully-coupled simulation and use them as input data for the simplified simulation, i.e. just solving the fluid flow. All computations are performed with our research code CFS++, which is based on the finite element (FE) method.

The presented results show that a pure fluid simulation with prescribed structural movement can substitute the fully-coupled approach. However, caution must be used to ensure accurate boundary conditions on the interface, and we found that only a pressure driven flow correctly responds to the physical effects when using specified motion.

1. Introduction

The human voice is the basis for verbal communication, i.e., speech. The primary voice signal is generated in the larynx by the two opposing oscillating vocal folds [8]. The entire process is a complex interaction of fluid mechanics, solid mechanics and acoustics. As the lungs compress, air flows through the larynx and forces the vocal folds to vibrate, which in turn creates a pulsating air stream. Pulsating airflow, vocal fold vibrations, and supraglottal air vortices are the source of the perceived acoustic sound. This phenomena is computed by our research code CFS++, which is based on the finite element (FE) method [16]. Thereby, the physical properties, as well as their interactions, are considered: fluid and structural mechanics.

This fully-coupled approach is very costly with respect to computational time. There are several methods to reducing the computational effort. One is to use multi-mass models as developed by Flanagan and Landgraf [9]. The computational costs are extremely low, but an accurate flow field cannot be represented and complex oscillatory modes of the vocal folds are not captured. Therefore, based on continuum mechanics, Alipour et al. [1,3] used a finite element method to simulate the vocal folds, while the flow is based on Bernoulli’s equation. However, to determine the phonation threshold pressure, a solution of the Navier–Stokes equations is necessary as suggested by de Vries et al. [7].

A second approach is to reduce the number of unknowns by assuming a 2D computational set-up and exploiting symmetry, as demonstrated by Bae and Moon [4] and Thomson et al. [23]. This approach is referred to as the hemilarynx approach and neglects any asymmetric flow, and therefore certain turbulence effects. Hofmans et al. [13] discussed the admissibility set-up by investigating an experimental set-up of an in vitro larynx model and concluded that turbulence effects take too much time to develop. In phonation situations with closing vocal folds, this argument may hold as the flow has only one cycle to completely develop after a glottis opening. There also exist phonation situations in which the vocal folds do not fully close or touch each other (i.e., glottis closure insufficiency [19]); the assumption of a symmetric flow field is not longer valid during these situations where there is no contact.

To circumvent the costly iteration between fluid dynamics and structural mechanics, Larsson and Müller [15], Luo et al. [17] and Zheng et al. [27,28] employed a staggered coupling algorithm¹. However, as shown by Förster et al. [10] and Causin et al. [6], a staggered coupling Dirichlet–Neumann scheme that couples an incompressible fluid and a flexible structure is not unconditionally stable—known as the artificial added mass effect.

Another method to reduce computational efforts, while still accounting for a realistic flow field, is the simulation of 3D flow with specified movement of the structure. Essentially, the complex coupling is replaced with simple boundary conditions. The consequences, shortcomings, and validity are discussed in this work. This type of approach was chosen by Schwarze et al. [22] and Šidlof et al. [25], but instead of a velocity profile as inflow condition, Šidlof set a fixed pressure at the inflow. A detailed overview over all different methodologies simulating the human phonation process is presented by Alipour et al. [2] and most recently by Mittal et al. [18].

The aim of this study is to analyze the impact on reducing a fully-coupled fluid–structure phenomena to a pure fluid simulation with prescribed structural motion. To achieve this investigation, structural displacements of a fully-coupled simulation are extracted and used as imposed motion for a straight forward flow simulation. Additionally, a number of variations to the pure fluid simulations, which include changes in fluid–structure interface conditions, pressure inlet and geometry, are examined. These variations imitate specific uncertainties or incorrect boundary conditions and are each elucidated in separate sections of the manuscript.

The paper is organized as follows: first, the geometric set-up of the larynx is introduced in conjunction with the multilayer vocal folds. In Section 2 the mathematical models are presented, describing the governing equations of fluid and solid mechanics, as well as the field interactions. For a detailed description of the methods and their implementation to solve the coupled problem by means of the finite element method, we refer to [16], which also covers validation with the experimental set up of [11]. Section 3 presents four different case studies and discusses these by comparing the volume flux through the glottis, as well as the vibration of the vocal folds. In Section 4, the paper closes with a discussion of the results.

2. Model of fluid–structure interaction

2.1. Geometric set-up

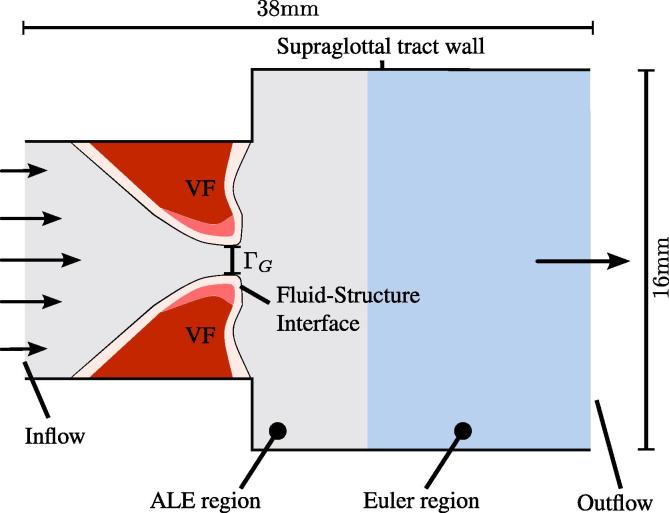
The geometric model consists of a simple channel with two elastic bodies inside representing the vocal folds. Through use of magnetic resonance imaging (MRI), Gömmel [12] extracted the geometry of the trachea, which shows that the vibration of the vocal fold covers only a part of the trachea. In our investigations, this is incorporated by narrowing the subglottal channel width as depicted in Fig. 1.

Fig. 1.

Fluid regions and boundary conditions. The glottis divides the fluid region into sub- and supraglottal area.

There are two prominent models to compute simulations of the vocal folds: (1) the “M5” model constructed by Scherer et al. [20,21], and (2) the model by Šidlof et al. [26] which uses an ex vivo plaster-casting methodology. A 2D version of the latter model was used in the subsequent simulations due to its complexity and realistic structure. This model has been improved by additionally considering different layers. The muscle, also called body, is at the base, and has a skewed trapezoidal form and supports the ligament. Both, the muscle and the ligament are covered by the lamina propria, which is approximately 1.2 mm thick at the base and reduces to half of its thickness at the tip of the vocal fold. The lamina propria is covered by a very thin tissue (0.05 mm) called epithelium, represented by a thin line in Fig. 2.

Fig. 2.

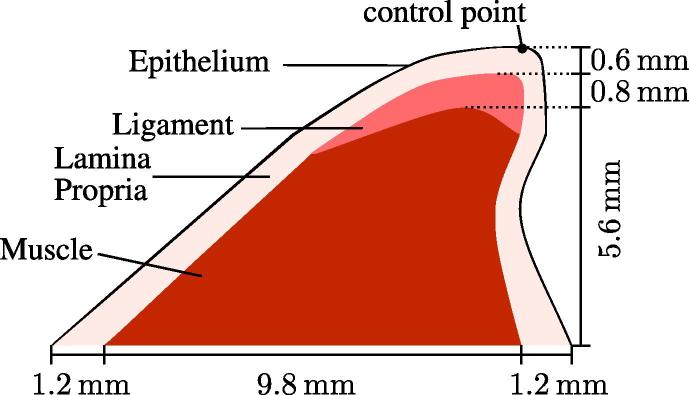
Geometry and material model of the vocal fold, consisting of four different regions. Dotted lines are reference lines for better readability.

Material parameters are still uncertain, as explained by Alipour et al. [2], as the thin and complex structure makes an experimental measurement difficult. Therefore, our material parameters rely on good estimation and comparison with different models. Additionally, an eigenfrequency analysis is done in advance to achieve a realistic vibrational frequency that mimics human phonation (Titze [24]). The elasticity modulus, used in the simulations, are given in Table 1. As 0 Poisson’s ratio a value of 0.45 is taken for all four tissue types.

Table 1.

Vocal fold material parameters for the four layer model.

Material	Elasticity modulus (kPa)
Muscle	30
Ligament	25
Lamina propria	20
Epithelium	50

2.2. Fluid mechanics

The flow can be regarded as incompressible for low Mach numbers (Ma < 0.3), as is the case in human phonation. This sets the fluid density ρ_f to a constant value and results in the incompressible Navier–Stokes’s equations, consisting of the following momentum and mass conservation equations:

$$\frac{\partial \mathbf{v}}{\partial t}+(\mathbf{v}·\nabla )\mathbf{v}+\nabla p-\nu \mathrm{\Delta }\mathbf{v}=\mathbf{0}\text{,}$$ (1)

$$\nabla ·\mathbf{v}=0\text{.}$$ (2)

In Eqs. (1) and (2) v denotes the fluid velocity, p the kinematic pressure $\left(p=\frac{P}{{\rho }_{\mathrm{f}}}\right)$, and $\nu \left(\nu =\frac{\mu }{{\rho }_{\mathrm{f}}}\right)$ the kinematic viscosity. To accurately capture the change in the fluid domain due to structural movement, the Arbitrary–Lagrangian–Eulerian (ALE) approach is used. Numerical instabilities, arising by convection dominants, are remedied by the streamline upwind Petrov–Galerkin (SUPG) method. A detailed description on the numerical schemes solving the Naviers–Stokes equations, can be found in [5], and we refer to [16] for a discussion on the implementation in our code.

2.3. Solid mechanics

To model the structural movement of the vocal folds, a linear elasticity model provided by Navier’s equation is applied

$$\nabla ·{\sigma }_{\mathrm{s}}={\rho }_{\mathrm{s}}\frac{{\partial }^2}{\partial t^2}\mathbf{u}\text{,}$$ (3)

and includes the Cauchy stress tensor σ_s, the solid density ρ_s and the displacement u. By introducing the tensor of elasticity [c] and the tensor of linear strain [S], Hooke’s law may be represented by

$${\sigma }_{\mathrm{s}}=[c][S]\text{.}$$ (4)

Furthermore, the linear strain–displacement is computed by

$$[S]=\frac{1}{2}(\nabla \mathbf{u}+{(\nabla \mathbf{u})}^T)\text{,}$$ (5)

and the elasticity tensor by

$$[c]=\left(\begin{array}{cccccc}{\lambda }_L+2{\mu }_L\hfill & {\lambda }_L\hfill & {\lambda }_L\hfill & 0\hfill & 0\hfill & 0\hfill \\ {\lambda }_L\hfill & {\lambda }_L+2{\mu }_L\hfill & {\lambda }_L\hfill & 0\hfill & 0\hfill & 0\hfill \\ {\lambda }_L\hfill & {\lambda }_L\hfill & {\lambda }_L+2{\mu }_L\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & {\mu }_L\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & {\mu }_L\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & {\mu }_L\hfill \end{array}\right)\text{.}$$

λ_L and μ_L are the Lamé parameters which are determined by elasticity modulus E and Poisson ration ν using the following equations:

$$\begin{array}{cc}\hfill & {\lambda }_L=\frac{\nu E}{(1+\nu )(1-2\nu )}\text{,}\hfill \\ \hfill & {\mu }_L=\frac{E}{2(1+\nu )}\text{.}\hfill \end{array}$$

Inserting Eqs. (4) and (5) into (3) results in the final partial differential equation (PDE) for linear elasticity:

$${\mathcal{B}}^T[c]\mathcal{B}\mathbf{u}={\rho }_{\mathrm{s}}\frac{{\partial }^2}{\partial t^2}\mathbf{u}\text{,}$$ (6)

with the differential operator $\mathcal{B}$, which is incorporated into the for the 2D plane strain case as

$$\mathcal{B}=\left(\begin{array}{cc}\frac{\partial }{\partial x}\hfill & 0\hfill \\ 0\hfill & \frac{\partial }{\partial y}\hfill \\ \frac{\partial }{\partial y}\hfill & \frac{\partial }{\partial x}\hfill \end{array}\right)\text{.}$$

2.4. Fluid–structure interaction

For a correct representation of the fluid–structure interaction, two conditions must be met at the common interface, Γ_fs between fluid and solid. First, the fluid velocity and structural velocity must be equal

$$\mathbf{v}=\frac{\partial }{\partial t}\mathbf{u}\mathrm{on}{\Gamma }_{\mathrm{fs}}\text{,}$$ (7)

which indicates that the fluid adheres to the structure. For a fixed wall, this corresponds to a so “no-slip” condition.

The second condition is the continuity of stress in the normal direction along the interface, indicating that fluid stress σ_f and solid stress σ_s must coincide, which is enforced by

$$[{\sigma }_{\mathrm{s}}]·\mathbf{n}=[{\sigma }_{\mathrm{f}}]·\mathbf{n}\mathrm{on}{\Gamma }_{\mathrm{fs}}\text{.}$$ (8)

Therefore, the acting fluid forces can be split up into a pressure and a viscous component:

$${\mathbf{f}}_{\mathrm{fs}}=[{\sigma }_{\mathrm{f}}]·\mathbf{n}={\displaystyle \underset{\mathrm{pressure}\mathrm{force}}{\underbrace{{\rho }_{\mathrm{f}}{\int }_{{\Gamma }_{\mathrm{fs}}}-\mathit{pI}·\mathbf{n}\mathrm{d}x}}}+{\displaystyle \underset{\mathrm{viscous}\mathrm{force}}{\underbrace{{\int }_{{\Gamma }_{\mathrm{fs}}}\mu (\nabla \mathbf{v}+{(\nabla \mathbf{v})}^T)·\mathbf{n}\mathrm{d}x}}}\text{.}$$ (9)

2.5. Boundary conditions

As an inflow condition, a fixed pressure is given 1 kPa and the outflow is given 0 Pa, which is consistent with realistic measurements by Holmberg et al. [14]. The trachea wall Γ_T is set to a no-slip condition

$$\mathbf{v}=\mathbf{0}\mathrm{on}{\Gamma }_T\text{,}$$ (10)

and vocal folds are fixed to the trachea, represented by

$$\mathbf{u}=\mathbf{0}\mathrm{on}{\Gamma }_T\text{.}$$ (11)

The interface boundary of fluid and structure is modeled as described in Section 2.4.

Fluid is considered to be at rest as the initial condition in the analysis. The first 200 time steps of the analysis are disregarded, such that the flow field is fully developed and the vocal folds vibrate periodically.

2.6. Numerical framework

To accurately resolve the flow structure, we performed a grid study (see Section 2.7) which resulted in 42.000 finite elements with quadratic basis function and, therefore, approximately 350.000 degrees of freedom for the flow velocity and pressure. To solve the PDE in time, the 2nd order backward differentiation formula (BDF2) with a time step size of 2.5 × 10⁻⁵ s was used. Five thousand time steps were performed, which resulted in t_end = 0.125 s. As stopping criterion, for solving the nonlinear Navier–Stokes equations an incremental L₂-norm (both for velocity and pressure) with an accuracy of 10⁻⁵ is chosen. To address the strong coupling, we performed iterations between the flow and structural mechanical field until the following incremental L₂-norm for the mechanical displacement was met

$$\Vert u_{n+1}^{k+1}-u_{n+1}^k{\Vert }_2<{10}^{-6}$$ (12)

where n is the time step counter and k is the iteration counter.

In [16] further details on solving the partial differential equations by means of the finite element formulation can be found.

2.7. Grid dependency

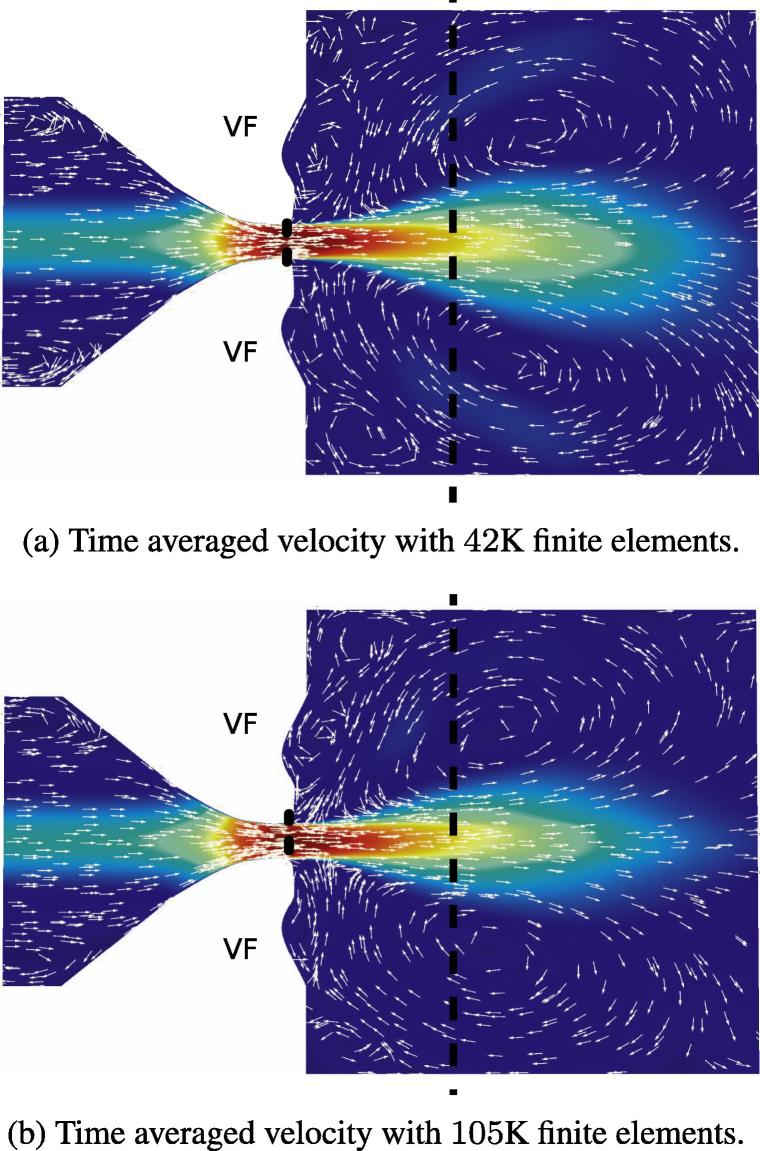
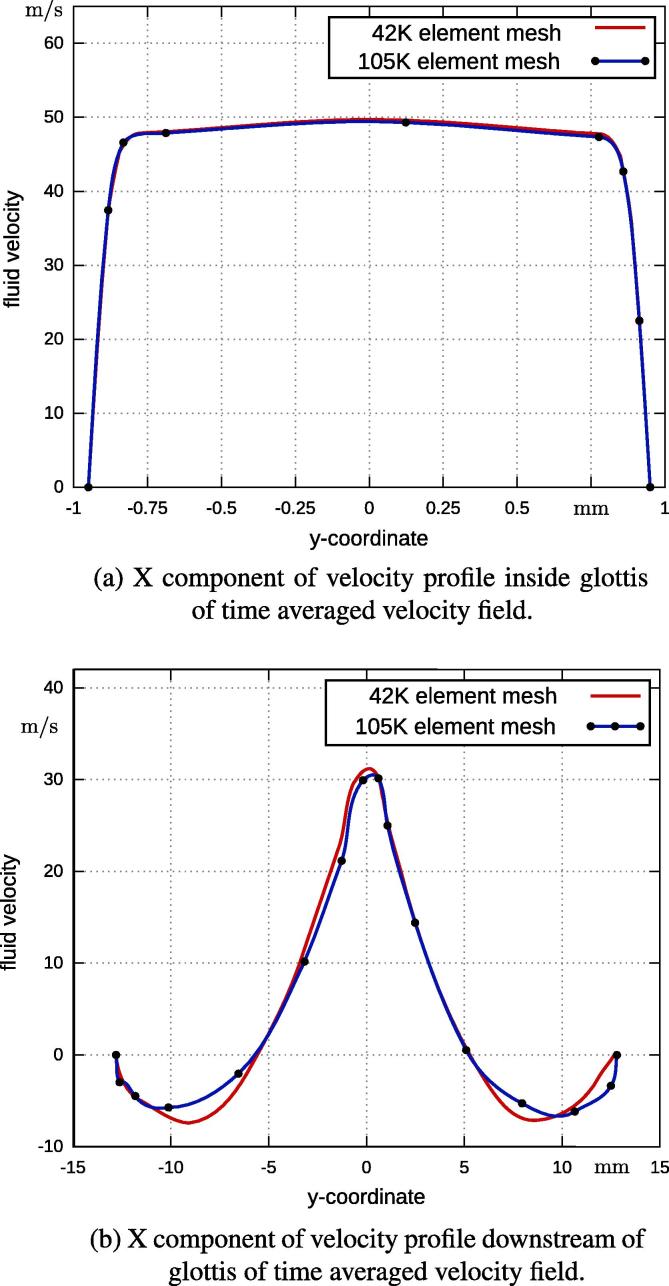
The influence of the computational mesh has been tested. A pure flow simulation and static geometry with a 42 K finite element grid was compared to a grid of 105 K elements. The time step size, number of steps, etc. were identical to values discussed in the previous section. The time averaged result of both mesh sizes are plotted in Fig. 3. Both simulations resulted in a similar pattern and position of the vortical structures. To provide a more detailed analysis, the velocity profile of two significant cross sections are compared; considering the main component, the x direction (vertical component). The location of the cross sections are indicated in Fig. 3: one is inside the glottis and the second downstream of the glottis. The comparison of the velocity profiles, as plotted in Fig. 4, demonstrate a good agreement in the cross section inside the glottis (see Fig. 4(a)), whereas the profiles deviate slightly at the second position. This indicates, that the coarse grid does not properly resolve the flow field downstream. Since the analysis of downstream flow field is not the aim of this work and the results for different mesh sizes are in good agreement, therefore, the 42 K finite element grid was used in the subsequent simulations.

Fig. 3.

Time averaged velocity field for different mesh sizes. Dashed line indicates the cross section displayed in the velocity profiles in Fig. 4. VF indicates the position of the vocal folds.

Fig. 4.

Comparison of velocity profiles for mesh sizes at two cross sections (see Fig. 3).

3. Results

The geometric set-up, as discussed in Section 2, the original model and will be referred to as such. Initially, a fully-coupled simulation is performed with the original model and the resulting vocal fold movement is extracted; this is used as the prescribed movement for the pure fluid flow simulation. The first study (Section 3.2) is a pure fluid simulation with prescribed movement and the velocity is set to v = 0 at the interface boundary Γ_fs.

The second study (Section 3.3) uses a lower inlet pressure of 800 Pa and sets the velocity field at the interface to the value recorded in the original set up.

In Section 3.4, slightly reformed vocal folds are used as shown in Fig. 9. To obtain a prescribed movement, the displacements from the fully-coupled simulations with the original vocal folds are projected onto the new shape. This case is then further altered by using a velocity inflow profile instead of a fixed pressure (Section 3.5).

Fig. 9.

Reformed vocal fold and outline of original geometry (solid black line).

We assess different scenarios to analyze certain simulation approaches, which are used to compute the human phonation process. Therefore, we focus on the impacts of using measurement data or estimates through observations (endoscopy) as prescribed vocal fold movement and boundary condition of a pure flow simulation. As a measure, the volume flux, Q_V, of the glottis is used and calculated using the following equation

$$Q_V(t)={\int }_{{\Gamma }_G(t)}\mathbf{v}·\mathbf{n}d\Gamma \text{,}$$ (13)

where Γ_G is the integration path inside the glottis (Fig. 1). Due to movement of the vocal folds, Γ_G varies in time.

3.1. Vocal fold vibration

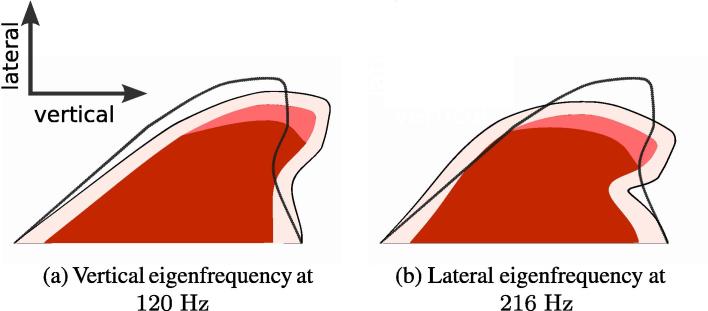
We begin with an eigenfrequency analysis of the vocal folds to determine the main frequencies of their natural vibration. The first two eigenfrequencies and with their shapes are shown in Fig. 5. The lateral movement (Fig. 5(a)) is of importance because it regulates the glottis width and, therefore, the fluid flow through the glottis. The reformed vocal folds have the first two eigenfrequencies at 122 Hz and 215 Hz. The eigenfrequencies of the two vocal folds are similar because their shapes do not differ much (see Fig. 9) and the material properties are the same.

Fig. 5.

Eigenform and eigenfrequency of the 2D vocal fold model with four layers. The original form is outlined on top of each eigenform.

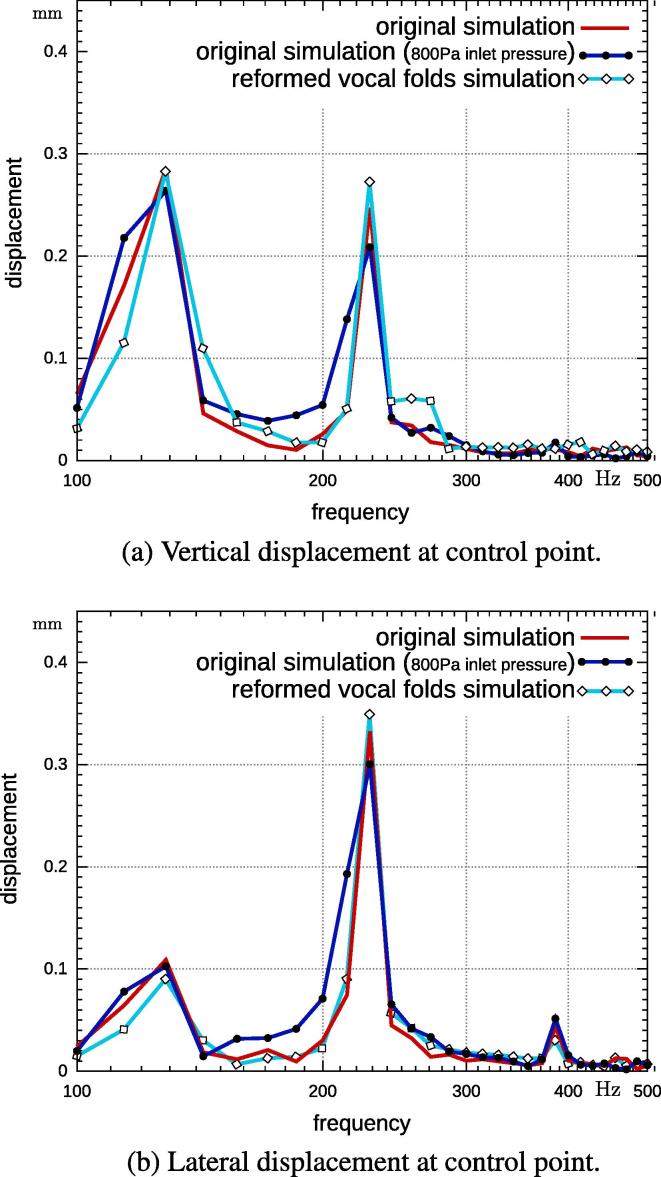
A control point on the vocal fold was chosen to monitor the vocal fold displacement. This point is located inside the glottis at the tip of the vocal fold, as shown in Fig. 2. The recorded displacements for all simulations are Fourier transformed and the results are displayed in Fig. 6. In Fig. 6(a), the vertical displacement is plotted and the two main peaks correspond to the first two eigenfrequencies of the vocal folds. The lateral movement is dominated by the second eigenfrequency and to a lesser degree at its second harmonic represented by a smaller peak. The amplitudes of the main frequencies are smaller for the case study of 800 Pa inlet pressure. This is due to weaker forces acting onto the vocal folds. Furthermore, frequencies between 120 Hz and 216 Hz are noticeably larger when compared to the original (1 kPa inlet pressure) simulation.

Fig. 6.

Vertical and lateral displacement as a function of frequency recorded at the control point on the vocal fold during three different fully-coupled fluid-structural simulations.

3.2. Case study: Homogeneous boundary condition (HBC)

In this case study, fluid simulations with specified movements are presented. All parameters are identical to the original set-up (i.e., geometry, boundary condition, apart from the fluid–structure interface). In the first pure fluid simulation, the interface velocity at the vocal folds is set to zero and in the second simulation, the fluid velocity is matched to the vocal fold velocity at the interface. Equal vocal fold and fluid velocity create the correct no-slip condition (NSC), which corresponds to the fully-coupled simulation.

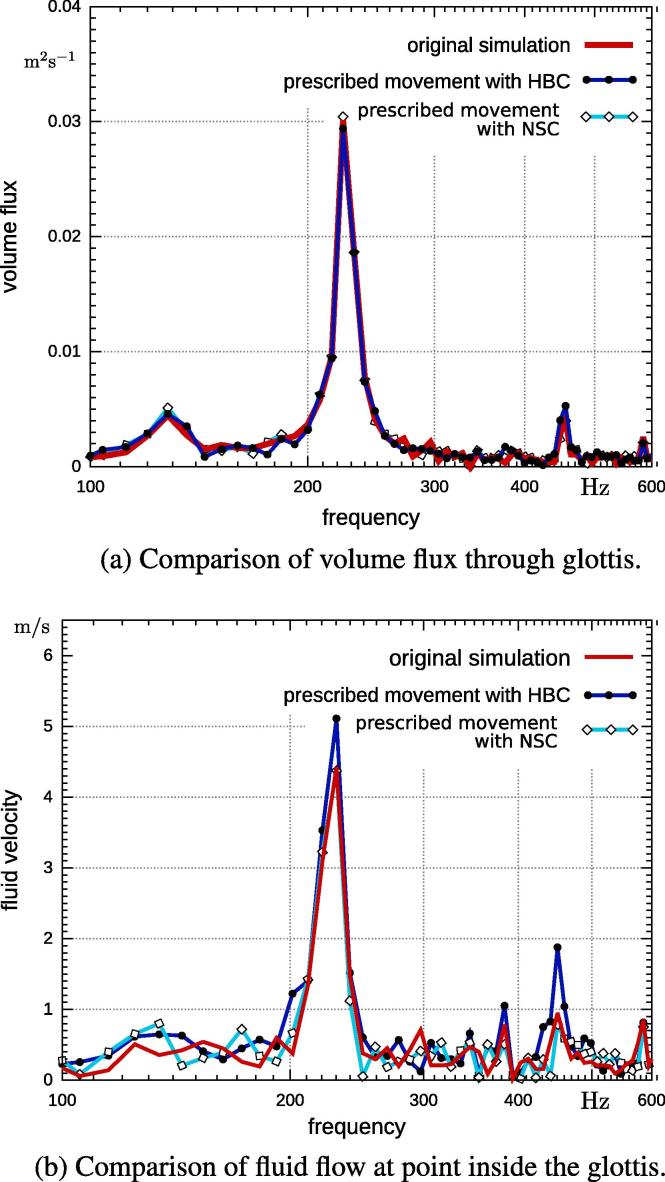
The volume flux of the original simulation and the prescribed simulations are displayed in Fig. 7(a). It shows a main frequency in the volume flux at 216 Hz, which corresponds to the second eigenfrequency of the vocal folds and their lateral movement, which mainly controls the fluid flow. The prescribed movements with the homogeneous boundary condition (HBC) and with no-slip condition (NSC) are in agreement with the fully-coupled simulation (i.e., frequency and amplitude coincide). However, the prescribed simulation with HBC differs from the other two models in amplitude of the characteristic frequencies at the center of Γ_G (Fig. 7(b)). In particular, the amplitude of the second harmonic is twice as high. These differences will likely have an impact on sound generation; the acoustic pressure field will be higher and the second harmonic will be dominant in contrast to the weaker fully-coupled simulation. The simulation with enforced no-slip condition, on the other hand, is in strong agreement and will result in a similar acoustic field as the fully-coupled simulation. In addition, the coupled scheme requires the iteration between fluid- and structural-mechanics. Therefore, because the algebraic system resulting from the Navier–Stokes equations needs to be solved three times more often, the overall simulation run time was three times longer.

Fig. 7.

Fluid field comparison in vertical direction of original simulation and pure fluid simulation with prescribed movement.

Mathematically, the fully-coupled simulation and the simulation case study with enforced no-slip conditions are equivalent and should result in identical results. However, the consistency of the two approaches can not be guaranteed in the discretized formulation due to the numerical approximation of the Navier–Stokes equations. In particular, after 100 time steps, the fully-coupled scheme performed approximately 1400 solve steps (solving the algebraic system of equations) and the pure flow simulation performed about 450. Therefore, identical numerical results over a long time period is not possible. During the first time steps, both approaches show identical flow fields but after the first approximately 200 time steps they start distinguishing themselves rapidly. The timing of when the two will differ may be delayed by reducing the error bound of the non-linear solver, but they will inevitable differ. To test for the effect of the error bound, the same simulations were performed with an error bound of 10⁻⁸ for the flow and coupling iteration (see Section 2.6); stopping criterion tolerance was reduced by a factor of 1.000. The deviation between both simulations was only be prolonged by about 100 time steps, which is minor considering the high increase in accuracy.

3.3. Case study: 800 Pa

Measuring the exact pressure in humans, which drives the phonation process, is difficult due to restricted access to the larynx. To simulate an inaccurate pressure measurement for a specific vocal fold vibration, we use prescribed movements obtained from the original simulation with a reduced inlet pressure of 800 Pa. To provide an accurate representation of the interface, the fluid velocity is set equal to the vocal fold velocities in Eq. (7), which corresponds to a no-slip condition (NSC).

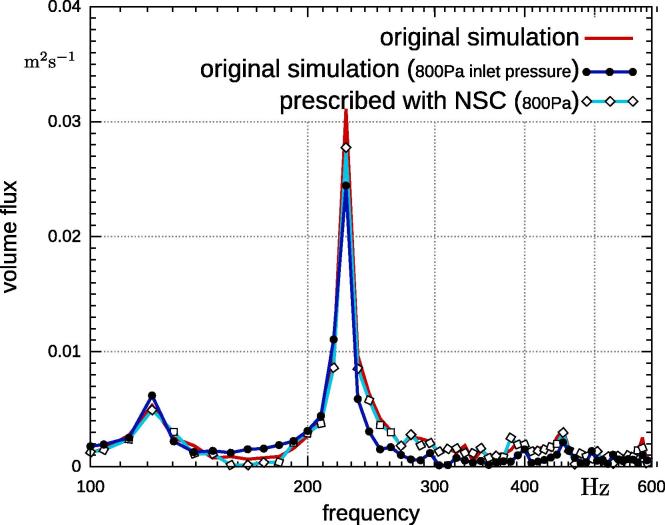
The resulting volume fluxes for the two fully-coupled simulations and the prescribed simulation with reduced inlet pressure are plotted in Fig. 8. The amplitude at the main frequency is reduced, in contrast to the original simulation, due to the lower pressure. However, it is higher than the peak amplitude of the fully-coupled case with 800 Pa inlet pressure, because the vocal folds open more. The increased opening can be deduced from the lateral displacement given in Fig. 6. Furthermore, reduced amplitudes at the frequency range of 120–216 Hz are found, which resembles the behavior of the original simulation.

Fig. 8.

Comparison of volume flux at glottis of original simulation, simulation with reduced pressure and prescribed movement with reduced pressure.

The difference in this frequency range, is due to the vocal fold vibration. The displacements of the original simulation (Fig. 6) reveals that the amplitudes in this frequency range are reduced as compared the fully-coupled simulation with 800 Pa inlet pressure. Therefore, it appears that, in regards to pressure inlet conditions, the flow characteristic is determined by the vocal folds movement. Consequently, the prescribed case does not imitate the 800 Pa fully-coupled simulation correctly because frequency components are lacking and the amplitude at the main frequency is higher.

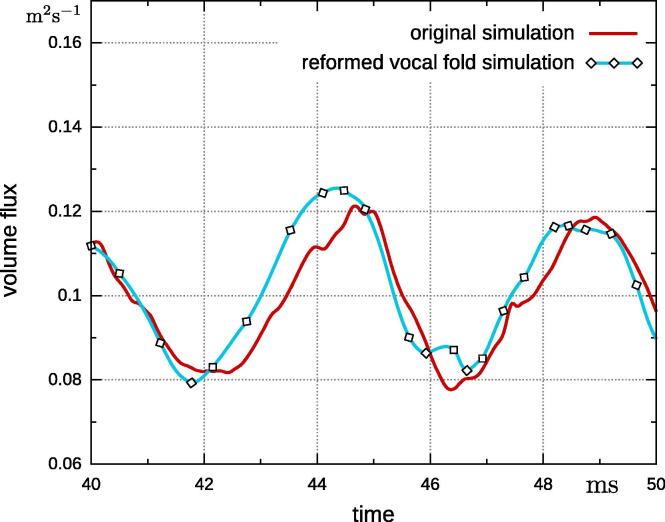
3.4. Case study: Reformed vocal folds

It is common practice to use observations of real vocal folds vibration as input for the numerical simulation. However, the geometry used is not identical to the observed or measured data. Instead, simplified models are acquired since patient specific vocal fold models are not yet state of the art. In this case study, we simulate a prescribed movement (i.e., acquired from measurements) and project the obtained displacements onto a different vocal fold shape. This demonstrates the effect of incorrect models or occurring measurement inaccuracies. In this case study, the two vocal fold models only slightly differ (Fig. 9) to maintain similar eigenfrequency and resulting main frequency of flow.

To obtain a preset movement for the new geometry, each finite element node on the fluid structure interface determines its nearest neighboring node of the original fully-coupled interface to obtain the displacement. The velocity is set accordingly (see (7)) and the inlet pressure in all three simulations is identical, set to 1.0 kPa.

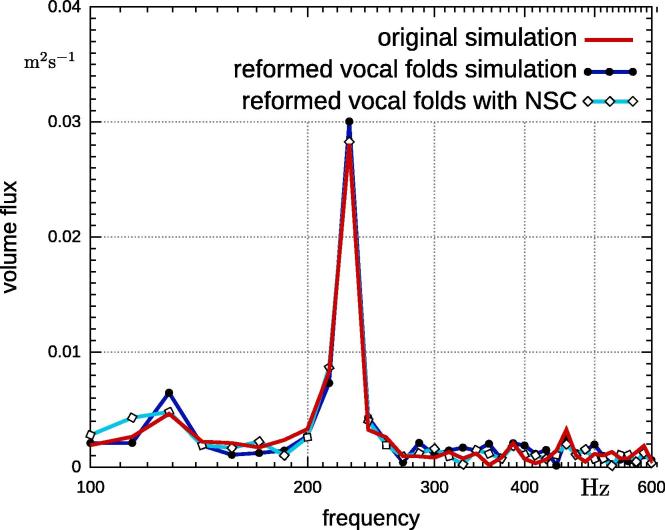
Although the geometry change is minor, there is an effect on the volume flux (Fig. 10). The volume flux at the two main frequencies is 7–8% higher for the fully coupled case with reformed vocal folds. It is likely a greater difference in the geometry will have a greater effect on the results. However, it should be noted that the prescribed movement does have the same characteristic peaks as the original fully-coupled simulation. This suggests that small measurement errors, in the vocal fold shape do not have a strong impact on the volume flux. Therefore, a fluid simulation with prescribed movement is feasible.

Fig. 10.

Comparison of volume flux at glottis of fully-coupled simulations with original and reformed vocal folds and simulation with prescribed movement on reformed vocal folds.

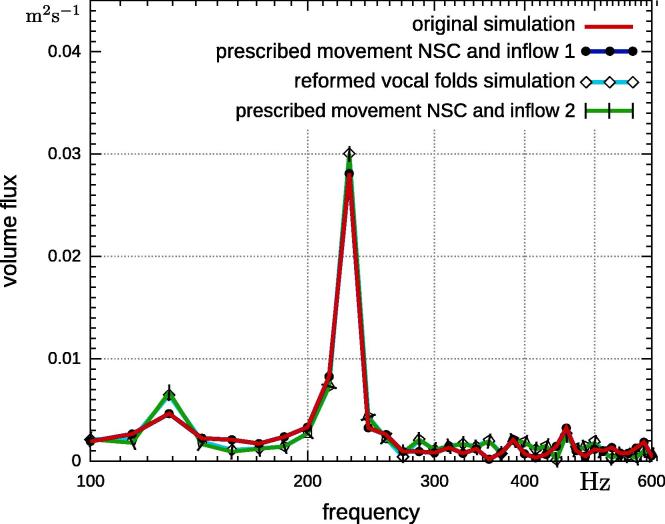
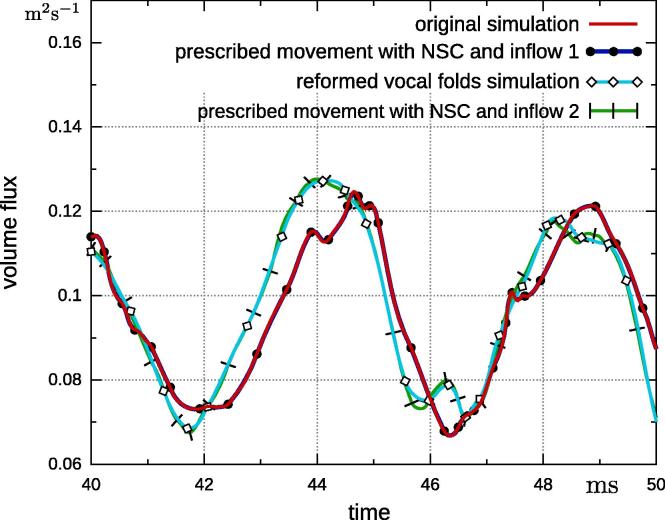
3.5. Case study: Reformed vocal folds with prescribed inflow

The basic model remains identical like in the previous section, e.g., reformed vocal folds, prescribed movement from the original set-up, no-slip condition. The only difference is that the inflow pressure was replaced by a parabolic velocity profile, which was extracted from the original simulation. A second simulation uses the inflow profile of the fully-coupled simulation with reformed vocal folds. The first inflow condition is referred to as “inflow 1”, while the inflow condition gained from the simulation with reformed vocal folds is referred to as “inflow 2”. A time interval of the volume flux obtained by these two inflow conditions is depicted in Fig. 11. Next, we performed simulations with prescribed movement obtained from the original simulation and projected it onto the reformed vocal folds; once with “inflow 1” and once with “inflow 2”. The results of the volume flux through the glottis do not appear to differ from previous findings (Fig. 12). However, a closer look shows that the simulations with the same inflow have an identical volume flux through the glottis, regardless if it is prescribed or fully-coupled. This observation becomes more clearer when the volume flux is visualized in time (see Fig. 13). Simulations with the same inflow also have the same flux through the glottis. This is especially interesting when the prescribed movements from the original simulation are applied, but “inflow 2” condition is used. This results in the same volume flux as the fully-coupled simulation with reformed vocal folds, however, the vocal fold motion is different. The structural displacement of the vocal folds does not have an effect on the volume flux through the glottis when velocity profiles are used as inflow condition.

Fig. 11.

Extraction of volume flux at inflow for the fully-coupled simulations with original and reformed vocal folds.

Fig. 12.

Comparison of volume flux at glottis of fully-coupled simulations with original and reformed vocal folds and simulations with prescribed movement on reformed vocal folds once with “inflow 1” and once with “inflow 2”.

Fig. 13.

Volume flux through glottis in time domain obtained by fully-coupled simulations with original and reformed vocal folds and simulations with prescribed movement on reformed vocal folds once with “inflow 1” and once with “inflow 2”.

This example illustrates the importance of fluid–structure interaction. Generally, a change in the fluid field will result in a change of the vocal folds displacement which, in turn, affect the flow field. However, in the investigated cases of driven inflow, the flow field does not influence the vocal fold movement.

4. Conclusion and summary

The presented work discusses the effect of using prescribed movements in a fluid–structure coupled problem by comparing four different scenarios of one way coupling with the fully coupled approach. First, the investigations show that a homogeneous boundary condition for the flow velocity at the coupling interface results in higher fluid velocities inside the glottis. Thus, one has to apply no-slip boundary conditions. Next, varying the inlet pressure (instead 1 kPa we used 800 Pa) results, not only, reduced volume fluxes at the main frequencies, but also in-between them, which is caused by the reduced oscillation amplitudes of the vocal folds. Furthermore, small deviations in the geometry of the vocal folds cause small differences in the volume flux (7–8%), compared to the fully-coupled computation. Finally, replacing the pressure driven flow by a prescribed inflow condition demonstrated that the volume flux was unaffected by the prescribed movement. Consequently, the motion of the vocal folds does not have a strong effect on the volume flux through the glottis, if velocity profiles are used as inflow condition.

A prescribed methodology has the advantage of significantly reducing the computational time, in this case by a factor 3. Although some agreement between the methodologies can be achieved, it is important to note the effects of the fluid flow on the acoustic sources and acoustic pressure. Higher flow velocities have an impact on the sound pressure level. A reduction or an increase of the flow amplitudes in a specific frequency range will also cause change in the acoustic field. Therefore, in certain scenarios (e.g., velocity profile inflow condition), a fully-coupled scheme cannot be replaced by a pure fluid simulation with prescribed movement.