Emergence of synchronous EEG spindles from asynchronous MEG spindles

Abstract

Sleep spindles are bursts of rhythmic 10–15 Hz activity, lasting ∼0.5–2 s, that occur during Stage 2 sleep. They are coherent across multiple cortical and thalamic locations in animals, and across scalp EEG sites in humans, suggesting simultaneous generation across the cortical mantle. However, reports of MEG spindles occurring without EEG spindles, and vice versa, are inconsistent with synchronous distributed generation. We objectively determined the frequency of MEG‐only, EEG‐only, and combined MEG‐EEG spindles in high density recordings of natural sleep in humans. About 50% of MEG spindles occur without EEG spindles, but the converse is rare (∼15%). Compared to spindles that occur in MEG only, those that occur in both MEG and EEG have ∼1% more MEG coherence and ∼15% more MEG power, insufficient to account for the ∼55% increase in EEG power. However, these combined spindles involve ∼66% more MEG channels, especially over frontocentral cortex. Furthermore, when both MEG and EEG are involved in a given spindle, the MEG spindle begins ∼150 ms before the EEG spindle and ends ∼250 ms after. Our findings suggest that spindles begin in focal cortical locations which are better recorded with MEG gradiometers than referential EEG due to the biophysics of their propagation. For some spindles, only these regions remain active. For other spindles, these locations may recruit other areas over the next 200 ms, until a critical mass is achieved, including especially frontal cortex, resulting in activation of a diffuse and/or multifocal generator that is best recorded by referential EEG derivations due to their larger leadfields. Hum Brain Mapp, 2011. © 2011 Wiley Periodicals, Inc.

INTRODUCTION

Oscillatory EEG phenomena are thought to reflect a primary thalamo‐cortical mechanism for the modulation, phasing, and integration of neuronal information processing across large numbers of cortical neurons [Buzsaki,2006]. Among the most intensely studied such phenomena are sleep spindles and their homologues which occur in anaesthetized or in vitro systems [Andersen and Andersson,1968; Contreras et al.,1997; Destexhe et al.,1998; Spencer and Brookhart,1961a,b]. Discovered 75 years ago [Loomis et al.,1935], spindles occur mainly in Stage 2 NREM sleep, with a frequency of 10–15 Hz and a duration of 0.5–2 s [Gibbs and Gibbs,1950].

Since spindles are a model for thalamo‐cortical synchronizing mechanisms, considerable effort has been devoted to understanding how synchrony arises and how much synchrony is present during spindles. Some animal models have found a slow propagation of spindles from a focal onset zone [Andersen and Andersson,1968; Kim et al.,1995], whereas others report a remarkable synchrony in widespread locations [Contreras et al.,1997]. The current consensus is that spindles during normal sleep are synchronous across the thalamus and cortex, but may become desynchronized after lesions, or in vitro, or under anesthesia [Contreras et al.,1997; Destexhe and Sejnowski,2003; McCormick and Bal,1997]. Elegant intracellular studies have found that spindles emerge from interactions between inhibitory cells in the thalamic reticular nucleus and bursting thalamocortical neurons, that then entrain this rhythm in their target cortical areas [Bazhenov et al.,2002]. Experimental data and computational models suggest a critical role for cortico‐thalamic projections in spindle synchrony [Contreras et al.,1997; Destexhe et al.,1998; Traub et al.,2005].

Widespread synchrony of spindle generators in humans has also been inferred from the high correlation of spindle discharges across widely dispersed scalp EEG channels [Contreras et al.,1997]. However, other studies found that multiple generators are necessary to account for the MEG field pattern [Gumenyuk et al.,2009; Ishii et al.,2003; Manshanden et al.,2002; Shih et al.,2000; Urakami,2008].

A more striking but less completely described dissociation between MEG and EEG is the occurrence of a spindle in one measurement modality but not the other. An early study noted that MEG spindles can be completely absent even when the EEG spindle is clear [Hughes et al.,1976]. A later single‐sensor study found that MEG spindles were more common but occurred only at vertex [Nakasato et al.,1990]. Yoshida et al. [1996] classified spindles as EEG‐only (30%), MEG‐only (20%), or both. However, since they only used seven sensors, some of this disparity may reflect incomplete sampling. In a study examining this question with whole head recordings of both EEG and MEG, Urakami [2008] remarked that MEG spindles can occur without EEG spindles but considered such events rare and did not analyze them. Similarly, Manshanden et al. [2002] noted that spindles could occur in either EEG or MEG or both, but did not quantify this phenomenon. We re‐examined these issues in the current study, using high density EEG and MEG, and objective spindle categorization. We found that MEG spindles often occur without significant EEG involvement. Comparison of such spindles with those occurring in both MEG and EEG suggests that spindles may appear first in a manner that is sometimes more efficiently recorded by MEG gradiometers, and that they become visible to referential EEG when they spread, especially to frontocentral areas.

METHODS

Participants and Recordings

We recorded the electromagnetic field of the brain during sleep from seven healthy adults (three males, four females, ages 20–35). Participants had no neurological problems including sleep disorders, epilepsy, or substance dependence, were taking no medications and did not consume caffeine or alcohol on the day of the recording. We used a whole‐head MEG scanner (Neuromag Elekta) within a magnetically shielded room (IMEDCO, Hagendorf, Switzerland) and recorded simultaneously with 60 channels of EEG and 306 MEG channels (Fig. 1). MEG SQUID (super conducting quantum interference device) sensors are arranged as triplets at 102 locations; each location contains one “magnetometer” and two orthogonal planar “gradiometers” (GRAD1, GRAD2). Throughout the text, the square root of the sum of the power of GRAD1 and GRAD2 is referred to as GRAD. Unless otherwise noted, MEG will be used here to refer to the gradiometer recordings. EEG electrodes were placed on the scalp in the standard 10‐10 montage, and referenced to an averaged mastoid. Electrode locations in individual subjects were recorded using a 3D digitizer (Polhemus FastTrack). HPI (head position index) coils were used to measure the spatial arrangement of head relative to the scanner. Four subjects had a full night's sleep in the scanner and three had daytime sleep recordings (2 h). Padding was provided under the arms and knees, and around the head and neck, to make the subjects more comfortable and minimize movements. Every 20 min, the recording was stopped, data were saved, HPI locations were remeasured, and recordings were restarted. Analyses were limited to epochs where the subject did not move between the beginning and end of the 20‐min recording. Sampling rate was either 1,000 Hz (down sampled by a factor of 2 for the final analysis) or 600 Hz. The continuous data were low‐pass filtered at 40 Hz. An independent component analysis (ICA) algorithm was used to remove ECG contamination [Delorme and Makeig,2004]. Sleep staging was confirmed by three neurologists according to Rechtschaffen and Kales' sleep classification [Rechtschaffen and Kales,1968].

Figure 1.

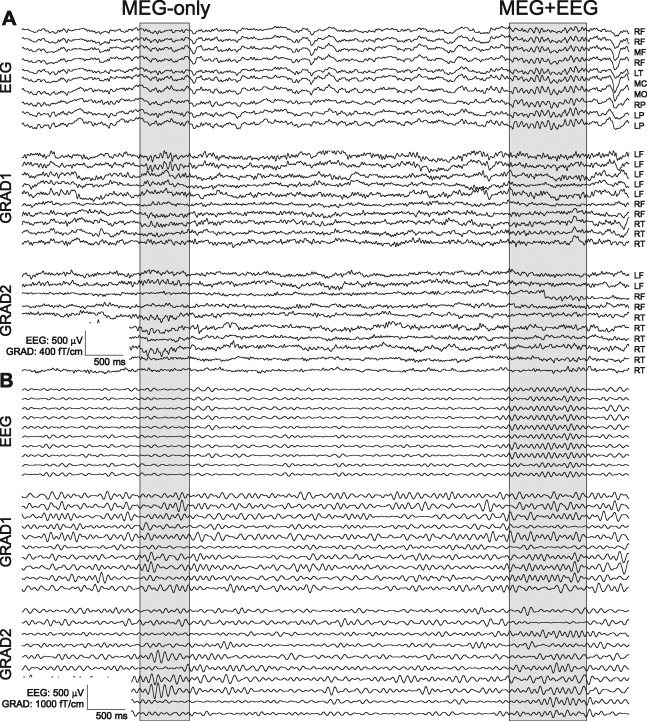
Example Mo (MEG‐only) and ME (MEG+EEG) spindles. For clarity, selected spindles in sample referential EEG and MEG gradiometer channels are highlighted in gray. Broadband (A) and 7–15 Hz bandpass (B) recordings are shown. Complete recording profiles are shown in Supporting Information Figures 1 and 2. L (Left), M (Middle), R (Right) F (Frontal), T (Temporal), C (Central), P (Parietal).

Sequential Power Spectral Density (SPSD) and Spindle Detection Algorithm

To objectively classify spindles as being manifested in the referential EEG, MEG gradiometers, or both, we calculated the power spectral density of EEG and MEG sensors during 30‐s long recording epochs. Epochs were chosen based on visual inspection as containing a relatively high density of EEG spindles during typical Stage 2 sleep and no artifacts. The choice of epochs to study was made without reference to the MEG recordings. Power was calculated in the frequency range of 7–15 Hz using windows 500‐ms long and moving steps of 100 ms (Fig. 2). Spindles were automatically detected from the resulting SPSD time‐series. Since the absolute size of MEG sensor recordings can be strongly influenced by the distance of the sensor from the cortical surface (due to the position of the head in the dewar), we first normalized the MEG for each sensor to its maximum across the 30‐s data segment. Then, each sensor's SPSD data were smoothed by five sequential passes of a three point smoothing filter. All resulting local maxima were found, and the standard deviation of these maxima was calculated across all sensors. The number of channels with maxima greater than two standard deviations above zero occurring within a 100‐ms window was counted. This count was squared, then convolved ten times with a three point smoothing filter, then normalized and the largest 80% were retained as spindles. These multiple steps had the effect of selecting epochs with spindle‐frequency power consistently above baseline for a sufficient period of time and across multiple channels. We compared the detection of EEG spindles by this computer algorithm to that of an experienced electroencephalographer in a random 30‐s epoch from each of the subjects. All of the 54 human‐detected spindles were also detected automatically. An additional 21 spindles detected automatically were not detected by the human observer. Upon examination, it was determined that these events could reasonably be considered spindles, but the human observer was using a higher internal threshold.

Figure 2.

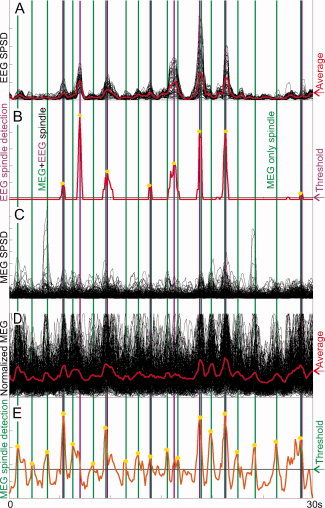
Automatic detection of EEG and MEG spindles. A. Power from 7 to 15 Hz in a 500 ms moving window (Sequential power spectral density: SPSD) is plotted for a 30‐s epoch of Stage 2 sleep for each EEG ch, normalized to the maximum value of the largest channel. The average of all channels is in red. B. Output of the EEG spindle detection algorithm (see Methods). The horizontal line indicates the detection threshold, and yellow stars denote automatically detected peaks, with maroon vertical lines allowing comparison of their timing to other panels. C. MEG SPSD for each channel, normalized to the maximum value of the largest channel. The average of all channels is in red. D. MEG SPSD for each channel, normalized to the maximum value of that channel. The average of all channels is in red. E. Output of the MEG spindle detection algorithm. The horizontal line indicates the detection threshold, and yellow stars the automatically detected peaks, with green vertical lines allowing comparison of their timing to other panels. Many MEG spindles have little or no corresponding EEG spindle. (For an additional example from another subject, see Supporting Information Fig. 1).

It should be noted that the classification of spindles as being present in both MEG gradiometers and in referential EEG (ME), versus in MEG gradiometers only (Mo) is not pure, absolute or necessarily even dichotomous in the sense of denoting two clearly distinct and non‐overlapping populations. Indeed, the distribution of EEG spindle‐frequency activation during MEG spindles was continuous, and while the threshold was slightly more lenient than that of an experienced electroencephalographer, the precise choice of the threshold was necessarily arbitrary. However, several different thresholds with this method, as well as other methods were used to categorize spindles as ME vs. Mo, without a change in the fundamental findings.

Amplitude, Coherence, and Topography

To compare the amplitude, coherence, and topography of ME vs. Mo spindles, we analyzed 1,000‐ms epochs of MEG gradiometer recordings centered on their peak of the spindle. After de‐trending, three different amplitude criteria were calculated for each epoch. The first amplitude criterion was RMS (root mean square) amplitude which is defined as the square root of the mean of the square of the waveform. Second was the Hilbert amplitude which was calculated as the mean of square root of the conjugate square of Hilbert transforms of the measured signal. For the coherence measures, Capon's nonparametric spectral estimation which is known as the minimum variance distortionless response (MVDR) was used. MVDR spectral estimation is based on the output of a bank of filters where the bandpass filters are data and frequency dependent [Benesty et al.,2005]. The MVDR may be advantageous over Welch's method in distinguishing the coherences of nearby frequencies. Here, the MVDR estimate of each possible gradiometer‐pair was calculated over 7–15 Hz. Then, the mean of these values were averaged over the sensor pairs to reach one number per spindle representing the mean within modality coherence for gradiometers over the entire 7–15 Hz range.

RESULTS

Visual inspection of raw traces from referential EEG and MEG gradiometer recordings (Fig. 1A) revealed spindles that were visible in both MEG and EEG (“ME” spindles) whereas others seemed to be recorded with MEG only (“Mo” spindles). This became clearer when the traces were band‐passed in the spindle frequency (Fig. 1B), and further when the power in this band was integrated over 500‐ms periods and plotted sequentially (Fig. 2). An example from another subject is shown in Supporting Information Figures 1 and 2. To quantify this phenomenon we used automatic detection in each modality followed by categorization based on coincidence detection. Finally, we tested if the Mo and ME spindles differ in their amplitude, coherence, number of channels involved, or topography.

Sequential Power Spectral Density (SPSD)

Sequential power spectral density (SPSD) in the spindle range was calculated using 500‐ms windows (sliding with 100 ms steps) for Stage 2 NREM sleep epochs with numerous spindles. Four 30‐s epochs were analyzed in each of the participants. This method is identical to that used by Contreras et al. [1997] as a key element supporting their argument for large‐scale synchrony. Plots of SPSD from referential EEG replicate the findings of Contreras et al. (but with more EEG channels): spindles are visible as clear peaks where essentially all channels are simultaneously active (Fig. 2A). Like EEG, MEG gradiometers also show large peaks when many channels are active, and these are generally at the same times as the EEG spindles (Fig. 2C). This was quantified by averaging the SPSD across all EEG channels, and similarly averaging the SPSD across all MEG channels, and then calculating the correlation coefficient between these two time‐series for each 30‐s segment. Results were averaged across four segments in every subject and across subjects; the mean of these coefficients was 0.66 ± 0.09. Thus, while EEG and MEG spindles tended to co‐occur, there were many times when they diverged.

Examination of Figures 1 and 2 also reveals that EEG channels are seldom individually active in this frequency range outside of frank spindles, whereas individual MEG channels can show a large amount of activity between spindles. Even during spindles, a given MEG sensor could begin and end its involvement asynchronously with the EEG or with other MEG channels. This was quantified by calculating the average correlation between all possible pairs of EEG channels during the 30‐s segments in a given subject, and then averaging these values across all four 30‐s segments for that subject. The similar average correlation was calculated for all pairs of GRAD1 channels, and this was averaged with the similar average across pairs of GRAD2 sensors. Across the seven subjects, the mean ± STD pairwise EEG correlation was 0.63 ± 0.08. In contrast the same measure for gradiometer channels was only 0.22 ± 0.10. Paired t‐test between these values demonstrated a significant difference (P < 0.00001).

Automatic MEG and EEG Spindle Detection

To objectively identify spindles in the MEG and EEG, we devised a method based on their SPSD (see Fig. 2 and Supporting Information Fig. 2). This was done independently for EEG (detecting a total of 295 peaks in all subjects) and MEG (detecting a total of 537 peaks), and the time of peak power was determined for each peak. Parameters were chosen so that the automatic detection closely matched the judgment of experienced electroencephalographers. We examined if the occurrence of a peak (indicating a spindle) in one modality implied that it also occurred in the other, while permitting a difference in peak latency ranging from 0 to 1,000 ms in 100‐ms steps. As is seen in Figure 3, the peak coincidence probability increased when greater temporal imprecision was allowed. For all the permitted lags, the probability of a peak in EEG‐SPSD given existence of an MEG‐SPSD peak was lower than the probability of occurrence of a peak in MEG‐SPSD given existence of an EEG‐SPSD peak. That is, referential EEG spindles were more likely to be accompanied by a MEG gradiometer spindle than the converse.

Figure 3.

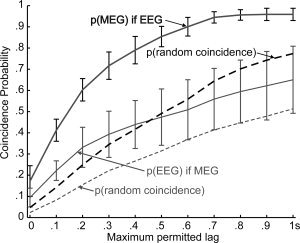
Probability of MEG vs. EEG spindle co‐occurrence. Spindles were automatically detected from MEG gradiometers and referential EEG, and their co‐occurrence at different delays is plotted. The thick black line shows the probability that an MEG spindle occurs given that an EEG spindle had, and the thin gray line shows the reverse relationship. Error bars are standard deviations across subjects. Dashed lines represent the probability of peak coincidence after the inter‐spindle intervals have been randomized. Both solid lines are greater than their corresponding dashed lines, indicating that spindles in the two measurement modalities do tend to occur together. The gray thin line is below the black thick line, indicating that most EEG spindles are accompanied by a MEG spindle, but not vice versa.

A maximum EEG vs. MEG spindle peak difference of 500 ms was chosen for the analyses described below, to correspond to the usual duration of a spindle of about 1 s. On the basis of this analysis, we divided the MEG‐SPSD peaks into two groups. Those that had a coincident EEG‐SPSD peak were categorized as ME spindles and those which did not were categorized as Mo spindles. Using these criteria, a total of 254 ME and 283 Mo spindles were automatically identified in the seven subjects. Across subjects, the mean and standard deviation of the number of Mo spindles were 40.42 ± 9.82, and of ME spindles were 36.28 ± 10.41. Consequently, the mean and standard deviation across subjects of the probability that an MEG spindle would occur given that an EEG spindle was detected was 0.85 ± 0.05. In contrast, the probability that an EEG spindle would occur given that an MEG spindle was detected was only 0.47 ± 0.13. A paired t‐test indicates that these proportions were significantly different (P < 0.001). Thus, about half of the MEG spindles have a corresponding EEG spindle during the integration period of 500 ms in any given subject. Spindles occurring only in EEG were rare and were not studied further here.

The expected coincidence rate under the null hypothesis of no relation between the peaks of EEG and MEG spindles was estimated by randomly and independently shuffling the inter‐peak intervals of each of the 28 epochs. The results, plotted as dashed lines in Figure 3, are consistently lower than the actual coincidence rates. At an allowed 500‐ms asynchrony, the mean ± standard deviation across subjects of the probability that an MEG spindle would occur given that an EEG spindle was detected was 0.65 ± 0.08, whereas the probability that an EEG spindle would occur given that an MEG spindle was detected was 0.37 ± 0.11. ANOVA was conducted with factors of permitted lag, target modality, and actual/randomized intervals. All main effects were significant, including, specifically, the main effect of actual vs. randomized intervals (F = 349 dF = 1, P < 0.00001). Thus, the times of occurrence of EEG and MEG were related, but nonetheless showed considerable independence.

Amplitude, Coherence, and Number of MEG Channels Involved in Mo vs. ME Spindles

We next examined the 1,000‐ms MEG epochs centered on the gradiometer spindle peaks, to determine if any differences could be found between ME and Mo spindles (Table I). We first tested if spindles become apparent in referential EEG when the MEG sensor signals (and thus their underlying sources) are larger. Indeed, the RMS amplitude of the GRADs was 13% greater for ME than Mo spindles (t test, P < 0.00001). However, this amplitude increase is not sufficient in itself to explain the 55% average increase in EEG amplitude between these conditions. Another possibility would be for the activity in the generators underlying the MEG signals to become more coherent, and thus summate more effectively. However, the average MVDR coherence between GRAD channels only increased by 1% from Mo to ME spindles, again a change that is too small to account for the large increase in EEG spindle amplitude. The coherence remained indistinguishable between ME and Mo spindles when considering frequencies from 10 to 15 Hz individually (see Fig. 4). These values were obtained by comparing all spindles in each category (“ME” and “Mo”). If we averaged first within a subject and then found the mean across subjects, similar values were obtained. We also obtained similar values when using different methods to estimate amplitude and power (please see Supporting Information Table S1). Similar results were also obtained when we made these calculations for just the GRAD channels exceeding criterion for participation in the spindle, or for just the top five channels in amplitude in every spindle. Thus, although MEG signals during spindles become moderately larger and perhaps slightly more coherent when they are accompanied by an EEG spindle, these increases do not seem sufficient to explain the large increase in EEG amplitude.

Table I.

Amplitude and Coherence in Mo vs. ME spindles. MEG and EEG amplitude, and MEG coherence, were calculated for spindles appearing in both MEG and EEG (ME) versus those appearing only in MEG (Mo). Calculations were made either by first averaging the results within each of the 7 subjects and then comparing across subjects (upper panel), or by comparing all 254 ME spindles to all 283 Mo spindles (lower panel). Calculations in each panel were repeated using all channels, only the ‘active channels’ for each spindle, or the 5 channels with the largest spindle activity in each spindle. Results were highly consistent in all comparisons.

Comparison across patients	MEG RMS power	EEG RMS power	Coherence between GRADs (MVDR)
All channels
Mo	1.98	4.8	0.244
ME	2.33	7.43	0.255
Ratio	1.18	1.55	1.03
t test P<	0.01	0	0
Active channels
Mo	1.97		0.253
ME	2.24		0.258
Ratio	1.14		1.02
t test P<	0.01		0.1
Top 5 channels
Mo	1.96		0.26
ME	2.22		0.26
Ratio	1.12		1
t test P<	0.02		0.98
Comparison across spindles	MEG RMS power	EEG RMS power	Coherence between GRADs (MVDR)
All channels
Mo	1.96	4.71	0.25
ME	2.3	7.42	0.25
Ratio	1.18	1.54	1.01
t test P<	0.0001	0.0001	0.017
Active channels
Mo	1.95		0.26
ME	2.22		0.26
Ratio	1.14		0.99
t test P<	0.001		0.15
Top 5 channels
Mo	1.94		0.27
ME	2.18		0.26
Ratio	1.12		0.97
t test P<	0.0001		0.2

Figure 4.

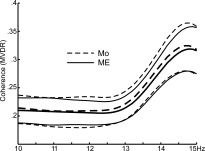
Coherence‐frequency relationship in ME versus Mo spindles. The average MVDR coherence between all pairs of gradiometers is plotted from 10 to 15 Hz. Although higher frequencies had higher coherence, this was similar for ME (solid) and Mo (dashed). Thick lines are means, thin standard deviation.

In contrast to these small or negligible differences in amplitude, and coherence between Mo and ME, we did find a large increase in the number of channels participating in the spindles between conditions. To evaluate if a given channel participated in a spindle, we first selected, using the automated algorithm, nonspindle periods as those periods that fell below the threshold line. Channels were considered to participate in the spindle if, at any point during that spindle, their PSD amplitude exceeded twice the standard deviation of their activity during the nonspindle periods. Based on this analysis, a mean of 20.9% of the GRAD channels participated in ME spindles, significantly greater than the 12.6% participating in Mo (nonpaired t test, P < 0.00001).

MEG Topography Differences Between Mo and ME Spindles

We also examined topography as a possible explanation for why some MEG gradiometer spindles were observed in referential EEG and others not. We reasoned that some locations of the generators underlying the MEG signals might project more effectively to the EEG sensors. Visualization of the average GRAD topography revealed no striking difference between Mo (Fig. 5A) versus ME (Fig. 5B) spindles besides amplitude. However, when the ratio is taken between these maps (Fig. 5C), it is clear that power increases to ME at some locations substantially more (>80%) than at others (<10% increase). Locations with greater increases are over prefrontal cortex, generally more anterior and toward the midline than the overall average topography. The significance of this topographical change was tested using ANOVA with factors of condition (Mo, ME) and topography (204 gradiometer channels) on the average power for each spindle, after normalization as suggested by McCarthy and Wood [1985]. Of interest is the interaction of condition and location (due to normalization, the main effect of condition was not significant). This interaction was highly significant (df 151,204; F = 4.31, P < 0.0001).

Figure 5.

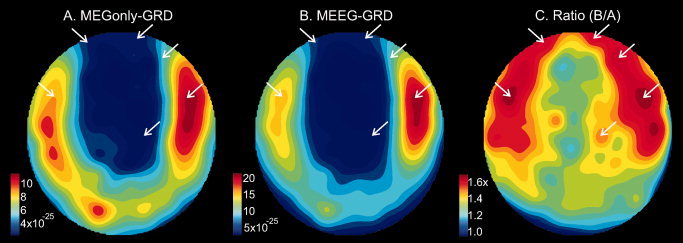
More frontal and midline MEG topography in spindles that are also seen with EEG. Topographic plots of MEG gradiometer spindle power during spindles observed only in MEG (A), in both MEG and EEG (B), and their ratio (C). Note the locations marked by white arrows in C, where the maximum signal increase was observed. These locations are anterior and toward the midline as compared to the maxima in A and B. The arrows are placed in the same locations in all three topoplots.

Time‐Course Differences Between MEG and EEG During ME Spindles

The finding that ME spindles involve more channels and a somewhat more frontal topography than Mo spindles suggests that the brain substrate of spindles which are recorded only by MEG may need to spread in order to also appear in the EEG. We tested this by examining the relative onsets of MEG and EEG discharges in ME spindles. The time‐courses of the PSD from each MEG gradiometer channel was first normalized to its maximum value in the 30‐s epoch. Then, all MEG gradiometer channel's PSDs in a given spindle were averaged together, and then normalized so that minimum to maximum ranged from 0 to 1. The same average was created for EEG and all of the spindles were then aligned to the peak (see Fig. 6). The average normalized EEG PSD values from 700 to 300 ms before its peak were significantly smaller than those of the normalized MEG PSD (paired t test, two‐tailed, P < 0.001), indicating that the MEG spindle onset precedes that of the EEG. A similar comparison of the curves during the fall of the spindle found that the MEG spindle terminated later than the EEG (paired t test, two‐tailed, P < 0.001). Taking 15% of maximum as the onset of the spindle discharge, the average curves suggest that the EEG spindle begins ∼190 ms after the MEG spindle. Using the same threshold, the EEG spindle ends ∼310 ms before the MEG spindle. If a threshold of 40% were chosen, then the corresponding values would be 100 and 140 ms. Thus, on average, the MEG gradiometer spindle both begins before and ends after the referential EEG spindle.

Figure 6.

Comparative time‐course of MEG and EEG power during ME spindles. A. Normalized power across all spindles and channels shows that MEG gradiometer activity (solid line) has increased to 15% of maximum ∼190 ms before the referential EEG (dashed line), and it falls to that level ∼320 ms after the EEG. Similarly, at 40% of maximum, MEG leads the EEG by 100ms during the rising phase, and lags it by 140 ms during the falling phase, of the spindle. B. The same pattern is seen in each of the subjects considered individually. For statistical analysis, the period from 700 to 300ms before the peak power was taken as the rise period, and from 300 to 700 ms after the stimulus to be the fall period (see text).

DISCUSSION

Our findings confirm previous studies showing dissociations in the visibility of spindles in MEG vs. EEG [Hughes et al.,1976; Manshanden et al.,2002; Nakasato et al.,1990; Urakami,2008; Yoshida et al.,1996]. The current study is the first to quantify this phenomenon using high‐density MEG and EEG recordings covering the entire head. We found that MEG spindles without EEG (Mo) often occur but not vice versa, suggesting that the neural substrate of referential EEG spindles may be dependent on the neural substrate of MEG gradiometer spindles, but not vice versa. Evidence for this was found in comparing the dynamics of MEG and EEG during spindles that were recorded with both modalities (ME), where the onset of the MEG spindle activity preceded that of the EEG spindle by about two cycles. This suggests that the substrate of the MEG spindle is usually activated first, and this may lead to activation of the neural substrate of the EEG spindle.

To gain insight into this process, we quantified the characteristics differentiating spindles where the MEG spindle substrate failed to engage that of the EEG (Mo) from those where it did (ME). MEG amplitude increased far less from Mo to ME spindles than did EEG (∼13% vs. ∼55%). Thus, the EEG amplitude increase cannot be explained by the MEG generators increasing in amplitude. Similarly, since the coherence between MEG sensors increased only slightly (∼1%) from Mo to ME spindles, an increase in the coherence of the generators underlying the MEG spindles is an unlikely explanation for why they sometimes become visible in the EEG. In contrast to these relatively small changes between Mo and ME spindles, the number of MEG sensors participating in the spindle increased ∼66%, and the topography shifted frontally.

These findings suggest that spindles may become visible in the referential EEG when a critical amount of cortex (reflected in the number of participating MEG gradiometers) becomes involved, especially in the frontal lobe. Under this hypothesis, MEG and EEG spindles represent the same generic types of underlying neural generators, with the difference being the number and location of such generators that need to be engaged for the spindle to be visible. An alternative hypothesis is that the neural generators of MEG vs. EEG spindles differ not only in number and location, but also in their basic circuitry, as we propose below. In either case, the current findings suggest that it will be necessary to revise models of spindles derived mainly from studies in animals which posit a single monolithic synchronous spindle generator during natural sleep [Contreras et al.,1997].

EEG and MEG both detect intracortical currents driven by active currents across pyramidal cell membranes [Hamalainen and Ilmoniemi,1994]. Thus, the ultimate candidate neuronal sources of EEG and MEG are identical, and the difference between them must arise from differences in the biophysics of how these sources do, or do not, propagate to the sensors. Because EEG is generated by extracellular currents, it is smeared by the CSF and skull intervening between cortex and scalp; MEG, generated by intracellular currents, is insensitive to these effects. The magnetic fields generated by radial current dipoles (i.e., perpendicular to the scalp, for example on the crowns of gyri), do not leave the head and so cannot be detected with MEG. In contrast, EEG measures both tangential and radial sources [Cohen and Cuffin,1983]. At a local level, the EEG and MEG are generated by current passing through different limbs of the same electrical circuit. However, due to biophysics, each referential EEG sensor records from a much larger cortical area (its “leadfield”) than each MEG gradiometer. Although this would seem to imply that any spindle recorded by MEG would also be seen with EEG, our results found the opposite to be true.

We propose that, paradoxically, the occurrence of MEG‐only spindles is precisely because of their small leadfields. If a focal spindle generator is in the center of the leadfield of a particular gradiometer then it will have a high SNR in that sensor, but in EEG sensors recording from the same source, the many other unrelated sources in their large leadfields would obscure the spindle, resulting in low SNR, possibly below detection threshold. Noise may be generated especially by radial generators in the crowns of gyri. These are closest to the sensors and thus the greatest contributors to EEG, but are invisible to MEG. Conversely, because EEG does integrate over such a large area, it is exquisitely sensitive to even weak sources when they are synchronous over this area. A completely synchronous and distributed source will be difficult to detect with MEG because it will largely cancel in sulcal cortex (because the dipoles in the opposite banks have opposite signs), and cannot be detected in gyral crown cortex because the source is radial. Thus, the biophysics of MEG and EEG propagation suggest that to some extent, they may be recording from different kinds of generators during spindles, highly focal vs. highly distributed, respectively. This hypothesis is supported by the observation that MEG gradiometers have generally low coherence with each other (∼0.25) during spindles, whereas referential EEG signals appear highly coherent (∼0.7) [Dehghani et al.,2010]. Furthermore, the frequency spectra of MEG and EEG during ME spindles are highly distinct, and this also implies distinct underlying neural generators [Dehghani et al., Doi:10.1016/j.clinph.2010.06.018].

These predictions are consistent with the reported relative amplitudes of referential EEG and MEG gradiometers to activation of focal versus distributed sources. Specifically, when measured as peak‐to‐peak amplitudes in μV and fT cm⁻¹, the ratio of EEG to MEG is about 0.04 for the response to electrical stimulation of the median nerve, at 20 ms, presumed to be a single focal dipole [Huang et al.,2007; Komssi et al.,2004]. In contrast, during the current spindle recordings the EEG to MEG ratio was about 2.0. Thus, if isolated focal sources were producing the MEG spindles of the observed amplitude, then the corresponding EEG spindles would only be about 2 μV in amplitude, about 50 times smaller than the observed EEG spindles and not detectable within the noise. This would suggest that EEG spindles are generated by a distributed source. Distributed sources decrease relatively little from the cortical surface to the scalp [Nunez and Silberstein,2000], and this can be inferred to be the case from combined recordings of ECOG and scalp EEG spindles, although this has not been systematically quantified [Asano et al.,2007; Nakabayashi et al.,2001]. Thus, the fact that EEG and MEG spindles can occur independently, as well as their relative amplitudes with respect to each other and to cortical recordings, are consistent with the possibility that MEG is recording from scattered focal asynchronous generators whereas EEG is recording from a highly distributed and coherent generator.

The proposal that MEG gradiometers record mainly from multiple asynchronous focal spindle generators whereas referential EEG records mainly from a single diffuse spindle generator would require that such distinct generating circuits exist for spindles. Indeed classical studies found that barbiturate spindles in cats can either be restricted to small thalamo‐cortical modules with largely independent durations, onsets, frequencies and phase, or be synchronous over wide areas [Andersen et al.,1967]. These focal vs. distributed spindles were identified with “augmenting” vs. “recruiting” responses that characterize cortical projections from the “specific” vs. “nonspecific” thalamus [Spencer and Brookhart,1961b], a distinction that is currently expressed as “matrix” vs. “core” systems [Jones,2001]. Thus, one model suggested by our data is that the EEG is more sensitive to spindles that are diffusely and synchronously generated by the matrix thalamocortical system, whereas the MEG is more sensitive to multiple focal asynchronous spindles generated by the core thalamocortical system. Both systems would be active during ME spindles, but mainly the core system would be active during Mo spindles.

Note that even if MEG gradiometers and referential EEG are seeing different neuronal sources, the current findings demonstrate that these sources are not occurring randomly with respect to each other. Intracellular studies have found that spindles emerge from interactions between inhibitory cells in the thalamic reticular nucleus and bursting thalamocortical neurons [Bazhenov et al.,2002]. The intrinsic conductances that underlie the bursting and refractoriness which drive the rhythmicity are active only in a restricted range of membrane potential [Destexhe and Sejnowski,2003]. This range occurs during Stage 2 sleep, resulting in spindles and other EEG characteristics. Although the physiology of matrix vs. core thalamic cells have not been separately determined, presumably they are similar, and this shared permissive context may be one source of the correlation demonstrated between MEG and EEG spindles, even if they do not share the same neural generators. Furthermore, connections between the matrix and core systems at several cortical and thalamic locations provide an opportunity for spindles in one system to recruit the other [Zikopoulos and Barbas,2007].

Such an interaction, starting in the core system and spreading to the matrix, could result in the observation reported here that when MEG and EEG spindles co‐occur, the spindle starts approximately two cycles earlier in the MEG. A recruitment of thalamo‐cortical domains within the core system is suggested by the finding that ME differ from Mo in having 66% more involved channels. Furthermore, the more frontal MEG topography of ME vs. Mo spindles, suggests that the recruitment of frontal areas may either activate a critical mass of domains, or trigger a widespread coherent diffuse generator necessary for the appearance of a spindle in the EEG. A special role of prefrontal areas 9, 13, and 46 in synchronizing thalamo‐cortical oscillations is suggested by their uniquely strong and widespread projections to the nucleus reticularis thalami in macaques [Zikopoulos and Barbas,2006]. In humans, Areas 9 and 46 are in the middle and superior frontal gyri, corresponding generally to where ME spindles evoked more power than Mo [Rajkowska and Goldman‐Rakic,1995].

These differences between EEG and MEG may have been smaller if more focal EEG derivations (bipolar or Laplacian), and/or less focal MEG magnetometers had been compared rather than referential EEG to MEG gradiometers. However, our intent is not to draw a general conclusion about EEG and MEG, but to note how biophysical differences between referential EEG and gradiometer MEG may reveal different aspects of the spindle generating system. Specifically, we hypothesize that referential EEG's biophysically‐determined sensitivity to diffuse activation allows it to record spindles generated by the matrix thalamocortical system, whereas gradiometer MEG's sensitivity to focal sources allows it to record spindles generated by the core system. Confirmation of this hypothesis will depend on intracranial recordings and modeling studies. The quantification in the current results provides essential constraints and checks on those models.

Supporting information

Additional Supporting Information may be found in the online version of this article.