Abstract
Probabilistic methods have the potential to generate multiple and complex white matter fiber tracts in diffusion tensor imaging (DTI). Here, a method based on dynamic programming (DP) is introduced to reconstruct fibers pathways whose complex anatomical structures cannot be resolved beyond the resolution of standard DTI data. DP is based on optimizing a sequentially additive cost function derived from a Gaussian diffusion model whose covariance is defined by the diffusion tensor. DP is used to determine the optimal path between initial and terminal nodes by efficiently searching over all paths, connecting the nodes, and choosing the path in which the total probability is maximized. An ex vivo high-resolution scan of a macaque hemi-brain is used to demonstrate the advantages and limitations of DP. DP can generate fiber bundles between distant cortical areas (superior longitudinal fasciculi, arcuate fasciculus, uncinate fasciculus, and fronto-occipital fasciculus), neighboring cortical areas (dorsal and ventral banks of the principal sulcus), as well as cortical projections to the hippocampal formation (cingulum bundle), neostriatum (motor cortical projections to the putamen), thalamus (subcortical bundle), and hippocampal formation projections to the mammillary bodies via the fornix. Validation is established either by comparison with in vivo intracellular transport of horseradish peroxidase in another macaque monkey or by comparison with atlases. DP is able to generate known pathways, including crossing and kissing tracts. Thus, DP has the potential to enhance neuroimaging studies of cortical connectivity.
Key words: anatomic connectivity, fiber tracking, structural connectivity
Introduction
The advent of diffusion tensor imaging (DTI) technology is enabling clinicians and neuroscientists to examine normal and impaired connectivity in the mammalian brain (Basser et al., 2000; Conturo et al., 1999; Mori et al., 1999; Pace and Pierpaoli, 1963; Parker et al., 2002a; Poupon et al., 2000). DTI encapsulates the directionality of water diffusion along fibers constituting tracts or bundles between these structures (Basser et al., 1994a; Le Bihan et al., 1989; Pierpaoli et al., 1996; Xue et al., 1999). The diffusion tensor, D, is a 3×3 tensor, that is, a symmetric matrix whose eigenvectors and eigenvalues define an ellipsoid that can describe the diffusive characteristics of water at each voxel in the image despite being at a lower resolution than that of the individual axons in the tracts (Basser et al., 1994a; Beaulieu, 2002). The principal eigenvector associated with the largest eigenvalue represents the direction of fastest diffusion of water in the volume. Application of these essential properties of water diffusion have led to the development of a wide range of methods for elucidating connectivity of gray matter structures and segmentation of white matter (WM) in the past decade (Basser and Jones, 2002; Johansen-Berg and Rushworth, 2009; Le Bihan et al., 2001; Mori and van Zijl, 2002; Ramnani et al., 2004; Tournier et al., 2011).
Fiber tracking methods can be generally classified as either deterministic (Basser et al., 2000; Conturo et al., 1999; Hageman et al., 2009; Mori et al., 1999; Poupon et al., 2000) or probabilistic (Acar and Yörük, 2009; Behrens et al., 2003; Friman and Westin, 2005; Jbabdi et al., 2007; Jonasson et al., 2005; Sherbondy et al., 2008). However, both approaches have limitations such as inability to discriminate crossing fibers, low signal-to-noise ratio (SNR), and poor tracking in regions of low anisotropy (Jbabdi and Johansen-Berg, 2011; Lazar and Alexander, 2003; Le Bihan et al., 2006; Moldrich et al., 2010; Mukherjee et al., 2008; Tournier et al., 2002). In particular, deterministic methods rely on tracking the principal eigenvector and thus do not continue tracking into regions in which anisotropy is typically low, and the principal eigenvector is a less reliable indication of fiber orientation. More recently, a new class of probabilistic methods has emerged that can overcome some of these shortcomings. Posing the problem as an optimization problem enables computation of a “shortest path” between chosen initial and terminal points that globally minimizes a sequentially additive energy constraint defined by the tensor in the spirit of the classical Djikstra's algorithm (Everts et al., 2009; Fout et al., 2005; Iturria-Medina et al., 2007; Lal, 2004; Lifshits et al., 2009; Merhof et al., 2006a, 2006b; Poynton et al., 2005; Zalesky, 2008; Zalesky and Fornito, 2009). These assign a probability distribution to the local orientation of fibers at each voxel, and use path finding methods to compute the optimal path between two regions.
This article focuses on the use of dynamic programming (DP) as the optimization procedure by implementing the algorithm originally developed by Lal (2004) and Poynton et al. (2005) in the widely used MRIStudio software (Jiang et al., 2006). In particular, the probabilistic law for diffusion in the Lal algorithm is modified to ensure that optimal paths through isotropic tensors are not affected by the magnitude of the tensor and then, a modification of cost per unit length as a connectivity metric, originally proposed by Poynton et al. (2005), is introduced to facilitate pruning of fibers that are not anatomically valid. An ex vivo macaque hemi-brain is used for validation, and the advantages of this approach as an alternative to using phantom data are discussed.
Methods
Probabilistic labeling of paths
By defining a node as the voxel center and a path as an initial node x0 and a set of direction vectors 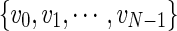 connecting nodes
connecting nodes 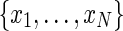 , a probability distribution can be induced on fiber tract orientation at each node, enabling the computation of the probability of a path as the product of the probabilities of the transitions between subsequent nodes along the path. A voxel j is in the neighborhood of voxel i if j is immediately adjacent to i in the 26-connected sense. There is a direct transition from node xi to node xj, representing the centers of voxels i and j, respectively, if and only if j is in the neighborhood of i. The state space of all nodes should be defined by appropriate thresholds on scalar quantities such as fractional anisotropy, ignoring voxels below a specified value. DP can then be used to compute the maximal probability path linking two nodes in the state space and the basic algorithm extended to compute K nonintersecting paths between a set of initial and terminal nodes.
, a probability distribution can be induced on fiber tract orientation at each node, enabling the computation of the probability of a path as the product of the probabilities of the transitions between subsequent nodes along the path. A voxel j is in the neighborhood of voxel i if j is immediately adjacent to i in the 26-connected sense. There is a direct transition from node xi to node xj, representing the centers of voxels i and j, respectively, if and only if j is in the neighborhood of i. The state space of all nodes should be defined by appropriate thresholds on scalar quantities such as fractional anisotropy, ignoring voxels below a specified value. DP can then be used to compute the maximal probability path linking two nodes in the state space and the basic algorithm extended to compute K nonintersecting paths between a set of initial and terminal nodes.
Since evidence suggests that the directionality of the diffusion depends on the orientation of axonal fibers, it is reasonable to assume that the orientation of fibers follows the same Gaussian distribution as that of the diffusion of water molecules (Alexander et al., 2000). With this assumption, the problem of tracking fibers is reduced to the problem of computing the path between two nodes in a graph that minimizes a cost function determined by the eigenvalues of the covariance representation of the quadratic form in a sequentially additive quadratic cost. More sophisticated probability models characterizing diffusion have recently been developed (Friman and Westin, 2005; Sherbondy et al., 2008; Tuch, 2004) and can be incorporated into this method as long as the probability distribution for the diffusion at a particular voxel remains locally defined.
It is essential that the probability of Gaussian diffusion over unit time be the same for isotropic diffusion; so, the diffusion tensor at voxel i, Di, is normalized by its trace Tr(Di), that is, 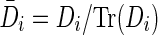 (Frandsen et al., 2007). Let
(Frandsen et al., 2007). Let 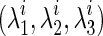 and
and 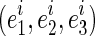 be, respectively, eigenvalues and unit eigenvector of Di such that
be, respectively, eigenvalues and unit eigenvector of Di such that 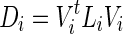 , where
, where 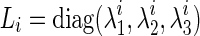 and
and 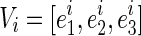 . If
. If 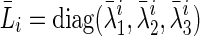 where
where 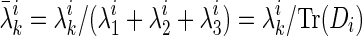 , it can be shown that
, it can be shown that 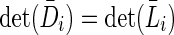 and
and 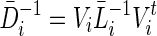 .
.
We need to define the probability associated with a transition between connected nodes xi and xi+1 to have a Gaussian distribution with covariance matrix 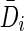 . Then, the probability of an N-length path πN(x0, xN) is given by the product of the quadratic form of the individual directional vectors dj between nodes along the path as
. Then, the probability of an N-length path πN(x0, xN) is given by the product of the quadratic form of the individual directional vectors dj between nodes along the path as
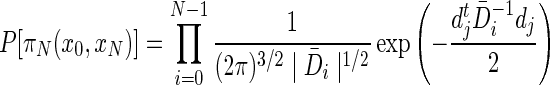 |
(1) |
that implicitly assumes diffusion between any adjacent voxel irrespective of length in a fixed time of τ=0.5 (Alexander et al., 2000).
By considering logarithms, the maximum probability N-length path π* (x0, xN) is given by the minimization of the negative log likelihood
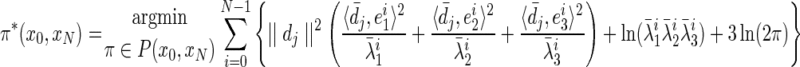 |
(2) |
where 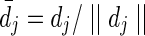 is the unit directional vector, and P(x0, xN) is the set of all paths between nodes x0 and xN; see Lal (2004) for proof. Note that the constant term is retained to ensure that the transition cost is positive. The path
is the unit directional vector, and P(x0, xN) is the set of all paths between nodes x0 and xN; see Lal (2004) for proof. Note that the constant term is retained to ensure that the transition cost is positive. The path 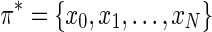 that minimizes this function is the optimal path.
that minimizes this function is the optimal path.
Dynamic programming
The problem of determining the optimal path reduces to one of computing the minimum energy path linking initial and terminal nodes in the state space. Let S be the finite collection of nodes of size ||S||=M and define ck(i, j) as the cost of the transition from 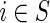 to
to 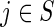 at time k. If the cost is additive over the length of the path, and the optimal path between two points is assumed to pass through no more than N nodes, then there may be as many as MN paths linking two nodes, assuming the most complex case in which all nodes are connected to each other, that is, have a valency of M. Carrying out a brute force search would require considering the cost associated with each of these paths, and such an approach would very quickly become computationally impractical as N and M become large. DP overcomes this problem, as it reduces the complexity of the search to order of NM2 by taking advantage of the fact that the cost function being minimized is sequentially additive. Note that while most practical implementations simplify the graph such that the connectedness or valency (V) of each node is less than M, for example, 6 or 26, the brute force search's performance will be in the order of MVN, which is still computationally impractical as N gets large.
at time k. If the cost is additive over the length of the path, and the optimal path between two points is assumed to pass through no more than N nodes, then there may be as many as MN paths linking two nodes, assuming the most complex case in which all nodes are connected to each other, that is, have a valency of M. Carrying out a brute force search would require considering the cost associated with each of these paths, and such an approach would very quickly become computationally impractical as N and M become large. DP overcomes this problem, as it reduces the complexity of the search to order of NM2 by taking advantage of the fact that the cost function being minimized is sequentially additive. Note that while most practical implementations simplify the graph such that the connectedness or valency (V) of each node is less than M, for example, 6 or 26, the brute force search's performance will be in the order of MVN, which is still computationally impractical as N gets large.
There are many ways of implementing DP. The present implementation is described in Algorithm 1 next. Let Hx be the set of nodes {n} such that a direct transition between x and n exists, the cost ck(xi, xj) for 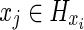 following the probabilistic model described by Equation (2), and ck(xi, xj)=∞ for
following the probabilistic model described by Equation (2), and ck(xi, xj)=∞ for 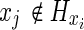 . The optimal N-length cost J0 (s) from s to t is given by the final step of the algorithm evaluated at i=s. Note that the algorithm permits the degenerate move from a node i to itself with cost ck(i, i)=0 for all i, thus allowing paths with length less than N to be included.
. The optimal N-length cost J0 (s) from s to t is given by the final step of the algorithm evaluated at i=s. Note that the algorithm permits the degenerate move from a node i to itself with cost ck(i, i)=0 for all i, thus allowing paths with length less than N to be included.
| Algorithm 1. Initialize: Jk (i)=∞ i≠t, Jk (t)=0 for all k; SN={t}; |
| For every k=N−1 to 0, |
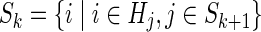 ; ; |
set ck (i, j) from Equation (2), 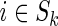 and and 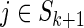 . . |
set 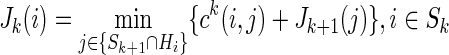
|
| end |
Here, the state space Sk is defined as the subset of nodes that can be reached from the initial node in k steps with a finite cost. This further optimizes the search pattern by only considering the restricted state spaces Sk ⊂ S at each iteration. Thus, many of the M2 paths at each iteration can be ignored without compromising the condition of optimality.
It follows that if the cost of the optimal k length paths from the initial node to all nodes in the state space is known, then the optimal k+1 length paths to all nodes in the state space can be found by examining at most M2 paths. So, since k is iterated from 0 to N−1, DP computes the optimal path by considering NM2 or fewer paths; instead of the MN paths, a brute force search would be required.
Computing a single optimal path between two regions has little practical use, as any two brain structures are linked by a bundle comprising multiple fibers. Thus, there is a need to find a most probable set of distinct fibers connecting the two regions. This is achieved by altering the state space as follows. Given an initial set of nodes S and a terminal set of nodes T, introduce two “dummy nodes” s and t into the state space, such that there is a transition from s to every node in S in the first time step with cost 0, and there is a transition from every node in T to node t with cost 0, at all time steps. Hence, 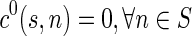 , and
, and 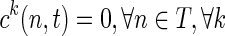 .
.
The path formed by removing the first and last arcs from the optimal path between nodes s and t is the optimal path between the sets of nodes S and T; see Lal (2004) for proof. So, the introduction of the “dummy nodes” into the state space allows for the computation of the optimal path between an initial set of nodes and a terminal set of nodes. So, to extend the search process to find K distinct paths between two sets of nodes, the DP algorithm is performed via a modification in the search space described in Algorithm 2 next.
One iteration of the DP algorithm gives the optimal path 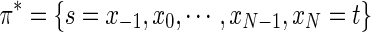 . Let Hx represent the neighborhood of node x. For all nodes xi, 0≤i≤N−1 along the optimal path π*, set Hxi=Ø. This step cuts off all the connections from the nodes along the path to all its neighboring nodes, effectively removing the nodes from the search space. The next iteration of the DP algorithm directly follows, which will find the most probable path in the modified search space, a path that is completely distinct from the previous paths found.
. Let Hx represent the neighborhood of node x. For all nodes xi, 0≤i≤N−1 along the optimal path π*, set Hxi=Ø. This step cuts off all the connections from the nodes along the path to all its neighboring nodes, effectively removing the nodes from the search space. The next iteration of the DP algorithm directly follows, which will find the most probable path in the modified search space, a path that is completely distinct from the previous paths found.
| Algorithm 2. Determine the optimal path from every node in S to xN , and let the optimal path from x−1 to xN be p1. Let F be a list of paths, initially empty. |
| Initialize p=p1, k′=1 and F[1]=p. |
| While an alternative to p exists and k′≤K |
For every 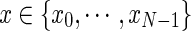
|
| update Hxi=Ø |
| end |
| set p equal to the optimal path from x−1 to xN, k′=k′+1 and F[k′]=p. |
| end |
The number of fibers K is a free parameter that can be empirically used. This can be done by generating a large number of fibers and selecting the first K generated fibers based on when the fibers begin to deviate from the bundle's true geometry and location. Unfortunately, this information may not be known a priori. If one chooses K sufficiently small, it is much less likely that a fiber generated will deviate to a great extent from the most optimal fiber in the bundle.
Connectivity metric
Following Lal (2004), Poynton et al. (2005) proposed a measure of the fiber bundle containing K fibers via 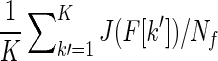 , where J(F[k′]) is the cost of a fiber, F[k′], computed from Equation (2) and Nf is the number of nodes along F[k′]. However, a more meaningful measure can be obtained from J(F[k′])/L(F[k′]), where L(F[k′]) is the length of the fiber, that can be construed as a connectivity metric (Jackowski et al., 2004; Marigonda and Orlandi, 2011; Merhof et al., 2006b; Parker et al., 2002b; Pichon et al., 2005).
, where J(F[k′]) is the cost of a fiber, F[k′], computed from Equation (2) and Nf is the number of nodes along F[k′]. However, a more meaningful measure can be obtained from J(F[k′])/L(F[k′]), where L(F[k′]) is the length of the fiber, that can be construed as a connectivity metric (Jackowski et al., 2004; Marigonda and Orlandi, 2011; Merhof et al., 2006b; Parker et al., 2002b; Pichon et al., 2005).
Data acquisition and processing via MRIStudio
Following Oishi et al. (2011), one rhesus monkey (Macaca mulatta) brain was perfusion fixed using 4% paraformaldehyde and scanned using a 4.7T Bruker scanner. A three-dimensional multiple spin-echo diffusion tensor sequence was used to acquire a set of diffusion-weighted images in seven linearly independent directions (Zhang et al., 2003). Parameters were as follows: echo time (TE)=32.5 ms, TR=0.7 sec, field of views (FOV)=80×58×60 mm (zero-filled to a data matrix=186×256×192 with nominal resolution 0.312×0.312×0.312 mm3), and b=1000 sec/mm2. Co-registered T2-weighted images with the same FOV were also acquired with the fast spin-echo sequence via TE=15 ms and TR=1 sec (Huang et al., 2006). A left-sided hemi-brain volume was then created with the data resampled to 0.2×0.2×0.2 mm3 and zero-filled matrix size 240×480×320. The dataset was transferred to a workstation and processed using MRIStudio (Jiang et al., 2006). After inspection, the six independent elements of the 3×3 diffusion tensor were calculated for each pixel by using the multivariate linear-fitting method. After diagonalization, three eigenvalues and three eigenvectors were obtained (Basser et al., 1994b) and used to calculate the fractional anisotropy. DP was implemented in MRIStudio to take advantage of the editing features such as Boolean operations developed for fibers generated by the Fiber Assignment by Continuous Tracking (FACT) algorithm. Three-dimensional screenshots of fibers were taken in CAWorks (www.cis.jhu.edu/software/caworks).
Anatomical regions of interest
Anatomical regions of interest (ROIs) were manually segmented in the T2 volume using the Schmahmann and Pandya (SP) atlas (Schmahmann and Pandya, 2006). The T2 modality was chosen, as it had a similar contrast as the atlas. It should be noted that electrophysiologic stimulation was not used to confirm anatomical correspondence and that with the exception of the putamen, it was necessary to include WM subjacent to the gray matter structure.
(1) Walker's area 46 encompasses the WM lying subjacent to the principal sulcal cortex (area 46) along its entire rostro-caudal extent.
(2) Dorsal Cingulum Bundle (CB) consists of the CB at the level of the cingulate motor area just rostral to the intersection of the central sulcus with the medial face of the hemisphere. The CB at this level is surrounded by the cortex of area 23, 30, and 29 medially and by cortical WM laterally.
(3) Ventral CB is situated in the WM protrusion that underlies the most caudal portion of the presubiculum and the transitional cortices (areas 29 and 30) forming the caudomedial lobule of Goldman–Rakic et al. (1984).
(4) Mediodorsal Thalamus is located in the ventral portion of the subcortical bundle (SB) just caudal to the decussation of the anterior commissure. This portion of SB forms a portion of the boundary between the rostral globus pallidus and the body of the caudate nucleus.
(5) Principal Sulcus Dorsal Bank is located in the cortex lining the dorsal bank of the principal sulcus (area 46), encompassing the middle third of the rostral-caudal extent of area 46 and stretching from the dorsal border with area 9 along the bank of the sulcus approximately two-third the distance to the depth of the sulcus.
(6) Principal Sulcus Ventral Bank is situated in the middle third of the rostrocaudal extent of the principal sulcal cortex (area 46) and stretches from the ventral lip of the sulcus to approximately two-third the distance to the depth of the sulcus.
(7) Frontal Superior Longitudinal Fasciculus II-Version A (SLFII-FrontalA) begins midway along the rostro-caudal extent of the principal sulcus and includes the cortex of the dorsal bank of the principal sulcus (area 46) and cortex on the lateral two-third of the superior frontal gyrus (area 9d). More caudally, the ROI extends into the cortex surrounding the superior spur of the arcuate sulcus (8Ad) and onto the adjacent cortex on the dorsal convexity (6d). Far caudally, this ROI is limited to the depths and medial bank of the superior arcuate sulcus (6d).
(8) Parietal Superior Longitudinal Fasciculus II-Version A (SLFII-ParietalA) is located in the cortex, forming the caudal half of the lateral bank of the intraparietal sulcus (area POa) and adjacent ventral convexity (areas PG and Opt).
(9) Frontal Superior Longitudinal Fasciculus II-Version B (SLFII-FrontalB) includes the nearly the entire dorsal bank of the principal sulcus (area 46), excluding only the rostral quarter. The ROI encroaches onto the adjoining dorsal convexity (area 9d), but only slightly. More caudally situated cortices (8Ad and 6d) were not included in order to generate kissing or crossing fibers with the arcuate fasciculus (AF; see below).
(10) Parietal Superior Longitudinal Fasciculus II-Version B (SLFII-ParietalB) includes nearly the entire lateral bank of the intraparietal sulcus (area POa), with only the rostral quarter not included, and the most caudal region of the cortex on the inferior parietal lobule (areas PG and Opt). Near the caudal tip of the lateral fissure, there is marginal encroachment of the ROI onto the cortex of the convexity (PFG). This ROI was intentionally made larger than that of SLFII-ParietalA to try to generate kissing or crossing fibers.
(11) Frontal Superior Longitudinal Fasciculus III (SLFIII-Frontal) is situated in the cortex forming the ventral bank of the inferior spur of the arcuate sulcus (areas 44, 6v) and in the caudal extension of premotor area 6v on the precentral gyrus.
(12) Parietal Superior Longitudinal Fasciculus III (SLFIII-Parietal) is located in the rostral parietal cortex just ventral to the rostral tip of the intraparietal sulcus (area PF) and encompassing the cortex between the intraparietal sulcus and the lateral fissure (areas PFG and PFop).
(13) Frontal Arcuate Fasciculus (AF-Frontal) consists of the cortex forming the ventral (area 8A) and dorsal banks (area 6d) of the superior spur of the arcuate sulcus. Note that the area 46/9 components of this ROI were intentionally excluded to generate kissing or crossing fibers.
(14) Temporal Arcuate Fasciculus (AF-Temporal) includes the cortex lining the dorsal bank of the superior temporal sulcus (area TPO) and caudal portions of the superior temporal gyrus (area Tpt) adjacent to TPO.
(15) Frontal Occipital Fasciculus (FOF-Frontal) extends rostrally from the approximate midpoint of the principal sulcus, where the ROI occupies the dorsal bank of the principal sulcus (46d). It extends onto the adjacent dorsal convexity (9d), encroaching on the adjacent medial cortex (9m). More caudally, the ROI includes the cortex surrounding the superior spur of the arcuate sulcus and bordering convexities (8Ad and 6d), as well as 46d. The most caudal portion of the ROI is present at the level where the principal sulcus ends and includes only the dorsal bank of the superior spur of the arcuate sulcus (6d).
(16) Frontal Occipital Fasciculus (FOF-PO) is located in the medial occipital lobe in the cortex lining the medial bank of the intraparietal sulcus (PO) and extending through the adjacent WM to include the cortex on the medial wall of the hemisphere (PGm). The most caudal origin of the FO (PO) was chosen as the second ROI in order to generate the full longitudinal extent of the FOF (as illustrated by Case 17 of SP).
(17) Fornix-Mammillary Bodies (MMB) includes the MMB of the thalamus.
(18) Fornix-Fimbria is located in the caudal most portion of the fimbria near the splenium of the corpus callosum. The fimbria at this level is situated just medial to the caudal extent of the lateral ventricle and to the caudal most, elongated portion of the caudate nucleus.
(19) Frontal Uncinate Fasciculus (UF-Frontal) is limited to a finger of WM lying subjacent to area 14 of the rostral orbitofrontal cortex in one coronal section (95) corresponding roughly to Section 20 of SP.
(20) Temporal Uncinate Fasciculus (UF-Temporal) also consists of a slender finger of WM located in the rostral temporal lobe between the amygdala and the lateral temporal cortices TE1, TE2 and extending ventrally to lie just subjacent to areas TL and 35. This ROI is restricted to one coronal section (164) that corresponds to Section 57 of SP.
(21) SP Motor Case 24 is situated in cortex lining the frontal operculum, or dorsal lip of the lateral fissure, in the precentral gyrus (areas 1 and 2).
(22) SP Motor Case 25 is located in the face representation cortex in the ventral precentral gyrus (area 4).
(23) SP Motor Case 26 is located in the hand motor area of the precentral gyrus (area 4).
(24) SP Motor Case 27 is situated in the motor trunk representation of the precentral gyrus (area 4).
(25) SP Motor Case 28 includes the dorsal portion of the precentral gyrus (area 4), corresponding to the foot motor area.
(26) SP Motor Case 29 is located on the medial surface of the superior frontal gyrus, just dorsal to the cingulate sulcus, in the rostral supplementary motor area associated with the face representation (area 6m).
(27) Putamen includes the entire rostro-caudal extent of the putamen. It extends from the rostral-most portion located ventrolateral to the anterior limb of the internal capsule (IC) to its most caudal portion lateral to the globus pallidus and dorsal to the tail of the caudate nucleus.
Delineation of fiber tracts with intracellular transport of horseradish peroxidase
A comparison with postmortem tracing data was performed via visual examination of histologically processed sections from a different Rhesus macaque monkey. This monkey had horseradish peroxidase (HRP) pellets implanted in the dorsal and ventral banks of the principal sulcus in order to identify fiber tracts connecting Walker's area 46 with other brain regions. Details of the surgical procedure, perfusion, and histological processing have been previously described (Selemon and Goldman-Rakic, 1985) (case 14). Eight HRP pellets were implanted in this monkey, resulting in a large injection site that encompassed the caudal two-third of the Walker's area 46 (Brodmann areas 9, 10) and encroached caudally on adjacent Brodmann areas 8 and medially on area 6 (see Figs. 8 and 9 in Selemon and Goldman–Rakic, 1985). This monkey also received an injection of tritiated amino acids in the posterior parietal cortex.
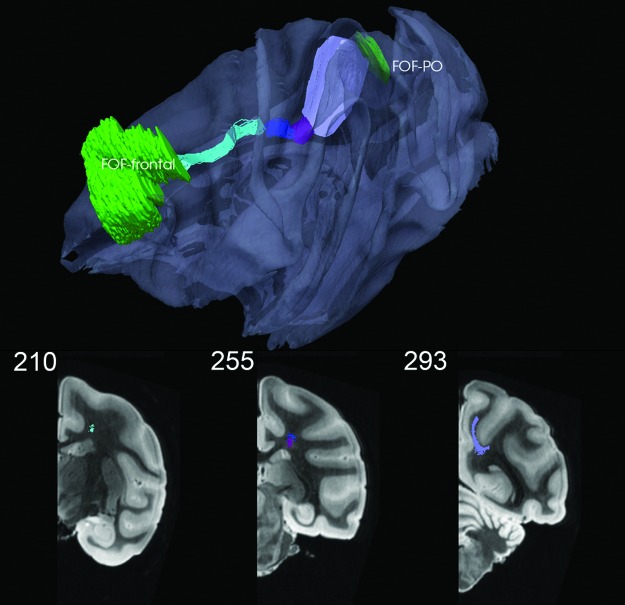
FIG. 8.
FOF-frontal to FOF-PO via four different bundles and three waystations. Here, the color code for the connection metric is not used. Coronal views shown in bottom row; see also movie at http://cis.jhu.edu/data.sets/macaque_hemi-brain_fiber_tracking/
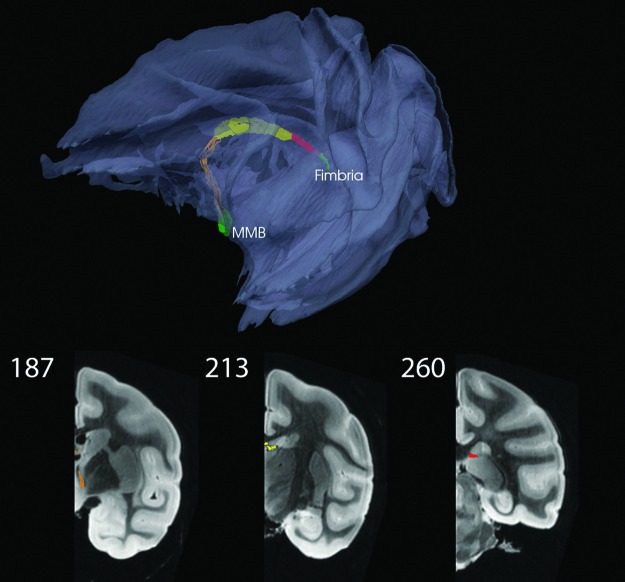
FIG. 9.
Fornix–Fimbria to mammillary bodies (MMB) via three different bundles and two waystations. Here, the color code for the connection metric is not used. Coronal views shown in bottom row; see also movie at http://cis.jhu.edu/data.sets/macaque_hemi-brain_fiber_tracking/
Results
Except where stated, the following results were obtained with a threshold of 0.4 for FA, which is consistent with Oishi et al. (2011).
Single transition cost
The cost of a transition from one node to seven possible adjacent nodes for different types of diffusion tensors is both tensor and length dependent (Table 1). This cost assessment is consistent with the Gaussian diffusion model first formulated by Alexander et al. (2000).
Table 1.
Transition Costs from One Node to Seven Adjacent Nodes via the Black Directional Vector (Top Row) Based on the Tensor Shape and Orientation at the Start Node (First Column)
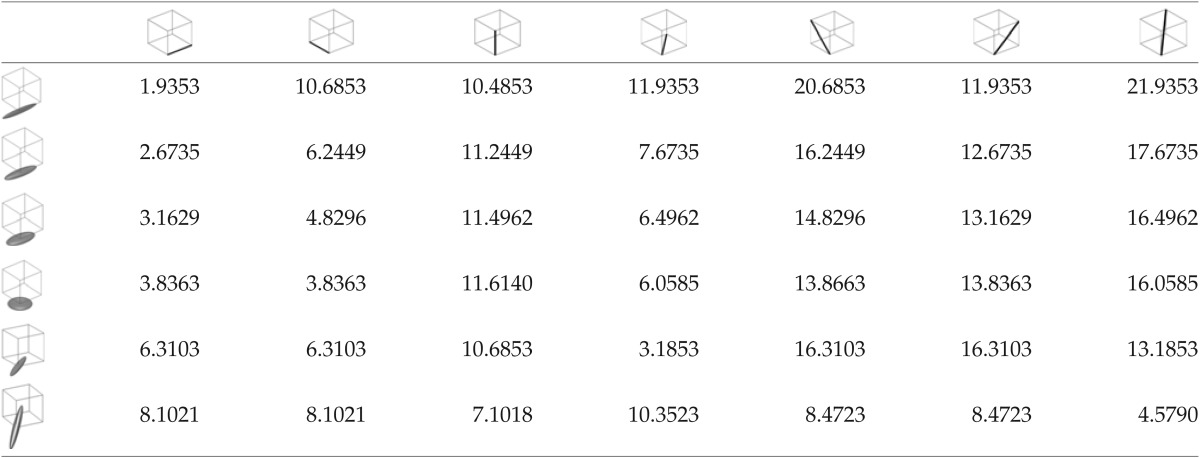 |
Caveats due to high anisotropy bias, resolution, and ROI proximity
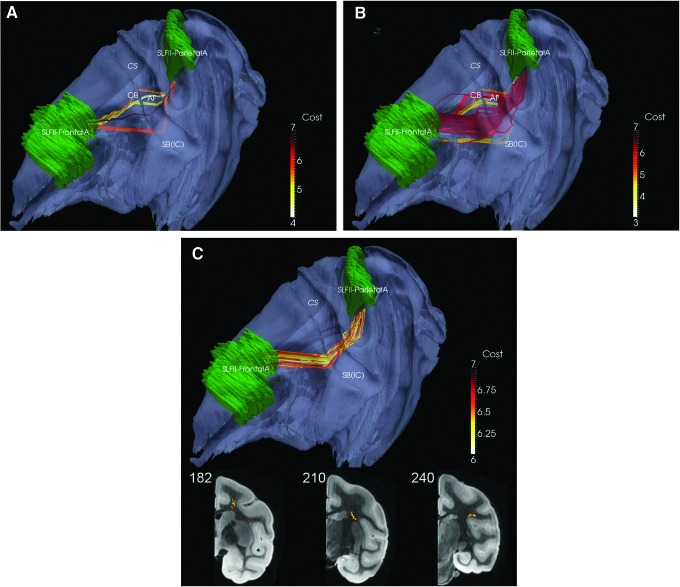
The number of fibers (K) should be as large as possible to resolve problems that arise due to fibers with high anisotropy bias and to closely aligned fiber bundles. These are illustrated by generation of SLFII using SLFII-FrontalA and SLFII-ParietalA ROIs with K=20 (Fig. 1A) in a comparison to generation of this same fiber bundle with K=200 (Fig. 1B). When K=20, three distinct paths are generated: one through the CB, one along the expected SLFII, and one through the IC and the SB. The deviant bundles through the CB and IC probably arise due to the strong projections from both frontal and parietal cortices to the CB and IC (Selemon and Goldman-Rakic, 1988). At this voxel resolution, DP is confounded by the close proximity of these frontal and parietal bundles in the CB and the IC. It should be noted, however, that the lateral bundle, that is, the one which courses through the SLFII, has lower cost (indicated by the lighter color) than the other two. At larger values of K such as 200 (Fig. 1B), the lower cost or equivalently higher probability SLFII bundle is partially masked by the presence of a fourth bundle, not seen with the fewer fibers, which appears to be a part of the AF and exhibits higher anisotropy bias than the one through the CB. A strategy which utilizes the connectivity metric-based color code to identify fibers for editing and then employs the AND/NOT editing feature in MRIStudio to prune these anatomically inconsistent fibers results in a representation of the SLFII that is consistent with the classic Schmahmann and Pandya (2006) anatomical tracings (Fig. 1C). Thus, several factors can generate incorrect fibers: the bias to high anisotropy, the tendency to pass from one to the other of two closely aligned fiber bundles, and the tendency to prefer shortest paths. To compensate for these factors, it is important to generate as many fibers as possible (K=200) and to use the color-coded connectivity metric to prune incorrect fibers.
FIG. 1.
Parietal Superior Longitudinal Fasciculus II-Version A (SLFII-ParietalA) to Frontal Superior Longitudinal Fasciculus II-Version A (SLFII-FrontalA): (A) K=20 fibers; (B) K=200 fibers; (C) K=67, after pruning. Central Sulcus (CS), arcuate fasciculus (AF), cingulum bundle (CB) and subcortical bundle (SB) [internal capsule (IC)] are marked as reference points. Coronal views for 1C shown in last row; see also movie at http://cis.jhu.edu/data.sets/macaque_hemi-brain_fiber_tracking/
The need for “way stations” in long association bundles
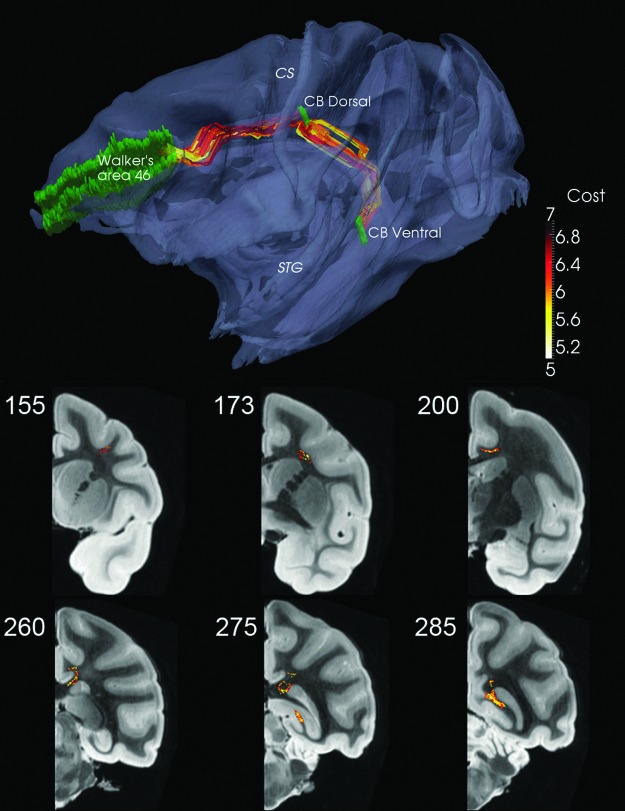
Some fiber bundles that exhibit a long traverse coupled with an extreme change of direction may require a “way station.” This is illustrated by the CB, a fiber bundle that connects many cortical areas with the hippocampal formation. Only connectivity between the dorsolateral prefrontal cortex (Walker's area 46) and the hippocampal formation was examined. In order to override the tendency for DP to prefer the shortest path between these two ROIs and thereby avoid the most caudal portion of the CB that curves around the splenium of the corpus callous, a third ROI, the dorsal CB was used as a way station (Fig. 2).
FIG. 2.
Walker's area 46 to CB Dorsal with K=49 and thence to CB Ventral with K=68. CS and the superior temporal gyrus (STG) are marked as reference points. Coronal views for Walker's area 46 to CB Dorsal shown in middle row and for CB Dorsal to CB Ventral in bottom row; see also movie at http://cis.jhu.edu/data.sets/macaque_hemi-brain_fiber_tracking/
Comparison with in vivo tract tracing
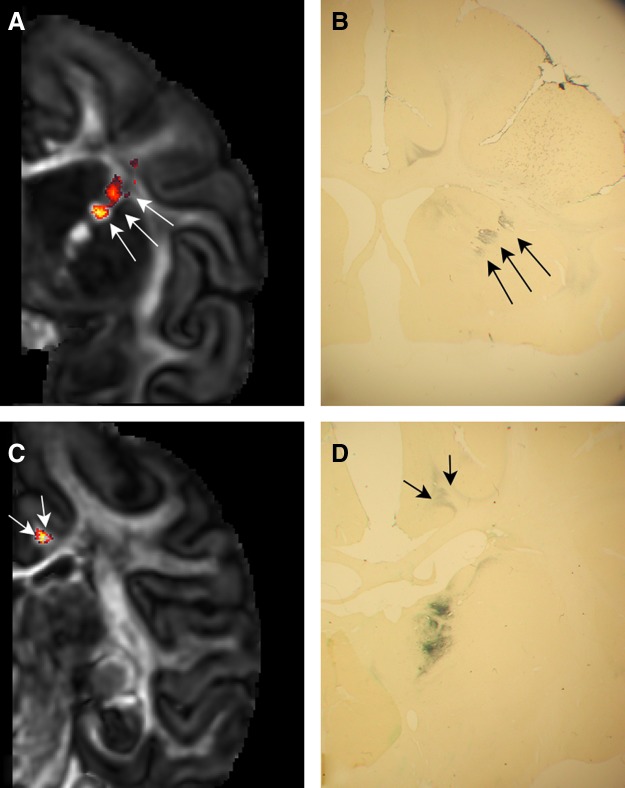
Coronal sections through a macaque brain in which HRP had been placed in the dorsolateral prefrontal cortex (Walker's area 46) and anterogradely transported into the fiber bundles of the CB and SB were compared with DP-generated fibers (Fig. 3). HRP-labeled fibers were found in the fiber bundles of the SB in the anterior limb of the IC (Fig. 3A, B) and in the CB (Fig. 3C, D).
FIG. 3.
Automated fiber tracking of the SB and CB in comparison to the same tracts shown via horseradish peroxidase (HRP) tract tracing. Arrows in (A, B) point to the SB as it courses through the anterior limb of the IC. Arrow heads in (C, D) show the CB encapsulated by the posterior cingulate cortex.
Short- and long-association cortico-cortical bundles
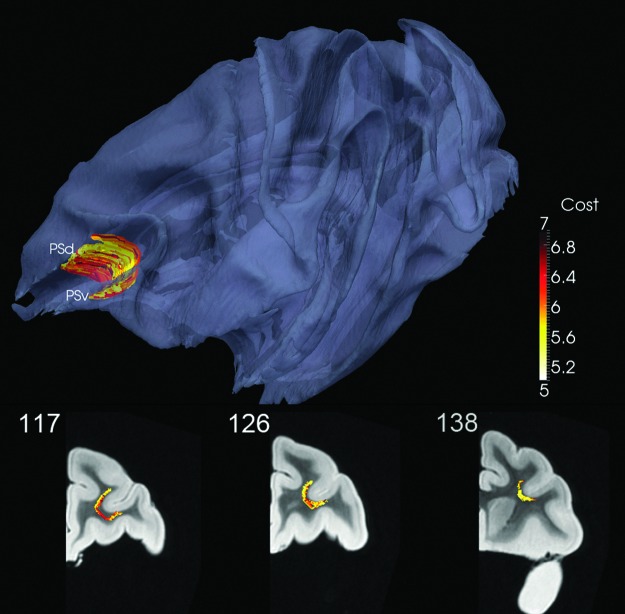
DP-generated fibers based on ROIs in the ventral and dorsal banks of the principal sulcus formed a short, U-shaped association cortico-cortical bundle in the WM beneath the fundus of the principal sulcus (Fig. 4). Note that no fibers traversed the geodesic between the two ROIs despite their proximity.
FIG. 4.
Principal sulcus (PS) from ventral (v) to dorsal (d) banks (K=200). Coronal views shown in bottom row; see also movie at http://cis.jhu.edu/data.sets/macaque_hemi-brain_fiber_tracking/
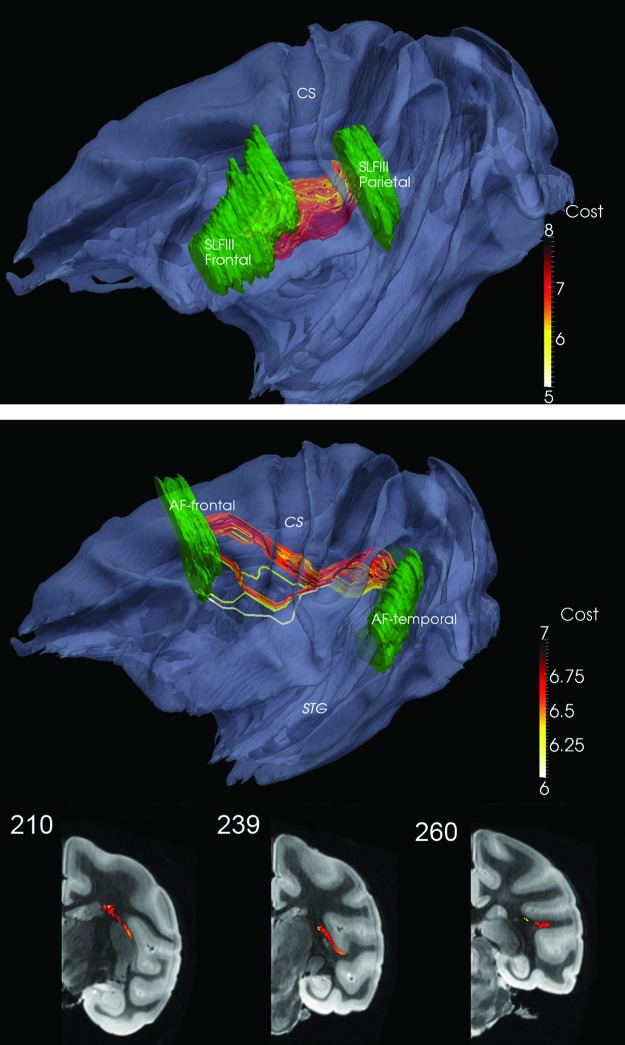
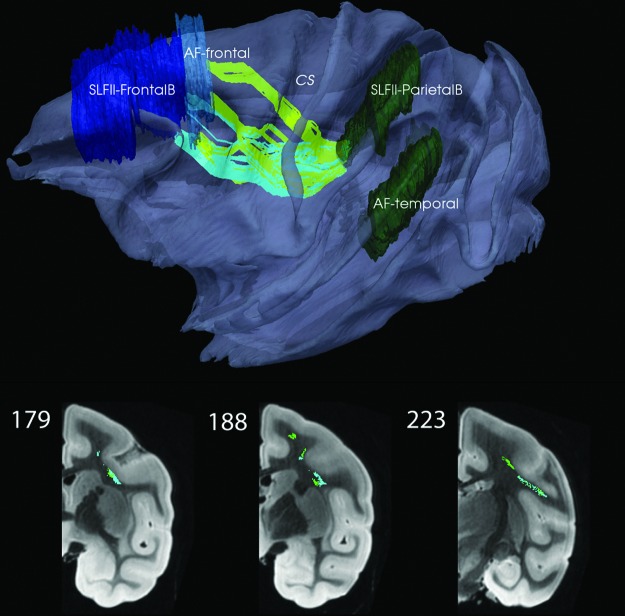
Long-association bundles for SLFIII and AF were generated (Fig. 5). In the latter case, it was necessary to use K=800 and to prune the inconsistent fibers that either due to high anisotropy bias or geodesic tendency were ranked higher; indeed, the highest rank of the fiber in the edited AF bundle (K=64) was 302. In addition, two bundles were generated with the SLFII-FrontalB and AF-Frontal as two separate start ROIs and the SLFII-ParietalB and AF-Temporal combined as one end ROI. The two edited bundles (K=104 and 82, respectively) are seen to merge, that is, cross or kiss as they approach the SLFII-ParietalB ROI (Fig. 6). In each case, K=400 was initially used with some of the fibers similar to those in Figure 5 edited out.
FIG. 5.
Top: SLFIII Frontal to Parietal (K=200). Middle: AF Frontal to Temporal (K=64). CS and STG are marked as reference points. Bottom: Coronal views of AF Frontal to Temporal; see also movie at http://cis.jhu.edu/data.sets/macaque_hemi-brain_fiber_tracking/
FIG. 6.
Two SLFII-FrontalB (light green, K=104) and AF-Frontal (light blue, K=82) bundles tracked to a combined SLFII-ParietalB and AF-Temporal. Contrast with the AF bundle from Figure 7. CS is marked as a reference point. Here, the color code for the connection metric is not used. Coronal views shown in bottom row; see also movie at http://cis.jhu.edu/data.sets/macaque_hemi-brain_fiber_tracking/
Association bundles for the UF (Fig. 7), FOF (Fig. 8), and fornix (Fig. 9) were also generated. The latter two proved to be challenging for several reasons. Both have relatively lower FA than adjacent bundles (corpus callosum, CB for the FOF, and, in addition, the anterior commissure, IC, and external medullary lamina of the thalamus for the fornix). So, it was necessary to lower the FA threshold from 0.4 to 0.1, which reflects the fact that FOF carries multiple tracts between different cortices (see Chapter 27 in Schmahmann and Pandya, 2006). Then, waystations were needed to prevent shunting into adjacent bundles. For the FOF, three waystations at coronal sections 241, 255, and 270, which respectively corresponded to sections 93, 97, and 105 in the SP atlas, were used with the four initial values of K=1000, 400, 200, and 400 reduced to 31, 56, 95, and 349, respectively, after editing. The result is a bundle that is consistent with Figure 19-2 of Schmahmann and Pandya (2006). From the PO, the fibers begin in the SLFI, separate into FOF proper, and then, become sandwiched between the corpus callosum and corona radiata while coursing rostrally toward the frontal lobe; see pages 234–236, 268, 272–276, and chapter 27 in Schmahmann and Pandya (2006).
FIG. 7.
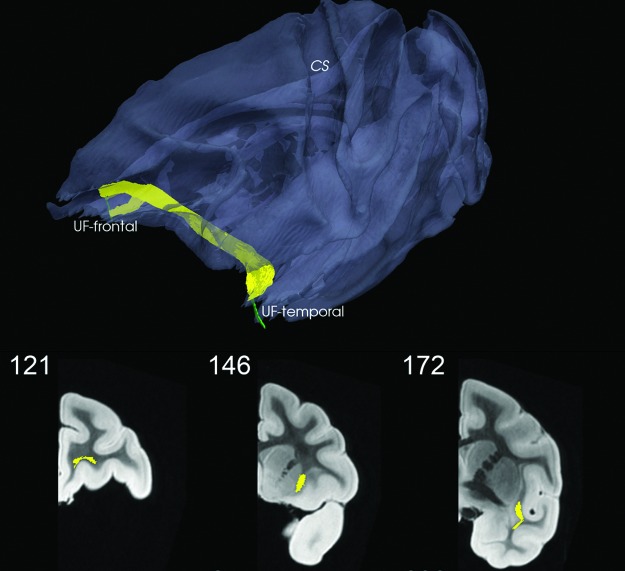
Uncinate fasciculus (UF) temporal to frontal (K=131). CS is marked as reference point. Here, the color code for the connection metric is not used. Coronal views shown in bottom row; see also movie at http://cis.jhu.edu/data.sets/macaque_hemi-brain_fiber_tracking/
For the fornix, which is technically a cortico-SB as the hippocampus is old cortex, two waystations were employed as suggested by Concha et al. (2005) and Saunders and Aggleton (2007). The waystations were located within the fornix in coronal sections 192 and 252 (corresponding to SP sections 69 and 97, respectively) and were used with the three initial values of K=200, 200, and 150 reduced to 8, 48, and 40, respectively, after editing. An additional difficulty was the proximity of the fornix to the mid-sagittal plane, which coincided with the boundary of the image volume.
Cortico-striatal bundles
Motor corticostriatal tracts were generated from six distinct cortical ROIs defined by SP Motor Cases 24 through 29 to the putamen (Fig. 10). Some overlapping of fiber bundles was observed, that is, kissing and crossing fibers, as well as a bifurcating and reconnecting bundle.
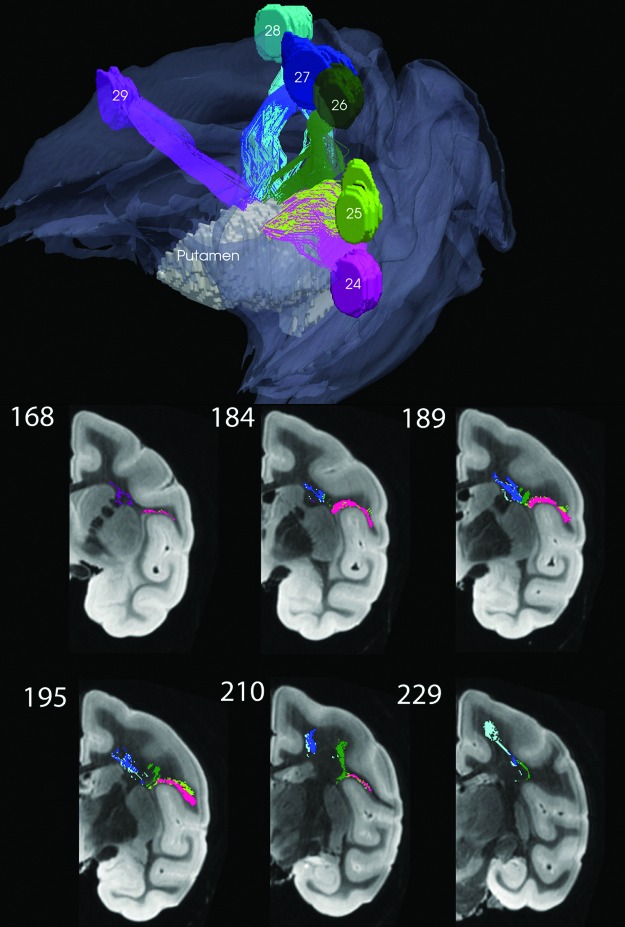
FIG. 10.
Tracts to the putamen from SP Motor Case 24 (light green, K=200), Case 25 (light blue, K=200), Case 26 (pink, K=161), Case 27 (green, K=159), Case 28 (blue, K=191), and Case 29 (purple, K=118). Here, the color code for the connection metric is not used. Coronal views shown in bottom row; see also movie at http://cis.jhu.edu/data.sets/macaque_hemi-brain_fiber_tracking/
Discussion
A probabilistic method for tracking of fiber bundles that utilizes DP minimization of a quadratic function based on the Gaussian form of the full DTI tensor has been developed. DP has been shown to generate realistic tracts, including crossing and kissing fibers in DTI images without need for multiple gradients. DP is computationally less intensive than other probabilistic tracking methods that have emerged in recent years due to its focus on generating tracts between user-specified ROIs and, thus, is hypothesis driven rather than exploratory (cf. Croxson et al., 2005). DP also uses the scoring method based on a connectivity metric, such as in Sherbondy et al. (2008).
The DP approach can be applied to more advanced, high angular-resolution (HAR) techniques albeit via a different cost function based on a probabilistic model. Although the limitations of Gaussian diffusion have been acknowledged, it continues to be widely used. This is because of several practical issues of the HAR approach: the large number of required diffusion encoding directions and, more importantly, the large b-values (typically more than 3000 sec/mm2). As demonstrated by Ben-Amitay et al. (2012), such values cause much of the MR signal to decay to the noise floor, resulting in poor SNR. More importantly, the large b-value leads to higher motion sensitivity and additional eddy current distortion, which are difficult to detect and correct because of low SNR. So, it is likely that research and clinical studies will continue to use standard DTI scans.
The DP approach is attractive with regard to DTI data; deterministic approaches such as those mentioned earlier are known to generate severe false-negative results, because if there is a voxel with an incorrect fiber orientation due to noise or complex anatomy, deviation from the real path occurs. Since the deterministic approaches are usually combined with knowledge-based anatomical constraints such as at least using at least two ROIs with known connectivity, the paths that deviate from real ones are eliminated. Likewise, the DP approach is driven by anatomical knowledge; the two locations with known connections are specified and the most probable path is searched, reducing the chance of false positives. This approach is more robust against noise, partial volume effect, and problematic regions with complex tract anatomy. It is, however, important to examine whether the reconstructed paths agree with known trajectories between the two specified locations.
DP falls within a class of computationally efficient pathfinding strategies that are beginning to be useful for tracking bundles. One is the A* approach (Richter et al., 2013), which was found to be more efficient than global optimization strategies such as Gibbs tracking (Reisert et al., 2011). In fact, DP was able to completely traverse the 2D spiral phantom, which could not be done with Gibbs tracking (see Fig. 3 in Richter et al., 2013). The strong principle of optimality used in DP states that all optimal paths comprise optimal sub-paths, and it is this fact which permits the reduction in complexity of the problem (Bertsekas, 1987). The cost function assumes an additive cost that depends locally only on the current node and path direction, which is equivalent to the strong principle of optimality. As mentioned earlier, the number of paths evaluated in a brute force approach would be in the order of MVN, where V is the connectedness, which in this case is 26. DP iteratively examines MV optimal sub-paths of ever-increasing length by assuming the strong principle of optimality, reducing the complexity to MVN and thereby making the problem tractable. Reducing V from 26 to 6 will still yield optimal paths, however at the price of a higher cost as exemplified by the transition costs for a skewed directional vector in the last row of Table 1. Since a larger neighborhood of 74 was used in the A* approach, it is possible to use a larger search space in the current software. However, the computational efficiency of the A* approach is dependent on the selection of an appropriate heuristic function. A poor choice can result in a brute force search. With DP, the reduction in search complexity is direct and independent of heuristics or other subjective conditions.
It might be argued that the feasibility of DP should be evaluated using phantom data such as PISTE (http://cubric.psych.cf.ac.uk/commondti) or FiberCup (www.lnao.fr/spip.php?rubrique79). However, it is perhaps more meaningful to generate tracts between anatomically defined ROIs using real data. So, a hemi-brain from a macaque was used as a viable means of understanding the capabilities and limitations of DP. Data used in this study for comparison or development of more sophisticated algorithms are being made available at http://cis.jhu.edu/data.sets/macaque_hemi-brain_fiber_tracking/
Indeed, the macaque brain has been previously used as a model for testing methods for studying WM tracts. Parker et al. (2002a) was the first to use the rhesus monkey to evaluate tractography methods, albeit at a low resolution. More recently, Hofer and Frahm (2008) used a 2.9T scanner to study tracts in a macaque DTI scan that was upsampled to 0.75 mm3 isotropic voxels. Using an FA threshold of 0.15, they used the FACT algorithm in MRIStudio (Mori et al., 1999) to generate several tracts. While the ROI seeds they used are different from those used here, the generated SLFII and somatosensory U-fibers are similar. Unlike DP, FACT was unable to deal with kissing and crossing fibers seen with HAR (Wedeen et al., 2008, 2012, ). Adluru et al. (2012) also used a deterministic approach to track several bundles with an FA threshold of 0.1–0.15 in a template of 0.5 mm3 resolution generated as a population average from 271 macaques from a 3T scanner.
DP has several limitations. First, there is inherent bias to high anisotropy and length. As can be seen from Figure 1, it is important to visualize the tracts for anatomical consistency as well as ensure that the ROIs are defined appropriately. Perhaps not surprisingly, due to the cost function, false tracts can be generated especially in the neighborhood of bundles with higher anisotropy as in the case of the FOF and the fornix. This problem is not uncommon even with probabilistic methods (Croxson et al., 2005). This confound can be addressed in one of two ways. One is by using a scoring system based on connectivity metric to ensure anatomically consistent bundles are generated; it is quite straightforward to show that the connectivity metric is approximately inversely proportional to the fractional anisotropy, that is, the lower the cost the higher the anisotropy. The other way is to exclude adjacent bundles from the search space as was done for the deterministic approach by Zhang et al. (2010). For example, generating the FOF and fornix was resolved by excluding adjacent bundles and using waystations with a lower FA threshold of 0.1. Second, the image resolution is insufficient to deal with fiber bundles emanating from designated ROIs that come in very close proximity to each other; hence, the importance of checking the fibers for consistency with known fiber pathways. Third, the method is dependent on high resolution or smooth data. Due to the nature of the 26-voxel neighborhood, it is possible for individual paths to turn 35–45° when passing through noisy or isotropic regions, but these can be masked by generating multiple fibers. Here, it will be helpful to know Contrast-to-Noise Ratio or SNR of the image being studied (Farrell et al., 2007; Kingsley, 2006). In addition, an option for smoothing fibers via tensioned B-splines was implemented but it was not used.
Though no direct comparisons with other methods were made, it is worth noting that Figure 2 could not be replicated by FACT because of the crossing fibers in the CB. In addition, given the FOF-Frontal and FOF-PO ROIs, FACT with a threshold of 0.1 generated a bundle that was more inferior to the true FOF going through the middle longitudinal fasciculus and Extreme Capsule (see Figs. 14-2 and 15-1 in Schmahmann and Pandya, 2006) similar to those generated by deterministic approaches (Adluru et al., 2012; Hofer and Frahm, 2008). This led to the inference of a macaque homologue of the human inferior FOF that does not exist (Catani et al., 2007; Schmahmann and Pandya, 2007).
Last but not the least, it is critically important to validate tracts with regard to staining of tracts via histological sections (Annese, 2012; Dauguet et al., 2006; Seehaus et al., 2013). In this regard, there was very close correspondence between tracts generated with DP and in vivo anterograde transport of HRP in a macaque brain. Generated tracts were also consistent with those from the Schmahmann and Pandya (2006) atlas. It should be possible to reproduce the tractography for the right hemisphere, but the focus on the left has been motivated by an ongoing study of histology and MRI analyses in a macaque model of fetal exposure to radiation in which only the left hemisphere is available (Ceritoglu et al., 2010; Selemon et al., 2013). It is worth noting that the vast majority of published tracer studies have traditionally focused on one side.
Extensions and modifications of DP are possible in several ways. First, a larger neighborhood than the 26-voxel one used here could allow for acute turns (Merhof et al., 2006a, 2006b; Richter et al., 2013). The approach to modify the DP state space to control curvature and torsion (Lal, 2004) can be applied to construct a Markov model in which the transition cost depends on the previous transition along the path. Thus, a Markovian approach (Iglesias et al., 2012) could be used to incorporate bending energy into the cost function (Poupon et al., 2000) for regularization. Adjusting the state space and cost function to be based on voxel triples (Collins et al., 2011) allows for more sophisticated regularization. It is also possible to incorporate Bayesian priors based on tensor coherence or dot-product with regard to a neighboring voxel (Fout et al., 2005; Merhof et al., 2006a, 2006b). Second, for lower-resolution data such as human DTI data, it may be necessary to subparcellate the initial and end ROIs into m and n smaller ROIs to generate m×n bundles each with K fibers, which would be similar to the example of subdividing the motor cortex to generate cortico-striatal tracts. To minimize the need for editing fibers or setting K too large, one could use a WM parcellation atlas such as that developed by Huang et al. (2006) to exclude regions from the state space to generate anatomically consistent bundles as suggested earlier. Furthermore, the connectivity metric provides a single value for each fiber, which could be helpful in studying bundles disrupted by disease and may provide a better alternative to calculating the average fractional anisotropy in the bundle. These limitations and extensions will be explored more fully, particularly in human data in subsequent papers.
Acknowledgments
The authors thank Joseph Hennessey, Hao Huang, Can Ceritoglu, Michael Bowers, Elizabeth Postell, Carolyn Zin, and Geoffrey Gunter for technical assistance. Research was supported by NIH grants (R01-AG020012, R01-EB003543, P41-EB015909, R01-EB000975, and P50-MH71616).
Author Disclosure Statement
No competing financial interests exist.
References
- Acar B. Yörük E. DT-MRI connectivity and/or tractography? Two new algorithms. In: Aja-Fernandez S, editor; de Luis Garcia R, editor; Tao D, editor; Li X, editor. Tensors in Image Processing and Computer Vision. London, UK: Springer-Verlag; 2009. pp. 335–353. [Google Scholar]
- Adluru N. Zhang H. Fox AS. Shelton SE. Ennis CM. Bartosic AM. Oler JA. Tromp do PM. Zakszewski E. Gee JC. Kalin NH. Alexander AL. A diffusion tensor brain template for rhesus macaques. Neuroimage. 2012;59:306–318. doi: 10.1016/j.neuroimage.2011.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander AL. Hasan K. Kindlmann G. Parker DL. Tsurudal JS. A geometric analysis of diffusion tensor measurements of the human brain. Mag Reson Med. 2000;44:283–291. doi: 10.1002/1522-2594(200008)44:2<283::aid-mrm16>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- Annese J. The importance of combining MRI and large-scale digital histology in neuroimaging studies of brain connectivity and disease. Front Neuroinform. 2012;6:13. doi: 10.3389/fninf.2012.00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ. Jones DK. Diffusion-tensor MRI: theory, experimental design and data analysis—a technical review. NMR Biomed. 2002;15:456–467. doi: 10.1002/nbm.783. [DOI] [PubMed] [Google Scholar]
- Basser PJ. Mattiello J. Le Bihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B. 1994a;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Basser PJ. Mattiello J. Lebihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994b;66:259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ. Pajevic S. Pierpaoli C. Duda J. Aldroubi A. In vitro fiber tractography using DT-MRI data. Magn Reson Med. 2000;44:625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Beaulieu C. The basis of anisotropic water diffusion in the nervous system—a technical review. NMR Biomed. 2002;15:435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
- Behrens TE. Johansen-Berg H. Woolrich MW. Smith SM. Wheeler-Kingshott CA. Boulby PA. Barker GJ. Sillery EL. Sheehan K. Ciccarelli O. Thompson AJ. Brady JM. Matthews PM. Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. Nat Neurosci. 2003;6:750–757. doi: 10.1038/nn1075. [DOI] [PubMed] [Google Scholar]
- Ben-Amitay S. Jones DK. Assaf Y. Motion correction and registration of high b-value diffusion weighted images. Magn Reson Med. 2012;67:1694–1702. doi: 10.1002/mrm.23186. [DOI] [PubMed] [Google Scholar]
- Bertsekas DP. Dynamic Programming. Englewood Cliffs, NJ: Prentice-Hall, Inc.; 1987. [Google Scholar]
- Catani M. Allin MP. Husain M. Pugliese L. Mesulam MM. Murray RM. Jones DK. Symmetries in human brain language pathways correlate with verbal recall. Proc Natl Acad Sci USA. 2007;104:17163–17168. doi: 10.1073/pnas.0702116104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceritoglu C. Wang L. Selemon LD. Csernansky JG. Miller MI. Ratnanather JT. Large deformation diffeomorphic metric mapping registration of reconstructed 3D histological section images and in vivo MR images. Front Hum Neurosci. 2010;4:43. doi: 10.3389/fnhum.2010.00043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins MD. Singh V. Alexander AL. Network connectivity via inference over curvature-regularizing line graphs. Lect Notes Comp Sci. 2011;6492:65–78. [Google Scholar]
- Concha L. Gross DW. Beaulieu C. Diffusion tensor tractography of the limbic system. AJNR Am J Neuroradiol. 2005;26:2267–2274. [PMC free article] [PubMed] [Google Scholar]
- Conturo TE. Lori NF. Cull TS. Akbudak E. Snyder AZ. Shimony JS. McKinstry RC. Burton H. Raichle ME. Tracking neuronal fiber pathways in the living human brain. Proc Nat Acad Sci USA. 1999;96:10422–10427. doi: 10.1073/pnas.96.18.10422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Croxson PL. Johansen-Berg H. Behrens TE. Robson MD. Pinsk MA. Gross CG. Richter W. Richter MC. Kastner S. Rushworth MF. Quantitative investigation of connections of the prefrontal cortex in the human and macaque using probabilistic diffusion tractography. J Neurosci. 2005;25:8854–8866. doi: 10.1523/JNEUROSCI.1311-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dauguet J. Peled S. Berezovskii V. Delzescaux T. Warfield SK. Born R. Westin C-F. 3D histological reconstruction of fiber tracts and direct comparison with diffusion tensor MRI tractography. Med Image Comput Comput Assist Interv. 2006;4190:109–116. doi: 10.1007/11866565_14. [DOI] [PubMed] [Google Scholar]
- Everts MH. Bekker H. Roerdink Jos BTM. Visualizing White Matter Structure of the Brain Using Dijkstra's Algorithm. In: Zinterhof P, editor; Lončarić S, editor; Uhl A, editor; Carini A, editor. Proceedings of the 6th International Symposium on Image and Signal Processing and Analysis (ISPA 2009); Salzberg, Austria. 2009. pp. 575–580. [Google Scholar]
- Farrell JA. Landman BA. Jones CK. Smith SA. Prince JL. Van Zijl PC. Mori S. Effects of signal-to-noise ratio on the accuracy and reproducibility of diffusion tensor imaging-derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5 T. J Magn Reson Imaging. 2007;26:756–767. doi: 10.1002/jmri.21053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fout N. Huang J. Ding Z. Visualization of Neuronal Fiber Connections from DT-MRI with Global Optimization. SAC’05: Proceedings of the 2005 ACM Symposium on Applied Computing; New York, NY: ACM Press; 2005. 2005. pp. 1200–1206. [Google Scholar]
- Frandsen J. Hobolth A. Ostergaard L. Vestergaard-Poulsen P. Vedel Jensen EB. Bayesian regularization of diffusion tensor images. Biostatistics. 2007;8:784–799. doi: 10.1093/biostatistics/kxm005. [DOI] [PubMed] [Google Scholar]
- Friman O. Westin C-F. Uncertainty in white matter fiber tractography. Lect Notes Comp Sci. 2005;8:107–114. doi: 10.1007/11566465_14. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. Selemon LD. Schwartz ML. Dual pathways connecting the dorsolateral prefrontal cortex with the hippocampal formation and parahippocampal cortex in the rhesus monkey. Neuroscience. 1984;12:719–743. doi: 10.1016/0306-4522(84)90166-0. [DOI] [PubMed] [Google Scholar]
- Hageman NS. Toga AW. Narr KL. Shattuck DW. A diffusion tensor imaging tractography algorithm based on Navier-Stokes fluid mechanics. IEEE Trans Med Imaging. 2009;28:348–360. doi: 10.1109/TMI.2008.2004403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofer S. Frahm J. In vivo mapping of fiber pathways in the rhesus monkey brain. Open Med Imaging J. 2008;2:32–41. [Google Scholar]
- Huang H. Walker M. Ying SH. Zee DS. Van Zijl PC. Mori S. 3D DT-MRI atlas of macaque brain. Proc Int Soc Magn Reson Med. 2006;14:440. [Google Scholar]
- Iglesias JE. Thompson PM. Liu CY. Tu Z. Fast approximate stochastic tractography. Neuroinformatics. 2012;10:5–17. doi: 10.1007/s12021-011-9113-2. [DOI] [PubMed] [Google Scholar]
- Iturria-Medina Y. Canales-Rodriguez EJ. Melie-Garcia L. Valdes-Hernandez PA. Martinez-Montes E. Aleman-Gomez Y. Sanchez-Bornot JM. Characterizing brain anatomical connections using diffusion weighted MRI and graph theory. Neuroimage. 2007;36:645–660. doi: 10.1016/j.neuroimage.2007.02.012. [DOI] [PubMed] [Google Scholar]
- Jackowski C. Kao CY. Qiu M. Constable RT. Staib LH. Estimation of anatomical connectivity by anisotropic front propagation and diffusion tensor imaging. Med Image Comput Comput Assist Interv. 2004;3217:663–671. [Google Scholar]
- Jbabdi S. Johansen-Berg H. Tractography: where do we go from here? Brain Connect. 2011;1:169–183. doi: 10.1089/brain.2011.0033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jbabdi S. Woolrich MW. Andersson JL. Behrens TE. A Bayesian framework for global tractography. Neuroimage. 2007;37:116–129. doi: 10.1016/j.neuroimage.2007.04.039. [DOI] [PubMed] [Google Scholar]
- Jiang H. Van Zijl PC. Kim J. Pearlson GD. Mori S. DTIStudio: resource program for diffusion tensor computation and fiber bundle tracking. Comput Methods Programs Biomed. 2006;81:106–116. doi: 10.1016/j.cmpb.2005.08.004. [DOI] [PubMed] [Google Scholar]
- Johansen-Berg H. Rushworth MF. Using diffusion imaging to study human connectional anatomy. Annu Rev Neurosci. 2009;32:75–94. doi: 10.1146/annurev.neuro.051508.135735. [DOI] [PubMed] [Google Scholar]
- Jonasson L. Bresson X. Hagmann P. Cuisenaire O. Meuli R. Thiran JP. White matter fiber tract segmentation in DT-MRI using geometric flows. Med Image Anal. 2005;9:223–236. doi: 10.1016/j.media.2004.07.004. [DOI] [PubMed] [Google Scholar]
- Kingsley PB. Introduction to diffusion tensor imaging mathematics: part III. tensor calculations, noise, simulations, and optimization. Concepts Magn Reson Part A. 2006;28A:155–179. [Google Scholar]
- Lal RM. The Johns Hopkins University; 2004. Tracking in Diffusion Tensor Imaging. MSE Thesis. [Google Scholar]
- Lazar M. Alexander AL. An error analysis of white matter tractography methods: synthetic diffusion tensor field simulations. Neuroimage. 2003;20:1140–1153. doi: 10.1016/S1053-8119(03)00277-5. [DOI] [PubMed] [Google Scholar]
- Le Bihan D. Mangin JF. Poupon C. Clark CA. Pappata S. Molko N. Chabriat H. Diffusion tensor imaging: concepts and applications. J Magn Reson Imaging. 2001;13:534–546. doi: 10.1002/jmri.1076. [DOI] [PubMed] [Google Scholar]
- Le Bihan D. Poupon C. Amadon A. Lethimonnier F. Artifacts and pitfalls in diffusion MRI. J Magn Reson Imaging. 2006;24:478–488. doi: 10.1002/jmri.20683. [DOI] [PubMed] [Google Scholar]
- Le Bihan D. Turner R. Macfall J. Effects of intravoxel incoherent motions (IVIM) in steady-state free precession (SSFP) imaging: application to molecular diffusion imaging. Magn Reson Med. 1989;10:324–337. doi: 10.1002/mrm.1910100305. [DOI] [PubMed] [Google Scholar]
- Lifshits S. Tamir A. Assaf Y. Combinatorial fiber-tracking of the human brain. Neuroimage. 2009;48:532–540. doi: 10.1016/j.neuroimage.2009.05.086. [DOI] [PubMed] [Google Scholar]
- Marigonda A. Orlandi G. A mathematical model for neuronal fibers. Commun Appl Ind Math. 2011;2:e-363. [Google Scholar]
- Merhof D. Enders F. Hastreiter P. Ganslandt O. Fahlbusch R. Nimsky C. Stamminger M. Neuronal fiber connections based on A*-pathfinding. In: Manduca A, editor; Amini AA, editor. Medical Imaging 2006: Physiology, Function, and Structure from Medical Images; San Diego, CA: SPIE; 2006a. p. 61431S-8. [Google Scholar]
- Merhof D. Richter M. Enders F. Hastreiter P. Ganslandt O. Buchfelder M. Nimsky C. Greiner G. Fast and accurate connectivity analysis between functional regions based on DT-MRI. Med Image Comput Comput Assist Interv. 2006b;4191:225–233. doi: 10.1007/11866763_28. [DOI] [PubMed] [Google Scholar]
- Moldrich RX. Pannek K. Hoch R. Rubenstein JL. Kurniawan ND. Richards LJ. Comparative mouse brain tractography of diffusion magnetic resonance imaging. Neuroimage. 2010;51:1027–1036. doi: 10.1016/j.neuroimage.2010.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S. Crain BJ. Chacko VP. Van Zijl PC. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol. 1999;45:265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Mori S. Van Zijl PC. Fiber tracking: principles and strategies–a technical review. NMR Biomed. 2002;15:468–480. doi: 10.1002/nbm.781. [DOI] [PubMed] [Google Scholar]
- Mukherjee P. Chung SW. Berman JI. Hess CP. Henry RG. Diffusion tensor MR imaging and fiber tractography: technical considerations. AJNR Am J Neuroradiol. 2008;29:843–852. doi: 10.3174/ajnr.A1052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oishi K. Huang H. Yoshioka T. Ying SH. Zee DS. Zilles K. Amunts K. Woods R. Toga AW. Pike GB. Rosa-Neto P. Evans A. Van Zijl PC. Mazziotta JC. Mori S. Superficially located white matter structures commonly seen in the human and the macaque brain with diffusion tensor imaging. Brain Connect. 2011;1:37–47. doi: 10.1089/brain.2011.0005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pace G. Pierpaoli W. Photodynamic effect of diidroquinidine on isolated hearts of mammals. Nature. 1963;199:915–916. doi: 10.1038/199915a0. [DOI] [PubMed] [Google Scholar]
- Parker GJ. Stephan KE. Barker GJ. Rowe JB. Macmanus DG. Wheeler-Kingshott CA. Ciccarelli O. Passingham RE. Spinks RL. Lemon RN. Turner R. Initial demonstration of in vivo tracing of axonal projections in the macaque brain and comparison with the human brain using diffusion tensor imaging and fast marching tractography. Neuroimage. 2002a;15:797–809. doi: 10.1006/nimg.2001.0994. [DOI] [PubMed] [Google Scholar]
- Parker GJ. Wheeler-Kingshott CA. Barker GJ. Estimating distributed anatomical connectivity using fast marching methods and diffusion tensor imaging. IEEE Trans Med Imaging. 2002b;21:505–512. doi: 10.1109/TMI.2002.1009386. [DOI] [PubMed] [Google Scholar]
- Pichon E. Westin CF. Tannenbaum AR. A Hamilton-Jacobi-Bellman approach to high angular resolution diffusion tractography. Med Image Comput Comput Assist Interv. 2005;8:180–187. doi: 10.1007/11566465_23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierpaoli C. Jezzard P. Basser PJ. Barnett A. Chiro GD. Diffusion tensor MR imaging of human brain. Radiology. 1996;201:637–648. doi: 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
- Poupon C. Clark CA. Frouin V. Regis J. Bloch I. Le Bihan D. Mangin JF. Regularization of diffusion-based direction maps for the tracking of brain white matter fasicles. Neuroimage. 2000;12:184–195. doi: 10.1006/nimg.2000.0607. [DOI] [PubMed] [Google Scholar]
- Poynton C. Lal R. Ratnanather JT. Mori S. Boatman D. Miller MI. Probabilistic Tracking of Fiber Pathways Using Dynamic Programming. Human Brain Mapping Conference; Toronto. 2005. [Google Scholar]
- Ramnani N. Behrens TE. Penny W. Matthews PM. New approaches for exploring anatomical and functional connectivity in the human brain. Biol Psychiatry. 2004;56:613–619. doi: 10.1016/j.biopsych.2004.02.004. [DOI] [PubMed] [Google Scholar]
- Reisert M. Mader I. Anastasopoulos C. Weigel M. Schnell S. Kiselev V. Global fiber reconstruction becomes practical. Neuroimage. 2011;54:955–962. doi: 10.1016/j.neuroimage.2010.09.016. [DOI] [PubMed] [Google Scholar]
- Richter M. Zolal A. Ganslandt O. Buchfelder M. Nimsky C. Merhof D. Evaluation of diffusion-tensor imaging-based global search and tractography for tumor surgery close to the language system. PLoS One. 2013;8:e50132. doi: 10.1371/journal.pone.0050132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saunders RC. Aggleton JP. Origin and topography of fibers contributing to the fornix in macaque monkeys. Hippocampus. 2007;17:396–411. doi: 10.1002/hipo.20276. [DOI] [PubMed] [Google Scholar]
- Schmahmann JD. Pandya DN. Fiber Pathways of the Brain. Oxford, New York: Oxford University Press; 2006. [Google Scholar]
- Schmahmann JD. Pandya DN. The complex history of the fronto-occipital fasciculus. J Hist Neurosci. 2007;16:362–377. doi: 10.1080/09647040600620468. [DOI] [PubMed] [Google Scholar]
- Seehaus AK. Roebroeck A. Chiry O. Kim DS. Ronen I. Bratzke H. Goebel R. Galuske RA. Histological validation of DW-MRI tractography in human postmortem tissue. Cereb Cortex. 2013;23:442–450. doi: 10.1093/cercor/bhs036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selemon LD. Ceritoglu C. Ratnanather JT. Wang L. Harms MP. Aldridge K. Begovic A. Csernansky JG. Miller MI. Rakic P. Distinct abnormalities of the primate prefrontal cortex caused by ionizing radiation in early or midgestation. J Comp Neurol. 2013;521:1040–1053. doi: 10.1002/cne.23217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selemon LD. Goldman-Rakic PS. Longitudinal topography and interdigitation of corticostriatal projections in the rhesus monkey. J Neurosci. 1985;5:776–794. doi: 10.1523/JNEUROSCI.05-03-00776.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selemon LD. Goldman-Rakic PS. Common cortical and subcortical targets of the dorsolateral prefrontal and posterior parietal cortices in the rhesus monkey: evidence for a distributed neural network subserving spatially guided behavior. J Neurosci. 1988;8:4049–4068. doi: 10.1523/JNEUROSCI.08-11-04049.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherbondy AJ. Dougherty RF. Ben-Shachar M. Napel S. Wandell BA. ConTrack: finding the most likely pathways between brain regions using diffusion tractography. J Vis. 2008;8:15.1–16. doi: 10.1167/8.9.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tournier JD. Calamante F. King MD. Gadian DG. Connelly A. Limitations and requirements of diffusion tensor fiber tracking: an assessment using simulations. Magn Reson Med. 2002;47:701–708. doi: 10.1002/mrm.10116. [DOI] [PubMed] [Google Scholar]
- Tournier JD. Mori S. Leemans A. Diffusion tensor imaging and beyond. Magn Reson Med. 2011;65:1532–1556. doi: 10.1002/mrm.22924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuch DS. Q-ball imaging. Magn Reson Med. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- Wedeen VJ. Rosene DL. Wang R. Dai G. Mortazavi F. Hagmann P. Kaas JH. Tseng WY. The geometric structure of the brain fiber pathways. Science. 2012;335:1628–1634. doi: 10.1126/science.1215280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedeen VJ. Wang RP. Schmahmann JD. Benner T. Tseng WY. Dai G. Pandya DN. Hagmann P. D'Arceuil H. De Crespigny AJ. Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers. Neuroimage. 2008;41:1267–1277. doi: 10.1016/j.neuroimage.2008.03.036. [DOI] [PubMed] [Google Scholar]
- Xue R. Van Zijl PC. Crain BJ. Solaiyappan M. Mori S. In vivo three-dimensional reconstruction of rat brain axonal projections by diffusion tensor imaging. Magn Reson Med. 1999;42:1123–1127. doi: 10.1002/(sici)1522-2594(199912)42:6<1123::aid-mrm17>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- Zalesky A. DT-MRI fiber tracking: a shortest paths approach. IEEE Trans Med Imaging. 2008;27:1458–1471. doi: 10.1109/TMI.2008.923644. [DOI] [PubMed] [Google Scholar]
- Zalesky A. Fornito A. A DTI-derived measure of cortico-cortical connectivity. IEEE Trans Med Imaging. 2009;28:1023–1036. doi: 10.1109/TMI.2008.2012113. [DOI] [PubMed] [Google Scholar]
- Zhang J. Richards LJ. Yarowsky P. Huang H. Van Zijl PC. Mori S. Three-dimensional anatomical characterization of the developing mouse brain by diffusion tensor microimaging. Neuroimage. 2003;20:1639–1648. doi: 10.1016/s1053-8119(03)00410-5. [DOI] [PubMed] [Google Scholar]
- Zhang Y. Zhang J. Oishi K. Faria AV. Jiang H. Li X. Akhter K. Rosa-Neto P. Pike GB. Evans A. Toga AW. Woods R. Mazziotta JC. Miller MI. Van Zijl PC. Mori S. Atlas-guided tract reconstruction for automated and comprehensive examination of the white matter anatomy. Neuroimage. 2010;52:1289–1301. doi: 10.1016/j.neuroimage.2010.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]