Slow oscillations of K_ATP conductance in mouse pancreatic islets provide support for electrical bursting driven by metabolic oscillations

Abstract

We used the patch clamp technique in situ to test the hypothesis that slow oscillations in metabolism mediate slow electrical oscillations in mouse pancreatic islets by causing oscillations in K_ATP channel activity. Total conductance was measured over the course of slow bursting oscillations in surface β-cells of islets exposed to 11.1 mM glucose by either switching from current clamp to voltage clamp at different phases of the bursting cycle or by clamping the cells to −60 mV and running two-second voltage ramps from −120 to −50 mV every 20 s. The membrane conductance, calculated from the slopes of the ramp current-voltage curves, oscillated and was larger during the silent phase than during the active phase of the burst. The ramp conductance was sensitive to diazoxide, and the oscillatory component was reduced by sulfonylureas or by lowering extracellular glucose to 2.8 mM, suggesting that the oscillatory total conductance is due to oscillatory K_ATP channel conductance. We demonstrate that these results are consistent with the Dual Oscillator model, in which glycolytic oscillations drive slow electrical bursting, but not with other models in which metabolic oscillations are secondary to calcium oscillations. The simulations also confirm that oscillations in membrane conductance can be well estimated from measurements of slope conductance and distinguished from gap junction conductance. Furthermore, the oscillatory conductance was blocked by tolbutamide in isolated β-cells. The data, combined with insights from mathematical models, support a mechanism of slow (∼5 min) bursting driven by oscillations in metabolism, rather than by oscillations in the intracellular free calcium concentration.

glucose-stimulated insulin secretion (GSIS) is a dynamic and oscillatory process. Under normal physiological conditions, pancreatic insulin secretion results in the appearance of pulses of plasma insulin in humans, mice, rats and dogs (28, 33, 36, 42). Mouse islets display diverse oscillatory patterns, consisting of slow (2–7 min), fast (<2 min), or compound (fast overlapped with slow) (22, 33). Oscillatory insulin secretion is clinically significant as it is lost or disturbed in patients with type 2 diabetes or their near relatives (34, 45). As pulses in insulin have very recently been shown to be more efficacious than continuous insulin at potentiating insulin action in the liver in vivo (27), the clinical manifestations of impaired insulin pulsatility in diabetics may cause reduced insulin pulsatility at the level of the liver, which in turn causes incomplete insulin suppression of hepatic glucose production. However, the mechanism underlying these diverse patterns both in vitro and in vivo has not been definitively established.

We as well as others (6, 43) have proposed that oscillations in glucose metabolism drive slow oscillations in islet membrane electrical activity due to the cyclic opening and closing of K_ATP channels as a result of fluctuations in the ATP/ADP ratio. An alternative mechanism has been proposed in which oscillations in metabolism are secondary to oscillations in cytosolic Ca²⁺ (8, 10, 11, 15, 16). In either case, the existence of metabolic oscillations should result in oscillations in K_ATP conductance (gK_ATP). Evidence for slow oscillations in gK_ATP to date includes the observation that single K_ATP channels slowly oscillate in on-cell membrane patches (12) and that β-cell input conductance differed between the active and silent phases of the oscillations (23). In contrast, Smith et al. (41) found that input conductance was the same during active and silent phases and concluded that oscillations in gK_ATP do not underlie oscillations in membrane potential.

To examine the mechanism underlying slow islet oscillations, we recorded electrical activity from β-cells in intact islets in situ. Total membrane conductance was measured during the active and silent phases of islet bursting while a β-cell on the islet surface was held in voltage clamp. β-Cell conductance was calculated from the slopes of current-voltage curves using ramps applied from a standard holding potential of −60 mV, either after switching from current to voltage clamp during different phases of bursting or by continually measuring conductance using repetitive voltage ramps from a fixed holding potential. We found that conductance oscillated, with a period similar to that of the slow bursting pattern. To determine if the oscillatory conductance was due to gK_ATP, the conductance was measured under experimental conditions where either the glucose concentration was altered or drugs selective for K_ATP channels were added. The conductance oscillations were abolished by the K_ATP blockers tolbutamide and glyburide or by applying saline containing 2.8 mM glucose or 11 mM glucose plus diazoxide to pharmacologically open K_ATP channels.

A striking feature of the oscillations we observed was that the membrane conductance was higher during the silent phase of the burst than during the active phase. This is compatible with models in which oscillations of gK_ATP are driven by primary metabolic oscillations, but not with several published models in which the oscillations are secondary to the effects of Ca²⁺ on metabolism. The implications of these results for understanding the underlying mechanism of islet oscillations are discussed in detail at the end of the paper.

MATERIALS AND METHODS

Preparation of Mouse Islets and Single β-Cells

Pancreatic islets were isolated from 3- to 4-mo-old male Swiss-Webster mice by using a previously published protocol (46). This protocol was carried out in accordance with the guidelines of the University of Michigan Committee on the Use and Care of Animals (UCUCA). Islets were picked by hand into fresh Krebs solution and then transferred to culture dishes containing RPMI 1640 supplemented with 10% FBS, glutamine, and penicillin-streptomycin. Islets were cultured overnight at 37°C in an incubator. Electrophysiological recordings were made from islets cultured for 72 h or less. Islets were dispersed into single β-cells by 10-min incubation in zero calcium solution containing 3 mM EGTA, 0.2% BSA, and 0.22% glucose to which was added 0.25% trypsin, followed by repeated pipetting. The cell suspension that resulted was then centrifuged and washed with culture medium, and then cells were plated onto glass coverslips.

Electrophysiology

Patch electrodes were pulled (P-97; Sutter Instruments) from borosilicate glass capillaries (Warner Instruments) and had resistances of 4–6 Mohm when filled with an internal buffer containing (in mM): 28.4 K₂SO₄, 63.7 KCl, 11.8 NaCl, 1 MgCl₂, 20.8 HEPES, and 0.5 EGTA at pH7.2. The electrodes were then backfilled with the same solution but containing amphotericin B at 0.36 mg/ml to allow membrane perforation. Islets were transferred from culture dishes into a 0.5-ml recording chamber. Solutions held at 32–34°C were driven through the bath by a gravity system at a rate of ∼1 ml/min. Islets were visualized using an inverted microscope (Olympus IX50). Pipette seals obtained were >2 G-ohms. Perforation was judged to be successful when the series resistance decreased to a steady-state level and membrane capacitance increased. Recordings were made using an extracellular solution containing (in mM): 140 NaCl, 3 CaCl₂, 5 KCl, 2 MgCl₂, 10 HEPES, and 11.1 or 2.8 glucose. β-Cells were identified by their lack of activity in 2.8 mM glucose and by the appearance of regular electrical bursting in external solution containing 11.1 mM glucose. Drugs were dissolved directly into saline solution daily using DMSO stocks; the final concentration of DMSO used was always ≤0.1%.

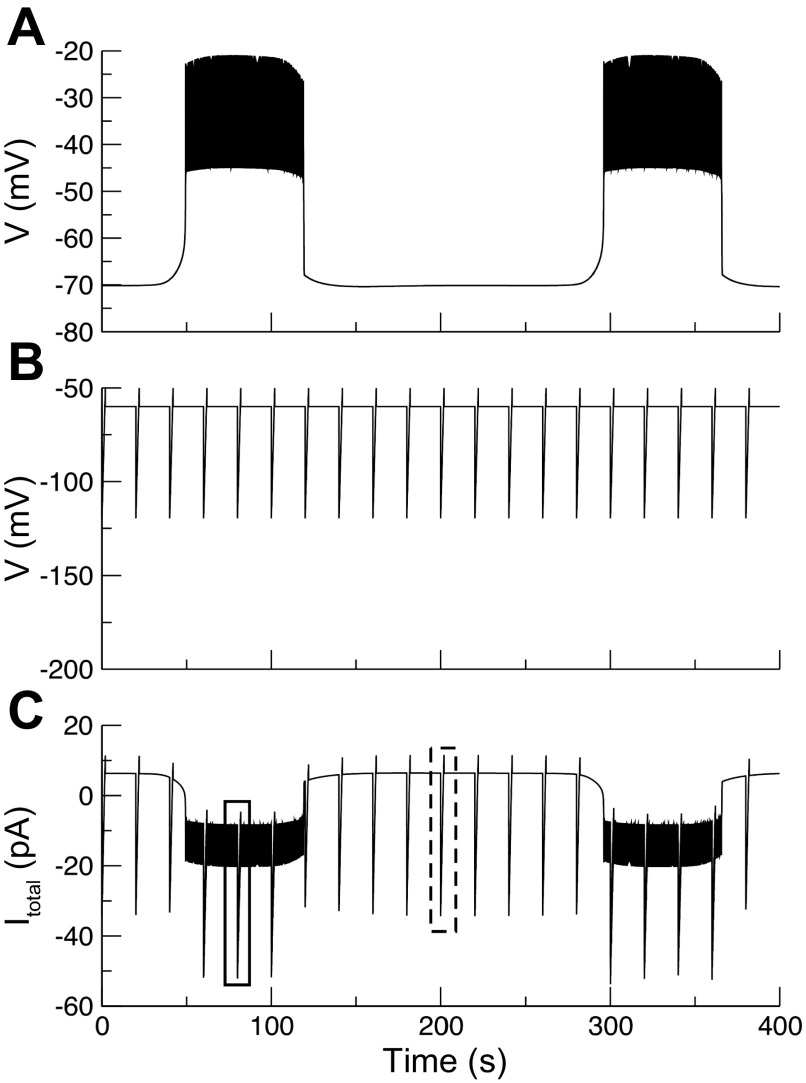
One β-cell in each intact islet was patched. After the perforated patch configuration in voltage clamp mode was established, membrane potential was recorded in current clamp (Fig. 1A). The cell was then subjected to one of two different voltage ramp protocols to measure current-voltage relationships (I-V).

Fig. 1.

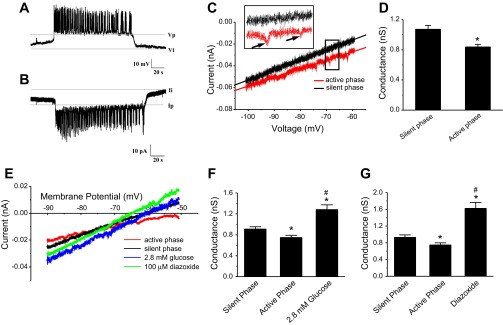
Recordings of peripheral islet cells in current clamp and voltage clamp and slope conductances measured under different conditions. A: patch-clamped cells in current-clamp mode were identified as β-cells by their characteristic bursting pattern. B: when the recording mode was switched to voltage clamp, inverted current bursts were seen, reflecting current from neighboring cells entering via gap junctions. The ratio of voltage differential to current differential yields an estimate of 1 nS coupling for the islet shown; the mean for 15 islets was 0.96 ± 0.01 nS. C: interrupted voltage ramp (IVR) protocol was used to generate current-voltage (I-V) curves in which the potential of the clamped cell was ramped from −100 to −60 mV. Invading action currents were taken as an indication that the rest of the islet was in its active phase (red); silent-phase trace indicated in black. Slope was estimated by linear curve fitting. D: in the presence of 11.1 mM glucose, conductance in the active phase was reduced compared with the silent phase (active-phase) conductance. E: representative I-V recording traces during voltage ramps. Voltage ramps were applied to islets exposed to saline containing 2.8 mM glucose or in the presence of 100 μM diazoxide in saline containing 11.1 mM glucose. Different slopes indicate that conductance is different under these conditions. F: islets exposed to 2.8 mM glucose have higher conductance than silent or active phases of islets in 11.1 mM glucose. G: conductance in the presence of diazoxide is higher than in silent or active phases in 11.1 mM glucose. *Significant difference from active phase; #significant difference from silent phase.

Interrupted voltage ramp (IVR).

Following the establishment of the whole cell configuration and the observation of stable electrical oscillations in current clamp, the recording mode was transiently switched from current clamp to voltage clamp during the silent or active phases. The cell was clamped at −60 mV in voltage clamp mode, and a 2-s voltage ramp from −120 to −50 mV (35 mV/s) was applied. Evoked currents were digitized at 10 kHz after filtering at 2.9 kHz. The protocols were generated using Patchmaster software (v2 × 32; HEKA Instruments).

Holding potential ramp (HPR).

Following the establishment of the whole cell configuration and the observation of stable electrical oscillations in current clamp, the recording mode was switched from current clamp to voltage clamp for the remainder of the experiment. The cell was voltage-clamped to a holding potential of −60 mV, and 2-s voltage ramps identical to the above were applied every 20 s. Active vs. silent phases were identified by the presence or absence of remote inward currents on the I-Vs that come from neighboring cells during the active spiking or the silent interburst phases, respectively.

Data Analysis

Analysis was carried out using Origin 7.0 software (Origin Labs, Northampton, MA). Membrane conductance was calculated from the slope of the current-voltage relations obtained between −100 and −60 mV, the region of the β-cell I-V that was mostly linear (Fig. 1C). Paired and unpaired t-tests were used to compare membrane conductances. Data shown are presented as means ± SE. Pulsatile analysis of K_ATP conductance in isolated mouse β-cells was carried out using the Cluster algorithm after determination of two point moving averages of raw data, as in (30).

Modeling

Mathematical modeling was used to verify the validity of our technique for measuring time-dependent gK_ATP and to predict the pattern of gK_ATP changes that should occur depending on the mechanism for these changes. We used a version of the Dual Oscillator model (DOM) (taken from Ref. 5) with a few parameter changes to produce slow rather than compound oscillations that are detailed in Table 1 and appendix iii. The model consists of 11 ordinary differential equations for membrane potential (V_m), K⁺ channel gating, concentrations of cytosolic Ca²⁺, endoplasmic reticulum Ca²⁺, ADP, the glycolytic intermediates glucose 6-phosphate (G6P) and fructose-1,6-bisphosphate (FBP), and the mitochondrial membrane potential and concentrations of NADH, ADP, and Ca²⁺. These 11 dynamic variables constitute two linked but separate oscillators, an electrical oscillator (EO) and a metabolic oscillator (MO). The EO is capable of oscillating when the MO is fixed, producing a variety of fast oscillations (6), and the MO is capable of oscillating when the EO is fixed, which can be manifested as small but robustly slow subthreshold fluctuations in cytosolic Ca²⁺ (4, 31). The multiple ways in which the two fundamental oscillations combine have been described schematically in Ref. 6 and analyzed mathematically in detail in Ref. 17. The model used here includes several well-characterized Ca²⁺-dependent effects on mitochondrial metabolism. In particular, Ca²⁺ flux into mitochondria decreases the mitochondrial membrane potential, decreasing the driving force for the production of ATP. In contrast, the ATP production is increased by the stimulatory action of mitochondrial Ca²⁺ on the activity of dehydrogenases. Finally, ATP is consumed by Ca²⁺ pumps in the plasma membrane and the endoplasmic reticulum. Of interest here are when the EO and MO combine to produce slow oscillations or mixed fast and slow oscillations, as we analyzed only gK_ATP in islets displaying slow- or mixed-type oscillations. To simulate cell-cell interactions in the islet (see Figs. 5 and 6), diffusive coupling of V_m, FBP, and G6P was implemented as in Ref. 44. Here, however, coupling is made asymmetric, as described in the next paragraph, to allow a two-cell ensemble to approximate an islet in which only one cell is voltage clamped. The parameters for each cell are the same for all figures except Fig. 7, A and C, where a contrasting model is displayed. Parameters that differ from the original version of the model (5) are listed in Table 1.

Table 1.

Parameters for simulations using the Dual Oscillator model

Parameter	Original	Figs. 6, 7, 8B&D	Fig. 8A&C
Electrical
gK(Ca) (pS)	300	100	100
gK(ATP) (pS)	16,000	10,000	18,000
Vm (mV)a	−20	−16	−16
kpmca (ms−1)	0.1	0.15	0.15
Metabolic
JGK (μM s−1)b	0.4	0.18	NA
K4 (μM)	220	1000	NA
kGPDH (μM ms−1)	0.0005	0.0005	0
JGPDH_bas (μM ms−1)	0.0005	0.0005	0.002

The main changes were a reduction in maximal K_ATP conductance (gK_ATP) and flux through glucokinase (GK) to increase the range of gK_ATP in order to conform to the observations in the present study. The other changes were needed to restore the period to about 5 min and adjust spike amplitude. See appendix iii for further details on parameter changes and IV for computer codes used in the simulations

^aHalf-maximal membrane potential for Ca²⁺ activation (not labeled in original)

^bUnits corrected from original paper (5).

Fig. 5.

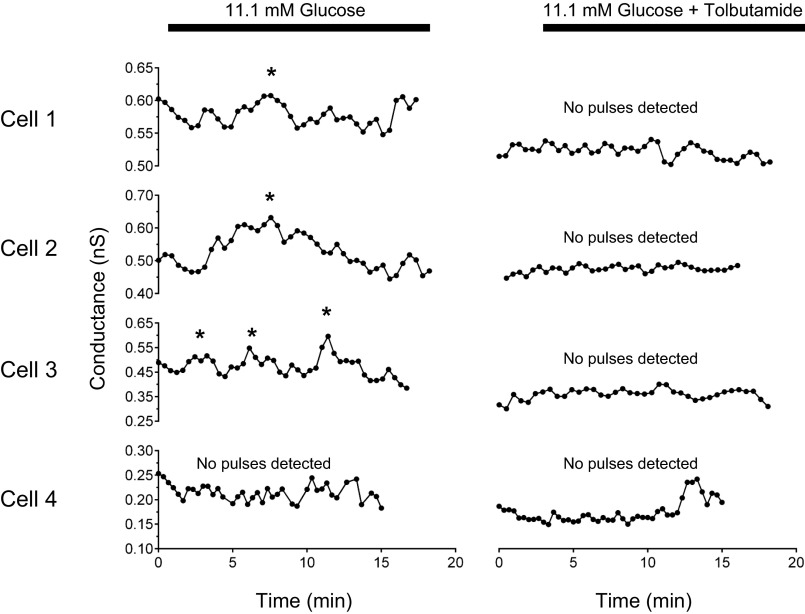
K_ATP conductance (gK_ATP) oscillations present in isolated β-cells were abolished by tolbutamide. Ramp voltage commands elicited oscillatory slope conductances in 3 of 4 isolated β-cells, detected using the Cluster algorithm (*, detected peaks). Tolbutamide (100 μM) blocked conductance oscillations and significantly decreased mean conductance (P < 0.05 with paired t-test). Data plotted are 2 point moving averages of raw conductance values.

Fig. 6.

Membrane potential in unclamped and clamped portions of the model islet and simulation of membrane current in the clamped cell. Simulation of an experiment where 2-s I-V ramps were applied once every 20 s. A: membrane potential in the unclamped supercell. B: membrane potential in the voltage clamped cell. C: current in the unclamped cell. Parameters for ionic currents and metabolism are the same as in Fig. 7, B and D (slow glycolytic bursting case), with the addition of diffusive coupling on V_m, FBP, and G6P. Coupling parameters in Eq. 1 in materials and methods were g_c = 10 pS and P = 0.01 for an effective coupling strength, as seen by the clamped cell equal to ∼500 pS. This agrees well with the empirical value estimated from the model using voltage and current differentials in A and C, respectively. Corresponding effective coupling strengths for FBP and G6P were 1.0 and 0.5 ms⁻¹, respectively.

Fig. 7.

Extraction of gK_ATP in the model islet. Values are taken from the holding potential ramp simulated in Fig. 4. A: I–V curves in the clamped cell during I–V ramps simulated in Fig. 5. Curves with oscillations were taken when the unclamped portion of the islet was in its active phase of bursting. B: linear curve fits to 2 representative I–V curves, 1 from a silent phase and 1 from an active phase (see boxed regions in Fig. 5C). C: actual gK_ATP in the clamped cell during each ramp (solid line); total slope conductance from linear fits as in B (○); and total conductance with coupling conductance removed (triangles). Filled symbols, active phase; open symbols, silent phase.

In an islet coupled through gap junctions producing synchronous bursting and in which one peripheral cell is voltage clamped, there are two distinct cell populations: those cells that are not clamped and which oscillate in synchrony, and a single cell whose voltage is clamped but which feels the effects of the other population via the electrical coupling.

To model this in a simple way, we represent the nonclamped cell population as a single bursting cell that we refer to as a “supercell” (39). This is a reasonable approximation, because the cells in the bursting population are synchronous; i.e., they are all doing approximately the same thing. Because this cell represents a large membrane area (the sum of the areas of all bursting cells), the effect of this supercell on the clamped cell via gap junctions will be large, whereas the effect of the clamped cell on the supercell will be small. Thus, the electrical coupling is effectively asymmetric. We denote the membrane potential of the clamped cell as V_m,1 and that of the supercell as V_m,2. The voltage equations then have the form

$$C_{m,1}\frac{d{V}_{m,1}}{dt}=-I_{ion,1}-I_{coup,1}+I_{app}$$

$$C_{m,2}\frac{d{V}_{m,2}}{dt}=-I_{ion,2}-I_{coup,2}$$

As cell 1 consists of the single voltage-clamped cell, it alone has I_app, which represents the current passed to maintain the command potential and is equal to the measured total current. When the system is in voltage clamp mode, the measured current has the form

$$I_{app}=I_{cap}+I_{ion,1}+I_{coup,1}$$

where I_cap = C_m,1dV_m,1/dt is the capacitive current and is non-zero only during the ramp. If an islet consists of N β-cells, then the fraction of membrane area in the single clamped cell is p = 1/(N − 1), while that of the supercell is 1 − p. The asymmetric coupling currents are then

$$I_{coup,1}=\frac{g_c}{2p}(V_{m,1}-V_{m,2})$$

$$I_{coup,2}=\frac{g_c}{2(1-p)}(V_{m,2}-V_{m,1})$$ (1)

A derivation of Eq. 1 can be found in appendix i.

The key point is that the effect of coupling on each population is inversely related to its size. If P = 0.5, as for two identical coupled cells, these become the usual symmetric expressions. In the simulations below, we take g_c = 10 pS and N = 101, so the clamped cell experiences ∼500 pS of coupling conductance whereas the supercell experiences effectively only ∼5 pS. Thus, the clamped cell is strongly affected by incoming coupling current, which is reflected in the measured I_app, but the supercell is only weakly affected and continues to spike and burst during the I-V ramps (see Fig. 5, A and B), as we have observed experimentally. The simplified representation of the islet makes transparent how this asymmetric response of the clamped and unclamped cells comes about.

We used the same approach for FBP and G6P, which are needed to synchronize the slow metabolic oscillations in islets. Those equations do not contain an applied current, but they do affect the measured I_app, since oscillating metabolites in the unclamped cells can diffuse into the clamped cell and affect ATP/ADP and hence gK_ATP.

Simulations were carried out using the program XPPAUT (14). Numerical solution of the ordinary differential equations was carried out by standard methods. Voltage clamp simulations were done with a variable step-size, 4th order Runge-Kutta method (Qualstp.RK4 in the XPPAUT menu) in order to handle the discontinuities introduced by voltage clamping. Current clamp simulations were done with a backward differentiation method (CVODE). The computer codes are included as supplementary files and described in appendix iv.

RESULTS

Membrane Conductance Was Higher During the Silent Phase Than During the Active Phase of the Electrical Oscillations

The whole cell perforated patch clamp technique was used to record the electrical activity of a peripheral islet cell, and individual β-cells were identified by their characteristic bursting pattern in 11.1 mM glucose (Fig. 1A). As in our previous studies, we observed mouse islets having fast and slow oscillatory patterns, so that the type of pattern was variable (6). We previously reported that at least some of this variability is due to the individual mouse being studied (33).

When the patch clamp was switched from current clamp to voltage clamp mode, the holding current oscillated, showing inverted bursts representing currents entering from neighboring cells (Fig. 1B), as previously seen by others (19, 37). The coupling conductance can be estimated by using Ohm's law from the product of the potential difference between the active and silent phases of the patched cell in current clamp times the current difference in voltage clamp (40). For the record shown in Fig. 1, A and B, the coupling conductance is ∼1 nS.

Figure 1C shows the results of an interrupted voltage ramp (IVR), in which the patch clamp was switched from current clamp to voltage clamp during the silent or active phases of the burst, as described in materials and methods. The I-V curves generated using the IVR were generally linear between −100 and −60 mV, with some curvilinear behavior seen at more depolarized potentials. The slope conductance calculated from ramp I-V for the cell shown was measurably lower during the active phase (red curve) than during the silent phase (black curve). Note that the active-phase curve is characterized by the presence of invading action currents or “notch currents” (identified in the inset in Fig. 1C on an expanded time scale by black arrows) that are presumed to occur due to the bursting activity of neighboring cells and are absent during silent-phase ramps. These notch currents were used to distinguish active-phase I-V curves from silent-phase I-V curves during repeated holding potential ramps (HPR; Fig. 2), when the burst pattern could not be directly observed. Repeating the IVR with 33 islets, we found that the mean silent-phase conductance was greater than the active-phase conductance (active-phase conductance, 0.84 ± 0.04 nS; silent-phase conductance, 1.07 ± 0.05 nS; n = 33, P < 0.01 by paired t-test; Fig. 1D). Although there were shifts in current levels between recordings, these likely reflect different levels of coupling conductance, but note that only the slopes of these curves were used to make inferences about gK_ATP. In addition, as shown in Fig. 5, gK_ATP oscillations were also observed in some completely isolated mouse β-cells held at −60 mV.

Fig. 2.

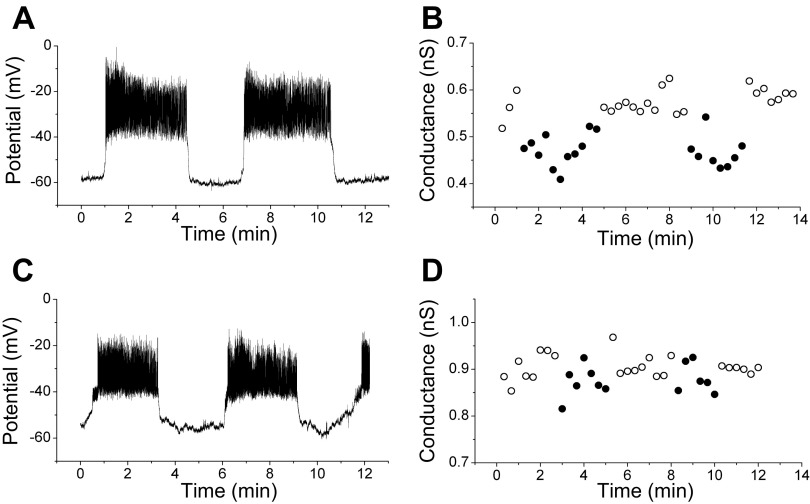
Islet conductance oscillates in 11.1 mM glucose. A: representative recording trace showing oscillatory membrane potential of an islet exposed to 11.1 mM glucose. B: oscillatory conductance values obtained using voltage ramps from the same β-cell held at −60 mV between ramps. The oscillation period was similar for voltage and conductance. Recordings were sequential, with conductance measured after establishing the presence of membrane potential oscillations. C: silent- (○) and active- (●) phase durations for all 11 islets tested.

We next determined how total conductance was effected by manipulations that influence the number of open K_ATP channels (Fig. 1E). We first used a low glucose concentration (2.8 mM), for which the islets were silent due to a large number of open K_ATP channels. In low glucose, the measured conductance was 1.28 ± 0.09 nS (n = 10), which was higher than that seen during either the corresponding silent phase (0.91 ± 0.04 nS, n = 10, P < 0.01, paired ANOVA) or the active phases triggered by 11.1 mM glucose (0.74 ± 0.04 nS, n = 10. P < 0.01; Fig. 1, E and F). We next tested the effect of diazoxide (DZ), a K_ATP channel opener (1). As shown in Fig. 1, E and G, islet conductance was significantly increased by 100 μM DZ (1.62 ± 0.14 nS, n = 11) compared with the silent (0.93 ± 0.06 nS) or active phases (0.75 ± 0.04 nS). Indeed, the conductance in DZ and 11.1 mM glucose was higher even than the conductance in 2.8 mM glucose alone, demonstrating that a sizeable fraction of K_ATP channels are still closed in 2.8 mM glucose.

β-Cell Conductance Slowly Oscillated Between the Silent and Active Phases of Bursting

The experiment above demonstrated that membrane conductance was higher in the silent phases than in the active phases of bursting. These determinations were made in islets that were switched to voltage clamp from current clamp during different phases of bursting. As an alternative method to more systematically investigate changes in β-cell conductance during bursting, we recorded ionic currents during 2-s voltage ramps applied every 20 s to β-cells held at −60 mV for the entire duration of the experiment [holding potential ramp (HPR) protocol]. One advantage of this approach is that it maintains a low Ca²⁺ level in the clamped cell, so that variations in ionic conductance due to changes in Ca²⁺ are minimized. In contrast, the effect of intrinsic metabolic oscillations on K_ATP conductance is maintained, provided that these oscillations persist at a fixed low Ca²⁺ level (evidence for this was given in Ref. 29).

Figure 2 shows an example of how the HPR protocol was used on an islet. After recording several cycles of β-cell electrical activity in current clamp in 11.1 mM glucose (Fig. 2A), we clamped cells to −60 mV, and the HPR protocol was initiated (2B). Sometimes, the holding current of superficial β-cells was steady, which we interpreted to mean that neighboring unclamped cells of the islet were in their silent phase of bursting. At other times, the measured holding current exhibited notches, which we interpreted to mean that the unclamped cells of the islet were in the active phase of bursting and the notches resulted from invading action potentials. Applying voltage ramps from −100 to −60 mV elicited smooth ramp I-V curves during the putative silent phases and notch-containing I-V curves during the putative active phases. As shown in Fig. 2, the conductance oscillated and was higher during the silent phases (open circles) than during the active phases (filled circles). Note that the period of the conductance oscillation is similar to that of the burst period, although the electrical bursting (2A) and the oscillating conductance changes (2B) were not measured simultaneously.

This procedure was repeated in a total of 11 islets, and the conductances are quantified in Fig. 2C. Each panel represents an individual islet, and the conductance for each silent (open circle) and active (filled circle) phase is shown. The mean active-phase conductance was lower than the mean silent-phase conductance in each islet tested. The average difference in conductance between active and silent phases was 0.117 ± 0.012 (SE) nS and was highly significant (P < 0.0001). In addition, the period of the conductance oscillations was similar to the burst period in all the islets we tested (not shown).

Oscillations in Islet Conductance Were Mediated by K_ATP Channels

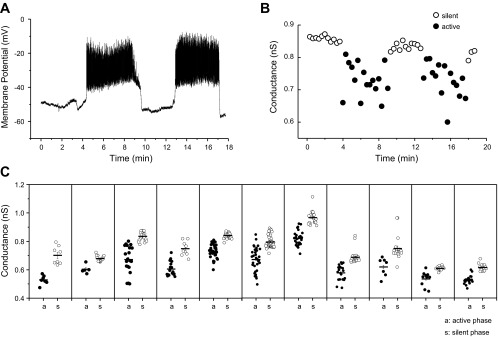
The conductance recorded and measured during the voltage ramps is expected to be mostly due to K_ATP channels and coupling conductance. However, to confirm this and to distinguish the two, we used tolbutamide, a K_ATP blocker, to test whether it reduced total slope conductance. In 11.1 mM glucose, addition of this agent converted the islet from a bursting state to a continuous spiking state (Fig. 3A). During bursting, the slope conductance in the islet shown oscillated between 0.88 and 0.75 nS in the silent and active phases, respectively, and was reduced to 0.52 nS by tolbutamide (Fig. 3B). More importantly, the conductance measured in the presence of tolbutamide did not exhibit slow oscillations but instead remained steady at a low value except for noisy fluctuations. The residual conductance is likely to consist mainly of coupling conductance, which is shown here to not exhibit slow oscillations and thus supports the model assumption that coupling conductance is constant. The residual conductance in this islet was ∼0.5 nS, comparable to the value obtained from the ratio of the current differential to the voltage differential (Fig. 1, A and B). Similar results were found in two other islets (not shown). This is consistent with the hypothesis that the conductance oscillations are due to K_ATP channels. In addition, the period of these changes in gK_ATP was quite similar to those we observed previously for the endogenous NAD(P)H oscillations of islets (29, 32) and for slow islet Ca oscillations (29, 32, 33) measured under identical conditions to those used here (overnight culture followed by a challenge of 11.1 mM glucose).

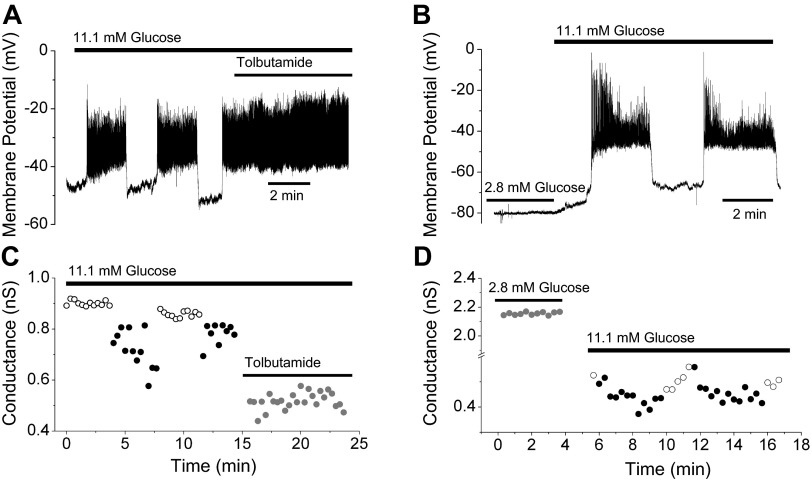
Fig. 3.

Conductance oscillations are abolished by tolbutamide or 2.8 mM glucose. A and B: in the presence of K_ATP blocker tolbutamide (200 μM), oscillations in membrane potential and conductance that were previously observed in a solution containing 11.1 mM glucose were subsequently abolished. Membrane potential after sulfonylurea exposure remained continuously depolarized, with fast spiking superimposed, and conductance declined to a lower level without oscillations under corresponding conditions. C: when exposed to 2.8 mM glucose, islets were hyperpolarized and did not burst (top). D: in low glucose, conductance was much larger than in 11.1 mM glucose and exhibited no oscillations.

Next, we examined the effects of changing the glucose concentration from a substimulatory level, in which the islet was silent, to a stimulatory level in which the islet was bursting (Fig. 3C). When islets (n = 3) were exposed to 2.8 mM glucose, the conductance was high and nonoscillatory, reflecting the large number of open K_ATP channels expected at this low glucose concentration. An increase in glucose to 11.1 mM reduced the conductance and initiated slow oscillations (Fig. 3D). This is again consistent with the hypothesis that the slowly oscillating conductance is mostly gK_ATP.

The simplest interpretation of the data in Figs. 2 and 3 is that conductance oscillations reflect fluctuating ADP/ATP levels and K_ATP channel activity due to intrinsic metabolic oscillations within individual β-cells. It is possible, however, that the conductance oscillations are secondary to oscillations in membrane potential and/or Ca²⁺ that occur during islet bursting. Although Ca²⁺ is unlikely to have risen due to entry through plasma membrane channels because of the voltage range used in the ramps (−100 to −50 mV), it is conceivable that Ca²⁺ could have diffused in from neighboring cells whose membrane potentials were oscillating. In this case, the elimination of conductance oscillations during the pharmacological manipulation of K_ATP channel activity might not reflect direct action at K_ATP channels but occur secondarily to the silencing of islet bursting and ablation of Ca²⁺ oscillations. We thus examined whether conductance oscillations were eliminated by blocking K_ATP channels only in the clamped cell while permitting oscillations in the remaining cells in the islet. We recorded membrane potential and applied HPR ramps using regular electrodes (Fig. 4, A and B) or electrodes filled with glyburide (200 μM; Fig. 4, C and D). Including glyburide in the pipette rather than the bath would be expected to limit the drug to the interior of the clamped cell and possibly a few of its neighbors. Glyburide was chosen in place of tolbutamide to block K_ATP channels due to its greater lipid permeability (47). As shown in Fig. 4C, membrane potential oscillations recorded in current clamp mode persisted in the presence of internal glyburide. These membrane potential oscillations could be due only to bursting occurring in neighboring cells and transmitted through gap junctions, and they confirm that the drug did not significantly perturb cells other than the clamped cell. Figure 4D shows the conductance obtained from HPR ramps applied to one islet in the presence of internal glyburide. In contrast to the membrane potential oscillations, the conductance oscillations were reduced in amplitude by glyburide in the pipette in five of six islets tested (in one islet glyburide had no effect at all on conductance oscillations). This implies that the conductance oscillations originated in the clamped cell, not its neighbors, and were in particular not the result of Ca²⁺ diffusing in from the neighbors.

Fig. 4.

Conductance oscillations are abolished in recordings using glyburide-filled electrodes. A and B: membrane potential and slope conductance oscillations recorded using the holding potential ramp (HPR) protocol in 11.1 mM glucose with a standard electrode. C and D: membrane potential and slope conductance recorded in the same islet and glucose concentration as shown in A but using a glyburide-filled electrode (200 μM); electrical oscillations were preserved, but conductance oscillations were abolished in 5 of 6 islets tested. Membrane potential oscillations that occur in neighboring cells are presumed to be transmitted to the voltage-clamped cell through gap junctional coupling. The hypothesis that conductance oscillation amplitude was lower in glyburide than in control was significant by unpaired t-test with P = 0.03 (0.118 ± 0.04 vs. 0.051 ± 0.06 nS).

Figures 3 and 4 taken together show that slow conductance oscillations were reduced or eliminated after pharmacological inhibition of gK_ATP. These data strongly support the hypothesis that the dominant oscillatory component of islet conductance we observed is gK_ATP.

gK_ATP Oscillations in Isolated β-Cells

As a further test for slow oscillations of gK_ATP, we applied ramp voltage clamp commands to single, isolated mouse β-cells. Figure 5 shows the conductances of four single β-cells in which we were able to record before and after addition of tolbutamide. Four were oscillatory (cells 1–3) as assessed by the Cluster algorithm (see materials and methods; identified peaks are denoted by asterisks), while one cell (cell 4) lacked pulsatility. For each of the four cells, the addition of 100 μM tolbutamide to the bathing solution reduced membrane conductance from 0.45 ± 0.005 nS to 0.37 ± 0.002 nS (P < 0.05 by paired t-test), and in all three cells where Cluster detected conductance oscillations these were eliminated by tolbutamide. Oscillations were also observed in 11.1 mM glucose for 8 of 11 single cells that were not exposed to tolbutamide. These oscillations had a mean period of 3.2 ± 0.4 min, which is within the typical range of slow metabolic oscillations in β-cells. These findings thus support our interpretation that gK_ATP can intrinsically oscillate in the absence of Ca²⁺ influx through voltage-gated Ca channels, as cells were held at −60 mV, below the activation voltage range of high voltage Ca channels, or from neighboring β-cells, as gap junctional coupling was absent.

Model-Based Validation of Conductance Oscillation Measurements

Since a pancreatic islet is an electrical syncytium consisting of a network of β-cells coupled via gap junctions (3), currents measured on the islet surface also include a contribution from neighboring β-cells that is passed into the clamped cell by the gap junctions. This is clearly the case here, as indicated by the notch currents in our voltage clamp traces. The coupling between cells is thus strong enough to transmit remote spikes to the clamped cell but not strong enough to suppress the spiking and bursting of the unclamped cells by the single clamped β-cell.

To aid in the interpretation of the time-dependent conductance data, we employed the Dual Oscillator model (DOM), which can produce slow bursting oscillations like those we observed. The simulations with the model illustrated in Figs. 6 and 7 and described below suggest that the experimental estimation of oscillation amplitude from the slope conductances obtained using our protocol is not seriously affected by coupling currents and is reliable.

A model islet can be constructed by electrically coupling many model β-cells. However, as described in materials and methods, a significant simplification can be achieved by taking advantage of the fact that β-cells within an islet burst in synchrony and so can be treated approximately as a “supercell”. Thus, one can investigate the effects of electrical coupling on a voltage-clamped peripheral cell by analyzing a model where a clamped cell is electrically coupled to an unclamped supercell.

We used this simplified islet model to ascertain whether oscillations in gK_ATP could be faithfully extracted by the ramp protocol used in the experiments when applied to a coupled islet. Figure 6 shows the simulated membrane potentials of the bursting β-cell subpopulation, modeled as a supercell (Fig. 6A), and the coupled voltage-clamped β-cell (Fig. 6B). The unclamped supercell continued oscillating despite the voltage clamp of the coupled cell since the coupling current passing into the supercell is small. In contrast, the effects of coupling are large in the clamped β-cell, since its membrane area is small compared with that of the supercell.

The total current predicted for the clamped cell is shown in Fig. 6C. One active-phase ramp is shown in the solid box and one silent-phase ramp in the dashed box. The rapid spikes during the active phase are reflected in the clamped cell as fast current spikes during the holding period. Coupling causes the total current in the clamped cell to oscillate positively during the silent phase and negatively during the active phase of supercell bursting (Fig. 6C). The effects of the voltage ramps in Fig. 6B are seen as large downward deflections that occur during both active and silent phases in Fig. 6C. The effective conductance experienced by the clamped cell is ∼0.5 nS, as can be seen by substituting the values g_c = 10 pS and p = 1/100 in Eq. 1. In contrast, the effective conductance experienced by the supercell is 5 pS, 100 times smaller, and the voltage deflections expected in Fig. 6A are not visible on the scale of the graph. We note that the number of islet cells used in the simulation is not critical, as use of >100 cells would not change the result (see appendix ii for further explanation).

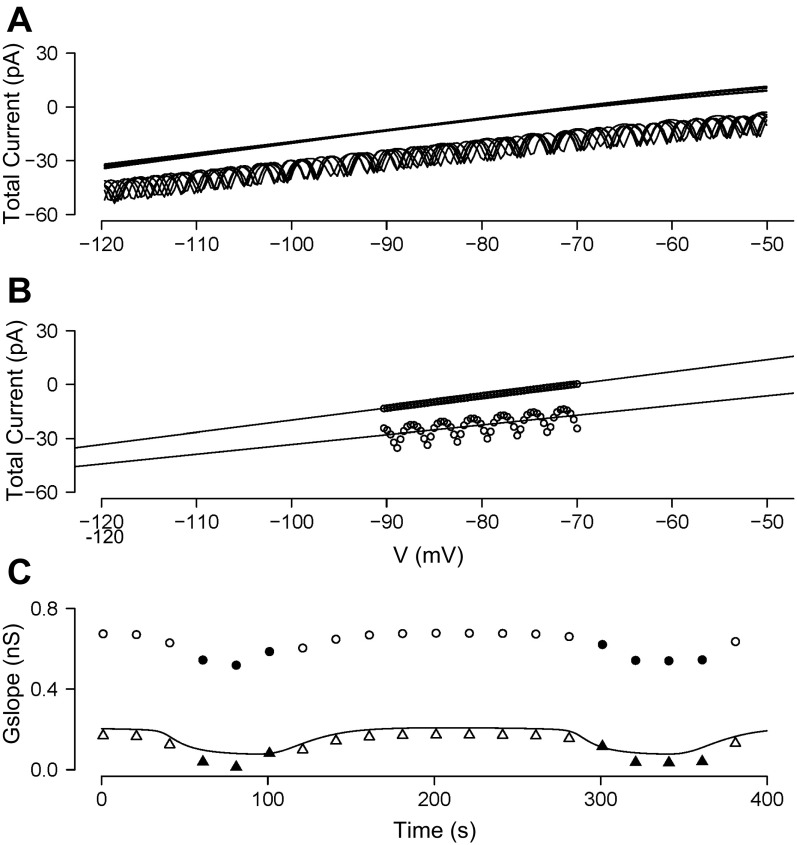
The ramp currents for each sweep from Fig. 6C are overlaid on the ramp voltages from Fig. 6B to give the simulated I-V traces shown in Fig. 7A. They correspond to the experimental I-V traces in Fig. 1B and again exhibit notch currents (seen here as small oscillations) as were observed in the experiments. The slope of the I-V curve is larger during the silent phase than during the active phase of the burst, and there is a clear vertical shift, which was expected from the drop in current in Fig. 6C and was also observed experimentally in Fig. 1B.

The model indicates that this shift is due to coupling current from the unclamped neighbors (Eq. 1). The coupling current causes only a vertical shift and not a change in slope for two reasons. First, we assumed in the model that coupling conductance is constant. This assumption is justified by Fig. 3A, where gK_ATP was blocked. Second, the voltage profile is nearly a square wave, alternating between the silent phase and plateau phase potentials, with only brief excursions to higher potentials. The coupling current thus acts like a constant-conductance leak current with a reversal potential that jumps when the unclamped cells switch between their silent and active phases. There is also a component due to membrane capacitance, but since this current is constant for all voltages (the rate of change of voltage is constant during a ramp) it makes no contribution to the slope.

In Fig. 7B, we used the model to simulate the experimental determination of slope conductance by fitting a straight line through two representative currents elicited between −90 and −70 mV, where the errors due to nonlinear voltage-dependent conductances are minimized. Figure 7C (circles; filled for active phase, open for silent phase) shows the conductance over time of the clamped cell. The extracted total slope conductance (circles) is much larger than the actual K_ATP conductance of the model clamped cell (solid line). Most of this discrepancy is accounted for by the coupling conductance, as shown by the triangles (filled, active phase; open, silent phase), representing the total conductance minus the coupling conductance. Thus, although the coupling conductance is large, it is an additive component and does not affect the estimation of the oscillation amplitude.

The amplitude of the conductance oscillation in the model is ∼0.16 nS, comparable to that observed in the experiments using HPR ramps (Fig. 2). Most importantly, both the total conductance and gK_ATP are lower during the active phase (filled triangles) than during the silent phase (open triangles) of the model burst as observed in the experiments (Fig. 7C; compare Figs. 1 and 2).

Low Conductance During the Active Phase Is Consistent with Slow Bursting Driven by Metabolic Oscillations

We have thus far established that the total conductance is higher during the silent phase of bursting than during the active phase and that this reflects the activity of K_ATP channels. What does this tell us about the mechanism of bursting in β-cells? We address this question using the DOM (see materials and methods and Refs. 5 and 6). In this model, oscillations in glycolysis can produce slow oscillations in the ATP/ADP ratio and thus slow oscillations in gK_ATP. The Ca²⁺ concentration also plays a role in electrical activity in the model; it acts directly on Ca²⁺-activated K⁺ channels and indirectly on ATP utilization via Ca²⁺ pumps and on ATP production via Ca²⁺-dependent dehydrogenases and Ca²⁺-dependent changes in the mitochondrial membrane potential. By changing parameter values, one can emphasize one feedback pathway over the others and thus produce slow bursting driven by glycolytic oscillations or, when the glycolytic oscillator is disabled, slow bursting driven solely by Ca²⁺ feedback. We can use these two modes of operation to determine what our data on gK_ATP oscillations tell us about the burst mechanism.

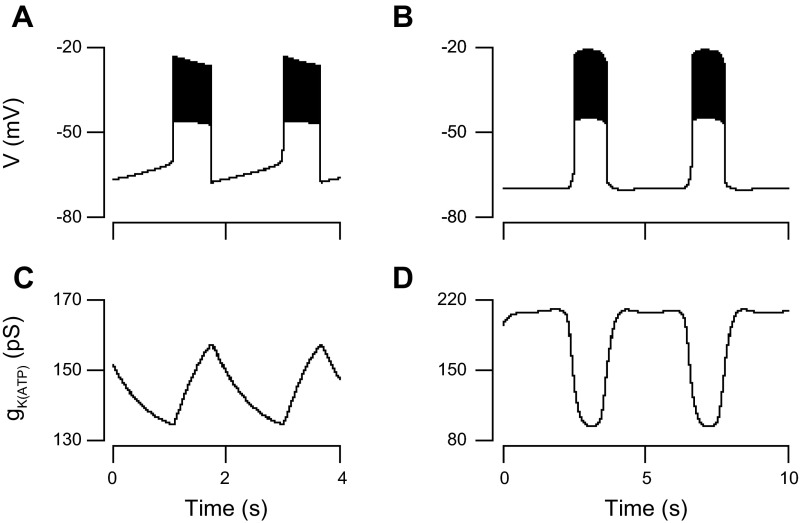
The observation that the conductance is higher during the silent phase than during the active phase of bursting might seem unsurprising at first glance, as increased K_ATP conductance would naturally result in hyperpolarized membrane potential, but the converse does not hold: hyperpolarized membrane potential does not imply that mean K_ATP conductance must be higher during the silent phase. In fact, in some models for islet oscillations, K_ATP conductance is lower during the silent phase (8, 15, 16). Here, we use the DOM to illustrate a case in which mean K_ATP conductance is the same in the active and silent phases. This occurs when the glycolytic oscillator is disabled and bursting is driven by slow changes in the ATP/ADP ratio driven by Ca²⁺. This is the basis for bursting in the Keizer-Magnus model (24, 25), which is actually a submodel of the DOM. In Keizer-Magnus mode, oscillations of gK_ATP are driven by the effect of Ca²⁺ to inhibit mitochondrial ATP production. Consequently, gK_ATP rises during the active phase and declines during the silent phase (Fig. 8, A and C). The mean gK_ATP is thus approximately the same in the active and silent phases, which is not compatible with our data. In contrast, when the glycolytic oscillator is operational (Fig. 8, B and D) and is the primary driver of gK_ATP changes, the active phase is initiated by a sharp rise in glycolytic flux (not shown), which reduces gK_ATP. The end of the glycolytic spike, due to depletion of F6P, allows gK_ATP to recover, ending the active phase. Thus, in glycolytic mode, gK_ATP is lower during the active phase than in the silent phase, in agreement with the experimental data we have presented here (Figs. 1, C and D, and 2).

Fig. 8.

Symmetrical gK_ATP in Keizer-Magnus model vs. asymmetrical gK_ATP when glycolysis oscillates. A: Membrane potential (A) and gK_ATP (C) for the Dual Oscillator model (DOM) in Keizer-Magnus mode (i.e., no glycolytic oscillations). Membrane potential (B) and gK_ATP (D) for the DOM in glycolytic oscillation mode. See text for interpretation and details.

DISCUSSION

In this study, we measured and analyzed membrane conductance changes during the glucose-dependent electrical oscillations of isolated mouse islets. To accomplish this, voltage ramps were applied to single β-cells residing on the surface of islets. We found that when the islet exhibited slow bursting oscillations the total conductance in the clamped cell oscillated with a period similar to the burst period (Fig. 2). When the islet was silent or in a tonic spiking state, the conductance in the clamped cell was constant, with small noisy fluctuations (Fig. 3). With pharmacological treatments (Figs. 3 and 4) and the aid of a mathematical model (Fig. 7), we demonstrated that these oscillations were due to oscillations in the conductance of the K_ATP current. Significantly, the conductance was lower during the active phase of the islet burst than during the silent phase (Figs. 1–4). Our model simulations show that this pattern is indicative of bursting driven by intrinsic metabolic oscillations rather than metabolic oscillations driven by changes in [Ca²⁺] (Fig. 8). Here, Ca²⁺ plays a permissive role, but metabolic oscillations can occur in the absence of Ca²⁺ oscillations (29).

The ionic conductance measured in this study over the voltage range of −100 to −60 mV was mediated in part by plasma membrane ionic conductances and in part by gap junction conductance. gK_ATP is expected to be the dominant intrinsic ionic conductance and to be nearly linear in this voltage range. We tested this hypothesis and found that the total conductance was greatest in 100 μM diazoxide, less in 2.8 mM glucose, still less in 11.1 mM glucose during the silent phase of the oscillations, and least during the active phase of the oscillations (Figs. 1 and 2). This sequence is consistent with the properties of gK_ATP. Moreover, bath application of the K_ATP channel blocker tolbutamide abolished the conductance oscillations, as did lowering the glucose concentration to 2.8 mM (Fig. 3). Additionally, conductance oscillations were also blocked by the addition of the K_ATP channel blocker glyburide to the patch pipette solution, rather than the bath, even though the neighboring cells continued to exhibit membrane potential oscillations (Fig. 4). The latter set of experiments showed that the conductance oscillations originated in the clamped cell and were not the result of Ca²⁺ diffusion from the neighbors. As Ca²⁺ is unlikely to have oscillated in the clamped cell during HPR ramps, this provides further support for the hypothesis that the oscillations in total slope conductance are mediated by gK_ATP and driven by oscillations in metabolism. Finally, conductance oscillations in cells isolated from islets were abolished by application of tolbutamide (Fig. 5).

The question of how gK_ATP is activated during the slow oscillations remains to be considered. There is experimental evidence that K_ATP channels can be activated by imposed elevations of Ca²⁺ (10, 20, 38) but that oscillations of metabolism can also occur in the absence of Ca²⁺ oscillations (29). We think it unlikely that the conductance oscillations that we observed were driven by Ca²⁺, for the following reasons. First, Ca²⁺ influx through the Ca²⁺ channels of the patched cell is expected to be minimal between −100 and −60 mV, as this is below the activation range of voltage-dependent Ca²⁺ channels. Second, although it is possible that Ca²⁺ could enter the clamped cell through gap junctions from unclamped neighbors and directly activate K_Ca or indirectly activate K_ATP channels, Ca²⁺ diffusion would likely be greatest when the neighboring cells are in their active phase. Thus, if this diffusion effect were large, one would expect to see increased conductance in the clamped cell during the active phase, in contrast to our observation that the slope conductance was lowest during the active phase. Also, as discussed above, we found that conductance oscillations were reduced or abolished when K_ATP channels were blocked in the clamped cell alone, which further argues against a major role for Ca²⁺ diffusion.

In addition to the effects on gK_ATP discussed above, Ca²⁺ provides negative feedback to its own elevation directly by activating K_Ca channels, as in many other cell types (18, 20). Moreover, because Ca²⁺ that enters the cell can then be exchanged for Na⁺, its rise can in turn indirectly activate electrogenic Na⁺-K⁺ pump activity (9, 15, 16). While these complex mechanisms can be difficult to disentangle experimentally, in our view, many of the disagreements in the literature about the importance of these various mechanisms can be resolved by carefully distinguishing between fast (period 10–120 s or so) and slow (period 3–10 min) islet oscillations. The DOM incorporates both classes of mechanisms of K_ATP channel activation and reproduces both fast and slow oscillations (6). According to this model, the effect of Ca²⁺ on K_Ca together with its effect on metabolism (and hence K_ATP conductance) is an important driver of the fast oscillations. The models described in Refs. 8, 11, 16, and 17 provide alternative explanations for the fast oscillations. All of those models involve fast oscillations in metabolism secondary to the fast Ca²⁺ oscillations, which is not in conflict with the data in this paper.

Input resistance fluctuations have been studied during fast oscillations to assess whether burst termination is mediated by the opening of a K⁺ channel or inactivation of an inward current. Atwater et al. (2) examined input resistance by injecting current pulses and recording the resultant voltage deflections. The input resistance increased during the silent phase, consistent with closure of a K⁺ channel, and decreased during the active phase, consistent with the opening of a K⁺ channel. This was interpreted as evidence in favor of a K_Ca channel as the primary pacemaker of fast bursting but could apply equally to the K_ATP channel, which had not been discovered at that time. Göpel et al. (20) also looked at input resistance during fast bursting, but by measuring current in response to 10 mV voltage-clamp steps around −70 mV (see their Fig. 3). They found no oscillation in input resistance, but we believe that with this protocol they would have seen the same oscillation that we saw if they had examined slow islets. Indeed, Larsson et al. (23) applied the same protocol to cells exhibiting slow oscillations and observed conductance variations similar to ours between active and silent phases.

In the DOM, K_ATP channels couple slow oscillations in metabolism (specifically ATP/ADP) to Ca²⁺-dependent electrical oscillations. However, electrical as well as Ca²⁺ oscillations persist in sulfonylurea type 1 receptor (SUR1) knockout mice that lack K_ATP channels (13, 21). Removal of a large hyperpolarizing K_ATP current should put islet cells into a continuous spiking state with an elevated Ca²⁺ level. Since this does not occur, it is likely that another K⁺ channel is upregulated in the knockout mice. If these channels are responsive to ATP/ADP, then this could explain why slow electrical and Ca²⁺ oscillations persist in SUR1 knockout mice. While models based on purely ionic mechanisms can certainly produce fast oscillations (for a recent example, see Ref. 7), in general these other models cannot simulate slow or mixed fast and slow oscillations.

In summary, we have shown that slope conductance obtained from voltage ramps in pancreatic islets exposed to stimulatory glucose oscillates, with a higher conductance in the silent than the active phase when the β-cells are held at −60 mV. These oscillations were further shown to be predominantly gK_ATP and likely were not driven by Ca²⁺ oscillations, which would be expected to increase the total conductance during the active phase, not decrease it. These results are compatible with the DOM but not models of slow islet oscillations that predict higher gK_ATP during the active phase. The novel approach that we have used in this paper should be useful for further studies to probe the endogenous conductances of pancreatic islets.

GRANTS

Work in the Satin laboratory was supported by National Institute of Diabetes and Digestive and Kidney Diseases grant RO1 DK-46409. A. Sherman was supported by the Intramural Research Program of the NIDDK. R. Bertram was supported by National Institute of Diabetes and Digestive and Kidney Diseases grant R01 DK-080714 and C. S. Nunemaker by RO1 DK-089182.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.R., A.S., R.B., P.B.G., and L.S.S. conception and design of research; J.R. performed experiments; J.R., A.S., R.B., P.B.G., C.S.N., C.D.W., and L.S.S. analyzed data; J.R., A.S., R.B., P.B.G., C.S.N., C.D.W., and L.S.S. interpreted results of experiments; J.R., A.S., and C.S.N. prepared figures; J.R., A.S., R.B., P.B.G., C.D.W., and L.S.S. drafted manuscript; J.R., A.S., R.B., P.B.G., C.S.N., C.D.W., and L.S.S. edited and revised manuscript; J.R., A.S., R.B., P.B.G., C.S.N., C.D.W., and L.S.S. approved final version of manuscript.

Appendix

I. Derivation of Eq. 1 in Main Text

Here, we derive Eq. 1 of materials and methods, which represents an islet as one clamped cell connected to an unclamped supercell representing the rest of the cells of the islet. We do the analysis for the more general situation of a heterogeneous islet as two coupled isopotential subpopulations with distinct properties and then specialize the final result, as this is no harder and the result can then be used in a range of applications. This formula has been used before but without a derivation to explain why it works (35). We assume that all properties are identical within each subpopulation but the two subpopulations can have different properties.

In general, the distinct islet subpopulations could be intermixed rather than contiguous, but simulations show that if the islet is reasonably well synchronized, an adequate approximation can be obtained by idealizing it as two spheres connected by a resistor representing the distributed gap junctional conductance. Let the membrane potential of the cells in the two populations be represented by the equations

$$C_{m,1,tot}\frac{d{V}_{m,1}}{dt}=-I_{ion,1,tot}-I_{coup,1,tot}$$

$$C_{m,2,tot}\frac{d{V}_{m,2}}{dt}=-I_{ion,2,tot}-I_{coup,2,tot}$$

where the subscript tot indicates that the quantities are total quantities for each population. We rewrite these in terms of quantities per cell:

$$N_1{C}_m\frac{d{V}_{m,1}}{dt}=-N_1{I}_{ion,1}-\frac{N_1+N_2}{2}{g}_c(V_1-V_2)$$

$$N_2{C}_m\frac{d{V}_{m,2}}{dt}=-N_2{I}_{ion,2}-\frac{N_1+N_2}{2}{g}_c(V_2-V_1)$$

where N₁ and N₂ are the numbers of cells in the two groups and the capacitances, currents, and conductances shown are per cell. The capacitance per cell is not subscripted, because we assume that all cells have the same surface area. The coupling currents have been written out as conductance times the voltage difference, and we assume that the gap junctions are symmetrical and identical and that all cell pairs are coupled. Note that the gap junctional conductance is scaled by half the number of cells in the islet since connections come in symmetrical pairs.

We divide both sides of both equations by N = N₁ + N₂ and define

$$p=\frac{N_1}{N_1+N_2}$$

resulting in

$$p{C}_m\frac{d{V}_{m,1}}{dt}=-p{I}_{ion,1}-\frac{1}{2}{g}_c(V_1-V_2)$$

$$(1-p)C_m\frac{d{V}_{m,2}}{dt}=-(1-p)I_{ion,2}-\frac{1}{2}{g}_c(V_2-V_1)$$

Finally, we divide the equations by p and 1 − p, respectively, to obtain

$$C_m\frac{d{V}_{m,1}}{dt}=-I_{ion,1}-\frac{1}{2p}{g}_c(V_1-V_2)$$

$$C_m\frac{d{V}_{m,2}}{dt}=-I_{ion,2}-\frac{1}{2(1-p)}{g}_c(V_2-V_1),$$

This result leads to Eq. 1 in the main text for the voltage clamp case. An equivalent result, without the factor of 2 in the coupling conductance, g_c, was previously obtained for a hippocampal neuron model, in which one sphere represented the soma and the other the dendritic tree (35). We verified that the factor of 2 is correct by using Ohm's law and the product of the current and voltage differences in the simulation of Fig. 5, according to the method described in Ref. 40. This two-compartment reduction was shown to be accurate for neurons with complex dendritic trees, with p, the ratio of soma to dendrite area, sufficient for predicting whether the neurons would show bursting behavior (26). We can restate the result for pancreatic islets as follows: Two isopotential compartments of unequal surface area, which can be represented by spheres, coupled by a symmetrical gap junction or axial resistance, can be transformed via scaling by surface area into two compartments of equal surface area with an asymmetrical (rectifying) gap junction.

II. Dependence of Results on Islet Size

The simulations for Figs. 6 and 7 were done using Eq. 1 in the main text and N = 101. Here, we show that making N larger would have little effect on the results.

Eq. 1 states that the effective coupling felt by the clamped cell and the supercell are

$$\frac{g_c}{2p}=\frac{g_c}{2}N$$

and

$$\frac{g_c}{2(1-p)}=\frac{g_c}{2}\left(\frac{N}{N-1}\right),$$

respectively, using p = 1/N.

To simulate an islet with N > 100, it is necessary to reduce g_c proportionally in order to keep the conductance felt by the clamped cell constant at the experimentally measured value. If we choose N = 1,000, for example, g_c must be reduced by a factor of 10. The factor N/(N − 1), in contrast, hardly changes. Consequently, the effect of the supercell on the clamped cell remains unchanged, but the effect of the clamped cell on the supercell, already negligible, becomes 10-fold smaller. Thus, the value of N does not change the results for slope conductance once N is sufficiently large, and our simulations (not shown) indicate that N = 101 is more than sufficiently large.

III. Parameter Changes from Previous Versions

The parameter changes from the original published version (5) are listed in Table 1, but here are some additional comments. The values in the column labeled “Original” produced compound oscillations. To obtain Figs. 6 and 7 and 8, B and D, we reduced ḡ_K(Ca) to give pure, slow oscillations. We reduced ḡ_K(ATP) and J_GK in order to increase the range of gK_ATP in accordance with the observations in this paper. To make Fig. 8, A and C, we converted the system to one equivalent to the Keizer-Magnus model by disabling the glycolytic oscillator. This was done by removing the connection between glycolysis and the mitochondria, which is mediated in the full DOM by the following equation for the flux through pyruvate dehydrogenase (PDH):

$$J_{PDH}=\frac{p_{1}NAD{H}_m}{p_{2}NA{D}_m+NAD{H}_m}\frac{C{a}_m}{p_3+C{a}_m}(J_{GPDH}+J_{GPDH\_bas}),$$

where J_{GPDH_bas} is the basal, nonoscillatory flux through glyceraldehyde-3-phosphate dehydrogenase (GPDH) and J_GPDH is the oscillatory flux through GPDH, taken to be in equilibrium with fructose-1,6-bisphosphate (FBP):

$$J_{GPDH}=k_{GPDH}\sqrt{FBP/(1\mu M)}$$

To disable the glycolytic oscillator in Fig. 8, k_GPDH was set to 0, and J_{GPDH_bas} was increased fourfold to compensate. The authoritative version of the equations is contained in the xppaut and Matlab files listed below in section IV.

IV. Source Files for the Simulations

The simulations were carried out with xppaut (14) using the files listed below as Supplementary Files. Matlab files for Fig. 8 are also included.

(xppaut and information on how to install and use it can be downloaded from: http://www.math.pitt.edu/∼bard/xpp/xpp.html).

A facsimile of each figure can be produced in xppaut by selecting Initialconds, Go with the mouse, or typing IG.

Fig6.ode: XPP code for Fig. 6, A and B. To see Fig. 6C, first type “G” (Graphic stuff) and “D” (Delete last curve), and then plot itot vs. tsec.

Fig7.ode: XPP code for Fig. 7A along with the membrane potential of the unclamped portion of the islet (V₂), scaled to fit in the window. This shows that the lower ramps with reduced slope and superimposed oscillations correspond to the time when the unclamped cells are spiking.

Fig8AC.ode: XPP code for Fig. 8A, the membrane potential of the model in Keizer-Magnus mode. To see Fig. 8C, plot gkatp vs. tmin.

Fig8AC.m: Matlab code for Fig. 8, A and C.

Fig8BD.ode: XPP code for Fig. 8B, the membrane potential of the model with glycolytic oscillator active. To see Fig. 8D, plot gkatp vs. tmin.

Fig8BD.m: Matlab code for Fig. 8, B and D.