Equifinality and its violations in a redundant system: multifinger accurate force production

Abstract

We explored a hypothesis that transient perturbations applied to a redundant system result in equifinality in the space of task-related performance variables but not in the space of elemental variables. The subjects pressed with four fingers and produced an accurate constant total force level. The “inverse piano” device was used to lift and lower one of the fingers smoothly. The subjects were instructed “not to intervene voluntarily” with possible force changes. Analysis was performed in spaces of finger forces and finger modes (hypothetical neural commands to fingers) as elemental variables. Lifting a finger led to an increase in its force and a decrease in the forces of the other three fingers; the total force increased. Lowering the finger back led to a drop in the force of the perturbed finger. At the final state, the sum of the variances of finger forces/modes computed across repetitive trials was significantly higher than the variance of the total force/mode. Most variance of the individual finger force/mode changes between the preperturbation and postperturbation states was compatible with constant total force. We conclude that a transient perturbation applied to a redundant system leads to relatively small variance in the task-related performance variable (equifinality), whereas in the space of elemental variables much more variance occurs that does not lead to total force changes. We interpret the results within a general theoretical scheme that incorporates the ideas of hierarchically organized control, control with referent configurations, synergic control, and the uncontrolled manifold hypothesis.

the equilibrium-point hypothesis has been, for the past half-century, one of the most controversial and influential hypotheses in the field of motor control (Feldman 1986; Feldman and Levin 1995). Recently, it has been developed in the form of a referent configuration (RC) hypothesis (Feldman 2009). Whereas the original equilibrium-point hypothesis described the neural control of a single muscle and muscle pairs acting at a joint (Feldman 1986), the RC hypothesis generalized the main ideas to the control of multimuscle, whole body actions involving redundant sets of effectors. According to the RC hypothesis, voluntary movements are produced by shifts of neural variables leading to changes in referent values for task-specific, salient variables given the external force field. Analysis of movement equifinality in the presence of transient force perturbations has been an important source of experimental evidence quoted as both supporting the equilibrium-point hypothesis (Bizzi et al. 1976; Kelso and Holt 1980; Latash and Gottlieb 1990; Schmidt and McGown 1980) and creating problems for it (DiZio and Lackner 1995; Hinder and Milner 2003; Lackner and DiZio 1994). Further discussions incorporated all of the mentioned observations into the equilibrium-point hypothesis (and the RC hypothesis) and emphasized that equifinality was not a universal phenomenon but expected only under certain experimental conditions (Feldman and Latash 2005).

Most of the cited studies of equifinality have not considered the fact that all natural movements are performed by redundant systems. The problem of motor redundancy (Bernstein 1967) emerges at any level of description of the system for movement production. Recently, this problem has been reformulated based on the principle of abundance (Gelfand and Latash 1998; Latash 2012). According to this principle, the apparent excess of elemental variables is not a computational burden for the central nervous system (CNS) but a rich apparatus that allows combining both stability and adaptability of movement patterns. This approach assumes that natural movements involve a scheme with a hierarchy of few-to-many transformations. In particular, a task-related low-dimensional input results in variable involvement of a larger (redundant) number of elemental variables that show covariation across repetitive trials stabilizing (reducing variance of) potentially important performance variables (Latash 2010).

This approach suggests that stability of overall performance is ensured by structured variance at the level of elements. The uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2007) provides a computational approach that allows quantifying two components of variance at the level of elemental variables with respect to a selected performance variable. One of these components (parallel to the UCM, V_UCM) does not affect the performance variable, whereas the other one (orthogonal to the UCM, V_ORT) does. There are other methods that study the structure of variance (reviewed in de Rugy et al. 2013; Tresch and Jarc 2009; Tresch et al. 2006), but the UCM-based analysis is particularly appropriate for our study because it provides direct links between variance in two spaces, those of a particular performance variable and of elemental variables.

A scheme combining the principle of abundance, the hierarchical control scheme, the idea of synergies, the UCM hypothesis, and control with RC (Latash 2010) allows making predictions with respect to phenomena of equifinality at different levels of analysis of a redundant system. In particular, this scheme predicts that a transient perturbation may be expected to result in equifinality at the level of task-related performance variables defined by an invariant RC at the highest, task-specific level but not necessarily at lower levels of elemental variables. Testing this hypothesis has been the main purpose of the study.

Note that, within the RC hypothesis, movement tasks and force production tasks are different peripheral outcomes of basically the same neural process (Feldman 1986). So, equifinality can be studied by using both transient force perturbation during a movement task and transient positional perturbations during a force production task. In this study, we used a device called the “inverse piano” (Martin et al. 2011a) that allows introducing positional perturbations (smooth changes in the finger configuration) during accurate force production tasks. We predicted that a transient change in position of a finger would lead to relatively small variance of the total force produced by four fingers of a hand (F_TOT) compared with variance in the space of elemental variables: commands to fingers. In other words, force changes by the fingers after a perturbation would be organized into a synergy stabilizing the total force (in a sense, V_UCM > V_ORT).

Fingers of the human hand are not independent force generators. When a person changes the force of a finger intentionally, other fingers also show unintentional force changes (lack of individuation or enslaving; Kilbreath and Gandevia 1994; Schieber 2001; Zatsiorsky et al. 1998). As a result, analysis of multifinger action can be performed using two sets of elemental variables, finger forces and hypothetical commands to fingers that can be changed by the person one at a time (finger modes; Danion et al. 2003; Zatsiorsky et al. 1998). We tested our main hypothesis in both spaces of elemental variables. Since enslaving typically leads to positive force covariation, we expected the synergic effects in the space of finger modes to be stronger than in the space of finger forces.

METHODS

Subjects

Eight self-reported right-handed subjects (6 males and 2 females) took part in this study (age: 27.8 ± 1.8 yr). All subjects were healthy and had no history of hand injury. All subjects gave informed, written consent in accordance with the procedures approved by the Office for Research Protections of the Pennsylvania State University.

Equipment

Data were recorded using an inverse piano device (for a detailed overview of the inverse piano, see Martin et al. 2011a). The device consisted of four unidirectional piezoelectric force transducers (208C02; PCB Piezotronics, Depew, NY) mounted on individual linear actuators (PS01-23x80; LinMot, Spreitenbach, Switzerland). The center-to-center distance between adjacent force sensors was 3 cm. Individual sensors could be adjusted in the longitudinal direction to accommodate different hands.

Data from the sensors were sent through an AC/DC conditioner (5134B; Kistler, Amherst, NY) to a 16-bit analog-to-digital converter (CA-1000; National Instruments, Austin, TX). A LabVIEW-based (National Instruments) program was used to collect the data at 300 Hz, provide visual feedback, and control the linear actuators through a controller (E400-AT; LinMot).

Experimental Procedure

The subjects sat in a chair facing the table with the setup and a 19-in. monitor placed 0.8 m away at eye level. The monitor was used to set tasks and provide visual feedback on F_TOT. The forearm was secured with straps to a foam surface, minimizing the contribution of the arm and shoulder joints. The proximal portion of the palm rested on the support, and no changes in the hand configuration were allowed (monitored by the experimenter). The protocol involved three tasks: maximal voluntary contraction (MVC), single-finger accurate ramp force production, and four-finger accurate force production.

MVC task.

During this task, the subjects were instructed to press as strongly as possible on the sensors with the four fingers. They were provided visual feedback on F_TOT. Subjects were given 5 s to reach MVC force. Two trials were performed with a 30-s rest interval, and the data from the trial with the higher peak force were used. The peak force produced by the individual fingers was used to set further tasks.

Single-finger accurate ramp force production task.

This task was performed by each of the four fingers as the task finger. During this task, the screen showed the subjects a sequence of three straight lines. Over the 1st 5 s, a horizontal line corresponded to 5% of the MVC of the task finger. Then, a slanted line led to 45% of the MVC of the task finger over 4 s. Then, a horizontal line corresponded to the 45% of MVC until the end of the trial (12 s total). The subjects were instructed to match the template by pressing with one finger while keeping all four fingers on force sensors. They were asked to pay no attention to force produced by those fingers. Two trials were conducted for each finger, and the fingers were tested in a random order. The data from this task were used to compute the enslaving matrix (see later) and convert force data into mode data at a later stage of synergy analysis.

Accurate four-finger force production task.

Subjects were given 5 s to produce a constant level of F_TOT = 15 N by pressing naturally with all four fingers. At the end of the 5-s interval (we will refer to it as stage 1), visual feedback on F_TOT disappeared. One second later, one of the force sensors was moved smoothly upward by 1 cm over a period of 0.5 s (we will address this manipulation as perturbation). No wrist motion occurred due to the small amplitude of the lifting motion; besides, the wrist and forearm were secured during the experiment as described earlier. The sensor stayed at the new, elevated position for 1 s (this interval will be referred to as stage 2) and then was lowered back to its starting position over a period of 0.5 s. The subjects were instructed to continue producing force for 2 s after the sensor was lowered (stage 3). The total time for each trial was 10 s. Subjects were instructed “do not interfere voluntarily with finger motion and force production” during the sensor motion. There were five conditions. Four of those involved perturbation applied to one of the fingers: I, index; M, middle; R, ring; and L, little. In the fifth condition, the feedback disappeared, but no finger was perturbed. Each condition was repeated 20 times. The 100 trials were presented in a random order. Breaks (30 s) were offered every 20 trials to prevent fatigue.

Data Processing

Initial data processing.

The force signals were filtered with a second-order, zero-lag Butterworth low-pass filter with a cutoff frequency of 20 Hz. Preperturbation (state 1) force values were obtained by averaging the force data from 3.00 to 3.25 s after the trial initiation. After the sensor was lifted (state 2), in the new steady-state, force values were averaged from 6.63 to 6.88 s. After the sensor was lowered to its initial position (state 3), the force values were averaged from 8.00 to 8.25 s (Fig. 1). During the course of the experiment, some subjects appeared to interfere voluntarily during the perturbation, resulting in uncharacteristically large force changes in state 3. The assumption of voluntary interference was made based on the large deviations of the force profile from the average force profiles across trials within the same condition. To mitigate effects of such unusual trials and to have a consistent criterion of trial acceptance across conditions, the four trials with the largest deviation of F_TOT from its average value across all of the trials within a given series for a given subject were removed. This resulted in 16 trials per subject for each condition that were used in further analysis.

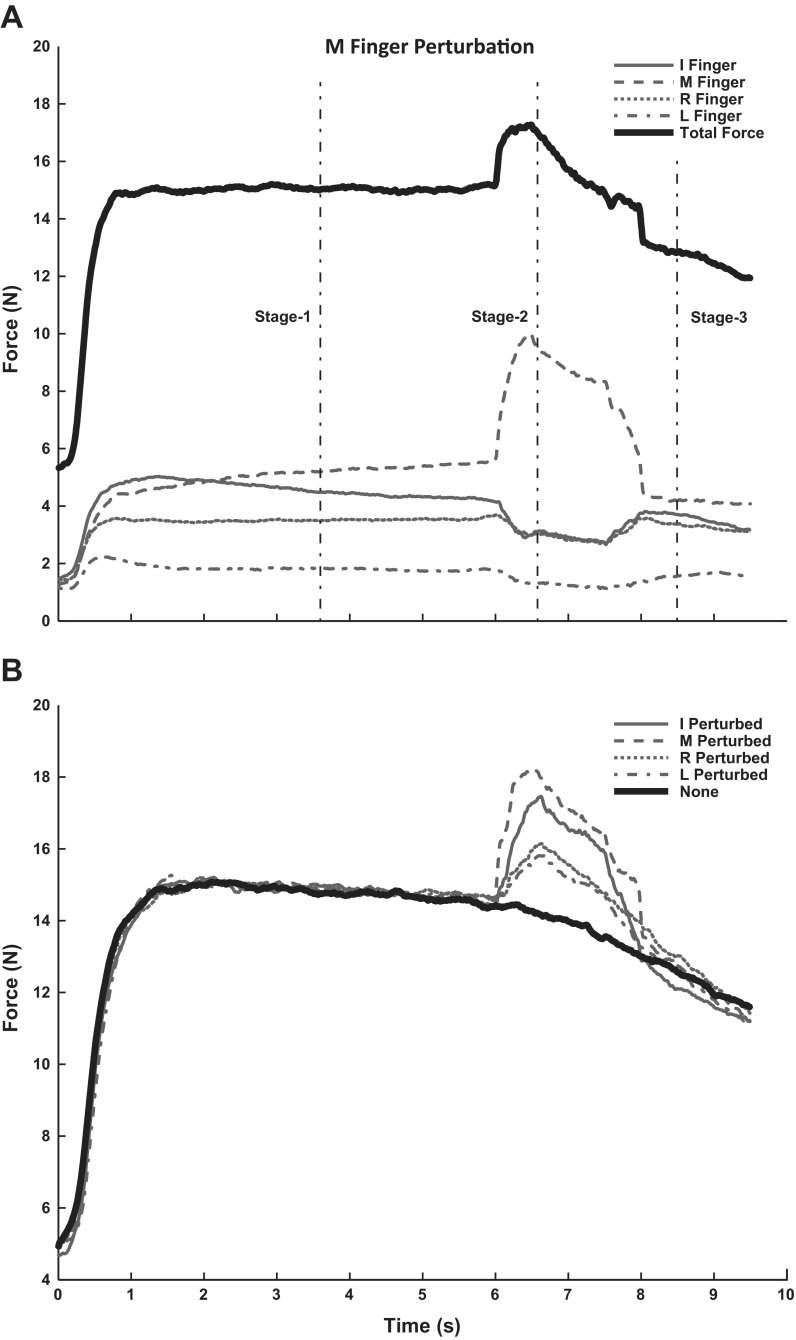
Fig. 1.

A: typical finger force profiles in a trial with middle-finger perturbation. The top force profile is total force (F_TOT). The times corresponding to the 3 stages are indicated by the vertical thin lines. I, index; M, middle; R, ring; L, little. B: an illustration of the F_TOT changes across conditions. Note the downward F_TOT drift after the visual feedback was turned off present in each of the conditions with and without perturbations.

Calculation of the enslaving matrix.

The single-finger ramp trials were used to calculate an enslaving matrix for each subject. This matrix reflects the fact that, when a person tries to change the force produced by one of the fingers, other fingers of the hand show unintentional force changes (Zatsiorsky et al. 1998, 2000). Since fingers are not independent force generators, the distribution of finger-force variance is not expected to be spherical even in the absence of any special neural control strategy. It may, by chance, be elongated along the UCM, computed for a selected performance variable or orthogonal to this UCM. To reduce effects of finger-force interdependence on the analysis of multifinger synergies stabilizing F_TOT (see later), we performed the analysis in two spaces, those of finger forces and finger modes. Finger modes are hypothetical neural commands that can be modified by the subject one at a time (Danion et al. 2003); they were computed from finger forces with the help of the enslaving matrix. To compute the enslaving matrix, the force values of each finger during the ramp were fit to the regression equation:

$${\text{F}}_{i,j}={\text{F}}_i^0+k_{i,j}\times {\text{F}}_{TOT,j}$$ (1)

where i = {I,M,R,L} and j = {I,M,R,L}. F_i,j is the force produced by finger i when finger j is the task finger. F_TOT,j is F_TOT produced when finger j is the task finger. The constants k_i,j were arranged in an enslaving matrix:

$$\left[\text{E}\right]=\left[\begin{array}{cccc}{k}_{\text{I},\text{I}}& k_{\text{I},\text{M}}& k_{\text{I},\text{R}}& k_{\text{I},\text{L}}\\ k_{\text{M},\text{I}}& k_{\text{M},\text{M}}& k_{\text{M},\text{R}}& k_{\text{M},\text{L}}\\ k_{\text{R},\text{I}}& k_{\text{R},\text{M}}& k_{\text{R},\text{R}}& k_{\text{R},\text{L}}\\ k_{\text{L},\text{I}}& k_{\text{L},\text{M}}& k_{\text{L},\text{R}}& k_{\text{L},\text{L}}\end{array}\right]$$ (2)

The diagonal entries of the enslaving matrix describe finger forces produced by commands directed at those fingers, whereas off-diagonal entries describe effects of finger nonindependence. The E matrix was used to convert finger-force values to mode values by the equation:

$$\left[\text{M}\right]={\left[\text{E}\right]}^{-1}\left[\text{F}\right]$$ (3)

where [M] is a 4 × 1 matrix of mode values, and [F] is a 4 × 1 matrix of finger-force values. We computed the E matrix in the initial condition only, when all of the finger sensors were at the same level. This was done to reduce the duration of the study. Enslaving matrices were quantified using the same device (the inverse piano) across a variety of finger positions including positions similar to those used in this study (Martin et al. 2011b); no major changes in these matrices were found across different finger-position combinations. Note also that the main comparisons within the study were performed before and after the transient finger lifting-lowering sequence when all fingers were at the same, initial position.

Analysis of multifinger synergies.

It is well-established that, in the absence of visual feedback, subjects show a slow, gradual decrease in the amount of force they produce even if they try to produce a constant force (Shapkova et al. 2008; Slifkin et al. 2000; Vaillancourt and Russell 2002). Our fifth condition (when no finger was raised) was used to control for this phenomenon.

Analysis of multifinger synergies stabilizing F_TOT was performed within the framework of the UCM hypothesis (Scholz and Schöner 1999). This analysis quantifies the variance of the elemental variables across repetitive trials in two subspaces: one that does not affect F_TOT (variance within the UCM, V_UCM) and the other that does (variance orthogonal to the UCM, V_ORT). We performed this analysis using two sets of elemental variables, finger forces and finger modes computed from the force values using the enslaving matrix [E]. This was done to explore robustness of the effects of the transient changes in finger position on the structure of variance in the space of elemental variables, forces or modes. The two corresponding sets of variance components will be addressed further as [V_UCM,ƒ; V_ORT,ƒ] and [V_UCM,m; V_ORT,m]. Analysis was performed using the difference of forces (or modes) between states 1 and 2 (ΔForce_2,1 or ΔMode_2,1) and states 1 and 3 (ΔForce_3,1 or ΔMode_3,1). Each of the variance indices was further normalized by the number of degrees of freedom in the corresponding subspaces (3 for the UCM and 1 for the ORT), and a synergy index was computed as:

$$\Delta V=\frac{V_{UCM}-V_{ORT}}{V_{TOT}}$$ (4)

where V_TOT stands for total variance, and each variance index is normalized per degree of freedom. If ΔV > 0, then a conclusion is drawn that the elemental variables are organized in a synergy stabilizing F_TOT. For further analysis, ΔV values were z-transformed using Fisher transformation adjusted to the boundaries of ΔV inherent to its computation, +1.33 and −4. This resulted in two transformed synergy indices computed using finger forces and finger modes as elemental variables, ΔV_f and ΔV_m, respectively.

Statistics.

Unless otherwise noted, data are presented in the text as means with standard errors. Normality was assessed by the Shapiro-Wilk test. Two-way ANOVAs were used with the factors Finger (4 levels: I, M, R, and L) and Finger-raised (specifying which finger was perturbed; 5 levels: I, M, R, L, and N, where N stands for the unperturbed case). To test the 1st hypothesis, we compared the variance indices between stages 1 and 3 using also a factor Variance (2 levels, V_UCM and V_ORT). To test the 2nd hypothesis, a 2-way ANOVA with factors Finger-raised and Analysis (2 levels, force space and mode space) was used. Tukey honestly significant difference test was used for post hoc analysis. Statistical significance was set at P < 0.05. Statistical tests were run in SPSS (Chicago, IL).

RESULTS

General Patterns of Force and Mode Changes

The subjects showed a consistent profile of force changes during the trials with perturbation. When a finger was lifted, its force increased, and the force of the other three fingers dropped. Overall, this resulted in an increase of F_TOT. When the finger was lowered back to its initial position, its force dropped while the force of the other three fingers showed an increase. There was also a general trend for all of the forces to drop slowly after the visual feedback was turned off. This trend was seen in trials with perturbations and in the control trials, when the visual feedback was turned off but no perturbation took place. On average, in the nonperturbed trials, F_TOT dropped by 3.1 ± 1.4 N, whereas the force drop in the perturbed trials was, on average, 3.7 ± 1.3 N.

Typical time profiles of finger forces are shown in Fig. 1A. Subjects achieved the state 1 force level of 15 N quickly, within 1–1.5 s after the start of the trial. During the perturbation applied to the middle finger, the force of that finger increased, whereas the forces of the other three fingers decreased. At the new steady-state (state 2), F_TOT showed a slow decrease. After the perturbation (state 3), F_TOT continued to show a general decreasing trend. This trend was similar across all conditions for some of the subjects (Fig. 1B). It could be more pronounced in trials with perturbations compared with nonperturbed trials in other subjects.

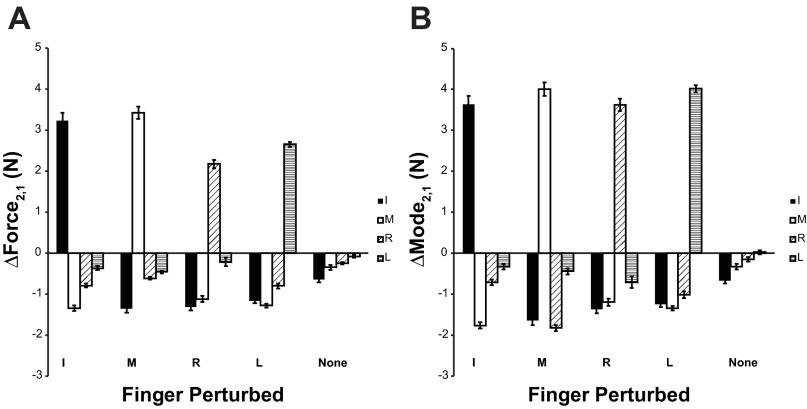
These patterns were analyzed using changes in both forces and modes between stages. As shown in Fig. 2, changes in both force and mode values between stages 2 and 1 (ΔForce_2,1 and ΔMode_2,1) for the perturbed fingers were positive, indicating that the force and mode values for the perturbed finger increased during state 2. Furthermore, ΔForce_2,1 and ΔMode_2,1 values for nonperturbed fingers were typically negative, indicating that force and mode values decreased during state 2 for those fingers. When no perturbation took place, both forces and modes of all four fingers showed a tendency to drop. The two-way ANOVA with factors Finger and Finger-raised run on ΔForce_2,1 and ΔMode_2,1 showed significant main effects of Finger (F_3,7 > 54.0; P < 0.001), Finger-raised (F_4,7 > 14.0; P < 0.001), and an interaction (F_12,7 > 600.0, P < 0.001). Post hoc Tukey tests confirmed that perturbation increased both force and mode values of the perturbed finger and led to their decrease in the other fingers.

Fig. 2.

Changes in finger forces (ΔForce; A) and modes (ΔMode; B) between stages 1 and 2 for each finger and condition. Averaged across-subjects values with standard error bars are presented.

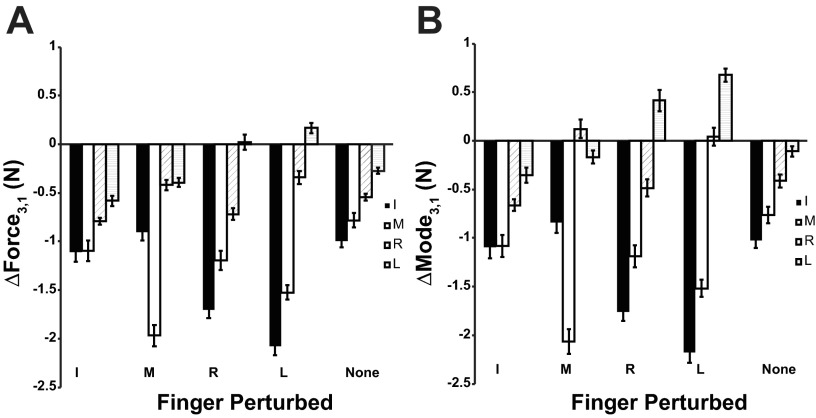
After the perturbed finger was lowered to its initial position, both forces and modes typically showed a decline in their values compared with stage 1. Figure 3 illustrates this with changes in forces and modes between stages 1 and 3 (ΔForce_3,1 and ΔMode_3,1). Although the values for ΔForce_3,1 and ΔMode_3,1 dropped for each finger in almost every condition, the values increased for the L finger in the R-raised and L-raised conditions. The drop in force and mode values was typically larger in conditions with finger perturbations compared with the nonperturbed condition. There are no obvious differences in the values between the perturbed and nonperturbed fingers (unlike the comparison between stages 1 and 2 illustrated in Fig. 2). The two-way ANOVA with factors Finger and Finger-raised confirmed significant main effects for Finger (F_3,2540 = 194.14; P < 0.001), Finger-raised (F_4,2540 = 7.07; P < 0.001), and an interaction (F_12,2540 = 21.60, P < 0.001) for ΔForce_3,1 and significant main effects of Finger (F_3,2540 = 200.58; P < 0.001) and an interaction (F_12,2540 = 20.39, P < 0.001) for ΔMode_3,1. The effect of Finger-raised for the ΔMode_3,1 analysis was under the significance level (P = 0.083). Post hoc Tukey tests confirmed that all four fingers showed a greater change of force in the perturbation trials than in the no-perturbation trial. However, a given perturbation condition did not affect the perturbed finger any differently than the other perturbation conditions.

Fig. 3.

ΔForce (A) and ΔMode (B) between stages 1 and 3 for each finger and condition. Averaged across-subjects values with standard error bars are presented.

Variance Analysis

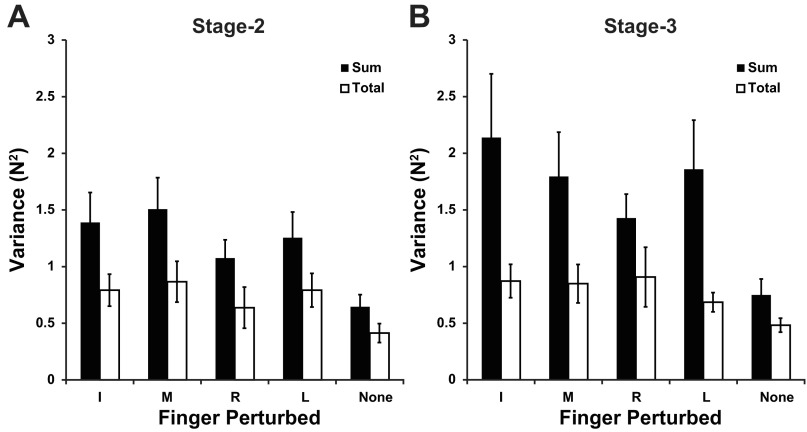
In both states 2 and 3, the variance of F_TOT computed across trials was less than the sum of the variances of individual finger forces (Fig. 4A). This was also true for the comparison between the variance of the total mode values and the sum of the variances of individual finger modes (Fig. 4B). This result indicates that the individual finger forces (modes) covaried to minimize variation of F_TOT. This was confirmed by a two-way ANOVA (Sum/Total × Finger-raised). Sum/Total indicated whether the variance was calculated as the sum of the individual finger variances or was the actual four-finger variance. Sum/Total showed a significant effect in state 2 (F_1,70 = 16.07, P < 0.001) and state 3 (F_1,70 = 20.45, P < 0.001), whereas Finger-raised also showed a significant effect in both state 2 (F_4,70 = 3.80, P < 0.01) and state 3 (F_4,70 = 2.66, P < 0.05). There were no significant interactions.

Fig. 4.

Sum of individual finger-force variances (black), and total variance of force (white) at state 2 (A) and state 3 (B). All variances were calculated on change in force data, that is ΔForce_2,1 and ΔForce_3,1.

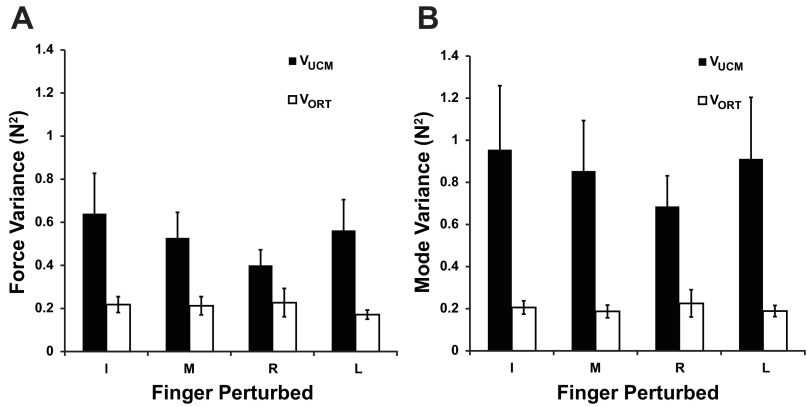
To mitigate the effects of the slow drop in force that happened across all condition, both with and without perturbation (Fig. 1B), we detrended the individual finger-force time profiles for each subject separately by subtracting the average across trials force time profiles in the nonperturbed condition. Changes in the detrended data between stages 1 and 3 were further analyzed within the framework of the UCM hypothesis: the total variance in the finger-force and finger-mode spaces was decomposed into two components parallel to the UCM (V_UCM) and orthogonal to the UCM (V_ORT; see methods). Figure 5 shows that, overall, V_UCM was greater than V_ORT across all conditions in both force and mode spaces. A two-way ANOVA (Variance × Finger-raiser) was performed to explore this observation. The Variance factor described whether the variance was in the UCM or orthogonal subspace. There was a main effect of Variance reflecting the fact that V_UCM was larger than V_ORT for both force and mode analyses (F_1,70 > 12.0, P < 0.001). There was a significant effect of Finger-raised (F_4,70 = 3.46, P < 0.05) for force analysis. Post hoc analysis confirmed that both variance components in the nonperturbed condition were smaller than in the index and middle finger raised conditions. In mode space, there was no significant Finger-raised effect and no significant interactions.

Fig. 5.

Two components of variance, within the uncontrolled manifold (V_UCM) and orthogonal to the UCM (V_ORT), computed in the space of finger forces (A) and modes (B). Averaged across-subjects data are presented with standard error bars.

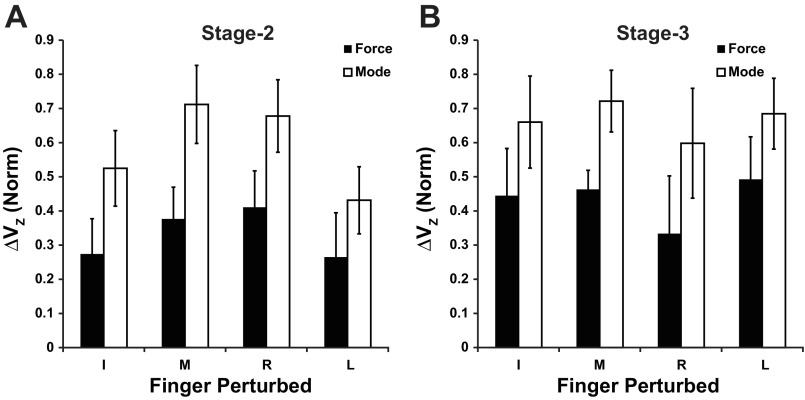
The observation of greater UCM variance was further confirmed in the calculation of the index of synergy, ΔV. As shown in Fig. 6, the z-transformed index of synergy (ΔV_z) in both force and mode space was >0 across all conditions. Furthermore, ΔV was greater in the mode space than in the force space. A two-way ANOVA (Analysis × Finger-raised) confirmed these observations. The Analysis factor described whether ΔV was computed in the force space or mode space. There was a significant effect of Analysis (F_1,70 = 8.93, P < 0.01) without other effects.

Fig. 6.

Z-transformed indices of synergy calculated in force space (black) and mode space (white) in state 2 (A) and state 3 (B). Averaged across-subjects data are presented with standard error bars.

DISCUSSION

The main hypothesis formulated in the Introduction has been confirmed. Indeed, in both finger-force and finger-mode spaces, significantly more variance was confined to the subspace (the UCM; Scholz and Schöner 1999) corresponding to no changes in F_TOT. In other words, there was more variance in the space of elemental variables than in F_TOT (Fig. 4). We can conclude, therefore, that equifinality after a transient perturbation may happen in the space of task-related performance variables but not in the space of elemental variables. Our secondary hypothesis has also been confirmed. Indeed, the difference between the amounts of variance within the UCM (V_UCM) and orthogonal to the UCM (V_ORT) was larger for analysis in the space of hypothetical commands to fingers (modes; Danion et al. 2003) compared with analysis in the space of finger forces. This was expected because the definition of modes eliminates the positive covariation among finger forces due to the phenomenon of enslaving (Zatsiorsky et al. 2000). Since positive covariation of forces is expected to add to V_ORT, its elimination increases the index of synergy stabilizing F_TOT.

Equifinality Within the RC Hypothesis

According to the RC hypothesis, digit force is a consequence of a difference between the actual and referent coordinates of the digit tip (Latash et al. 2010; Pilon et al. 2007). The actual coordinate was manipulated in our study using the inverse piano, whereas the referent coordinate was expected to be unchanged under the “do not intervene voluntarily” instruction (Feldman 1966; Latash 1994). Within this simplified scheme, a transient perturbation is not expected to change the final equilibrium state of the system (equifinality); note that the equilibrium state is a combination of digit tip position and force.

Several studies questioned this simplified account by showing that violations of equifinality can occur in unusual, destabilizing force fields when the forces were motion-dependent and acted only during the movement, not at the new steady-state. Such studies used Coriolis forces in a centrifuge (DiZio and Lackner 1995; Lackner and DiZio 1994) and velocity-dependent forces generated by a torque motor to add force proportional to velocity and acting in the direction of the velocity (“negative damping,” Hinder and Milner 2003). Further discussion (Feldman and Latash 2005) clarified that, even under the do not intervene voluntarily instruction, central input into neural structures controlling the action can be modified by such factors as velocity dependence, reflex effects from sensory receptors in other parts of the body, and history effects. Besides, it is possible that subjects are unable to ignore unusual, destabilizing perturbations and, despite the explicit instruction, could not help but change their voluntary command to the involved effectors translating into changes in their RC.

Our study is different from most of the cited ones in two important aspects. First, it uses a positional perturbation and analyzes changes in forces, whereas most earlier studies used force perturbations and analyzed coordinate changes. Note that, within the RC hypothesis, movement and force production are different peripheral outcomes of essentially identical control processes. Both result from a discrepancy between the actual and referent coordinates, but forces are produced when there is an external stop preventing motion toward the referent coordinate, and movements are seen when there is no such stop. Second, earlier studies did not explicitly consider the problem of motor redundancy and did not ask whether equifinality is equally observed at different levels of analysis of the hierarchical neuromotor system involved in all natural actions.

Hierarchical Synergic Control of Natural Actions

Our understanding of the neural control of natural movements is based on several axioms (reviewed in Latash 2010). First, we view the neural control system as a physical/physiological system, not a computational one (Latash 2012; Shadmehr and Wise 2005). Second, we view it as a hierarchical system where, at each level, a few-to-many transformation takes place organized in a synergic way with central back-coupling loops (Latash et al. 2005). As a result, these transformations allow the output of each level to vary as long as these variations are organized primarily within the UCM for the variable defined by the input. Third, the whole system involves a global feedback organized with respect to task-specific performance variables that makes sure that the action results in accurate performance of those variables. Fourth, the input at each level represents subthreshold depolarization of the target neuronal membranes (Feldman 2011).

The RC hypothesis assumes the existence of the mentioned hierarchy where the upper level specifies a set of referent values (a RC) for relatively few task-specific variables. These variables may be expected to show equifinality in response to transient perturbations (under certain conditions; see Feldman and Latash 2005). The mentioned sequence of few-to-many transformations, however, allows for an infinite number of combinations of elemental variables compatible with the same values of the few task-specific variables. So, equifinality at lower levels may be violated because of deviations of elemental variables along the UCMs. Moreover, the relatively low stability of a redundant system along the UCM contributes to deviations of the system of elemental variables along the UCM and is expected to lead to relatively high V_UCM values as observed in our experiment.

In the case of multifinger-force production, we analyzed the task at two levels. The upper level is the task level, which dictates that during stage 1 the four fingers together produced the required F_TOT. At this level, one may view F_TOT as being produced by a “virtual finger” (cf. Arbib et al. 1985) resulting from a discrepancy between the actual and referent coordinates for that imagined digit. The lower level is the individual finger level where we used two types of analysis, of finger forces and of finger modes. It has been shown that during steady-state force production under visual feedback, variance of F_TOT and the corresponding V_ORT component of variance at the finger force/mode level are very low. In contrast, V_UCM is much higher, resulting in large values of the synergy index (Olafsdottir et al. 2005). Since actual fingertip coordinates stayed unchanged in those studies (and in our stage 1), this fact means that referent coordinates for individual fingers varied across trials, whereas the referent coordinate for the virtual finger stayed relatively unchanged. This is an example of a few-to-many transformations organized in a synergic way mentioned in the previous paragraph.

The analysis does not have to stop at the individual finger level. One may ask whether fingertip force is stabilized by covaried activation of the numerous flexors and extensors contributing to the action of that finger (cf. the notion of multimuscle-mode synergies, Krishnamoorthy et al. 2003). One can go one step further and ask whether muscle activation is stabilized by covaried involvement of individual motor units. These levels of analysis are beyond the scope of the current study.

The UCM Concept and Stability of Action

The scheme described briefly in the previous section naturally leads to different dynamic stability in different directions within the space of elemental variables. These differences can be probed using external changes in the force field (Latash et al. 2005; Mattos et al. 2011; Yang et al. 2007) or using across-trials analysis of variance under the assumptions that natural variability results in varying initial conditions and changes in the time-varying state of the system (Scholz and Schöner 1999; Scholz et al. 2000). The latter method has been primarily used to explore stability of redundant systems in support of the concept of the UCM (reviewed in Latash et al. 2007).

Several studies have shown that response to a perturbation happens to a large degree within the UCM, i.e., along directions with lower stability (Mattos et al. 2011, 2013; Scholz et al. 2000). So, a transient perturbation used in our study was expected to lead to deviations primarily along the UCM within the spaces of finger forces/modes. Indeed, we observed changes in finger forces in opposite directions, an increase in the force of the perturbed finger and a drop in the force of the other three fingers when the perturbed finger was lifted and a drop in the force of the perturbed finger accompanied by an increase in the other finger forces when the perturbed finger was lowered (Fig. 1A). Note that lifting a finger is expected to be transmitted mechanically to other fingers of the hand and lead to a drop in their forces. Although such effects could contribute to force changes observed during the finger lifting and lowering processes, their contribution has been estimated as small (Martin et al. 2011a) leading to a conclusion on a major role of neural components in those counterdirectional force changes. We also emphasize that the main results of our study were obtained in the comparison of finger forces (and modes) before and after the lifting-lowering sequence when all of the fingers were at the same position.

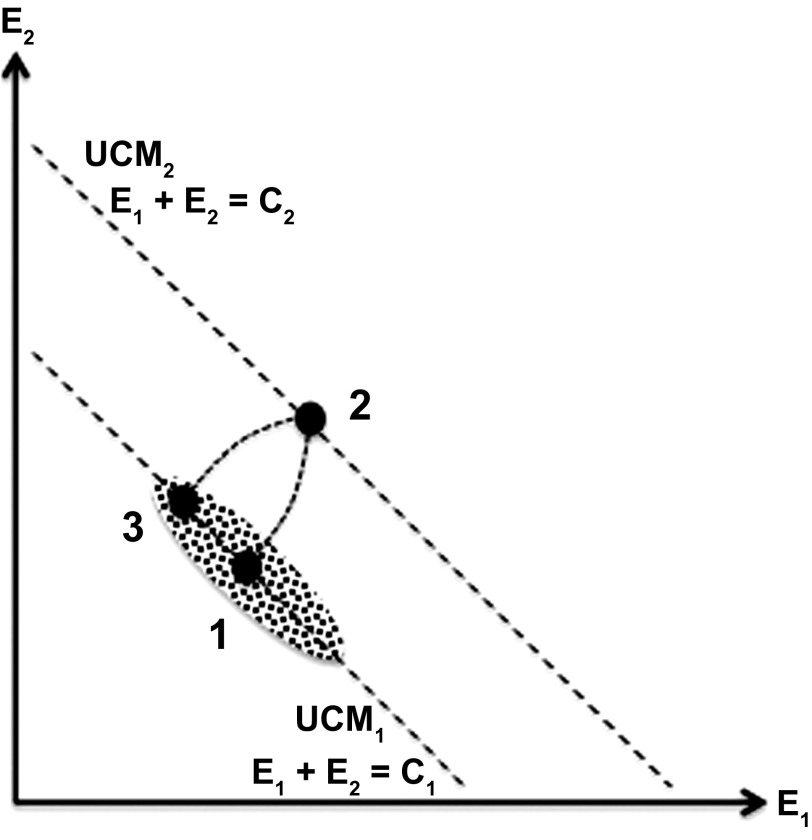
The concept of stability in a redundant system is illustrated in Fig. 7 for a task of producing a constant sum of two elemental variables, E₁ and E₂. If the task E₁ + E₂ = C₁ is performed multiple times, a cloud of data points is expected elongated along the UCM for this task shown by the dashed line in Fig. 7. If a perturbation leads to a change in (E₁ + E₂) so that the sum becomes different (C₂ in Fig. 7), much of the deviation in the E space is expected to happen along the UCM. If now the perturbation is removed, equifinality is expected in the task space (the system returns to the UCM corresponding to the original task E₁ + E₂ = C₁). However, it will not return to the same point on the UCM resulting in a nonzero deviation along the direction corresponding to no changes in the C variable.

Fig. 7.

An illustration of a task of producing a constant sum (C) of 2 elemental variables, E₁ and E₂. If a perturbation leads to a change in (E₁ + E₂), much of the deviation occurs along the UCM. After the perturbation is removed, equifinality is expected in the task space (the system returns to the initial UCM) but not in the {E₁; E₂} space, resulting in a non-0 deviation along the UCM.

It is well-known that, when subjects produce a constant force under visual feedback and then feedback is turned off, there is a slow decline of F_TOT (Shapkova et al. 2008; Slifkin et al. 2000). In terms of the RC hypothesis, this decline is associated with an unintentional drift of the referent coordinate. One could expect such a drift to be variable across trials. So, despite our attempts to mitigate the effects of this drift on our analysis by using the nonperturbed condition, we expected the drift to lead to higher V_ORT. However, even in the presence of such potentially inflated V_ORT, V_UCM was still significantly higher, showing that in conditions of transient changes in external conditions equifinality can be expected in the space of task-related performance variables but not necessarily in the space of elemental variables.

Similar conclusions have been reached in earlier studies of trunk-assisted reaching (Adamovich et al. 2001; Ma and Feldman 1995). In those studies, different trajectories in the joint configuration space were observed that maintained relative consistency of the endpoint trajectory depending on whether the trunk contributed to the movement or the trunk motion was mechanically blocked. Both those studies and our results support the general idea on the role of redundancy in stabilizing the task performance. The fact that we observed significantly larger variance within the UCM compared with orthogonal to the UCM direction using two sets of variables, finger forces and finger modes, emphasizes the robustness of the main finding.

Concluding Comments

The main message of the study is that transient perturbations applied to a redundant system lead to relatively small changes in a task-related performance variable (equifinality). In contrast, relatively large deviations are seen in directions within the UCM computed for that variable. These results are readily incorporated into a motor control scheme combining the idea of control with referent body configuration with the idea of synergic control of redundant (actually abundant) sets of elements.

GRANTS

The study was in part supported by National Institutes of Health grants NS-035032 and AR-048563.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

V.M.Z. and M.L.L. conception and design of research; L.W. performed experiments; L.W. and M.L.L. analyzed data; V.M.Z. and M.L.L. interpreted results of experiments; L.W. and M.L.L. prepared figures; L.W. and M.L.L. drafted manuscript; L.W., V.M.Z., and M.L.L. edited and revised manuscript; L.W., V.M.Z., and M.L.L. approved final version of manuscript.