Significance
Animal cells continuously move, divide, and transmit forces by actively reorganizing their internal scaffold or cytoskeleton. Molecular motors pull actin filaments together and generate contraction of the cytoskeleton underneath the cell membrane. We address the detailed mechanism of contraction by using a minimal in vitro assay: a liposome membrane to which we attach actin filaments and molecular motors in a controlled manner. We reproduce contraction like in cells. We show that the scaffold needs to be tightly attached to the membrane for efficient contraction, but, under some conditions, efficient contraction can lead to liposome destruction. These results suggest that cells must precisely control their contractility to remain intact during cellular events.
Keywords: actomyosin contractility, biomimetism, active gels, soft condensed matter
Abstract
Animal cells actively generate contractile stress in the actin cortex, a thin actin network beneath the cell membrane, to facilitate shape changes during processes like cytokinesis and motility. On the microscopic scale, this stress is generated by myosin molecular motors, which bind to actin cytoskeletal filaments and use chemical energy to exert pulling forces. To decipher the physical basis for the regulation of cell shape changes, here, we use a cell-like system with a cortex anchored to the outside or inside of a liposome membrane. This system enables us to dissect the interplay between motor pulling forces, cortex–membrane anchoring, and network connectivity. We show that cortices on the outside of liposomes either spontaneously rupture and relax built-up mechanical stress by peeling away around the liposome or actively compress and crush the liposome. The decision between peeling and crushing depends on the cortical tension determined by the amount of motors and also on the connectivity of the cortex and its attachment to the membrane. Membrane anchoring strongly affects the morphology of cortex contraction inside liposomes: cortices contract inward when weakly attached, whereas they contract toward the membrane when strongly attached. We propose a physical model based on a balance of active tension and mechanical resistance to rupture. Our findings show how membrane attachment and network connectivity are able to regulate actin cortex remodeling and membrane-shape changes for cell polarization.
Animal cells constantly adapt their shape as they move and divide. Events like cytokinesis (1) and motility (2) require concerted remodeling of the actin cytoskeleton and the plasma membrane. A crucial cell module that drives cellular shape changes is the actomyosin cortex beneath the cell membrane, which produces contractile forces that squeeze the cell forward during migration or constrict it during division. The cell cortex is a thin actin network of thickness ∼0.2 µm (3), which is tightly attached to the plasma membrane (4, 5). On the molecular scale, contractile forces are generated by myosin II motor proteins, associated into bipolar filaments (6), which use adenosine 5′-triphosphate (ATP) to exert pulling forces on actin filaments.
To drive cell-shape changes, these forces must be communicated to the plasma membrane, which requires membrane–actin attachment (7–9) through, for example, proteins from the ERM (ezrin, radixin, moesin) family (10–13). Several in vivo studies provide evidence that cortex–membrane attachment strongly influences contractile processes. For instance, blebbing at the cell poles due to transient detachment of the cortex from the membrane serves to release excess cortical tension during cytokinesis, which is crucial to achieve proper division (14). In early Caenorhabditis elegans embryos, myosin-driven contraction drives long-range cortical flow of actin along the membrane, which is crucial to establish cell polarity and asymmetric cell division (15). It is increasingly recognized that cortex remodeling and cell-shape changes depend on a balance between the active forces generated by motors and the passive forces originating from cortex (visco)elasticity and cortex–membrane adhesion (16). However, the microscopic basis of this force balance remains unclear. It is difficult to resolve this question directly in cells, because manipulation by drugs or genetic methods can also affect the dynamics of the underlying cytoskeleton via specific signaling pathways (17).
An alternative approach is to use either cell-free extracts (18, 19) or systems reconstituted from a minimal set of purified cellular components (20). These approaches have been successfully used to show that contractility of bulk actomyosin networks depends on the kinetic parameters of the motors (21–23), as well as on the presence of actin cross-linkers that allow build-up of stress (24, 25). A recent study of 2D actomyosin networks attached to flat model biomembranes showed that actin–membrane anchoring also influences cortex contractility (26). However, although this biomimetic assay can address actin–membrane adhesion, it cannot address the influence of membrane deformability on cortex remodeling and shape change.
Here, we reproduce active contractility in a cell-like system, where actomyosin cortical networks are anchored to a liposome membrane. Cortices linked to the outer leaflet of the liposome membrane mimic the cell cortex as well as intracellular organelles like endosomes (27). Low linkage or cross-link density promote active cortex rupture, which breaks the symmetry and causes passive elastic retraction of the network to one pole of the liposome. In contrast, high membrane anchorage and high network cross-link density promote active compression of the liposomes by cortex contraction. We further show that when the cortices are instead connected to the inner leaflet of the liposome membrane, actin–membrane linkage strongly biases the directionality of cortex contraction. Our results shed light on the physical mechanisms that control contraction events during cell division, motility and endosome-shape changes.
Results
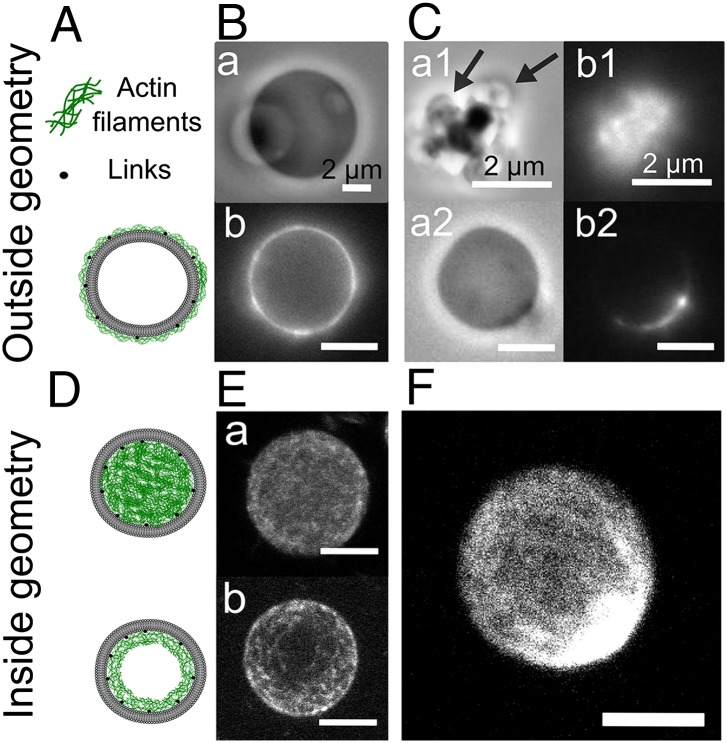
To mimic the cellular cortex, we anchor actin filaments to a liposome membrane and add myosin II motors purified from rabbit skeletal muscle. Motors assemble into bipolar filaments of an approximate length of 0.7 µm containing around 100 myosins (24). Actin filaments that contain 1/400 of biotinylated actin monomers carry an average of one biotin link per micrometer and are strongly bound via streptavidin or neutravidin to biotinylated lipids of the liposome membrane. The strength of actin–membrane anchoring can, thus, be tuned by changing the fraction of biotinylated lipids in the membrane. To test the influence of geometry, we attach the actin shell either on the outer leaflet of the liposome membrane (Fig. 1 A and B) or to its inner leaflet (Fig. 1 D and E).
Fig. 1.
Liposomes with a biomimetic actin-myosin cortex with two distinct geometries: outside geometry (Upper) and inside geometry (Lower). (A and D) Scheme of a liposome with actin filaments attached to the outside or inside by actin–membrane linkers. (B and C) Phase contrast images (a, a1, and a2) and actin fluorescence images (b, b1, and b2) of liposomes containing 1% biotinylated lipids in the absence (B) or in the presence (C) of myosin. (E and F) Confocal image of fluorescent encapsulated actin in low attachement condition (E, a) and in High attachment condition (E, b) in the absence or in the presence (F) of myosin. (Scale bars: 5 µm unless otherwise indicated.)
Cortex Formation in Different Geometries and Active Contraction.
Actin filaments of 4-µm length are attached to the outside of liposomes and cover the entire liposomes, forming shells of a constant average thickness h on the order of half a micron (Fig. 1B and Fig. S1). “Strong” or “weak” attachment respectively refers to 1 or 0.1 mol % of biotinylated lipids. The thickness and total amount of bound actin is independent of attachment strength as long as the incubation time is longer than 15 min (Fig. S2). When myosin filaments are injected into the solution, the actin distribution becomes heterogeneous in 90% of all liposomes (357 of 390 in six independent experiments) independently of their attachment strength (Fig. S3, first two bars), which is a clear signature of contractile behavior (Fig. 1C and Fig. S1B). Importantly, we also find that reducing filament length strongly reduces the occurrence of contraction, from 90% to only 7% of all liposomes (Fig. S3). This observation indicates that contraction requires sufficiently high network connectivity, consistent with prior findings for bulk actomyosin networks (22). Note that streptavidin can mediate both filament–membrane and filament–filament attachments (i.e., that the strong attachment and weak attachment cases differ in both membrane attachment strength and network connectivity).
Interestingly, we observe two markedly different contractile behaviors for any given population of contracting liposomes: either liposomes are crushed and actin filaments form a dense cluster together with membrane fragments (Fig. 1C, a1, black arrows) or liposomes remain intact and actin peels away along the membrane and accumulates at one pole (Fig. 1 C, a2 and b2). Various controls (Fig. S3) confirm that actin-network contraction originates exclusively from active contraction by myosin filaments.
Upon injection of fluorescently labeled myosin, time-lapse imaging clearly reveals that fluorescent myosin spots appear at the surface of the liposomes. These discrete spots have a diffraction-limited size and likely represent 0.7-μm filaments. Sometimes, we observe brighter myosin spots, which likely represent small clusters of myosin filaments (Fig. S4). The spatial distribution of the myosin spots appears to be random and the outcome of cortex contraction appears to be independent on how the myosin spots are distributed. Interestingly, contraction always starts after around three separate spots of myosin are bound (Fig. S4). Although this number is an underestimate because of the epifluorescence observation, this indicates that a few myosin filaments only are required for shell contraction.
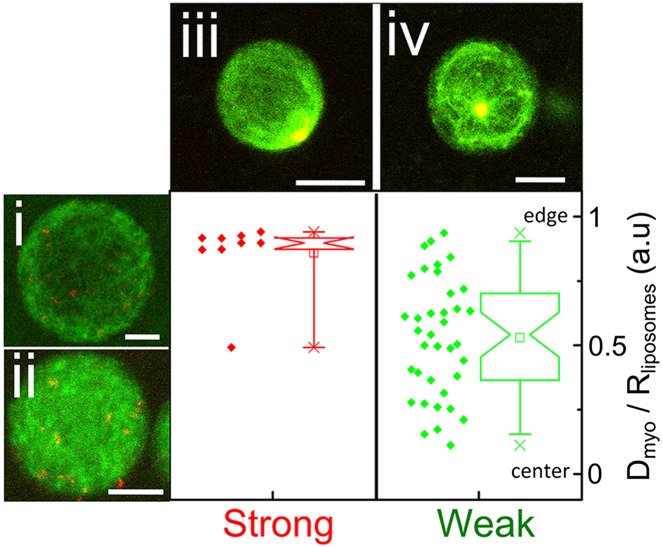
To test the role of geometry on the contraction behavior, we compare the “outside geometry” with the one of cortices anchored to the inner leaflet of the liposome membrane. To this end, we encapsulate biotinylated actin filaments together with neutravidin cross-linkers and myosin by hydration of a film of lipids as recently developed (Fig. S5) (28, 29). The actin filaments form a homogeneous peripheral shell in 90% of the liposomes in the strong attachment condition (2 mol% biotinylated lipids) and in 84% of the liposomes in weak attachment conditions, attained in the absence of biotinylated lipids (Fig. 1E). This observation is consistent with previous reports (30) and reflects spatial confinement of actin filaments forced to adopt a peripheral localization to reduce their bending energy, because their persistence length (31) and contour lengths are similar to the diameter of the liposomes (Fig. S5). The thickness of the actin shells increases with liposome radius, indicating that the amount of membrane-adsorbed actin is proportional to the volume-to-surface ratio, consistent with previous reports (Fig. S5) (32). In about 10% of the liposomes, the actin forms a space-filling “bulk” network. Incorporation of biotin-neutravidin membrane anchors does not influence the percentage of liposomes with a shell, nor the shell thickness or actin encapsulation efficiency (Fig. S5). When myosin is encapsulated together with actin inside liposomes, about 10% of the liposomes contain myosin at a level that is detectable by confocal microscopy. We trigger myosin contraction by warming the samples from 4–20 °C. Time-lapse imaging of liposomes inside a temperature-controlled chamber reveals that the motors contract the actin network in less than 1 min in the presence of cross-linkers (Fig. S6). In all cases, the myosin motors eventually form one dense cluster surrounded by a compacted actin network (Fig. 2, iii and iv). In the absence of cross-linkers, no contraction occurs (Fig. 2, i and ii). To test the influence of membrane anchorage, we compare liposomes containing 2% and 0% biotinylated lipids. As in the outside geometry, we observe a marked influence of actin–membrane anchoring: strongly anchored cortices contract toward the membrane (Fig. 2, iii), whereas nonanchored cortices mainly contract inward to form a dense actomyosin cluster away from the membrane (Fig. 2, iv).
Fig. 2.
Effect of cortex cross-linking and actin–membrane attachment on cortex contraction in the inside geometry. Confocal images of actin (green) and myosin (red) inside liposomes in the absence of cross-linkers (i and ii) or in the presence of cross-linkers and either strong attachment (iii) or weak attachment (iv). (Scale bars: 5 µm.) Plots are the distance of the myosin cluster from the center of the liposome (Dmyo) normalized by the liposome radius, Rliposome, for different liposomes (n = 9 for strong attachment and n = 37 for weak attachment). Box plots show the mean value (small square), maximum and minimum values (crosses), and 5th and 95th percentiles (whiskers).
Dynamics of Contraction in the Outside Geometry.
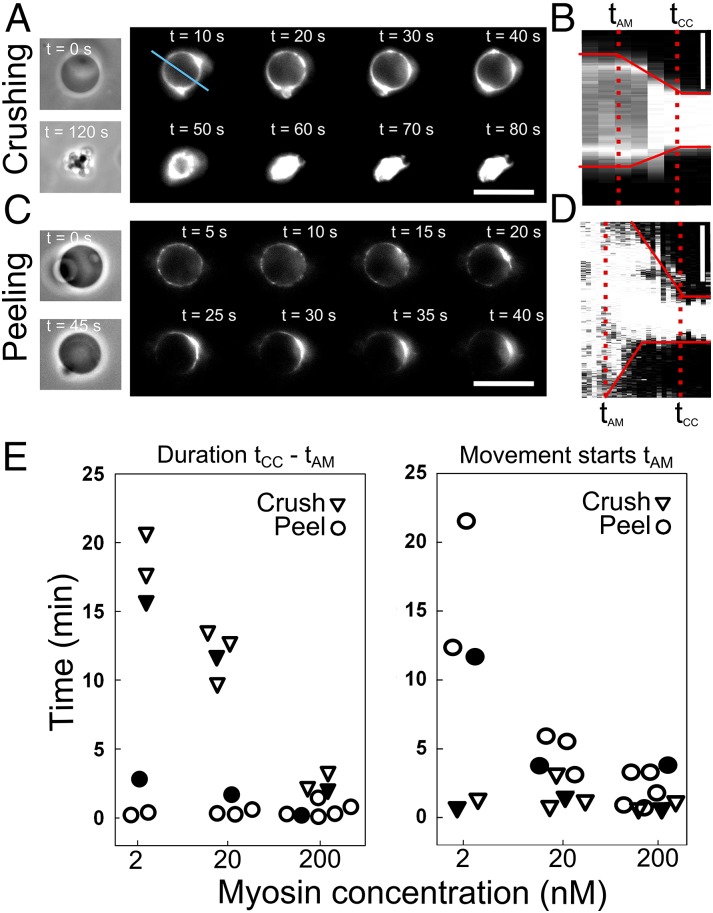
Experimentally, it is most convenient to characterize the dynamics of contraction in the outside geometry, where contraction can be triggered by myosin injection (Fig. 3). From kymographs, we define the following characteristic times (indicated in Fig. 3 B and D): time 0 corresponds to myosin injection in the observation chamber, tAM is the onset time for actin movement, and tCC is the time at which actin movement stops. The total duration of each contraction event is then tCC − tAM.
Fig. 3.
Outside geometry: kinetics of vesicle crushing and cortex peeling. Images taken by phase contrast (A and C, Left) and epifluorescence (A and C, Right). Time lapse images (A and B) of contractile liposomes and kymograph along the blue line in A and along the liposome contour (D). (Scale bars: A and C, 10 µm; B and D, 5 µm.) Conditions were as follows: 1% biotinylated lipids and 20 nM myosin. (E) Characteristic times: duration of contraction, tCC − tAM, for crushing (triangles) and peeling (circles) (Left); time where actin starts to move, tAM (Right). Open symbols indicate weak attachment conditions; solid symbols indicate strong attachment conditions. All symbols are spaced for clarity.
We observe markedly different kinetics of contraction during liposome crushing versus cortex peeling. In the presence of 2 nM myosin, the duration of crushing (tCC − tAM) is 18 ± 2 min, corresponding to a velocity of crushing of about 0.8 ± 0.5 µm/min, which is about 10 times slower than the peeling velocity (Fig. 3E, Left). However, at the same myosin concentration, the onset time tAM elapsed before peeling starts is much longer than the onset time for liposome crushing (Fig. 3E, Right). The dependence of the kinetics on myosin concentration is also markedly different for crushing and peeling liposomes. In case of crushing, tAM is independent of motor density and its average value is 1.5 ± 1 min, whereas the duration of contraction strongly decreases with increasing motor density, indicating that crushing is driven by active contraction. In contrast, the duration of contraction during peeling is independent of motor density and is on average 0.7 ± 0.5 min (90% confidence). This observation suggests that contraction during peeling is not actively driven but is rather the result of passive, elastic retraction, although we cannot exclude a small contribution of active contraction after the initiation of peeling (Discussion). The time tAM for peeling to start does depend strongly on motor density, going down from 15.2 ± 3 min to 1.8 ± 1.4 min (average values) when the myosin concentration is increased from 2 to 200 nM. These observations suggest that peeling may require a sufficient tension that reached faster in the presence of more myosin.
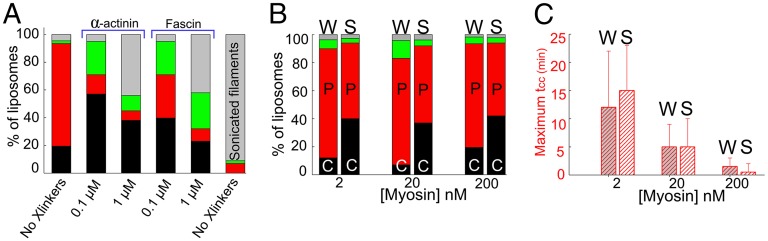
If peeling represents passive elastic retraction of a ruptured cortex, we expect that increased cross-linking of the cortex should protect cortices from rupturing and peeling. We confirm that the presence of cross-linkers like α-actinin or fascin reduces the occurrence of peeling and instead promotes liposome crushing (Fig. 4A). Moreover, less peeling and overall less contraction is observed at a higher concentration of cross-linkers (Fig. 4A).
Fig. 4.
Effect of membrane anchoring and actin cortex cross-linking on cortex contraction in the outside geometry. (A and B) Percentage of liposomes crushing (black bar), peeling (red bar), undetermined cases (green bar), or noncontracting. Data are from at least three independent experiments, with ∼100 liposomes in each case. (B and C) Weak attachment condition (W) and strong attachment condition (S). (A) Varying level of cortex connectivity (200 nM myosin in all cases in weak attachment condition). (B) Effect of myosin concentration and attachment condition on contraction outcome. (C) Maximum measured contraction time, of all contracting cases (crushing and peeling) as a function of myosin concentration.
If peeling is driven by cortex rupture followed by elastic cortex retraction, we expect that weakening the attachment of actin filaments to the membrane should promote peeling. Indeed, when we lower the percentage of biotinylated lipids in the membrane, we observe a marked increase of the occurrence of peeling and a reduction of the occurrence of crushing (Fig. 4B). Interestingly, this shift in behavior is independent of the myosin concentration. Although the probability of peeling versus crushing is strongly dependent on membrane-attachment strength, the onset time and contraction duration of both peeling and crushing are independent of attachment strength. The time at which crushing or peeling stops, tCC, is constant for a given myosin filament concentration and has an average value of 17 ± 4 min for 2 nM myosin, 8 ± 4 min for 20 nM myosin, and 2 ± 1.5 min for 200 nM myosin. The maximal contraction time tCC, defined as the time at which the whole liposome population (about 100) has contracted, is also independent of membrane attachment strength (Fig. 4C). However, the maximal contraction time strongly decreases when the myosin concentration is raised from 2 to 200 nM, from 12 ± 10 min to 1.5 ± 1.5 min, for weak attachment condition (Fig. 4C, “W” bars), and from 15 ± 8 min to 0.5 ± 1.5 min in strong attachment condition (Fig. 4C, “S” bars). All together, these results indicate that more attachment promotes crushing but does not affect the overall contractile property of the actin shell.
Discussion
Our biomimetic model system allows us to study the physical mechanisms by which contractile actomyosin cortices change cell shape. We anchor actin-myosin networks to liposome membranes with the geometry of a cell. Unlike assays with actomyosin networks reconstituted on supported lipid bilayers (26), our system can address the influence of cortex contraction on membrane shape. The advantage of such cell-like model systems is that they permit precise control over the molecular composition of the system and its geometry, with actin either anchored inside or outside.
Cortex Connectivity and Membrane Attachment Govern Contraction Outcome.
We find in both inside and outside geometries that motor-driven contraction requires a minimum level of network connectivity (Fig. 2 i and ii and Fig. 4, right bar), consistent with previous observations in bulk networks (22–25, 33). The striking finding is that actin–membrane anchoring governs the outcome of cortex contraction. In the “inside geometry,” anchoring decides whether the cortex contracts toward the membrane or detaches and contracts inwards. In the outside geometry, lowering the density of biotinylated lipid anchors in the membrane promotes cortex peeling, whereas increasing the density of membrane anchors promotes liposome crushing.
Physical Mechanism That Governs Crushing Versus Peeling.
In both cases of crushing and peeling, a threshold quantity of myosin filament is needed to induce contraction (Fig. S4). However, crushing is much slower than peeling but is accelerated at higher motor densities.
Crushing is characterized by the bursting of the liposome under the influence of actomyosin contraction, possibly attributable to pore opening. The slow rate of contraction may be attributable to the decrease in liposome volume upon contraction that generates a resisting osmotic pressure, similar to observations in live cells (34). Indeed, reducing the osmotic resistance to contraction by osmotically deflating liposomes generates exclusively crushed liposomes (Fig. S7). There is also an additional resisting force that is a frictional force of hydroporosity attributable to the hydraulic permeability of the membrane and actin network through which the solution transits, which is difficult to estimate. Nevertheless, the presence of membrane bulges after the contraction (Fig. 1C, a1, arrows) suggests a pressure release mechanism.
Unlike crushing, the duration of peeling (tCC – tAM) does not depend on myosin concentration. However, motor activity is needed to trigger peeling, presumably by causing spontaneous cortex rupture and/or detachment from the membrane. We find that the initiation time (tAM) where peeling starts strongly decreases with increasing myosin concentration, indicating that peeling only occurs if the built-up cortical tension is high enough. Together, these observations strongly support an elastic retraction mechanism for peeling. Interestingly, cortex breakage is preceded by thinning of the actin cortex (Fig. S8), reminiscent of the thinning of the actin network at the front of droplets or beads moving through an actin polymerization-based mechanism that generates elastic stresses in the actin network (35, 36). If there is some contribution of active contraction after peeling initiation, we expect an increase of the velocity of peeling over time, which is not observed in our experiments.
What governs the bias toward crushing or peeling? The physical mechanism of peeling we propose, based on cortex rupture followed by elastic retraction, is similar to the spontaneous symmetry breaking of actin shells that actively polymerize around a spherical surface (37). Polymerizing shells fracture once the tangential stress or tension attributable to actin filament growth is sufficient. Analogously, we propose that actomyosin cortices rupture once sufficient tension is built up by myosin motors bound to the actin network. Thus, we expect that increasing the myosin density should reduce the initiation time for cortex rupture, which is consistent with our observations (Fig. 3E). We can also directly test whether motors mechanically stress the cortices by locally photodamaging the actin cortex (37). We find that local actin disruption leads to cortex peeling away from the damaged region only in the presence of myosin motors (Fig. S9), indicating indeed the presence of cortical tension generated by myosin motors. Cross-linking the cortex prevents peeling because the initial fracture is disfavored (Fig. 4). Collectively, our data, thus, strongly support a mechanism where peeling is initiated by symmetry breaking through a fracture of the cortex, followed by a (passive) elastic retraction. We, therefore, anticipate that the bias of peeling versus crushing should be governed by a critical level of tension. Note that liposomes often deform before peeling, which may indicate that peeling can be preceded by crushing (38). For a given network structure, peeling occurs when the motor driven tension exceeds this critical tension, whereas crushing occurs when the tension is below this critical tension (Fig. 5). Tension threshold is higher because the fracture is more difficult to open, in agreement with our results, where keeping the same myosin concentration and, therefore, the same tension but adding cross-linkers prevents peeling (Fig. 4A).
Fig. 5.
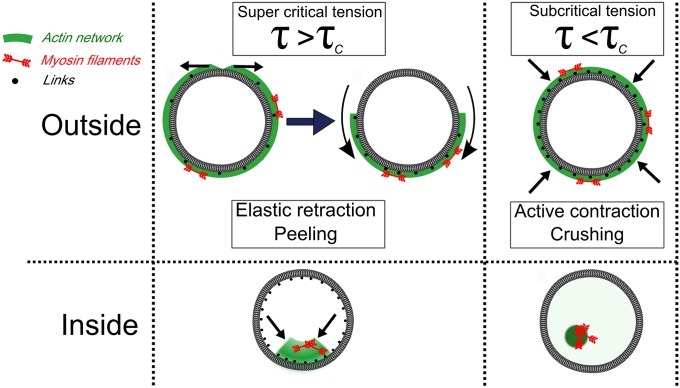
Effect of geometry and actin–membrane anchoring on myosin-driven cortex contraction. In the outside geometry (Upper), myosin motors build up cortical tension, τ . If τ exceeds the critical tension, τC, for network rupture, the cortex will elastically retract, resulting in cortex peeling toward one side of the liposome. If the cortex is strongly anchored or strongly cross-linked, the tension remains subcritical and the motors will instead actively compress and crush the liposome. In the inside geometry (Lower), motors contract strongly anchored cortices toward the membrane, whereas they contract and detach weakly anchored cortices away from the membrane.
Force Analysis and Estimates of Characteristic Times and Critical Tensions.
During cortex peeling, forces exerted on the actin shell are parallel to the membrane and act only against the viscous resistance of the lipid bilayer. The total friction force of the gel with the membrane per liposome is given by 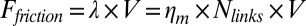 , where
, where 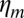 is the membrane friction, which is on the order of 10−6 Pa.s.m (39),
is the membrane friction, which is on the order of 10−6 Pa.s.m (39), 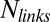 is the total number of links, which is on the order of 105 per liposome (about one link per 50 nm2),
is the total number of links, which is on the order of 105 per liposome (about one link per 50 nm2), 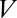 is the peeling velocity, and
is the peeling velocity, and 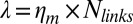 is the friction coefficient. Before peeling, the actin shells have a typical elastic modulus E of about 104 Pa (40) and a thickness e of about 500 nm, corresponding to a spring constant
is the friction coefficient. Before peeling, the actin shells have a typical elastic modulus E of about 104 Pa (40) and a thickness e of about 500 nm, corresponding to a spring constant 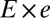 for the corresponding unfolded elastic sheet. Therefore, an elastic peeling mechanism would give a characteristic duration time
for the corresponding unfolded elastic sheet. Therefore, an elastic peeling mechanism would give a characteristic duration time 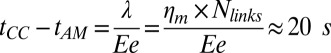 (Fig. 3E). This estimate is in good agreement with the experimental value of 42 ± 30 s, providing strong support for our physical model for peeling. Moreover, we can now also estimate the critical tension
(Fig. 3E). This estimate is in good agreement with the experimental value of 42 ± 30 s, providing strong support for our physical model for peeling. Moreover, we can now also estimate the critical tension 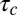 for peeling as the ratio of the prestress generated by the motors to the length L (characteristic size) of the network. Because an average of three myosin filaments are bound, each composed of a number Nm of ∼100 motors with a duty cycle (DC) between 5% and 18% (41, 42), each motor pulling with a force Fm of ∼3.5 pN (43), and the liposome size L is around 10 μm, we obtain an estimate of the tension
for peeling as the ratio of the prestress generated by the motors to the length L (characteristic size) of the network. Because an average of three myosin filaments are bound, each composed of a number Nm of ∼100 motors with a duty cycle (DC) between 5% and 18% (41, 42), each motor pulling with a force Fm of ∼3.5 pN (43), and the liposome size L is around 10 μm, we obtain an estimate of the tension 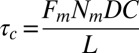 between
between 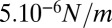 and
and 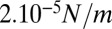 . This is a rough estimate, but it is interesting to notice that it is comparable to, although one order of magnitude lower than, values measured for cellular actin cortices (44).
. This is a rough estimate, but it is interesting to notice that it is comparable to, although one order of magnitude lower than, values measured for cellular actin cortices (44).
Under strong attachment conditions, myosin contractile forces cause liposome crushing in the outside geometry. Note that decreasing membrane attachment by decreasing the number of biotinylated lipids in the membrane not only weakens the attachment of actin filaments but also reduces the connectivity of the actin network itself: one streptavidin molecule, when binding a biotinylated lipid and a filament, can still provide two other binding sites for cross-linking actin filaments. We propose that strong attachment conditions, thus, prevent rupture of the actin shell by motor-driven cortical tension. It is interesting that in the inside geometry, cortex contraction does not deform the membrane. Instead, the actin is partly peeled or torn away from the membrane. This effect most likely reflects dragging of lipid/streptavidin anchors in the plane of the membrane (45). Alternatively, pulling of lipids out of the membrane may contribute to cortex detachment, given that the biotin–streptavidin bond is stronger than the lipid–membrane bond (46), or actin-filament rupture may occur (26).
Relevance for Cell-Shape Changes.
During cell-shape changes, the actin cortex is not merely a passive, adaptive structure, but it actively participates in establishing cell shape. Active forces generated by the actomyosin cortex are transmitted to the membrane and to the extracellular environment through actin–membrane anchors, which results in cell polarization and movement. We achieved the reconstitution of actomyosin networks of different geometries on a liposome membrane showing that the geometry, the membrane anchoring of actin networks, and their connectivity are key factors in controlling the outcome of myosin-driven contraction. In our experiments, the advantage of the outside geometry assay is that the cortex composition can be precisely controlled in a temporally defined manner, which is difficult to achieve when cortices are formed inside liposomes. We find that crushing is slower than peeling because osmotic pressure works against it. In cells, where the geometry is inside-out, cortical tension is also opposed by osmotic pressure (33). Although cells likely have additional machineries to avoid failure, actomyosin contractility can under some conditions lead to tissue tear-off at the scale of a cell layer in developing fly embryos (47). Moreover, the fact that the actin cortex can rupture in cells (analogous to peeling in our liposomes) has been observed and analyzed (48).
Cells, by regulating the connectivity of the actin cortex and the strength of membrane attachment, can thus achieve different modes of contraction to drive large-scale shape changes during processes like cell motility. Cells normally change shape without membrane rupture or large scale changes in volume. Therefore, our results highlight the need for cells to use additional mechanisms to maintain a contractile network attached at the cell surface and to prevent contractile forces from rupturing this attachment or the membrane itself.
Materials and Methods
Lipids, reagents, and proteins are listed in SI Materials and Methods.
Forming Actin Shells on the Outside of Liposomes (Outside Geometry).
Liposomes are first incubated with 160 nM streptavidin for 15 min and then diluted 30 times. In these conditions, biotinylated lipids are saturated by streptavidin, as confirmed by the observation that increasing streptavidin concentration leads to the same percentage of contracting liposomes and the same occurrence of crushing or peeling (Results and Fig. S3). This is confirmed by the fact that the concentration of biotinylated lipids is at least three orders of magnitude lower than the concentration of streptavidin during incubation. A bulk solution of 40 µM actin monomers (Cytoskeleton) containing 10% fluorescently labeled actin and 1/400 biotinylated actin monomers is polymerized at 1 µM by diluting 40 times in the working buffer (25 mM imidazole, 50 mM KCl, 70 mM sucrose, 1 mM Tris, 2 mM MgCl2, 1 mM ATP, 0.1 mM DTT, 0.02 mg/mL casein, adjusted at a pH 7.4) for 1 h in the presence of 1 µM of phalloidin (to prevent depolymerization). Actin filaments are then diluted 10-fold to 0.1 µM, mixed with streptavidin-coated liposomes, and incubated for 15 min. The mix is diluted five times for observation with myosin, to reduce background fluorescence from actin filaments. Fluorescent myosin filaments are locally injected on the liposomes. The average length of actin filaments is L = 3.9 ± 1.6 µm (n = 30 filaments), as measured by transmission electron microscopy (Fig. S10).
Reconstitution of Actin Networks and Actin–Myosin Networks Inside Liposomes (Inside Geometry).
G-actin (made in-house) is polymerized in the I buffer [25 mM imidazole⋅HCl (pH 7.4), 1 mM DTT, 0.1 mM MgATP, 50 mM KCl, 2 mM MgCl2, 280 mM sucrose, 0.5% (vol/vol) glycerol, 2 mM trolox, 2 mM protocatechuic acid and 0.1 μM protocatechuate 3,4-dioxygenase]. An enzymatic system is included to regenerate ATP, composed of 1.33 mM creatine phosphate and 766 units per milliliter creatine phosphokinase. Actin concentration is 23.8 μM, including 30 mol% or 20 mol% of AlexaFluor 488-labeled actin and 0.25 mol% of biotinylated actin. If present, we use 120 nM neutravidin and either 238 or 476 nM myosin, including 10 mol% fluorescently labeled myosin (the results were similar for both myosin concentrations). The average length of the actin filaments is 13 µm, as measured by the total internal reflection fluorescence microscopy (Fig. S10).
Supplementary Material
Acknowledgments
We thank D. Levy and A. Di Cicco for electron microscopy; J. LeeTinWah for myosin 2 functionality tests; A. Yamada for the experiments using ADP-Myosin; and J. Lemiere, M. Bussionnier, and M. Kuit-Vinkenoog for protein preparation. We also thank B. Alonso Latorre and N. Becker for discussions, F. van der Linden and B. Gentry for actin-length distribution, S. Roth for 3D detection and image analysis, and C. Marques for advice on the precursor method. This work was supported by French Agence Nationale de la Recherche (ANR) Grants ANR 09BLAN0283 and ANR 12BSV5001401, Fondation pour la Recherche Médicale Grant DEQ20120323737, a Vidi grant from the Netherlands Organization for Scientific Research (NWO), and the Foundation for Fundamental Research on Matter, which is part of NWO. K.C. acknowledges a fellowship from the ARC.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1221524110/-/DCSupplemental.
References
- 1.Mabuchi I, Okuno M. The effect of myosin antibody on the division of starfish blastomeres. J Cell Biol. 1977;74(1):251–263. doi: 10.1083/jcb.74.1.251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Huxley HE. Muscular contraction and cell motility. Nature. 1973;243(5408):445–449. doi: 10.1038/243445a0. [DOI] [PubMed] [Google Scholar]
- 3.Clark AG, Dierkes K, Paluch EK. Monitoring actin cortex thickness in live cells. Biophysical Journal. 2013;105(3):570–580. doi: 10.1016/j.bpj.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Morone N, et al. Three-dimensional reconstruction of the membrane skeleton at the plasma membrane interface by electron tomography. J Cell Biol. 2006;174(6):851–862. doi: 10.1083/jcb.200606007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bray D, White JG. Cortical flow in animal cells. Science. 1988;239(4842):883–888. doi: 10.1126/science.3277283. [DOI] [PubMed] [Google Scholar]
- 6.Svitkina TM, Verkhovsky AB, McQuade KM, Borisy GG. Analysis of the actin-myosin II system in fish epidermal keratocytes: Mechanism of cell body translocation. J Cell Biol. 1997;139(2):397–415. doi: 10.1083/jcb.139.2.397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kunda P, Pelling AE, Liu T, Baum B. Moesin controls cortical rigidity, cell rounding, and spindle morphogenesis during mitosis. Curr Biol. 2008;18(2):91–101. doi: 10.1016/j.cub.2007.12.051. [DOI] [PubMed] [Google Scholar]
- 8.Rosenblatt J. Mitosis: Moesin and the importance of being round. Curr Biol. 2008;18(7):R292–R293. doi: 10.1016/j.cub.2008.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tsujioka M, et al. Talin couples the actomyosin cortex to the plasma membrane during rear retraction and cytokinesis. Proc Natl Acad Sci USA. 2012;109(32):12992–12997. doi: 10.1073/pnas.1208296109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bretscher A, Edwards K, Fehon RG. ERM proteins and merlin: Integrators at the cell cortex. Nat Rev Mol Cell Biol. 2002;3(8):586–599. doi: 10.1038/nrm882. [DOI] [PubMed] [Google Scholar]
- 11.McClatchey AI, Fehon RG. Merlin and the ERM proteins—regulators of receptor distribution and signaling at the cell cortex. Trends Cell Biol. 2009;19(5):198–206. doi: 10.1016/j.tcb.2009.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Charras GT, Hu CK, Coughlin M, Mitchison TJ. Reassembly of contractile actin cortex in cell blebs. J Cell Biol. 2006;175(3):477–490. doi: 10.1083/jcb.200602085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gautreau A, Poullet P, Louvard D, Arpin M. Ezrin, a plasma membrane-microfilament linker, signals cell survival through the phosphatidylinositol 3-kinase/Akt pathway. Proc Natl Acad Sci USA. 1999;96(13):7300–7305. doi: 10.1073/pnas.96.13.7300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sedzinski J, et al. Polar actomyosin contractility destabilizes the position of the cytokinetic furrow. Nature. 2011;476(7361):462–466. doi: 10.1038/nature10286. [DOI] [PubMed] [Google Scholar]
- 15.Munro E, Nance J, Priess JR. Cortical flows powered by asymmetrical contraction transport PAR proteins to establish and maintain anterior-posterior polarity in the early C. elegans embryo. Dev Cell. 2004;7(3):413–424. doi: 10.1016/j.devcel.2004.08.001. [DOI] [PubMed] [Google Scholar]
- 16.Salbreux G, Charras G, Paluch E. Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 2012;22(10):536–545. doi: 10.1016/j.tcb.2012.07.001. [DOI] [PubMed] [Google Scholar]
- 17.de Curtis I, Meldolesi J. Cell surface dynamics - how Rho GTPases orchestrate the interplay between the plasma membrane and the cortical cytoskeleton. J Cell Sci. 2012;125(Pt 19):4435–4444. doi: 10.1242/jcs.108266. [DOI] [PubMed] [Google Scholar]
- 18.Field CM, et al. Actin behavior in bulk cytoplasm is cell cycle regulated in early vertebrate embryos. J Cell Sci. 2011;124(Pt 12):2086–2095. doi: 10.1242/jcs.082263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pinot M, et al. Confinement induces actin flow in a meiotic cytoplasm. Proc Natl Acad Sci USA. 2012;109(29):11705–11710. doi: 10.1073/pnas.1121583109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ershov D, Stuart MC, van der Gucht J. Mechanical properties of reconstituted actin networks at an oil–water interface determined by microrheology. Soft Matter. 2012;8(21):5896–5903. [Google Scholar]
- 21.Maruyama K, Watanabe S. The role of magnesium in the superprecipitation of myosin B. J Biol Chem. 1962;237:3437–3442. [PubMed] [Google Scholar]
- 22.Bendix PM, et al. A quantitative analysis of contractility in active cytoskeletal protein networks. Biophys J. 2008;94(8):3126–3136. doi: 10.1529/biophysj.107.117960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Koenderink GH, et al. An active biopolymer network controlled by molecular motors. Proc Natl Acad Sci USA. 2009;106(36):15192–15197. doi: 10.1073/pnas.0903974106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Soares e Silva M, et al. Active multistage coarsening of actin networks driven by myosin motors. Proc Natl Acad Sci USA. 2011;108(23):9408–9413. doi: 10.1073/pnas.1016616108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Thoresen T, Lenz M, Gardel ML. Reconstitution of contractile actomyosin bundles. Biophys J. 2011;100(11):2698–2705. doi: 10.1016/j.bpj.2011.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Murrell MP, Gardel ML. F-actin buckling coordinates contractility and severing in a biomimetic actomyosin cortex. Proc Natl Acad Sci USA. 2012;109(51):20820–20825. doi: 10.1073/pnas.1214753109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liebl D, Griffiths G. Transient assembly of F-actin by phagosomes delays phagosome fusion with lysosomes in cargo-overloaded macrophages. J Cell Sci. 2009;122(Pt 16):2935–2945. doi: 10.1242/jcs.048355. [DOI] [PubMed] [Google Scholar]
- 28.Tsai FC, Stuhrmann B, Koenderink GH. Encapsulation of active cytoskeletal protein networks in cell-sized liposomes. Langmuir. 2011;27(16):10061–10071. doi: 10.1021/la201604z. [DOI] [PubMed] [Google Scholar]
- 29.Mertins O, da Silveira NP, Pohlmann AR, Schröder AP, Marques CM. Electroformation of giant vesicles from an inverse phase precursor. Biophys J. 2009;96(7):2719–2726. doi: 10.1016/j.bpj.2008.12.3928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Limozin L, Bärmann M, Sackmann E. On the organization of self-assembled actin networks in giant vesicles. Eur Phys J E Soft Matter. 2003;10(4):319–330. doi: 10.1140/epje/i2002-10118-9. [DOI] [PubMed] [Google Scholar]
- 31.Isambert H, et al. Flexibility of actin filaments derived from thermal fluctuations. Effect of bound nucleotide, phalloidin, and muscle regulatory proteins. J Biol Chem. 1995;270(19):11437–11444. doi: 10.1074/jbc.270.19.11437. [DOI] [PubMed] [Google Scholar]
- 32.Pontani LL, et al. Reconstitution of an actin cortex inside a liposome. Biophys J. 2009;96(1):192–198. doi: 10.1016/j.bpj.2008.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Köhler S, Bausch A. Contraction mechanisms in composite active actin networks. PLoS One. 2012;7(7):e39869. doi: 10.1371/journal.pone.0039869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Stewart MP, et al. Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature. 2011;469(7329):226–230. doi: 10.1038/nature09642. [DOI] [PubMed] [Google Scholar]
- 35.Bernheim-Groswasser A, Wiesner S, Golsteyn RM, Carlier M-F, Sykes C. The dynamics of actin-based motility depend on surface parameters. Nature. 2002;417(6886):308–311. doi: 10.1038/417308a. [DOI] [PubMed] [Google Scholar]
- 36.Trichet L, Campàs O, Sykes C, Plastino J. VASP governs actin dynamics by modulating filament anchoring. Biophys J. 2007;92(3):1081–1089. doi: 10.1529/biophysj.106.091884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.van der Gucht J, Paluch E, Plastino J, Sykes C. Stress release drives symmetry breaking for actin-based movement. Proc Natl Acad Sci USA. 2005;102(22):7847–7852. doi: 10.1073/pnas.0502121102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Carvalho K, et al. Actin polymerization or myosin contraction: Two ways to build up cortical tension for symmetry breaking. Phil Trans R Soc B. 2013;368(1629):20130005. doi: 10.1098/rstb.2013.0005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Murrell M, et al. Spreading dynamics of biomimetic actin cortices. Biophys J. 2011;100(6):1400–1409. doi: 10.1016/j.bpj.2011.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Marcy Y, Prost J, Carlier M-F, Sykes C. Forces generated during actin-based propulsion: A direct measurement by micromanipulation. Proc Natl Acad Sci USA. 2004;101(16):5992–5997. doi: 10.1073/pnas.0307704101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Harris DE, Warshaw DM. Smooth and skeletal muscle myosin both exhibit low duty cycles at zero load in vitro. J Biol Chem. 1993;268(20):14764–14768. [PubMed] [Google Scholar]
- 42.Guilford WH, et al. Smooth muscle and skeletal muscle myosins produce similar unitary forces and displacements in the laser trap. Biophys J. 1997;72(3):1006–1021. doi: 10.1016/S0006-3495(97)78753-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Finer JT, Simmons RM, Spudich JA. Single myosin molecule mechanics: Piconewton forces and nanometre steps. Nature. 1994;368(6467):113–119. doi: 10.1038/368113a0. [DOI] [PubMed] [Google Scholar]
- 44.Bergert M, Chandradoss SD, Desai RA, Paluch E. Cell mechanics control rapid transitions between blebs and lamellipodia during migration. Proc Natl Acad Sci USA. 2012;109(36):14434–14439. doi: 10.1073/pnas.1207968109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Fenz SF, Merkel R, Sengupta K. Diffusion and intermembrane distance: Case study of avidin and E-cadherin mediated adhesion. Langmuir. 2009;25(2):1074–1085. doi: 10.1021/la803227s. [DOI] [PubMed] [Google Scholar]
- 46.Evans E. Probing the relation between force—lifetime—and chemistry in single molecular bonds. Annu Rev Biophys Biomol Struct. 2001;30:105–128. doi: 10.1146/annurev.biophys.30.1.105. [DOI] [PubMed] [Google Scholar]
- 47.Martin AC, Gelbart M, Fernandez-Gonzalez R, Kaschube M, Wieschaus EF. Integration of contractile forces during tissue invagination. J Cell Biol. 2010;188(5):735–749. doi: 10.1083/jcb.200910099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Paluch E, Piel M, Prost J, Bornens M, Sykes C. Cortical actomyosin breakage triggers shape oscillations in cells and cell fragments. Biophys J. 2005;89(1):724–733. doi: 10.1529/biophysj.105.060590. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.