Crystalline polymorphism induced by charge regulation in ionic membranes

Significance

The crystallization of molecules with polar and hydrophobic groups, such as ionic amphiphiles and proteins, is of paramount importance in biology and biotechnology. This combined X-ray scattering and theoretical study demonstrates how crystalline order within membranes formed by coassembled cationic and anionic amphiphiles can be controlled by varying pH and molecular tail length. Our work suggests design of bilayer membranes with specific crystalline arrangements at ambient temperature and physiologically relevant pH environments with suitable choice of headgroup and tail. Changes in crystallinity are likely to affect molecular diffusion rates across membranes and may enable control over the encapsulation and release of molecules within the membrane. Moreover, pH-induced crystalline transformations are likely used by organisms to control metabolic flow in harsh environments.

Abstract

The crystallization of molecules with polar and hydrophobic groups, such as ionic amphiphiles and proteins, is of paramount importance in biology and biotechnology. By coassembling dilysine (+2) and carboxylate (–1) amphiphiles of various tail lengths into bilayer membranes at different pH values, we show that the 2D crystallization process in amphiphile membranes can be controlled by modifying the competition of long-range and short-range interactions among the polar and the hydrophobic groups. The pH and the hydrophobic tail length modify the intermolecular packing and the symmetry of their crystalline phase. For hydrophobic tail lengths of 14 carbons (C₁₄), we observe the coassembly into crystalline bilayers with hexagonal molecular ordering via in situ small- and wide-angle X-ray scattering. As the tail length increases, the hexagonal lattice spacing decreases due to an increase in van der Waals interactions, as demonstrated by atomistic molecular dynamics simulations. For C₁₆ and C₁₈ we observe a reentrant crystalline phase transition sequence, hexagonal–rectangular-C–rectangular-P–rectangular-C–hexagonal, as the solution pH is increased from 3 to 10.5. The stability of the rectangular phases, which maximize tail packing, increases with increasing tail length. As a result, for very long tails (C₂₂), the possibility of observing packing symmetries other than rectangular-C phases diminishes. Our work demonstrates that it is possible to systematically exchange chemical and mechanical energy by changing the solution pH value within a range of physiological conditions at room temperature in bilayers of molecules with ionizable groups.

Nature uses electrostatic interactions among positively and negatively charged groups to induce the organization of biomolecules into highly complex structures that respond to ionic changes (1, 2). The structure of the aggregates at specific ionic conditions is intimately related to its function. Therefore, understanding the mechanisms that control the structure of molecules with hydrophobic and polar groups at physiological conditions is of great importance in molecular biology and biotechnology. In particular, amphiphilic molecules that have polar ionizable groups, such as proteins and lipids, can change their structures and functions in response to the pH and the concentration of ions in the solution (3), thereby affecting their physical properties and functions. For example, the structure of lipid membranes affects the structure and activity of membrane-bound proteins (4–6). Furthermore, the intermolecular packing density and structure are known to affect the molecular diffusion rates of water and ions across membranes (7, 8). Changing the packing density of molecules within membranes could also be useful for controlling encapsulation and release efficiency of molecules inside a vesicle (9). Additionally the spacing between amphiphilic molecules within a membrane may control the capacity to encapsulate or release amphiphilic molecules within the bilayer, such as the proteins that reside inside lipid membranes (10) and possibly hydrophobic drugs. Therefore, it is important to explore different approaches to adjust the structure of lipid membranes.

At the mesoscale level, crystalline membranes are essential for many bacteria (11), bacterial microcompartments (12), and archaea (13) to survive in extreme environments including high salinity. These organisms take various polyhedral geometries that are characteristic of crystalline closed shells (14, 15). The presence of polar and hydrophobic groups in their wall envelopes and the fact that they survive at low pH values and disintegrate or become spherical (the shape of closed liquid membranes) when divalent metal ions are chelated (11, 13) suggest that their crystallization is triggered by electrostatic interactions. Divalent ion-induced crystallization of anionic membranes has been recently studied (16, 17), but crystallization changes induced by pH variations in bilayers are unknown. Here, we study pH effects in crystalline membranes of coassembled amphiphiles with carboxylate and dilysine headgroups, whose pK_a values are about 5.5 (18) and 10 (19), respectively.

Simple mixtures of cationic and anionic amphiphiles exhibit some of the behaviors of highly complex natural membranes. They self-assemble into a large variety of membrane structures, including closed-shell vesicles, via the electrostatic interactions between the cationic and the anionic surfactant headgroups (20–22). Catanionic vesicles formed from coassembled cationic and anionic amphiphiles show stability for long periods and can be formed spontaneously without sonication or extrusion (20, 23). The assembly of such amphiphilic molecules with ionizable groups into bilayer membranes offers a unique opportunity to systematically analyze the subtle balance of electrostatics, entropy, hydrophobicity, and short-range interactions in their structure. Therefore, these membranes can provide important insight about membrane dynamics and may have useful biomedical applications such as drug delivery (24).

The phase behavior of cationic and anionic amphiphiles is determined by many parameters, such as the amphiphile mixing ratio, concentration, and molecular structure (25–27). We recently studied mixtures +3 cations and –1 anions forming catanionic membranes (14). The molecular packing of these membranes showed a hexagonal to rectangular-C to hexagonal phase transition with increasing pH, resulting in significant changes to the membrane morphology. These membranes appear to be stable to salt (up to 500 mM NaCl) in contrast to other ionic coassembled systems that are very sensitive to charge screening (28, 29). To be useful as models for biological membranes or for potential applications in drug delivery, the range of accessible temperatures is very limited, so other parameters to control crystalline order must be considered. The pH range of physiological media can vary considerably between different tissues. For example, it is known that a microenvironment in tumors is more acidic than in normal tissues (30–32). Therefore, it is important to understand the internal membrane structure and the consequent membrane morphology as a function of pH. Because the variation of pH within a particular localized environment is small, other parameters like molecular structure must also be considered to control the internal membrane structure at a specific pH.

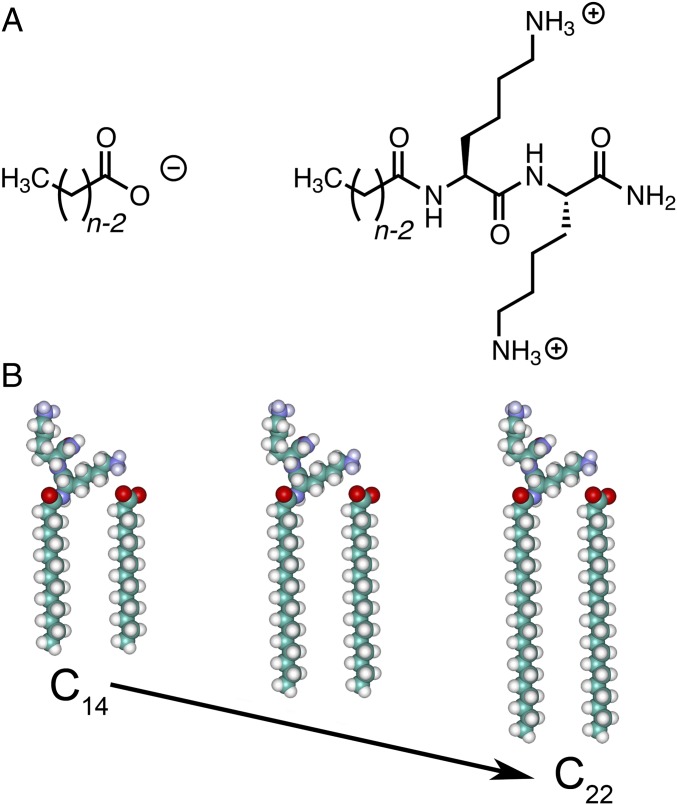
We study here the molecular packing in catanionic membranes formed from +2 dilysine cationic amphiphiles and –1 fatty acids (Fig. 1A) as a function of solution pH and amphiphile tail length (Fig. 1B). The solution pH controls the degree of ionization of the cationic and the anionic headgroups, whereas the tail length determines the strength of the intermolecular van der Waals interactions, as shown by atomistic molecular dynamics (MD) simulations. Simultaneous small- and wide-angle X-ray scattering (SAXS and WAXS) are used to measure the membrane thickness and the crystalline packing of the amphiphiles in the membrane plane.

Fig. 1.

(A) Charged amphiphiles used for ionic coassembly: –1 fatty acid (C_n-1-COOH) with +2 dilysine (C_n-K₂). (B) Schematic representations of the pairs of cation and anion with different tail length from n = 14 to n = 22 used to form bilayers.

Results and Discussion

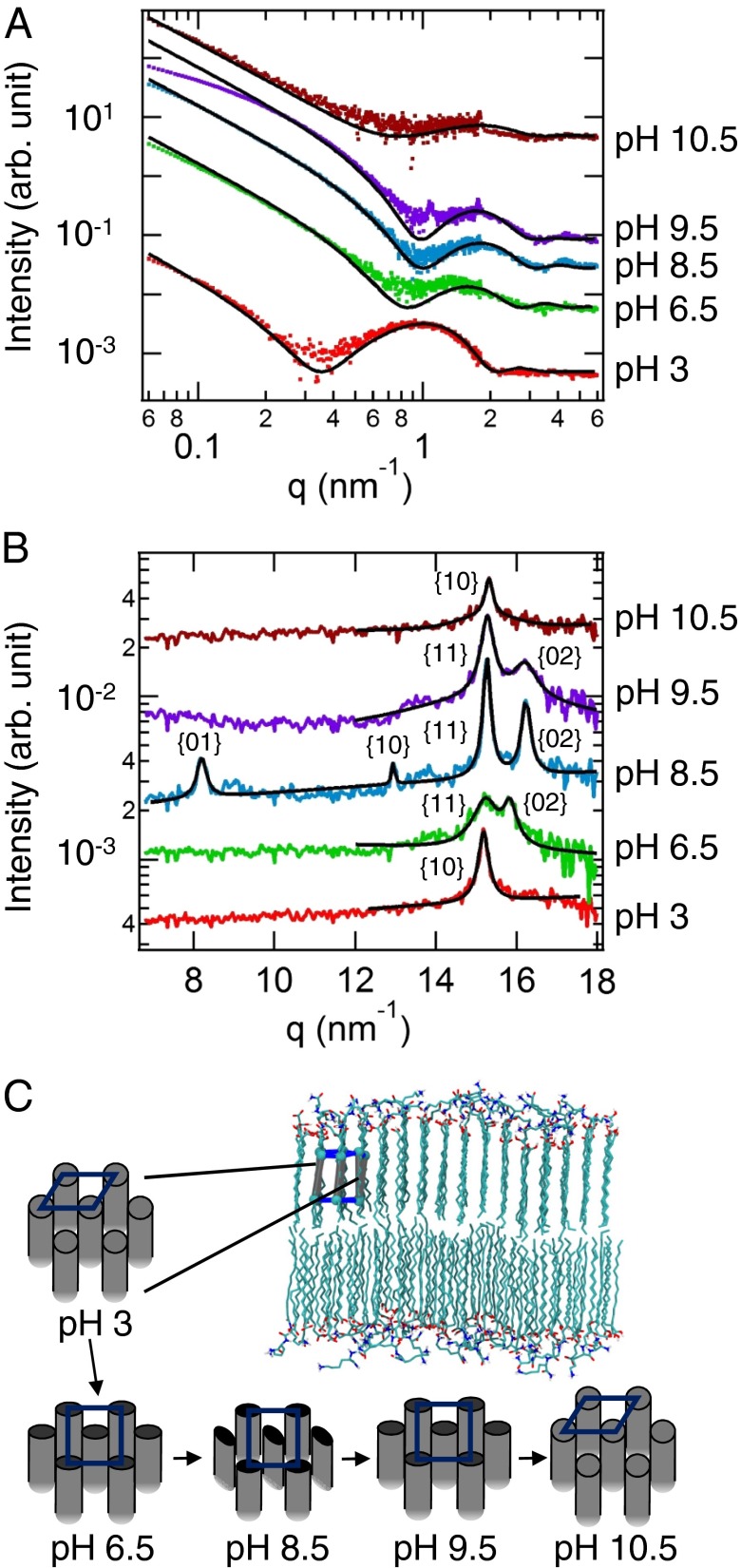
To understand the effect of solution pH on catanionic mixtures, we first investigated solutions of oppositely charged amphiphiles with a given tail length. Specifically, we observed the coassembly of N-palmitoyl dilysine (C₁₆-K₂) and palmitic acid (C₁₅-COOH). In aqueous solution by itself, C₁₆-K₂ forms micelles and C₁₅-COOH is insoluble. Simultaneously collected SAXS–WAXS data provide in situ information on the nanoscale morphology and atomic length scale crystallinity, respectively. Fig. 2A shows the processed SAXS data for the mixture of these amphiphiles as a function of scattering vector (q = 4πsinθ/λ) at various solution pH values. Regardless of the solution pH, the SAXS intensity in the Porod region (q < 0.3 nm⁻¹) decreases as ∼ q^–2, indicating scattering from 2D membranes, as illustrated in Fig. 2C. The SAXS-derived estimates for the bilayer membrane thicknesses are listed in Table 1. For C₁₆ mixtures, the bilayer thickness is highest at pH 3 (∼5.8 nm). For pH ≥ 6.5, the bilayer thickness is nearly a constant ∼4.0 nm. The reduction in the bilayer thickness with increasing pH has been previously also observed for mixtures of N-palmitoyl trilysine (C₁₆-K₃) and C₁₅-COOH and was explained by atomistic MD simulations, which showed that at high pH there exists extensive interdigitation of the hydrophobic tails of the molecules comprising the two leaflets of the bilayer (14).

Fig. 2.

(A) In situ SAXS and (B) WAXS data showing the background-subtracted scattered intensity versus the scattering vector q for mixtures of palmitic acid (C₁₅-COOH) and cationic N-palmitoyl dilysine (C₁₆-K₂) as the pH is increased from 3 to 10.5. The datasets are offset vertically for clarity. The black lines are the fits. Deviations in the SAXS fits are likely due to sample polydispersity. (C) Schematic representations for the bilayer model at pH 3, 6.5, 8.5, 9.5, and 10.5. Changes are observed in the packing of the alkyl tails into a hexagonal, rectangular-C, or rectangular-P lattice.

Table 1.

Lattice parameters and membrane thicknesses obtained from X-ray scattering for mixtures of anion C₁₅-COOH and cation C₁₆-K₂ (Fig. 2 B and C)

pH	Crystal form	Domain size, nm	Lattice const, nm	Area per molecule, nm2	Membrane thickness, nm
3	Hexagonal	24	a = 0.477	0.197	5.8
6.5	Rectangular-C	13	a = 0.483	0.192	4.2
			b = 0.795
8.5	Rectangular-P	33	a = 0.484	0.188	3.8
			b = 0.775
9.5	Rectangular-C	23	a = 0.484	0.188	4.0
			b = 0.775
10.5	Hexagonal	36	a = 0.474	0.195	3.3

Although the features in the SAXS data describe the nanometer-scale morphology of the bilayers, the diffraction peaks in the WAXS region (q ≥ 7 nm⁻¹) arise from the crystalline packing of alkyl tails of the molecules forming the bilayer membranes. Fig. 2B shows the WAXS data for the C₁₆ catanionic mixture at different pH values. For the C₁₆ catanionic mixtures, the number and the position of the diffraction peaks, and thus the crystalline packing of the alkyl tails, sensitively depend upon the solution pH. For pH 3 and pH 10.5, a single diffraction peak is observed and is putatively attributed to a hexagonal packing of the molecular tails. This is because the cross-sectional area/tail A_t calculated for pH 3 and pH 10.5 (Table 1) are close to A_t ∼0.20–0.21 nm² for cylindrically disoriented alkanes in their fully extended conformation, commonly described as a rotator phase (33). By contrast, solutions at pH 6.5 and pH 9.5 exhibit two diffraction peaks, which are indicative of a rectangular-C (centered) structure in which each unit cell is occupied by two molecules with the same orientation of the molecular backbone planes. At pH 8.5, four diffraction peaks are observed and the peak positions indicate a 2D rectangular-P (primitive) lattice with two molecules per unit cell. Within a rectangular-P unit cell, the orientation of the alkyl tail backbone plane for the molecule at the center of the cell is different from that for the alkyl tails occupying the unit cell vertices, as shown schematically in Fig. 2C. The observed diffraction peaks in the low q region are not due to ordering of the cationic headgroups (see calculations in SI Appendix).

The pH-dependent effects on the 2D crystal phase and area/tail (A_t) can be qualitatively explained by the pH-driven ionization of the cationic and the anionic components of the membrane. Specifically, at low pH the carboxylic acid headgroups (pK_a ∼5.5) (18) are largely undissociated (neutral), whereas the amines in the dilysine headgroups (pK_a ∼10) (19) are mostly protonated (cationic). In catanionic mixtures, the pK_a value for the carboxylic acid is expected to decrease and the pK_a value for the protonated lysine is expected to increase relative to their bulk pK_a values (14, 34, 35). At intermediate pH (∼8.5), both the carboxylic acids and the lysine amines are fully ionized, whereas at very high pH the carboxylic acids are fully ionized and the lysines are mostly neutral. Therefore, the attractive electrostatic interactions between the cations and the anions reach a maximum at intermediate pH (Table 1).

The observed hexagonal–rectangular-C–rectangular-P–rectangular-C–hexagonal sequence of 2D crystal phase transitions with increasing pH (Fig. 2C) is consistent with the pH-driven ionization changes of the cationic and anionic headgroups described above. At pH 3 and pH 10.5, where the electrostatic attractions between the headgroups are expected to be weak, the orientationally disordered molecular tails pack into a hexagonal lattice (14, 33, 36). At pH 6.5 and 9.5, the enhanced electrostatic interactions lead to a higher packing density, which necessarily requires orientational ordering of the backbone planes of the alkyl tails. Therefore, a distortion of the hexagonal lattice is expected and is manifested by assembly into 2D rectangular-C lattices. At pH 8.5, where the electrostatic attractions are expected to be close to a maximum, the lattice is rectangular-P with the highest packing density. As the cohesive interactions are maximized at this pH, the molecules must reorient to achieve denser packing. The rectangular-P lattice of C₁₆ mixtures indeed has an A_t ∼0.188 nm², which is close to the minimum area per tail (0.1875 nm² for herringbone packing) of alkyl tails found in Langmuir films (33). Here it is worth noting that the lattice parameters for the rectangular-P and the rectangular-C lattices (Table 1) are smaller by ∼2–4% from the universal curve of lattice parameters for alkyl tail packing in Langmuir films (33). These deviations likely result from the strong electrostatic attractions between the cationic and anionic headgroups present in our study, but absent in Langmuir film studies. Consistent with this interpretation, the lattice parameters for our hexagonal lattices (weak electrostatic interactions) fall within the range of values for the hexagonally packed alkyl tails in Langmuir films.

In the previous study of the mixture of N-palmitoyl trilysine and palmitic acid, no rectangular-P was observed at intermediate pH, where the electrostatic attractions should be highest (14). The bulkier trilysine headgroup may limit the extent of close intermolecular packing, as suggested by the larger area per tail (A_t ∼ 0.192 nm² at pH 8.5). These observations show that the solution pH provides a facile pathway to reversibly control the crystalline phases of ionic membranes and the molecular packing density by modulating the electrostatic interactions between oppositely charged amphiphilic headgroups.

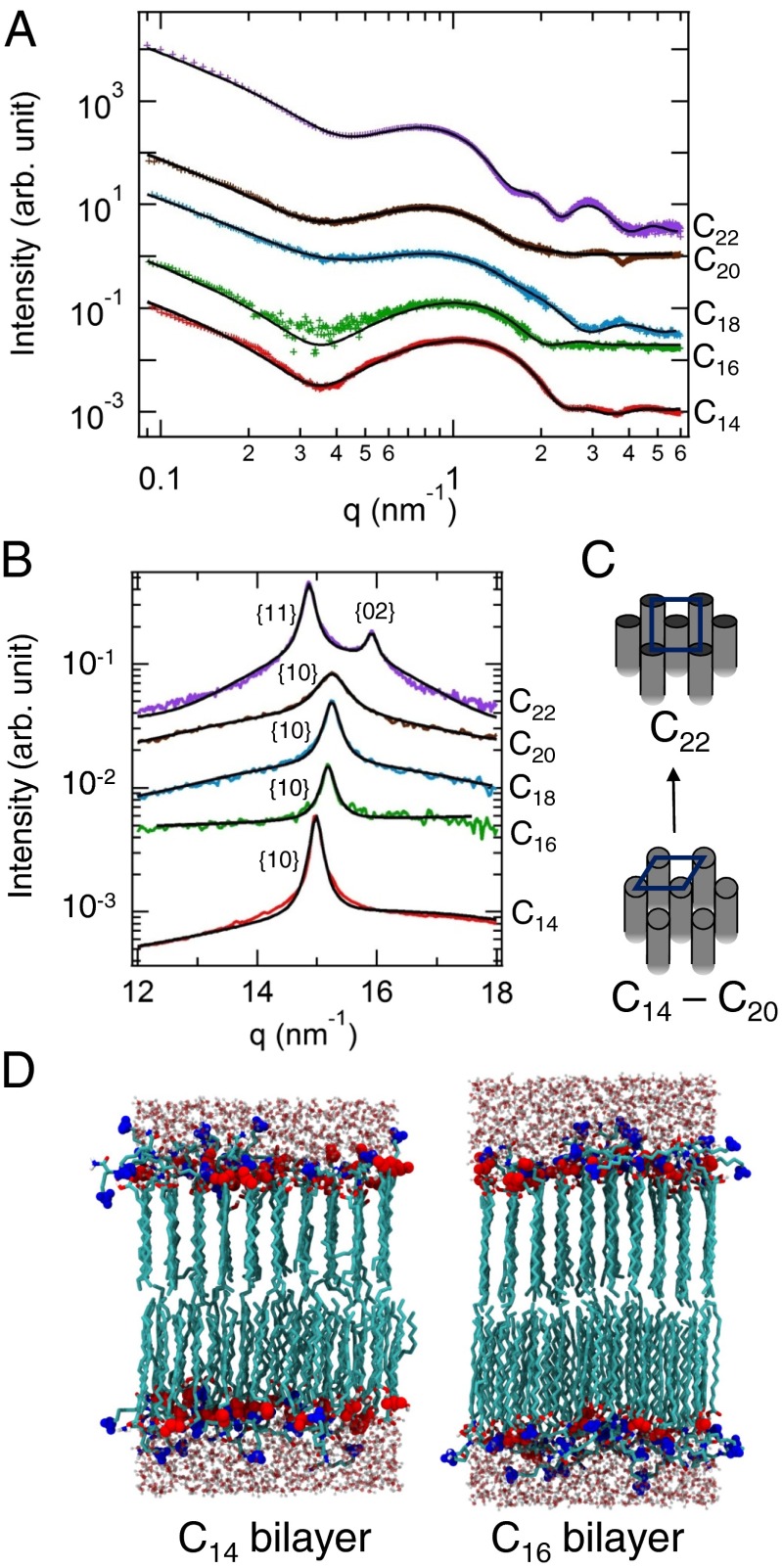
Because biological media typically operate within a narrow pH range, it is valuable to understand other factors that control amphiphile crystallization at a particular pH. For this reason, we also explored the 2D packing of amphiphiles with longer or shorter tail lengths. The other systems we studied have the same cationic and anionic headgroups, but tail length C₁₄, C₁₈, C₂₀, or C₂₂. The samples are prepared by mixing each cation with the carboxylic acid of the same alkyl tail length (Fig. 1B). Fig. 3A shows the processed SAXS data for C_n (n = 14, 16, 18, 20, and 22) mixtures in water at pH 3. In each system the cations alone formed micelles in solution (SI Appendix, Fig. S2). Similar to the case of C₁₆, mixtures of C₁₄, C₁₈, C₂₀, and C₂₂, each coassemble into bilayers that are stable over long periods (days). The SAXS data are fitted using a model that accounts for both bilayer membranes and spherical micelles (see SI Appendix for details). This model is chosen because SAXS profiles from solutions of the cations alone show strong scattering from micelle structures (SI Appendix, Fig. S2). As expected, the thickness of each membrane increases with alkyl tail length (Table 2). Fig. 3B shows the WAXS data for C_n (n = 14, 16, 18, 20, and 22) mixtures at pH 3. For the C₁₄, C₁₆, C₁₈, and C₂₀ mixtures, a single diffraction peak in the WAXS region indicates a hexagonal packing of the alkyl tails. In contrast, a rectangular-C phase is observed for C₂₂ mixtures. The van der Waals interactions between the C₂₂ tails are stronger than the shorter tails within the bilayers at a fixed temperature. Therefore, the longer tails are more sensitive to the orientation of neighboring tails, resulting in the rectangular-C phase.

Fig. 3.

(A) In situ SAXS and (B) WAXS data showing the background-subtracted scattered intensity versus the scattering vector q for mixtures of catanionic amphiphiles as the tail length n is increased from 14 to 22. The datasets are offset vertically for clarity. The black lines are the fits. (C) Schematic representations showing changes in molecular packing with tail length. (D) Snapshots of the atomistic MD simulations on C₁₄ and C₁₆ systems. Carbon atoms are colored cyan; the headgroups of the charged amphiphiles are highlighted in blue for NH₃⁺ or red for COO^–. Water molecules are shown explicitly.

Table 2.

Lattice parameters and membrane thicknesses obtained from X-ray scattering for mixtures of anion and cation at different tail lengths (n) at pH 3 (Fig. 3 B and C)

Tail length	Crystal form	Domain size, nm	Lattice const, nm	Area per molecule, nm2	Membrane thickness, nm
14	Hex	30	a = 0.487	0.205	5.6
16	Hex	24	a = 0.477	0.197	5.8
18	Hex	21	a = 0.477	0.197	7.5
20	Hex	12	a = 0.477	0.197	7.6
22	Rect-C	29	a = 0.500	0.197	8.0
			b = 0.789

The area per molecule by MD is 0.207 nm² and 0.200 nm² for tail length 14 and 16, respectively.

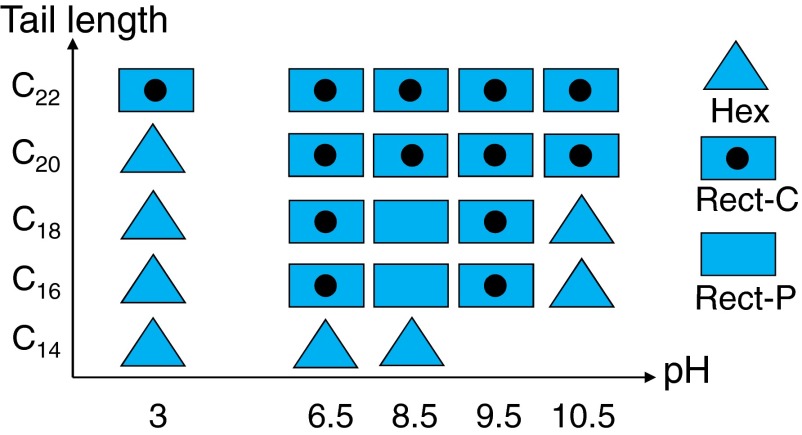
These results show how varying solution pH and tail length can affect the packing of molecules within a bilayer membrane. To fully understand the relationship between the hydrophobic tails and the charged headgroups, we also investigated membranes formed from this series of amphiphiles over a range of pH values (SI Appendix). Based on the results, we are able to generate the 2D phase diagram shown in Fig. 4. The shorter tailed surfactant C₁₄ shows crystalline membranes with a hexagonal lattice across the pH range studied here. As discussed above, for C₁₆ the change in electrostatic interaction between adjacent headgroups due to pH has a very strong effect on the crystalline order of the tails. The C₁₈ mixture gives very similar phase transitions as a function of pH. As the tail length increases to C₂₀, there is a hexagonal to rectangular-C crystalline structure transition with increasing pH. The longest tail (C₂₂) is dominated by van der Waals interactions among the tails and shows only rectangular-C packing across all pH values. It is possible that the rectangular-P structure exists over a very narrow pH range, as in the cases of C₁₆ and C₁₈ mixtures. This bilayer formed by coassembly of weak acids and weak bases has a strong capacity for self-buffering, making it experimentally difficult to attain precise pH values (±1 pH unit). Nevertheless, the pH-dependent changes in the A_t are similar to those observed in C₁₆ and C₁₈, where A_t reaches a maximum around pH 8.5 (SI Appendix, Table S6). In summary, the packing of intermediate length tails (C₁₆, C₁₈, and C₂₀) within the catanionic membrane is highly sensitive to the pH, whereas the packing of the shortest tail (C₁₄) and longest tail (C₂₂) is less sensitive.

Fig. 4.

Phase diagram showing the formation of membrane and amphiphile packing structure of catanionic mixture as a function of pH and tail length.

Atomistic MD simulations show remarkable agreement with the experiments in the C₁₄ and C₁₆ systems at pH 3 (Fig. 3D). The calculated peak positions extracted from the simulations match the experimental WAXS results (SI Appendix, Fig. S9). The simulation results show that the amphiphiles pack in hexagonal lattice in both cases, with a reduction in the area per molecule from 0.207 nm² (C₁₄) to 0.200 nm² (C₁₆). The simulations also reveal an enhancement in the van der Waals interactions from –27 k_BT to –33 k_BT per hydrocarbon tail when the tail length n increases from 14 to 16, which suggests a gain of ∼2 k_BT per hydrocarbon atom in the crystalline membrane structure (17). The hydration of lipid bilayers has been studied previously by MD simulations in systems with charged groups such as dimyristoylphosphatidylcholine (DMPC) lipid bilayers (37), which showed that the average number of hydrogen bonds per lipid oxygen atom varies depending on its position within the lipid. Specifically, the oxygen atoms of the phosphate group in contact with water were found to have a higher probability to form hydrogen bonds compared with the ester oxygen atoms. There are also studies on the structure of water close to hydroxyl groups (38). However, the hydration of cationic–anionic bilayers is unknown. Our MD calculations of the radial distribution function show that the strength of the correlation (SI Appendix, Fig. S10) between the NH₃⁺ headgroups (from cationic amphiphiles) and water is much stronger than between the COO^– headgroups (from anionic amphiphiles) and water, as the NH₃⁺ group from the long lysine side chain is more exposed to the aqueous medium. The coordination number of water molecules around the headgroups of NH₃⁺, COO^–, and COOH (from uncharged anionic amphiphiles) is smaller for C₁₆ than for C₁₄, whereas the coordination number between the COO^– around NH₃⁺ is similar in both cases (SI Appendix, Table S11). The simulations suggest that the reduced intermolecular spacing within the membrane from C₁₄ to C₁₆ is promoted by the enhancement of van der Waals interactions and the water distribution around the amphiphiles, whereas the electrostatic attraction between the oppositely charged headgroups remains the same in both cases. That is, the competition of van der Waals forces with electrostatic interactions between the cationic and anionic groups is not solely responsible for their coassembly into bilayers. In addition, the interactions between the amphiphiles’ polar headgroups and water seem to play a key role in the energetics of coassembly.

Finally, we note that our previous studies (14) on +3/−1 amphiphilic membranes showed that the symmetry of the crystalline bilayer influences the mesoscale morphology of the membrane. In particular, we showed that lower symmetry crystal structures (rectangular-C) inhibit the formation of closed crystalline shells. Instead, vesicles readily formed when the tails of the amphipiles are packed in a hexagonal lattice, which we corroborate here by cryogenic transmission electron microscopy (cryo-TEM) at pH 3 (SI Appendix, Fig. S14). In this present study we find that the pH value not only modifies the molecular packing, but also the size of the crystalline domains (Table 1), which is also found to be strongly dependent on the tail length of the amphiphiles (Table2).

Conclusions

Our results demonstrate that crystalline order within catanionic membranes can be controlled by varying pH or molecular tail length. Previous work has shown only hexagonal packing of molecules within catanionic membranes where the ionization state of the cationic component does not depend on pH (25, 39). In contrast, the ionization state of each of the molecules studied here is pH dependent, which enables us to control the membrane crystal structure by varying the degree of ionization among the headgroups. The solution pH controls the ionization state of the headgroups, thereby regulating the electrostatic interactions between neighboring molecules and the water around the headgroups. Increasing the alkyl tail length strengthens the van der Waals interactions between hydrophobic tails of adjacent molecules. These results produce a complete analysis of how the hydrophobic and hydrophilic parts of the molecules interact and contribute to crystalline packing within bilayers at a constant temperature. Our work suggests design of bilayer membranes with specific crystalline arrangements at ambient temperature and physiologically relevant pH environments with suitable choice of headgroup and tail. The reentrant transitions in crystalline symmetry and molecular packing observed as the solution pH increases are due to the delicate balance of hydrophobic and hydrophilic interactions. We foresee that the ability to control intermolecular spacing and arrangements may enable control over the encapsulation and release of molecules within the membrane. Changes in crystallinity are also likely to affect rate of diffusion of molecules across the membrane (7–9), which is important for a liposome-based drug delivery system. Moreover, pH-induced crystalline transformations are likely used by organisms, including archaea and bacteria, to control metabolic flow in harsh environments.

Materials and Methods

Synthesis.

All Fmoc–amino acids and Rink 4-methylbenzhydrylamine (MBHA) amide resin were purchased from Novabiochem Corporation. All other reagents and solvents for peptide synthesis were purchased from Aldrich, Mallinckrodt, or TCI and used as provided. The synthesis of each N-alkanoyl dilysine (C_n-K₂) was performed using standard solid-phase peptide synthesis methods as described previously (14). Briefly, peptides were grown on Rink Amide MBHA resin, using 4.0 equivalents of an Fmoc-protected amino acid, 3.95 molar equivalents of 2-(1H-benzotriazole-1-yl)-1,1,3,3-tetramethyluronium hexafluorophosphate (HBTU), and 6.0 equivalents of N,N-diisopropylethylamine (DIEA) for each residue coupled to the resin. The fatty acid tail was subsequently coupled to the N terminus of the peptide by adding 8.0 molar equivalents of each fatty acid to the peptide in the presence of 7.95 molar equivalents of HBTU and 12 molar equivalents of DIEA. The peptide was then cleaved from the resin, and amino acid side groups were deprotected in 95% trifluoroacetic acid (TFA), 2.5% triisopropylsilane (TIS), and 2.5% deionized water. TFA was removed by rotary evaporation. Peptides were purified by preparative HPLC on a Varian Prostar 210 HPLC system using a Waters Atlantis C-18 30 × 250 mm column under a slow elution gradient of 98–0% water and acetonitrile (0.1% TFA). Product-containing fractions were confirmed by electrospray ionization mass spectrometry (Agilent 6510 Q-TOF LC/MS), combined, and lyophilized after removing acetonitrile by rotary evaporation to afford the desired amphiphiles as their trifluoroacetate salts.

Sample Preparation.

The cationic dilysine amphiphiles (C_nK₂) were dissolved in deionized water (resistivity ∼18 MΩ⋅cm) at a concentration of 4 mM (C₁₆–C₂₂) or 12 mM (C₁₄). The coassembled solution for each tail length was prepared by adding the dilysine cation solution to a centrifuge tube containing an excess of the solid fatty acid (three equivalents) with the same hydrocarbon tail length. These solution concentrations were picked to ensure an excess of the carboxylic acid and maximize the coassembly of the oppositely charged amphiphiles. The fatty acids used in the present study are not water soluble at room temperature. To dissolve the fatty acids and thus to promote coassembly in solution, the mixtures were heated to 80 °C for 60 min. (C₂₂ samples had to be heated to 90 °C to ensure complete dissolution.) The samples were then cooled to room temperature and centrifuged at ∼7,000 × g for 5 min to remove precipitates, which contained the undissolved fatty acids. The pH of these solutions after heating and cooling was ∼3. The solution pH of each sample (except pH 3) was adjusted with 1 M NaOH just before X-ray measurements. It is worth noting that no assembly was observed for the cation-only solutions or mixed samples prepared using a shorter C₁₂ tail at 4 mM.

X-Ray Scattering.

SAXS and WAXS data were collected simultaneously by two separate CCD X-ray areal detectors at the DND 5ID-D and 12ID undulator beamlines of the Advanced Photon Source (APS) at the Argonne National Laboratory. The sample solutions were injected through a capillary tube flow-cell at room temperature to reduce radiation damage. Data were collected at an incident photon energy of 10.00 keV (wavelength λ = 0.1240 nm). For purposes of background subtraction, SAXS–WAXS data were also collected from the empty capillary and from the pure water containing capillaries (no amphiphiles). The exposure time for each CCD image was 10 s, and five images were taken for each sample. The 2D SAXS–WAXS patterns were converted into 1D radial intensity patterns by Fit2D, I(2θ), by circular integration, and the 1D profiles were thereafter averaged over the five sets of data for each sample. All of the X-ray data reported here are a result of at least two independent measurements and are fully reproducible.

Atomistic MD Simulations.

Classical atomistic MD simulations are performed using the package GROMACS (version 4.5.5) (40). The latest version of the GROMOS96 54A7 United-Atom force field (41) is used for the amphiphile molecules with water molecules modeled by the Simple Point Charge model. The force field has been validated in our previous work (14) in reproducing well the crystalline structures of mixtures of trivalent cationic (C₁₆-K₃) and monovalent anionic (C₁₅-COOH) amphiphiles. Two systems representing different hydrocarbon tail lengths of C₁₄ and C₁₆, respectively, are investigated. In both of the systems, the ionization degree of palmitic acid molecules of 30% (see SI Appendix, Table S9 for the compositions) is used to mimic the low pH condition (pH ∼ 3) (14). The simulations are started from pseudobilayer structures (akin to Fig. 3D) to speed up the process for equilibrium structures. The electrostatic interactions are calculated via the Particle Mesh Ewald method (42) and the short-range Lennard–Jones 12–6 interactions are truncated at 1.2 nm with the long-range dispersion corrections applied to the energy and pressure. The simulations are performed for a duration of 50 ns for the C₁₄ system and a longer duration of 400 ns for the C₁₆ system. The temporal calculations of the area per amphiphile molecule support that around 20 ns is long enough to equilibrate the bilayer structures for both systems (SI Appendix, Fig. S8). Therefore, the trajectories from the last 20 ns for the C₁₄ system, the last 100 ns for the C₁₆ system, are used for the subsequent data collection and analysis.