The sequencing bias relaxed characteristics of Hi-C derived data and implications for chromatin 3D modeling

Abstract

The 3D chromatin structure modeling by chromatin interactions derived from Hi-C experiments is significantly challenged by the intrinsic sequencing biases in these experiments. Conventional modeling methods only focus on the bias among different chromatin regions within the same experiment but neglect the bias arising from different experimental sequencing depth. We now show that the regional interaction bias is tightly coupled with the sequencing depth, and we further identify a chromatin structure parameter as the inherent characteristics of Hi-C derived data for chromatin regions. Then we present an approach for chromatin structure prediction capable of relaxing both kinds of sequencing biases by using this identified parameter. This method is validated by intra and inter cell-line comparisons among various chromatin regions for four human cell-lines (K562, GM12878, IMR90 and H1hESC), which shows that the openness of chromatin region is well correlated with chromatin function. This method has been executed by an automatic pipeline (AutoChrom3D) and thus can be conveniently used.

INTRODUCTION

The increasing applications of chromosome conformation capture-based techniques (1–4), especially Hi-C (5) and its derivatives (6–9), have prompted the development of theoretical methods for reconstructing 3D chromatin structures. Several chromatin 3D modeling methods (5,6,8,10–14) have been raised based on the physical theory and/or optimization theory, which validates the link between chromatin 3D structures and genomic functions (15). In the original Hi-C article, Liebeman-Aiden and colleagues (5) adopted polymer model together with Monte Carlo simulation to reveal the potential principle of chromatin folding. Various Monte Carlo procedures were further developed to simulate chromatin 3D structures by fitting Hi-C data (10,13,16). Alternatively, Duan et al. (6) proposed a constrained optimization strategy to reconstruct chromatin 3D structure of budding yeast, which was then applied to fission yeast with some modifications (14). Kalhor et al. (8) developed another kind of optimization-based approach to predict the population of chromatin structures. More recently, a Bayesian framework was raised to infer the chromatin spatial organization and evaluate the structural variations (12).

However, the wide use of these methods is limited by the sequencing biases of Hi-C derived data. First, it is pointed out that the raw Hi-C chromatin interactions have systematic biases resulted from experiment, such as restriction enzymes, GC content and sequence uniqueness (17). The current bias reduction and 3D modeling schemes only focus on the sequencing bias within the same experiment caused by differences in enzyme efficiency and sequence coverage for different chromatin regions (5,8,17–19) but neglect the bias arising from another important factor, experimental sequencing depth. Our following work will show that experimental sequencing depth can significantly change the distribution of the observed chromatin interaction frequency, which is tightly coupled with the recognized bias for chromatin regions. Therefore, the chromatin 3D structures modeled through conventional methods cannot be reasonably compared among different experiments. Second, a lot of modeling approaches are performed at megabase resolution because it is difficult to reduce systematic bias at higher resolution. It is known that functional structural rearrangement often occur in genomic sizes ranging from hundreds of kilobases to megabases (20). Thus, the low-resolution modeling can only provide information on global chromatin structure but prevent its application for investigating 3D structure of functional chromatin regions.

These concerns stimulated our interest to propose a novel strategy to reduce sequencing-dependent biases by normalizing Hi-C data with the inherent characteristics of chromatin interactions. We identified a sequencing-bias-relaxed parameter, which can represent regional chromatin structure at multi-scale genomic resolution, and used it to establish an approach for chromatin 3D modeling. As a consequence, this method not only allows the comparisons among chromatin structures derived from different chromatin regions and experiments but also can be automatically executed at high resolution. To our knowledge, this is the first approach devoted to automatic chromatin 3D modeling for structural comparison. Considering that most researchers focus their studies on specific chromatin regions, the automatic pipeline (AutoChrom3D) in this article was used to model chromatin regions with genomic size ranging from hundreds of kilobases to megabases at 8 kb resolution. However, the structure of chromatin region with larger size can also be modeled at lower resolution by using this method.

MATERIALS AND METHODS

Data sources and processing

The Hi-C derived chromatin interactions for human cell lines K562 and GM12878 were generated by Liebeman-Aiden et al. (5) and Kalhor et al., respectively (8), and the human cell lines IMR90 and H1hESC were generated by Dixon et al. (9). The ChIP-Seq libraries for cell line IMR90 were generated by Hawkins et al. (21), and other RNA-Seq, ChIP-Seq and DNase-Seq libraries were downloaded from ENCODE (22). Hi-C raw data processing refers to the previous pipeline (8), and main steps are briefly introduced here. It is known that the pair-end sequencing can surpass the ligation junction in some reads (8). To improve the mappability of this part of reads, all reads are scanned to identify the existence of potential ligation junctions for the expected sequence ‘AAGCTAGCTT’ from HindIII libraries, and then the junction and all bases after the 3′ of the junction are removed. The kept reads are then aligned to the reference human genome hg19 by using bwa-0.6.1-r104 with default settings. Only the uniquely mapped paired-reads (mapping quality > 30 for both reads) are selected for the next processing. The pairs that originated from PCR duplication are removed, and the pairs without enzyme restriction site after the downstream 500 bp is also removed to exclude incomplete exonuclease action. Finally, all pairs aligned <10 000 bp are considered as self-ligation and further eliminated from data set. The detailed information on the read number of each library can be found in Supplementary Table S1.

Chromatin representation

Chromatin is represented by the bead-on-a-string model, in which a bead consists of one or several consecutive fragments digested by restriction enzyme (HindIII). The chromatin is represented as consecutive beads, where is the genomic length of investigated chromatin region and is the chromatin resolution. Beads are carefully fitted to the required resolution by considering the fragment length distribution. The interaction frequency map is defined as an matrix, , and the entry is the observed interaction frequency between beads and . Without specific explanation, the following calculations are based on the selected chromatin regions.

Structure parameter determination

At the given resolution and genomic distance , chromatin interaction frequencies are averaged by , where and represent and beads in the chromatin region respectively, and is the total number of bead pairs satisfying . The exponent parameter is calculated as the derivative of against . Only bead pairs within are used in our calculation because fluctuates greatly outside this genomic distance for many functional regions. The structure compaction of a given chromatin region is defined as the normalized exponent parameter:

where and are the derivatives calculated from chromatin region and whole genome, respectively. Chromatin interaction coverage is derived from chromatin structure compaction with modifications:

where coverage varies from 0 to 1. Only chromatin regions with coverage higher than 5% were used in data analysis and structure modeling in this work.

Data evaluation and filtering

The probability of observing the interaction frequency for bead pair that satisfies is modeled using the Poisson model, where the parameter can be estimated from the interaction set by maximum likelihood. We treat every with specific genomic distance as an independent Poisson model to reduce the impact of genomic distance on the observed interaction frequency. Then the interaction frequency between beads and is evaluated by a P-value, which is used to filter unreliable interactions. These selected chromatin interactions are used in subsequent calculations.

Interaction strength recalculation

The range of interaction frequencies at high resolution is limited, but the interactions with the same frequency can be surrounded by totally different neighbor interactions (Supplementary Figure S1). The square window is used to calculate the density of neighbor interactions as following equation: , where , is the interaction density of the square window centered at , and is the window size (set to 5 in this work). Parameter denotes the random variable for the set , and only interaction sets for are used in next calculations. The interaction strength is recalculated through linear transformation: , where is a parameter, which is proportional to the bead radius. The standard deviation of decreases with increasing to narrow the change in stronger interaction frequency . Then every interaction strength can be recalculated by using the aforementioned calculation for existing . To further eliminate outliers, the top 5% calibrated interaction frequencies are set to the maximum threshold of the rest ones, whereas the bottom 5% interaction frequencies are removed.

Spatial distance conversion and normalization

The flexibility of chromatin region is considered by following the method proposed by Kalhor et al. (8). The radius of the region is defined in the following formula according to geometry: , where and are the genomic lengths of the modeled region and the whole genome, respectively, and the nuclear radius is set to 3.5 based on prior knowledge (23). The nuclear occupancy varies from to , defining the regional flexibility range from to . Correspondingly, the diameter of flexible bead ranges from to where is the bead resolution. The minimum and maximum values of nuclear occupancy are set to be and by following the published data (24). Different values of nuclear occupancy are used to reconstruct chromatin structures to evaluate their potential impact (Supplementary Table S2). The maximum value of nuclear occupancy does not change the modeling a lot, whereas the increase of minimum nuclear occupancy makes the predicted structures bigger in overall. However, there is no significant change of the relative structural openness among different parameter values as shown by Pearson correlation coefficient, indicating that the selection of these parameter would not change the conclusions.

To normalize the disparate data sets into unified input to chromatin structure predictor, the piecewise linear function based on the characteristics of chromatin interaction are used in the spatial distance conversion. It is known that interaction frequency decreases when genomic distance increases (5,11). Our calculation shows that in all experimental data sets, the genomic distances can be generally separated into three parts according to the decrease patterns (Supplementary Figure S2). Although the genomic sizes 160 kb and 1.2 Mb are just simple estimates in this separation, this result is well consistent with the hierarchical organization of chromatin structures, in which genomic size 1.2 Mb coincides with the size of topology-associated domains and 160 kb coincides with the size of sub-domains (9,15). The piecewise function is used to distinguish these parts in spatial distance conversion. Together with the aforementioned chromatin structure compaction and region radius, the interaction strength is converted to spatial distance by using two linear transformations determined by three points: , and . The parameters and represent the maximum and minimum (), respectively, and is the corresponding quantile calculated from data set (Supplementary Figure S2). , and are set to , and , respectively (Supplementary Figure S3). The spatial distance for interaction is calculated by using the following equation:

The 3D chromatin structure prediction and measurement

After the spatial distance conversion, the Cartesian coordinates of the investigated chromatin region are solved by a non-linear constrained optimization:

where denotes the Euclidian distance between beads and .

Radius of gyration is used to measure the compaction of chromatin structure: , where denotes the Cartesian coordinates, is the geometric center, and smaller radius of gyration indicates denser chromatin structure.

Sequencing data normalization

To conduct reasonable inter cell-line comparisons for epigenomic signals, the epigenomic signals from different experiments are normalized by following a previous procedure with some modifications (25). To be consistent with our region size, the 500 kb window is used to scan the genome to calculate its average signal strength with 5 kb sliding in each step. The corresponding background and foreground quantiles are used to normalize the experimental data set by using the equation , where is the regional position, and is the averaged signal density of chromatin region from original data set by eliminating no-signal positions. To find the optimal background and foreground , the original signal density 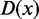is plotted in an ascent order, and the most stably increased part is chosen to perform normalization (Supplementary Figure S4). The raw PolyA+ RNA-Seq signals from whole cell are used for normalization and analysis in the same way as epigenomic signals. In this work, the raw RNA-Seq rather than annotated genes are used, as chromatin 3D structures are more significantly correlated to whole RNA expression.

Region selection and comparison

For intra cell-line comparison, the active and inactive regions with 800 kb genomic size are selected by using DNaseI hypersensitivity sites (DHS) as an indicator (26). These selected active regions show consistently stronger DHS signals than inactive regions in all cell lines (Supplementary Figure S5). Pearson correlation is performed to investigate the relationship between radius of gyration and epigenomic signal for every cell line.

For every two cell-line comparison, 20 chromatin regions with considerable structural differences are selected based on the criterion that the value of chromatin structure compaction in one cell line is significantly larger than that in another cell line (Supplementary Figure S6). Finally, 120 chromatin regions are randomly selected to perform inter cell-line comparison for all cell-line pairs. The 500 kb genomic size domains are selected here because most epigenetic domains are smaller than ∼200 kb in genomic size (20), which makes the inter cell-line comparison a little more sensitive to genomic size than intra cell-line comparison. However, we also performed inter cell-line comparisons on 800 kb domains, and the results are largely consistent (see ‘Results and Discussion’ section). In the two cell-line comparison, if the regional epigenomic signal and radius of gyration are both larger or smaller in one cell line than that in another cell line, this region is considered to be positively correlated one. Otherwise, they are considered to be negatively correlated one. The numbers of positively correlated regions () and negatively correlated regions () are then used to calculate the significance by , where varies from −1 to 1.

RESULTS AND DISCUSSION

Dependence of regional interaction bias on sequencing depth in Hi-C derived data

Four human cell lines with considerably different Hi-C sequencing depths K562 (5), GM12878 (8), IMR90 and H1hESC (9) were selected to explore the impact of sequencing depth on regional bias, based on the finding that the topological domains are stable among different cell lines in mammalian species (9). To conduct a more strict comparison by eliminating potential structural variations among different cell lines, available biological replicates in cell lines IMR90 and H1hESC, denoted as IMR90-R1, IMR90-R2, H1hESC-R1 and H1hESC-R2, respectively, were used in the comparison. Because the sequencing depths of replicates in the cell line K562 is extremely low, the biological replicates were merged for analysis in this experiment. In the cell line GM12878, there are only technical but not biological replicates. However, there exist two independent Hi-C derived experiments on this cell line from a previous study (8). The two experiments were performed by two related but different technologies: classical Hi-C and tethered Hi-C (called TCC). It is reported that TCC can reduce noises on Hi-C, especially the noises on the inter-chromosomal interactions (8). Though different technologies can generate potential sequencing differences, it is not likely that the noise-reduction in TCC will significantly influence our analysis and modeling as only intra-chromosomal interactions are used in our analysis on selected chromatin regions. Without specificity, GM12878-T and GM12878-H are used to represent the experiments with higher and lower sequencing depths, respectively, in this work.

First, typical chromatin regions were randomly selected in four cell lines to perform interaction frequency comparison by using DHS as indicator (Supplementary Table S3). Though the detailed DHS distribution can change in different cell lines, the statistical test shows that the selected DHS-rich chromatin regions exhibit significantly stronger signals than DHS-poor chromatin regions in all four cell lines (Supplementary Figure S5). These regions were further identified as either active or inactive by using epigenomic signals because the genome has a tendency to cluster into active and inactive regions (20). Figure 1a illustrates that the sequencing bias for chromatin regions is tightly coupled with that from sequencing depth. In the cell line H1hESC, there is no statistical difference in interaction frequency between active and inactive regions in the lower sequencing-depth biological replicate, but significant difference is observed in the higher sequencing-depth biological replicate. As for the cell line IMR90, it is the higher sequencing-depth biological replicate showing no significant interaction frequency change between two sets of regions, whereas lower sequencing-depth replicate shows significant difference. The exactly same situation to IMR90 is observed in the two independent experiments on the same cell line GM12878. The reversal trend occurs in the cell line H1hESC, with the interaction frequency of inactive regions being significantly higher than the frequency of active regions (Figure 1a).

Figure 1.

Statistical analysis of chromatin structure parameter on different regional and experimental Hi-C data sets (*P < 0.05, **P < 0.01, ***P < 0.001). (a) Statistics of the distribution of averaged interaction frequency in different regional and experimental data sets. In all, 31 active and 31 inactive regions were randomly selected in seven Hi-C experiments from four human cell lines K562, GM12878, IMR90 and H1hESC, with the genomic size of 800 kb. The relative values between active and inactive regions change significantly in different experiments, showing that the sequencing depth greatly affects the relative values of averaged interaction frequency between active and inactive regions. (b) Statistics of the distribution of regional exponent parameter. The exponent parameter can well distinguish the structure compaction of active regions from inactive regions. However, the absolute values of this parameter change among different experiments. (c) Box plot of the distribution of the normalized exponent parameter. Except for the higher value in active regions compared with inactive regions, the normalized parameter smoothes the original difference in Figure 1b, which makes chromatin region compaction comparable among different experiments.

We next partitioned whole genome into chromatin regions with 800 kb for each one, which was used to evaluate the impact of sequencing depth on interaction frequency in a genome-wide scale. To reduce the impact of chromatin structural stochasticity, only the chromatin regions with enough interaction coverage were considered to be stable ones since these regions generally show higher percentage of reproducible chromatin interactions (Supplementary Figure S7). Finally, 1923 regions were selected for subsequent analysis. Then all partitioned chromatin regions were sorted in an ascent/descent order according to their averaged interaction frequencies, and Spearman correlation was used to define to what extent the position order of chromatin region can change when sequencing depth changes (Table 1). The low correlation, especially between cell lines, indicates that chromatin interaction frequencies undergo dramatic position changes among different experiments when sequencing depth changes, consistent with the comparison of active and inactive regions mentioned above. These results together provide the evidence of the dependence of regional interaction bias on sequencing depth.

Table 1.

Statistical analysis of the influence of sequencing depth on averaged interaction frequency and regional exponent parameter

	H1hESC-R1	H1hESC-R2	IMR90-R1	IMR90-R2	GM12878-T	GM12878-H	K562
H1hESC-R1		0.85, 0.9(*)	0.56, 0.78(***)	0.57, 0.79(***)	0.87, 0.67(***)	0.4, 0.52(*)	0.31, 0.48(**)
H1hESC-R2	0.85, 0.9(*)		0.53, 0.85(***)	0.38, 0.85(***)	0.7, 0.71	0.05, 0.55(***)	0.13, 0.51(***)
IMR90-R1	0.56, 0.78(***)	0.53, 0.85(***)		0.9, 0.96(***)	0.51, 0.7(**)	0.27, 0.57(***)	0.3, 0.5(**)
IMR90-R2	0.57, 0.79(***)	0.38, 0.85(***)	0.9, 0.96(***)		0.58, 0.7(**)	0.56, 0.56	0.38, 0.5(*)
GM12878-T	0.87, 0.67(***)	0.7, 0.71	0.51, 0.7(**)	0.58, 0.7(**)		0.56, 0.67(*)	0.35, 0.51(**)
GM12878-H	0.4, 0.52(*)	0.05, 0.55(***)	0.27, 0.57(***)	0.56, 0.56	0.56, 0.67(*)		0.41, 0.42
K562	0.31, 0.48(**)	0.13, 0.51(***)	0.3, 0.5(**)	0.38, 0.5(*)	0.35, 0.51(**)	0.41, 0.42

The first number is the Spearman correlation coefficient between two Hi-C derived experiments calculated from all 1923 chromatin regions for averaged interaction frequency, and the second number is for regional exponent parameter. The correlation coefficients from 23 individual chromosomes are used to test the difference between the first and the second numbers (*P < 0.05, **P < 0.01, ***P < 0.001).

Sequencing-bias-relaxed parameter for chromatin structure modeling

The difficulty of normalizing Hi-C derived data sets from disparate regions and experiments lies in selecting an inherent chromatin structure parameter independent of sequencing biases. To address this challenge, we analyzed the local dependence between interaction frequency and genomic distance. Previous genome-wide analyses (5,7,11) on Hi-C data have shown that the chromatin interaction frequency is inversely proportional to genomic distance by following the power–law relationship, where the exponent parameter represents the global chromosome structure property. Here, we further showed that the power–law relationship remains consistent for different regional and experimental data sets by reanalyzing the aforementioned chromatin regions (Supplementary Table S3). As shown in Figure 1b, the regional exponent parameter can well distinguish active from inactive regions in every independent experiment. We performed Spearman correlation analysis again on this regional exponent parameter as we did on interaction frequency. Our results show that this parameter is much more stable in position order under different experimental sequencing depth (Table 1). For the biological replicates in the same cell line, the regional exponent correlations significantly improve from 0.85 to 0.9 for H1hESC and 0.9 to 0.96 for IMR90, compared with the interaction frequency correlation. More dramatic changes are observed in the inter cell-line comparisons. Most inter cell-line correlations from interaction frequency are below 0.4, even smaller than 0.2 in some cases, whereas the correlations from regional exponent are above 0.5 in almost all cases. All these results imply that this regional exponent can be a potential candidate to represent inherent structural characteristics of Hi-C derived data.

Though the regional exponent order largely remains, its absolute value still undergoes significant change when sequencing depth changes (Figure 1b). To make the parameter comparable among different experimental data sets, this regional exponent is normalized by the chromosomal exponent determined by experiment. Our calculation shows that this normalized parameter is comparable among different experiments for both active and inactive regions, with active regions exhibiting statistically higher values (Figure 1c). Altogether, our results argue that this normalized exponent is a sequencing-bias-relaxed parameter of chromatin structure (Supplementary Figure S8).

Pipeline of AutoChrom3D

AutoChrom3D uses this derived structure parameter to normalize chromatin interactions with the attempt of chromatin structure comparison. First, the local structure compaction parameter of chromatin region is computed by using raw data. To reduce the negative effects of noisy and weak interactions on structure prediction, the Poisson model is used to evaluate the credibility of chromatin interactions, and only those interactions that represent most stable structure patterns are selected. Considering that most interaction frequencies are extremely low in some data sets, the square window is used to calibrate interaction strength by taking neighbor interactions into consideration (Supplementary Figure S1). The calibrated interaction strength is then transformed to spatial distance by using the structure compaction parameter to perform normalization. Finally, the normalized spatial distances are used to predict chromatin structure via a nonlinear constrained optimizer (Figure 2). As the chromatin structures reconstructed by our approach capture the structural characteristics by relaxing the coupled sequencing biases, they can be used for both intra and inter cell-line structural comparison.

Figure 2.

The pipeline of AutoChrom3D.

Method validation and application

To verify the applicability of AutoChrom3D, the four human cell lines mentioned earlier in the text, K562, GM12878, IMR90 and H1hESC were selected for subsequent statistical analysis. Different biological replicates in the same cell line were merged, and GM12878-T was used in structural analysis. Radius of gyration was used to measure the compaction of modeled chromatin structure. To investigate the relationship between chromatin 3D structure and epigenetic state, seven epigenetic markers available for all cell lines, H3K4me1, H3K4me3, H3K9ac, H3K27me3, H3K9me3, H3K36me3 and K3K79me2, were used to represent different chromatin states and functions. In these epigenetic markers, H3K4me1 and H3K4me3 represent the enhancer and promoter signals, respectively, and H3K9ac generally occur concomitantly with these two signals, reflecting that the enhancer and promoter are active or not. H3K27me3 is the polycomb signal, H3K9me3 is a heterochromatin signal, and H3K36me3 and H3K79me2 are two markers to reflect transcription activity (27,28). Two additional signals are included in the analysis: GC-content and RNA-Seq, in which GC-content represents the overall gene density of chromatin region and RNA-Seq directly shows the transcription level.

We first applied AutoChrom3D to perform intra cell-line structural analysis. Fluorescence in situ hybridization (FISH) experiment (29) has shown that the active regions are more open than the inactive regions by using chromatin areas ranged from several megabases to tens of megabases in human primary female fibroblast, which was verified by several other cell lines (30). We grouped these active and inactive FISH regions into 1 Mb chromatin regions (Supplementary Table S4) and reconstructed 3D chromatin structures for each one. Figure 3a illustrates the structures predicted by AutoChrom3D for one region from these FISH areas. The two structures well capture the structural difference between the two regions, with the radius of gyration of the active region significantly larger than that of the inactive region (0.176 µm versus 0.138 µm). Calculations from other cell lines show the similar results (Supplementary Figure S9). Our statistical analysis on these FISH regions shows that the active regions generally exhibit higher spatial distance than inactive regions in four cell lines (Figure 3b and Supplementary Figure S10), consistent with previous FISH experiments (29,30).

Figure 3.

Intra cell-line chromatin 3D structure comparisons. (a) The 3D structures of active region (Chr11: 60 150 000–61 150 000) and inactive region (Chr11: 84 195 021–85 195 021) predicted from the cell line IMR90 at 8 kb resolution, and the corresponding genomic/epigenomic signals. The top and bottom panels show the genomic/epigenomic signals for active and inactive regions respectively. (b) Averaged spatial distances of FISH active and inactive chromatin regions from the cell line IMR90. (c) Box plot showing the statistically larger radius of gyration in active regions compared with inactive regions. (d) Pearson correlation between radius of gyration and genomic/epigenomic signals for four cell lines.

To further compare the active and inactive chromatin regions in 3D structure, the aforementioned active and inactive chromatin regions (Supplementary Table S3) were used for 3D structure modeling and comparison. It can be seen that the 3D structures of active chromatin regions are statistically more open than those of inactive regions (Figure 3c). To investigate the relationship between chromatin structure and state, Pearson correlation between radius of gyration and every selected chromatin state marker was calculated on these selected chromatin regions for all cell lines. As shown in Figure 3d, GC-content is positively correlated to radius of gyration, implying that gene-dense chromatin regions are generally more open in 3D space than gene-poor regions. Correspondingly, the active signals (H3K4me1, H3K4me3 and H3K9ac), the transcription signals (H3K36me3, H3K79me2 and RNA-Seq) and even the polycomb signal H3K27me3 also show strong positive correlations to radius of gyration. It is not surprising to observe the positive correlation for H3K27me3, as previous studies have already shown that H3K27me3 is closely associated with high CpG density (28,31). Contrary to those signals, heterochromatin signal H3K9me3 is negatively correlated to radius of gyration in overall, with the exceptions indicating the complicated situations in biological system.

We next applied AutoChrom3D to perform inter cell-line structural analysis. To our knowledge, a previous 5C work (32) on human functional domain α-Globin in cell lines K562 and GM12878 is the only study on modeling chromatin 3D structures for inter cell-line comparison. Figure 4 illustrates the chromatin structures predicted from our method. Our work is highly consistent with the previous 5C work, with the cell line K562 exhibiting more open chromatin structure and stronger active signals than GM12878 (0.117 µm versus 0.105 µm). However, the structures from our method are considerably more compacted than those in the 5C work, especially in K562. This is because Hi-C captures whole-genome chromatin interactions, but the number of detectable interactions in 5C depends on the designed probes. This difference also implies the potential and advantage of Hi-C data in regional chromatin 3D modeling.

Figure 4.

Inter cell-line chromatin 3D structure comparisons. The chromatin 3D structures of human α-Globin domain (Chr16: 60 002–559 999) are modeled at 8 kb resolution for cell lines K562 and GM12878, and the corresponding genomic/epigenomic signals are shown.

To statistically compare the differences in regional structure and activity among different cell lines, 120 chromatin regions with considerable structural differences were selected to conduct comparisons for every two cell lines (Supplementary Table S5). GC-content is eliminated from inter cell-line comparison because the four cell lines do not differ in GC-content for the same chromatin region. It can be seen that the cell line with stronger active signals (H3K4me1, H3K4me3 and H3K9ac) and transcription signals (H3K36me3 and RNA-Seq) statistically exhibits more open chromatin 3D structure than the cell line with weaker signals (Figure 5 and Supplementary Figure S11). By contrast, heterochromatin signal H3K9me3 mainly show negative relationship to the openness of chromatin structure in almost all inter cell-line comparisons. The situation for polycomb signal H3K27me3 is a little more complicated, with negative correlation to chromatin structural openness in some cases but not in other cases. Some minor exceptions can be observed not only because of the complication of biological systems but also because of the difficulty in finding the best way to normalize different kind of sequencing data among different cell lines. In overall, these results are highly consistent with the intra cell-line analysis.

Figure 5.

Statistical analysis on the relationship between chromatin epigenetic state change and 3D structural rearrangement.

Our comparative analyses partly reveal the relationship between chromatin 3D structure and functional state. The results from intra cell-line comparisons actually show that gene-rich chromatin regions are generally more open in 3D structure than gene-poor regions (33). As gene-rich chromatin regions have more regulatory elements, such as enhancer and promoter, these regions often show stronger active signals (H3K4me1, H3K4me3 and H3K9ac), transcription signals (H3K36me3, H3K79me2 and RNA-Seq) and even CpG-associated repressed signal H3K27me3. By contrast, the gene-poor regions are generally heterochromatin regions, showing stronger H3K9me3 signal. The inter cell-line comparisons provide some insights on the relationship between chromatin epigenetic state change and 3D structural rearrangement (34,35). The active signals H3K4me1, H3K4me3 and H3K9ac show that the activation of chromatin epigenetic state is significantly associated with the opening of chromatin 3D structure, accompanied by stronger transcription signals H3K36me3 and RNA-Seq, whereas the inactivation marked by H3K9me3 is often associated with the chromatin structure closing. The silencing marked by H3K27me3 is also related to the structure closing, but the situation is a little complicated in this signal partly due to its diverse distribution patterns in chromatin regions. The negative correlation of H3K27me3 in inter cell-line comparison does not mean inconsistence with the positive correlation in intra cell-line comparison, as the comparison of structural rearrangement for same chromatin region is totally different from comparison of different kinds of chromatin regions.

CONCLUSION

In this work, we show that the bias of chromatin interaction is significantly dependent on sequencing depth, and the normalized regional exponent can relax the coupled sequencing biases and represent the inherent characteristics of chromatin structure. We then propose a method to automatically reconstruct chromatin structures by using this sequencing-bias-relaxed structure parameter to normalize chromatin interactions. Together with 1D genomic and epigenomic data, this method can powerfully interpret the relationship between 3D chromatin structures and genome functions through intra and/or inter cell-line comparisons. However, it should bear in mind that as a first effort devoted to automatic chromatin 3D modeling for structural comparison, there is ample space to improve the modeling method to give more accurate 3D chromatin structures.

All predicted chromatin structures in this work, the source code and web service of this method are available at http://ibi.hzau.edu.cn/3dmodel/.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Funding for open access charge: National Natural Science Foundation of China [31200951]; National Basic Research Program of China [973 project, 2012CB721000]; the Fundamental Research Funds for the Central Universities [2011PY142, 2011PY027 and 2013SC02].

Conflict of interest statement. None declared.