Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2013 Aug 27;29(21):2722–2728. doi: 10.1093/bioinformatics/btt473

lDDT: a local superposition-free score for comparing protein structures and models using distance difference tests

Valerio Mariani 1,2,†, Marco Biasini 1,2,†, Alessandro Barbato 1,2, Torsten Schwede 1,2,*
PMCID: PMC3799472  PMID: 23986568

Abstract

Motivation: The assessment of protein structure prediction techniques requires objective criteria to measure the similarity between a computational model and the experimentally determined reference structure. Conventional similarity measures based on a global superposition of carbon α atoms are strongly influenced by domain motions and do not assess the accuracy of local atomic details in the model.

Results: The Local Distance Difference Test (lDDT) is a superposition-free score that evaluates local distance differences of all atoms in a model, including validation of stereochemical plausibility. The reference can be a single structure, or an ensemble of equivalent structures. We demonstrate that lDDT is well suited to assess local model quality, even in the presence of domain movements, while maintaining good correlation with global measures. These properties make lDDT a robust tool for the automated assessment of structure prediction servers without manual intervention.

Availability and implementation: Source code, binaries for Linux and MacOSX, and an interactive web server are available at http://swissmodel.expasy.org/lddt

Contact: torsten.schwede@unibas.ch

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The knowledge of a protein’s 3D structure enables a wide spectrum of techniques in molecular biology, ranging from rational design of mutagenesis experiments for the elucidation of a protein’s function to drug design. While the rapid development of DNA sequencing techniques has been providing researchers with a wealth of genomic data, experimental structure determination techniques require substantially more effort, and consequently the gap between the number of known protein sequences and the number of known protein structures has been growing continuously. To fill this gap, various computational approaches have been developed to predict a protein’s structure starting from its amino-acid sequence (Guex et al., 2009; Moult, 2005; Schwede et al., 2009). Despite remarkable progress in structure prediction methods, computational models often fall short in accuracy compared with experimental structures. The biannual CASP experiment (Critical Assessment of techniques for protein Structure Prediction) provides an independent blind retrospective assessment of the performance of different modeling methods based on the same set of target proteins (Moult et al., 2011).

One of the main challenges for the CASP assessors is to define appropriate numerical measures to quantify the accuracy with which a prediction approximates the experimentally determined structure. In the course of the CASP experiment, model comparison techniques have evolved to reflect the current state of the art of prediction techniques: In the first installments of CASP, root-mean-square deviation (RMSD) between a prediction and the superposed reference structures was used in various forms as the main evaluation criterion (Hubbard, 1999; Jones and Kleywegt, 1999; Martin et al., 1997; Mosimann et al., 1995). However, RMSD has several characteristics that limit its usefulness for structure prediction assessment: the score is dominated by outliers in poorly predicted regions while at the same time it is insensitive to missing parts of the model, and it strongly depends on the superposition of the model with the reference structure.

To overcome some of the limitations of RMSD in the context of CASP, the Global Distance Test (GDT) was introduced in CASP4 (Zemla, 2003; Zemla et al., 2001). In contrast to RMSD, the GDT is an agreement-based measure, quantifying the number of corresponding atoms in the model that can be superposed within a set of predefined tolerance thresholds to the reference structure. For each threshold, different superpositions are evaluated and the one giving the highest number is selected. The final GDT score is then calculated as the average fraction of atoms that can be superposed over a set of predefined thresholds (0.5, 1, 2 and 4 Å for GDT-HA and 1, 2, 4 and 8 Å for GDT-TS, respectively). One of the advantages of GDT is that strongly deviating atoms do not considerably influence the score. At the same time, missing segments in the predictions lead to lower scores. Besides GDT, several other scores for model comparison have been developed to overcome the limitations of RMSD (Olechnovic et al., 2013; Siew et al., 2000; Sippl, 2008; Zhang and Skolnick, 2004).

One of the main limitations of measures based on global superposition becomes evident when applied to flexible proteins composed of several domains, which can change their relative orientation naturally with respect to each other (Fig. 1). Typically in those cases, the global rigid-body superposition is dominated by the largest domain, and as a consequence, the smaller domains are not correctly matched, resulting in artificially unfavorable scores. In CASP, the effects of domain movement are reduced by splitting the target into the so-called assessment units (AUs), that are evaluated separately. The definition of AUs is carried out by visual inspection, and is therefore time-consuming. Furthermore, the criteria used to define the AU are often subjective (Clarke, et al., 2007; Kinch et al., 2011). Grishin et al. have proposed an approach to numerically support this decision by analyzing the variability among the predictions for a specific target (Kinch et al., 2011).

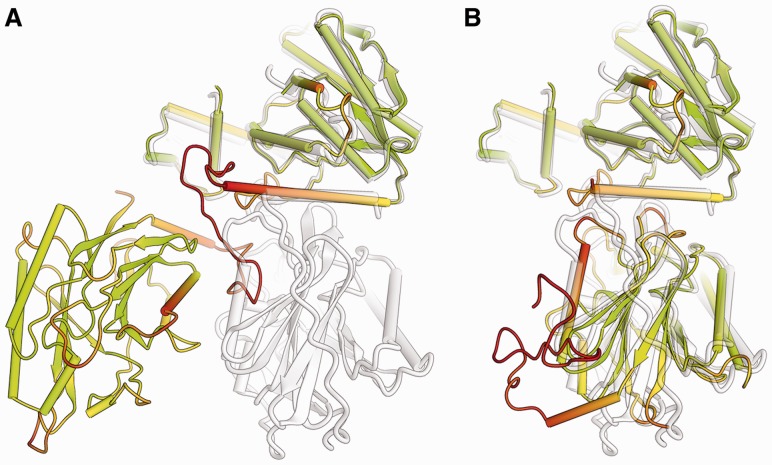
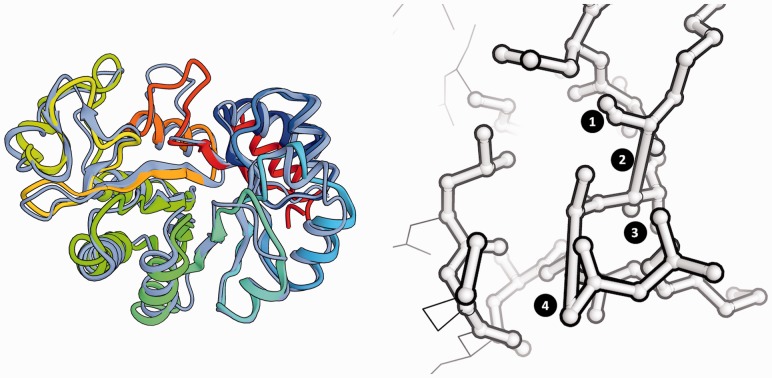
Fig. 1.

Fig. 1.

Open in a new tab

Comparison of predicted protein structure model with its reference structure for CASP target T0542. The target structure (shown in gray) consists of two domains. In (A), a predicted model (TS236, in color) is shown in full length, with the first domain superposed to the target. For graphical illustration, (B) shows the two domains in the prediction separated according to CASP AUs and superposed individually to the target structure. In both panels, the model is colored according to full-length lDDT scores following a traffic-light-like red-yellow-green gradient, with red corresponding to low values of the lDDT, green to high values and yellow to average values. As superposition-free method, lDDT is insensitive to relative domain orientation and correctly identifies segments in the full-length model deviating from the reference structure

Local superposition-free measures based on rotation-invariant properties of a structure are an attractive alternative to overcome several of the shortcomings outlined before. For example, dRMSD—the distance-based equivalent of RMSD—is used in chemoinformatics to assess differences in ligand poses in binding sites (Bordogna et al., 2011). In CASP9, the local Distance Difference Test (lDDT) score was introduced, assessing how well local atomic interactions in the reference protein structure are reproduced in the prediction (Mariani et al., 2011). More recently, other non–superposition-based scores have been proposed, e.g. CAD score based on residue–residue contact areas (Olechnovic et al., 2013), measures using residue contact similarity (Rodrigues et al., 2012) or the recall, precision, F-measure (RPF)/DP score, which was initially developed to evaluate the quality of nuclear magnetic resonance (NMR) structures (Huang et al., 2012). Also, the SphereGrinder score (Kryshtafovych et al., 2013) was used for the assessment of local accuracy of refinement targets in CASP9 (MacCallum et al., 2011).

Initially, most of the scores used in structure prediction assessment aimed at the evaluation of the protein backbone or fold, thereby focusing on carbon α (Cα) atom positions. However, with increasing accuracy of prediction methods for template-based models, the focus of the assessment has shifted to the evaluation of the atomic details of a model. In CASP7, the first scores based on local atomic interactions were introduced in the form of HBscore, which quantifies the fraction of hydrogen bond interactions in the target protein correctly reproduced in the model (Battey et al., 2007; Kopp et al., 2007). In CASP8, several scores for assessing the local modeling quality were introduced (main chain reality score, hydrogen bond correctness, rotamer correctness and side-chain positioning) (Keedy et al., 2009), as well as an evaluation of the stereochemical realism and plausibility of models using the MolProbity score (Chen et al., 2010).

In this article, we expand the initial concept of lDDT. Because the lDDT score considers all atoms of a prediction including all side-chain atoms, it is able to capture the accuracy of, e.g. the local geometry in a binding site, or the correct packing of a protein’s core. We discuss its properties with respect to its low sensitivity to domain movements, and the significance that can be assigned to the absolute score values. Furthermore, we introduce the concept of using multiple reference structures simultaneously, and incorporate stereochemical quality checks in its calculation. We finally illustrate how lDDT can be used to highlight regions of low model quality, even in models of multi-domain proteins where domain movements are present.

2 METHODS

2.1 The lDDT

lDDT measures how well the environment in a reference structure is reproduced in a protein model. It is computed over all pairs of atoms in the reference structure at a distance closer than a predefined threshold Ro (called inclusion radius), and not belonging to the same residue. These atom pairs define a set of local distances L. A distance is considered preserved in the model M if it is, within a certain tolerance threshold, the same as the corresponding distance in 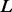Inline graphic. If one or both the atoms defining a distance in the set are not present in M, the distance is considered non-preserved. For a given threshold, the fraction of preserved distances is calculated. The final lDDT score is the average of four fractions computed using the thresholds 0.5 Å, 1 Å, 2 Å and 4 Å, the same ones used to compute the GDT-HA score (Battey et al., 2007). For partially symmetric residues, where the naming of chemically equivalent atoms can be ambiguous (glutamic acid, aspartic acid, valine, tyrosine, leucine, phenylalaine and arginine), two lDDTs, one for each of the two possible naming schemes, are computed using all non-ambiguous atoms in M in the reference. The naming convention giving the higher score in each case is used for the calculation of the final structure-wide lDDT score.

The lDDT score can be computed using all atoms in the prediction (the default choice), but also using only distances between Cα atoms, or between backbone atoms. Interactions between adjacent residues can be excluded by specifying a minimum sequence separation parameter. Unless explicitly specified, the calculation of the lDDT scores for all experiments described in this article has been performed using default parameters, i.e. Ro = 15 Å, using all atoms at zero sequence separation.

2.2 Multireference lDDT

The lDDT can be computed simultaneously against multiple reference structures of the same protein at the same time. The set of reference distances L includes all pairs of corresponding atoms, which, in all reference structures, lie at a distance closer than the reference threshold Ro. For each atom pair, the minimum and the maximum distances observed across all the reference structures are compared with the distance between the corresponding atoms in the model M being evaluated. The distance is considered preserved if it falls within the interval defined by the minimum and the maximum reference distances or if it lies outside of the interval by less than the predefined length threshold. The fraction of preserved distances is computed like in the single reference case.

2.3 Stereochemical quality checks

To account for stereochemical quality and physical plausibility of the model being evaluated, the calculation of the lDDT can take violations of structure quality parameters into account. Here, stereochemical violations in the model are defined as bond lengths and angles with values that diverge from the respective average reference value derived from high-resolution experimental structures (Engh and Huber, 1991, 2006) by more than a predefined number of standard deviations (12σ by default; see Supplementary Material). Interatomic distances between pairs of non-bonded atoms in the model are considered clashing if the distance between them is smaller than the sum of their corresponding atomic van der Waals radii (Allen, 2002), within a predefined tolerance threshold (by default 1.5 Å). Tolerance thresholds can be defined for each pair of atomic elements independently.

In case where the side-chain atoms of a residue show stereochemical violations or steric clashes, all distances that include any side-chain atom of this residue are considered as not preserved for the lDDT calculation. In case the back-bone atoms are involved in stereochemical violations or steric clashes, all distances that include any atom of the residue are treated as not preserved.

2.4 Determination of the optimal inclusion radius Ro

To determine the optimum value of the inclusion radius parameter Ro for lDDT, an analysis of predictions of all multidomain targets evaluated during the CASP9 experiment (Kinch et al., 2011; Mariani et al., 2011) was carried out (see Supplementary Table S1 for a complete list). GDC-all scores for predictions covering >50% of the target protein sequence were computed based on the AUs definitions by the CASP9 assessors (Kinch et al., 2011). A weighted whole target GDC-all score was computed for each target as the average GDC-all scores of its AUs weighted by the AU size. GDC-all scores are an all-atom version of GDT with thresholds from 0.5 to 10 in steps of 0.5 Å. GDC-all scores were computed using LGA version 5/2009 (Zemla, 2003), using a 4Å cut-off for the sequence-dependent superposition.

lDDT scores were calculated for the whole targets by including all residues that are covered by any AU, and in an AU-based form using the same weighting scheme already applied to GDC-all scores. The inclusion radius parameter was varied in the range from 2 to 40 Å, and the correlation R2 score between the distribution of weighted averaged GDC-all scores and the distribution of lDDT scores was computed and plotted against the value of the inclusion radius (Figs. 2 and 3).

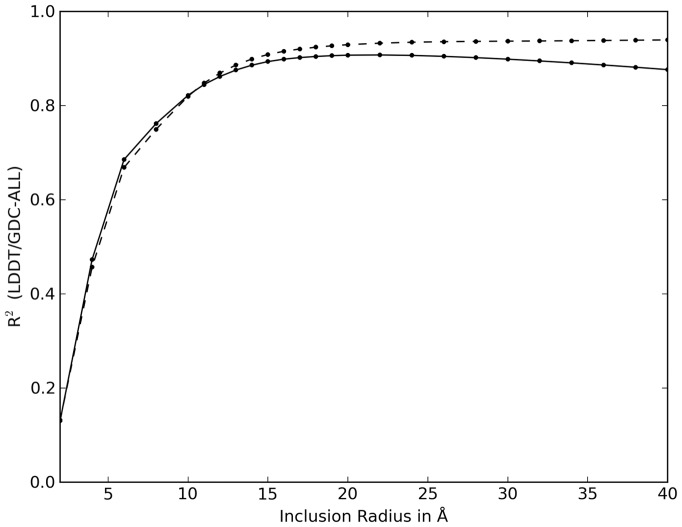
Fig. 2.

Fig. 2.

Open in a new tab

Determination of the optimal inclusion radius parameter Ro. Pearson correlation (R2) between whole target lDDT scores (solid line) and domain-based weight-averaged lDDT score (dashed line) versus domain-based weight-averaged GDC-all scores for different values of the inclusion radius parameter Ro were computed over all CASP9 predictions for multidomain targets

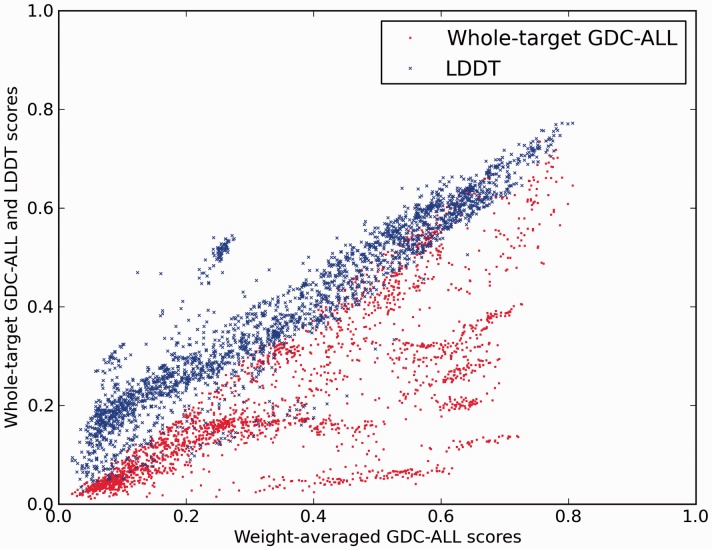
Fig. 3.

Fig. 3.

Open in a new tab

Correlation between whole structure GDC-all and lDDT scores and domain-based weight-averaged GDC-all scores. For CASP9 predictions of multidomain targets, GDC-all scores (red dots) and lDDT scores (blue dots) were computed against the whole unsplit target structures. For the lDDT scores, the default value of 15 Å for the inclusion radius was used

2.5 Validation of baseline scores for different folds

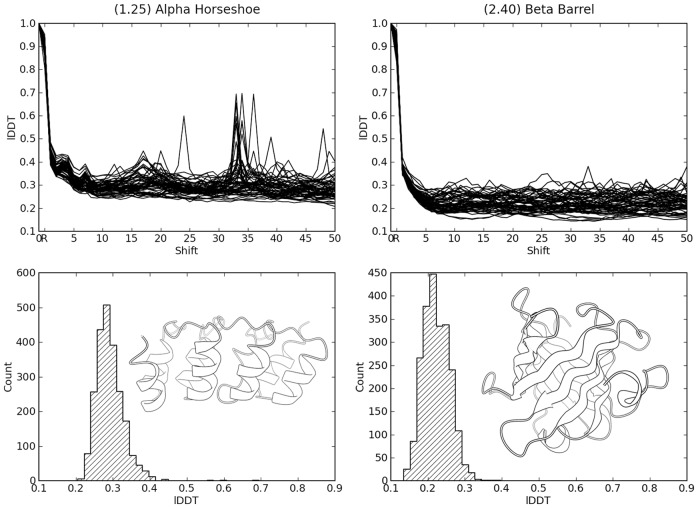
To analyze the influence of the protein fold of the assessed structure on the lDDT score, pseudorandom models were created for different architectures in the CATH Protein Structure Classification system (Cuff et al., 2011) using the following procedure: representative domains longer than 50 residues were selected as evenly as possible among the topologies of the CATH classification. For each domain, side-chain coordinates were removed and then rebuilt using the SCWRL software package (with default parameters) (Krivov et al., 2009). Pseudorandom models representing threading errors were then generated by shifting all residues by one alignment position in a backbone-only model, and rebuilding the side-chains with SCWRL4, and computing the corresponding lDDT score. The procedure was repeated iteratively until a threading error of 50 residue positions was reached. This method is loosely based on the approach described in Shi et al. (2009). In Figure 4, we show the results for CATH Architecture entries 1.25 (Alpha Horseshoe) and 2.40 (Beta-barrel), each represented by 60 example structures.

Fig. 4.

Fig. 4.

Open in a new tab

Baseline lDDT scores for models with simulated threading errors. lDDT scores of pseudo-models with threading errors for two examples of different CATH Architectures are shown: Alpha Horseshoe (left) and Beta Barrel (right). The lDDT score is plotted as a function of the introduced threading error (top). The histograms (bottom) show the distribution of these ‘baseline’ scores for threading error offset >15 residues for the two architectures. The structure inlays show an example structure of the respective CATH Architecture. Peaks at large off-sets indicate repetitive structural elements with locally correct arrangement

For estimating lDDT scores of random protein pairs, 200 protein models with wrong fold were generated by selecting pairs of structures with different CATH topologies, generating models by rebuilding side chains on the backbone of the other protein, and computing lDDT scores for these decoy models. The median of the resulting distribution was 0.20, with a 0.04 mean absolute deviation.

2.6 Implementation and availability

lDDT has been implemented using the OpenStructure framework (Biasini et al., 2010). Source code, standalone binaries for Linux and Mac OSX, as well as an interactive web server are available at http://swissmodel.expasy.org/lddt/. The web server has been implemented using the Python Django and JavaScript jQuery frameworks; it supports all the major browsers.

3 RESULTS AND DISCUSSION

We have developed the lDDT as a new superposition-free measure for the evaluation of protein structure models with respect to a reference structure. In the following, we will discuss the choice of the optimal inclusion radius parameter Ro to achieve low sensitivity to domain movements, and analyze baseline scores for lDDT for different fold architectures. We will discuss the application of lDDT for assessing local correctness of models, including stereochemical plausibility. Finally, we will present an approach for assessing a model simultaneously against several reference structures, e.g. a structural ensemble from NMR.

3.1 Optimal choice of the inclusion radius parameter R0 makes lDDT largely insensitive to domain movements

3.1.1 Determination of the optimal inclusion radius

The nature of the lDDT score is ultimately determined by the choice of the inclusion radius parameter Ro. For low values of the inclusion radius, only short-range distances are assessed, and the accuracy of local interactions has a major impact on the final value of the lDDT score. On the other hand, when the value of the inclusion radius parameter is high, the evaluation of long-range atomic interactions gains a bigger contribution in the final score, and the final lDDT score turns into a representation of the global model architecture quality.

For assessing the accuracy of protein models, the inclusion radius should be high enough to give a realistic assessment of the overall quality of the model, but at the same time, the lDDT score should not lose its ability to evaluate the modeling quality of local environments. Especially, scores should not be influenced by changes of domain orientation between the model and the target structures. The optimal value of the inclusion radius parameter Ro has been determined on a dataset comprising all CASP9 predictions for multidomain targets, and the corresponding assignment of AUs as defined by the CASP9 assessors. Weighted GDC-all scores were calculated as weighted averages of the AU-based scores (see Materials and Methods for details). Hence, the weighted GDC-all scores can be considered to be largely devoid of the influence of domain movements. lDDT scores were then computed using both the full target structures and, in a weight-averaged AU-based form, for a range of Ro, values from 1 to 40 Å. For each threshold, we calculated the correlation with the weight-averaged GDC-all scores for the same predictions. We used GDC-all (and not the more common Cα-based GDT) score to compare two all-atoms measures on the same set of data. The results are shown in Figure 2. The conclusions presented in this article, however, also hold when using GDT as reference measure.

For small values of the Ro parameter, the two types of lDDT scores essentially reduce to a contact map overlap measure (Vendruscolo et al., 1999) and the correlation with global scores such as GDC-all is rather low. As the inclusion radius increases, longer-range interactions are being evaluated and the correlation shows a steep increase as the lDDT score starts to reflect the global quality of the model. For large values of Ro, where inter-domain relationships start playing a more significant role and domain movements start to influence the whole-target lDDT score, its correlation begins to decrease slowly. However, the slow decrease in correlation for values of the inclusion radius >24 Å (Fig. 2) shows the stability of the whole-target lDDT score with respect to the influence of domain movements. Even including all inter-atomic distances in the calculation (Ro = ∞), which maximizes the effect of domain movement, does not significantly lower the correlation with domain-based GDC-all scores (R2 = 0.82). Based on this analysis, we selected a default value of 15 Å for the inclusion radius Ro. This allows the lDDT score to avoid the drawbacks that affect measures based only on very local characteristics, e.g. contact map overlap.

3.1.2 Sensitivity analysis versus relative domain movements

Proteins consisting of multiple domains can exhibit flexibility between their domains, which can often be experimentally observed in the form of structures with different relative orientations of otherwise rigid domains. In many cases, these relative movements play a functional role. From a modeling assessment perspective, however, the analysis of the relative orientation of the domains must therefore be separated from the assessment of the modeling accuracy of the individual domains.

The insensitivity to relative domain movement makes the lDDT score a good choice for the unsupervised evaluation of predictions of multidomain structures, in contrast to scores based on global superposition. To illustrate this behavior, Figure 3 shows lDDT and GDC-all scores computed on full-length structures as a function of the AU-based weight-averaged GDC-all scores (x-axis). As expected, the correlation between the two types of GDC-all scores is rather poor (R2 = 0.58), whereas the correlation between the AU-based GDC-all scores and the lDDT scores is good (R2 = 0.89). The hybrid nature of the lDDT score allows it to be global enough to evaluate the modeling quality of the protein domains, but local enough to be only marginally affected by their relative orientations in the compared structures. When using the lDDT score to evaluate predictions, it is not necessary to split the target structure in separate domains, whose identification can be a complex and time-consuming procedure. The absolute lDDT score values show a dependency on the structural architecture of the protein being modeled (see Section 3.2 later in the text). For example, a small group of predictions off-diagonal (GDC-all between 0.2 and 0.35, lDDT between 0.4 and 0.6) belonging to target T0629 show a high correlation within the group, but the slope is different from other targets. The elongated trimeric structure of T0629 has relatively few intra-chain contacts and is mainly stabilized by interactions between chains. Thus, local interactions within a chain are mainly limited to trivial nearest neighbor contacts that are easily satisfied in predictions, which explain the higher lDDT scores. For reference, the correlation between the lDDT and GDC-all scores for single-domain CASP9 targets is shown in Supplementary Fig. S2).

3.2 Validation of lDDT score baselines for different protein folds

Because lDDT scores express the percentage of inter-atomic distances present in the target structure that are also preserved in the model, a value of ‘0’ corresponds to 0 conserved distances, and ‘1’ to a perfect model. However, these extreme values are in practice rarely observed, even in extremely high and low-quality models. At the high-accuracy end, fluctuations in surface side chain conformations will result in values <1. For very low accuracy models, still some local inter-atomic distances will be preserved if the model has at least a stereochemically plausible structure and features some secondary structure elements. In the context of protein model assessment, two types of baseline values are of interest: the expected score when comparing two random structures, and scores for models with correct folds but including threading errors.

In principle, the first value could be estimated using Flory–Huggins polymer solution theory (Flory, 1969; Huggins, 1958), e.g. as done for the determination of RPF/DP values for NMR structures (Huang et al., 2012). However, because protein structures are rich in rigid structural elements like α-helices and β-sheets, where the relative local positions are restricted, they show in general a higher number of preserved local distances than random polymers. Based on these considerations, we decided to empirically derive lDDT baseline scores by comparing a reference structure with a set of well-defined decoy models. A comparison of the Flory–Huggins and decoy-based analysis can be found in the Supplementary Materials. The average lDDT score when comparing random structures, i.e. protein models with different architectures (see Materials and Methods), is 0.20 (±0.04). For estimating the effect of alignment shifts in models with otherwise correct fold and stereochemistry, we created pseudomodels starting from the original protein structure and introducing threading errors of increasing magnitude for different representative structure architectures from CATH (Cuff et al., 2011). We then compared the pseudomodels with the original structure, computing their lDDT scores against it.

Here, we show the results for CATH architecture entries 1.25 (Alpha Horseshoe) as example for proteins rich in α-helices, and 2.40 (Beta-barrel) as representative for a β-sheet protein (Fig. 4). The plots at the top of each panel show the value of the lDDT scores (on the y-axis) for 60 pseudomodels as a function of the magnitude of the threading error (residue offset) on the x-axis. For large threading errors, the lDDT scores converge to a ‘baseline’ range of scores, which appear to be largely independent of the threading error magnitude. We considered scores in this range to be typical lDDT scores for a low-quality model with the same architecture as the target structure. For models in the Alpha Horseshoe architecture, the average baseline lDDT score is ∼0.28, whereas for the Beta barrel class, the value of 0.22 is lower, illustrating the influence of the architecture of the protein. This indicates that the lower boundary of the lDDT score can vary as a function of the architecture of the target protein, which influences the comparison of absolute raw scores of models for different folds, but not of models of the same architecture. This is a common behavior of most structure comparison measures.

One interesting feature in Figure 4 is the presence of several peaks at larger threading errors (e.g. around residue 34) in the Alpha Horseshoe architecture example. These peaks correspond to internal repeats in the structure, which give rise to locally correct models when the threading shift coincides with the size of the repeat.

3.3 Local model accuracy assessment

Modeling errors are typically not homogenously distributed over the model, but are localized, e.g. in template-based models often in segments that had to be remodeled de novo. Residue-based lDDT scores quantify the model quality on the level of a residue’s environment. The low sensitivity of lDDT to relative domain movements also applies to per-residue scores. As shown in Figure 1, local lDDT scores are not dominated by different domain orientations between the target and the model structures, but correctly reflect the accuracy of the local atomic environment surrounding the residue under investigation in the model. Figure 1 shows a superposition of the structure of target T0542 (in light gray) with prediction by group TS236 (colored according to the full-length lDDT score). The models represent each of the two individual domains with high accuracy, but their relative domain orientation does not correspond to the target structure. Superposition-based scores would assign a high score to one of the domains but not to the other, or require scoring based on isolated domain. As illustrated on the right panel (Fig. 1), residues with low lDDT score correspond to regions of large local structural divergence between the two domain structures, irrespective of the domain movement between them. As expected, low local scores can also be detected at the interface between the two domains where the interactions cannot be modeled correctly without knowing their relative orientation in the target.

3.4 Stereochemical realism assessment

Although validation of the stereochemical plausibility of protein models is a routine procedure for experimental structure determination, e.g. in X-ray crystallography (Read et al., 2011), this is not a common practice in theoretical modeling. Depending on the applied method, models generated in silico may reveal rather unrealistic stereochemical properties. Typically, numerical scores applied in retrospective model assessment compute a measure for the average atomic dislocation between the reference structure and the model, without considering the stereochemical quality of the latter. Consequently, two models with similar average atomic displacements may nevertheless differ significantly in their stereochemical plausibility, and some models might include atomic arrangements that are physically impossible.

To address this question, lDDT incorporates a stereochemical plausibility check, which assesses two aspects of model quality: the lengths of chemical bonds and the widths of angles in the model structure. Bond and angle measurements are compared with a set of standard parameters derived from high-resolution crystal structures (Engh and Huber, 2006). A stereochemical violation is defined as a parameter deviating from the expected values by more than a specified number of standard deviations (default: 12σ; see Supplementary Material). Inter-atomic distances between non-bonded atoms in the model are compared with the sum of their Van der Waals radii (Allen, 2002), and a violation (‘clash’) is assigned if two atoms are closer than the sum of the Van der Waals radii, allowing a certain tolerance (default: 1.5 Å). When calculating the lDDT score, all distances involving side-chain atoms of a residue involved in any type of stereochemical violations in the model are considered as non-preserved. In cases where backbone atoms are involved in stereochemical violations, all distances involving this residue are considered non-preserved. This approach leads to the lowering of the final lDDT score of a model according to the extent of the structure’s stereochemical problems (Fig. 5).

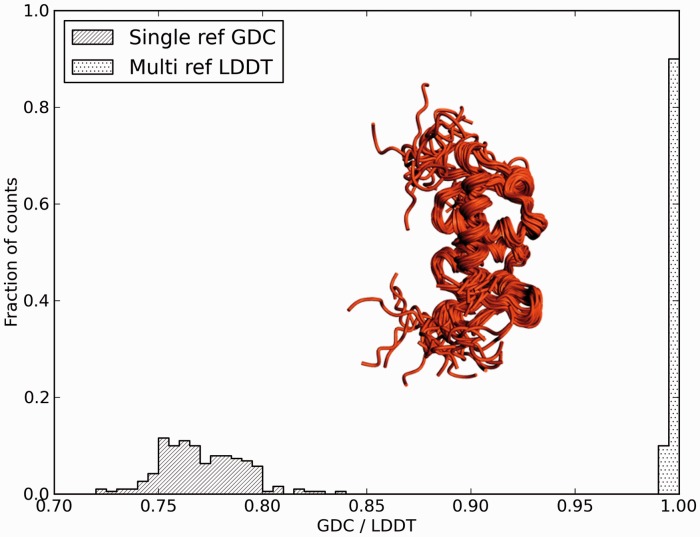
Fig. 5.

Fig. 5.

Open in a new tab

Assessing stereochemical plausibility. This example illustrates the stereochemical quality checks on lDDT score for a model (TS276, left side as ribbon representation) for target T0570-D1 with unrealistic stereochemistry (close-up, right). Residues with too short (1) or too long (2) chemical bonds, as well as those with close atomic interactions (3) or impossible bond angles (4), result in lower scores during the lDDT computation

As an example, Figure 5 shows the CASP9 prediction TS276_1 for target T0570-D1. The backbone of the prediction can be superposed accurately to the backbone of the target structure (left panel), and the prediction has indeed a high GDT-HA score (0.814). Displacement-based all-atom scores do not immediately reveal the problems, with a GDC-all score of 0.705 and an lDDT score without stereochemical checks of 0.682. However, when the lDDT score includes stereochemical check, the lDDT score drops to 0.571. Panel B shows a close-up of the region around residue alanine 21, where several stereochemical violations are evident.

3.5 Multireference structure comparison

The typical situation for protein structure prediction assessment is to compare a model against a single reference structure. There are, however, cases where several equivalent reference structures are available, e.g. structural ensembles generated by NMR, crystal structures with multiple copies of the protein in the asymmetric unit (non-crystallographic symmetry) (e.g. target T603 in CASP9), or independently determined X-ray structures for the same protein at different experimental conditions. In these cases, no structure can be considered more reliable than any other. However, owing to the choice of different templates, models often have a higher similarity to one or the other reference structure, and the choice of reference for the evaluation score can lead to very different results for models of equal quality.

In case of the lDDT, the following approach allows to evaluate a model simultaneously against an ensemble of reference structures: for each pair of atoms, we define an acceptable distance range by taking the minimal and maximal distance observed across all references where the atoms are present. If, in any of the reference structures, the distance is longer than the inclusion radius Ro, this distance is considered a long-range interaction, and is ignored. For the assessment, the corresponding distance in the model is considered preserved, when it falls inside the acceptable range or outside of it by less than a predefined threshold offset.

One obvious application of the multi-reference lDDT score is the evaluation of models against NMR structure ensembles. For example, in the case of CASP9 target T0559 (PDBID: 2L01), an ensemble of 20 NMR structures has been experimentally determined. Selecting one single chain from the ensemble as reference to evaluate prediction models would be an arbitrary decision, artificially favoring some models that are closer to that specific structure. To estimate the effect of selecting a single reference structure, all structures in the ensemble were in turn used as a ‘model’ and evaluated against all the others. Using traditional pairwise comparison with GDC-all scores (Fig. 6, striped bars), fluctuations of almost 12 GDC points around an overall low value of 0.77 are observed. To avoid this, variable regions of the ensemble are often excluded from the assessment (Clarke et al., 2007; Kinch et al., 2011; Mao et al., 2011).

Fig. 6.

Fig. 6.

Open in a new tab

Comparing a model against an ensemble of reference structures. The experimental reference structure for CASP target T0559 (human protein BC008182, PDBID:2L01) is an ensemble of NMR structures. The graph shows the effect of selecting a single structure as reference (GDC-all values as striped bars) in contrast to the multireference lDDT implementation (dotted bars). For this example, each structure within the ensemble was selected in turn as reference and compared with the other members

Ideally, this situation should be avoided, and a prediction should not be rewarded or penalized for being more similar to one member of the ensemble than to another. The multireference version of the lDDT score has been developed to overcome this problem by sampling the conformational space covered by the ensemble and compensating for its variability. Using the same example, the multireference lDDT score, which uses one chain as a ‘model’ and all the others together as multireferences, shows a spread of <1% (Fig. 6, dotted bars), indicating its robustness when scoring a model against an ensemble of equivalent reference structures. Recently, methods using elastic network models have been proposed to computationally explore the intrinsic flexibility landscape for a single reference protein (Perez et al., 2012).

4 CONCLUSION

In this article, we describe the lDDT score, which combines an agreement-based model quality measure with (optional) stereochemical plausibility checks. We have demonstrated its low sensitivity with respect to domain movements in case of multidomain target proteins, which allows for automated assessment without the need for manually splitting targets into AUs. We also have shown that local atomic interactions are well captured and local lDDT scores faithfully reflect the modeling quality of sub-regions of the prediction. In addition, we present an approach to compare models against multiple reference structures simultaneously without arbitrarily selecting one reference structure for the target, or removing parts that show variability. Additionally, as an agreement-based score, lDDT is robust with respect to outliers.

One disadvantage of the lDDT score is that it does not fulfill the mathematical criteria to be a metric. However, the same is true for most scores commonly applied for structure comparison such as GDT, or RSMD based on iterative superposition when comparing models with different number of atoms. We consider lDDT particularly suited for the evaluation of predictions for the same target protein, e.g. in the context of the CASP and CAMEO (www.cameo3d.org) experiments. For these kind of applications, unlike, e.g. for clustering protein structures, we do not see the lack of metric properties as a significant limitation.

Supplementary Material

Supplementary Data
supp_29_21_2722__index.html (1.1KB, html)

ACKNOWLEDGEMENT

The authors gratefully acknowledge the financial support by the SIB Swiss Institute of Bioinformatics.

Conflict of Interest: none declared.

REFERENCES

  1. Allen FH. The Cambridge Structural Database: a quarter of a million crystal structures and rising. Acta Crystallogr. B. 2002;58:380–388. doi: 10.1107/s0108768102003890. [DOI] [PubMed] [Google Scholar]
  2. Battey JN, et al. Automated server predictions in CASP7. Proteins. 2007;69(Suppl. 8):68–82. doi: 10.1002/prot.21761. [DOI] [PubMed] [Google Scholar]
  3. Biasini M, et al. OpenStructure: a flexible software framework for computational structural biology. Bioinformatics. 2010;26:2626–2628. doi: 10.1093/bioinformatics/btq481. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bordogna A, et al. Predicting the accuracy of protein-ligand docking on homology models. J. Comput. Chem. 2011;32:81–98. doi: 10.1002/jcc.21601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chen VB, et al. MolProbity: all-atom structure validation for macromolecular crystallography. Acta Crystallogr. D Biol. Crystallogr. 2010;66:12–21. doi: 10.1107/S0907444909042073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Clarke ND, et al. Domain definition and target classification for CASP7. Proteins. 2007;69(Suppl. 8):10–18. doi: 10.1002/prot.21686. [DOI] [PubMed] [Google Scholar]
  7. Cuff AL, et al. Extending CATH: increasing coverage of the protein structure universe and linking structure with function. Nucleic Acids Res. 2011;39:D420–D426. doi: 10.1093/nar/gkq1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Engh RA, Huber R. Accurate bond and angle parameters for X-ray protein structure refinement. Acta Crystallogr. A. 1991;47:392–400. [Google Scholar]
  9. Engh RA, Huber R. International Tables for Crystallography. Vol. F, ch. 18.3. John Wiley & Sons, Ltd; 2006. Structure quality and target parameters; pp. 382–392. [Google Scholar]
  10. Flory PJ. Statistical mechanics of chain molecules. New York: Interscience Publishers; 1969. [Google Scholar]
  11. Guex N, et al. Automated comparative protein structure modeling with SWISS-MODEL and Swiss-PdbViewer: a historical perspective. Electrophoresis. 2009;30(Suppl. 1):S162–S173. doi: 10.1002/elps.200900140. [DOI] [PubMed] [Google Scholar]
  12. Huang YJ, et al. RPF: a quality assessment tool for protein NMR structures. Nucleic Acids Res. 2012;40:W542–W546. doi: 10.1093/nar/gks373. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hubbard TJ. RMS/coverage graphs: a qualitative method for comparing three-dimensional protein structure predictions. Proteins. 1999;37(Suppl. 3):15–21. doi: 10.1002/(sici)1097-0134(1999)37:3+<15::aid-prot4>3.3.co;2-q. [DOI] [PubMed] [Google Scholar]
  14. Huggins ML. Physical chemistry of high polymers. New York: Wiley; 1958. [Google Scholar]
  15. Jones AT, Kleywegt GJ. CASP3 comparative modeling evaluation. Proteins. 1999;(Suppl. 3):30–46. doi: 10.1002/(sici)1097-0134(1999)37:3+<30::aid-prot6>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
  16. Keedy DA, et al. The other 90% of the protein: assessment beyond the Calphas for CASP8 template-based and high-accuracy models. Proteins. 2009;77(Suppl. 9):29–49. doi: 10.1002/prot.22551. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kinch LN, et al. CASP9 target classification. Proteins. 2011;79(Suppl. 10):21–36. doi: 10.1002/prot.23190. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kopp J, et al. Assessment of CASP7 predictions for template-based modeling targets. Proteins. 2007;69(Suppl. 8):38–56. doi: 10.1002/prot.21753. [DOI] [PubMed] [Google Scholar]
  19. Krivov GG, et al. Improved prediction of protein side-chain conformations with SCWRL4. Proteins. 2009;77:778–795. doi: 10.1002/prot.22488. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kryshtafovych A, et al. CASP Prediction Center infrastructure and evaluation measures in CASP10 and CASP ROLL. Proteins. 2013;81 doi: 10.1002/prot.24399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. MacCallum JL, et al. Assessment of protein structure refinement in CASP9. Proteins. 2011;79(Suppl. 10):74–90. doi: 10.1002/prot.23131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Mao B, et al. Improved technologies now routinely provide protein NMR structures useful for molecular replacement. Structure. 2011;19:757–766. doi: 10.1016/j.str.2011.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Mariani V, et al. Assessment of template based protein structure predictions in CASP9. Proteins. 2011;79(Suppl. 10):37–58. doi: 10.1002/prot.23177. [DOI] [PubMed] [Google Scholar]
  24. Martin AC, et al. Assessment of comparative modeling in CASP2. Proteins. 1997;29(Suppl. 1):14–28. doi: 10.1002/(sici)1097-0134(1997)1+<14::aid-prot4>3.3.co;2-f. [DOI] [PubMed] [Google Scholar]
  25. Mosimann S, et al. A critical assessment of comparative molecular modeling of tertiary structures of proteins. Proteins. 1995;23:301–317. doi: 10.1002/prot.340230305. [DOI] [PubMed] [Google Scholar]
  26. Moult J. A decade of CASP: progress, bottlenecks and prognosis in protein structure prediction, Curr. Opin. Struct. Biol. 2005;15:285–289. doi: 10.1016/j.sbi.2005.05.011. [DOI] [PubMed] [Google Scholar]
  27. Moult J, et al. Critical assessment of methods of protein structure prediction (CASP)–round IX. Proteins. 2011;79(Suppl. 10):1–5. doi: 10.1002/prot.23200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Olechnovic K, et al. CAD-score: a new contact area difference-based function for evaluation of protein structural models. Proteins. 2013;81:149–162. doi: 10.1002/prot.24172. [DOI] [PubMed] [Google Scholar]
  29. Perez A, et al. FlexE: using elastic network models to compare models of protein structure. J. Chem. Theory Comput. 2012;8:3985–3991. doi: 10.1021/ct300148f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Read RJ, et al. A new generation of crystallographic validation tools for the protein data bank. Structure. 2011;19:1395–1412. doi: 10.1016/j.str.2011.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Rodrigues JP, et al. Clustering biomolecular complexes by residue contacts similarity. Proteins. 2012;80:1810–1817. doi: 10.1002/prot.24078. [DOI] [PubMed] [Google Scholar]
  32. Schwede T, et al. Outcome of a workshop on applications of protein models in biomedical research. Structure. 2009;17:151–159. doi: 10.1016/j.str.2008.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Shi S, et al. Analysis of CASP8 targets, predictions and assessment methods. Database. 2009;2009:bap003. doi: 10.1093/database/bap003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Siew N, et al. MaxSub: an automated measure for the assessment of protein structure prediction quality. Bioinformatics. 2000;16:776–785. doi: 10.1093/bioinformatics/16.9.776. [DOI] [PubMed] [Google Scholar]
  35. Sippl MJ. On distance and similarity in fold space. Bioinformatics. 2008;24:872–873. doi: 10.1093/bioinformatics/btn040. [DOI] [PubMed] [Google Scholar]
  36. Vendruscolo M, et al. Statistical properties of contact maps. College Park, MD: American Physical Society; 1999. [Google Scholar]
  37. Zemla A. LGA: a method for finding 3D similarities in protein structures. Nucleic Acids Res. 2003;31:3370–3374. doi: 10.1093/nar/gkg571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Zemla A, et al. Processing and evaluation of predictions in CASP4. Proteins. 2001;45(Suppl. 5):13–21. doi: 10.1002/prot.10052. [DOI] [PubMed] [Google Scholar]
  39. Zhang Y, Skolnick J. Scoring function for automated assessment of protein structure template quality. Proteins. 2004;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_29_21_2722__index.html (1.1KB, html)
supp_btt473_Supplementary-Data.pdf (753.3KB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES