Efficient inference of local ancestry

Abstract

Motivation: The inference of local ancestry of admixed individuals at every locus provides the basis for admixture mapping. Local ancestry information has been used to identify genetic susceptibility loci.

Results: In this study, we developed a statistical method, efficient inference of local ancestry (EILA), which uses fused quantile regression and k-means classifier to infer the local ancestry for admixed individuals. We also conducted a simulation study using HapMap data to evaluate the performance of EILA in comparison with two competing methods, HAPMIX and LAMP. In general, the performance declined as the ancestral distance decreased and the time since admixture increased. EILA performed as well as the other two methods in terms of computational efficiency. In the case of closely related ancestral populations, all the three methods performed poorly. Most importantly, when the ancestral distance was large or moderate, EILA had higher accuracy and lower variation in comparison with the other two methods.

Availability and implementation: EILA is implemented as an R package, which is freely available from the Comprehensive R Archive Network (http://cran.r-project.org/).

Contact: jyangstat@gmail.com

1 INTRODUCTION

Since the completion of human genome project in 2003 (Collins et al., 2003), it is feasible to conduct a case–control study to identify disease-susceptible loci using millions of single-nucleotide polymorphisms (SNPs). Unlike the family-based linkage analysis, the case–control design provides an easier way to access large samples for studying complex diseases. The case–control design is especially useful when dealing with a late onset disease in which the parental genotype is usually difficult to obtain. However, a genome-wise association study based on the case–control design may yield false-positive findings because of population admixture that is attributed to individuals descended from multiple ancestral population groups. Specifically, alleles that differ in frequency between ancestral populations may be falsely found to be associated with diseases that are also more prevalent in one ancestral population than the other.

Several approaches have been developed to account for population admixture in genetic association studies. One approach is the genomic control (Devlin and Roeder, 1999), which calculates an inflation factor to adjust the testing statistic and hence the P-value. Another approach is to identify the genetic background using principle component analysis and then adjust the testing statistic using significant eigenvectors (Price et al., 2006). However, it is challenging to infer local ancestry for admixed individuals because the true ancestral information is a mixture of haplotypes with varied lengths, each of which can be traced back to its original ancestry.

To infer local ancestry using SNP data, we face the following challenges. First, given that most SNPs only have three different genotypes, if we only use the genotype information at a given locus, we would have limited power to infer local ancestry for that locus and also such power would depend on whether the SNPs differ in frequency between the ancestral groups. Second, the number of generations since admixture occurred must be taken into account in this kind of analysis because it is inversely related to the length of genomic regions derived from any given group. Although the number of generations is rarely known, we can infer the boundaries of these ancestral blocks by identifying regions where the ancestral haplotypes differ on either side. Therefore, the challenge becomes how to identify the breakpoint or transition point for ancestral blocks within an individual’s genome. Third, the majority of existing models assume linkage equilibrium under which the analysis only needs to use unlinked markers but is at risk of losing power because of excluding potential ancestral informative markers. This simple approach is particularly questionable for the SNPs that are genotyped on platforms with dense coverage.

In this study, we developed a new method for efficient inference of local ancestry (EILA) in admixed individuals based on three steps that were designed to deal with the existing methodological challenges. The first step assigns a numerical score (with a range of 0–1) to genotypes in admixed individuals to better quantify the closeness of the SNPs to a certain ancestral population. The second step uses fused quantile regression to identify breakpoints of the ancestral haplotypes. In the third step, the k-means classifier is used to infer ancestry at each locus. The major strength of EILA is that it relaxes the assumption of linkage equilibrium and uses all genotyped SNPs rather than only unlinked loci to increase the power of inference. Another important strength of this method is its higher accuracy and lower variation in comparison with competing methods. These strengths are demonstrated by the simulation study in Section 4.

2 THE EILA METHOD

In this section, we consider an admixed population descended from two ancestral populations. Extension to more than two ancestral populations is discussed in Section 3.3. We also assume the samples of ancestral populations are available so that we can infer ancestral genotype distributions. Based on these assumptions, we infer local ancestry using three samples: one study sample of admixed individuals with unknown local ancestry and two reference samples from different ancestral populations. Sections 2.1–2.3 describe technical details of the EILA method.

2.1 Mapping admixed genotypes onto continuous scores

Define 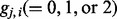as the number of reference alleles for an individual i at locus j. Genotypes from the reference ancestral populations are denoted by the superscript A and B. Given a collection of n₁ individuals from Ancestry A and n₂ individuals from Ancestry B, we define a score 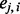for the observed admixed genotype 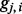as the probability that 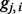is descended from Ancestry A:

Unlike 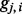that is a discrete variable with little information about the closeness of the SNPs to a certain ancestral population, 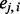is a continuous variable (with the range 0–1) that has an intuitive interpretation. Suppose that we have a set of closely linked SNPs from an admixed individual and that the two segments flanking these SNPs are descended from Ancestry A, the majority of 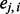would be close to 1. However, if the segments are descended from Ancestry B, the majority of 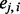would be close to 0. In another situation where one segment is descended from Ancestry A and the other segment from Ancestry B, the average of 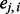would be ∼0.5. Because the event 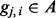is binary, the logistic regression is a natural choice for calculating the score .

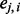2.2 Using fused quantile regression to identify breakpoints of the ancestral haplotypes

For an admixed individual i, the first step of EILA generates a sequence of scores 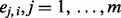. Define 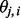to be a smooth series. Using the fused quantile regression proposed by Eilers and de Menezes (2005), we can estimate 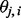by finding the value that minimizes

(1)

Equation (1) contains two terms: the first term is a median regression that is robust to outliers; the second term is a penalty that determines the smoothness of 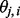using the tuning parameter 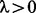. When λ is small, the effect of the penalty is small, so the fitted value of 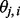is very close to the observed 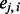. On the other hand, when λ is large, the penalty term dominates, so the 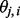’s in proximity are similar. The choice of λ is discussed in detail in Section 3.2.

In summary, the fitted curve has plateaus and sudden jumps between them. The plateau indicates that all of the SNPs within this region are in one of three cases: (i) descended from Ancestry A, (ii) descended from Ancestry B or (iii) equally admixed. The jumps between plateaus are possible breakpoints between ancestral blocks. The fused quantile regression is used in this step to achieve two goals: one is to smooth SNP scores within admixed individuals and the other is to infer the location of breakpoints for ancestral blocks.

2.3 Using k-means classifier to infer local ancestry

Given the breakpoints for each admixed individual identified in the previous step, we propose to infer the local ancestry for each segment between breakpoints using the k-means classifier because of its efficiency and accuracy in assigning local ancestry. It is important to note that all SNPs in each segment are used in this step to achieve high power of inference.

To classify genomic segments into Ancestry A, Ancestry B or equally admixed, we need the corresponding three types of SNP distributions. Although we have samples from ancestral populations A and B, we do not have samples that are known to have equal admixture from these two ancestral populations at every locus. Our approach for dealing with this issue is to simulate first-generation admixed individuals through random mating of two individuals of whom one is randomly selected from Ancestry A and the other from Ancestry B. The random mating process is repeated many times to generate a sample of equally admixed individuals. In practice, the number of simulated admixed individuals would be equal to the average number of individuals in populations A and B.

To infer local ancestry for each segment between breakpoints using unsupervised k-means classification, we define the test set as all SNPs within the segment being studied. The training set consists of the corresponding segments from the simulated sample of equally admixed individuals along with the two reference samples from the ancestral populations A and B. Note that the ancestral statuses for the training set are known but the ancestral status for the test set is unknown. We use the k-means classifier to train the three reference samples in the training set and to identify the three centroids (or means) corresponding to the three reference populations. To infer the local ancestry of the test segment, we find the centroid nearest to the test segment. This procedure is repeated until every segment of unknown local ancestry SNPs for every admixed individual in the study sample has been classified.

3 IMPROVEMENT AND EXTENSION OF THE EILA METHOD

The direct implementation of the EILA method for high-throughput arrays requires a huge amount of computer memory and computation time. For example, we found that when the total number of SNPs was 20 000, the fused quantile regression implemented in R required >192-GB RAM, which is beyond the capacity of most computers. For 10 000 SNPs, it took 10 h on 2.53 GHz Intel(R) Xeon(R) CPU running R under Linux. Thus, for Genome-Wide Human SNP Array 6.0 (Affymetrix Inc., Santa Clara, CA) that contains >70 000 SNPs on chromosome 1, the required computer memory and computation time are not practically feasible. Sections 3.1 and 3.2 describe our approaches to drastically improve the computational efficiency (it took only 0.6 s rather than 10 h for 10 000 SNPs on the same machine). Section 3.3 extends the EILA to the case of three ancestral populations.

3.1 Improving fused quantile regression

The simplest way to improve computational efficiency is to adopt the Frisch–Newton method following the recommendation of Eilers and de Menezes (2005) and Koenker (2005). The computation time of this method is, however, proportional to the third power of the number of SNPs. In addition, the required computer memory for the Frisch–Newton method at the scale of high-throughput arrays is not feasible in most settings. Thus, we propose the following two approaches to increase the computational efficiency without losing accuracy of breakpoint identification. First, we used the Wilcoxon rank-sum test to compare the distributional difference between the two reference samples at each locus. For every M base pairs, we selected 1 SNP with the smallest P-value. Our preliminary analysis found that 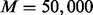is sufficient for fused quantile regression to identify the breakpoints without missing any potential ones. Second, because even 1 SNP per 50 000 bp requires a lot of computation time to fit the fused quantile regression on one whole chromosome, we further improved the algorithm by fitting the fused quantile regression piecewise. That is, we partitioned the whole chromosome into several segments, each of which has a length between 10 and 25 MB. As our purpose is to identify breakpoints, fitting fused quantile regression in each partition does not affect breakpoint identification.

3.2 Choice of the tuning parameter

In Section 2.2, we briefly explain that the function of the tuning parameter λ of the fused quantile regression is to control the smoothness of the fitted curve. In this section, we provide the technical details of how to choose the tuning parameter.

One approach commonly adopted in quantile regression is the Schwarz information criterion [SIC; (Schwarz, 1978)] under which the optimal value of λ (i.e. the one that minimizes SIC) can only be determined empirically. This is, however, a time-consuming process, especially for a large number of SNPs, and thus is not practical in genetic data analysis. Furthermore, we conducted a simulation study fitting the fused quantile regression with various values of λ on simulated admixed samples (see Section 4.2 for the detailed procedure of data generation) and found that SIC is not an effective approach to determine the optimal λ. For example, Figure 1 based on our simulation results shows that any λ value >8 could be the optimal value.

Fig. 1.

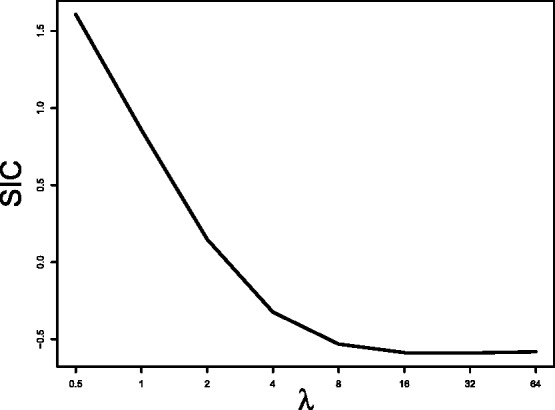
The relationship between SIC and λ based on simulation

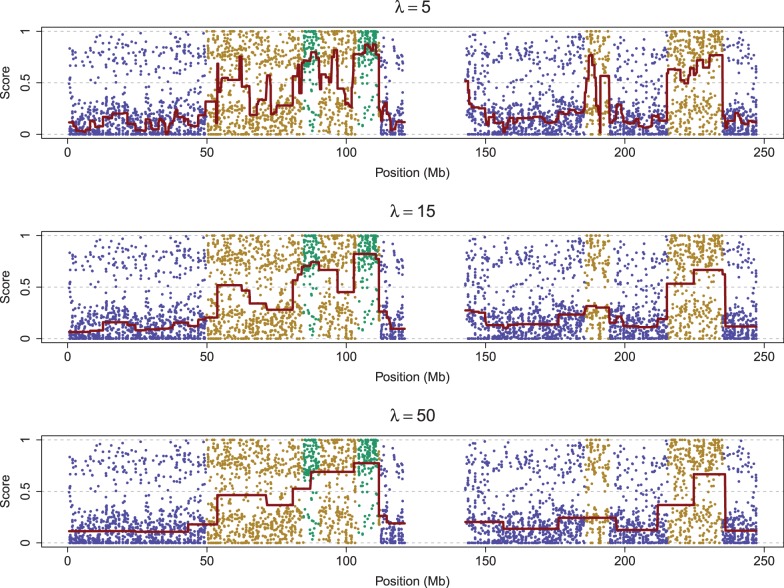
Instead of the SIC approach, we propose a simulation approach to find the optimal λ. We evaluated the relationship between λ and breakpoints by using the fused quantile regression with various values of λ to fit simulated data resulting from the procedure described in Section 4.2. Figure 2 displays the simulation results based on three values of λ: 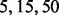in the top, middle and bottom panels, respectively. The blue points indicate that both alleles of the corresponding SNP were descended from AncestryA; the green points indicate that both alleles were descended from Ancestry B; and the brown points indicate that two alleles were descended from Ancestries A and B. The red lines are the fitted lines of fused quantile regression that are between the 0 and 0.5 horizontal lines in the region of blue points, between the 0.5 and 1 horizontal lines in the region of green points and in proximity to the 0.5 horizontal line in the region of brown points. The true breakpoints are at the boundary of regions with different colors.

Fig. 2.

The relationship between λ and breakpoint identification based on a simulation study (the red lines are the fitted fused quantile regression with 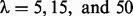; the blue points indicate both alleles were descended from Ancestry A; the green points indicate both alleles were descended from Ancestry B; the brown points indicate the two alleles were descended from Ancestries A and B)

The top panel of Figure 2 shows that the fitted fused quantile regression with a small value of λ (e.g. 5) detected all true breakpoints and yet had short segments that tended to result in low power in local ancestry inference because very few SNPs can be used in the k-means clustering. On the other hand, the bottom panel shows that the fitted fused quantile regression with a large value of λ (e.g. 50) had long segments and also tended to miss many breakpoints. The middle panel, otherwise, shows a compromise between the two when 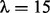, which was the largest value at which all true breakpoints can be identified in the simulation and thus was chosen to be the optimal value. The results in Section 4 show that the EILA method with this particular λ value performs well in comparison with two competing methods, HAPMIX and LAMP, under different ancestral distributions and number of generations.

3.3 Extension to three ancestral populations

It is straightforward to extend our method to the case of three ancestral populations (e.g. A, B and C) for which there are three possible pairs (i.e. A–B, B–C, and A–C). Following the steps in Sections 2.1 and 2.2, we can identify a set of breakpoints for each pair of ancestral populations. For example, the breakpoints S_AB of the A–B pair can be identified using the admixed sample and ancestral samples from populations A and B. For the other two ancestral pairs, the breakpoints S_BC and S_AC can be identified in similar ways. The set of breakpoints for these three ancestral populations, S_ABC, is thus the collection of breakpoints from the three sets, .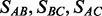

To infer local ancestry for each segment specified by the breakpoints S_ABC, we can follow the procedure in Section 2.3 to simulate an admixed sample from each pair of the three reference samples. Using the k-means classifier with 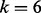based on the three reference samples and three simulated admixed samples, we can assign each unknown segment for each individual in the study sample to one of the six possible ancestral populations.

4 SIMULATION STUDY

We evaluated the performance of the proposed EILA method in comparison with two existing methods for inference of local ancestry, the LAMP and Hapmix, by conducting a simulation study based on ancestral data from the International HapMap Project http://www.hapmap.org/. The two competing methods are described in Section 4.1. Section 4.2 delineates the procedure for simulating admixed samples. The results of the simulation study are presented in Section 4.3.

4.1 The LAMP and Hapmix methods

The first competing method is the LAMP (Sankararaman et al., 2008) that was shown to have higher efficiency and accuracy than older methods such as the SABER (Tang et al., 2006) and the Structure (Pritchard et al., 2000). The LAMP method is based on sliding windows of contiguous SNPs across the entire chromosome. In each window, a cluster algorithm is used to estimate the probability that an SNP is descended from Ancestry A, Ancestry B or the admixed population. The majority vote among all windows covering this SNP is then used to infer its local ancestry.

Another competing method used to compare with the proposed method is the HAPMIX (Price et al., 2009). Unlike the LAMP that uses ancestral frequencies for local ancestry inference, HAPMIX assumes that the phased samples from unadmixed populations are available. The inference method builds on the Hidden Markov Model where the hidden state represents the ancestral status based on phased data. HAPMIX estimates the likelihood of the observed admixed segment that is a better match with one ancestral population than the other. The central idea is to use dense SNPs to model linkage disequilibrium in the ancestral populations to improve the local ancestry inference. However, this method may be sensitive to the accuracy of phased ancestral data.

4.2 Procedure of simulating admixed samples

Our simulation study was designed based on the publicly accessible data from ancestral samples of the International HapMap Project so that the results can be easily generalized to real data situations. We used the Affymetrix Genome-Wide Human SNP Array 6.0 for chromosome 1 as the SNP set. There are 11 populations in HapMap, which are listed in Table 1. The upper triangle of Table 1 shows the abbreviations of population names and the distance between each pair of populations using the root-mean-square difference (RMSD) of the reference alleles; the values listed in the lower triangle are the ratio of the RMSD of a particular pair to the RMSD of the reference pair CHB/CHD (Han Chinese in Beijing/Chinese in Metropolitan Denver), which has the smallest value of RMSD among all pairs. We simulated all pairwise admixed samples from the HapMap ancestral samples. Among them, the following six pairs have been chosen to be the focus of the simulation experiments because of the common interest in studying them and the wide range of differences represented by them: CEU/YRI and GIH/YRI represent the high level of difference; CEU/MEX, GIH/MEX and GIH/CEU are at the moderate level; and CEU/TSI represents the low level (CEU: Utah residents with Northern and Western European ancestry from the CEPH collection; GIH: Gujarati Indians in Houston, Texas; MEX: Mexican ancestry in Los Angeles, California; TSI: Toscani in Italia; YRI: Yoruba in Ibadan, Nigeria).

Table 1.

The RMSD values based on chromosome 1 using independent samples from HapMap

Population	ASW	CEU	CHB	CHD	GIH	JPT	LWK	MEX	MKK	TSI	YRI
ASW		0.1851	0.2232	0.2251	0.1803	0.2240	0.0753	0.1781	0.0776	0.1835	0.0720
CEU	4.79		0.2011	0.2043	0.1142	0.2022	0.2300	0.1083	0.1937	0.0515	0.2370
CHB	5.78	5.21		0.0386	0.1687	0.0588	0.2501	0.1590	0.2267	0.2047	0.2556
CHD	5.83	5.29	1.00		0.1701	0.0641	0.2516	0.1621	0.2291	0.2068	0.2576
GIH	4.67	2.96	4.37	4.40		0.1689	0.2184	0.1169	0.1859	0.1145	0.2264
JPT	5.80	5.24	1.52	1.66	4.37		0.2509	0.1595	0.2277	0.2056	0.2562
LWK	1.95	5.95	6.48	6.52	5.65	6.50		0.2177	0.0771	0.2279	0.0595
MEX	4.61	2.80	4.12	4.20	3.03	4.13	5.64		0.1845	0.1112	0.2253
MKK	2.01	5.01	5.87	5.93	4.81	5.89	2.00	4.78		0.1900	0.0942
TSI	4.75	1.33	5.30	5.35	2.96	5.32	5.90	2.88	4.92		0.2355
YRI	1.86	6.14	6.62	6.67	5.86	6.63	1.54	5.83	2.44	6.10

Note: Population descriptors.

ASW, African ancestry in Southwest USA; CEU, Utah residents with Northern and Western European ancestry from the CEPH collection; CHB, Han Chinese in Beijing, China; CHD, Chinese in Metropolitan Denver, Colorado; GIH, Gujarati Indians in Houston, Texas; JPT, Japanese in Tokyo, Japan; LWK, Luhya in Webuye, Kenya; MEX, Mexican ancestry in Los Angeles, California; MKK, Maasai in Kinyawa, Kenya; TSI, Toscani in Italia; YRI, Yoruba in Ibadan, Nigeria.

To simulate ancestral samples, the genotypes at each locus were generated using the allele frequencies estimated from HapMap ancestral populations. We simulated 60 ancestral samples on chromosome 1 for each ancestry. For each pair of ancestral samples from HapMap, we defined one as Ancestry A and the other as Ancestry B. To generate one admixed individual from Ancestries A and B for g generations, we simulated 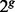individuals with the probability τ from Ancestry A and the probability 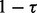from Ancestry B. The resulting 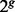individuals thus served as the ancestry of the admixed individual. The next generation of size 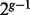was derived by randomly pairing the 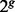individuals and having each pair generate one child. This process of random mating was executed recursively to simulate g generations. We simulated 30 admixed individuals from Ancestries A and B by repeating the process of generating one admixed individual 30 times. We also set the recombination rate at the commonly adopted level of 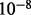/bp (Nachman and Crowell, 2000).

4.3 Simulation results

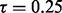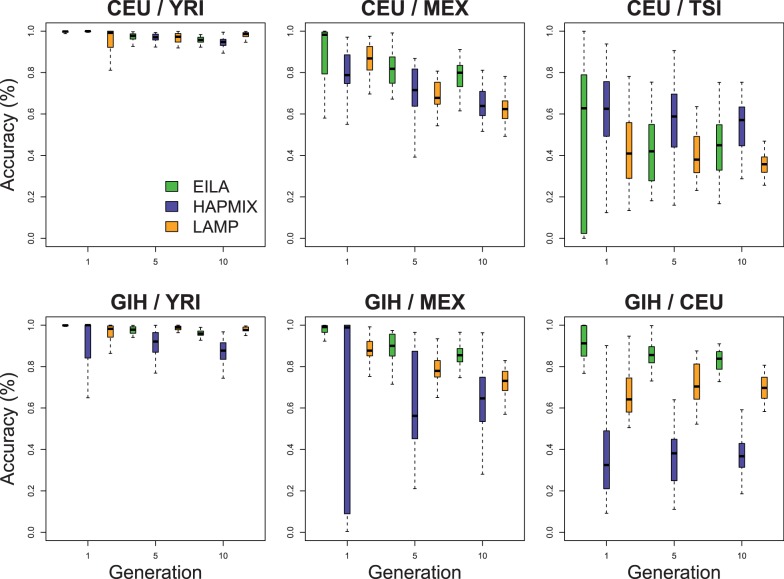
This section compares the performance of three competing methods (EILA, HAPMIX and LAMP) when and the time since admixture (measured in the number of generations) is varied: 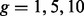. The accuracy of local ancestry inference for each method was calculated for each admixed individual. Figure 3 shows the boxplots of the accuracy rates among the simulated 30 admixed individuals from the same ancestral pair under each configuration of the method and the number of generations. This figure consists of six panels, each of which corresponds to an ancestral pair including CEU/YRI, CEU/MEX, CEU/TSI, GIH/YRI, GIH/MEX and GIH/CEU.

Fig. 3.

The boxplots of the accuracy of local ancestry inference using EILA, HAPMIX and LAMP

The major factor that affects the accuracy of local ancestry inference is the ancestral distance (i.e. RMSD). For ancestral populations with a large RMSD such as CEU/YRI (RMSD = 0.237), all three programs had high average accuracy rates (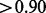). For moderately related ancestral populations such as CEU/MEX (RMSD = 0.108), the average accuracy rates ranged from 0.62 to 0.86 across the methods. For closely related ancestral populations such as CEU/TSI (RMSD = 0.051), the average accuracy rates of local ancestry inference ranged from 0.35 to 0.60 across the methods.

In comparison with HAPMIX and LAMP, EILA had higher accuracy and lower variation when the ancestral distance was large or moderate (i.e. all ancestral pairs but CEU/TSI). In the case of closely related ancestral populations such as CEU/TSI, all the three methods performed poorly (the average accuracy rate 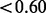). Although HAPMIX performed slightly better than the other two methods for the CEU/TSI pair, its performance appeared to be heavily dependent on the quality of phased ancestral samples. Particularly, for any simulated admixed samples involving GIH ancestral population, HAPMIX had lower accuracy and higher variation in comparison with the other two methods. We also conducted paired t-tests to compare the differences in average accuracy between EILA and LAMP and between EILA and HAPMIX. The results show that the average accuracy of EILA was significantly higher than the other two methods (P 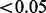) for all the ancestral pairs, except for the pairs of CEU/YRI and CEU/TSI. To benchmark the computational efficiency of the three programs, we measured the total time to infer local ancestry for the 30 admixed individuals simulated in our study. The total computation time was 332 s for EILA, 116 s for HAPMIX and 552 s for LAMP. Thus, the computational efficiency of EILA is comparable with that of the other two programs in practical settings.

We also evaluated the effect of the time since admixture on the accuracy of local ancestry inference. When 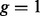, all the simulated admixed individuals had no breakpoints for ancestral segments (i.e. all SNPs were either descended from one ancestral population or admixed from the two ancestral populations). Thus, this situation was used to evaluate whether any of the methods require the existence of breakpoints. The result shows that none of the methods failed in such a situation. Overall, all the three methods performed worse as the time since admixture became longer (i.e. more generations). This effect was, however, relatively small in comparison with the effects of ancestral distances and analytical methods.

5 CONCLUSIONS

This study contributes to the field by developing a statistical method, EILA, to efficiently infer local ancestry in admixed individuals based on the three steps that were designed to deal with the existing methodological challenges. The major strength of EILA is that it relaxes the assumption of linkage equilibrium and uses all genotyped SNPs rather than only unlinked loci to increase the power of inference. We also propose new approaches to improve the computational efficiency of the EILA method drastically and extend it to the case of three ancestral populations. The R package EILA implementing the EILA method will be available at http://cran.r-project.org/.

Our simulation results show that the ancestral distance is the major factor affecting the accuracy of local ancestry inference. The accuracy rates decreased as the ancestral distance decreased. When the ancestral distance was large or moderate, EILA had higher accuracy and lower variation in comparison with the two competing methods, HAPMIX and LAMP. In the case of closely related ancestral populations, all the three methods performed poorly. In terms of computational efficiency, EILA performed as well as the other two methods. Overall, all the three methods performed worse as the time since admixture became longer. This effect was, however, relatively small in comparison with the effects of ancestral distances and analytical methods.

Funding: National Institutes of Health (NIH) grants (K01 AA016591 and R01 AI079139). The content is solely the responsibility of the authors and does not necessarily represent the official view of the NIH.

Conflict of Interest: none declared.