Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2013 Sep 10;29(21):2714–2721. doi: 10.1093/bioinformatics/btt489

Accounting for epistatic interactions improves the functional analysis of protein structures

Angela D Wilkins 1,2, Eric Venner 3, David C Marciano 1, Serkan Erdin 4, Benu Atri 3, Rhonald C Lua 1, Olivier Lichtarge 1,2,3,*
PMCID: PMC3799481  PMID: 24021383

Abstract

Motivation: The constraints under which sequence, structure and function coevolve are not fully understood. Bringing this mutual relationship to light can reveal the molecular basis of binding, catalysis and allostery, thereby identifying function and rationally guiding protein redesign. Underlying these relationships are the epistatic interactions that occur when the consequences of a mutation to a protein are determined by the genetic background in which it occurs. Based on prior data, we hypothesize that epistatic forces operate most strongly between residues nearby in the structure, resulting in smooth evolutionary importance across the structure.

Methods and Results: We find that when residue scores of evolutionary importance are distributed smoothly between nearby residues, functional site prediction accuracy improves. Accordingly, we designed a novel measure of evolutionary importance that focuses on the interaction between pairs of structurally neighboring residues. This measure that we term pair-interaction Evolutionary Trace yields greater functional site overlap and better structure-based proteome-wide functional predictions.

Conclusions: Our data show that the structural smoothness of evolutionary importance is a fundamental feature of the coevolution of sequence, structure and function. Mutations operate on individual residues, but selective pressure depends in part on the extent to which a mutation perturbs interactions with neighboring residues. In practice, this principle led us to redefine the importance of a residue in terms of the importance of its epistatic interactions with neighbors, yielding better annotation of functional residues, motivating experimental validation of a novel functional site in LexA and refining protein function prediction.

Contact: lichtarge@bcm.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Protein functional sites and their key residue determinants are important to elucidate the molecular details underlying protein function (Laskowski and Thornton, 2008), design drugs (Hardy and Wells, 2004), engineer proteins (Thyme et al., 2009) and predict protein function (Erdin et al., 2010). The experimental gold standard to map these sites is alanine scanning (Clackson and Wells, 1995; Onrust et al., 1997), but this approach is rarely exhaustive and limited by the availability of biologically relevant assays.

Therefore, complementary, inexpensive and scalable approaches search for functional sites and residues by analyzing the vast evolutionary record of protein sequences computationally (Aloy et al., 2001; Buslje et al., 2010; Casari et al., 1995; Engelen et al., 2009; Glaser et al., 2003; Halabi et al., 2009; Innis, 2007; Pupko et al., 2002; Pazos et al., 2006; Valdar, 2002). The Evolutionary Trace (ET) (Lichtarge et al., 1996; Mihalek et al., 2004) identifies functionally important residue positions by finding sequence substitution patterns correlated with divergences among homologs, thereby explicitly taking phylogenetic relationships into account. ET predictions have been extensively validated experimentally (Onrust et al., 1997; Rajagopalan et al., 2006; Ribes-Zamora et al., 2007; Rodriguez et al., 2010; Shenoy et al., 2006; Sowa et al., 2000, 2001) and through large-scale retrospective predictions of functional sites (Yao et al., 2003) and protein functions (Venner et al., 2010). These studies point to a number of general and consistent observations in well-structured protein domains: (i) sequence positions may be ranked by evolutionary importance; (ii) most important sequence residues cluster structurally (Madabushi et al., 2002); (iii) these structural clusters predict functional sites (Yao et al., 2003), such that (iv) small structure–function motifs called 3D templates based on these clusters can predict protein function on a genomic scale (Erdin et al., 2010; Kristensen et al., 2008; Venner et al., 2010; Ward et al., 2008). The evolutionary principles that give rise to these useful patterns remain unclear.

This work suggests that epistasis drives these patterns. Traditionally, epistasis means interactions between genes; however, it is also recognized as a major force in molecular evolution of individual proteins (Breen et al., 2012). Strong epistatic interactions occur between contact residues (Ortlund et al., 2007), presumably because function and adaptation are intimately related to mutual interaction and variation of physically neighboring residues. Indeed, improving the clustering quality of evolutionarily important residues improves predictions of functional sites (Mihalek et al., 2006a, b; Wilkins et al., 2010). In that light, the clustering of these residues simply reflects the fundamental epistatic coupling of neighbors.

These observations motivate a series of hypotheses. We hypothesize that if epistasis and function constrain residue neighbors during selective pressure, then evolutionary importance should distribute smoothly over a protein structure. If so, optimizing ET rank smoothness, for example, by selecting sequences appropriately, should improve predictions of functional sites, molecular determinants and functions. Thereby, a modified ET algorithm could directly enforce smoothness and improve predictions by focusing primarily on epistatic interactions.

Our results show that, in practice, we can assess ET rank smoothness by treating the structure as a network, or graph, of amino acid nodes, linking these nodes by edges indicating structural contact and applying the discrete Laplacian operator from a graph theory to quantify ET smoothness. Selections of input sequences that minimize the smoothing function constructed from the Laplacian operator then led to better functional site analyses by ET. Moreover, a new inherently smoother pair-interaction Evolutionary Trace (piET) algorithm built to measure the importance of neighbor-to-neighbor residue pairs, instead of single residues, improves functional site predictions in retrospective study and in an experimental application on Escherichia coli LexA—a protein that triggers the SOS response through which bacteria evolve drug resistance. Finally, piET improves large-scale functional annotations. Together, these data show that the smoothest structural distribution of evolutionary importance reflects functional information best, and that epistatic interactions are strongly reflective of the effective distance between residues.

2 METHODS

2.1 Measuring the smoothness of a rank distribution

To measure the smoothness of ET ranks over a protein, we treat the structure as a graph. The nodes of this graph are the residues, and its edges indicate adjacent sequence residues or close contacts in the known structure. This focus on neighbors is because they will likely experience most strongly the impact of a substitution. The Laplacian operator (Chung, 1997) is the discrete graph counterpart of the standard Laplacian operator used to measure smoothness in a continuous function, and it is computed with two matrices: the adjacency matrix, denoted A, which specifies which residues contact each other in the protein structure (within a minimum atom–atom distance of four Angstroms); and the degree matrix, denoted D, which describes the number of residues adjacent to residue i. Specifically, A is defined as

graphic file with name btt489m1.jpg (1)

This simple form could eventually be made to account for the number of atom–atom contacts, their apparent distances, electrochemical propensities and other attributes of residue neighbor interactions. The degree matrix, D, is a function of 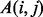Inline graphic

graphic file with name btt489m2.jpg (2)

The Laplacian operator L is then defined as 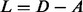Inline graphic. Following standard practice, we may measure the smoothness of any vector field x distributed across the nodes of a graph defined by A through the quadratic form of its Laplacian (Chung, 1997), which is also referred to as the smoothing function, and defined by

graphic file with name btt489m3.jpg (3)

In this work, the vector field x is the relative evolutionary importance (ET rank) of each residue given by the real-value Evolutionary Trace (rvET) algorithm (Mihalek et al., 2004), which measures the size of a phylogenetic divergence associated with a substitution at each sequence position. A short review of this algorithm can be found in Supplementary Materials. By convention, lower values of 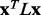Inline graphic indicate smoother distributions of the xi over the protein structure, meaning that the difference in ET ranks is smaller between residues that are in contact.

2.2 Functional determinant test set

The dataset of functional determinants was taken from a previous work (Wilkins et al., 2010). The gold standard functional sites for protein–ligand interactions are defined by the database PDBsum (Laskowski et al., 2005). The protein–protein functional sites are the residues within five Angstroms of the residues in the complexed proteins. To obtain a multiple sequence alignment (MSA) for each query protein, a set of sequences was retrieved with BLAST (Altschul et al., 1997) (using NCBI’s non-redundant protein sequence database, the BLOSUM62 substitution matrix and default parameters). The top 500 homologs with an e-value better than 0.05 were retrieved from NCBIInline graphics Protein database. After we generated alignments, the set was curated to remove sequences with sequence identity <26% and length <70% when compared with query. The homologues were then realigned after curation.

2.3 Measures of overlap and clustering

To assess the recovery of known functional sites in proteins, we calculate an overlap z-score zo between top-ET ranked positions and the ‘gold standard’ functional site, based on the hypergeometric distribution. We first calculate the mean m and the variance 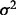Inline graphic of the hypergeometric distribution

graphic file with name btt489m4.jpg (4)

where N is defined as the length of the query protein, M is the number of residues that make up the functional site and n is the number of residues that fall under a certain ET rank-coverage. We then calculate the hypergeometric z-score 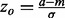Inline graphic, where a is the actual number of functional site residues at a particular ET rank. Each ET rank can be associated with a distinct z-score. To access performance at multiple ranks, we developed the overlap measure 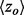Inline graphic, which is the average z-score over ET ranks that fall within a particular coverage range,

graphic file with name btt489m5.jpg (5)

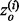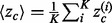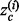Typically, we find that the most useful ET predictions are in the top 20%. Inline graphic is the overlap z-score corresponding to the residues within a certain ET percentile rank i. The sum is over K unique evolutionary ranks for residues that fall within the top 20% cutoff. The measure of clustering is calculated in a similar fashion, Inline graphic where Inline graphic are found analytically and have already been discussed at length in Mihalek et al., (2003).

2.4 Sequence selection simulation

To test smoothing, 30 000 ET analyses ran on randomly constructed MSAs. Each alignment starts from a default alignment (described in previous section) from which randomly sequences are removed, such that the number of sequences removed was randomly chosen between 25 and the total number of sequences in the starting alignment. 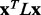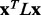The new set of ET ranks leads to unique values of smoothing function Inline graphic and average overlap z-score Inline graphic. The multiple ET analyses are binned based on the value of the smoothing function Inline graphic. The average 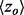Inline graphic was then found for the individual bins to evaluate the correlation.

2.5 Residue–residue evolutionary importance

To motivate our approach, we reasoned that although mutations operate on individual residues, natural selection filters these mutations based on how they perturb molecular interactions. Hence, neighboring residues, i, j, should share evolutionary constraints and their importance ranks should be closely related as observed by the clustering of top-ranked residues within proteins (Madabushi et al., 2002) and their mirroring across molecular interfaces (Raviscioni et al., 2005). If so, we should focus measures of importance directly on molecular interactions rather than on individual residues. By measuring the evolutionary importance of the link between residues, 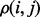Inline graphic, we could then infer the importance of i from the average of 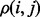Inline graphic over all its neighbors j. In essence, a residue’s importance throughout evolution would be borne of its epistatic interactions with neighboring residues. To implement this strategy and compute the evolutionary importance of the link between two neighboring residues 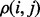Inline graphic, we followed an ET strategy. Residues ranked highly by ET have been shown to knock out (Ribes-Zamora et al., 2007) or swap functions (Rodriguez et al., 2010), while control mutations to poorly ranked residues were neutral. We can extend this same approach to a pair of residues, where the residue pair 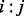Inline graphic is more informative if its sequence variations (among 20 × 20 = 400 possible unique states) correspond to greater evolutionary tree divergences, i.e. those that are closer to the tree root. The piET algorithm therefore applies the standard rvET procedure to pairs of residues within the MSA, to measure these residue–residue patterns in the context of the evolutionary tree. 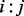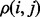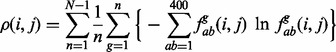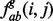The evolutionary importance of a structural neighbor pair Inline graphic is denoted by Inline graphic where,

graphic file with name btt489m6.jpg (6)

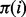where Inline graphic is the frequency of the pair of an amino acid ab of a type within group g of the sub-alignment in the n-th set of sub-alignments. The number of possible nodes in the evolutionary tree is N – 1 where N is the number of sequences in the alignment. The factor Inline graphic was adapted from a previous study (Mihalek et al., 2004) to give weight to the individual sub-alignments based on their location in the phylogenetic tree. The rvET algorithm couples the phylogenetic tree to the pattern of variation of a pair of residues, viewed as a single evolving unit (Supplementary Fig. S1). Once the importance of every pair is available, the piET rank Inline graphic of an individual residue i is calculated by averaging 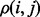Inline graphic over all its neighbors,

graphic file with name btt489m7.jpg (7)

As previously defined in Equation (2), 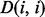Inline graphic is the number of residues in contact with residue i (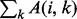Inline graphic). This equation for 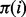Inline graphic factors shared evolution of the contact residues into the ET phylogenetic framework.

2.6 Evolutionary trace annotation

To test the piET algorithm in a large-scale application, we substituted it in place of rvET into the Evolutionary Trace Annotation (ETA) algorithm and asked whether it improved ETA predictions. ETA is a suite of programs for automated discovery of protein function based on their structure. It identifies protein structures that may have identical biochemical functions based on whether they share small structural motifs composed of top-ranked ET residues (Erdin et al., 2010; Kristensen et al., 2008; Ward et al., 2008). In brief, ETA defines structural motifs by (i) mapping ET ranks onto the surface of a protein structure, (ii) detecting clusters of important amino acids and (iii) selecting six top-ranked amino acids from the cluster. The geometry of the alpha carbon atoms of these six residues define a 3D template that is then searched for, by geometric similarity, in the protein data bank (PDB) (Berman et al., 2000). Specificity is enhanced by filtering matches based on evolutionary and structural similarity and ensuring that protein structures match each other reciprocally. These matches are used to construct a network, as previously described (Venner et al., 2010), in which nodes are protein structures and edges indicate functional similarity, as detected by the ETA algorithm. We label this network with known functional information and use a diffusion model to control the propagation of those labels through the network, leading to predictions of function for protein structures currently lacking function annotations. If using piET instead of rvET causes ETA predictions to improve, it suggests that piET is a more useful metric of evolutionary importance.

2.7 Functional annotation test set

The function annotation tests included past query and target sets (Ward et al., 2008; Wilkins et al., 2010). The query set included 1217 structural genomics enzymes annotated to the third or fourth level of the Enzyme Commission (EC) classification. The target set is the subset of the 2008PDB90 (Hobohm et al., 1992), which contains 17 234 proteins, which contains 4387 enzymes with four-digit EC annotations. The combination of the query and target sets resulted in a network of 17 952 proteins among which 5105 are annotated as enzymes. Each protein in the test set was assigned a single enzymatic function.

2.8 Network construction and diffusion

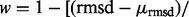
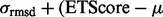
Networks were built and predictions followed as previously described (Venner et al., 2010). Briefly, an ETA template match was converted into a real-valued (edge) weight by averaging the mean evolutionary distance and the rmsd: 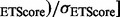Inline graphic Inline graphic Inline graphic. ETA outputs an rmsd and ETScore for each template match. ETScore summarizes the average difference in evolutionary importance (ET Rank) between matched residues and rmsd is the average distance between the atoms in the structures of the matched templates. Additionally, 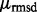Inline graphic is the average rmsd over all template matches, 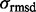Inline graphic is the standard deviation of all rmsds. Likewise, 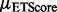Inline graphic is the average ETScore over all template matches and 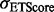Inline graphic is the standard deviation of all ETScores.

Graph diffusion passes functional information between proteins that share similar ETA templates (Venner et al., 2010). We can represent our knowledge of protein enzymatic function as y, a vector of labels representing whether a protein i is associated with a particular EC number (yi). Diffusion of the available information (in this case EC number) leads to a new label, f. We can solve for f by minimizing the following:

graphic file with name btt489m8.jpg (8)

In this expression, the first term is the loss function and represents the difference between initial and final labels. The second term is the smoothness of the new label f in the context of the Laplacian matrix L. The diffusion coefficient μ balances the loss of the initial labels against the smoothness. The previous equation has a closed form solution

graphic file with name btt489m9.jpg (9)

where I is the Identity matrix. The diffusion coefficient μ is calculated as previously shown (Venner et al., 2010).

2.9 Network integration

To test for complementary functional information in rvET and piET, the networks were merged into a single network (Tsuda et al., 2005). We perform diffusion with multiple networks by solving for

graphic file with name btt489m10.jpg (10)

where Lk represents the Laplacian form of network k. 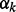Inline graphic is weighting factor that represents the importance of each network in the combination. We can find 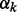Inline graphic by minimizing 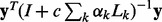Inline graphic. To simplify the minimization problem, we set the additional restriction 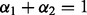Inline graphic (because in this case we have only two networks), and solved using the brute force optimization procedure in the scientific python package (SciPy: Jones, 2001). We are then able to solve for f for a particular y vector that represents a specific enzymatic function (EC number). We solve with a different y for each enzymatic function represented in the network, thus associating every protein in the test set with every function. To compare these values, we normalize to a z-score 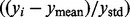Inline graphic. For each protein, the function with the highest z-score is our predicted enzymatic function for that protein, and we use the z-score as a confidence measure in the prediction.

3 RESULTS

3.1 Smoothing the evolutionary importance rank distribution improves functional site predictions

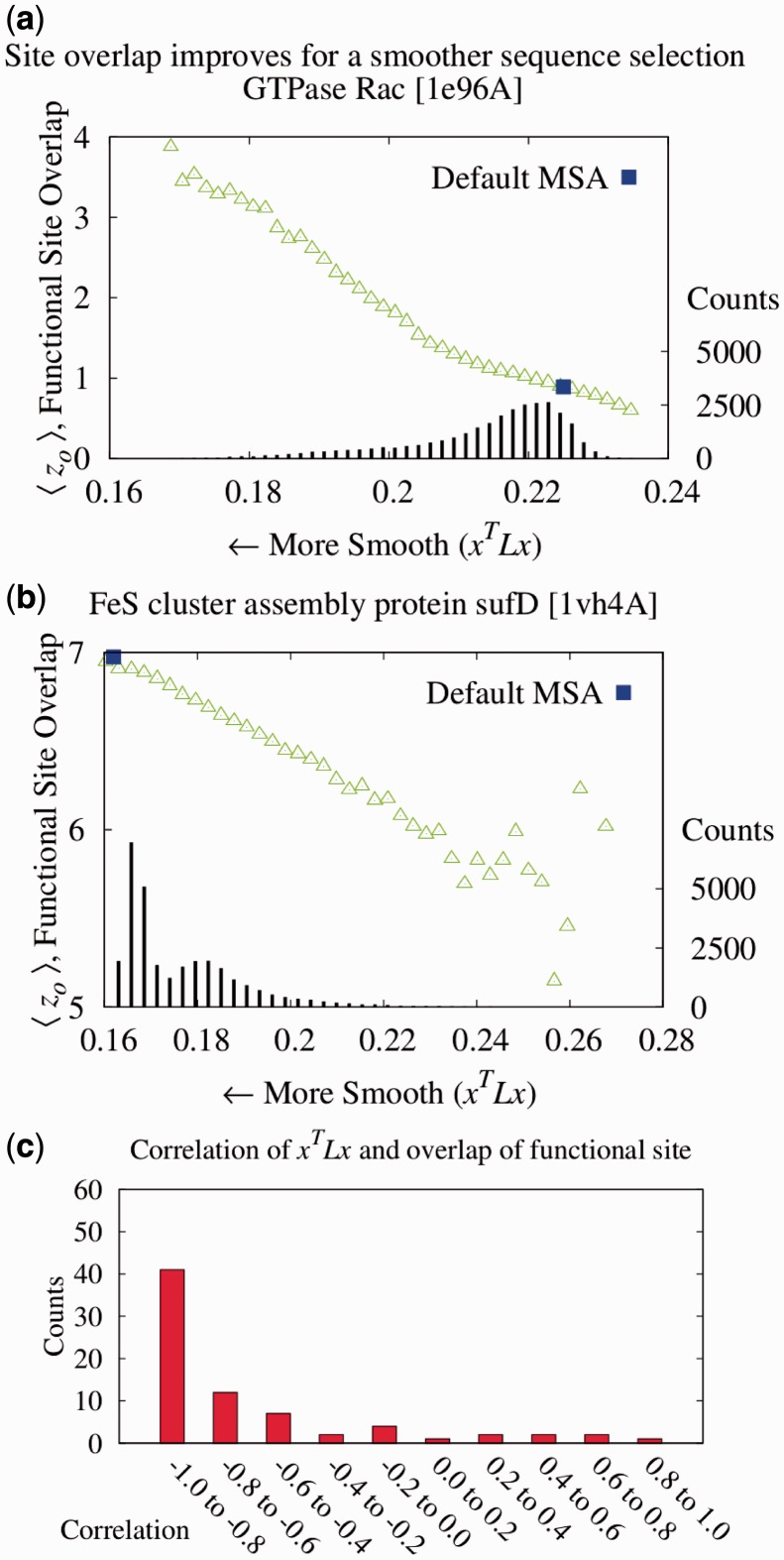
To test whether ET rank smoothness correlates with the quality of functional site predictions, we applied the Laplacian operator to the ET rank distributions on 74 diverse proteins bound to various substrates, cofactors, DNA or proteins (see ‘Methods’ section). For each protein, a large number of alternative MSAs was randomly generated from a default sequence alignment (Fig. 1). This gave rise to multiple ET rank distributions, each one with its unique smoothness, 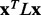Inline graphic and overlap z-score between top-ranked residues and the functional sites annotated in the pdb files (details found in ‘Methods’ section). In most cases (81%), the correlation was strong (Fig. 1c). Exceptions included five proteins with inverse correlations (>0.4) when the ET clusters identified a functional site other than the one referenced in the pdb file gold standard. For instance, in the rhodopsin structure [PDBID 1f88], ET found the G-protein interaction determinants instead of the retinal binding site noted in the crystal structure (Berman et al., 2000). A specialized difference ET analysis would be needed to identify that site, which is specific to visual receptors (Madabushi et al., 2004). A few proteins had small correlation because the functional site prediction was robust and insensitive to the randomization procedure. Nevertheless, averaging over all 74 proteins, including these anomalies, the smoothest sequence selection improved the smoothing function 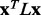Inline graphic by 12.6%; it increased the traditional clustering z-score 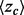Inline graphic by 12.9%, and it raised the overlap z-scores 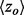Inline graphic by 8.6%. In a second sequence simulation experiment (Supplementary Material), we found that the number of sequences had little influence on the correlations and improvement in functional site prediction. These data show a strong association between improved functional site annotations and smoother distributions of evolutionary importance rankings.

Fig. 1.

Fig. 1.

Open in a new tab

To establish that smoother ET ranks are a desirable feature, we showed that smoothness correlated with the quality of functional site prediction. MSAs of proteins with known functional sites were randomized by selecting a random number of sequences and then analyzed with the rvET algorithm. Every variation in the alignment leads to a new distribution of ET ranks and, in turn, a unique value of the smoothness within the structure (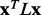Inline graphic) and functional site overlap measure (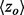Inline graphic). The individual analyses were then binned and counted (black lines) based on the value of 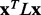Inline graphic where the average overlap measure (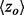Inline graphic) for the analyses in each bin was found (green triangle). Higher 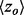Inline graphic implies better site prediction and lower 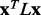Inline graphic implies a smoother distribution of ET ranks over structure. In both cases there is a steady and strong improvement in functional site overlap as smoothness increases, showed by the average overlap z-score 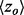Inline graphic for the corresponding bins in the histogram (green). (a) In the GTPase Rac structure [PDBID 1e96A, Human] the default MSA (Blue) did not significantly recover the known binding site, whereas the smoother ET ranks from sequence selection did. (b) By contrast, in the example the structure for FeS cluster assembly protein sufD [PDBID 1vh4A, E.coli], the default MSA (blue) is already smoother than most of the randomly generated alternatives. (c) The value of the smoothing function 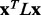Inline graphic for the random input sequences correlates with functional site overlap. The average correlation over the 74 proteins was −0.65

3.2 New Algorithm identifies functional determinants

These results justified a search for an Evolutionary Trace algorithm that is inherently smoother, dubbed piET, which was benchmarked and compared with rvET on the same test set used above Section 3.1. piET produced striking gains: 41% better smoothing, evaluated with the quadratic form of the Laplacian rose; 58% better clustering z-scores 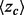Inline graphic among top-ranked residues; and 23% better overlap z-score 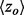Inline graphic against known sites. These functional site prediction improvements were generally consistent across proteins, Figure 2. Hence, the recovery of functional sites improves significantly with an algorithm that measures the importance of residue interactions first, and only deduces the importance of each residue second. This strategy embodies the notion that smoothness is the byproduct of shared evolutionary constraints among interacting residue neighbors. Its success demonstrates that the phylogenomics of piET brings correlated evolution to light, and that one of its hallmarks is the structural smoothness of evolutionary importance.

Fig. 2.

Fig. 2.

Open in a new tab

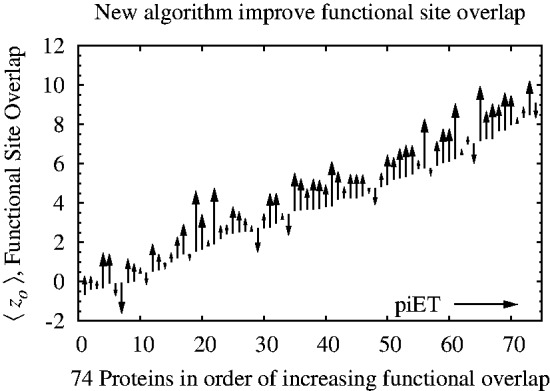
Smoothing the distribution of ET ranks in the protein structure improves the detection of functional residues. A set of 74 proteins was tested for improvement in functional site detection with the piET algorithm. The figure shows the consistent improvement in overlap z-score 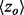Inline graphic for the individual proteins in the test set

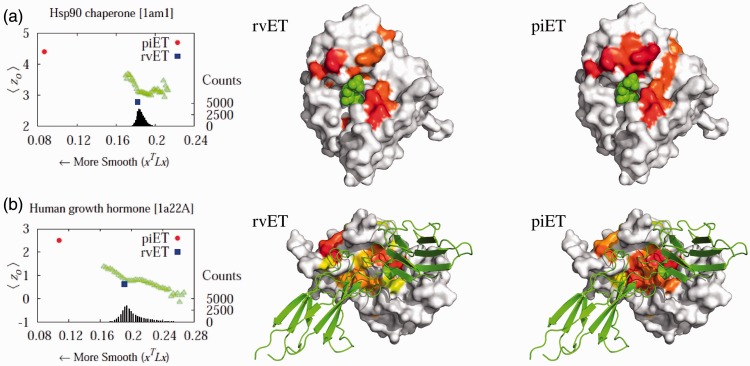
To illustrate these gains in a specific example we next turned to Hsp90, a eukaryotic chaperone critical for protein folding and involved in cell cycle regulation, steroid hormone responsiveness and signal transduction among many other processes. Its functions depend on ATP hydrolysis and the crystallized structure [PDBID 1am1] identifies the ATP–ADP binding sites. Although rvET identified some residues proximal to this site involved in ATP hydrolysis, piET identifies a much larger evolutionarily important site in that region (Fig. 3a), and the overlap z-score 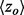Inline graphic increased more than 2-fold (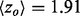Inline graphic to 4.39). In fact, piET also outperforms the rvET optimized by choosing the smoothest outcome after randomization of the sequence input. In a second example, piET predicted the protein–protein interface for the growth hormone and hormone receptor complex [PDBID 1a22] better. Although the rvET had picked important residues in this functional region of the growth hormone, the evolutionary important site with piET is better resolved (Fig. 3b) and statistically more significant (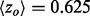Inline graphic to 2.51). In a third example, rvET found the dimer site of the sufD structure [PDBID 1vh4] well, and no randomization of the input sequences could improve this result. Yet, piET sharply raises the statistical significance of the site (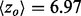Inline graphic to 8.95), Supplementary Figure S3. These representative examples show that piET is inherently smoother than rvET, and that this translates into better clustering among top-ranked ET residues and better functional site identification.

Fig. 3.

Fig. 3.

Open in a new tab

Functional site prediction improves with piET algorithm. The piET algorithm (red) produces a ‘smoother’ distribution and captures the known functional site better than both the rvET algorithm (blue) and the simulation (green). (a) The top 10% residues for Hsp90 chaperone [PDBID 1am1] are marked on the protein surface for algorithms, rvET and piET. The piET algorithm scored more top-ranked residues close to the known protein–ligand site with ADP as shown. (b) The protein–protein interface of hormone and receptor complex [PDBID 1a22] is better identified with the new algorithm. The residues ranked in the top 20% for the respective algorithms, piET and rvET, are shown in prismatic color where the residues marked red are the most evolutionarily important residuess

3.3 Highlighting functional regions in LexA

To demonstrate functional site prediction, piET was next focused on LexA, a well-studied protein that regulates the SOS response to DNA damage in E.coli (Butala et al., 2009). On direct interaction with recombinase A (RecA), LexA dimers self-cleave their DNA binding domain and thus lift transcriptional repression of more than 40 genes, including some that mediate error-prone DNA repair and subsequent escape from genotoxic stress (Butala et al., 2009). The DNA binding and catalytic sites of LexA have been identified but not its RecA interaction site. Although recently rvET suggested a novel composite LexA binding site on RecA (Adikesavan et al., 2011), no such candidate site is apparent on LexA.

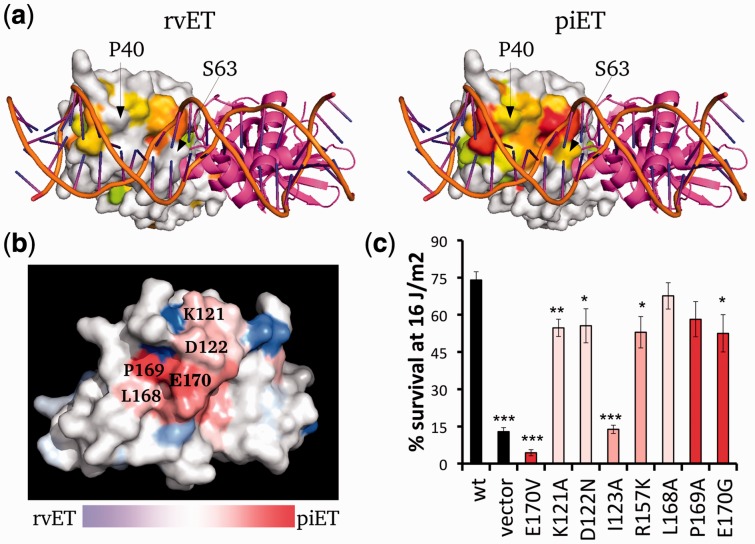
First, piET improved the identification of the known DNA binding site and active site of LexA. While rvET for the most part does not find a cluster of top-ranked residues at the DNA binding site, except for a few nearby residues (Fig. 4a, left panel), piET fully recovers that site (Fig. 4a, right panel). The statistical significance of these predictions (Supplementary Fig. S4) were similar regardless of whether the reference LexA structures was bound to DNA (as in PDBID 3jsp) or not (as in PDBID 1jhh). Moreover, this improvement is not at the expense of loss of ET signal elsewhere in the protein: piET identifies the catalytic active site even better than rvET (Supplementary Fig. S4). Thus, previously characterized sites of LexA are better resolved by piET.

Fig. 4.

Fig. 4.

Open in a new tab

The piET algorithm provides better biological understanding of LexA. (a) The piET algorithm identifies the DNA binding site of LexA better when compared with the rvET analysis (PDBID 3jsp). The residues deemed to be in the top 30% are colored based on evolutionary importance where red is considered the most important. (b) piET identifies a novel cluster of residues. The rvET–piET difference scale is calculated by taking the normalized difference of the rank percentiles. Residues are marked red (piET) or blue (rvET) when the residue is significantly more important to respective method. (c) Mutations at this new LexA site disrupt DNA damage survival. *P < 0.05, **P < 0.01 and ***P < 0.001

Next, we considered a small novel cluster of residues on the LexA structure identified by piET, shown in Figure 4b. piET ranked these residues as 14% more evolutionarily important (rmsd is 3%) on average than rvET. They are in immediate contact with each other and form a tight cluster, therefore fulfilling a hallmark of a functional site not previously recognized. Previously, a single E170V mutation at this site proved important for LexA self cleavage (Lin and Little, 1989). To extend this observation, we performed additional mutations within the piET-identified site neighboring E170. These mutations disturbed LexA function in response to ultraviolet-induced DNA damage, confirming that these residues form a previously unrecognized LexA functional site (Fig. 4c). Together these data show that piET pinpoints functional residues and active sites significantly better than rvET, even in a complex multifunctional protein. In LexA, this leads to the discovery of a novel functional site, possibly pointing to a binding site for RecA.

3.4 piET improves annotation of enzymatic function

To test whether piET also captures functional information on a large scale, we constructed separate function prediction networks with rvET–ETA and piET–ETA. These contained 17 952 proteins (nodes), and 115 784 and 114 542 ETA matches (edges) in the piET and rvET networks, respectively. The diffusion model (Venner et al., 2010) predicted enzymatic function and confidence scores on a test set of 1070 structural genomics enzymes with existing annotations, based on 5105 annotated proteins in the network. Whenever possible, these predictions were up to the fourth level EC number, which describes not only the chemical reaction but also its substrate. In this test, the piET algorithm performed slightly better, with a small improvement (Supplementary Fig. 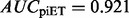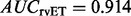S5) in area under the curve (Inline graphic compared with Inline graphic).

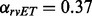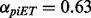To test whether these piET and rvET networks were redundant or complementary, we merged them into a single network (Tsuda et al., 2005). This method creates a weighted combination based on the connectivity of the individual Laplacian matrices and without need for training. The network mixture coefficients were Inline graphic and Inline graphic. The first incorrect prediction of this combined network occurs at 8.1% coverage, and it is preceded by 86 correct ones (Supplementary Fig. S5). By contrast, the first incorrect prediction the rvET or piET networks alone occurred at 30 and 31, respectively. This is of practical importance, as the high confidence predictions are generally the ones we would act on experimentally. The individual algorithms mix in mistakes sooner, and by merging networks we can reduce mistakes. At 100% coverage, the merged network method was 4.3% more accurate and the area under the curve improved to 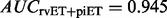Inline graphic. Both the rvET and the piET algorithms for detecting evolutionary importance focus the ETA on different but complementary functional sites. ETA performed best when the algorithms were integrated, showing that each algorithm is providing relevant but unique functional information.

4 DISCUSSION

This study adds in three significant ways to a long-term effort to identify functional sites. First, we show that the spatial distribution of evolutionary information (measured here by ET rank) in a folded structure is smooth. This complements the original notion of ET clusters (Lichtarge et al., 1996) with a mathematically simple interpretation that lends itself to computation via the Laplacian operator of a graph. This discrete Laplacian operator is fundamental to networks (Chung, 1997), and here it enables optimization in sequence selection better than the diverse measures of clustering used before (Wilkins et al., 2010). These were entirely empirical and useful to suggest the simplifying notion of smoothness. We show when we consider the functional linkage between residues, we can better interpret sequence information.

The second improvement builds on this notion of smoothness to develop an algorithm that focuses on a residue’s interactions with neighbors. The method first scores the importance of these interactions and then averages over the neighbor interactions to give the total importance of each residue. This is consistent with prior suggestions (Gutteridge et al., 2003; Raviscioni et al., 2005) that natural selection operates based less on the intrinsic character of an amino acid, than on the nature of its couplings to other residues, here primarily those in its immediate surrounding. Previous studies have noted improvement in predictions when they average evolutionary information for residues over sequence (Capra and Singh, 2007; Pei and Grishin, 2001) and structure (Panchenko et al., 2004; Teppa et al., 2012). We add to this work by quantifying the shared evolutionary pattern between residues near in structure. These interactions are the essence of the residue’s function. Though the method is currently limited to structural information, we can use the constantly improving homology-modeling algorithms (Roy et al., 2010) or databases of pre-computed homology models (Bordoli and Schwede, 2012).

Third, we show how these results follow logically from epistatic interaction among residues. Other methods focused on pairwise interactions via covariation (Pazos and Valencia, 2008), thermodynamic (Maksay, 2011) or energetic coupling (de la Lande et al., 2010). Networks of such correlations often lead to clusters of pathways although their interpretation is not straightforward (Chi et al., 2008). By contrast, clusters of ET residues lead to functional sites shown independently to be highly significant compared with other methods [see Supplementary Materials in Rausell et al. 2010, and extensively tested experimentally in a large variety of proteins (Lichtarge and Wilkins, 2010)]. These validations included mapping and then recoding of allosteric determinants of both interprotein and intraprotein signaling pathways (Rodriguez et al., 2010).

In summary, this work finds and exploits the fact that epistatic forces mold evolution and, as a result, leads to the smooth distribution of evolutionary importance throughout protein structures. This smoothness stems from the functional linkage of residues typically nearby in conformation, a hallmark of epistasis. This basic property leads to new algorithms for computing the evolutionary importance of (a) residue–residue interaction among neighbors, and (b) individual residues. In turn, this substantially improves functional site analysis and function prediction in test sets while also verified experimentally by predicting a novel site in LexA. This should prove useful in guiding protein engineering and mutations to the most relevant parts of a protein. A server performing piET calculations is available at our site: http://mammoth.bcm.tmc.edu/uet.

Supplementary Material

Supplementary Data
supp_29_21_2714__index.html (1KB, html)

ACKNOWLEDGEMENT

The authors thank Panagiotis Katsonis, Andreas M. Lisewski and Ilya Novikov for helpful discussion.

Funding: National Institutes of Health (NIH-GM079656, NIH-GM066099, NLM 5T15LM07093); National Science Foundation (NSF CCF-0905536, NSF DBI-1062455).

Conflict of Interest: none declared.

REFERENCES

  1. Adikesavan AK, et al. Separation of recombination and SOS response in Escherichia coli RecA suggests LexA interaction sites. PLoS Genet. 2011;7:e1002244. doi: 10.1371/journal.pgen.1002244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Aloy P, et al. Automated structure-based prediction of functional sites in proteins: applications to assessing the validity of inheriting protein function from homology in genome annotation and to protein docking. J. Mol. Biol. 2001;311:395–408. doi: 10.1006/jmbi.2001.4870. [DOI] [PubMed] [Google Scholar]
  3. Altschul S, et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Berman H, et al. The protein data bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bordoli L, et al. Automated protein structure modeling with swiss-model workspace and the protein model portal. In: Orry AJW, Abagyan R, editors. Homology Modeling, volume 857 of Methods in Molecular Biology. 2012. pp. 107–136. Humana Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Breen MS, et al. Epistasis as the primary factor in molecular evolution. Nature. 2012;490:535538. doi: 10.1038/nature11510. [DOI] [PubMed] [Google Scholar]
  7. Butala M, et al. The bacterial lexa transcriptional repressor. Cell. Mol. Life Sci. 2009;66:82–93. doi: 10.1007/s00018-008-8378-6. 10.1007/s00018-008-8378-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Buslje CM, et al. Networks of high mutual information define the structural proximity of catalytic sites: implications for catalytic residue identification. PLoS Comput. Biol. 2010;6:e1000978. doi: 10.1371/journal.pcbi.1000978. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Capra JA, Singh M. Predicting functionally important residues from sequence conservation. Bioinformatics. 2007;23:1875–1882. doi: 10.1093/bioinformatics/btm270. [DOI] [PubMed] [Google Scholar]
  10. Casari G, et al. A method to predict functional residues in proteins. Nat. Struct. Biol. 1995;2:171–178. doi: 10.1038/nsb0295-171. [DOI] [PubMed] [Google Scholar]
  11. Chi C, et al. Reassessing a sparse energetic network within a single protein domain. Proc. Natl Acad. Sci. USA. 2008;105:4679–4684. doi: 10.1073/pnas.0711732105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chung FRK. Spectral Graph Theory. American Mathematical Society; 1997. [Google Scholar]
  13. Clackson T, Well JA. A hot spot of binding energy in a hormone-receptor interface. Science. 1995;267:383–386. doi: 10.1126/science.7529940. [DOI] [PubMed] [Google Scholar]
  14. de la Lande A, et al. Surface residues dynamically organize water bridges to enhance electron transfer between proteins. Proc. Natl Acad. Sci. USA. 2010;107:11799–11804. doi: 10.1073/pnas.0914457107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Engelen S, et al. Joint evolutionary trees: a large-scale method to predict protein interfaces based on sequence sampling. PLoS Comput. Biol. 2009;5:e1000267. doi: 10.1371/journal.pcbi.1000267. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Erdin S, et al. Evolutionary trace annotation of protein function in the structural proteome. J. Mol. Biol. 2010;396:1451–1473. doi: 10.1016/j.jmb.2009.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Glaser F, et al. ConSurf: identification of functional regions in proteins by surface-mapping of phylogenetic information. Bioinformatics. 2003;19:163–164. doi: 10.1093/bioinformatics/19.1.163. [DOI] [PubMed] [Google Scholar]
  18. Gutteridge A, et al. Using a neural network and spatial clustering to predict the location of active sites in enzymes. J. Mol. Biol. 2003;330:719–734. doi: 10.1016/s0022-2836(03)00515-1. [DOI] [PubMed] [Google Scholar]
  19. Halabi N, et al. Protein sectors: evolutionary units of three-dimensional structure. Cell. 2009;138:774–786. doi: 10.1016/j.cell.2009.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hardy JA, et al. Searching for new allosteric sites in enzymes. Curr. Opin. Struct. Biol. 2004;14:706–715. doi: 10.1016/j.sbi.2004.10.009. [DOI] [PubMed] [Google Scholar]
  21. Hobohm U, et al. Selection of representative protein data sets. Protein Sci. 1992;1:409–417. doi: 10.1002/pro.5560010313. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Innis CA. siteFiNDER—3D: a web-based tool for predicting the location of functional sites in proteins. Nucleic Acids Res. 2007;35:W489–W494. doi: 10.1093/nar/gkm422. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kristensen DM, et al. Prediction of enzyme function based on 3D templates of evolutionarily important amino acids. BCM Bioinformatics. 2008;9:17. doi: 10.1186/1471-2105-9-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Laskowski R, et al. PDBsum more: new summaries and analyses of the known 3D structures of proteins and nucleic acids. Nucleic Acids Res. 2005;33:D266–D268. doi: 10.1093/nar/gki001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Laskowski RA, Thornton JM. Understanding the molecular machinery of genetics through 3D structures. Nat. Rev. Genet. 2008;9:141–145. doi: 10.1038/nrg2273. [DOI] [PubMed] [Google Scholar]
  26. Lichtarge O, Wilkins A. Evolution: a guide to perturb protein function and networks. Curr. Opin. Struct. Biol. 2010;20:351–359. doi: 10.1016/j.sbi.2010.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Lichtarge O, et al. An evolutionary trace method defines binding surfaces common to protein families. J. Mol. Biol. 1996;257:342–358. doi: 10.1006/jmbi.1996.0167. [DOI] [PubMed] [Google Scholar]
  28. Lin LL, Little JW. Autodigestion and RecA-dependent cleavage of Ind mutant LexA proteins. J. Mol. Biol. 1989;210:439–452. doi: 10.1016/0022-2836(89)90121-6. [DOI] [PubMed] [Google Scholar]
  29. Madabushi S, et al. Structural clusters of evolutionary trace residues are statistically significant and common in proteins. J. Mol. Biol. 2002;316:139–154. doi: 10.1006/jmbi.2001.5327. [DOI] [PubMed] [Google Scholar]
  30. Madabushi S, et al. Evolutionary trace of G protein-coupled receptors reveals clusters of residues that determine global and class-specific functions. J. Biol. Chem. 2004;279:8126–8132. doi: 10.1074/jbc.M312671200. [DOI] [PubMed] [Google Scholar]
  31. Maksay G. Allostery in pharmacology: thermodynamics, evolution and design. Prog. Biophys. Mol. Biol. 2011;106:463–473. doi: 10.1016/j.pbiomolbio.2011.01.001. [DOI] [PubMed] [Google Scholar]
  32. Mihalek I, et al. Combining inference from evolution and geometric probability in protein structure evaluation. J. Mol. Biol. 2003;331:263–279. doi: 10.1016/s0022-2836(03)00663-6. [DOI] [PubMed] [Google Scholar]
  33. Mihalek I, et al. A family of evolution-entropy hybrid methods for ranking protein residues by importance. J. Mol. Biol. 2004;336:1265–1282. doi: 10.1016/j.jmb.2003.12.078. [DOI] [PubMed] [Google Scholar]
  34. Mihalek I, et al. Evolutionary and structural feedback on selection of sequences for comparative analysis of proteins. Proteins. 2006a;63:87–99. doi: 10.1002/prot.20866. [DOI] [PubMed] [Google Scholar]
  35. Mihalek I, et al. A structure and evolution guided monte carlo sequence selection strategy for multiple alignment-based analysis of proteins. Bioinformatics. 2006b;22:149–156. doi: 10.1093/bioinformatics/bti791. [DOI] [PubMed] [Google Scholar]
  36. Onrust R, et al. Receptor and betagamma binding sites in the alpha subunit of the retinal G protein transducin. Science. 1997;275:381–384. doi: 10.1126/science.275.5298.381. [DOI] [PubMed] [Google Scholar]
  37. Ortlund EA, et al. Crystal structure of an ancient protein: evolution by conformational epistasis. Science. 2007;317:1544–1548. doi: 10.1126/science.1142819. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Panchenko AR, et al. Prediction of functional sites by analysis of sequence and structure conservation. Protein Sci. 2004;13:884–892. doi: 10.1110/ps.03465504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Pazos F, et al. Phylogeny-independent detection of functional residues. Bioinformatics. 2006;22:1440–1448. doi: 10.1093/bioinformatics/btl104. [DOI] [PubMed] [Google Scholar]
  40. Pazos F, Valencia A. Protein co-evolution, co-adaptation and interactions. EMBO J. 2008;27:2648–2655. doi: 10.1038/emboj.2008.189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Pei J, Grishin NV. AL2CO: calculation of positional conservation in a protein sequence alignment. Bioinformatics. 2001;17:700–712. doi: 10.1093/bioinformatics/17.8.700. [DOI] [PubMed] [Google Scholar]
  42. Pupko T, et al. Rate4Site: an algorithmic tool for the identification of functional regions in proteins by surface mapping of evolutionary determinants within their homologues. Bioinformatics. 2002;18:S71–S77. doi: 10.1093/bioinformatics/18.suppl_1.s71. [DOI] [PubMed] [Google Scholar]
  43. Rajagopalan L, et al. Essential helix interactions in the anion transporter domain of prestin revealed by evolutionary trace analysis. J. Neurosci. 2006;26:12727–12734. doi: 10.1523/JNEUROSCI.2734-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Rausell A, et al. Protein interactions and ligand binding: from protein subfamilies to functional specificity. Proc. Natl Acad. Sci. USA. 2010;107:1995–2000. doi: 10.1073/pnas.0908044107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Raviscioni M, et al. Correlated evolutionary pressure at interacting transcription factors and dna response elements can guide the rational engineering of dna binding specificity. J. Mol. Biol. 2005;350:402–415. doi: 10.1016/j.jmb.2005.04.054. [DOI] [PubMed] [Google Scholar]
  46. Ribes-Zamora A, et al. Distinct faces of the Ku heterodimer mediate DNA repair versus telomeric functions. Nat. Struct. Mol .Biol. 2007;14:301–307. doi: 10.1038/nsmb1214. [DOI] [PubMed] [Google Scholar]
  47. Rodriguez G, et al. Evolution-guided discovery and recoding of allosteric pathway specificity determinants in psychoactive bioamine receptors. Proc. Natl Acad. Sci. USA. 2010;107:7787–7792. doi: 10.1073/pnas.0914877107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Roy A, et al. I-TASSER: a unified platform for automated protein structure and function prediction. Nat. Protocols. 2010;5:725–738. doi: 10.1038/nprot.2010.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Shenoy S, et al. Beta-arrestin-dependent, G protein-independent ERK1/2 activation by the beta2 adrenergic receptor. J. Biol. Chem. 2006;281:261–273. doi: 10.1074/jbc.M506576200. [DOI] [PubMed] [Google Scholar]
  50. Sowa M, et al. Prediction and confirmation of a site critical for effector regulation of RGS domain activity. Nat. Struct. Biol. 2001;8:234–237. doi: 10.1038/84974. [DOI] [PubMed] [Google Scholar]
  51. Sowa ME, et al. A regulator of G protein signaling interaction surface linked to effector specificity. Proc. Natl Acad. Sci. USA. 2000;97:1483–1488. doi: 10.1073/pnas.030409597. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Teppa E, et al. Disentangling evolutionary signals: conservation, specificity determining positions and coevolution. implication for catalytic residue prediction. BMC Bioinformatics. 2012;13:235. doi: 10.1186/1471-2105-13-235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Thyme SB, et al. Exploitation of binding energy for catalysis and design. Nature. 2009;461:1300–1304. doi: 10.1038/nature08508. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Tsuda K, et al. Fast protein classification with multiple networks. Bioinformatics. 2005;21(Suppl. 2):ii59–ii65. doi: 10.1093/bioinformatics/bti1110. [DOI] [PubMed] [Google Scholar]
  55. Valdar W. Scoring residue conservation. Proteins. 2002;43:227–241. doi: 10.1002/prot.10146. [DOI] [PubMed] [Google Scholar]
  56. Venner E, et al. Accurate protein structure annotation through competitive diffusion of enzymatic functions over a network of local evolutionary similarities. PLoS One. 2010;5:e14286. doi: 10.1371/journal.pone.0014286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Ward RM, et al. De-orphaning the structural proteome through reciprocal comparison of evolutionarily important structural features. PLoS One. 2008;7;3:e2136. doi: 10.1371/journal.pone.0002136. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Wilkins AD, et al. Sequence and structure continuity of evolutionary importance improves protein functional site discovery and annotation. Protein Sci. 2010;19:1296–1311. doi: 10.1002/pro.406. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Yao H, et al. An accurate, sensitive, and scalable method to identify functional sites in protein structures. J. Mol. Biol. 2003;326:255–261. doi: 10.1016/s0022-2836(02)01336-0. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_29_21_2714__index.html (1KB, html)
supp_btt489_Wilkins-Lichtarge-supplemental.pdf (835.3KB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES