Structured illumination quantitative phase microscopy for enhanced resolution amplitude and phase imaging

Abstract

Structured illumination microscopy (SIM) is an established microscopy technique typically used to image samples at resolutions beyond the diffraction limit. Until now, however, achieving sub-diffraction resolution has predominantly been limited to intensity-based imaging modalities. Here, we introduce an analogue to conventional SIM that allows sub-diffraction resolution, quantitative phase-contrast imaging of optically transparent objects. We demonstrate sub-diffraction resolution amplitude and quantitative-phase imaging of phantom targets and enhanced resolution quantitative-phase imaging of cells. We report a phase accuracy to within 5% and phase noise of 0.06 rad.

1. Introduction

In biological microscopy, there has been a continued drive towards increasing imaging resolution for relevant samples [1]. In many cases, this drive translates to designing better optical systems to optimize for aberrations and resolution to achieve diffraction-limited performance [2]. However, in cases where better resolution is still required, this drive leads to a need to extend the imaging resolution to beyond the system’s diffraction limit. Such a need has driven the development of many unique sub-diffraction imaging techniques that have made large impacts for microscopy.

This set of techniques can largely be divided into two classes. The first class of techniques is targeted towards cases where the sample is coherently illuminated and diffracts into the imaging system’s aperture [3]. In such cases, the general strategy to obtain sub-diffraction resolution makes use of the fact that imaging resolution is simply one of several degrees of freedom that describe the imaging system. Though the total number of degrees of freedom is invariant, it is possible to sacrifice less desired ones, such as temporal, polarization, or field-of-view constraints, to improve the final image resolution to beyond the conventional diffraction limit [4, 5]. Of closest relevance to this work are spatiotemporal encoding and oblique illumination schemes, which either simultaneously or sequentially tilt different regions of a sample’s spatial frequency spectrum into the system’s aperture. The final image will then have a net frequency support synthesized from all the individual diffraction-limited frequency regions, which is ultimately responsible for the image’s sub-diffraction resolution [6–10]. This is a central theme in most synthetic aperture techniques.

The second class of sub-diffraction resolution imaging techniques is a more recent development that has found great impact in biological fluorescence imaging. By appropriately utilizing properties of fluorophores, one can visualize a fluorescent sample at “super” resolutions beyond the diffraction limit. This class of “super-resolution” techniques is further subdivided into two main categories. The first main category is based on single molecule localization, where individual fluorescent emitters are localized at sub-diffraction resolution for each raw acquisition, and then aggregated into one final super-resolved image. Examples of such techniques include photoactivated localization microscopy (PALM) and stochastic optical reconstruction microscopy (STORM) [11, 12]. The second category of super-resolution techniques uses spatially modulated excitation to narrow the effective imaging point-spread-function. Either this is done directly, as in stimulated emission depletion (STED) and ground-state depletion (GSD), or indirectly after post-processing, as in structured illumination microscopy (SIM) [13–16]. Of these super-resolution techniques, SIM holds the unique advantage of potential extension to non-fluorescent samples, and has shown exciting potential for such cases [6, 8, 10, 17, 18].

In this work, we describe another such extension of SIM that allows high-contrast and enhanced-resolution imaging of transparent samples via quantitative phase contrast. In the biological sciences, quantitative phase profiles of cells allow determination of cellular structure and composition with minimal sample preparation. Especially in cases where conventional preparation techniques, such as fixation, staining, or fluorescent tagging, may affect cellular functions and limit biological insight, quantitative phase imaging (QPM) offers an important alternative [19–22]. In other cases, such as determining cellular path lengths or refractive index, QPM is one of the few available options. However, due to the coherent laser illumination required for QPM, the diffraction-limited resolution for QPM is less than that of typical incoherent imaging systems [1]. This work uses structured illumination of the sample to extend all the quantitative capabilities of QPM to sub-diffraction resolution for coherent imaging, thus matching the imaging resolution of QPM to that of its conventional, incoherent imaging counterparts.

2. Theory

2.1. Off-axis digital holography

We review below the basics of complete reconstruction (amplitude and phase) of a sample by off-axis digital holography. Consider the complex transmittance of a sample, given by $x(r)$, under some illumination field pattern, given by $i(r)$, that is optically passed through a system and generates a coherent image at the camera, given by $y(r)$. Here, r is the 2D spatial coordinate vector. This coherent image is then interfered by an off-axis reference wave, given by $U_r(r)=\exp (-jk\cdot r)$. Here, proportionality constants are disregarded for mathematical simplicity and k is defined as the direction vector. The net interference pattern at the camera will then be given by:

$$\begin{array}{l}n\left(r\right)={\left|y\left(r\right)+U_r\left(r\right)\right|}^2\\ \text{=}1+{\left|y\left(r\right)\right|}^2+y\left(r\right)\exp \left(-j ·kr\right)+y^{*}\left(r\right)\exp \left(j k·r\right)\end{array}$$ (1)

The third and fourth terms sum together to describe the carrier heterodyne frequency, a key indicator for holographic data, which consists of the complete image information multiplied by opposite phase shifts. These spatial multiplications by the phase shifts results in frequency shifts of the image information by $k\cdot r$ and $-k\cdot r$ in Fourier space. If the optical system is designed such that these frequency shifts separate the image spectra from the DC-centered support of the first two terms of Eq. (1), then $y(r)$ can be completely reconstructed, amplitude and phase, via digital filtering and simple Fourier manipulations [1].

2.2. Enhancing resolution via structured illumination

In typical SIM, because the fluorescent, spatially incoherent, emission is detected from the sample, the intensity at the image plane is a linear transform of the sample structure. Here, the spatially coherent diffraction, not fluorescence, from the sample is detected, and thus the image field is a linear transform of the sample transmittance function [3]. Assuming that the illumination and detection arms of the optical system are both limited by the same numerical aperture (NA), we can write

$$y\left(r\right)=h_c\left(r\right)\otimes \left[x\left(r\right)·\left[h_c\left(r\right)\otimes i\left(r\right)\right]\right]$$ (2)

where ⊗ is the convolution operator, $h_c(r)$ is the system’s coherent point spread function, and the steps outlined above are taken to recover $y(r)$ from holographic raw data. Fourier transforming, we get,

$$Y\left(\omega \right)=H_c\left(\omega \right)·\left[X\left(\omega \right)\otimes \left[H_c\left(\omega \right)·I\left(\omega \right)\right]\right]$$ (3)

where is the spatial coordinate vector, $Y\left(\omega \right),H_c\left(\omega \right),X\left(\omega \right),andI\left(\omega \right)$ are the Fourier transforms of $Y\left(r\right),h_c\left(r\right),x\left(r\right),andi\left(r\right)$ respectively, and $H_c\left(\omega \right)$ is defined as the system’s transfer function. In the case of plane wave illumination, $i\left(r\right)=1$, $I\left(\omega \right)=\delta \left(\omega \right)$, and Eq. (3) becomes a spatially low pass filtering equation, $Y_{BF}\left(\omega \right)=H_c\left(\omega \right)\cdot X\left(r\right)$, where $H_c\left(\omega \right)$ sets the system’s diffraction limit. From coherent diffraction theory [3], we know that $H_c\left(\omega \right)$ acts as a tophat filter that sharply rejects spatial frequencies with magnitude beyond some cutoff, say ${\omega }_c$, and passes all other frequencies.

We now describe how to obtain an enhanced resolution image containing spatial frequencies $\left|\omega \right|>{\omega }_c$ without physically using a larger aperture. In the case of an illumination field set by two interfering beams, we have $i(r)=\cos ({\omega }_0\cdot r+{\varphi }_n)$, where $\left|{\omega }_0\right|\le {\omega }_c$ is the illumination’s frequency vector. Fourier transforming and substituting into Eq. (3), we see that the corresponding acquisition will have a Fourier distribution of the form,

$$Y_n\left(\omega \right)=H_c\left(\omega \right)·\left[X\left(\omega -{\omega }_0\right) e^{-j {\varphi }_n}+X\left(\omega +{\omega }_0\right) e^{j {\varphi }_n}\right]$$ (4)

Here, as in conventional SIM, we see that this raw acquisition contains high frequency content beyond the diffraction limit, incorporated into terms $X\left(\omega -{\omega }_0\right)$ and $X\left(\omega +{\omega }_0\right)$, shifted into the system’s passband. As in conventional SIM, by phase-stepping $i(r)$, we can linearly solve for $X\left(\omega -{\omega }_0\right)$ and $X\left(\omega +{\omega }_0\right)$ and demodulate them back to their appropriate positions in Fourier space to reconstruct the image $Y_{SI}\left(\omega \right)=H_{eff}\left(\omega \right)\cdot X(r)$, where $H_{eff}\left(\omega \right)$ is now the effective system transfer function of plane wave illumination given by

$$H_{eff}\left(\omega \right)=H_c\left(\omega -{\omega }_0\right) +H_c\left(\omega +{\omega }_0\right)$$ (5)

It is clear from Eq. (5) that $H_{eff}\left(\omega \right)$ has a larger frequency support than $H_c\left(\omega \right)$, and thus $Y_{SI}\left(\omega \right)$ is more highly resolved than $Y_{BF}\left(\omega \right)$ along the orientation set by ${\omega }_0$. Interestingly, because $H_{eff}\left(\omega \right)$ does not contain a non-shifted region of frequency information, it actually loses diffraction limited information along the orientation orthogonal to ${\omega }_0$, which is directly in contrast with conventional SIM. However, this “gap” Fourier space is filled out by repeating this procedure with rotations of the illumination pattern. Maximal resolution gain is achieved when $\left|{\omega }_0\right|={\omega }_c$, and corresponds to a gain by a factor of two. Conventional deconvolution procedures can be used to reshape the final transfer function before inverse Fourier transforming to reconstruct the enhanced-resolution image [23], which has amplitude and quantitative phase information of the sample at sub-diffraction resolutions. We call this technique structured-illumination quantitative phase microscopy (SI-QPM).

We note that from Eq. (4), extended resolution images can theoretically be reconstructed by taking only 2 phase-stepped raw acquisitions per rotation; taking more, however, increases SNR and fidelity of reconstruction, and we usually take 6 raw acquisitions instead of 2, as mentioned in the experimental descriptions below. We also note that the heterodyne carrier and the structured illumination frequencies are physically distinct, and that the two frequencies, though simultaneously visible in the image, give independent information about the sample. We describe this in more detail later.

3. System design

The optical system designed to experimentally test this SI-QPM framework was based on a Mach-Zehnder off-axis interferometric transmission microscope. We show the schematic of our optical system below in Fig. 1 . Single spatial mode 532 nm illumination was provided by a frequency-doubled solid-state Nd:YAG laser (Coherent, Inc.) transmitted through a single-mode optical fiber (Thorlabs, 460HP). Collimated light from the fiber was split into sample and reference arms of the Mach-Zehnder interferometer. In the sample arm, the beam was further split into diffraction orders by a ronchi diffraction grating (DG, Edmund Optics, 50 lpmm). These orders were directed through a 4f system (L1 → OBJ) and filtered so that only the +/− 1 orders interfered at the sample to create the sinusoidal structured pattern. The transmitted diffraction pattern from the sample was then coherently imaged by a second 4f system (OBJ → L2) onto the surface of a CMOS camera (Pixelink, Ottawa, ON). This coherent image at the CMOS camera was interfered with an off-axis reference wave for amplitude/phase reconstruction. The modulation depth of this interference was maximized by tuning the optical path delay (OPD) element in the reference arm. Rotation and phase-stepping the illumination pattern was possible by mounting the DG on a rotational mount on a lateral translation stage.

Fig. 1.

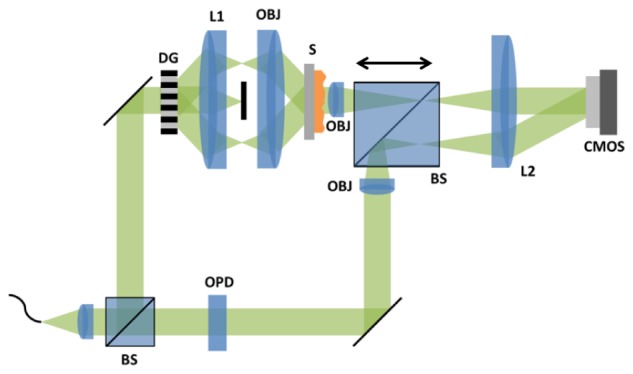
Optical system based on an off-axis interferometric transmission microscope configuration. Single mode 532 nm Gaussian beam illumination is split into sample and reference arms of interferometer by a beam splitter (BS). In the sample arm, the first 4f system Fourier filters through only the +/− 1 orders of the diffraction grating (DG) and images them onto the sample (S) plane to create a structured illumination pattern. The resulting sample diffraction is coherently imaged via the second 4f system to a CMOS camera and interfered by the reference wave.

Both 4f systems in the sample arm used identical objectives lenses (OBJ), so that their NA defined the limiting aperture of the system. In the experimental results shown below, imaging of the amplitude calibration, phase calibration, and biological cell samples were done with objectives with NAs of 0.4, 0.25, and 0.65, respectively (Newport M-20X, M-10X, and M-40X). For these objectives, the diffraction limited frequency supports were measured to be $1\mu m^{-1},0.5\mu m^{-1},1.5\mu m^{-1}$, corresponding to diffraction limited resolutions of $1\mu m^{-1},2\mu m^{-1},0.6\mu m^{-1}$, respectively. For each objective, lens L1 was chosen so that the +/− 1 diffraction orders from DG are focused to the edge of the objective’s pupil (focal lengths for L1 were f = 250, 250, and 200 mm for the M-20X, M-10X, and M-40X objectives, respectively). Lens L2 (f = 300 mm) was chosen to magnify the image of the sample onto the CMOS camera. Note that the angle at which the reference wave hits the imaging plane, which directly affects the carrier frequency heterodyned with the sample’s image, is determined by both L2 and the lateral positioning of the second beamsplitter (BS). By laterally translating BS, this carrier frequency can be easily tuned. To digitally filter the relevant sample information, as described in Section 2.1, this carrier frequency needs to be beyond the diffraction limited support of the image. This includes the frequency of the structured illumination pattern at the image plane, which is possible because the structured pattern on the sample is magnified (ie NA is lowered) by the second 4f system in the sample arm. In the end, this carrier frequency is fundamentally limited by the camera, and should be tuned using the BS so that it approaches the Nyquist sampling rate given by the camera pixel size. To achieve enhanced resolution up to twice the diffraction limit, two orthogonal rotations of the DG, with 6 phase-steps per rotation, are used. Of course, a more isotropic filling of Fourier space can be achieved with more rotations.

4. Results

4.1. Enhanced resolution amplitude imaging of calibration chart

To verify the resolution enhancement framework explained above, a 1951 USAF test target was first imaged, with diffraction limited resolution of 1µm, as a calibration sample for enhanced resolution imaging. This calibration sample was composed of opaque chrome bars set on a transparent glass background and was imaged transmissively. Note that this target is an amplitude object (ie phase profiles of this object do not carry useful information) and thus only the diffraction limited and extended resolution amplitude images of the object are compared below.

Figure 2 below outlines the off-axis holographic processing used to reconstruct amplitude field information at the image plane from a single acquisition in the orthogonal (i.e., wide-field) illumination (a-d) and structured illumination (e-h) cases. In both cases, the raw detected image was the interference pattern (a,e) generated at the image plane of the camera when the coherent image of the sample was mixed with the off-axis reference plane wave. In the case of structured illumination of the sample (e), however, the coherent image included the structured interference at the sample and thus the net raw interferogram consisted of competing interferences between the normal carrier frequency and the sample’s structured illumination. We digitally filtered and DC centered the region of Fourier space corresponding to the sample image information (outlined by yellow dashed circle in (b,f)) and inverse Fourier transformed to reconstruct the final images (d,h). In the reconstructed amplitude image in the case of structured illumination (h), we see the sinusoidal structured illumination pattern overlayed on the sample structure. Phase stepping this pattern, of course, is what ultimately allows enhanced resolution reconstruction, as discussed below.

Fig. 2.

Holographic reconstruction is shown for orthogonal (i.e., wide-field) illumination (a-d) and structured illumination imaging (e-h) before post-processing for enhanced resolution. (a,e) Raw interferograms at image plane are shown for orthogonal and structured illumination imaging and (b,f) associated Fourier spectra. In inset of (a) note the horizontal fringes from off-axis reference wave illumination, and in inset of (e) note overlapping horizontal fringes from off-axis reference wave illumination and vertical fringes from structured illumination (c,g) Digitally filtered and DC centered spectra from (b,f) and corresponding (d,h) inverse Fourier reconstructions are shown.

We note again that the heterodyned carrier frequency needs to lie beyond the frequency support of the image to allow proper holographic reconstruction. Though this carrier frequency occurs as a structured pattern on the image, it is purely used for amplitude and phase reconstruction, and cannot be used for enhancing imaging resolution of the sample. This is because the carrier frequency occurs from interaction with the sample’s image, which was already low-passed filtered by the system’s limiting aperture before hitting the image plane; ie at the image plane, there is no enhanced resolution to be obtained via further structured illumination.

To perform enhanced resolution amplitude field imaging, 6 raw acquisitions are acquired such as is shown in Fig. 2(e) with incrementally phase stepped illuminations at two rotation angles. In Figs. 3(b) and 3(c) below, extended resolution component images are shown with their corresponding Fourier spectra for sinusoidal illumination rotations of 0° and 90°. Adding (b) and (c) gives (d), which is the final extended resolution amplitude field reconstruction. The extended resolution information in (d) allowed clear and sharp visualization of the USAF Group 9 bars, which were all beyond the original diffraction limit and completely blurred out in the diffraction limited image (a). Note that we have filled out Fourier space with only two rotations. By using more rotations, we could fill out Fourier space more isotropically with a linearly growing computation cost.

Fig. 3.

Enhanced resolution reconstruction showing Fourier spectra (i) and associated amplitude of inverse Fourier transform (ii). (a) Diffraction limited image of sample under orthogonal (wide-field) illumination (b,c) Enhanced resolution field amplitude reconstructions from horizontal and vertical sinusoidal structured illumination of the sample (d) Final enhanced resolution amplitude reconstruction containing enhanced resolution information from both orientations

4.2. Enhanced resolution quantitative phase imaging

This technique is also demonstrated for extended resolution quantitative phase imaging. For this demonstration, the sample of choice was a blazed diffraction grating, where the blazed grooves acted as phase ramps spaced at $D=1.6\mu m$ apart, below our diffraction-limited resolution of 2 µm. The grating was imaged in air ($n_1=1$). The procedure used to perform enhanced resolution phase imaging was identical to that illustrated for amplitude imaging in Section 4.1 above, except that we now reconstructed phase, rather than amplitude maps. Only one orientation of structured illumination pattern was used since the grating had spatial frequencies in only one orientation. More orientations would be required for samples with 2D spatial frequency distribution.

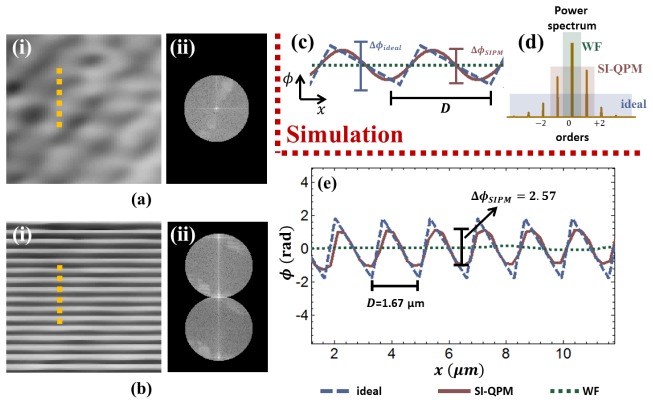
To demonstrate the quantitative nature of the enhanced-resolution phase images, the expected phase values from imaging the blazed grating are simulated. The grating was made of glass B270 ($n_2=1.523$) and had a groove depth of 700 nm, which results in a phase delay of of $\Delta {\varphi }_{ideal}=\frac{2\pi }{\lambda }D(n_2-n_1)$ across the grating. A numerically simulated phase profile (assuming constant amplitude transmittance) of this blazed grating is shown with the dashed blue line in Fig. 4(c) and the associated power-spectrum is shown in Fig. 4(d). We note that this power-spectrum is composed of distinct orders encoding the grating’s periodic profile. From the Fourier diffraction theorem, this spectrum is physically observed at the pupil plane of the imaging objective. The system was designed such that the objective’s aperture can physically only pass the 0th order under orthogonal illumination. By inverse Fourier transforming to simulate diffraction-limited imaging, the resulting diffraction-limited image of the grating completely low-pass filters out the grating phase structure and has a flat phase profile, as shown in dashed green in Fig. 4(c). This profile, of course, has no useful structural information about the sample. Simulating the enhanced resolution framework as described above allows to increase the net imaging bandwidth by a factor of two, which allows us to pass the +/− 1 orders and to image the fundamental spatial frequency of the grating, shown by the solid pink in Fig. 4(c). The maximum phase delay in this fundamental spatial frequency was found via simulation to be $\Delta {\varphi }_{SIPM}=2.7rad$. The image information that accounts for the difference between $\Delta {\varphi }_{ideal}$ and $\Delta {\varphi }_{SIPM}$ (i.e., the spatial frequencies describing the sharp edges of the sawtooth pattern) lie in the orders beyond the +/− 1, which lie beyond even by the enhanced resolution passband.

Fig. 4.

(a) Diffraction-limited and (b) enhanced-resolution images and corresponding Fourier spectrum of a blazed grating are shown. (c) We simulate the phase profile of ideal (blue dashed line), diffraction-limited (WF, green dashed line), and enhanced-resolution (SI-QPM, pink solid line) imaging of the grating and show the corresponding bandpasses on the sample’s power spectrum. (e) This simulation is experimentally verified by taking cross-cuts from the diffraction-limited and enhanced-resolution images, as shown in dashed yellow in (a,b), and comparing to the expected ideal simulated blaze profile.

Experimental confirmation was performed for these simulated results. Figures 4(a) and 4(b) shows the experimental quantitative phase images and associated Fourier spectra for diffraction-limited (WF) and enhanced resolution (SI-QPM) imaging, respectively, of the phase grating. Other than speckle noise, which we treat as a coherent imaging artifact, no sample structure is observed in the WF phase image. In contrast, the grating’s structure is clearly visible in the SI-QPM image. Cross-cuts of the WF and SI-QPM phase images taken along the yellow dashed lines are plotted with respect to the simulated phase profile of the grating in Fig. 4(e) As expected from the simulations, the WF cross-cut has no useful sample information while the SI-QPM cross-cut contains the grating’s fundamental spatial frequency. The measured phase difference across the SI-QPM profile is $\Delta {\varphi }_{SIPM}=2.57rad$, which is in good agreement with the expected $2.7rad$ from simulation (within 5%) and thus demonstrates SI-QPM’s ability to reliably provide quantitative phase information at sub-diffraction resolution. The main contributor to any phase error is expected to be speckle noise, which had a variance measured to be ${\sigma }_{speckle}^2=0.06$ for our particular system.

4.3. Enhanced resolution quantitative phase imaging on cells

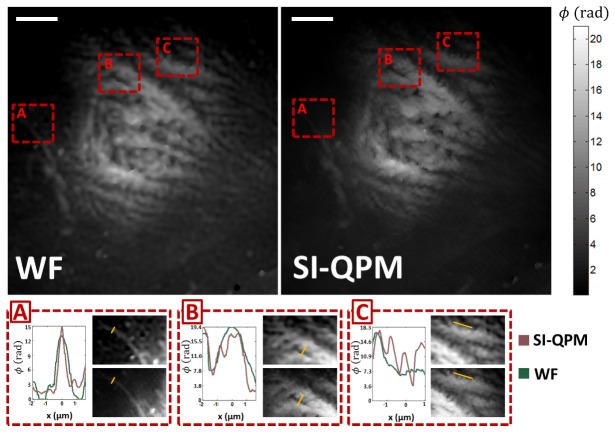
Finally, we illustrate enhanced resolution imaging of biologically relevant phase samples. For this, isolated mesenchymal cells from umbilical cord blood were obtained from the Carolina Cord Blood Bank at Duke University and imaged using SI-QPM. All procedures complied with policies determined by the Duke University Institutional Review Board. Each cell type was seeded at a density of 50 x 10⁴ cells/cm² on 4-well glass chambers (Lab-Tek). The samples were cultured for 48 hours before being fixed with cold methanol for 5 minutes. These samples were unstained and transparent and were treated as pure phase objects. Diffraction-limited (WF) and extended resolution (SI-QPM) phase images of these cells are compared in Fig. 5 below, where an individual mesenchymal cell was fixed while undergoing mitosis and imaged with 600 nm diffraction limited resolution. Biologically, the nuclear material is known to condense at the start of mitosis in preparation of cell division. Indeed, we see that much of the phase signal (i.e. longer optical path lengths) in Fig. 5 below were localized to within the nucleus, where the heterogeneous distribution of condensed nuclear material was clearly visible with high signal and contrast. We note again that this high signal/contrast visualization of the cell was made possible without any extrinsic contrast agents and derived purely from the intrinsic distribution of intracellular phase delays. This high signal/contrast visualization of the intricate nuclear condensate, in turn, offers fine features that were resolvable only by enhanced resolution, which we explore below

Fig. 5.

Comparison are of diffraction limited (WF) and enhanced resolution (SI-QPM) quantitative phase imaging of mesenchymal stem cells. Images are color-coded for quantitative phase delays through the sample. Scale bars on upper left correspond to 10 µm. Close-up comparisons of 3 regions (A,B,C) are shown below along with an associated line profile (marked in yellow).

We selected three intracellular regions-of-interest (ROIs) for closer inspection (A,B,C) that contain information about the morphology of the nuclear material. ROI-A focuses on an extension of the nuclear lamina that projected out into the cellular cytoplasm. ROI-B zooms in on a crevice between adjacent nuclear condensate and ROI-C focuses on fine features at the edge of a single nuclear condensate. In all cases, the improvement of image quality due to the addition of enhanced resolution information is clearly visible when considering SI-QPM compared to WF. Cross-sectional line profiles from each of these ROIs are plotted to quantitatively illustrate this resolution improvement and observe finer fluctuations of intracellular phase delays for SI-QPM, corresponding to the finer features that are only present due to extended resolution.

5. Discussion

In this work, the theory of conventional SIM has been expanded to allow for enhanced resolution amplitude/phase imaging of samples. Experimental results have been shown that validate this theory by obtaining enhanced resolution images of amplitude and phase samples through SI-QPM. We now compare this SI-QPM approach to conventional SIM, as well as to our earlier described technique structured oblique illumination microscopy (SOIM) [8].

We first note that in SIM/SOIM systems, the sample is typically imaged via epi- mode, and thus the illumination and detection arms of the system share the same limiting aperture. Therefore, maximum resolution gain is achieved when the illumination spatial frequencies are set to the edge of the system passband, which results in a factor of two improvement over the diffraction limit. Analogously, the illumination and detection arms of the SI-QPM system were designed with equal numerical aperture and thus the theoretical resolution is also twice the diffraction limit. However, unlike SIM/SOIM, the SI-QPM system images the sample through a transmission configuration, and thus the limiting apertures for illumination and detection are physically distinct. Thus, it is possible to use a larger NA for illumination than detection. This would allow greater than 2x the diffraction-limited resolution (with respect to the detection NA), allowed by the greater illumination NA, with all the benefits of larger field-of-view and longer depth-of-field, as allowed by the lower detection NA. The transmission configuration was selected for SI-QPM since most phase samples of interest back-scatter negligibly. If a sample does largely back-scatter, phase information would be less relevant and it would be optically simpler to achieve extended resolution imaging via SOIM.

We also note the mathematical similarity between SI-QPM and SIM reconstruction. In SIM, the measured intensity distribution at the image plane is a linear transform of the fluorescent emission distribution at the sample, and thus super-resolution reconstruction requires a simple linear inversion process. In SI-QPM, the sample is illuminated with a coherent field, and therefore the measured field pattern at the image plane is a linear transform of the complex transmittance at the sample plane. Thus, extended-resolution via SI-QPM is also achieved linearly. This is in direct contrast to SOIM, where the measured intensity at the image plane is not linearly related to the amplitude transmittance, and hence extended-resolution must be obtained by solving a non-linear system [8].

There is a crucial difference between SIM and SI-QPM. SI-QPM images the sample through coherent diffraction, not fluorescent emission. Thus, when we create the sinusoidal structured pattern on the sample via 2- beam interference, we are essentially doing simultaneous oblique illumination microscopy for each illumination beam. This directly leads to realizing that each individual illumination beam multiplexes regions of frequency content, individually diffraction limited but shifted over different regions of the sample’s spectrum, into the system’s detection aperture. The reconstruction process is then essentially a separation of these multiplexed components and though the final reconstructed image has a frequency support greater than that of the diffraction-limit, each enhanced-resolution component could be obtained using a single, properly oriented, illumination beam. This is in contrast to SIM, where the achieved resolution gain cannot be attributed to any single beam, regardless of orientation. Thus, though the post-processing reconstruction procedures for SIM and SI-QPM are almost identical, the associated optical phenomena are quite different, and we refrain from using the term “super-resolution”, a phrase often associated with SIM, to describe SI-QPM. In this respect, both SI-QPM and SOIM have substantial similarities to synthetic aperture techniques.

In the end, however, SI-QPM (and SOIM) allows imaging of non-fluorescent samples at resolution levels up to twice the diffraction limited resolution of coherent imaging. Furthermore, SI-QPM allows high contrast, quantitative, sub-diffraction imaging of phase samples, a class of samples that has remained largely untouched by most sub-diffraction imaging. This, of course, finds particular biological relevance when imaging cells that are inherently transparent. Conventional methods to image such cells with high contrast and resolution may include fixing and staining the cells, which kills the cells, or using fluorescent tags, which may affect cellular function dynamics. SI-QPM offers an alternative to obtain high contrast, high resolution images of cell morphology and dynamics with minimal sample preparation.

6. Conclusion

We have introduced the technique of SI-QPM which combines structured illumination microscopy with quantitative phase microscopy to allow extended resolution imaging of phase and amplitude samples. We show this concept at work for enhanced resolution imaging of a calibrated test target (amplitude object), a blazed phase grating with known profile (phase object), and mesenchymal cells. In all cases, high contrast images were reconstructed that had a spatial frequency support exceeding that of the system’s diffraction limit. This work has particular relevance towards imaging of unstained and largely transparent cells, where the information is encoded in the sample’s phase rather than amplitude distribution. Thus, being able to image sub-diffraction features on a phase object is a unique and biologically important ability that SI-QPM allows.