A super-resolution ultrasound method for brain vascular mapping

Abstract

Purpose: High-resolution vascular imaging has not been achieved in the brain due to limitations of current clinical imaging modalities. The authors present a method for transcranial ultrasound imaging of single micrometer-size bubbles within a tube phantom.

Methods: Emissions from single bubbles within a tube phantom were mapped through an ex vivo human skull using a sparse hemispherical receiver array and a passive beamforming algorithm. Noninvasive phase and amplitude correction techniques were applied to compensate for the aberrating effects of the skull bone. The positions of the individual bubbles were estimated beyond the diffraction limit of ultrasound to produce a super-resolution image of the tube phantom, which was compared with microcomputed tomography (micro-CT).

Results: The resulting super-resolution ultrasound image is comparable to results obtained via the micro-CT for small tissue specimen imaging.

Conclusions: This method provides superior resolution to deep-tissue contrast ultrasound and has the potential to be extended to provide complete vascular network imaging in the brain.

INTRODUCTION

It is becoming apparent that small vessel pathology plays an integral role in many diseases (cancer, Alzheimer's Disease¹) and functions of the brain,^{2, 3} but we lack the technology to properly assess these structures, limiting our understanding and ability to direct treatment. Using Computed Tomography (CT), vessels below 400 μm in diameter are not consistently detected,⁴ while clinical Magnetic Resonance Imaging (MRI) has a limit of approximately 300 μm for vessel detection.⁵ More recent studies in humans have shown that subtraction CT angiography, which is ionizing and requires injection of iodine contrast agent, can still fail to delineate small cerebral arteries such as the ophthalmic arteries.⁶ MRI remains a costly imaging modality with limited availability, particularly at higher field strengths (3 T or 7 T) where a greater number of vessels can be detected.^{7, 8} At 1.5 tesla, MR angiography is limited to detecting first order branches of the Circle of Willis.⁸ Ultrasound, a more affordable and portable modality, has found limited use in the brain due to the ultrasound attenuating and aberrating effects of the skull bone that increase with increasing ultrasound frequency.⁹ Thus, ultrasound imaging in the brain has been limited to narrow acoustic windows in the skull and low frequencies that are less affected by the skull bone. However, since axial resolution for pulse-echo sonography depends on pulse length, which increases with decreasing frequency, this approach sacrifices resolution and has limited the use of ultrasound to imaging major vessels.^{10, 11}

Here, we use a passive technique similar to those previously used in acoustics¹² and seismic imaging,¹³ modifications of which have more recently been investigated to map cavitation activity during ultrasound therapy.^{14, 15} With passive beamforming techniques both the phase and amplitude information of the received signals are considered and axial resolution primarily depends on frequency and array aperture, and not on pulse length.¹⁶ Additionally, the intensity of the scatter response can be integrated over time to hugely improve the signal to noise ratio (SNR).¹³ Finally, to overcome the skull attenuation we use a low frequency transmit array, and to increase the resolution we use a full hemispherical sparse receiver array. Large aperture transmit arrays are standard place in transcranial ultrasound therapy research,^{17, 18} but have not been used for brain imaging. Micrometer-size gas bubbles are exceptional scatters of ultrasound and have been used as intravascular contrast agents for over two decades.^{19, 20} With our hemispherical array, and using passive beamforming, we can optimize the imaging resolution for a given frequency and achieve sufficient SNR to image single bubbles through a human skullcap. Here we transcranially excite single microbubbles flowing through a tube phantom and generate three-dimensional maps of the bubbles, using a bubble-based phase correction technique, similar to those proposed by others for phase correction of the transmit beam,^{21, 22} but modified to apply to the receive case. The result is a high resolution, transcranial, diffraction limited image of the tube phantom.

However, it has been known for some time that the position of a distinct source within an image can be determined to a much greater level of accuracy than the point spread function (PSF).²³ This has been applied to optics to allow imaging well beyond the diffraction limit.²⁴ We utilized these ideas, and the fact that the bubbles move with the blood flow, and developed a method to enhance the three-dimensional resolution of our trans-skull imaging beyond the diffraction limit.

METHODS AND MATERIALS

Experimental setup and measurements

The experimental setup is illustrated in Fig. 1a. We obtained images, through an ex vivo human skullcap, of a spiral phantom with a nominal internal tube diameter of 255 μm. The receiver array consisted of 128 piezo-ceramic disc elements (Del Piezo Specialties, LLC., West Palm Beach, FL) sparsely distributed in a pseudo-random configuration over a whole hemisphere to optimize the imaging resolution. The elements had a diameter of 2.54 mm and center frequencies of 612 kHz. Waveforms from the receiver array were captured using a 128 channel receiver (SonixDAQ, Ultrasonix, Richmond, B.C., Canada). The sampling rate was 10 MHz.

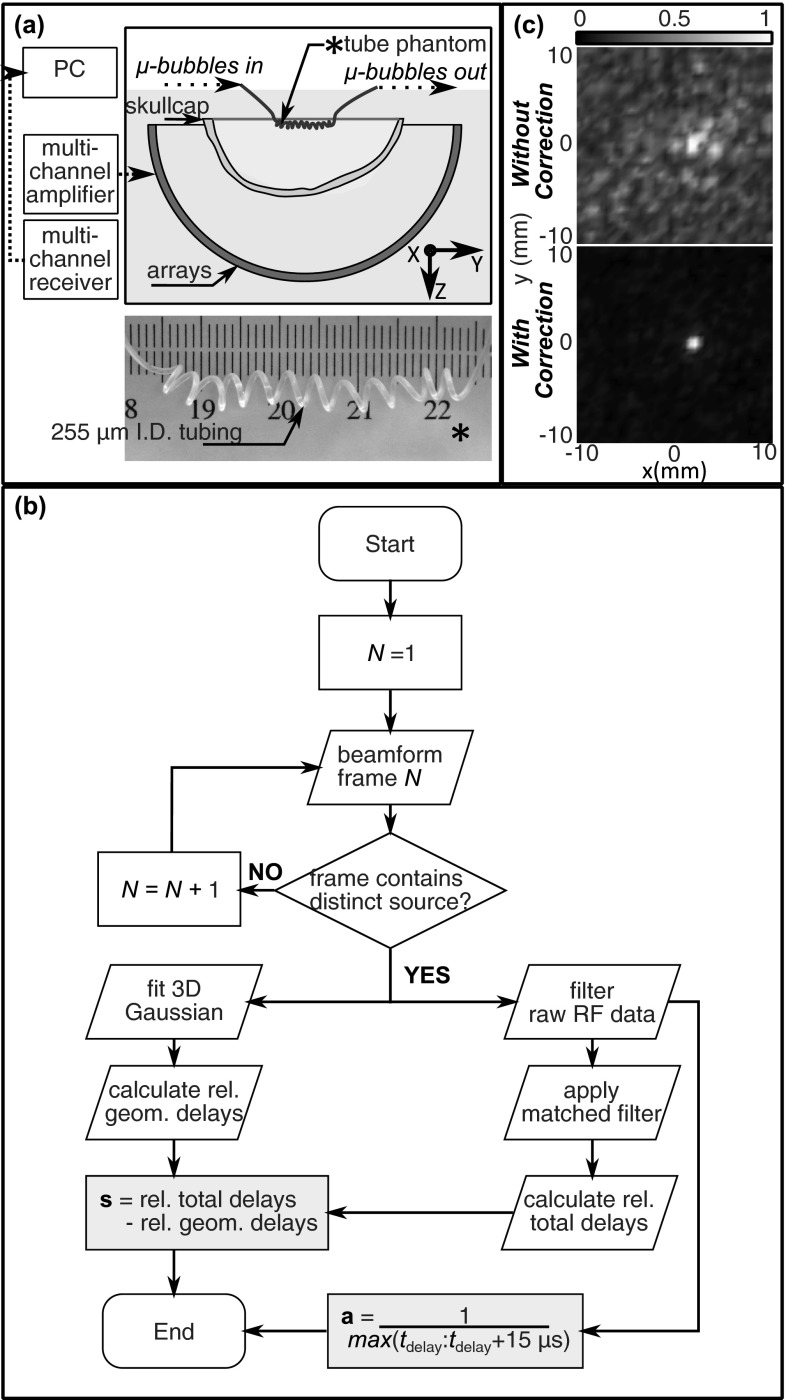
Figure 1.

(a) Illustration of the experimental setup and photograph of the imaging phatom. (b) Flow chart illustrating the method for calculating the phase {s} and amplitude {a} correction terms. (c) Normalized z-projection images (2 cm stack) of a single bubble reconstructed without (top) and with (bottom) phase and amplitude correction to account for the abberating effects of the skull.

The ultrasound was generated using a subset of 128 elements from a previously described 30 cm diameter, 1372 element hemispherical transcranial therapy array.¹⁸ The transmit elements have a center frequency of 306 kHz and were driven using a 128 channel driving system (Verasonics, Inc., Redmond, WA). Bursts were five cycles in length and were repeated at a rate of 10 Hz. Based on prior measurements with a calibrated fiber-optic hydrophone (Precision Acoustics, Ltd., Dorset, U.K.), it was estimated that focal pressures between approximately 0.15 and 0.35 MPa (Mechanical Index (MI) = 0.25–0.59) were achieved through the skull. The use of separate transmit and receive arrays served multiple purposes. First, the narrowband receiver elements tuned to two times the driving frequency provided good sensitivity to the harmonic bubble activity. The receiver elements were also sufficiently narrowband as to suppress the strong reflections of the transmitted pulse from the skull bone and avoid saturating the received signals. Finally, smaller diameter elements were used on receive in order to maintain good directivity at the higher receive frequency.

The transducer was placed in a rubber-lined tank filled with degassed, deionized water. An ex vivo human skullcap was degassed in a vacuum jar for 2 h prior to the experiment. The skullcap was placed in the tank and a tube phantom was placed near the geometric focus of the array (15 cm focal length). The tube phantom was made from 255 μm internal diameter polytetrafluoroethylene tubing (Cole-Parmer, Vernon Hills, IL). To make the spiral, the tube was wrapped tightly around a brass rod with external diameter of 2.5 mm and repeatedly heated and quenched. After removing the tube from the brass rod, the phantom relaxed to the shape of an irregular spiral with an approximate diameter of 3 mm and pitch of 3–3.5 mm.

Water was gravity fed through the phantom at a rate of approximately 0.23 ml/min. This flow rate would be reasonable in some of the smaller cerebral vasculature. This is based on reported flow rates in humans in the middle cerebral artery (6.5 mm diameter) of 127 ml/min.²⁵ The transmit focus was electronically steered through a 12 × 12 × 12 mm³ volume with a step size of 2 mm, recording the received waveforms at each location. Definity™ microbubbles (1–3 μm mean diam., Lantheus Medical Imaging, North Billerica, MA) in water at an approximate concentration of 1600 bubbles/ml, or 12 mm of tubing per bubble were then fed through the phantom and the volume scan was repeated. The concentration of bubbles was estimated based on a maximum of 1.2 × 10¹⁰ bubbles per ml of undiluted agent immediately following activation (http://www.definityimaging.com/pdf/DEFINITY%20Prescribing%20Information%20515987-0413.pdf), and assuming a loss of 50% of the bubble population due to handling.²⁶ A conservative estimate based on published work in humans¹¹ would suggest that the concentrations used in this study are approximately one one-thousandth of those in the blood stream for transcranial Doppler ultrasound.

Data analysis

All data processing was performed offline in MATLAB (Mathworks, Natick, MA). The reference scans of the tube containing water were first subtracted line by line from the bubble measurements in order to suppress the reflections from the skull. Then the individual frames were reconstructed at normal resolution, and super-resolution image processing was applied to the reconstructed images as described in Secs. 2B1, 2B2. In the remainder of the article “a frame” refers to a reconstructed image from a single excitation pulse. “A scan” refers to a composite image comprised of frames where each frame represents a different transmit focus and where the transmit focus was systematically scanned through the imaged volume. “A complete image” refers to the final composite image composed of frames from multiple scans of the same volume.

Image reconstruction–normal resolution

Frames were reconstructed using geometric delays to beamform the images over the reconstruction grid, with or without the inclusion of additional delay and amplitude compensation terms to account for the effects of the skull. The intensity value assigned to a voxel in the reconstructed frame can be mathematically expressed as the summation of the magnitude of the power spectrum over a frequency band having a bandwidth of M discrete points centered about a center frequency having discrete index m_c:

$$I\left(\mathbf{r}\right)=\sum _{m=m_c-\frac{M}{2}}^{m_c+\frac{M}{2}}{\left|\sum _i{Q}_i\left(\mathbf{r};f_m\right)\right|}^2,$$ (1)

where I(r) is the intensity at a point r = (x,y,z) in the reconstruction grid, and Q_i(r;f_m) is the value at the mth frequency band of the discrete Fourier transform of the time-delayed waveform for receiver i and point r, q_i(r;t_n), over a window of N points:

$$Q_i\left(\mathbf{r};f_m\right)=\sum _{n=n_0}^{n_0+\left(N-1\right)}{q}_i\left(\mathbf{r};t_n\right)\times e^{-j2\pi mn/N}.$$ (2)

The time delayed waveform q_i(r;t_n) can be expressed as

$$q_i\left(\mathbf{r};t_n\right)=a_i\times p_i\left(t_n+\frac{‖{\mathbf{r}}_i-\mathbf{r}‖}{c}-S_i\right),$$ (3)

where a_i is an amplitude correction term, p_i(t) is the pressure value recorded by element i at time t, r_i is a vector of the coordinates of receiver element i, c is the speed of sound in the medium, s_i is a delay term to compensate for the effect of the skull on the waveform received by element i, and ∥.∥ represents the Euclidean norm. For a given skull geometry and orientation, the skull delay parameters s_i will be a function of the source location and receiver element location, but over a small reconstruction grid it is acceptable to use a single correction per element for all the grid points since the sound is incident on the same skull regions.²⁷ Previously this assumption has been found to hold true for transmit focusing over a 24 mm radial steering range at 0.81 MHz and with elements having individual surface areas of 283 mm².²⁷ Thus at 612 kHz and with surface areas of 5 mm²/element, this assumption should hold true over the reconstruction grid used in this study (20 × 20 × 20 mm³). For the same reason, and since variations due to spherical spreading will be small over a small volume, the amplitude correction terms a_i can also be approximated by a single correction per element over a small reconstruction grid.

The skull delay and amplitude correction terms were determined from the acoustic emissions from a single bubble. The method for calculating the phase and amplitude corrections is outlined in Fig. 1b. The signals from the single bubble were captured and processed as described above to obtain a frame without phase or amplitude correction (Fig. 1c, top panel). From this initial frame, the source position was estimated by fitting a three-dimensional Gaussian to the reconstructed data. The fit was performed over a 5 × 5 × 5 mm³ volume about the point of peak intensity. The Gaussian was given a fixed standard deviation (σ_x = σ_y = 0.55 mm, σ_z = 1.15 mm) in each of the three dimensions based on the experimentally determined PSF of the receive array near the geometric focus but allowed translation and rotation in the fit. The rotation of the Gaussian was allowed in order to account for tilting of the focal volume when steering off axis, as well as a slight rotation of the array with respect the Cartesian coordinate system to which the array elements were originally registered. No large rotations which could bias the fit by tipping the axial PSF into the transverse plane were observed. The size of the Gaussian remained fixed when the Gaussian was translated since large changes were not expected over the small reconstruction volume.²⁸ Next, the geometric delays associated with this source location were determined. A matched-filter was then used to determine the total time delays between the receive elements. The individual channels were digitally filtered with a narrowband fourth-order Butterworth band-pass filter (400–800 kHz) prior to applying the matched filter. The skull delays were determined as the difference between the total time delays, calculated by applying the matched filter to the individual RF lines, and the geometric delays, calculated from the positional estimate of the bubble in the uncorrected frame. The final delays were expressed as leading or lagging with respect to a single reference channel. The amplitude correction terms were determined as the reciprocal of the maximum value in each channel over a 15 μs time window over the bubble response, as identified by the matched filter. The amplitude correction terms normalized the bubble response at each receiver in a similar manner to the amplitude correction method described by White et al.²⁹ for correcting amplitudes on transmit.

The final phase and amplitude corrected frames were produced using a time window of 40 μs and a frequency interval of 100 kHz centered about 600 kHz. The bottom panel of Fig. 1c shows an example of a phase and amplitude corrected frame.

By scanning the transmit focus through a volume we were able to excite different bubbles in different portions of the phantom, to create an image of the larger structure. Three hundred forty three frames were captured during each complete scan of the volume. Frames that did not contain one clear source were discarded. This was performed by eliminating all frames that contained a local maximum with intensity greater than or equal to 50% of the global maximum in the frame. To make a complete image of the tube the remaining frames were normalized to themselves and then combined, taking the maximum pixel projection. Multiple scans of the same volume were performed to create the final normal resolution image.

Super-resolution image processing

To obtain the high resolution images, a three-dimensional Gaussian was fit to the aberration corrected frames in the same manner as for performing the skull aberration corrections. This was performed for each of the frames containing a clear source. High resolution frames were plotted as a Gaussian centered at the estimated source location and having standard deviations in the three dimensions equal to the uncertainties on the position estimate. The amplitudes of the plotted Gaussians were the same across all frames. The complete high resolution image was obtained by combining the normalized frames and taking the maximum pixel projection. Five frames used in the normal resolution image were not included in the final high resolution image because the uncertainties on their positional estimates were deemed outliers. Uncertainties of magnitude greater than 1.5 times the interquartile range beyond the third quartile were considered outliers. A smooth three-dimensional spline approximating the data centerline was drawn. The radial distances of the bubble positions from the centerline were calculated.

Microcomputed tomography (micro-CT)

The micro-CT image of the spiral phantom was obtained in a SCANCO micro-CT 100 scanner (SCANCO Medical, Brüttisellen, Switzerland). Following the ultrasound experiments, the spiral phantom was embedded in 2% agar gel in the same vertical orientation as the measurements. The micro-CT images could therefore be manually rigidly registered, without scaling or shear, to the super-resolution ultrasound images for direct comparison. Two fiducials were placed in the phantom to mark the approximate position of the ultrasound measurements. The scans (55 kVp, 200 μA, 11 W) were reconstructed with a 34 × 34 × 34 μm³ voxel size. The micro-CT stack was processed in ImageJ (National Institutes of Health, Bethesda, Maryland). The interior of the tube was manually segmented. The segmentation was imported into Matlab and the average vessel radius over the imaged length was calculated.

RESULTS

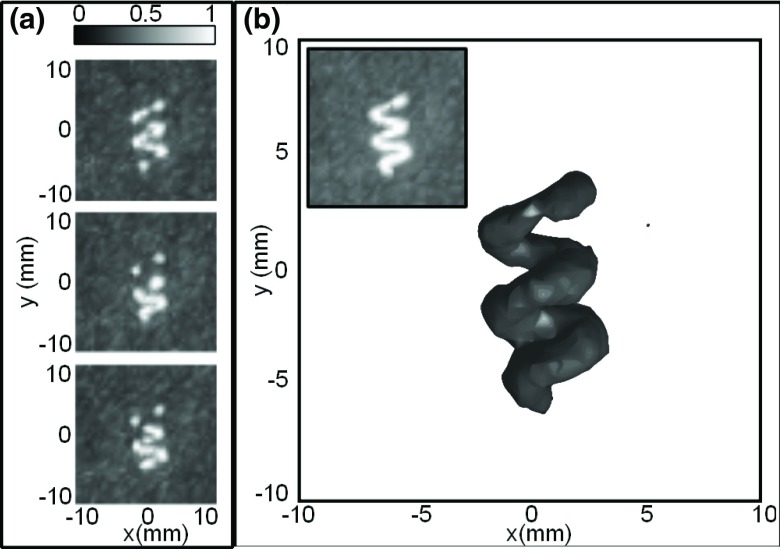
Figure 2a shows the composite images produced by three different complete scans of the imaged volume. Since the contrast agent was very dilute, a single scan produced only a partial image of the phantom. However, since the bubbles move with the flow, performing multiple scans of the same volume produced a complete image of the tube in 3D [Fig. 2b]. This image is composed of 445 frames, of a total of 3000 frames captured, containing clear individual bubbles.

Figure 2.

(a) Normalized intensity maximum pixel z-projection images (2 cm stacks) from three different scans of the phantom volume. (b) 3D rendering of the maximum pixel projection image from all scans, with the −3 dB isosurface shown. The z-projection grayscale image of the same volume is inset.

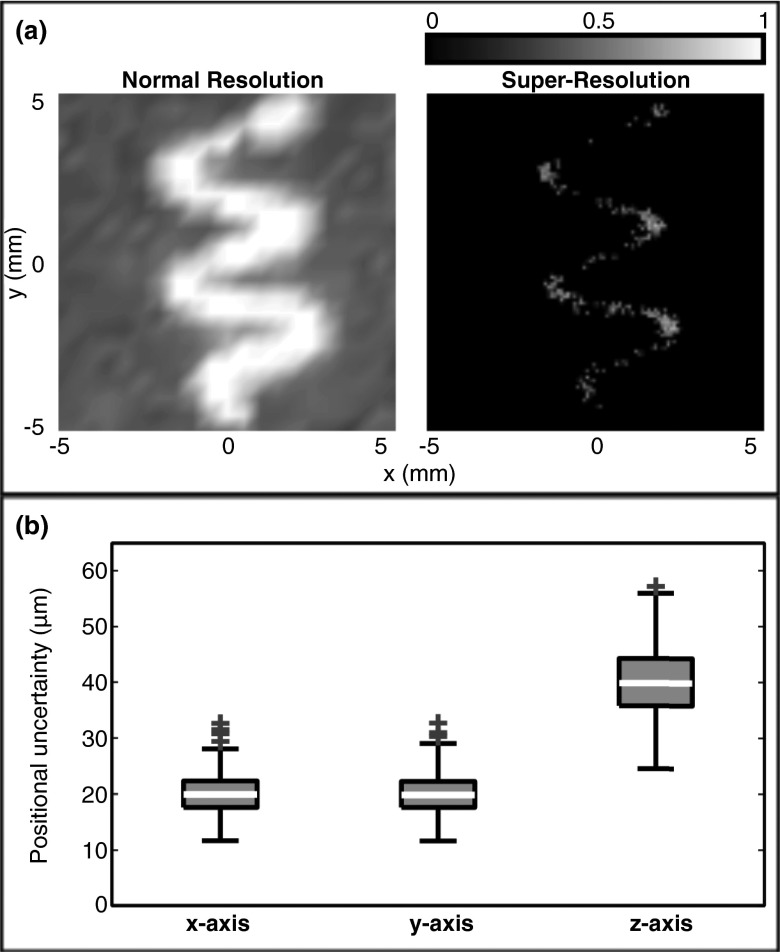
Super-resolution image processing was applied to the 445 individual, aberration corrected frames that comprise Fig. 2b. After discarding outlier fits (5 of 445), 440 super-resolution images of individual bubbles were combined to produce Fig. 3a. The uncertainties on the positional fits are illustrated in Fig. 3b. The uncertainties were standard deviations and were calculated from the 95% confidence interval on the fit, taking the 95% confidence interval to be the mean ± two standard deviations. The mean uncertainties (mean ± S.D.) on the fits were 20 ± 3 μm in the x and y directions, and 40 ± 6 μm in the z direction, or approximately 1/120 and 1/60 of the ultrasound wavelength at the received frequency (612 kHz).

Figure 3.

(a) Normalized intensity maximum pixel z-projection images (2 cm stacks) at (left) normal resolution, and (right) after applying the super-resolution image processing. (b) Box and whisker plot showing the uncertainty on the positional estimates along the three axes. The outliers (crosses) are those points greater than 1.5 times the interquartile range beyond the third quartile.

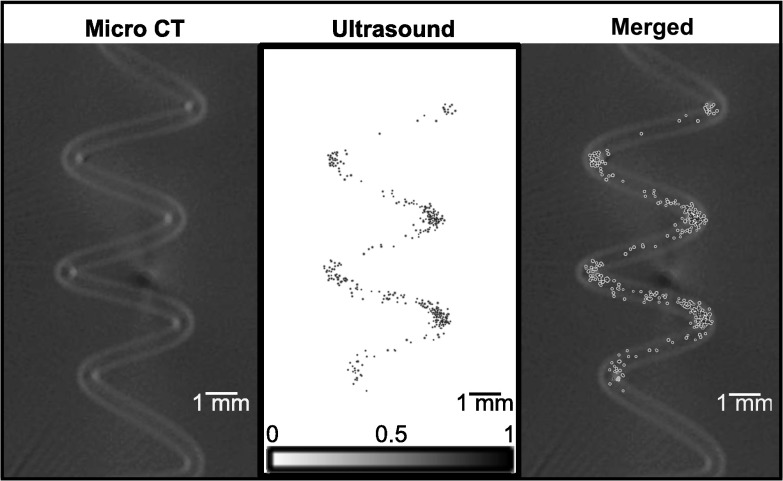
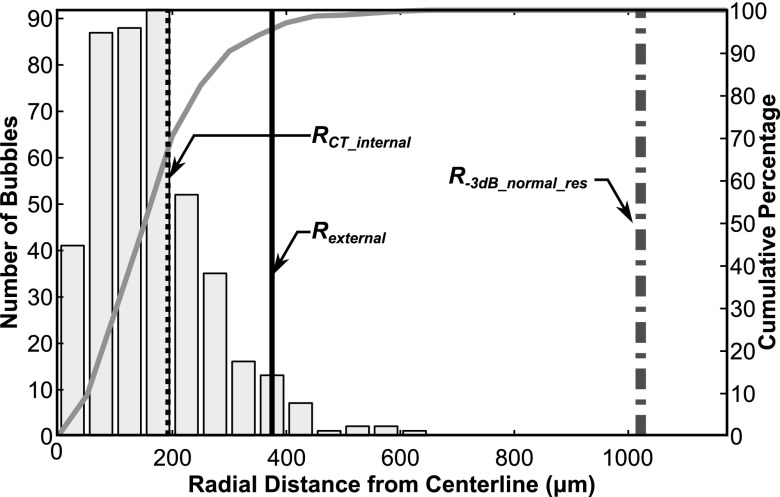
In Fig. 4, a direct comparison is shown between the resulting high resolution bubble image obtained through the human skull and the micro-CT image of only the tube phantom. Normalized intensities of less than 0.1 in the bubble image in Fig. 4 are displayed as transparent. Figure 5 shows the distribution of bubbles as a function of radial distance from the centerline of the bubble data. From the segmentation of the micro-CT data the average tube radius was found to be 192 μm. 70% of the bubbles were found to lie within 200 μm of the ultrasound image centerline, while 95% of the bubble positions were found to lie within a 375 μm radius of the centerline. The nominal exterior radius of the vessel was 375 μm. In contrast, at normal resolution the average tube radius was estimated to be 1.02 mm.

Figure 4.

Z-projections of (left) the micro-CT image of the tube phantom, (center) the high resolution ultrasound image of the microbubbles, and (right) the micro-CT image and ultrasound image manually rigidly aligned.

Figure 5.

Histogram showing the distribution of bubbles as a function of radial distance from the estimated tube centerline. The solid gray curve indicates the cumulative distribution.

DISCUSSION

The large aperture array, passive beamforming and phase correction techniques used in this study produced a clear, minimally distorted normal resolution image of the tube phantom through the skullcap. From Fig. 2b, the phantom structure is already clearly discernible from this initial diffraction limited image. The spiral diameter and pitch are both approximately 3–3.5 mm, suggesting that without further image processing this technique would already be suitable for imaging of large vascular structures in the brain, such as the Circle of Willis and its branching arteries.

The application of the super-resolution image processing greatly improved the image resolution. Although some movement of the phantom may have occurred during the gel embedding process, from Fig. 4 it can be seen that the micro-CT and bubble images show good correlation. The spread of the mapped bubbles is larger than the lumen in some areas. However, it can be seen that this technique still provides a great improvement over the normal resolution imaging in representing the true structure size, with a good representation of the shape of the phantom. The bubble spreading most likely results from errors in the estimate of the phase delays used to correct the initial images for skull effects. More complex phase correction techniques may be developed that could further improve image quality, and improve vessel size estimates.

The area over which this technique could be used remains to be investigated. A simulation study has shown that passive beamforming with this array should work well over a large region of the skull cavity.²⁸ However, in practice reflections from the skull bone or shielding effects may limit how close to the skull bone bubbles can be detected.

Since the detected bubbles are on the order of 1–3 μm in diameter, this technique may in the future be used to image down to capillary level with proper optimization of the transmit and receive arrays and frequencies. What makes this approach unique is its ability to produce high resolution images transcranially and at depth, making it highly relevant to clinical brain imaging. Although in this study there was no intervening tissue between the skull and phantom, we were able to isolate activity in different parts of the phantom. The presence of intervening tissue will attenuate the signals and propagation through the tissue may contribute to harmonic signals, which could affect image quality. In the normal resolution images the sidelobes can already be seen to have a speckle-like effect surrounding the tube image. This effect may be worse in vivo. The RF-line reference subtraction used in this study may help reduce the effects of the intervening tissue. However, other strategies may also be necessary to counter these effects. Expansion of the array to a greater number of elements would improve the beamformed image quality and reduce sidelobes. An alternative strategy would be to lengthen the excitation pulse and the time window over which the beamforming occurs, both of which should improve the image SNR.²⁸ Techniques such as pulse inversion imaging³⁰ or subharmonic imaging,³¹ which are contrast specific, may also improve image quality.

In vivo, the tight focusing on both transmit and receive should work in a similar manner to isolate single bubbles within the transmit focus. However, if multiple bubbles are located within the focus, the super-resolution technique should still be feasible as long as the sources are separated enough so that they are detected as individual sources.²⁸ Then multiple Gaussians could be fit to the data. Techniques in optical imaging have already been developed to address localizing multiple proteins within a single image.²⁴ By imaging multiple bubbles during each transmit pulse the overall imaging time could also be shortened since fewer frames would be required to produce a complete image. The time-of-flight for a burst to reach and return from the geometric focus is 200 μs. Therefore pulses could be reasonably sent every 500 μs, a 2kHz PRF. Thus the data in this study would take 1.5 s to capture, and a 10 × 10 × 10 cm³ volume would take approximately 15 min if each frame had no more than one bubble.

All processing was performed offline; however, real-time or near real-time implementation of these techniques would be possible with appropriate hardware. The resulting system would be low cost and capable of complete vascular imaging in the brain, with a huge impact on diagnostic and functional brain imaging, as well as our understanding of brain disorders. The results show resolution that is superior to any other deep tissue contrast ultrasound imaging and thus may also be able to enhance ultrasound imaging in other parts of the body with suitable array geometry and operation frequency modifications for the given anatomical site.

CONCLUSION

We have demonstrated a technique for achieving high resolution transcranial ultrasound images of vascular structures using passive beamforming techniques, noninvasive phase correction and super-resolution image processing. This technique has the potential to be extended to image the vascular network in the brain down to capillary level.