A microfluidic device for simultaneous measurement of viscosity and flow rate of blood in a complex fluidic network

Abstract

Blood viscosity has been considered as one of important biophysical parameters for effectively monitoring variations in physiological and pathological conditions of circulatory disorders. Standard previous methods make it difficult to evaluate variations of blood viscosity under cardiopulmonary bypass procedures or hemodialysis. In this study, we proposed a unique microfluidic device for simultaneously measuring viscosity and flow rate of whole blood circulating in a complex fluidic network including a rat, a reservoir, a pinch valve, and a peristaltic pump. To demonstrate the proposed method, a twin-shaped microfluidic device, which is composed of two half-circular chambers, two side channels with multiple indicating channels, and one bridge channel, was carefully designed. Based on the microfluidic device, three sequential flow controls were applied to identify viscosity and flow rate of blood, with label-free and sensorless detection. The half-circular chamber was employed to achieve mechanical membrane compliance for flow stabilization in the microfluidic device. To quantify the effect of flow stabilization on flow fluctuations, a formula of pulsation index (PI) was analytically derived using a discrete fluidic circuit model. Using the PI formula, the time constant contributed by the half-circular chamber is estimated to be 8 s. Furthermore, flow fluctuations resulting from the peristaltic pumps are completely removed, especially under periodic flow conditions within short periods (T < 10 s). For performance demonstrations, the proposed method was applied to evaluate blood viscosity with respect to varying flow rate conditions [(a) known blood flow rate via a syringe pump, (b) unknown blood flow rate via a peristaltic pump]. As a result, the flow rate and viscosity of blood can be simultaneously measured with satisfactory accuracy. In addition, the proposed method was successfully applied to identify the viscosity of rat blood, which circulates in a complex fluidic network. These observations confirm that the proposed method can be used for simultaneous measurement of viscosity and flow rate of whole blood circulating in the complex fluid network, with sensorless and label-free detection. Furthermore, the proposed method will be used in evaluating variations in the viscosity of human blood during cardiopulmonary bypass procedures or hemodialysis.

INTRODUCTION

Cardiovascular diseases (CVDs) are caused by several factors including hypertension, diabetes, obesity, and smoking.^{1, 2, 3} The blood of patients with CVDs represents altered hemorheological properties, which cause to impair microcirculatory functions including blood flow regulations and gas exchanges.⁴ During a cardiopulmonary bypass procedure, blood hemolysis is severely increased when blood is exposed to high shear stress, depending on membrane oxygenator as well as circulating pump types.⁵ Blood viscosity, which is determined by various factors such as plasma viscosity,⁶ haematocrit,⁷ deformability,^{8, 9, 10} and aggregation,^{11, 12, 13} has been considered as one of the promising parameters for effectively monitoring variations in physiological and pathological conditions.

A microfluidic platform, which can promise high potential for point-of-care-test (POCT),^{14, 15} has several advantages including small volume consumption, and disposability. Based on the microfluidic platform, several viscosity measurement methods such as extensional flow,¹⁶ capacity sensor,¹⁷ capillary force,^{18, 19} comparator,^{20, 21} quartz crystal microbalance (QCM),²² laser-induced capillary wave,²³ and multiple microfluidic channels²⁴ have been recently proposed. Most of these methods were focused on pure liquids rather than blood including cellular components. Few of these methods have been applied to measure blood viscosity, only as a stand-alone approach.^{19, 24, 25} Given that blood flow rate is not specified in a microvascular network, blood viscosities were routinely measured for wide ranges of shear rates, with the assumption that blood behaves as a non-Newtonian fluid. Thus, blood viscosity identification should be conducted at a specified flow rate, where blood circulates in a complex fluidic network. Blood viscosity has been recently monitored using an electrical impedance technique under in-vivo condition.⁷ The method requires calibration procedures using blood samples under in-vitro condition. Such calibration procedure, which uses specific blood samples, might potentially include measurement errors because blood viscosity strongly depends on several factors. The previous method will be meaningfully applied in comparative studies because hemorheology parameters are distinctively altered depending on in-vivo and in-vitro conditions.²⁶ In addition, the measurement of blood flow rate from flow-rate sensors^{27, 28} results in several issues such as sensor contamination and complex calibration procedures owing to variation in blood viscosity with respect to the various factors. To resolve these problems, measuring blood flow rate in a microfluidic channel, even without a flow-rate sensor is generally required. Therefore, blood viscosity can be measured in a complex fluidic network including a cardiovascular bypass,⁵ or extracorporeal bypass loop,²⁹ even at an unspecified flow rate.

In this study, we proposed a novel microfluidic device for monitoring variations in viscosity and flow rate of blood circulating in complex fluidic networks, in a semi-continuous manner. Based on three sequential flow controls in a microfluidic channel, the viscosity and flow rate of blood are simultaneously measured with label-free and sensorless detection. Considering the fact that most previous methods were applied to identify blood viscosity for a given flow rate, the proposed method has a distinctive advantage because of its capability to measure blood viscosity and flow rate simultaneously. Thus, the proposed method can be applied to measure blood viscosity in complex fluidic networks, at an unspecified flow rate. Additionally, the proposed method does not require fully integrated sensors, fluorescent particle-based labeling technique, and a complex calibration procedure. Blood viscosity is identified using 1x PBS (Phosphate Buffered Saline) solution as a reference fluid, which can be regarded as a self-calibration. For performance demonstration of the proposed method, the proposed method was applied to evaluate the viscosity and flow rate of human blood with respect to (a) specified flow rates through a syringe pump and (b) unspecified flow rates through a peristaltic pump. In addition, the proposed method was applied to measure viscosity of rat blood which circulates in complex fluidic network that includes a rat, a pinch valve, a reservoir, a peristaltic pump, and the microfluidic device.

SIMULTANEOUS MEASUREMENT OF VISCOSITY AND FLOW RATE OF BLOOD

Proposed method

In this study, a novel microfluidic device was adopted to measure the viscosity and flow rate of blood circulating in complex fluidic circuits simultaneously. Based on three-step sequential microflow controls, the viscosity and flow rate of blood are measured with label-free and sensorless detection. To demonstrate this proposed method, a symmetric microfluidic device, which is composed of two half-circular chambers, two side channels with multiple indicating channels, and one bridge channel connecting to both ends of the side channels, is carefully designed. To minimize flow fluctuations in the microfluidic device, and to avoid viscosity reduction in microfluidic channels,³⁰ the half-circular chamber is carefully designed to have spacious cavity (diameter = 22 mm, depth = 50 μm). In addition, each side channel has 25 identical indicating channels (width = 300 μm, depth = 50 μm) to monitor the fluidic motions of both fluids.

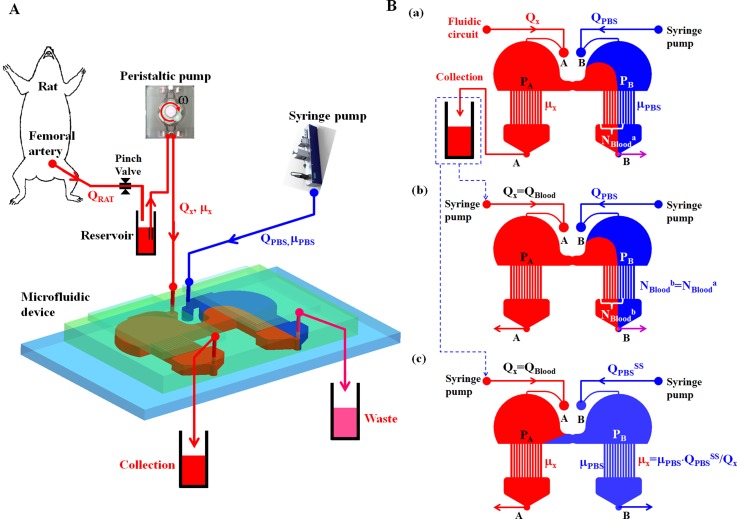
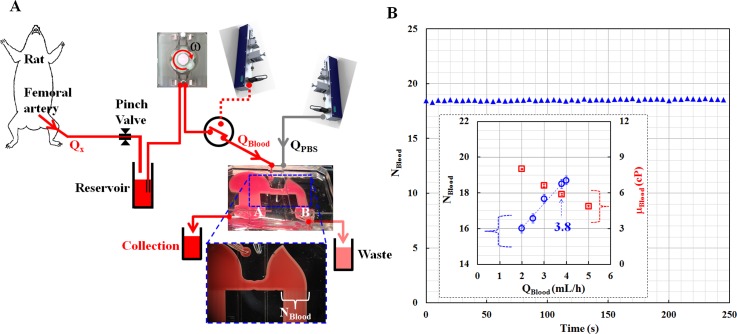
As illustrated in Fig. 1A, the microfluidic device is installed within a complex fluidic network that includes a rat, a reservoir, a pinch valve, a peristaltic pump, and a syringe pump. Rat blood as a test fluid was supplied from femoral artery to the microfluidic device using a peristaltic pump (MP-1000, Tokyo Rikakikai Co., Japan). To identify the viscosity (μ_x) and flow rate (Q_x) of rat blood, a PBS solution (reference fluid) was delivered using a syringe pump (neMESYS, Centoni GmbH, Germany) at a specific flow rate (Q_PBS). Additionally, the viscosity of PBS solution (μ_PBS) was measured in advance with a conventional viscometer (DV-II, Brookfield, USA). Both fluids were passed through the two outlets (A, B).

Figure 1.

Schematics of the proposed working principle using three sequential flow controls in a microfluidic device for simultaneously measuring viscosity and flow rate of blood in a complex fluidic network. (A) A complex fluidic network is composed of a rat, a pinch valve, a reservoir, a peristaltic pump, a syringe pump, and a microfluidic device. To identify the viscosity (μ_x) and flow rate (Q_x) of rat blood, PBS solution is delivered using the syringe pump, at a specific flow rate (Q_PBS). (B) Three sequential flow controls for measuring viscosity and flow rates of blood in the fluidic network. (a) At the first step, blood and PBS solution are delivered into the inlets (A, B). The flow rate of the PBS solution (Q_PBS) was carefully selected to make blood sample invade into right side channel. The number of indicating channels filled with blood in the right side channel was continuously monitored as N_Blood^a. During the first step, the blood sample was collected from the outlet (A). (b) In the second step, the unknown flow rate of blood (Q_x) can be identified as Q_x = Q_Blood by controlling a specific flow rate of blood (Q_Blood) to satisfy that N_Blood^b is equal to N_Blood^a. (c) At the last step, blood viscosity (μ_x) can be estimated by checking the hydrodynamic balance condition, where reversal flow of blood occurs in the bridge channel.

As shown in Fig. 1B, three-step sequential flow controls are applied to identify viscosity and flow rate of blood circulating in a fluidic network. At the first step [Fig. 1B1], rat blood and PBS solution are simultaneously delivered into inlets (A) and (B), respectively. To collect pure blood samples from the outlet (A), the flow rate of the PBS solution (Q_PBS) is carefully controlled to cause the blood to move to the right direction in the bride channel, and invade into the right-side channel owing to the pressure difference (P_A > P_B). The number of indicating channels filled with the blood in the right side channel is consistently monitored as N_Blood^a. In the second step [Fig. 1B2], the collected blood is supplied into the inlet (A) using a syringe pump. Additionally, the PBS solution is supplied into the inlet (B), with the same flow rate (Q_PBS) as the first step. To identify the unknown flow rate of blood (Q_x), a specific flow rate of blood (Q_Blood) is precisely controlled to satisfy that the number of indicating channels filled with blood (N_Blood^b) is equal to N_Blood^a, which is monitored in the first step (i.e., N_Blood^b = N_Blood^a). During the second step, the unknown flow rate of blood can be identified as Q_x = Q_Blood. At the last step [Fig. 1B3], the blood sample is supplied into the inlet (A) with the same flow rate (Q_Blood) as the second step. Blood viscosity (μ_x) can be identified by checking the hydrodynamic balance condition, where a reversal flow occurs in the bridge channel. By appropriately controlling the flow rate of the PBS solution as Q_PBS = Q_PBS^SS, the direction of blood flow immediately changes from right to left in the bridge channel, under the hydrodynamic balance condition (i.e., P_A = P_B). Using this hydrodynamic balancing method in the symmetric microfluidic device, blood viscosity formula (μ_x) is simply derived as, μ_x = μ_PBS·Q_PBS^SS/Q_Blood. Thus, the viscosity of blood (μ_x) can be easily measured by monitoring the specific flow rate of PBS solution (Q_PBS^SS), with the known viscosity of the PBS solution (μ_PBS) and the identified flow rate of blood (Q_Blood). In addition, most of the indicating channels in the left side channel are filled with blood.

Taking into account the fact that we can measure experimentally instantaneous viscosity at each flow rate condition, we assumed that the blood behaves as a Newtonian fluid at a specific flow rate (i.e., experimental approach) instead of a representative viscosity for whole flow-rate regimes of interest (i.e., theoretical approach). Based on this approach which has been regarded as acceptable one in a conventional viscometer, a shear rate of blood at the specific flow rate is approximately estimated in each indicating channel with a rectangular cross-section (width = w, depth = h).²⁵ Thus, the shear rate formula of blood in the rectangular channel is estimated as

$$\dot{\gamma }=\frac{32Q_{\mathit{B}\mathit{l}\mathit{o}\mathit{o}\mathit{d}}}{\pi {\mathit{ND}}^3}.$$ (1)

In Eq. 1, D and N indicate the hydraulic diameter for the rectangular channel, and the number of the indicating channels.

Analytical formula for evaluating the flow stabilization effect

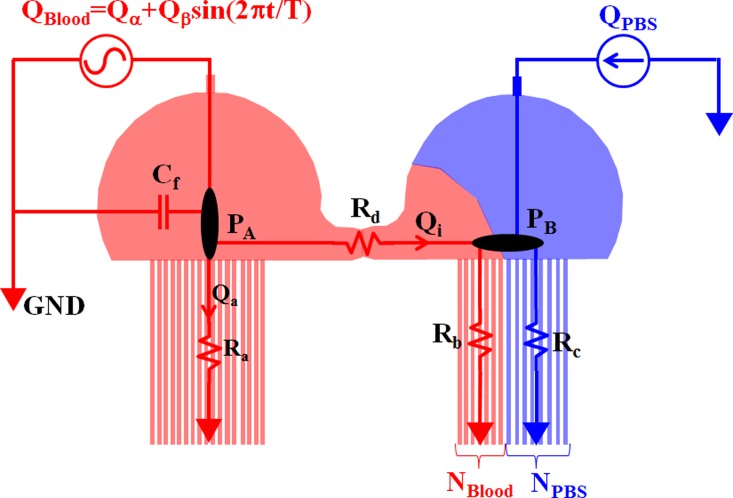
For convenience, we assume that blood moves to right direction in the bridge channel owing to a pressure difference (P_A > P_B). The left side channel is then filled with pure blood. Meanwhile, the right side channel is partially filled with blood and PBS solution. For mathematical representation, a simple fluidic circuit model for the proposed microfluidic device is established using fluidic resistances (R_a, R_b, R_c, R_d), membrane compliance (C_f), and flow rates (Q_Blood, Q_PBS), as shown in Fig. 2. In other words, fluidic resistances are used to model frictional losses in the channels. Under the dynamic flow rate, compliance effect owing to the left half-circular chamber is modeled as compliance (C_f), which is involved in reducing fluctuations of blood flow. Here, we assume that the effect of membrane compliance is reasonably negligible under the constant flow rate of PBS solution, in the right half-circular chamber. According to the mass conservation law at point “A”, a relationship between the blood flow rate (Q_Blood) and the pressure (P_A) is derived as

$$C_f\frac{d{P}_A(t)}{\mathit{d}\mathit{t}}+\frac{P_A(t)}{R_a}+Q_i(t)=Q_{\mathit{B}\mathit{l}\mathit{o}\mathit{o}\mathit{d}}(t).$$ (2)

In Eq. 2, the flow rate of blood supplied by the syringe pump (Q_Blood) is described as

$$Q_{\mathit{B}\mathit{l}\mathit{o}\mathit{o}\mathit{d}}(t)=Q_{\alpha }+Q_{\beta }\sin \left(\frac{2\pi t}{T}\right).$$ (3)

In Eq. 3, Q_α and Q_β denote the mean flow rate and the amplitude of oscillating flow rate with a period (T), respectively. In addition, the flow rate of blood passing through the bridge channel (Q_i) is expressed as follows:

$$Q_i(t)=\frac{P_A(t)-P_B(t)}{R_d}.$$ (4)

Considering the fact that the left side channel is only filled with blood, the flow rate of the blood moving through the left side channel (Q_a) can be expressed as Eq. 5

$$Q_a(t)=\frac{P_A}{R_a}.$$ (5)

Unlike the left side channel, the right side channel consists of two compartments that are filled with blood and PBS solution, respectively. Given that each compartment has the same pressure, the following relationship should be unexceptionally satisfied as Eq. 6

$$Q_i\cdot R_b=Q_{\mathit{P}\mathit{B}\mathit{S}}\cdot R_c.$$ (6)

Using Eqs. 3, 4, 5, 6, the following equation can be derived by converting the pressure (P_A) into the flow rate (Q_a)

$$R_a{C}_f\frac{d{Q}_a(t)}{\mathit{d}\mathit{t}}+Q_a(t)=Q_{\alpha }-\frac{R_c}{R_b}{Q}_{\mathit{P}\mathit{B}\mathit{S}}+Q_{\beta }\sin \left(\frac{2\pi t}{T}\right).$$ (7)

In solving Eq. 7, the flow rate through the left side channel (Q_a) is analytically derived as follows:

$$Q_a(t)=Q_{\alpha }-\frac{R_c}{R_b}{Q}_{\mathit{P}\mathit{B}\mathit{S}}+\frac{Q_{\beta }}{\sqrt{1+{\left(\frac{2\pi }{T}\right)}^2{\tau }^2}}\sin \left(\frac{2\pi t}{T}-{\tan }^{-1}\left(\frac{2\pi \tau }{T}\right)\right),$$ (8)

where τ indicates the time constant which is expressed as τ = C_f·R_a.

Figure 2.

Mathematical representation of the proposed microfluidic device using a discrete fluidic circuit model. The fluidic circuit was developed using fluidic resistances (R_a, R_b, R_c, R_d), membrane compliance (C_f) owing to the half-circular chamber, and flow rates (Q_Blood, Q_PBS). To evaluate the effect of membrane compliance on the flow stabilization, the flow rate of blood was periodically delivered into the microfluidic device as Q_Blood = Q_α + Q_β sin (2πt/T). Here, T indicates the period of blood flow rate. However, the PBS solution was supplied at a constant flow rate as Q_PBS.

A pulsation index (PI = [Q_max − Q_min]/[2Q_ave], Q_max: maximum flow rate, Q_min: minimum flow rate, Q_ave: average flow rate) is used to quantify the effect of time constant (τ) on the flow stabilization in the microfluidic device.

Based on the definition of PI and the analytic flow rate formula [Eq. 8], the PI is simply derived as follows:

$$PI=\frac{Q_{\beta }}{Q_{\alpha }-\frac{R_c}{R_b}{Q}_{\mathit{P}\mathit{B}\mathit{S}}}\cdot \frac{1}{\sqrt{1+{\left(\frac{2\pi }{T}\right)}^2{\tau }^2}}.$$ (9)

According to Eq. 9, PI depends on several parameters that include flow rates of blood and PBS solution (Q_α, Q_β, Q_PBS) as well as fluidic resistances (R_b, R_c) in the right side channel. In addition, the PI strongly depends on the time constant (τ) and period (T) of the blood flow rate. It also behaves as a typical low-pass filter (LPF). Thus, based on Eq. 9 as the LPF, the unknown time constant (τ) can be estimated as τ ≈ T_c/2π using the cut-off time (T_c). In other words, the time constant can be experimentally identified by measuring the cut-off time (T_c) from the dynamic response curve [i.e., PI vs. time period (T)].

MATERIALS AND METHODS

Fabrication of microfluidic device and sample preparation

A master replica molder with a rectangular cross-section (depth = 50 μm) was fabricated by using MEMS technologies including photolithography and deep reactive-ion etching. Polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning, USA) was poured on the master molder. After curing at 80 °C for 3 h, the PDMS was peeled off the master molder. First, after treating oxygen plasma (CUTE, Femto Science, Korea) on the PDMS and a glass substrate, the microfluidic device was prepared by bonding the PDMS on the glass substrate. Second, a glass substrate of suitable size was bonded on the top of each half-circular chamber to avoid extreme deformation owing to high active pressures. Human red blood cells (RBCs) were provided by a blood bank (Daegu-Kyeongbuk Blood Bank, Korea). The human blood samples with varying hematocrits ranging from 20% to 50% were adjusted by carefully adding RBCs or plasma. During all experiments, 1x PBS solution (pH 7.4, Bio Solution, Korea) was applied as the reference fluid to prevent rupture of the RBC membrane due to a different osmotic pressure.

Experimental setup

The microfluidic device was mounted on a stereo microscope (Stemi 2000-C, Zeiss, Germany) equipped with a digital camera (D700, Nikon, Japan). Microscopic images were captured with a magnification of 0.68×. In addition, the change of flow direction in the bridge channel of the microfluidic device was continuously monitored using the digital camera. Depending on experimental conditions, blood samples were supplied into the microfluidic device using a peristaltic pump or a syringe pump (neMESYS, Centoni Gmbh, Germany). However, blood and PBS solution using the syringe pump were supplied into the microfluidic device to identify blood viscosity and the flow rate. All experiments were conducted at consistent room temperature (25 °C). The viscosity of PBS solution was measured in advance as 1.00 ± 0.05 cP using a commercial viscometer (DV-II, Brookfield, USA) which requires 16 mL for each measurement.

Preparation of rat model

According to POSTECH Ethics Committee, all experiments were performed while enduring that the procedures are appropriate and humane. A male Sprague–Dawley rat (nine weeks old, body weight of 0.275 kg) was anesthetized with an intramuscular injection of ketamine (100 mg/kg) and xylazine (10 mg/kg). The rat was placed in the supine position on a plastic pad after anesthesia. During all experiments, heparin (1000 IU/mL/kg) was injected in the tail vein of the rat to prevent blood clotting in vascular conduits. After injecting heparin, the rat was placed on the plastic pad for 10 min. Thereafter, the left femoral artery was cannulated with one end of a polyethylene tubing (ID = 0.58 mm, PE-50, BD Intramedic^TM, USA) filled with heparin (10 IU/mL). The other end of the polyethylene tubing was connected to the blood reservoir. A pinch valve was applied to control the blood flow rate from the rat. The other polyethylene tubing (ID = 0.5 mm, thickness = 0.45 mm) was employed to connect the blood reservoir to the microfluidic device. Thus, the blood in the reservoir was delivered into the microfluidic device by the peristaltic pump, which had been operated for 30 min. At the end of the experiment, the rat was sacrificed under an anesthetic state.

RESULTS AND DISCUSSION

Flow stabilization in the microfluidic device

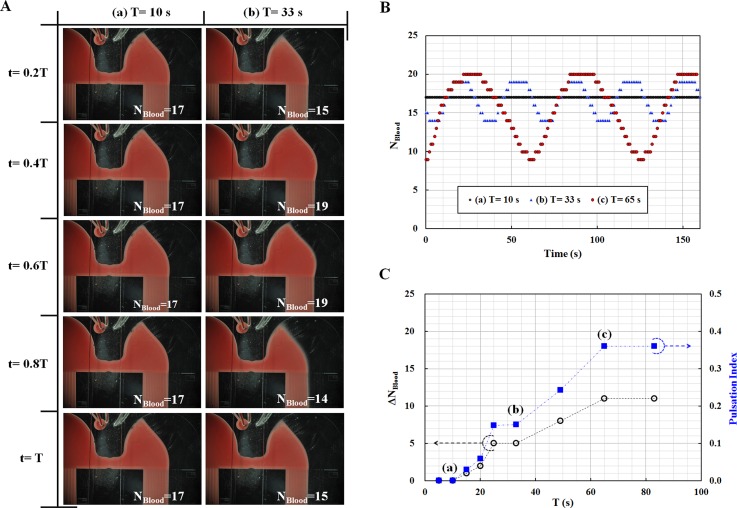
To evaluate the flow stabilization effect owing to membrane compliance of the half-circular chamber in the microfluidic device, PI was measured with respect to various periods of blood flow rate, which range from 5 s to 83 s. Blood flow rate was set as Q_Blood = 7 + 5sin (2πt/T) mL/h using a syringe pump. Here, T indicates the period of blood flow rate. Additionally, the flow rate of PBS solution was supplied at Q_PBS = 5 mL/h, using a syringe pump. As shown in Fig. 3A, the number of indicating channels filled with blood in the right side channel (N_Blood) can be counted from each microscopic image. As a result, N_Blood was consistently remained as 17, at a period of 10 s [Fig. 3A1]. However, N_Blood was periodically changed from 15 to 19 at a period of 33 s [Figs. 3A2]. Based on microscopic images captured for three periods [(a) T = 10 s, (b) T = 33 s, (c) T = 65 s], the number of indicating channels filled with blood in the right side channel (N_Blood) was summarized with respect to time. As represented in Fig. 3B, the number of N_Blood tends to increase gradually, even at a longer period rather than a shorter period. This result implies that the N_Blood behaves as a LPF. To analyze the fluidic behaviors quantitatively, variations in N_Blood(ΔN_Blood) and PI were estimated with respect to various periods. As shown in Fig. 3C, both ΔN_Blood and PI tend to increase gradually depending on period T. PI remains constant when the period is over 65 s. Based on these experimental results, cut-off time (T_c) is estimated at 49 s. Based on the relationship between the cut-off time and time constant, the time constant of the microfluidic device is estimated approximately as τ ≈ 8 s, owing to the half-circular chamber. From these results, we found that the half-circular chamber causes flow fluctuations to be completely removed as ΔN_Blood ≈ 0 when the period of periodic flow injection is shorter than 10 s. However, ΔN_Blood periodically varies to 11, at longer periods (T > 65).

Figure 3.

Quantitative evaluations of flow stabilization resulting from the membrane compliance of the half-circular chamber. (A) Microscopic images showing the number of indicating channels filled with blood in the right side channel (N_Blood) at two different periods [(a) T = 10 s, (b) T = 33 s]. (B) Temporal variations in N_Blood with respect to three different periods [(a) T = 10 s, (b) T = 33 s, (c) T = 65 s]. (C) Temporal variations in the number of indicating channels filled with blood (ΔN_Blood) and PI (Pulsation Index) with respect to various periods ranging from 5 s to 83 s. Flow fluctuations were completely removed as ΔN_Blood ≈ 0 in a short period (i.e., T < 10 s).

Blood viscosity measurement for given flow rate

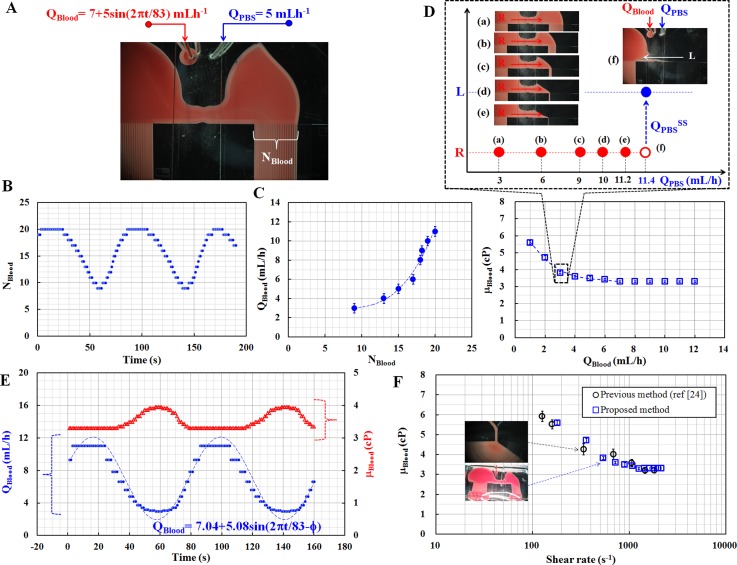
To demonstrate the performance of the proposed method, the blood sample (H_ct = 40%) and PBS solution were delivered into the microfluidic device, using a syringe pump. As illustrated in Fig. 4A, the flow rates of the two fluids are set as Q_Blood = 7 + 5 sin (2πt/T) mL/h and Q_PBS = 5 mL/h, respectively. After considering the dynamic responses with respect to various periods, the blood flow rate with a long period (T = 83 s) was carefully selected to identify blood viscosity, especially under dynamic flow-rate conditions. On the other hand, the flow rate of the PBS solution was kept constant at 5 mL/h. At the first step, the number of indicating channels filled with blood in the right side channel (N_Blood) was measured for 200 s, as shown in Fig. 4B. The results indicate that N_Blood changes periodically, and has the same period as the blood flow rate (T = 83 s), which is delivered by the syringe pump. In the second step, the blood samples collected from the outlet (A) during the first step were applied to obtain two relationships (N_Blood vs. Q_Blood, μ_Blood vs. Q_Blood). The flow rate of the PBS solution was kept consistent at 5 mL/h. First, as shown in Fig. 4C, the relationship between Q_Blood and N_Blood is obtained as a regression formula (i.e., Q_Blood = 0.0039N_Blood³ − 0.0861N_Blood² + 0.6508N_Blood+ 1.2749, R² = 0.976) by measuring N_Blood with respect to various flow rates of blood (Q_Blood). Next, blood viscosity was identified using the proposed method, with respect to various flow rates of blood, which range from 2 mL/h to 12 mL/h. As illustrated in Figs. 4D1 to 4D4, microscopic images were captured at a fixed blood flow rate of 3 mL/h (i.e., Q_Blood = 3 mL/h) to monitor reversal flows in the bridge channel with respect to various flow rates of PBS solution (Q_PBS). This experimental result shows that reversal flow occurs in the bridge channel, at a specific flow rate of the PBS solution (i.e., Q_PBS = 11.4 mL/h). Using the viscosity formula, blood viscosity is identified as 3.8 ± 0.05 cP, at a blood flow rate of 3 mL/h. By repeating similar procedures for various flow rates of blood, blood viscosity was measured with respect to various flow rates of blood, as shown in Fig. 4D. The relationship between μ_Blood and Q_Blood is then obtained as a regression formula (i.e., μ_Blood = −0.0192Q_Blood³ + 0.3264Q_Blood²− 1.907Q_Blood + 7.2426 cP, R² = 0.992), at a blood flow rate of less than 7 mL/h (i.e., Q_Blood < 7 mL/h). Above a blood flow rate of 7 mL/h, blood viscosity remains consistent at 3.3 ± 0.05 cP.

Figure 4.

Performance demonstration of the proposed method for given blood flow rates supplied by the syringe pump. (A) Flow rate of blood was controlled as sinusoidal function (Q_Blood = 7 + 5 sin (2πt/83) mL/h). The flow rate of PBS solution was carefully fixed at 5 mL/h. The number of indicating channels filled with blood in the right side channel was designated as N_Blood. (B) Temporal variations of N_Blood for a given flow rate of blood. (C) Relationship between blood flow rate (Q_Blood) and N_Blood (D) Relationship between blood viscosity (μ_Blood) and blood flow rate (Q_Blood). (E) Temporal variations of viscosity (μ_Blood) and flow rate (Q_Blood) of blood were estimated by using the two relationships. (F) Quantitative comparison of viscosity values obtained using the proposed method and the previous method.²⁴

As shown in Fig. 4E, based on the two relationships, the flow rate and viscosity of blood (Q_Blood, μ_Blood) are estimated by converting the N_Blood obtained during the first step of the experiment. As expected, the flow rate and viscosity have a reciprocal relationship, at a blood flow rate of less than 7 mL/h (i.e., Q_Blood < 7 mL/h). To evaluate the measurement accuracy of the blood flow rate, a curve fitting was conducted by assuming the flow rate of blood as Q_Blood = Q_a + Q_b sin (2πt/83−ϕ)). Based on the regression analysis, the two unknown parameters (Q_a, Q_b) are estimated as 7.04 and 5.08, respectively. This result implies that the proposed method is able to measure blood flow rate with sufficient accuracy. Next, using blood viscosity vs. flow rate as shown in Fig. 4D, a shear rate for corresponding blood flow rate is estimated using the shear rate formula. To compare the accuracy of blood viscosity measured by the proposed method, the previous microfluidic viscometer²⁴ was used to measure viscosity of the same blood samples. As shown in Fig. 4F, the blood viscosity values measured by the proposed method are in good agreement with the ones obtained by the previous method,²⁴ with respect to various shear rates.

Therefore, we conclude that the proposed method is able to simultaneously measure viscosity and flow rate of blood with sufficient accuracy, even under periodically varying dynamic flow conditions.

Blood viscosity measurement for unknown flow rate

As shown in Fig. 5A, to measure blood viscosity (μ_x) under an unknown flow rate (Q_x), blood samples (H_ct = 40%) in a reservoir was supplied into the microfluidic device using the peristaltic pump, which operated at a pumping speed of 2 (i.e., ω = 2). The PBS solution was delivered into the microfluidic device using the syringe pump. During this experiment, the flow rate of PBS solution (Q_PBS) was carefully set to 5 mL/h. The left-side channel was exclusively filled with the blood. The blood was then continuously returned to the reservoir from the outlet (A). However, the right-side channel was partially filled with blood and PBS solution, which were removed from the outlet (B). Thus, most of the blood samples were circulated in the closed fluidic network including the peristaltic pump, the left side channel in the microfluidic device, and the reservoir.

Figure 5.

(A) Schematic diagram for measuring blood viscosity under an unknown flow rate supplied by a peristaltic pump. Most of the blood samples were circulated in the closed fluidic network, which includes a reservoir, a peristaltic pump, and the left side channel of the microfluidic device. (B) Temporal variations of blood flow rate with a periodic (T = 2.92 ± 0.12 s), supplied by the peristaltic pump which operated at a pumping speed of ω = 2. After passing through the half-circular chamber of the microfluidic device, the fluctuations in blood flow rate was completely removed owing to the compliance effect of the chamber. The number of indicating channels filled with blood in the right side channel (N_Blood) was kept consistent at 15 (N_Blood = 15), which is equivalent to the blood flow rate of Q_Blood = 5 mL/h, as identified by the experimental procedure using the blood samples collected from the outlet (A). (C) Variations of viscosity (μ_Blood) and flow rate (Q_Blood) of blood sample with respect to hematocrits ranging from 20% to 50%. (D) Variations in N_Blood and Q_Blood with respect to the pumping speeds from ω = 2 to ω = 3. The inset represents the relationship between Q_Blood and N_Blood.

As represented in Fig. 5B, the peristaltic pump induces flow fluctuations with a period of 2.94 ± 0.12 s, which was measured by using a microfluidic device without a half-circular chamber. Because the period is sufficiently shorter than the time constant (τ ≈ 8 s) resulting from the membrane compliance of the half-circular chamber, the flow fluctuations are completely removed. Therefore, the number of indicating channels filled with blood (N_Blood) in the right side channel was consistently monitored as 15. Simultaneously, the blood samples collected in the reservoir were supplied into the microfluidic channel using the syringe pump instead of the peristaltic pump. As a result, the blood flow rate is kept consistent at 5 mL/h by maintaining N_Blood at 15.

The flow rate and viscosity of the blood were measured using blood samples with various hematocrits ranging from 20% to 50%. As shown in Fig. 5C, insets (a) and (b) indicate N_Blood = 13 (H_ct = 30%) and N_Blood = 15 (H_ct = 40%), respectively. As expected, the blood viscosity tends to increase gradually from 2.36 ± 0.05 cP to 6.59 ± 0.05 cP with respect to hematocrits. Using the shear rate formula, the shear rate of the blood is estimated at 898.6 s⁻¹. The experimental result is comparable with the previous result, in terms of dependency on hematocrit.³¹ In addition, at a fixed pumping speed of 2 (i.e., ω = 2), the flow rate of blood is consistently identified as 5 mL/h regardless of hematocrits. This indicates that the peristaltic pump provides a constant flow rate, independent of fluidic resistance variation.

Lastly, for the blood with 50% hematocrit (H_ct = 50%), N_Blood was measured depending on pumping speeds which range from ω = 2 to ω = 3. As shown in Fig. 5D, N_Blood tends to increase in a linear fashion depending on the pumping speed. Using the relationship between Q_Blood and N_Blood as shown in the inset, Q_Blood also tends to increase linearly with respect to the pumping speeds.

From these performance tests of the proposed method, we conclude that the proposed method can measure blood viscosity with sufficiency and consistency, even at unspecified flow rate of blood.

Blood viscosity measurement in complex fluidic network

As a final demonstration, blood viscosity of rat blood circulating within a complex fluidic network was measured. As shown in Fig. 6A, the microfluidic device was installed in a complex fluidic network that includes the rat, a pinch valve, a reservoir, and a peristaltic pump. The rat blood was delivered at an unspecified flow rate (Q_x) by adjusting the pinch valve, which was located between femoral artery and the blood reservoir. The blood in the reservoir was supplied into the microfluidic device using the peristaltic pump at a pumping speed of 2 (i.e., ω = 2). Meanwhile, the PBS solution was delivered using the syringe pump at the flow rate of 5 mL/h (i.e., Q_PBS = 5 mL/h). The left side channel was only filled with the blood. The blood was then collected from the outlet (A). However, the right side channel was partially filled with blood and PBS solution, which were removed from the outlet (B). Next, the number of indicating channels filled with blood in the right side channel (N_Blood) was continuously monitored for 250 s. As shown in Fig. 6B, N_Blood is kept consistent at 18–19. To identify the viscosity and flow rate of blood, the collected blood and PBS solution were simultaneously supplied into the microfluidic device using the syringe pump. Two distinctive relationships (N_Blood vs. Q_Blood, μ_Blood vs. Q_Blood) were experimentally obtained, as summarized in the inset of Fig. 6B. According to the relationship, the blood flow rate is supplied at 3.8 mL/h into the microfluidic device using the peristaltic pump. As expected, blood behaves as a non-Newtonian fluid. The blood viscosity of the rat is identified as 5.89 ± 0.08 cP at a blood flow rate of 3.8 mL/h (i.e., Q_Blood = 3.8 mL/h, $\dot{\gamma }$ = 683.0 s⁻¹). In addition, the hematocrit of the rat blood was measured as 54.3% ± 0.3% using a centrifugal-based hemocytometer. After separating the plasma from the blood using a centrifugal-separator, the plasma viscosity was measured as 1.23 ± 0.01 cP.

Figure 6.

(A) Schematic diagram for measuring the viscosity and flow rate of blood circulating in a complex fluidic network that includes a rat, a pinch valve, a reservoir, a microfluidic device, a peristaltic pump, and a syringe pump. The flow rate of PBS solution was carefully maintained at 5 mL/h. In addition, the peristaltic pump was operated at a pumping speed of ω = 2. (B) Temporal variations in the number of indicating channels filled with blood in the right side channel (i.e., N_Blood vs. time). The inset represents two distinctive relationships (N_Blood vs. Q_Blood, μ_Blood vs. Q_Blood). Thus, the viscosity of rat blood is identified as 5.89 ± 0.08 cP at a blood flow rate of 3.8 mL/h.

Based on these experimental demonstrations, we conclude that the proposed method using three sequential flow controls in the microfluidic channel is capable of monitoring temporal variations in the viscosity and flow rate of whole blood with sufficient accuracy, even at an unknown blood flow rate.

CONCLUSION

In this study, we suggested a novel microfluidic device for measuring viscosity and flow rate of blood in a complex fluidic network. Based on three sequential microflow controls, the viscosity and flow rate of blood are simultaneously measured with label-free and sensorless detection. To demonstrate this proposed method, we carefully designed a twin-shaped microfluidic device, which is composed of two half-circular chambers, two side channels with multiple indicating channels, and one bridge channel connecting the two side channels. Using the microfluidic device, three sequential flow controls were applied to identify the viscosity and flow rate of blood circulating in the complex fluidic network. To supply consistent fluidic flow in the microfluidic device, the effects of flow stabilization owing to the half-circular chamber were extensively investigated using the mathematical modeling and experimental investigations. In addition, an analytical formula of PI was derived using a discrete fluidic circuit model for the proposed microfluidic device. Based on the PI formula, the time constant contributed by the half-circular chamber is estimated as 8 s. Furthermore, the flow fluctuations resulting from the operation of peristaltic pump are completely removed, particularly during periodic flow injections with a short periods of less than 10 s (T < 10 s).

To demonstrate the performance of the proposed method, it was applied to evaluate the viscosity and flow rate of blood with respect to (a) specified flow rate via a syringe pump and (b) unspecified flow rate via a peristaltic pump. As a result, the flow rate and viscosity of blood were simultaneously measured with sufficient accuracy, compared with the reference flow rate and the results obtained using the established method, respectively. In addition, the proposed method was successfully used to measure the viscosity of rat blood circulating in a complex fluidic network that includes a rat, a pinch valve, a reservoir, a peristaltic pump, and the microfluidic device.

Based on the experimental demonstrations in this study, the proposed method is found to be a promising tool for effectively measuring the viscosity and flow rate of whole blood circulating in a complex fluid network, without fully-integrated sensors, and tedious labeling procedures. In the near future, the proposed method will be applied to evaluate temporal variations in blood viscosity during cardiopulmonary bypass procedures or hemodialysis.