Recovery from Slow Inactivation in K⁺ Channels is Controlled by Water Molecules

Abstract

The bacterial K⁺ channel KcsA can be used to help elucidate questions about channel inactivation and recovery at the atomic level. Although KcsA contains only a pore domain, without voltage-sensing machinery, it has the structural elements necessary for ion conduction, activation and inactivation^1–7. Available X-ray structures of KcsA provide an atomic view of the four most important functional states in which the intracellular gate is either closed or open, and the selectivity filter is either conductive or inactivated^8–10. Application of a specific stimulus opens the intracellular gate of a K⁺ channel (activation), yielding a transient period of ion conduction until the selectivity filter spontaneously undergoes a conformational change toward a non-conductive state (inactivation). Removal of the stimulus closes the gate and allows the selectivity filter to interconvert back to its conductive conformation (recovery). In this manuscript, a series of long molecular dynamics (MD) simulations reveal how the selectivity filter is sterically locked in the inactive conformation by buried water molecules bound behind the selectivity filter. Potential of mean force calculations show how the recovery process is affected by the buried waters and the rebinding of an external K⁺ ion. A kinetic model deduced from the simulations shows how releasing the buried waters can stretch the timescale of recovery to seconds. This leads to the prediction that reducing the occupancy of the buried waters by imposing a high osmotic stress should accelerate the rate of recovery, which was verified experimentally by measuring the recovery rate in the presence of 2M sucrose.

Macroscopic current measurements show that the KcsA channel inactivates within 1–3 seconds and that recovery takes place in 5–20 seconds, depending on the external K⁺ concentration^2,3. When the filter is in the conductive state, it is occupied by several K⁺ ions arranged in single file over five binding sites (S0 to S4); ion occupancy is considerably reduced when the filter is in the non-conductive inactivated state because it is “pinched” at the central glycine residue of the signature sequence TTVGYGD. The conductive conformation of the filter is virtually unchanged when the gate is closed or open. The “pinched” non-conductive conformation of the filter is similar in the open-inactivated conformation and in the closed structure crystallized at low K⁺ concentration, indicating that the latter provides a realistic representation of the KcsA channel in the closed-inactivated state ¹⁰.

Although available X-ray crystal structures reveal the conformations of the functional states, they do not explain the experimentally observed timescales. Recovery from inactivation is an extremely slow, ion-dependent process.¹³ (Fig. 1). Yet, the structural difference between the conductive and non-conductive filter is less than ~1Å root-mean-square (RMS), barely larger than the thermal fluctuations of proteins under ambient conditions (Fig. 1d). According to a naïve Eyring rate theory argument, the long timescale corresponds to an activation free energy barrier of about 15–20 kcal/mol, a value that is difficult to reconcile with the very slight structural difference between the conductive and inactive filter (Fig. S1). Explaining the molecular origin of the extraordinarily long timescale of the recovery process stands is an unresolved issue.

Figure 1. Gating, inactivation and recovery in KcsA channels.

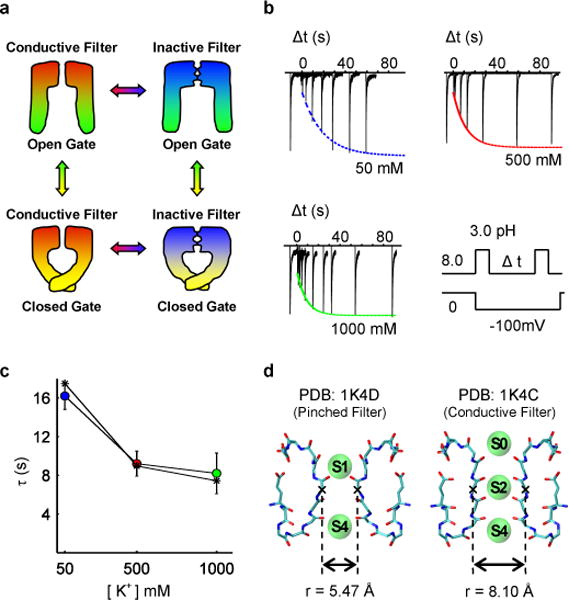
(a) Schematic depiction of the four dominant functional states. (b) Recovery of the selectivity filter from slow-inactivation measured from inward K⁺ current during a double pulse protocol that cycles the intracellular gate from open (inactivating the filter) to closed (promoting filter recovery) to open (for measuring the extent of recovery). The fraction of recovered channels increases as a function the inter-pulse duration (Δt) in each of the 3 patches, and may be fit to a single exponential function. (c) The fit time constants for recovery for various symmetric K⁺ concentrations demonstrate that K⁺ accelerates recovery. Results based on a kinetic model are shown as dashed line with asterisks. (d) The conductive state of the selectivity filter compared to the pinched state is characterized by a relatively small increase in the minimum inter-subunit distance between backbone atoms of the filter and an increase in ion occupancy.

To identify the barrier to an immediate recovery, a MD simulation of KcsA with the non-conductive filter and the closed gate was carried out in the presence of a high K⁺ concentration. While these conditions were designed to favor a spontaneous transition of the filter towards the conductive state, the filter remained in the non-conductive state during the 17 μs long simulation (Fig. 2a). Throughout the simulation, the selectivity filter stayed near the crystallographic conformation 1K4D and no ion translocation event was observed (Fig. S2). The stability of the non-conductive filter over this long timescale indicates that the simulation captured the rate-limiting step opposing a rapid recovery of the filter.

Figure 2. MD simulations reveal mechanism of recovery from inactivation.

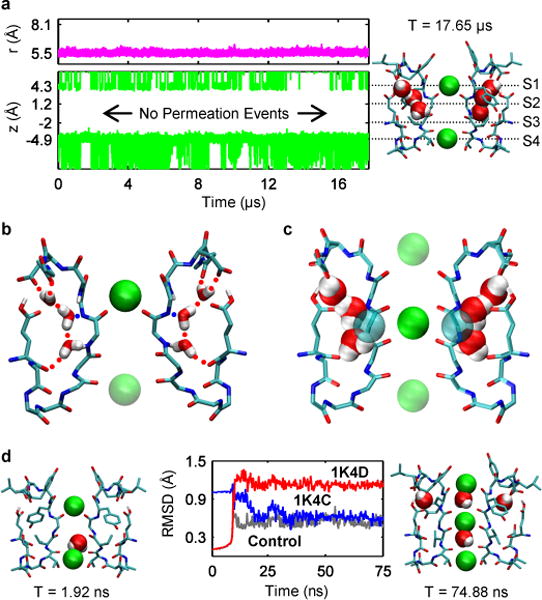
(a) Results from a simulation of the pinched filter show the width of the filter remained near r = 5.5Å where r is defined as the cross-subunit distance between the Cα atoms of glycine 77 (magenta line, top plot). Plot of the height of K⁺ ions, z, above the center of mass of the selectivity filter (green traces, bottom plot). Projection of the aforementioned plot onto a snapshot of the selectivity filter at the end of the simulation (right). (b) Network of hydrogen bonds match each water with two donors and an acceptor keeping waters trapped behind the selectivity filter throughout the simulation. (c) Water positions behind the pinched filter of 1K4D sterically clash with the conductive filter 1K4C. Rendering both water positions from 1K4D and the Cα glycine atoms from 1K4C as van der Waals spheres reveals that unfavorable steric clashes of ~1 Å in magnitude would exists between the protein and waters. (d) In simulations without water behind the filter, the RMS distance of the pinched filter relative to its original crystallographic coordinates (red) increases as the RMS distance to the conductive filter in 1K4C (blue) decreases. The RMS distance versus 1K4C falls to ~0.6 Å, comparable with a control simulation (dark grey) starting from the conductive filter 1K4C.

Examination of the 17 μs trajectory led us to focus on three buried water molecules in a ~8Å long cavity located behind the selectivity filter of each subunit. While water molecules bound near the protein surface are expected to undergo rapid dynamical fluctuations and exchange easily with the bulk¹⁴, the buried waters maintained distinct positions and orientations throughout the entire simulation. The buried waters are stabilized by a network of water-water and water-protein hydrogen bonds (Fig. 2b), displaying long residence times (Table S1). The buried waters thereby become an integral part of the protein structure when the selectivity filter is in the pinched conformation. On average, a given subunit cavity is occupied by 3 buried waters ~99% of the time as each cavity releases its waters into the bulk every 10–15 μs and refills in 80–100 ns (Fig. S5). The Tyr82 side-chain acts as a lid, controlling access to the cavity. In the cavity, the buried waters remain near the location observed in the structure with the pinched non-conductive filter (1K4D), which is also consistent with nuclear magnetic resonance (NMR) data^5,15. The outermost water molecule is observed in the X-ray structure of the conductive filter (1K4C), while the two others are absent. Structural modeling shows that the latter would clash with the backbone Cα of the central glycine residue (Gly77) if the filter adopted a conductive conformation (Fig. 2c). These results suggested that the presence of the buried water molecules bound behind the filter locks its conformation into the pinched non-conductive state and prevents a spontaneous transition toward the conductive state.

To demonstrate that these “inactivating waters” prevent recovery, MD simulations were carried out in which the inactivating waters removed (Fig. 2d). Within a few nanoseconds, the filter made a transition towards the conductive conformation (1K4C). The recovery transition was accompanied by K⁺ ions translocating inward toward the filter from the extracellular side and the binding of water molecules behind the filter at the positions observed in 1K4C. While one K⁺ ion moved to the site S2 of the filter, another entered the site S0 from the extracellular bulk. These two K⁺ ions, combined with a third K⁺ ion in S4 that remained present at its initial location during the entire simulation, resulted in a “S0-S2-S4” ion configuration in the filter. The involvement of K⁺ ions is expected, since the timescale of recovery increases at low extracellular K⁺ concentration. To further clarify the role of the ions, MD simulations were carried out with no free K⁺ ions in solution. In all cases, the filter remained in the pinched non-conductive conformation, consistent with the experimental observation that low extracellular K⁺ inhibits recovery. In contrast, additional simulations in 1M KCl showed that whether or not a K⁺ ion was initially bound in the site S4 or in the intracellular cavity of the channel, a K⁺ ion entered the filter from the extracellular side to bind to the site S2. Additional MD experiments were carried out to determine the outcome from different intermediate starting conditions (Table S2), indicating that the most likely pathway leading to recovery requires the absence of all 3 inactivating from all 4 subunits to permit the binding of an external K⁺ ion to the filter.

To characterize the free energy landscape controlling the recovery process, we calculated the 2D potential of mean force (PMF) as a function of the pinched glycine Cα-Cα distance of the filter r and the position of the external K⁺ ion Z (Fig. S6), with and without the inactivating waters (Fig. 3). These two states illustrate the energetic interplay between the inactivating waters and the external K⁺ ion on the recovery process. When the inactivating waters are present, no significant free energy barrier is encountered to move a K⁺ ion from the bulk to the binding site S1 of the pinched filter (Fig. 3a). However, the binding of an external K⁺ and its subsequent transition to the binding sites S2 or S3 is energetically forbidden if all the inactivating waters are present: the free energy landscape rises sharply, up to 30 kcal/mol relative to the local minimum, as the K⁺ is brought deeper into the filter toward the site S2 along the Z coordinate. The large energy barrier is because the non-conductive filter is too narrow for a K⁺ ion to fit through. The energy barrier to gradually open the filter to a conductive conformation is also highly unfavorable, rising by ~25 kcal/mol when an ion is in the site S1. Opening the pinched filter by moving along the r coordinate is opposed by a large free energy barrier because the backbone of the filter clashes with the buried inactivating waters. The PMF with the inactivating waters removed is markedly different (Fig. 3b). Once a K⁺ ion reaches the site S1, the recovery process becomes energetically downhill. A free energy basin guides the recovery process as the free energy decreases. The filter first makes a transition from the pinched to the conductive conformation, the ion in S1 then permeates down to the site S2, ending in a conformation that is highly similar to the 1K4C structure. In the absence of inactivating waters, the channel will spontaneously and rapidly recover to a conductive conformation upon the binding of a K⁺ ion from the extracellular solution; the filter remains locked in the non-conductive state, even with an incoming external K⁺ ion, as long as the inactivating waters are present.

Figure 3. 2D free energy landscape of the recovery process.

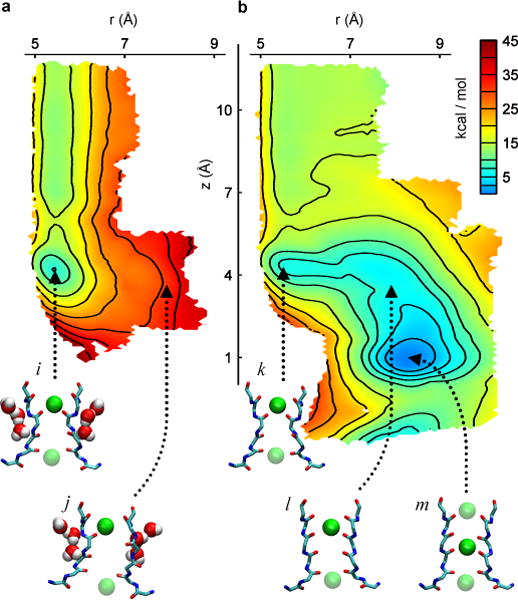
The horizontal reaction coordinate r describes the width of the selectivity filter and is defined as the cross-subunit distance between the Cα atoms of glycine 77. The vertical reaction coordinate z is the height of a K⁺ ion relative to the center of mass of the selectivity filter. (a) PMF calculated with inactivating waters present behind the selectivity filter. The pinched filter rests in a free energy minimum with a K⁺ in position S1 (snapshot i). The transition from a pinched to a conductive conformation (snapshot j) of the selectivity filter is impeded by a ~25 kcal/mol free energy barrier relative to the local minimum, resulting in an unstable conformation of the conductive filter. (b) PMF calculated with the inactivating waters absent. The pinched filter with a K⁺ ion in position S1 (snapshot k) recovers spontaneously, following the downhill slope of the free energy landscape. The filter recovers to a conductive conformation by moving first to an open conformation (snapshot l) before ions in the filter adopt a conductive configuration (snapshot m).

These experiments suggest that two factors control the conformational transition of the selectivity filter from the non-conductive pinched state to the conductive state: the release of the inactivating waters and the binding of an external K⁺ ion. The buried inactivating waters act as gate-keepers, locking the filter in the pinched non-conductive conformation; the binding of an external K⁺ ion cannot lead to recovery if they are present. The external K⁺ ion binding to the filter acts as a catalyst for the final step; releasing the inactivating waters does not lead to recovery without the binding of an external K⁺ ion. The inactivating waters must first be released to unlock the pinched state, and an external K⁺ ion must then bind to the filter to catalyze the final step to recovery.

Although these simulations suggest a plausible mechanistic scenario, a complete and spontaneous recovery from inactivation event was not observed during these experiments. The recovery process, which occurs on a timescale of ~10 seconds, is longer than what can be achieved with state-of-the-art computing technologies. Despite these limitations, it is important to bridge the results from MD experiments to the extremely long timescales of the recovery process observed in macroscopic current measurements. For this purpose, we rely on a kinetic model (Fig. 4a) based on the assumption that occupancy of the cavity of each of the four subunits by inactivating waters is independent and uncorrelated, and that recovery can proceed to its final stage through the binding of an external K⁺ ion only after all the inactivating waters have been released. While it is possible that recovery might occur very infrequently under different circumstances (Table S2), these constraints capture the dominant mechanism of recovery. Occupancy changes take place with forward and backward rates of k_f and k_b, followed by a final concerted step corresponding to the binding of an external K⁺ ion to the selectivity filter. By virtue of the stoichiometric constraint posed by the 4 subunits, the timescale of recovery predicted by this model is tens of seconds (Fig 1c, dashed line) using microscopic rates that are consistent with the current MD simulations (Fig 4). Moreover, the model displays the correct sensitivity to the external concentration of K⁺, becoming slower at low concentration and reaching a plateau at high concentration.

Figure 4. Role of water molecules in recovery process.

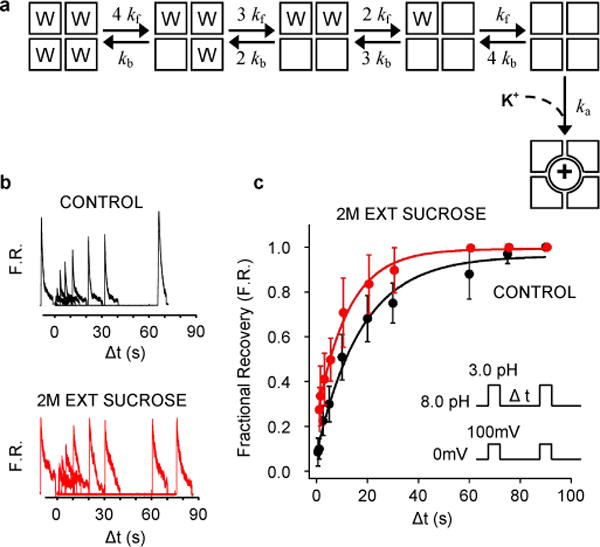
(a) Kinetic scheme incorporating the main findings of the MD simulations. The model was used to produce the simulated recovery times as function of [K⁺] shown in Figure 1c (dashed line) using the rate constants are 1/k_f=11μs, 1/k_b=79ns, 1/k_a=8.3 ns × (150mM/[K⁺]). When starting the kinetic model in the state with no inactivating waters, the channel reaches the active conductive state rather than the fully inactive state with a probability of ~0.5 at 50 mM of [K⁺]. This probability rises to ~0.7 at 150 mM of [K⁺]. (b and c) Effect of external sucrose on the time-course of recovery. (b) Outward currents recorded with external 5K⁺/145 mM NMG and internal 150 mM K⁺ in the absence and presence of 2M external sucrose. (c) Fractional recovery (F.R.) from 8 patches plotted as a function of the inter-pulse interval.

This mechanism predicts that lowering the occupancy of the subunit cavities by inactivating waters should accelerate the rate of recovery from inactivation. This is consistent with the experimentally observed hydrostatic pressure dependence of recovery for the Shaker K⁺ channel ¹⁶, which indicates that ~8 water molecules must be released from the inactivated state to return to the conductive filter. An alternative approach to vary the occupancy of the cavities is by applying a high osmotic stress to the external solution: increasing the osmotic stress from the external solution should accelerate the process of recovery¹⁷. The stability of the inactivating waters in 2M sucrose would decrease due to the high osmotic stress, which should lead to a more rapid time of recovery (Fig. S7). To test this prediction, we measured the rate of recovery of wild-type KcsA channel in the presence of 5 mM of K⁺ and 2M sucrose in the external solution (Fig. 4b). Without sucrose, the recovery time averaged from the two sets of 8 values is 17.06 + 4.75 sec, and in the presence of sucrose it decreases to 12.21 + 3.73 sec, consistent with our prediction (mean + SD; Fig. S7). While the overall effect is small (the waters bound to one subunit are destabilized by only ~0.7 k_BT), protein dynamics and the diffusion and binding of an external K⁺ ion to the selectivity filter that is critical to catalyze recovery are expected to slow down in viscous environment¹⁸. The fact that the recovery process is accelerated in 2M sucrose—despite a viscosity that is 30 times that of pure water—is strong evidence that the applied osmotic stress decreased the occupancy of the gatekeeper inactivating water molecules locking-in the non-conductive state of the selectivity filter.

Our MD simulations and macroscopic current measurements suggest that the selectivity filter of K⁺ channels functions as a ligand-gated pore through a built-in osmometer, where water molecules from the external solution are the “ligands” responsible for the gating stimulus. It is unlikely that such a mechanism could play an important physiological role in higher organisms, as there are negligible variations in internal osmotic strength; however, it is possible that such a mechanism could regulate bacterial K⁺ channels, as microorganisms are often exposed to widely varying external conditions. Examination of homology models of various K⁺ channels indicates that the subunit cavities are conserved structurally and in terms of the hydrogen bonding interactions that they could provide through the peptide backbone (Fig S3), suggesting that the role of inactivating waters acting as gate-keepers of the pinched non-conductive filter is likely to be conserved in the K⁺ channel superfamily.

Methods summary

Initial coordinates for the Molecular Dynamic (MD) simulations were taken from the crystal structures 1K4C and 1K4D. Crystallographic waters around the single subunit in each of the two crystal structures were placed around all four subunits in the tetramer. Residues were assigned their standard protonation state at pH 7.0, except for residue Glu71, which was protonated. The channel was embedded in a bilayer of POPC lipids and solvated in 1M KCl using the web service CHARMM-GUI (total number of atoms: 45898). All-atom simulations were run using the CHARMM PARAM27M force field²⁰ under constant NVT conditions at a temperature of 310K. MD simulations were carried out on the special purpose computer Anton²¹ on loan to the Pittsburgh Supercomputer Center (PSC). A total of 114 MD simulations were carried out starting from different initial conditions with respect to the inactivating water molecules, for an aggregate total time of 29.5 μs of MD.

FULL METHODS

Initial coordinates for the Molecular Dynamic (MD) simulations were taken from the crystal structures 1K4C and 1K4D. Crystallographic waters around the single subunit in each of the two crystal structures were placed around all four subunits in the tetramer. Residues were assigned their standard protonation state at pH 7.0, except for residue Glu71, which was protonated. The channel was embedded in a bilayer of POPC lipids and solvated in 1M KCl using the web service CHARMM-GUI (total number of atoms: 45898). All-atom simulations were run using the CHARMM PARAM27 force field²⁰ under constant NVT conditions at a temperature of 310K. MD simulations were carried out on the special purpose computer Anton²¹ on loan to the Pittsburgh Supercomputer Center (PSC). A total of 114 MD simulations were carried out starting from different initial conditions with respect to the inactivating water molecules, for an aggregate total time of 29.5 μs of MD (Table S2). The 2D PMFs (Fig. 3) with respect to the two coordinates r and z (Fig. S6) were calculated from Replica Exchange Molecular Dynamic (REMD) simulations²² using NAMD 2.9 (ref ²³), which were carried out on the petaflop supercomputer Jaguar, located at the National Center for Computational Sciences (NCCS). The region of interest in the (r, z) space was covered by a grid of equally spaced US windows; initial coordinates for the windows were taken from the unbiased trajectories or by slowly dragging neighboring configurations. For the first PMF (Fig. 3a), the 3 inactivating waters initially bound to each of the 4 subunits were trapped using flat-bottom harmonic distance restraints (flat portion spanned 8 Å). In the second PMF carried out without inactivating waters (Fig. 3b), restrained dummy particles (i.e., no interactions with the channel) were introduced to prevent re-entry of water from the bulk region. The first PMF comprises 137 windows while the second consists 226 windows, which were simulated with US/H-REMD (exchanges attempted every 1ps) for more than 0.5 ns for equilibration and more than 1ns for data accumulation. The results were unbiased using the weighted histogram analysis method (WHAM) ²⁴.

Electrophysiological measurements were made by patch clamp recordings in channel-reconstituted liposomes prepared as described earlier^25,26. Purified protein was reconstituted in asolectin vesicles (in 1:100 (mass:mass) protein to lipid ratio) by dilution with 200 mM KCl and 10 mM MOPS buffer at pH 7.0. Residual detergent was further removed by incubation with biobeads (Bio-Rad Laboratories). Channel-incorporated liposome suspension was then centrifuged for 2 h at 100,000 g and the pellet was resuspended in 60 μl of KCl/MOPS buffer. A drop of the proteoliposome was placed on a glass slide and dried overnight in a desiccator at 4°C. The sample was then rehydrated with 20 μl of buffer, which yielded giant liposomes. This preparation was suitable for patch clamp recordings after ~2 h. Currents were recorded 10mM MOPS buffer with indicated salt concentration. For measurements under KCl gradient, N-methyl-D-glucamine was used to replace KCl in the pipette. Recording pipettes were pulled from thin-walled borosilicate glass and heat polished such that they had a bath resistance of 1–2 MΩ when filled with 200 mM KCl, 10 mM MOPS solution. All measurements in this study were conducted in the inside-out configuration of the patch clamp technique. Experiments were performed at room temperature (20–22°C). Currents were elicited in response to pH jumps from 8.0 to 3.0 using an RCS-160 fast solution exchanger (Biologic) fed by gravity. Macroscopic currents were sampled at 5 kHz using Axon 200-B patch-clamp amplifier. For each experiment in the absence or presence of sucrose, the fractional recovery was measured at different inter-pulse intervals. There are 8 sets of experiment without sucrose, and 8 with sucrose. For the two conditions, the average recovery curve and its standard deviation was determined from the 8 different sets, and the time constant was determined from a single-exponential least-square fit. To determine if the recovery time constant in the absence and presence of sucrose is significantly different, we fitted each of the 8 individual data sets (for the two conditions) by a single exponential and determined the recovery time constant for each experiment. The two sets of 8 values were subjected to an unpaired Student t-test (DoF=14), which yielded a p-value of 0.03969.

The two 2D PMFs shown in Figure 3 were calculated using umbrella sampling (US) molecular dynamics (MD) simulations following a stratification strategy in which the region of interest in the space of the two reaction coordinates is covered by a grid of equally spaced US window simulations. To improve the statistical sampling, the US calculations were performed using Hamiltonian Replica Exchange MD (US/H-REMD) simulations (also called US window swapping).²⁸ Initial coordinates for the US windows were taken from the unbiased trajectories carried out on Anton. Initial coordinates for the missing windows were obtained by gradually dragging neighboring windows along the reaction coordinates to the center of each of the missing windows.

Initial coordinates for the first PMF came from the 17μs long unbiased MD simulation of the stable, pinched filter (Figure 2A). Windows taken from this trajectory already contained 3 inactivating water molecules lodged behind the selectivity filter in the cavities of each of the four subunits. A series of flat-bottom harmonic distance restraints were added between channel atoms and the water oxygen of the inactivating waters to ensure that they remained present behind the filter. The flat portion of the restraints spanned 8 Å above the pore helix of the channel – providing the water molecules freedom to move around a region of space purposefully designed to be larger than the overall size of the cavity. The initial coordinates for the second PMF came from the MD trajectory of the recovery process (Figure 2D), providing windows spanning the conformational transition from the pinched to the conductive filter. Windows taken from this trajectory lacked all inactivating water molecules behind the filter. To maintain the system in this occupancy state during the US/H-REMD simulations, dummy atoms (no non-bonded interactions with the channel) positioned above the pore helix were introduced in order to repel any water molecule trying to enter into the cavities behind the filter from the bulk region.

The first PMF comprised 137 windows while the second PMF consisted of 226 windows spanning the complete recovery process. All windows were equilibrated ≥ 0.5ns before starting REMD. Exchange attempts were made every 1000 steps (or 1ps of simulation of time), and neighboring windows were swapped if the Metropolis Monte Carlo exchange probability was satisfied. US/H-REMD simulations for the two PMFs were run for more than 1ns. The total aggregate simulation time used to produce the 2 US/H-REMD calculations is more than 800 ns. Windows were unbiased using the Weighted Histogram Analysis Method (WHAM),^29,30 which only required that the umbrella sampling windows were generated according to Boltzmann statistics.