Abstract
A polarizable force field of saturated phosphatidylcholine-containing lipids based on the classical Drude oscillator model is optimized and used in molecular dynamics simulations of bilayer and monolayer membranes. The hierarchical parameterization strategy involves the optimization of parameters for small molecules representative of lipid functional groups, followed by their application in larger model compounds and full lipids. The polar head group is based on molecular ions tetramethyl ammonium and dimethyl phosphate, the esterified glycerol backbone is based on methyl acetate, and the aliphatic lipid hydrocarbon tails are based on linear alkanes. Parameters, optimized to best represent a collection of gas and liquid properties for these compounds, are assembled into a complete model of dipalmitoylphosphatidylcholine (DPPC) lipids that is tested against the experimental properties of bilayer and monolayer membranes. The polarizable model yields average structural properties that are in broad accord with experimental data. The area per lipid of the model is 60 Å2, slightly smaller than the experimental value of 63 Å2. The order parameters from nuclear magnetic resonance deuterium quadrupolar splitting measures, the electron density profile, and the monolayer dipole potential are in reasonable agreement with experimental data, and with the non-polarizable CHARMM C36 lipid force field.
Keywords: DPPC, Bilayer, Monolayer, Drude Force Field
1 INTRODUCTION
Classical molecular dynamics (MD) simulations based on detailed atomic models represent a powerful approach to understand complex biomolecular systems. To obtain meaningful results from such simulations, however, using an accurate molecular mechanical force field (FF) is of paramount importance. The most commonly used biomolecular force fields approximate the complex quantum mechanical (QM) Born-Oppenheimer energy surface governing the interaction between molecules with simple analytical functions.1–8 Electrostatic interactions are modeled on the basis of simple point charges with fixed constant values optimized to mimic the average interaction between molecules in different environments.9 These fixed charged models are thus designed to account for induced polarization in a mean-field average way. In real molecules, however, the electron density is not static but must respond to the local electric fields. and the accuracy of fixed charge models becomes questionable in complex heterogeneous systems.
These issues take on a special importance in the case of biological membranes, where the molecular environment undergoes dramatic variations over microscopic length-scales. Within a distance of 10–15 Å corresponding to the polar head group region of a phospholipid bilayer membrane, the environment shifts from the high dielectric of bulk water to the low dielectric non-polar hydrocarbon core at the membrane interior. This complexity poses a particular challenge to models that employ fixed atomic charges. For instance, it is expected that the molecular dipole of a water molecule changes from a value close to the gas phase dipole (|μ|=1.8 Debye), in the electrostatically non-polar core of a membrane, to a dipole that is enhanced in magnitude (2.5 < |μ| < 3.0 Debye), in the bulk water region. Such a trend is ignored in fixed charge models, where the dipole is constrained at a value that reflects a mean bulk water-like environment. Furthermore, the dielectric response of the non-polar hydrocarbon region is not expected to be well represented by fixed charge models. While an effective mean charge distribution can be an acceptable approximation in regions where the dielectric response is dominated by the re-orientation of permanent dipoles, as it is in bulk water, it is a poor approximation in regions where the dielectric response is dominated by electronic polarization, as for non-polar hydrocarbons. The local dielectric constant of the hydrocarbon core of a membrane, which should have a value of about 2,10,11 is about 1 in fixed charge models. The lack of induced polarization in fixed charge models of hydrocarbons has a significant impact on the dipole potential at the membrane water interface, a property that strongly affects the permeation of charged species.12 In such models the dipole potential is approximately twice as large as that determined from experiment.
To improve the accuracy of MD simulations of biological membrane systems, we have developed and parameterized a polarizable FF for phospholipid molecules based on the classical Drude oscillator model.11,13 The chemical environment of a biological membrane is complex, which makes teasing out and attributing the various energetic contributions to specific terms in the FF a challenge. A reasonable strategy to determine the optimal parameters of the FF is to focus on the properties of small compounds that are representative of the various functional groups in a phospholipid. High level QM calculations can be used to probe interactions in the gas phase, while experimental measurements of thermodynamic, transport, and dielectric properties of pure substances can be used to infer energetic contributions to interactions in condensed phase environments. The larger molecule is then constructed from a set of well-characterized building blocks. In addition to simplifying the parameterization procedure, this strategy makes it possible to increase the transferability of the resulting FF. For phosphatidylcholine lipids, alkane molecules are used to model the aliphatic tails, ester molecules to model the esterified glycerol backbone, and the molecular ions of ammonium and phosphate model the head group. The protocol for the parameterization of the ester group of molecules and larger model compounds used to determine parameters that interface between functional groups will be discussed in detail, while the parameterization for the alkane models and molecular ions will be briefly summarized below.
A complete polarizable model of dipalmitoylphosphatidylcholine (1,2-dipalmitoyl-sn-glycero-3-phosphocholine), or DPPC, is assembled and used to carry out MD simulations of solvated bilayer and monolayer membranes. DPPC, one of the most extensively studied components of biological membranes, is an ideal benchmark system to assess the new polarizable FF. The results from the simulations are then compared against those from the CHARMM C36 model,2 which is perhaps the most accurate non-polarizable lipid FF currently available. The average structure of the membrane model is assessed by comparing to the experimentally determined area per lipid, bilayer thickness and monolayer surface tension. Measurements of the electron density profile and NMR order parameters are used to probe bilayer structure in greater detail. The electrostatics of the model are compared to measurements of the interface potential of a lipid monolayer spread on an air-water interface.
2 PARAMETERIZATION METHODOLOGY
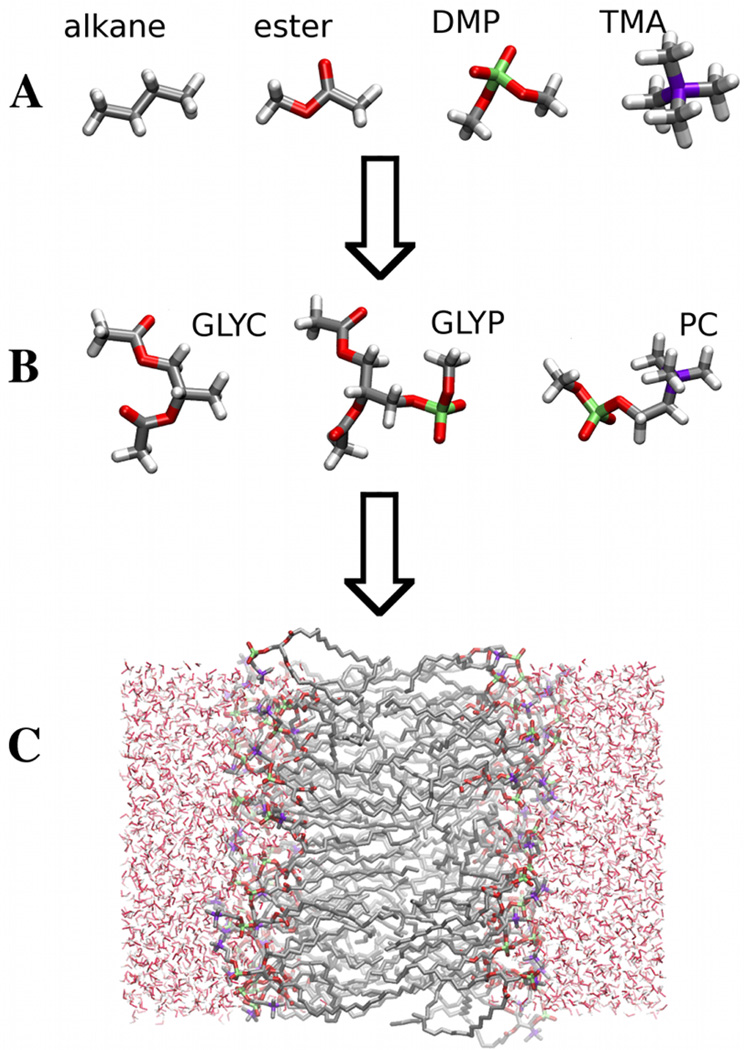
The basic strategy used to determine the parameters for the Drude phospholipid model is illustrated schematically in Figure 1: (A) parameters are determined for small molecule analogs of the functional groups that constitute the macromolecule; (B) larger model compounds are then used to determine parameters associated with intra-molecular degrees of freedom that lie at the interface between functional groups; and (C) MD simulations of the DPPC bilayer and monolayer are used to test the model.
Figure 1.
The figure illustrates the three stage process used to determine parameters for the model. (A) Model parameters are first calibrated against properties of small organic molecule analogs of functional groups of the phospholipid. (B) Torsional degrees of freedom that lie at the interface between functional groups are calibrated against QM calculations for an esterified glycerol compound (GLYC) a phospho-glycerol compound (GLYP) and a phosphatidyl choline compound are used to determine model parameters that lie at the interface between functional groups. (C) Simulations of a DPPC bilayer are used to test the model.
For all small molecules, the parameters were optimized using reference gas phase QM data via a grid search in parameter space and validated against available experimental data. QM data are calculated with QCHEM14 or the Gaussian 03/09 suite of programs.15,16 To perform QM computations efficiently without compromising accuracy, different levels of theory and basis set are chosen depending on the application. The MP2/6-31G(d) level provides a sufficient degree of accuracy in the optimization of gas phase geometries for neutral molecules and cations,17 whereas the MP2/6-31+G* level is used for anions. For each small molecules, all possible minimum energy rotamer configurations for the molecule are identified with CHARMM starting with an initial set of guess values for torsion parameters12 and reasonable sets of dihedral angle values about the central bond of the torsion. QM geometry optimizations starting with the set of unique FF rotamer configurations are performed and the set of distinct QM rotamer configurations are used in parameter optimization. The MP2/aug-cc-pVTZ single point energy is calculated for each resulting QM optimized rotamer configuration.
2.1 Electrostatic parameters
Electronic polarization effects are incorporated in the model by the addition of classical Drude oscillators.18 In this model, a mobile auxiliary charged particle is attached by a harmonic spring to a given atom. A charge of opposite sign is assigned to the atom and the electroneutral pair forms a classical Drude oscillator able to polarize in response to an external field. For each particle i, the model comprises core atomic charges, q(i), that are associated with the unpolarized charge distribution of the molecule, as well as the charges associated with the electro-neutral oscillators, i.e., the Drude charges, (on the nucleus) and (on the auxiliary Drude particle). In the current model, Drude oscillators are only added to heavy atoms (non-hydrogen) with the positive end anchored to the atomic site. The total potential energy associated with the Drude oscillators has the form„
| (1) |
where Uelec is the sum over all Coulombic interactions between core charges q(i) located at , and the Drude charges and are located at and respectively. The displacement vector for the Drude particle with respect to the parent nucleus is defined as , with a magnitude of . The contribution Uself, is the self-energy of the Drude oscillators, which may take the form of isotropic or anisotropic harmonic restraints. Most atoms are approximated to be isotropically polarizable. In this case, the Drude oscillators are treated as harmonic springs with the following self-energy (1/2) , where KD is the spring constant for the Drude oscillator. For atomic sites bearing lone pairs, such as oxygen, the core charge is restrained to off-atom virtual sites and the atomic polarizability is anisotropic. To model this, an anisotropic Drude oscillator is employed for such atoms, and its self-energy is given by (1/2) , where the force constant tensor KD is diagonal in a local reference frame that is fixed with respect to the parent molecular group. In the spirit of the Born-Oppenheimer approximation, the Drude particles associated with the electronic polarization can be relaxed to their energy minimum for any given nuclear configuration. The result is an equilibrium between the force of the Drude spring in the local frame and the electrostatic force from the total external electric field. This condition can be written in a form analogous to the self-consistent field (SCF) treatment for atomic point dipoles. In practice, the SCF treatment is computationally prohibitive and an extended Lagrangian scheme with a dual-thermostat is used to propagate the dynamics.13 Greater detail regarding the potential function used is provided in references.13,19 The non-electrostatic portion of the potential function has been discussed elsewhere.1
As in standard fixed charge FFs, the interactions between core charges corresponding to 1–2 (neighbor) and 1–3 (next-neighbor) pairs are subsumed by explicit bonding terms in the potential energy, Uint, and necessarily excluded from the electrostatic energy. Similarly, the interactions of the Drude oscillators with core charges are excluded for 1–2 and 1–3 pairs, though Coulomb interactions between Drude oscillators (i.e., dipole-dipole interactions) corresponding to 1–2 and 1–3 atom pairs are included but shielded by a damping function Sij(rij). The general form of the shielding function used in this work is,20
| (2) |
where rij is the distance between the particles forming the Drude-nucleus oscillators, αi is the trace of the atomic polarizability tensor and ai are the Thole damping parameters that modulate the shielding strength of Sij. The interactions involving all core charges and all Drude oscillators are included without shielding for all 1–4 pairs and beyond.
A critical feature in the development of a polarizable model is determining appropriate parameters to describe the atomic polarizability. In the current model, atomic polarizabilities are assumed to be independent of their environment. However, studies of the dispersion properties in crystals21–24 and electronic structure calculations25 have found a significant environmental impact on the atomic polarizabilities of halides. Studies have also found evidence for similar environmental effects on the polarizability of water.26 A possible explanation for these observations argues that electron repulsion between neighboring molecules in the condensed phase can impede the electronic response of a molecule, effectively reducing the molecular polarizability relative to the gas phase. The implication for the development of an optimal polarizable FF is to seek values that capture the effective response in a dense liquid-like environment as the target data. This is justified because the simulation of aqueous solvated biomolecules is ultimately the system of primary interest.
To determine electrostatic parameters, a map of the electrostatic potential (ESP) that surrounds a molecule is evaluated on a set of specified grid points using QM calculations.19,27,28 The lowest energy rotamer of the molecule is typically used for constructing the ESP maps. To measure the electronic response of the molecule a series of perturbed maps of the ESP are computed by placing a single +0.5e test charge at a set of chemically relevant positions around the molecule. The same calculations are repeated using the Drude model, restricting the force constant tensor of each oscillator to be isotropic. Optimal parameters are chosen to minimize the difference between the unperturbed and perturbed ESP maps from the QM and FF models according to:
| (3) |
where {q, α, a} are the set of core charges, Drude polarizability, and atom-based Thole damping parameters that define the electrostatic potential energy of the model. An additional restraint, , is used to ensure that the optimized parameters do not deviate appreciably from chemically significant values. Lone pair positions are chosen based on the local QM ESP in the vicinity of the lone pair and further optimized based on interactions of the respective model compounds with water. Details of the restrained fitting scheme employed here can be found in Anisimov et al.28 and Harder et al.27
Density-functional theory provides an efficient means of evaluating the electrostatic potential maps used to fit electrostatic parameters of the Drude model.28,29 The QM electrostatic potential calculations are evaluated using the B3LYP functional30,31 and the aug-cc-pVDZ basis set, a combination that has been shown to give good agreement with molecular polarizabilities and gas phase dipole moments.28 The electrostatic parameter fitting of the FF was carried out using a modified version of the FITCHARGE module in CHARMM.32
2.2 Lennard-Jones parameters
The Lennard-Jones (LJ) parameters of the non-polarizable CHARMM FF33 were used as an initial guess for the parameters of the Drude model for molecular ions. A set of models, generated on a grid in the LJ parameter space, are selected based on their agreement with the QM gas phase interaction data. Interaction energies and distances between the model compound and either a rare gas atom or a water molecule are used as initial target data. The gas phase interaction data between the ion and water is typically found to be sufficient to determine appropriate LJ parameters. The hydration free energy of the molecular ions serves as a test of the model validity in the condensed phase, and may be used as additional target data for final adjustment of the LJ parameters if necessary.
In the present work, final QM interaction energies are computed at the MP2/6-311+G(3df,2p) level which includes additional polarization and diffuse functions to ensure a faithful polarization response. Interaction energies are evaluated as the difference between the energy of the complex and the respective monomers and include the removal of basis set superposition error.34 An exception is made for interactions dominated by dispersion effects, where a higher level of theory and larger basis set become necessary. Interactions between the model compound and rare gas atoms are therefore evaluated at the MP3/6-311++G(3d,3p) level without the correction for basis set superposition.35 Optimized interaction energies and distances between the model compound and individual water molecules or rare gas atoms are obtained by scanning the energy along selected intermolecular distance coordinates. The geometry of the molecule is held fixed at the QM optimized conformation and the water molecule is held fixed at the experimental gas phase geometry.
For the esters, the LJ parameters are optimized by varying the parameters and simulation of the bulk liquid. For each parameter set, the molar volume (Vm) is calculated from the volume of the constant pressure simulation box per molecule. The enthalpy of vaporization is calculated from the average change in energy upon formation of the dense system,
| (4) |
where 〈U〉liq and 〈U〉vap are the average energies for the bulk liquid and the gas phase. The static dielectric constant is computed from,36
| (5) |
where the system dipole, , corresponds to a unit cell containing N molecular dipoles at an average volume 〈V〉 and temperature T. The infinite frequency dielectric response, ε∞, is calculated from,
| (6) |
where 〈⋯〉f indicates an average over induced-dipole fluctuations only. The average is obtained from Drude oscillators moving according to Langevin dynamics at a temperature T with all nuclei frozen in configurations extracted from MD simulations.
The agreement between experimental and simulation estimates for the liquid molecular volume, the enthalpy of vaporization and dielectric constant are used to select the best set of LJ parameters. The ability to reproduce the crystal lattice is also tested to further verify the validity of the model. In the case of esters, pair specific interactions (NBFIX)37 with water are quantified using QM minimum energy ester-water dimer configurations that sample the important hydrogen bonding environments around the two ester oxygen atoms and the corresponding energies. For the ester carbonyl oxygen atom, a cone with lateral height of 3 Å is defined with the carbonyl oxygen atom at the vertex and the carbonyl vector, pointing towards the carbonyl oxygen atom, defines the axis passing through the center of the cones base. Water oxygen atoms are placed on the base of this cone such that the angle subtended between nearest neighbor water oxygen atoms and the base center is 10°. One hydrogen atom per water molecule is oriented along the straight line joining the water and carbonyl oxygen atoms. The second hydrogen atom of water is oriented randomly. For the ether oxygen of the ester molecules, a cone with lateral height of 3 Å is defined with the ether oxygen at the vertex and the line from the vertex bisecting the C-O-C reflex angle defines the axis of the cone. Water molecules are placed on the base of this cone analogous to the case of the carbonyl oxygen atom. Starting with these 72 dimer configurations, full QM geometry minimizations are performed using the MP2/6-31G* basis set. The unique QM minimum energy dimer configurations are identified and single point energies are calculated at the MP2/aug-cc-pVTZ level of theory. The same procedure is repeated for all rotamers of the ester molecule that have energies within 10 kcal/mol of the rotamer global energy minimum.
The NBFIX parameter optimization was started with an initial set of parameters corresponding to the Lorentz-Berthelot combination rules. For each QM dimer configuration, m, the set of distances between atom i of water and heavy atom j of the ester molecule was calculated. The QM pair interaction energy, , is also calculated. Starting with the m’th QM dimer configuration, the FF was used to minimize the dimer energy. The set of distances and pair interaction energy are calculated analogously for the FF minimum energy configuration. The NBFIX parameters are optimized by minimizing the following objective function
| (7) |
where λ1 = 10−6. In practice, an additional harmonic restraint is placed to prevent the NBFIX parameters from drifting more than 0.1 from the reference parameters obtained using the Lorentz-Berthelot mixing rules.
2.3 Intra-molecular parameters
Using the non-bonded parameters and electrostatic model, equilibrium internal bonded term parameters were optimized against crystal data from a survey1 of the Cambridge Crystal Data Bank.38 Bonded term force constants were optimized against QM calculations of the vibrational spectra. Vibrational spectra were computed at the MP2/6-31G(d) level with a scale factor of 0.943439 in the parameterization of intra-molecular bond force constants. Analysis of the vibrational spectra was performed with the MOLVIB module40 in CHARMM using the internal coordinate assignment suggested by Pulay.41
2.4 Dihedral parameters
Parameters associated with torsional degrees of freedom were optimized against one dimensional relaxed potential energy scans as well as rotamer energies in order to balance the local and global QM target data. Starting from the global minimum or a rotamer configuration with energy within 5 kcal/mol from the global minimum, QM relaxed potential energy scans were performed using Gaussian 0916 for torsions involving non-hydrogen atoms only. Thus, for a molecule with N such torsions, N − 1 are kept fixed while one dihedral angle was scanned from −180 to 180° in increments of 10°. All configurations during the scans are extracted and single point energy calculations at the MP2/aug-cc-pVTZ level of theory are performed. For each configuration, i, obtained from each scan, the torsion parameters are set to zero and the FF energy from the non-torsional degrees of freedom, , is calculated. The QM energies, , are shifted such that the global minimum energy configuration has zero energy. For torsion parameter optimization, the following objective function was defined:
| (8) |
where is a normalization constant, V0 is a global energy scale shift factor, the subscript R and S correspond to rotamer and scan configurations, and , the index i runs over the total number of configurations from the scans, the index j runs over all rotamers for the molecule, and
| (9) |
where Ndist is the number of distinct torsions based on the atom types with each having a unique set of parameters, Nrep(m) is the number of distinct dihedral angles of type m in the molecule, and Nk is the maximum allowed multiplicity in the series expansion. FF torsion parameters of the Drude model are adjusted to give the best agreement between the QM and FF data from the scans and rotamers by minimizing the objective function. When using pre-optimized parameters from other molecules, they are excluded from the optimization although their contribution to the objective function is included.
3 COMPUTATIONAL DETAILS
All molecular dynamics (MD) simulations were performed with the programs CHARMM32 or NAMD42,43 which have been recently extended to support the Drude force field. The electrostatic degrees of freedom are minimized at the outset of the simulation and propagated dynamically along with the nuclei using a special dual-thermostat to keep the Drude oscillators at a low temperature.13 For appropriately chosen kinetic variables so-called extended Lagrangian simulations provide an accurate and efficient alternative to a self-consistent field solution at each time step of the simulation.13,44 A mass of 0.4 amu is typically added to the free end of the Drude oscillator and subtracted from the reference heavy atom. Although the Drude oscillator dynamics has been shown to be approximately adiabatic with this choice of mass45 they are coupled to an additional thermostat at a temperature T* of 1 K.
CHARMM utilizes dual Nosé-Hoover thermostats, one each for the nucleus and Drude-nucleus pairs, and Anderson-Hoover barostat46,47 to control the temperature and pressure of the bulk system.13 Temperature in the monomer simulations was controlled by a Langevin thermostat.48 A modified velocity-Verlet algorithm is used to integrate the equations of motion48 and the SHAKE/Roll and RATTLE/Roll procedure49,50 was used to constrain covalent bonds to hydrogens. Periodic boundary conditions were used in all liquid simulations. A particle mesh approximation to the Ewald sum with “tin foil" boundary conditions is used to evaluate the Coulombic interactions in the liquid simulations51 with a real space cutoff of 12 Å, an Ewald splitting parameter of 0.34 Å−1 a grid spacing of about 1.0 Å and a 6th order interpolation of the charge to the grid. A potential switching function between 10–12 Å is used for the LJ potential and a long range correction to the energy and pressure from the LJ potential is included.48 NAMD on the other hand utilizes a dual-Langevin thermostat43 and the Brünger-Brooks-Karplus method52 to integrate the Langevin equation for bulk simulations. The equations of motion are integrated with a 1 fs time step. All liquid simulations are performed at 1 atm.
Neat liquid simulations of systems containing 216 molecules were performed at 298 K and 1 atm. Simulations are run for 150 ps and data is collected over the last 100 ps except for methyl acetate for which the simulation was run for a total of 2.5 ns. The dielectric constant is evaluated from the average of 5 independent simulations. The hydration free energies were computed from a box containing 211, 118, and 120 water molecules and one molecule of methyl acetate, dimethyl phosphate and tetramethyl ammonium, respectively. The dispersive and repulsive contributions to the free energy were split using Weeks-Chandler Andersen decomposition of the LJ energy.53 The electrostatic and dispersive contributions were evaluated by thermodynamic integration. The integration was partitioned into 10 windows and performed using the trapezoid rule. The repulsive part of the free energy was evaluated from free energy perturbation using a protocol discussed elsewhere.54,55 Averages in the free energy calculations were taken from the last 250 ps of a 500 ps simulation for each window. An isotropic long range correction to the free energy is included.48 Error bars for the free energy were estimated from a block average of three 500 ps simulations.48
Simulations of the DPPC bilayer membranes consisted of 72 DPPC molecules, 36 per membrane leaflet, and 2189 water molecules. The simulations were started from a pre-equilibrated configuration from a C36 simulation of the DPPC bilayer that was graciously provided by Dr. Jeff Klauda. The membrane lies in the (x,y) plane with the normal to the interface along the z-direction. The simulation temperature was selected to be 323 K and initial Boltzmann distributed velocities were assigned randomly by NAMD using an initial seed for the random number generator. The temperature of the Drude oscillator was fixed at 1 K and a reflective hard-wall constraint was used to impose a maximum distance of 0.3 Å between the Drude particle and its parent atom; details are presented in Appendix 7. The simulations used a time step of 1 fs and all interactions were calculated at every time step. Periodic boundary conditions were applied along the three principal directions. Isotropic long range corrections to the energy and pressure for the LJ interactions were included as a simple approximation to the full correction in NAMD.
A total of three simulations starting with the same configuration but different initial velocities were performed with NAMD in the NPT ensemble for the Drude FF. In these simulations, the polarizable water model SWM4 based on the Drude FF was used.45 For comparison, one additional simulation was carried out using NAMD for the non-polarizable C36 FF.2 In this simulation, the non-polarizable water model TIP3P was used.56 An important point worth noting here is that the Drude model uses potential-switching for handling pair interactions, unlike the C36 additive model which uses force-switching2 instead. For all NPT bilayer simulations, the system was equilibrated for 25 ns and configurations were saved for analysis every 1 ps from the next 25 ns of the simulation.
The starting configuration used for the NPT simulations was also selected for constant area simulations of the Drude bilayer in the NPNAT ensemble with area per lipid fixed at 62 and 64 Å2. The system was equilibrated for 25 ns and the trajectory over the next 25 ns of the simulation was saved for analysis. The configuration at the end of 25 ns for the 62 Å2 area simulation was selected for a 1 ns initial simulation at an area of 61 Å2. The resulting configuration was used for a 50 ns simulation of a bilayer with area of 60 Å2. The configuration at the end of 1 ns of this simulation was used as the starting point for a 1 ns constant area simulation with area of 59 Å2. The final configuration was used for the 50 ns bilayer simulations at an area of 58 Å2. The starting configuration for the simulation at the constant area of 66 Å2 was generated in a similar stepwise manner starting with the configuration at the end of the 25 ns trajectory for the 64 Å2 simulation. Thus, a total of five constant area simulations were performed in the NPNAT ensemble for the Drude FF for 50 ns. Two 50 ns simulations using the C36 FF were also performed each at an area of 62 and 64 Å2.
Initial configurations for monolayer-water system were constructed from the final configurations obtained from the NPNAT simulations for the appropriate area. The air-monolayer-water-monolayer-air system is constructed by translating the bilayer leaflets and extending the unit cell along the membrane normal to 250 Å. Consequently, the number of DPPC and water molecules is the same as for the bilayer simulation. A total of five monolayer NVT simulations were performed at areas of 58, 60, 62, 64 and 66 Å2. The final configuration of the monolayer simulation with area of 62 Å2 was selected and all DPPC molecules removed. The resulting water slab with 2189 molecules was used for a 75 ns NVT simulation of the air-water interface. Periodic boundary conditions were applied for all DPPC monolayer and air-water interface simulations.
4 RESULTS AND DISCUSSION
The parameter optimization and validation in the present study builds up from models of small molecules that correspond to small molecular fragments of DPPC. These molecular fragments were then linked to create larger model compounds for which the FF parameters, related to molecular connectivities between the smaller model compounds, were supplemented. This stage of the optimization largely focused on torsion parameters. The final stage of the process involved creation of the full lipid FF followed by testing it in simulations of monolayers and bilayers. Results from this stage of the parameterization fed back into the small model aspect of the process when unsatisfactory results were obtained in the case of the bilayer simulations. Central to the overall quality of the FF is a proper treatment of the non-bonded aspect of the model. In lieu of more direct quantitative assessments of effective molecular polarizabilities in condensed phase environments, we have chosen an approach that employs bulk liquid properties to make empirical adjustments to the model polarizabilities.19,37,55,57–59
Previous experience with the C36 FF indicates that the methyl acetate (MAS) moiety is a critical element in the lipid model. Therefore, a number of polarizable models of MAS with the same electrostatic parameters but different LJ parameters were tested. The final model is determined by considering the enthalpy of vaporization, molecular volume and dielectric constant of the neat liquid as well as reproduction of the crystal lattice. For the molecular ions the polarizabilities were determined based on a recent study of atomic ions with a polarizable model based on Drude oscillators.60 This study found atomic polarizabilities for cations that are approximately equal to the gas phase value and a polarizability that is scaled down by 30% for anions gave hydration free energies that are in good agreement with experiment.
4.1 Model compounds and force field parameters
4.1.1 Alkanes
Parameters for the hydrocarbon tails of the lipid molecules are taken from the parameterization of a polarizable Drude model for alkane molecules.10 The molecular polarizability of the isolated molecules and the dielectric constants of the condensed phases, calculated as part of the present study, are summarized in Table 1 for ethane and butane. Alkane molecules are non-polar and properties such as the density and enthalpy of vaporization of uniform neat alkane liquids are more sensitive to dispersion effects associated with the LJ terms then the electrostatic parameters of the model. Though polarization effects do not manifest to a significant degree in the marginal field environment that comprise alkane liquids, the molecular polarizability of alkane molecules is significant.10 Because alkanes lack a permanent dipole, the dielectric permittivity of neat liquid alkanes is almost entirely due to the electronic polarization response. The molecular polarizability is well represented by the current Drude alkane FF as is the dielectric constant of the liquid.10
Table 1.
Polarizability and dielectric constant of Drude models for selected alkane compounds. Dielectric properties are evaluated at T=184.55 K and 272.65 K, respectively. Experimental data is from Ref.64
| α (Å3) | ε | |||
|---|---|---|---|---|
| Molecule | Experiment | Drude | Experiment | Drude |
| Ethane | 4.47 | 4.06 | 1.76 | 1.71 |
| Butane | 8.20 | 8.01 | 1.81 | 1.80 |
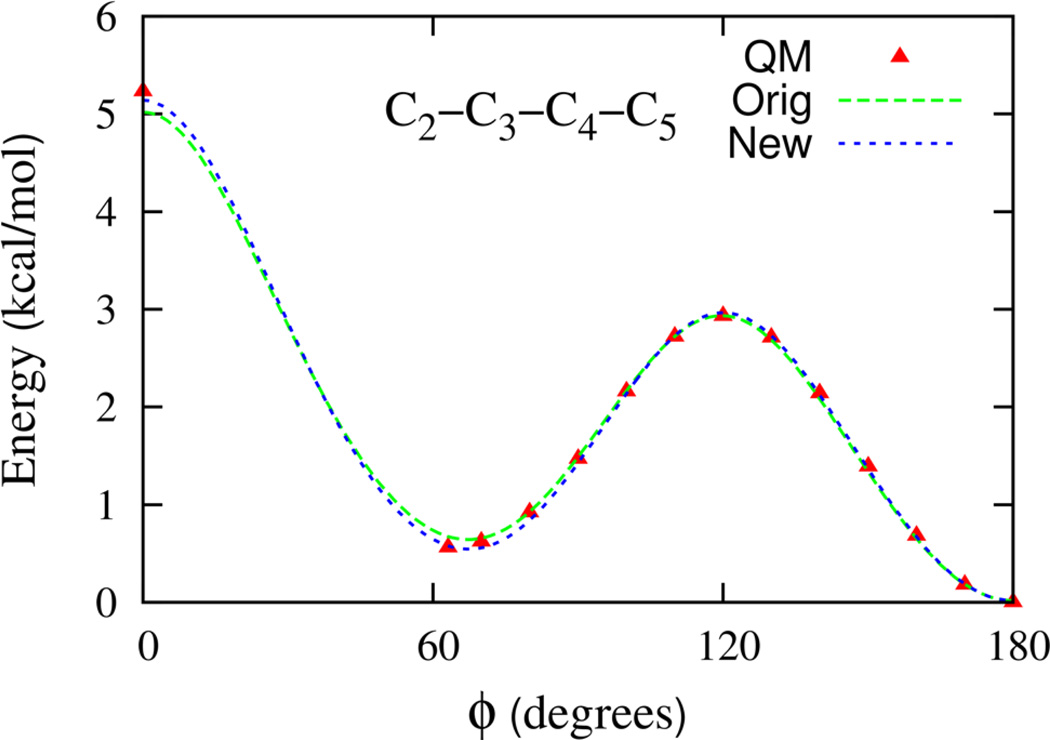
The hydrocarbon torsion parameters lead to overall good agreement between QM and FF torsion surfaces. In view of the importance of the relative population of trans-gauche configurations in the DPPC hydrocarbon tail for membrane properties, we revisited the agreement between QM and FF torsion surfaces. The 1-D potential energy scan for the C-C-C-C torsion of an isolated n-heptane molecule based on the original torsion parameters is shown in Figure 2. The FF was found to overestimate the energy of the gauche conformation by 0.1 kcal/mol, as compared to the QM scan. To improve the agreement between FF and QM 1-D scans, the torsion parameters were modified. The 1-D scan resulting from this modification is also presented in Figure 2 for comparison with the original FF and QM data. The agreement between the gauche energy is now improved, while the trans-gauche barrier height is minimally affected. Heptane rotamer energies61 were also found to be in slightly better overall agreement with QM energies.
Figure 2.
The torsion energy surfaces for heptane. The C2–C3–C4–C5 dihedral is scanned while keeping all other dihedrals fixed at 180°. The QM data is from Klauda et al. J. Phys. Chem. B 109, 5305 (2005) as is computed using the MP2:CC method described therein. The Orig model is the best fit of the QM data and New corresponds to the FF gauche state stabilized by an additional 0.1 kcal/mol required for better agreement with the QM data.
4.1.2 Dimethylphosphate and tetramethylammonium
Parameters for the phosphate portion of the phosphatidylcholine head group are based on a Drude model of the dimethylphosphate anion (DMP) and summarized in the Supporting information. The electronic properties of the DMP model are presented in Table 2. The model polarizability of 7.8 Å3 is smaller than the QM value of 10.6 Å3. The underestimation of the gas phase molecular polarizability is consistent with the renormalized atomic polarizabilities used in the parameterization of polarizable halide models.60,62 The positive moiety of the phosphatidylcholine head group is based on the parameterization of the tetramethyl ammonium cation (TMA) and optimized FF parameters are included in the Supporting information. The electronic properties of the TMA model are presented in Table 2. The molecular polarizability shown in Table 2, agrees well with the QM value. This is consistent with a recent parameterization of polarizable cationic atoms that base the model atomic polarizability on the gas phase polarizability of the ion.60,62
Table 2.
Electronic properties of dimethyl phosphate(DMP) and tetramethyl ammonium(TMA). Shown are the trace of the molecular polarizability. The unit of length is Å.
| Molecule | Properties | QM | CHARMM | Drude |
|---|---|---|---|---|
| DMP | TR(ᾱ) | 10.6 | N/A | 7.8 |
| TMA | TR(ᾱ) | 8.0 | N/A | 8.1 |
4.1.3 Esters
Ester compounds serve as the analogs of the esterified link to the glycerol backbone. Parameters for the Drude ester model are based on a detailed parameterization of MAS. Electrostatic parameters are determined by following the procedure discussed in Section 2. The QM and FF electrostatic potential data used to fit the parameters are computed for a monomer of MAS that is fixed in the QM optimized trans conformation which is the predominant conformation found in lipid structures. The electrostatic parameters were fitted directly to the gas phase QM data. The resulting dipole moment and polarizability are presented in Table 3 and are in good agreement with the reference QM values. The fitted Drude model electrostatic parameters are provided in the Supporting Information.
Table 3.
The molecular dipole and polarizability of methyl acetate. The QM properties are calculated at the B3LYP/aug-cc-pVDZ level.
| Properties | μx | μy | μz | μ | αxx | αyy | αzz | TR(ᾱ) |
|---|---|---|---|---|---|---|---|---|
| Exp | 1.7 | 6.9 | ||||||
| QM | 0.3 | 1.9 | 0.0 | 1.9 | 8.3 | 7.1 | 5.5 | 6.9 |
| Drude | 1.38 | 1.18 | 0.0 | 1.83 | 8.4 | 6.8 | 5.4 | 6.9 |
The LJ parameters for the polarizable Drude FF for N-methyl acetamide (NMA) and ethers are used as the initial guess for MAS about which a grid search in LJ parameter space is performed. The methyl LJ parameters and the Rmin for the carbonyl oxygen are kept fixed at the NMA values. LJ parameter sets for all other atoms are constructed about the origin such that Emin varies by ±0.05 kcal/mol and Rmin varies by ±0.05 Å for a total of 243 grid points including the origin. For each grid point, condensed phase simulations are performed for the gas phase and neat liquid to finalize the ester LJ parameters for the Drude FF.
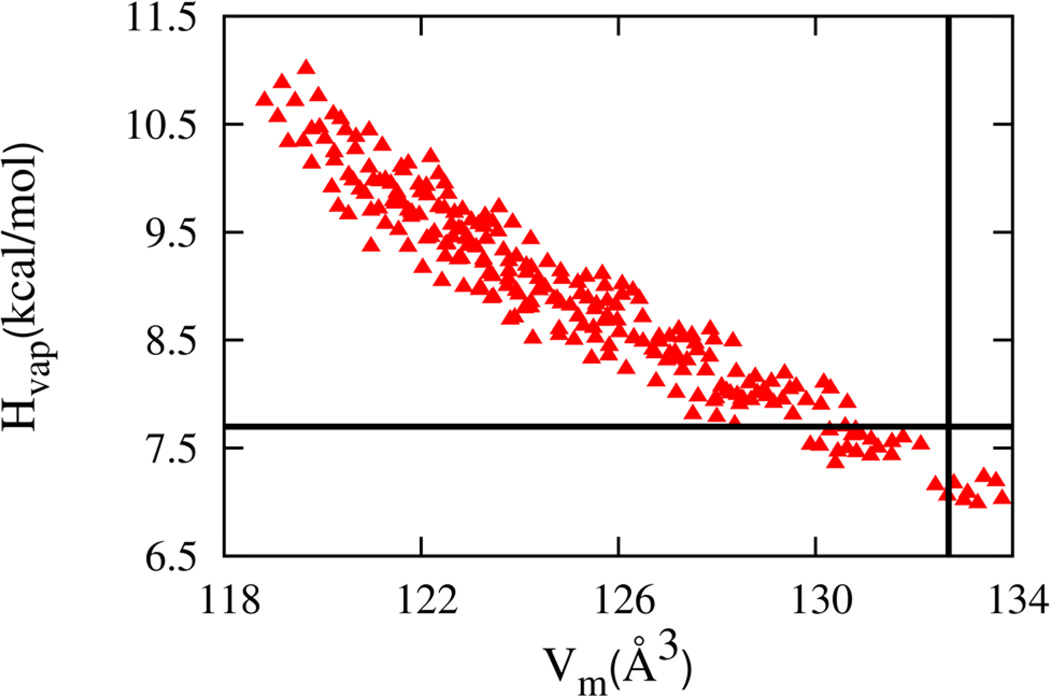
The results for Vm and Hvap are plotted in Figure 3. Each point corresponds to a different combination of LJ parameters. The enthalpy varies monotonically but nonlinearly with the molecular volume over the range of LJ parameter variation. Overall, decreasing the volume brings molecules closer together in the liquid and increases attractive interactions leading to a larger enthalpy. From the set of LJ parameters, those which give molar volume and enthalpy of vaporization within 2% of the experimental values of 132.7 Å3 63 and −7.8 kcal/mol,64 respectively, is selected for further analysis.
Figure 3.
The enthalpy of vaporization and molecular volume of neat methyl acetate liquid simulations for the Drude model (red triangles). The experimental values are shown as black lines.
To aid in selecting an appropriate LJ parameter set, the dielectric constant of liquid MAS is computed for the selected models. Dielectric properties provide a sensitive measure of the condensed phase electrostatic behavior of a molecule and can help discriminate between the different LJ parameter sets. For each model short-listed based on Vm and Hvap values, the dielectric constant is calculated and the results summarized in the Supporting information. The model with dielectric constant closest to the experimental value of 6.765 was selected as the MAS model. Both the static and infinite frequency dielectric constants of the models are summarized in Table 4. The infinite frequency response (ε∞) is due to the polarization of electron densities and is therefore directly sensitive to the effective electronic polarizability of the molecules in the condensed phase. The static dielectric constant is sensitive to both the size of the individual molecular dipoles that comprise the liquid and their orientational correlation.66 Because the dielectric constant in the model is slightly overestimated in the model, the implication is that the dipole moment or the orientational correlations must be enhanced compared to experiment. Finally, the stability of the methyl acetate crystal for the optimal model is verified and the data is presented in the Supporting Information.
Table 4.
Thermodynamic properties of methyl acetate at 298 K.
The quality of the MAS model is further tested by transferring the parameters to the following esters : ethyl acetate, methyl propionate, methyl butyrate and isopropyl acetate. The enthalpy of vaporization and molar volumes for these bulk liquids from simulations and experiments are presented in Table 5. The agreement is satisfactory for all the properties presented, further justifying the application of the parameters based on MAS to the lipid.
Table 5.
Thermodynamic properties of ester series at 298K. The models are based on the Drude model of methyl acetate. Experimental data is from Reference.95
| Molecule | ΔH (kcal/mol) | < υ > (Å3) | ||
|---|---|---|---|---|
| Experiment | Drude | Experiment | Drude | |
| Ethyl Acetate | −8.5 | −9.1 ± 0.5 | 163.6 | 165.4 ± 7.7 |
| Methyl Propionate | −8.6 | −9.0 ± 0.4 | 160.9 | 165.5 ± 9.1 |
| Methyl Butyrate | −9.7 | −10.0 ± 0.4 | 189.9 | 194.2 ± 6.4 |
| Isopropyl Acetate | −8.9 | −9.2± 0.5 | 194.5 | 192.4 ± 8.3 |
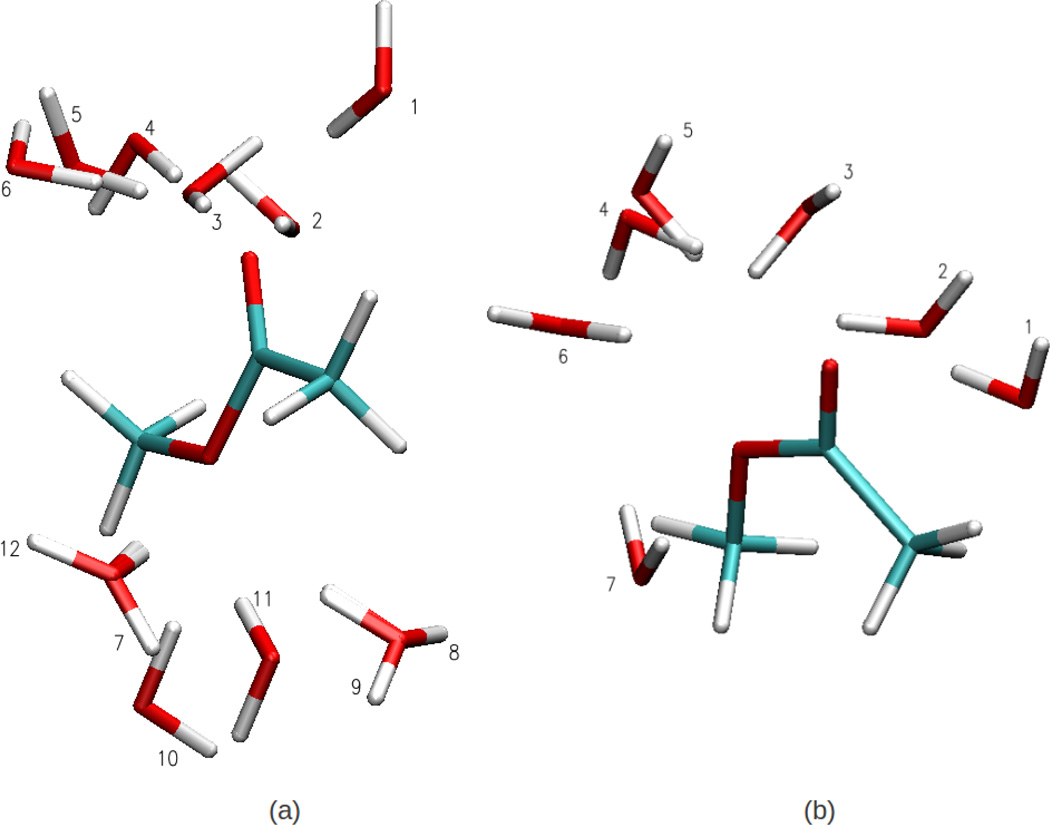
With the optimized LJ parameters for MAS, using the Lorentz-Berthelot for the water/MAS interactions leads to a hydration free energy of −6.2 kcal/mol, a value significantly more favorable than the experimental value of −3.4 kcal/mol.67 To improve the hydration behavior of MAS, for the cis- and trans-rotamers of MAS, minimum interaction energies and distances were obtained via full QM geometry optimizations for MAS-water dimers, as depicted in Fig. 4. The NBFIX parameters were optimized by matching the FF and QM dimer configurations as well as energies. The energies for the optimized FF and QM configurations are presented in Table 6. The overall agreement is better for the cis rotamer of MAS than the trans rotamer. For the trans-MAS rotamer, the contribution of some dimer configurations to the error in reproducing the QM dimer energies is significant. This may be ascribed to the QM dimer configurations not corresponding to a local minimum energy configuration or due to a deficiency in the FF. The overall root mean squared error for all rotamers is 0.51. The resulting NBFIX parameters were then utilized in the hydration free energy calculation for MAS and lead to a value of −3.7 kcal/mol, which is in satisfactory agreement with the experimental value. The final set of LJ and NBFIX parameters are presented in the Supporting Information.
Figure 4.
Methyl Acetate-Water dimer conformations for the (a) Cis and (b) Trans (methyl orientation with respect to carbonyl oxygen) methyl acetate conformations used to evaluate pair specific interaction energies between methyl acetate with water.
Table 6.
Summary of gas-phase interaction energies for heterodimers of methyl acetate with water as shown in Fig. 4. The pair interaction energy for the QM and FF minimum energy dimer configurations is presented along with the mean squared (MSD) errors.
| Configurations | Cis | Trans | ||
|---|---|---|---|---|
| QM | Drude | QM | Drude | |
| 1 | −5.96 | −5.92 | −6.53 | −6.62 |
| 2 | −4.94 | −6.25 | −4.64 | −4.72 |
| 3 | −5.50 | −6.25 | −4.50 | −4.71 |
| 4 | −3.85 | −5.92 | −4.97 | −4.86 |
| 5 | −5.56 | −6.25 | −5.18 | −5.22 |
| 6 | −4.94 | −6.25 | −4.72 | −4.48 |
| 7 | −3.59 | −3.69 | −4.64 | −4.71 |
| 8 | −3.49 | −3.69 | −2.23 | −3.24 |
| 9 | −3.59 | −3.70 | ||
| 10 | −3.37 | −3.69 | ||
| 11 | −3.95 | −3.59 | ||
| 12 | −3.48 | −3.69 | ||
| RMSD error | 0.76 | 0.14 | ||
| average RMSD error | 0.51 | |||
4.2 Optimization of the dihedrals parameters
Parameters for the Drude FF associated with the torsional degrees of freedom found in the phospholipid but not encompassed by the small molecule compounds are determined in this stage of the parameterization. To determine the appropriate parameters, three larger compounds that contain the relevant degrees of freedom associated with combining the smaller model compounds are now examined. Again, QM computations of conformational energies are used to provide the fundamental target data used to calibrate the parameters. The three compounds, which are illustrated in section B of Figure 1, include propylene glycol diacetate, a compound representative of the esterified glycerol backbone region of the lipid that will be referred to as “GLYC”, and propylene glycol diacetate phosphate, a model compound that encompasses the glycerol backbone region as well as the phosphate group that will be referred to as “GLYP”, and finally phosphatidylcholine, a model compound of the phosphatidyl choline head group that will be referred to as “PC”.
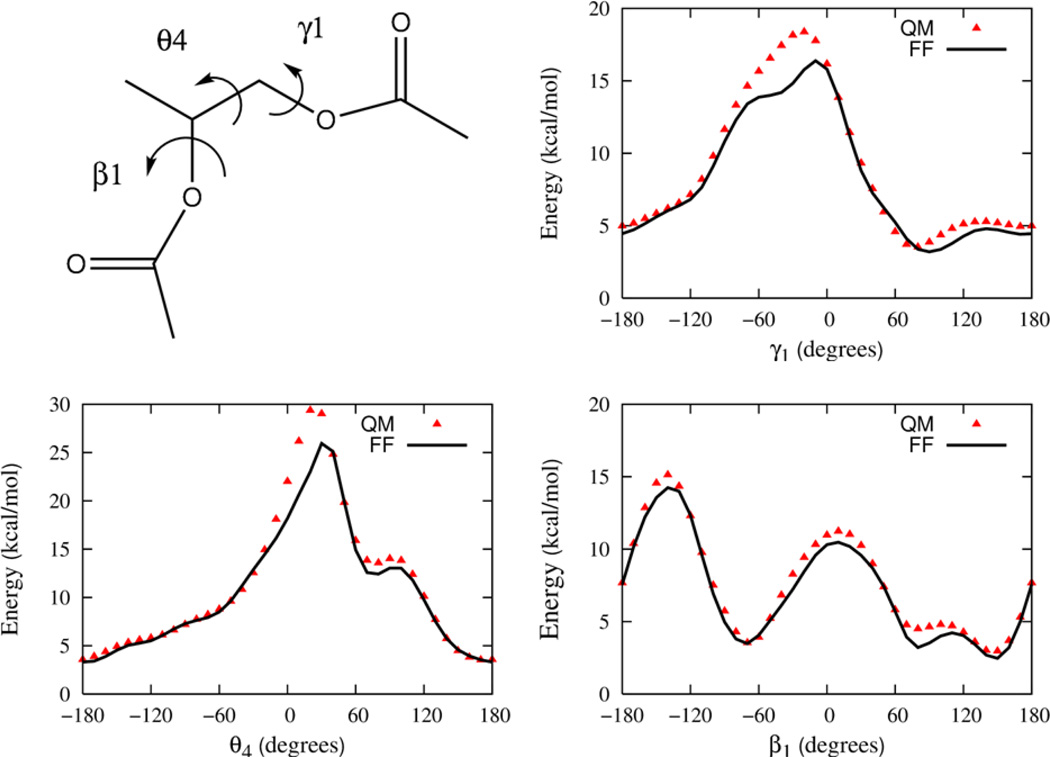
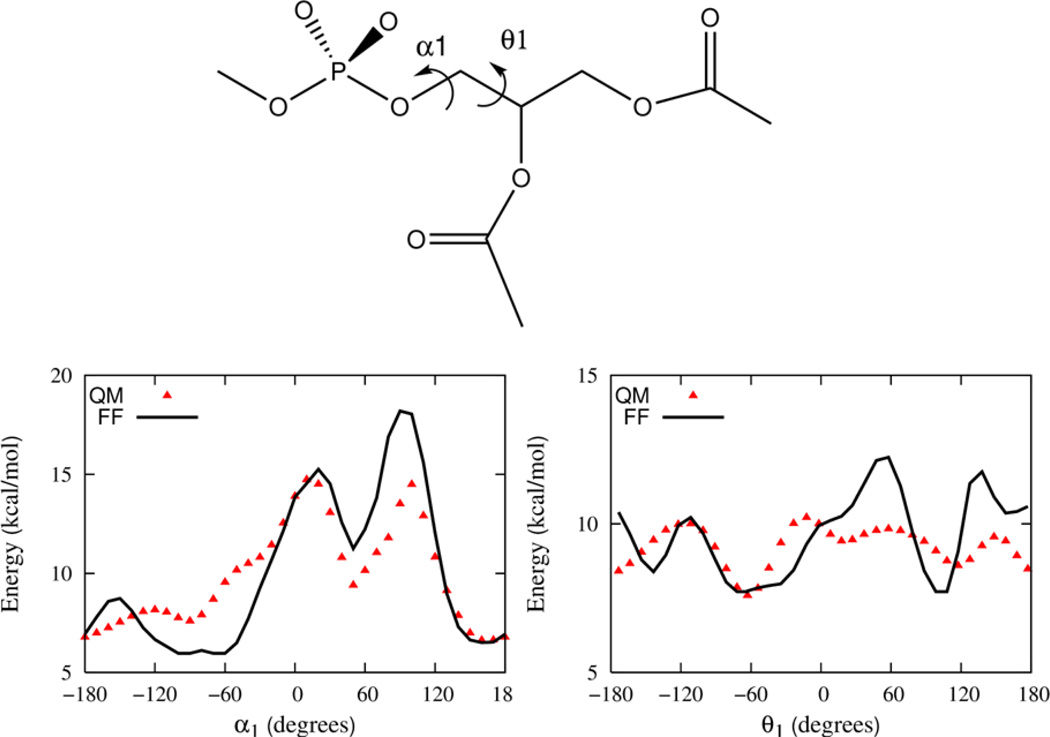
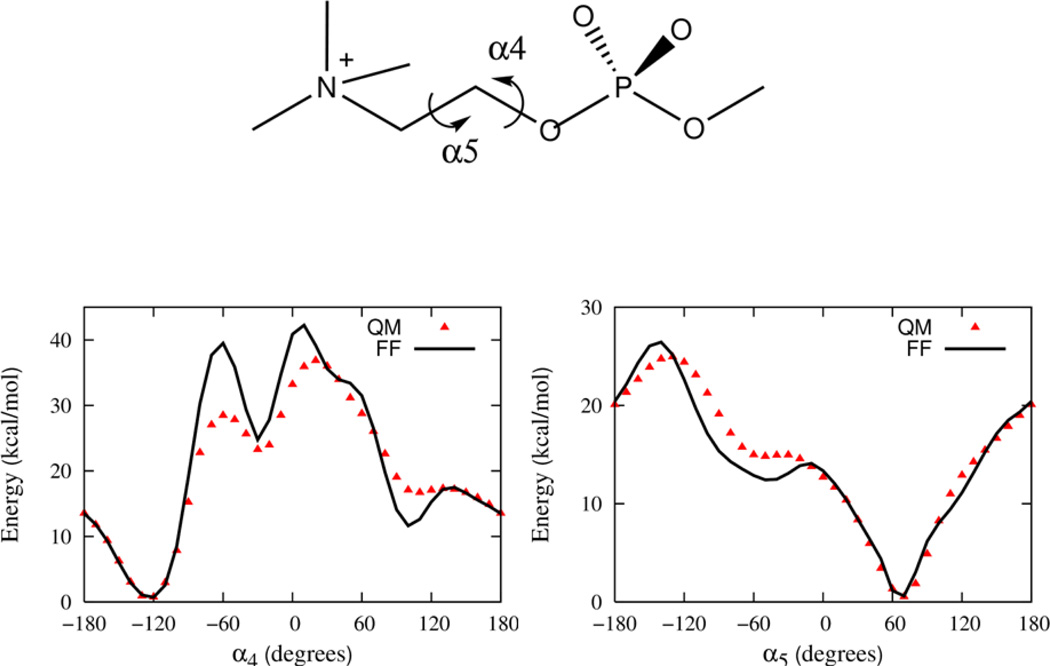
A full sampling of the conformational space of torsions would be extremely challenging, even for the GLYC, GLYP and PC compounds as they each contain 5, 9 and 5 rotatable bonds, respectively. The torsions specifically examined here are labeled in Figures 5, 6 and 7, respectively. Additional scans of the dihedral angles are not shown in these figures, but are used in the parameter optimization.
Figure 5.
The 1-D relaxed energy profile as a function of dihedral angle in the glycerol backbone model compound (GLYC) for γ1, θ4 and β1. Energies are offset relative to the energy minimum rotamer conformation. The rotamer configuration is (β1 = −68.3, β2 = −176.5, θ4 = 170.73, γ1 = 77.3 and γ2 = −178.5.
Figure 6.
The energy profile as a function of dihedral angle in the glycerol backbone model compound (GLYP). A single dihedral angle is probed holding the others fixed starting with a rotamer configuration γ2 = −167.9, γ1 = 87.6, θ4 = 170, β1 = 141.4, β2 = −169.9, θ1 = −178, α1 = −92.1, α2 = −72.1 and α3 = −70.3.
Figure 7.
The energy profile as a function of dihedral angle in the head group model compound PC. A single dihedral angle is probed holding the others fixed starting with a rotamer configuration α2 = −77.2, α3 = −61.6, α4 = −124.4, α5 = 70.1, and α6 = −175.4.
Prior to the torsion optimization for these compounds, we optimize the torsions for all the esters. For the GLYC compound, the targeted torsions are β1, θ4 and γ1. (The dihedral angle nomenclature for DPPC is used throughout and summarized in the Supporting information.) A rotamer search identified twenty six distinct QM rotameric states that comprise the GLYC model. For the global minimum configuration, the additional ester torsions, β2 and γ2, are in the approximately trans state as observed experimentally due to the large energy barrier to rotation associated with these degrees of freedom. The energy profiles from the QM model are shown in Figure 5 along with the best fit FF energy profiles and the agreement between the two is good.
The model compound GLYP, shown in Figure 1, is used to parameterize the θ1 and α1 dihedrals of the lipid. In total, nine dihedrals characterize the conformational states of GLYP. Dihedrals for β1, θ4 and γ1 corresponding to the 26 rotamers of GLYC and the global energy minimum of DMP (gauche-gauche) are fixed and a rotamer search performed for the remaining two angles. QM optimizations were carried out for a total of 297 rotameric states and the quality of agreement between FF and QM energies is included in the Supplementary Information. Using a rotamer with energy about 5 kcal/mol above the global minimum, relaxed potential energy profiles are constructed to determine the barrier heights for the θ1 and α1 degrees of freedom. Dihedral parameters for the Drude model are refined to give the best agreement with this QM data and the optimized 1D profiles are presented in Figure 6. The overall agreement between QM and FF profiles for α1 is good but for θ1, some notable difference in the shape of both the minima and maxima are apparent. Additional optimization of these dihedral parameters alone did not improve the overall quality of the fits and given the quality of the final DPPC model in mono- and bilayer simulations additional adjustments were not deemed necessary.
A model of the phosphatidylcholine head group (PC) is illustrated in Figure 1 and is used to determine parameters for dihedral potentials associated with the α4 and α5 torsions that modulate the conformational flexibility of the head group. Once again dihedral parameters are optimized against 1D energy profiles and rotamers. Figure 7 shows the relaxed potential energy scans for α4 and α5 starting with a low energy rotamer obtained from the QM data along with the surface from the final Drude model. Clearly, the position of the minima as well as the low energy part of the scans are well reproduced although the agreement of the barriers is less ideal.
4.3 DPPC bilayer simulations
4.3.1 Scattering data
The overall structure of the lipid bilayer from simulations can be validated against experiments by comparing the form factor which is measured through X-ray and neutron scattering experiments. The form factor is related to the average electron density profile, ρ(z), via a Fourier transform
| (10) |
where d is the length of the unit cell perpendicular to the bilayer and ρW is the electron density of pure water.
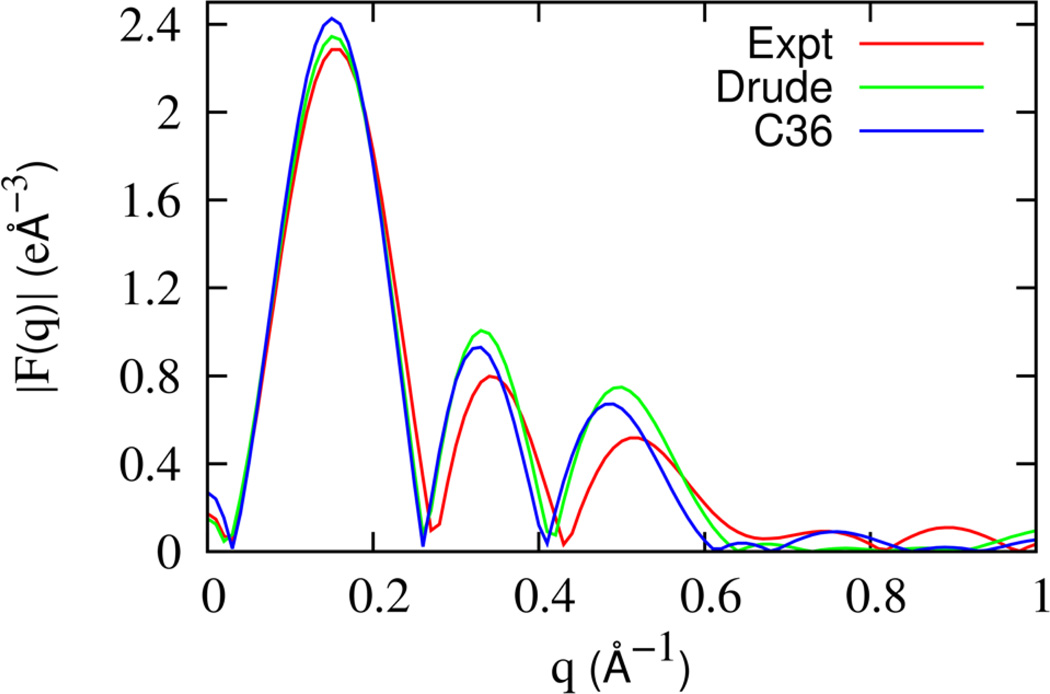
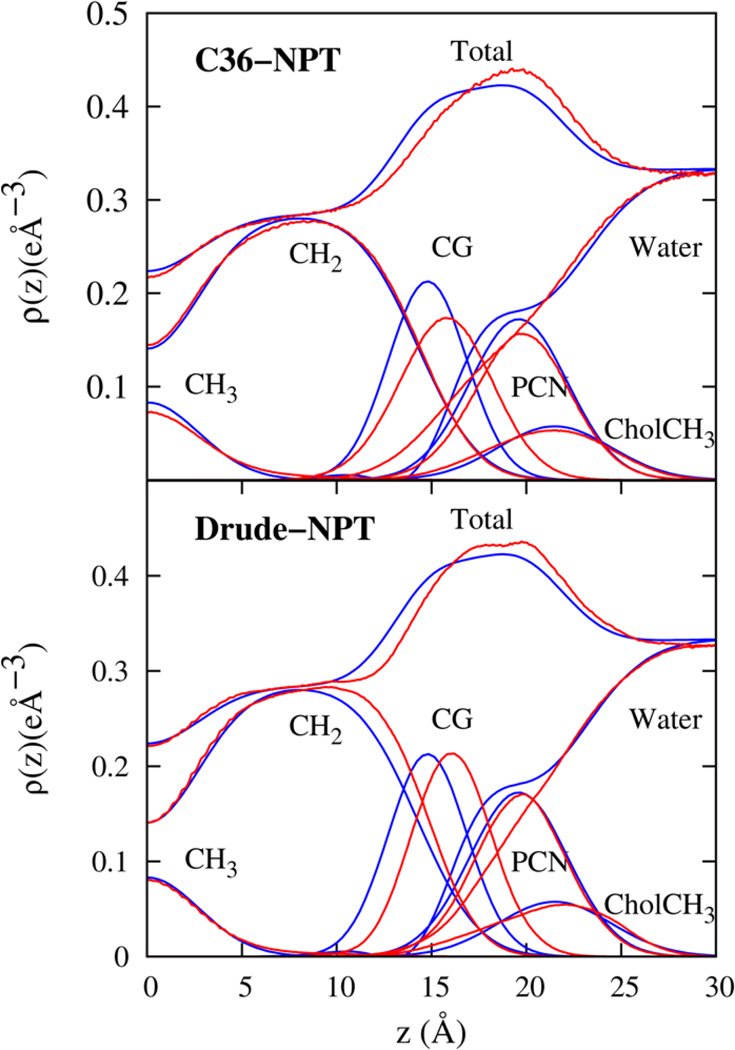
In recent work, the average structure of the DPPC bilayer was resolved and modeled by a simultaneous analysis of Neutron and X-ray scattering experiments by Kucerka et al.68 The Scattering Density Profiles (SDP) model of Kucerka et al.68 partitions the electron density of the bilayer system into contributions from the aliphatic methyl (CH3), aliphatic methylene (CH2), carbonyl and glycerol (CG), phosphate and CH2CH2N (PCN), and the three methyl groups of Choline (CholCH3). A Gaussian functional form is assigned to the volume probability distribution for all components, except for water and CH2. The hydrocarbon volume probability distribution is fit to an error function and the CH2 distribution can be extracted from the difference between the hydrocarbon distribution and the Gaussian aliphatic methyl distribution. The water probability distribution function is deduced indirectly by subtracting the total volume probability arising from the lipid components from unity throughout the system. The parameters for the different volume probability were obtained by fitting the form factors and are listed in Ref.68 The total electron density profile of the SDP model was calculated from the volume probability distribution function and transformed numerically to obtain the experimental form factor. In Figure 8, the form factor calculated from the total electron density profile calculated from the simulations are presented along with experimental data. There is good overall agreement between the Drude FF and experimental form factors. The Drude model appears to be slightly better than the C36 FF in reproducing the position of the peaks in |F(q)|.
Figure 8.
The x-ray scattering form factor for the DPPC bilayer system obtained by transforming the electron density profile from (a) Analytic model representing experimental data68 (red), (b) Drude model (green) and (c) C36 model (blue).
The availability of analytic functional forms and appropriate parameters in the SDP model for the five lipid components makes it possible to perform a detailed comparison of the electron density profiles for each lipid component calculated from simulations with experiments. All electron density profiles are presented in Figure 9. Both Drude and C36 FFs capture the general features of the electron density profile, which has peaks in the region of the lipid head groups and has a minimum in the center of the membrane. Deviation of the simulated form factor from experimental data are quantified with mean quadratic differences, χ2. The value of χ2 is 0.02 and 0.01 for the Drude and C36 FFs, respectively. Thus, the electron density profile from the Drude FF is in good agreement with experimental results, while the C36 FF is slightly better. For a more quantitative comparison between the FF and experimental data, it would be useful to compare the simulated form factor with the raw experimental data instead of the analytic fit. However, given the good quality of the fit to the experimental data at small wavelengths, small differences between the fit and experimental data are not expected to significantly compromise the overall comparison of bilayer structure in simulations with the real system. Furthermore, the large scatter in experimental data at large wavelengths makes a comparison with the simulation data difficult.
Figure 9.
The electron density profiles for the DPPC bilayer system as obtained from the NPT simulations of the C36 and Drude lipid models (blue lines) compared with experimental data68 (red lines). The heavy atom electron density is partitioned according to chemical groups as defined in Ref.68 and summarized in the text.
For the DPPC components, the Drude FF performs quite well for CH3, PCN and CholCH3. The peak in the CH2 electron density is slightly shifted towards the glycerol region compared to the experimentally resolved distribution. The CG electron density profile shows a corresponding shift towards the water phase although the peak height and width of the distribution compares well with experiments. Overall, the Drude FF leads to a bilayer with total electron density profile in good agreement with experimental data. For comparison, the C36 FF leads to good agreement for the CH3, CH2 and CholCH3 components. The CG and PCN peaks are broader and slightly shifted with respect to the experimental data as reported in Ref.2 The experimental data suggests penetration of water up to the glycerol region, but we do not see this for the Drude and C36 FFs since the finite size of the simulation box effectively reduces the interface undulations of the bilayer that could allow for this extra hydration to be visible in the SDP model.
4.3.2 Membrane Volume, Area per Lipid, and Surface Tension
The volume occupied by a membrane provides a coarse measure of its structure. For single component bilayers this structure can be expressed on volume per lipid basis (VL) that can be further decomposed into a per lipid area (A) and a membrane thickness (D) per leaflet. The bilayer volume and its components are sensitive to the interfacial surface tension which can be expressed as a function of the normal (PN) and transverse (PT) components of the pressure tensor,69
| (11) |
The surface tension so obtained is on a per leaflet basis. Because the system is axially symmetric, it adopts a constant normal pressure that is equal to the external pressure in the environment (1 atm). In contrast, the transverse pressure is functionally dependent on the depth along the bilayer normal. Roughly speaking the transverse pressure consists of contracting forces due to the hydrophobic effect at the interface between water and the membrane core which is balanced by inter-lipid interactions within the membrane.70 In equilibrium, these opposing forces balance such that the integrated transverse pressure is equal to PN and the surface tension vanishes. As such the tension free volume components of a FF model provide a measure of accuracy for the balance of molecular forces along the bilayer normal.
The volume occupied by a lipid molecule in a bilayer is experimentally well characterized and has an accepted value of 1229 Å3.68 We determine the equilibrium volume of the system from the NPT simulations using the lipid Drude and C36 FFs starting with an area/lipid of about 62.5 Å2 using NAMD. The average total volume (VT) of the simulation box is calculated from the box dimensions. Using the average density of SWM445 and TIP3 water models,56 the volume of a cubic box containing 2189 water molecules, VW, is calculated. The volume per lipid molecule is then estimated as VL = (VT − VW) /NL where NL = 72 is the number of lipid molecules in our system. The volume data from experiment and simulations are presented in Table 7. The Drude FF overestimates the lipid volume by an amount smaller than the volume occupied by a water molecule (about 30 Å3). For comparison, the C36 FF slightly underestimates the lipid volume with respect to experimental data. The Drude bilayers VL is clearly in better agreement with experiments than the C36 model.
Table 7.
Dimensions of the per lipid volume (VL), area per lipid from simulation (A), Luzzatti thickness (LB), and area per lipid A0 = 2VL/LB.
| Model | VL (Å3) | A (Å2) | LB (Å) | A0 (Å2) |
|---|---|---|---|---|
| Experiment68 | 1229 | 63 ±1 | 39.1 | 62.8 |
| C36 | 1233 ± 1.0 | 62.6 ± 3 | 39.42 | 63.2 |
| Drude | 1237 ± 0.8 | 60 ± 2 | 40.5 | 61.1 |
A measure of the bilayer thickness is the Luzzatti thickness (LB), which corresponds to the distance between the Gibbs dividing surface for water on either side of the bilayer. The experimentally accepted value is 39.1 Å.68 The position of the Gibbs surface is identified from the Drude and C36 model volume probability distribution for water as described in Ref.68 and the resulting values of LB are included in Table 7. The C36 model accurately reproduces the Luzzatti thickness whereas the Drude model overestimates it.
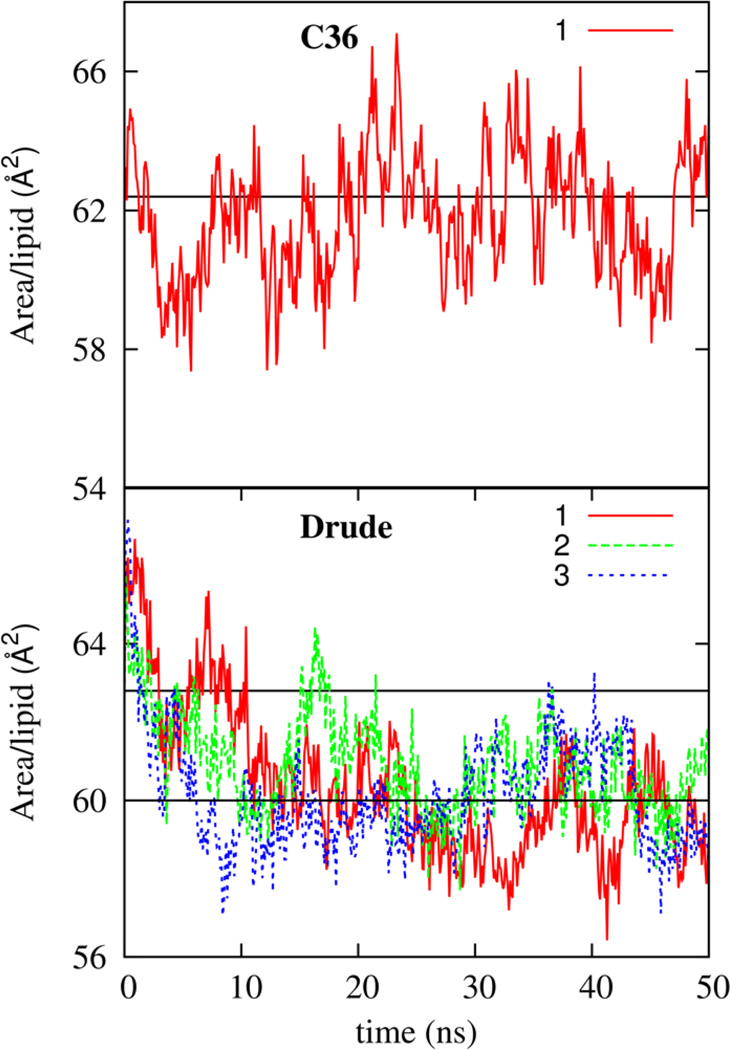
Based on the lipid volume and Luzzatti thickness, the SDP model estimates an area per lipid, A0, from A0 = 2VL/LB. The experimental value for A0 from Drude and C36 FFs are presented in Table 7. The Drude FF leads to lead to an A0 value smaller that the experimental value of about 62.78. In comparison, to this, the C36 FF leads to better agreement between A0 and experimental area of the bilayer. Of course, in simulations, it is straightforward to estimate the per lipid area (A) of the bilayer from the lateral box dimension. Shown in Figure 10 is the evolution of the area per lipid for the C36 FF as a function of simulation time. The reference experimental value is in the range 62–64 Å2.68,71,72 Consistent with the previously reported bilayer simulations with the C36 FF,2 the area per lipid stabilizes at approximately 62.8 Å2. Figure 10 includes the area per lipid for the Drude FF from three independent simulations. On average, the bilayer area stabilizes to a value approximately equal to 60 Å2, which is in reasonable agreement with experimental values. The stability of the bilayer was further verified by extending the simulation time to 150 ns and this data is presented in the Supporting Information. Taking into consideration finite size affects73 the Drude FF leads to a bilayer area of about 62 Å2, which is in good agreement with experimental estimates. For both the Drude and C36 FFs, A0 slightly exceeds A, but the difference is larger by at about 1.1 Å3 for the Drude FF. This discrepancy highlights a possible limitation of using A0 as the correct area per lipid, or using the volume of the bulk simulation box for water for determining VL or some shortcoming in the Drude FF.
Figure 10.
The time variation of the NPT bilayer area per lipid for one simulation with the CHARMM C36 lipid FF and for three simulations with the final Drude model. Also shown with straight lines are the average magnitude of the area per lipid of 60 Å2 for the Drude FF and the experimental value of 62.8 Å2 which is reproduced by the C36 FF.
Another way of validating the value of A is by noting that the equilibrium area per lipid in the NPT ensemble is the area at which the surface tension vanishes, i.e., a zero-surface tension simulation. It is possible to confirm the accuracy of the NPT simulations by calculating the surface tension from constant area NPANT simulations, with the area per lipid ranging from 58 to 66 Å2. The estimated surface tension values are presented in Table 8. The zero surface tension area per lipid can be identified as lying between 58 and 60 Å2 for the Drude FF.
Table 8.
Dependence of the surface tension(γ) (in mN/m) on the bilayer area per lipid (Å2) from constant area simulations at 323K.
| Area per lipid | 58 | 60 | 62 | 64 | 66 |
|---|---|---|---|---|---|
| γ | −3.2±0.6 | 3.5±0.3 | 8.7± 0.3 | 9.3±0.4 | 12.1±0.4 |
4.3.3 NMR data
Measurements of the quadrupolar splitting of the resonance signal of H2 nuclei can provides a detailed probe of bilayer structure. In the liquid crystalline phase the conformations of lipid molecules are axially averaged on the time scale of the experiment and the splitting frequency depends functionally on the angle, θ, made by the associated C-D bond with respect to the interface normal.74 The splitting frequency is linearly proportional to the order parameter, SCD, which is the second Legendre polynomial of the angle θ,
| (12) |
where cos(θ) is the angle formed by the C-D bond with respect to the bilayer normal.
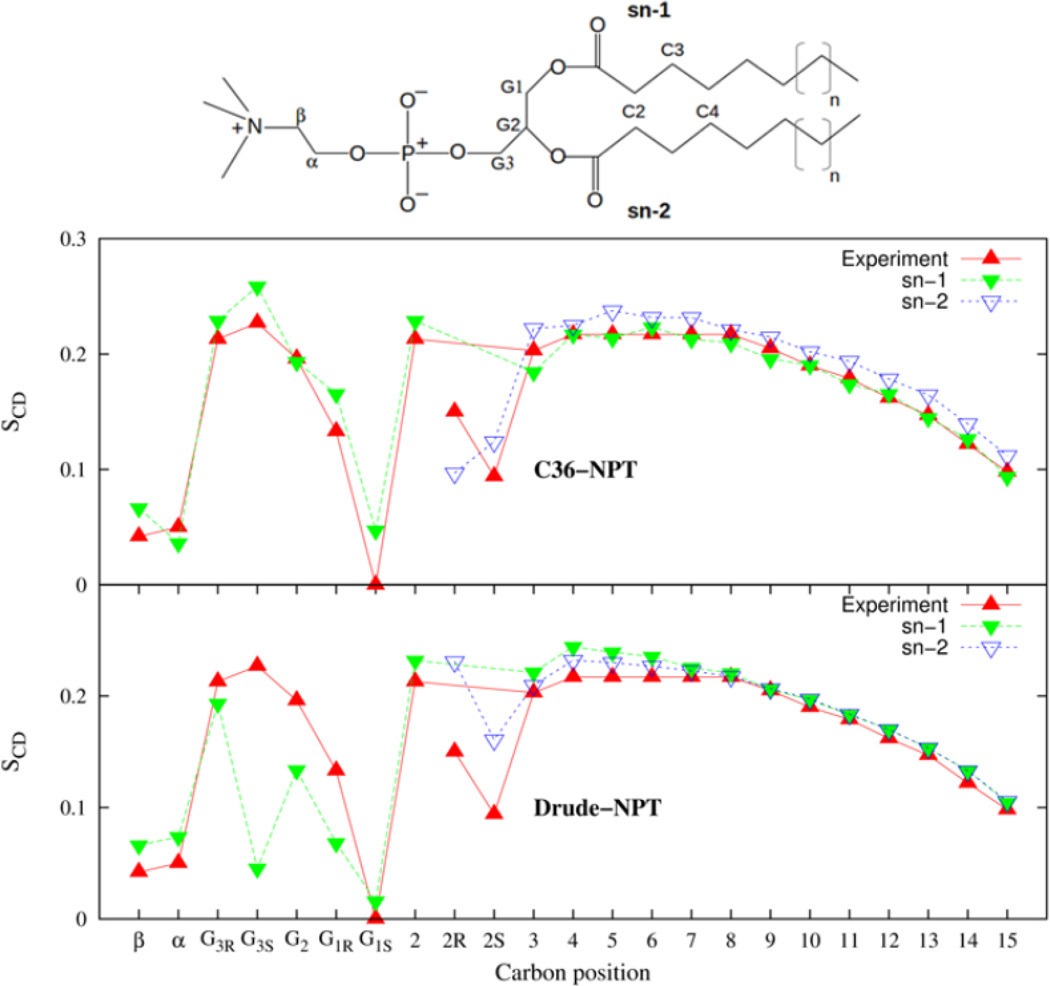
By selective deuteration of lipids, measurements of the quadrupolar splitting provide a means of determining the conformational order of C-D bonds at different positions along the lipid molecule. The order parameters are sensitive to the area per lipid of the bilayer and comparison between models with the same area is preferable. However, for the sake of comparing results for the same thermodynamic state, we compare order parameters resulting from the Drude and C36 FFs, disregarding the equilibrium area per lipid.
The order parameters calculated at various positions in the glycerol region and along the aliphatic tails of the lipid are shown in Figure 11 for the Drude and C36 FFs. Along the aliphatic tails the order parameter is larger near the head group region, reflecting the imposed order of the tethered head groups to the water interface. This order decreases along the chains falling towards the isotropic limit as one moves away from the head group of the lipid molecule. This trend is captured with good precision by both the Drude and C36 FFs. Along most of the aliphatic tails, the pair of hydrogens of each chain display equivalent values of SCD. This equivalence breaks down at the C2 position where the sn-2 chain is tilted near the glycerol region while the sn-1 chain is on average parallel.75,76 This results in lower values for the order parameters associated with the hydrogens on the sn-2 chain compared to the sn-1 chain and this feature is seen in the C36 bilayer simulation. By comparison, for the Drude model the order parameter for one C-D of the sn-2 chain is comparable to the sn-1 chain value while the other is smaller. A shift of the sn-2 C-D order parameters by 0.05 would bring the splitting into better agreement with experiments.
Figure 11.
Deuterium order parameters associated with the C-D bonds of the DPPC bilayer for the C36 and Drude models.
In the glycerol region the carbons are labeled G1–G3. A nonequivalence in the signal from the hydrogens at the G1 and G3 position of the glycerol moiety is also seen in the experimental order parameters. At the G1 position, the split is well represented by both the Drude and C36 FFs. For the G2 and G3S positions, the C36 FF performs better. The order parameters for the C36 FF are in overall better agreement with experimental data. This is not surprising since the C36 FF torsion parameter optimization targeted the reproduction of order parameters. Finally, the head group carbons, labeled α and β give order parameters that are both close to zero, experimentally. This is reproduced well by the Drude and C36 FFs. Examination of the dihedral angle distribution for the glycerol linker region constructed from the Drude and C36 simulations, presented in Supporting information, shows differences between the Drude and C36 FFs. Therefore, re-optimization of torsion parameters focusing on these torsional degrees of freedom will be performed in a future update of the FF.
The 31P chemical shift anisotropy (CSA) measured from NMR experiments is also a source of information about the average bilayer structure. The CSA is,
| (13) |
where
| (14) |
and,
| (15) |
In Eqs. (14) and (15), σ(t) is the instantaneous second-rank shielding tensor
| (16) |
where σii and êi(t) are, respectively, the instantaneous magnitude and direction of the principal tensor components, and x̂, ŷ, and ẑ are unit vectors in the lab frame (the bilayer normal is assumed to be in the ẑ direction). The 31P chemical shift tensor was taken from Ref.77 The anisotropy calculated from the simulation is summarized in Table 9. Experimental measurements place the value at −47 ppm,78 which is slightly smaller that the value computed from simulation for the polarizable FF. In contrast the C36 FF underestimates this value somewhat giving a value of −35 ppm. Thus, the Drude and C36 FFs bracket the experimental chemical shift anisotropies and leave room to improve the model as evidenced by the poor reproduction of the deuterium order parameter at selected positions near the head group region of the lipid. This also indirectly provides information about the tilt of the vector between the phosphorus and nitrogen atoms in the PC group with respect to the interface plane. Recent experiments estimate this angle to be 27 °.79 Our simulations with the Drude and C36 FFs lead to tilt angles of 26.8 ± 0.2° and 27.2 ± 0.3° respectively, both in good agreement with experiments.
Table 9.
Chemical Shift Anisotropy from 31P-NMR measurements in ppm. Principal axis values of the 31P chemical shift tensor (−76,−17,110) were taken from ref.77 Experimental data is from Ref.78 extrapolated to T=323 K.
| Model | Δσa |
|---|---|
| Exp. | −47 |
| C36 | −36 ± 29 |
| Drude | −54 ± 24 |
4.4 Lateral diffusion
An important aspect of membrane is the rate of lateral diffusion of lipid molecules within the 2D-plane of the bilayer leaflets. A number of experimental techniques have been employed for measuring the diffusion coefficient for lipids in bilayers and the results range from 0.1 to 22.4×10−7cm2/s (as discussed in Ref80) depending on the experimental technique employed. The long time diffusion coefficient estimated from NMR or photobleaching experiments81,82 is 1.52 × 10−7cm2/s, whereas neutron scattering place the short time diffusion coefficient83 at 12 × 10−7cm2/s.
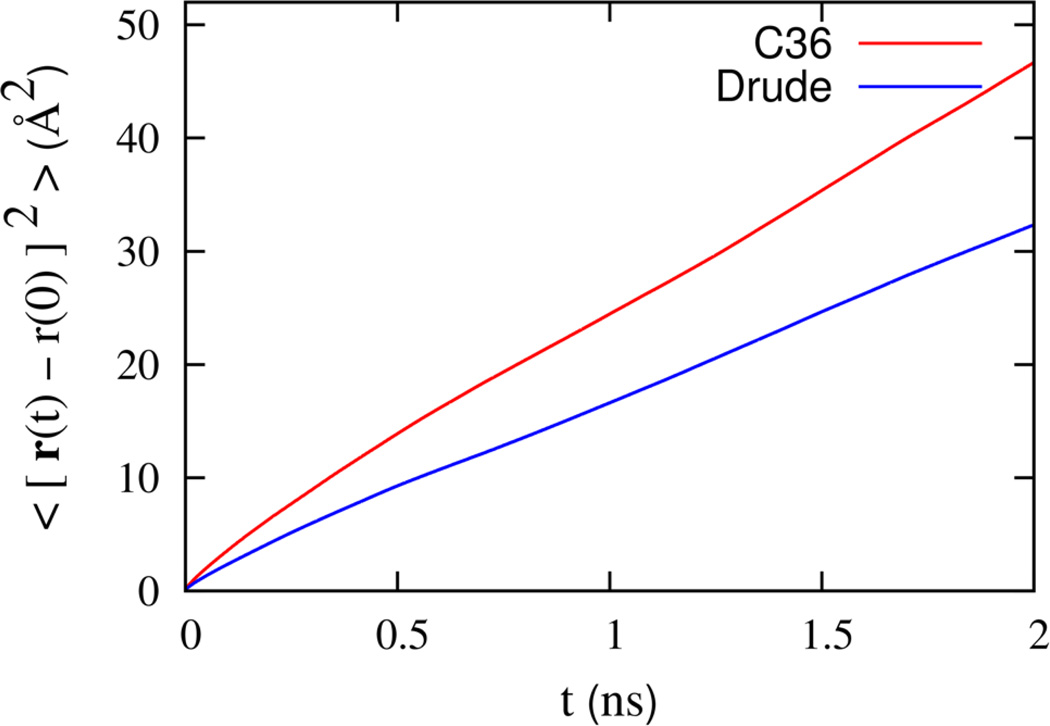
The mean square displacement calculated from the Drude and C36 simulations is shown in Figure 12. The calculated mean squared displacement for the Drude FF represents an average from three trajectories of 75 ns each. The result for the C36 FF was obtained from a single trajectory of 100 ns. At short times (t ≤ 0.5 ps), the mean squared displacement grows non-linearly with time before reaching a linear regime over longer times. This nonlinearity is suggestive of transient sub-diffusive motion, where each lipid molecule is caged by its neighbors. Local motion yields the rapid increase at short time, while more infrequent jumps give rise to the slower diffusion at longer times. At the time scales presented here (up to ~ 2 ns), the mean squared displacement starts to become linear. The effective diffusion constant at short time can be deduced from neutron scattering measurements;83 its value is 12 × 10−7 cm2/s. The short-time diffusion constants extracted from the simulations are 12.9 and 8.5 × 10−7 cm2/s, for the C36 and Drude FFs, respectively. A similar result (14 × 10−7 cm2/s) was previously obtained from the C27r FF.84
Figure 12.
In-plane mean square displacement of the DPPC molecules in the bilayer for C36 and Drude models over a broad time scale (bottom).
The long-time diffusion coefficient extracted from the simulations are 5.6 and 3.9 × 10−7cm2/s for the C36 and Drude FFs, respectively. A simple linear fit was performed for the time range 1–2 ns. Both estimates are larger than the available long time experimental values. However, as shown by Klauda et al,84 it is important to note that finite size artifacts are significant for small lipid patches. This can be appreciated by comparing previous results for the C27r force field;84 diffusion coefficient of 2.92 × 10−7 cm2/s and 0.95 × 10−7 cm2/s were obtained from simulations comprising 72 and 288 DPPC molecules, respectively. Thus, one should not expect quantitative agreement with experimental values from simulations based on a small bilayer of 72 lipids. The purpose of the present analysis is mainly to compare FFs. While further computations will be needed to fully characterize the models, it seems clear that, over the entire time scale examined, the diffusive movements of the lipids with the Drude FF are slower than in C36. This is expected since water diffusion with the polarizable SWM4 model45 is about twice slower than with the TIP3P model.56
4.5 DPPC monolayer simulations
The Drude DPPC model can be further tested against experimental surface tension and surface pressure data for lipid monolayers spread on a water-air sub-phase. For monolayer systems, the surface tension is measured at a fixed surface area. At the temperature under consideration (323 K), the bare water-air interface has an experimental surface tension value of γ0 = 67.9 dyn/cm.85 Upon addition of lipid, the surface tension decreases. This perturbation of the bare water-air tension, is the surface pressure induced by the monolayer,
| (17) |
where γ0 is the water/vapor surface tension and γ is the surface tension after addition of lipids to the interface. The surface tension is calculated from simulations at area per lipid of 58, 60, 62, 64 and 66 Å2 and presented in Table 10 along with the surface pressure. The Drude FF gives surface tensions and surface pressure values in reasonable agreement with experimental data86 over the entire range of areas considered here. For comparison, the C36 FF is not as successful in reproducing the monolayer surface tension over the same range of areas using the same truncation scheme. Given the fairly inaccurate air/water surface tension by the TIP3P water model,56 it is not surprising that the C36 monolayer simulations lead to poorer agreement with experiments. Accurate reproduction of the air/water surface tension by the polarizable SWM4 model45 is a significant reason for its better performance.
Table 10.
Monolayer surface pressure and surface tension in mN/m evaluated from Eq. (17); the pure water-air surface tension is 64 for the SWM4 model45 and 68 dyn/cm from experiment.86
| Area Per Lipid | Experiment | Drude | ||
|---|---|---|---|---|
| Π | γ | Π | γ | |
| 58 | 44 | 24 | 49 | 15±8 |
| 60 | 37 | 31 | 37 | 27±3 |
| 62 | 32 | 36 | 33 | 31±4 |
| 64 | 27 | 41 | 29 | 35±5 |
| 66 | 25 | 43 | 13 | 51±9 |
4.5.1 Membrane dipole potential
The nonrandom orientation of molecular dipoles at the water-membrane interface gives rise to a surface potential that affects the permeation of charged species across the membrane. The measured permeabilities imply an electrostatic potential difference, that interacts with the ion, of approximately 200 mV.87 This potential difference is traditionally equated to the potential difference encountered by a test charge traversing the same interface, which is otherwise known as the Galvani potential.88 In a membrane bilayer, such a characterization is complicated by the nature of the membrane interface. Specifically, the potential measured across points in different media, here (between bulk water and the interior of the membrane) is dependent on a quadrupole moment of the molecular charge density in addition to the orientation of molecular dipoles.89 This quadrupole contribution does not vanish in isotropic systems and is sensitive to details of the molecular charge density that lie within the van der Waals surface of the molecule, a physical regime that is inconsequential to inter-molecular interactions.90 The quadrupole contribution depends solely on the environment at the end points of the potential measurement, and strictly vanishes, only when the material environment at these positions is the same. For the lipid bilayer and similar systems, the end points are not the same and consequently the bilayer dipole potential is of dubious physical significance. For instance, it does not reflect the physical potential felt by a molecular species that penetrates the membrane interface.91
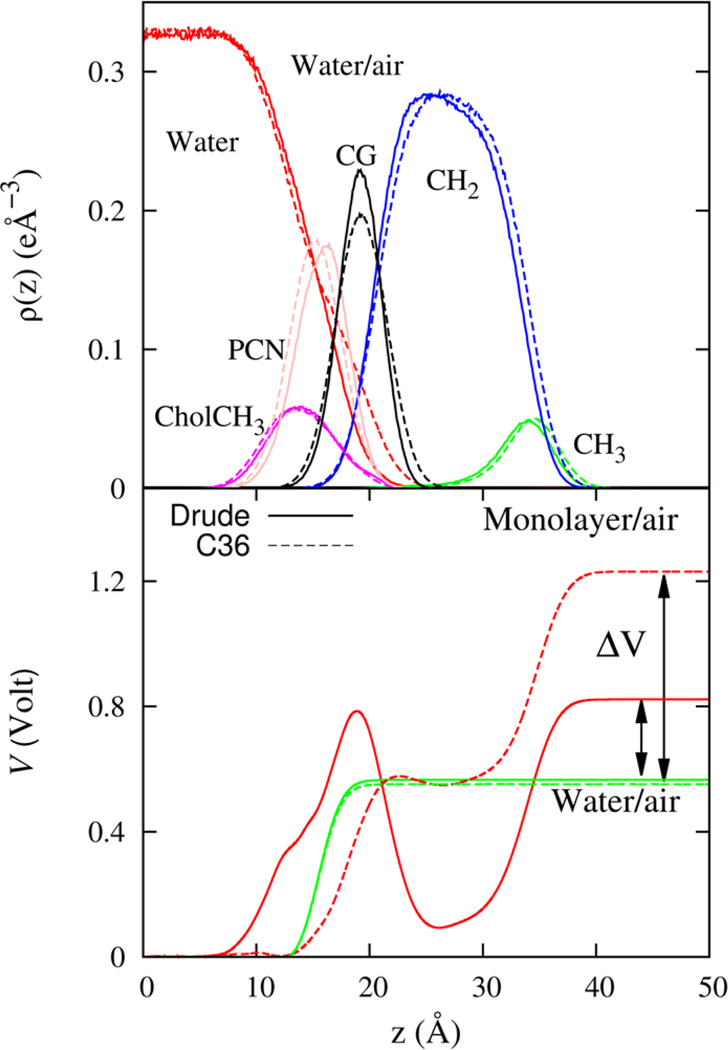
A physical measure of the impact that the membrane dipole potential has, on the configuration of a charged species, is provided by measurements on lipid monolayers.90 The experimentally accessible observable is the electrostatic potential difference, ΔV, measured across a lipid monolayer spread on an air-water interface with respect to the bare air-water sub-phase.
Shown in Figure 13 is the potential profile computed from molecular simulations of the lipid monolayer and water-air systems. The electrostatic potential profile is calculated from the average system charge density as a solution to the Poisson equation.12,45 The potential difference ΔV is shown in the figure and its magnitude is 0.28 V for the Drude FF. This estimate for the polarizable FF was found to be in reasonable agreement with experimental values that range from 0.2 to 0.4 V92,93 although it is somewhat smaller that the typically accepted value of 0.35 V. Decreasing the area per lipid to 60 Å2, which is closer to the NPT value for the area, leads to a potential difference of 0.33 and this is in much better agreement with the experimental value. In view of the smaller area for the bilayer in the NPT simulation, it is conceivable that corrections to the torsion parameters could lead to a slightly different orientation for the DPPC molecule in the bilayer and this could improve the electrostatic potential.
Figure 13.
Monolayer-air heavy atom electron density profiles (top) and the electrostatic potential profile (bottom) for the Drude (solid line) and C36 (dashed line) models. Also shown is the water-air electrostatic potential profile for the polarizable SWM4 and non-polarizable TIP3 water models. The area of cross-section corresponds to monolayer area per lipid fixed at 62 Å2.
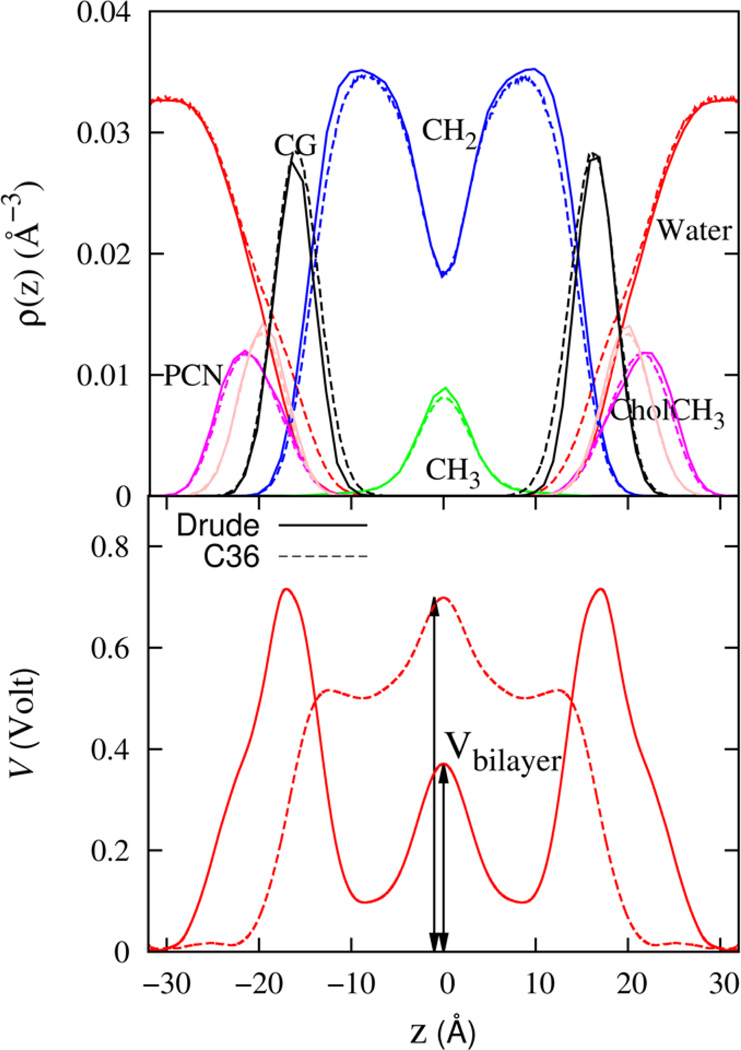
To understand the relationship between the physical observable, ΔV, of the monolayer and the Galvani potential in a bilayer, we consider a simple approximation. Presuming the water/lipid interface is structurally similar in both the bilayer and monolayer systems, the bilayer potential can be related to ΔV through two additional interfaces,
| (18) |
where, Vbilayer is the potential difference between bulk water and the membrane core of the bilayer, Vwater−air, is the potential difference from pure water to air and Vhydrocarbon−air is the potential difference from a hydrocarbon liquid to air. Individually, the three potentials to the right of Eq. (18), are unphysical, representing measurements between different materials. Together, the potential is a measure between common air environments that is analogous to the monolayer system potential. Figure 14 shows the profile of the electrostatic potential that is computed from simulations with the Drude FF. The potential difference between bulk water and the membrane core (Vbilayer) is 0.38 V for the Drude FF, and 0.7 V for the C36 FF. Since the number density profiles for all the molecular components of the DPPC molecule are quite similar the Drude and C36 simulations (see Figure 9), the major difference between the electrostatic profiles for the two models must primarily be due to differences in electrostatic representation of the hydrocarbon, water and water-headgroup interactions. Induced polarization in the interfacial region, where the average electric field is the largest, is a particularly important feature that cannot be captured by a FF with fixed partial charges.
Figure 14.
Membrane bilayer heavy atom number density profiles (top) and the electrostatic potential profile (bottom) for the Drude (solid line) and C36 (dashed line) models.
5 SUMMARY
Polarizable force fields for molecular compounds resembling the functional groups in a phospholipid molecule are parameterized against gas and liquid phase properties. Dimethylphosphate and tetramethyl-ammonium are used to represent the zwitterionic head group of a phosphatidylcholine lipid. Methyl acetate is used as the basis for the esterified glycerol backbone and linear alkanes are used to represent the hydrocarbon lipid tails. The polar compounds give both accurate gas phase interactions with water and hydration free energies. Additional condensed phase data including the enthalpy of vaporization, neat liquid density, and dielectric constant are used to determine parameters for the esters. The large molecular fragments are used to optimized the torsional degrees of freedom missing from the small molecule FF. Final parameters are then used to assemble the phospholipid FF. Simulations of lipid bilayers and monolayers are conducted to test the properties of the model membrane.
The polarizable FF reproduces the electron density profile, volume per lipid, area per lipid of the bilayer, and the surface tension as well as surface pressure properties of the lipid monolayer reasonably well. Additionally, the FF reproduces most of the deuterium order parameters determined from NMR spectra well, even though they were not targeted in FF optimization. This is in contrast to the C36 FF, which does target the order parameters during the FF optimization. Deviations from experimental values helped identify the salient shortcomings of the current FF, and these will be improved in subsequent work. Any FF for simulation of lipids should perform well for at least these properties. Polarizability is specifically found to play a crucial role in the dipole potential of the the membrane which is well reproduced by the Drude FF and not by the non-polarizable additive C36 FF. Thus, it would be beneficial to employ the Drude lipid FF in membrane protein simulations particularly with the polarizable Drude FF for proteins (under development) for maximum compatibility between lipid and protein force fields.
Supplementary Material
Acknowledgment
This work was supported by the National Institute of Health through grant GM-072558. The simulations were performed using computational resources at the LCRC, Argonne National Lab, and the Extreme Science and Engineering Discovery Environment (XSEDE) supported by National Science Foundation grant number OCI-1053575. E. H. would like to thank Troy Whitfield for helpful discussions.
Appendix: Drude Oscillator Hard-Wall Constraint
Infrequently, a Drude particle can go far away from its nucleus leading to unstable simulations. This phenomenon was more prominent in the case of the negatively charged anions with a large polarizability.62 To prevent such over-polarization of the Drude oscillators, a steep anharmonic restraining potential was introduced.62 However, the anharmonic restraint makes it necessary to use a shorter time-step of 0.5 fs to integrate the equations of motion, which undermines the efficiency of the simulation. To resolve this issue, we introduced the hard-wall constraint to enforce the upper limit of the distance between the Drude and the nucleus which makes MD simulations stable with 1 fs time step.
We consider a typical Drude-nucleus pair forming an oscillator (the atom index i is omitted for clarity). T* is the temperature of the thermostat coupled with the Drude oscillator. The mass of the nucleus and the Drude particle are denoted as mN and mD respectively. The positions are represented as rN and rD, then the vector from the nucleus to the Drude particle is defined as rND = rD − rN. The velocities are denoted as vN and vD. The distance between the nucleus and the Drude particle is typically not allowed to exceed Lw = 0.2Å. Hard-wall constraint is imposed after new positions are calculated in velocity-Verlet algorithm.94 If the distance between the nucleus and the Drude particle is larger than Lw (|rND| > Lw), the positions and velocities of the nucleus and the Drude particle will be adjusted along the direction of the bond vector (rND) as following. The velocities of the nucleus and the Drude particle projected along the vector rND/|rND| are written as,
| (19) |
and
| (20) |
The velocity of the center of mass along rND/|rND| is written as,
| (21) |
We assume that the relative velocity between the nucleus and the Drude particle projected along rND/|rND| is scaled down to when |rND| hits the reflecting wall (|rND| = Lw) and the directions of the velocities relative to the center of mass along the bond vector are reversed for both particles. The velocities relative to the center of mass along rND/|rND| after velocity rescaling read,
| (22) |
| (23) |
The new positions of the nucleus and the Drude particle are,
| (24) |
| (25) |
The new velocities of the nucleus and the Drude particle are,
| (26) |
| (27) |
The change in the pressure tensor upon a collision with the a hard reflecting wall is,
| (28) |
where Δt is the time step in MD simulations.
Footnotes
Supporting Information
Model compound force field parameters for model compounds and their thermodynamic properties, as well as other properties of the DPPC bilayer are presented in the Supporting Information. This information is available free of charge via the Internet at http://pubs.acs.com
Contributor Information
Alexander D. MacKerell, Jr., Email: alex@outerbanks.umaryland.edu.
Benoît Roux, Email: roux@uchicago.edu.
References
- 1.MacKerell AD, Jr, Bashford D, Bellott M, Dunbrack RL, Jr, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 2.Klauda JB, Venable RM, Freites JA, O’Connor JW, Tobias DJ, Mondragon-Ramirez C, Vorobyov I, MacKerell AD, Jr, Pastor RW. Update of the CHARMM All-Atom Additive Force Field for Lipids : Validation on Six Lipid Types. J. Phys. Chem. B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pastor RW, MacKerell AD., Jr Development of the CHARMM Force Field for Lipids. J. Phys. Chem. Lett. 2011;2:1526–1532. doi: 10.1021/jz200167q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jorgensen WL, Maxwell DS, Tirado-Rives J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- 5.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Jr, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, A Kollman P. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and, Organic Molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- 6.Dickson CJ, Rosso L, Betz RM, Walker RC, Gould IR. GAFFlipid: A General Amber Force Field for the Accurate Molecular Dynamics Simulation of Phospholipid. Soft Matter. 2012;8:9617–9627. [Google Scholar]
- 7.van Gunsteren WF, Billeter SR, Eising AA, Hünenberger PH, Krüger P, Mark AE, Scott WRP, Tironi IG. Biomolecular Simulation: The GROMOS96 Manual and User Guide. Hochshulverlag AG/ETH Zurich; 1996. [Google Scholar]
- 8.Piggot TJ, Piñeiro Á, Khalid S. Molecular Dynamics Simulations of Phosphatidylcholine Membranes: A Comparative Force Field Study. J. Chem. Theory Comput. 2012;8:4593–4609. doi: 10.1021/ct3003157. [DOI] [PubMed] [Google Scholar]
- 9.MacKerell AD., Jr Empirical Force Fields for Biological Macromolecules: Overview and Issues. J. Comp. Chem. 2004;25:1584–1604. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 10.Vorobyov IV, Anisimov VM, MacKerell AD., Jr Polarizable Empirical Force Field for Alkanes Based on the Classical Drude Oscillator. J. Phys. Chem. B. 2005;109:18988–18999. doi: 10.1021/jp053182y. [DOI] [PubMed] [Google Scholar]
- 11.Lamoureux G, MacKerell AD, Jr, Roux B. A Simple Polarizable Model of Water based on Classical Drude Oscillators. J. Chem. Phys. 2003;119:5185–5197. [Google Scholar]
- 12.Harder E, MacKerell AD, Jr, Roux B. Many-Body Polarization Effects and the Membrane Dipole Potential. J. Am. Chem. Soc. 2009;131:2760–2761. doi: 10.1021/ja806825g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lamoureux G, Roux B. Modeling Induced Polarization with Classical Drude Oscillators: Theory and Molecular Dynamics Simulation Algorithm. J. Chem. Phys. 2003;119:3025–3039. [Google Scholar]
- 14.Shao Y, Molnar LF, Jung Y, Kussmann J, Ochsenfeld C, Brown ST, Gilbert ATB, Slipchenko LV, Levchenko SV, O’Neill DP, et al. Advances in methods and Algorithms in a Modern Quantum Chemistry Program Package. Phys. Chem. Chem. Phys. 2006;8:3172–3191. doi: 10.1039/b517914a. [DOI] [PubMed] [Google Scholar]
- 15.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr, Vreven T, Kudin KN, Burant JC, et al. Gaussian 03, Revision C.02. Wallingford, CT: Gaussian, Inc.; 2004. [Google Scholar]
- 16.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, et al. Gaussian 09 Revision A.1. Wallingford CT: Gaussian Inc.; 2009. [Google Scholar]
- 17.Vorobyov I, Anisimov VM, Greene S, Venable RM, Moser A, Pastor RW, MacKerell AD., Jr Additive and Classical Drude Polarizable Force Fields for Linear and Cyclic Ethers. J. Chem. Theory and Comput. 2007;3:1120–1133. doi: 10.1021/ct600350s. [DOI] [PubMed] [Google Scholar]
- 18.Drude P. The Theory of Optics. 91 and 93 Fifth Ave., New York: Longmans, Green, and Co.; 1902. [Google Scholar]
- 19.Harder E, Anisimov VM, Whitfield T, AD MacKerell J, Roux B. Understanding the Dielectric Properties of Liquid Amides from a Polarizable Force Field. J. Phys. Chem. B. 2008;112:3509–3521. doi: 10.1021/jp709729d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Thole BT. Molecular Polarizabilities Calculated with a Modified Dipole Interaction. Chem. Phys. 1981;59:341–350. [Google Scholar]
- 21.Coker H. Empirical Free-Ion Polarizabilities of the Alkali Metal, Alkaline Earth Metal, and Halide Ions. J. Phys. Chem. 1976;80:2078–2084. [Google Scholar]
- 22.Mahan GD. van der Waals Coefficient Between Closed Shell Ions. J. Chem. Phys. 1982;76:493–497. [Google Scholar]
- 23.Fowler PW, Madden PA. In-Crystal Polarizabilities of Alkali and Halide Ions. Phys. Rev. B. 1984;29:1035–1042. [Google Scholar]
- 24.Jemmer P, Fowler PW, Wilson M, Madden PA. Environmental Effects on Anion Polarizability:âĂL’ Variation with Lattice Parameter and Coordination Number. J. Phys. Chem. A. 1998;102:8377–8385. [Google Scholar]
- 25.Valderrama E, Wheatley RJ. An Environmental Pseudopotential Approach to Molecular Interactions: Implementation in MOLPRO. J. Comp. Chem. 2003;24:2075–2082. doi: 10.1002/jcc.10353. [DOI] [PubMed] [Google Scholar]
- 26.Morita A. Water Polarizability in Condensed Phase: ab initio Evaluation by Cluster Approach. J. Comp. Chem. 2002;23:1466–1471. doi: 10.1002/jcc.10169. [DOI] [PubMed] [Google Scholar]
- 27.Harder E, Anisimov VM, Vorobyov IV, Lopes PEM, Noskov SY, MacKerell AD, Jr, Roux B. Atomic Level Anisotropy in the Electrostatic Modeling of Lone Pairs for a Polarizable Force Field Based on the Classical Drude Oscillator. J. Chem. Theory and Comput. 2006;2:1587–1597. doi: 10.1021/ct600180x. [DOI] [PubMed] [Google Scholar]
- 28.Anisimov VM, Lamoureux G, Vorobyov I, Huang N, Roux B, MacKerell AD., Jr Determination of Electrostatic Parameters for a Polarizable Force Field Based on the Classical Drude Oscillator. J. Chem. Theory and Comput. 2005;1:153–168. doi: 10.1021/ct049930p. [DOI] [PubMed] [Google Scholar]
- 29.Kaminski GA, Stern HA, Berne BJ, Friesner RA, Cao YX, Murphy RB, Zhou R, Halgren TA. Development of a Polarizable Force Field for Proteins via ab initio Quantum Chemistry: First Generation Model and Gas Phase Tests. J. Comp. Chem. 2002;23:1515–1531. doi: 10.1002/jcc.10125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Becke AD. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 31.Lee C, Yang W, Parr RG. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 32.MacKerell AD, Jr, Brooks B, Brooks CL, III, Nilsson L, Roux B, Won Y, Karplus M. CHARMM: The Energy Function and Its Parameterization with an Overview of the Program. In: Schleyer PvR, Allinger NL, Clark T, Gasteiger J, Kollman PA, Schaefer HF, III, Schreiner PR., editors. Encyclopedia of Computational Chemistry. Vol. 1. Chichester: John Wiley & Sons; 1998. p. 271. [Google Scholar]
- 33.Schlenkrich M, Brickman J, MacKerell AD, Jr, Karplus M. In: Biological Membranes: A Molecular Perspective from Computation and Experiment. Merz KM, Roux B, editors. Birkhäuser Boston: 1996. [Google Scholar]
- 34.Boys SF, Bernardi F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970;19:533–566. [Google Scholar]
- 35.D Yin D, MacKerell AD., Jr Combined ab initio/Empirical Approach for Optimization of Lennard-Jones Parameters. J. Comp. Chem. 1998;19:334–338. doi: 10.1002/jcc.1166. [DOI] [PubMed] [Google Scholar]
- 36.Leeuw SWD, Perram JW, Smith ER. Computer Simulation of the Static Dielectric Constant of Systems with Permanent Electric Dipoles. Annu. Rev. Phys. Chem. 1986;37:245–270. doi: 10.1146/annurev.pc.37.100186.001333. [DOI] [PubMed] [Google Scholar]
- 37.Baker CM, MacKerell AD., Jr Polarizability Rescaling and Atom-based Thole Scaling in the CHARMM Drude Polarizable Force Field for Ethers. J. Mol. Model. 2010;16:567–576. doi: 10.1007/s00894-009-0572-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Allen FH. The Cambridge Structural Database: A Quarter of a Million Crystal Structures and Rising. Acta Crystallogr. B. 2002;58:380–388. doi: 10.1107/s0108768102003890. [DOI] [PubMed] [Google Scholar]
- 39.Scott AP, Radom L. Harmonic Vibrational Frequencies:âĂL’ An Evaluation of HartreeâĹŠFock, MöllerâĹŠPlesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors. J. Phys. Chem. 1996;100:16502–16513. [Google Scholar]
- 40.Kuczera K, Wiorkiewiez-Kuczera J, Karplus M. MOLVIB. CHARMM program [Google Scholar]
- 41.Pulay P, Fogarasi G, Pang F, Boggs JE. Systematic ab initio Gradient Calculation of Molecular Geometries, Force Constants, and Dipole Moment Derivatives. J. Am. Chem. Soc. 1979;101:2550–2560. [Google Scholar]
- 42.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalé L, Schulten K. Scalable Molecular Dynamics with NAMD. J. Comp. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Jiang W, Hardy DJ, Phillips JC, MacKerell AD, Jr, Schulten K, Roux B. High-Performance Scalable Molecular Dynamics Simulations of a Polarizable Force Field based on Classical Drude Oscillators in NAMD. J. Phys. Chem. Lett. 2011;2:87–92. doi: 10.1021/jz101461d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Harder E, Kim B, Friesner RA, Berne BJ. Efficient Simulation Method for Polarizable Protein Force Fields: Application to the Simulation of BPTI in Liquid Water. J. Chem. Theory and Comput. 2005;1:169–180. doi: 10.1021/ct049914s. [DOI] [PubMed] [Google Scholar]
- 45.Lamoureux G, Harder E, Vorobyov IV, Roux B, MacKerell AD., Jr A Polarizable Model of Water for Molecular Dynamics Simulations of Biomolecules. Chem. Phys. Lett. 2006;418:245–249. [Google Scholar]
- 46.Martyna GJ, Klein ML, Tuckerman M. Nosé-Hoover Chains: The Canonical Ensemble via Continuous Dynamics. J. Chem. Phys. 1992;97:2635–2643. [Google Scholar]
- 47.Martyna GJ, Tobias DJ, Klein ML. Constant Pressure Molecular Dynamics Algorithms. J. Chem. Phys. 1994;101:4177–4189. [Google Scholar]
- 48.Allen MP, Tildesley D. J. Computer Simulation of Liquids. New York: Oxford University Press Inc.; 1987. [Google Scholar]
- 49.Martyna GJ, Tuckerman ME, Tobias DJ, Klein ML. Explicit Reversible Integrators for Extended Systems Dynamics. Mol. Phys. 1996;87:1117–1157. [Google Scholar]
- 50.Andersen HC. Rattle: A ’Velocity’ Version of the Shake Algorithm for Molecular Dynamics Calculations. J. Comput. Phys. 1983;52:24–34. [Google Scholar]
- 51.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 52.Brüenger A, Brooks CB, III, Karplus M. Stochastic Boundary Conditions for Molecular Dynamics Simulations of ST2 Water. Chem. Phys. Lett. 1984;105:495–500. [Google Scholar]
- 53.Weeks JD, Chandler D, Andersen HC. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971;54:5237–5247. [Google Scholar]
- 54.Deng Y, Roux B. Hydration of Amino Acid Side Chains: Nonpolar and Electrostatic Contributions Calculated from Staged Molecular Dynamics Free Energy Simulations with Explicit Water Molecules. J. Phys. Chem. B. 2004;108:16567–16576. [Google Scholar]
- 55.Anisimov VM, Vorobyov IV, Roux B, MacKerell A., Jr Polarizable empirical force field for the primary and secondary alcohol series based on the classical Drude model. J. Chem. Theory Comput. 2007;3:1927–1946. doi: 10.1021/ct700100a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating LiquidWater. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 57.Noskov SY, Lamoureux G, Roux B. Molecular Dynamics Study of Hydration in Ethanol-Water Mixtures Using a Polarizable Force Field. J. Phys. Chem. B. 2005;109:6705–6713. doi: 10.1021/jp045438q. [DOI] [PubMed] [Google Scholar]
- 58.Lopes PEM, Lamoureux G, Roux B, MacKerell AD., Jr Polarizable Empirical Force Field for Aromatic Compounds Based on the Classical Drude Oscillator. J. Phys. Chem. B. 2007;111:2873–2885. doi: 10.1021/jp0663614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Baker CM, Anisimov VM, MacKerell AD., Jr Development of CHARMM Polarizable Force Field for Nucleic Acid Bases Based on the Classical Drude Oscillator Model. J. Phys. Chem. B. 2011;115:580–596. doi: 10.1021/jp1092338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lamoureux G, Roux B. Absolute Hydration Free Energy Scale for Alkali and Halide Ions Established from Simulations with a Polarizable Force Field. J. Phys. Chem. B. 2006;110:3308–3322. doi: 10.1021/jp056043p. [DOI] [PubMed] [Google Scholar]
- 61.Klauda JB, Brooks BR, MacKerell AD, Jr, Venable RM, Pastor RW. An ab initio Study on the Torsional Surface of Alkanes and its Effect on Molecular Simulations of Alkanes and a DPPC Bilayer. J. Phys. Chem. B. 2005;109:5300–5311. doi: 10.1021/jp0468096. [DOI] [PubMed] [Google Scholar]
- 62.Yu H, Whitfield TW, Harder E, Lamoureaux G, Vorobyov I, Anisimov VM, MacKerell AD, Jr, Roux B. Simulating Monovalent and Divalent Ions in Aqueous Solutions using a Drude Polarizable Force Field. J. Chem. Theory Comput. 2010;6:774–786. doi: 10.1021/ct900576a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Iglesias M, Orge B, Canosa JM, Rodŕiguez A, Domingues M, neiro MMP, Tojo J. Thermodynamic Behavior of Mixtures Containing Methyl Acetate, Methanol, and 1-Butanol at 298.15 K: application of the ERAS Model. Fluid Phase Equilibria. 1998;147:285–300. [Google Scholar]
- 64.Lide DR. CRC Handbook of Chemistry and Physics. 93rd/ed. Boca Raton, Fla.: Crc;; Taylor and Francis [distributor]; 2012. [Google Scholar]
- 65.Shirke RM, Chaudhary A, More NM, Patil PB. Dielectric Measurements on Methyl Acetate + Alcohol Mixtures at (288, 298, 308, and 318) K using the Time Domain Technique. J. Chem. Eng. Data. 2000;45:917–919. [Google Scholar]
- 66.Höchtl P, Boresch S, Bitomsky W, Steinhauser O. Rationalization of the Dielectric Properties of Common Three-Site Water Models in terms of their Force Field Parameters. J. Chem. Phys. 1998;109:4927–4938. [Google Scholar]
- 67.Kelly CP, Cramer CJ, Truhlar DG. Aqueous Solvation Free Energies of Ions and IonâĹŠWater Clusters Based on an Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton. J. Phys. Chem. B. 2006;110:16066–16081. doi: 10.1021/jp063552y. [DOI] [PubMed] [Google Scholar]
- 68.Kučerka N, Nagle JF, Sachs JN, Feller SE, Pencer J, Jackson A, Katsaras J. Lipid Bilayer Structure Determined by the Simultaneous Analysis of Neutron and X-Ray Scattering Data. Biophys. J. 2008;95:2356–2367. doi: 10.1529/biophysj.108.132662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kirkwood JG, Buff FP. The Statistical Mechanical Theory of Surface Tension. J. Chem. Phys. 1949;17:338–343. [Google Scholar]
- 70.Marsh D. Lateral Pressure in Membranes. Biochim. Biophys. Acta. 1996;1286:183–223. doi: 10.1016/s0304-4157(96)00009-3. [DOI] [PubMed] [Google Scholar]
- 71.Mills TT, Toombes GES, Tristram-Nagle S, Smilgies D-M, Feigenson GW, Nagle JF. Order Parameters and Areas in Fluid-Phase Oriented Lipid Membranes Using Wide Angle X-Ray Scattering. Biophys. J. 2008;95:669–681. doi: 10.1529/biophysj.107.127845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Kučerka N, Tristram-Nagle S, Nagle JF. Closer Look at Structure of Fully Hydrated Fluid Phase DPPC Bilayers. Biophys. J. 2006;90:L83–L85. doi: 10.1529/biophysj.106.086017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Lindahl E, Edholm O. Mesoscopic Undulations and Thickness Fluctuations in Lipid Bilayers from Molecular Dynamics Simulations. Biophys. J. 2000;79:426–433. doi: 10.1016/S0006-3495(00)76304-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Klauda JB, Venable RM, MacKerell AD, Jr, Pastor RW. Current Topics in Membranes. Vol. 60. Elsevier; 2008. pp. 1–48. [Google Scholar]
- 75.Seelig A, Seelig J. Dynamic Structure of Fatty Acyl Chains in a Phospholipid Bilayer Measured by Deuterium Magnetic Resonance. Biochemistry. 1974;13:4839–4845. doi: 10.1021/bi00720a024. [DOI] [PubMed] [Google Scholar]
- 76.Seelig A, Seelig J. Bilayers of Dipalmitoyl-3-sn-Phosphatidylcholine: Conformational Differences Between the Fatty Acyl Chains. Biochim. Biophys. Acta. 1975;406:1–5. doi: 10.1016/0005-2736(75)90037-1. [DOI] [PubMed] [Google Scholar]
- 77.Herzfeld J, Griffin R, Haberkorn RA. Phosphorus-31 Chemical-Shift Tensors in Barium Diethyl Phosphate and Urea-Phosphoric Acid: Model Compounds for Phospholipid Head-Group Studies. Biochem. 1978;17:2711–2718. doi: 10.1021/bi00607a003. [DOI] [PubMed] [Google Scholar]
- 78.Niederberger, Seelig J. Phosphorus-31 Chemical Shift Anisotropy in Unsonicated Phospholipid Bilayers. J. Am. Chem. Soc. 1976;98:3704–3706. doi: 10.1021/ja00428a053. [DOI] [PubMed] [Google Scholar]
- 79.Semchyschyn DJ, Macdonald PM. Conformational Response of the Phosphatidylcholine Headgroup to Bilayer Surface Charge: Torsion Angle Constraints from Dipolar and Quadrupolar Couplings in Bicelles. Magn. Reson. Chem. 2004;42:89–104. doi: 10.1002/mrc.1333. [DOI] [PubMed] [Google Scholar]
- 80.Poger D, Mark AE. Lipid Bilayers: The Effect of Force Field on Ordering and Dynamics. J. Chem. Theory Comput. 2012;8:4807–4817. doi: 10.1021/ct300675z. [DOI] [PubMed] [Google Scholar]
- 81.Vaz WLC, Clegg RM, Hallmann D. Translational Diffusion of Lipids in Liquid Crystalline Phase Phosphatidylcholine Multibilayers - A Comparison of Experiment with Theory. Biochemistry. 1985;24:781–786. doi: 10.1021/bi00324a037. [DOI] [PubMed] [Google Scholar]
- 82.Scheidt HA, Huster D, Gawrisch K. Diffusion of Cholesterol and its Precursors in Lipid Membranes Studied by 1H Pulsed Field Gradient Magic Angle Spining NMR. Biophys. J. 2005;89:2504–2512. doi: 10.1529/biophysj.105.062018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Tabony J, Perly B. Quasielastic Neutron Scattering Measurements of Fast Local Translational Diffusion of Lipid Molecules in Phospholipid-Bilayers. Biochim. Biophys. Acta. 1991;1063:67–72. doi: 10.1016/0005-2736(91)90354-b. [DOI] [PubMed] [Google Scholar]
- 84.Klauda J, Brooks BR, Pastor RW. Dynamical Motions of Lipids and Finite-Size Effect in Simulations of Bilayers. J. Chem. Phys. 2006;125:144710. doi: 10.1063/1.2354486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Lemmon EW, McLinden MO, Friend DG. Thermophysical Properties of Fluid Systems. In: Linstrom PJ, Mallard WG, editors. NIST Chemistry WebBook, NIST Standard Reference Database Number 69. Gaithersburg, MD: National Institute of Standards and Technology; 2005. [Google Scholar]
- 86.Crane JM, Putz G, Hall SB. Persistence of Phase Coexistence in Disaturated Phosphatidylcholine Monolayers at High Surface Pressures. Biophys. J. 1999;77:3134–3143. doi: 10.1016/S0006-3495(99)77143-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Schamberger J, Clarke RJ. Hydrophobic Ion Hydration and Magnitude of the Dipole Potential. Biophys. J. 2002;82:3081–3088. doi: 10.1016/S0006-3495(02)75649-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Aveyard R, Haydon DA. An Introduction to the Principles of Surface Chemistry. Cambridge, UK: Cambridge University Press; 1973. [Google Scholar]
- 89.Wilson MA, Pohorille A, Pratt LR. Surface Potential of the Water Liquid-Vapor Interface. J. Chem. Phys. 1988;88:3281–3286. doi: 10.1063/1.453923. [DOI] [PubMed] [Google Scholar]
- 90.Harder E, Roux B. On the Origin of the Electrostatic Potential Difference at a Liquid-Vacuum Interface. J. Chem. Phys. 2008;129:234706. doi: 10.1063/1.3027513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Vorobyov I, Bekker B, Allen TW. Electrostatics of Deformable Lipid Membranes. Biophys. J. 2010;98:2904–2913. doi: 10.1016/j.bpj.2010.03.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Smaby JM, Brockman HL. Surface Dipole Moments of Lipids at the Argon-Water Interface. Biophys. J. 1990;58:195–204. doi: 10.1016/S0006-3495(90)82365-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Wang L. Measurements and Implications of the Membrane Dipole Potential. Annu. Rev. Biochem. 2012;81:615–635. doi: 10.1146/annurev-biochem-070110-123033. [DOI] [PubMed] [Google Scholar]
- 94.Frenkel D, Smit B. Understanding Molecular Simulation. London: Academic Press; 2002. [Google Scholar]
- 95.Majer V, Svoboda V. Enthalpies of Vaporization of Organic Compounds: A Critical Review and Data Compilation. Oxford: Blackwell Scientific Publications; 1985. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.